分治法实验心得
递归与分治算法心得

递归与分治算法心得
递归与分治算法是算法设计中常见的两种方法,它们在解决问题时都采用了“分而治之”的思想,将问题分解成更小的子问题,然后通过递归调用或者合并子问题的解来得到原问题的解。
通过我的学习和实践,我深刻认识到了递归与分治算法的重要性和优势。
首先,递归算法可以使问题的描述更加简单明了。
通过将问题转化为自身的子问题,我们可以建立起更为简洁优美的数学模型。
其次,递归算法可以使问题的解决过程更加自然。
在递归过程中,我们可以利用已知的子问题解决同类问题,实现代码的复用和模块化。
此外,递归算法还可以解决一些重要的数学问题,如斐波那契数列和二分查找等。
分治算法则更加注重问题的分解和合并。
它将问题划分成若干个规模相同或相近的子问题,然后将子问题的解合并起来得到原问题的解。
这种方法在解决某些复杂问题时具有很大的优势。
例如,在排序算法中,归并排序采用了分治算法的思想,将待排序的序列分成两个长度相等的子序列,然后递归地对子序列排序,最后将子序列合并成有序序列。
这种算法具有较高的稳定性和灵活性,常常被应用于海量数据的排序任务中。
总之,递归与分治算法是算法设计中不可或缺的两种方法。
在解决问题时,我们应该根据具体情况选择合适的算法,并在实践中不断探索、总结和优化。
只有这样,我们才能更好地应对日益复杂多变的计算机科学挑战。
分治法的个人总结

分治法是一种算法设计策略,它将问题划分为较小的子问题,然后通过解决子问题来解决原始问题。
个人总结如下:
分解问题:分治法首先将原始问题分解为规模较小的子问题。
这可以通过递归地将问题划分为更小的部分来实现。
分解问题的关键是确保每个子问题都是原始问题的规模的一个子集。
解决子问题:每个子问题都可以通过相同的算法来解决。
递归地应用相同的算法,直到达到基本情况,也就是子问题可以直接解决的规模。
合并解决方案:一旦解决了子问题,就将它们的解合并起来,形成原始问题的解。
这通常涉及对子问题的解进行组合,以获得原始问题的最终解。
适用性:分治法适用于那些可以自然地分解为子问题的问题。
它在解决许多常见问题时非常有效,如排序、搜索、计算最大值和最小值、归并等。
时间复杂度:分治法通常在每个子问题上执行相同的操作,并且子问题的数量通常是对数级别的。
因此,分治算法的时间复杂度通常可以表示为递归深度的多项式。
常见的时间复杂度包括O(nlogn)和O(n^2)。
并行化:由于分治法的子问题通常是相互独立的,因此它很适合并行化处理。
可以同时处理多个子问题,然后将它们的解合并起来。
这使得分治法在并行计算中具有较好的可扩展性。
总的来说,分治法是一种强大的算法设计策略,它通过将问题分解为子问题并递归地解决它们,然后将子问题的解合并起来,从而解决了许多复杂的问题。
它在算法设计和并行计算中都具有广泛的应用。
算法实验报告

实验一分治与递归算法的应用一、实验目的1.掌握分治算法的基本思想(分-治-合)、技巧和效率分析方法。
2.熟练掌握用递归设计分治算法的基本步骤(基准与递归方程)。
3.学会利用分治算法解决实际问题。
二 . 实验内容金块问题老板有一袋金块(共n块,n是2的幂(n≥2)),最优秀的雇员得到其中最重的一块,最差的雇员得到其中最轻的一块。
假设有一台比较重量的仪器,希望用最少的比较次数找出最重和最轻的金块。
并对自己的程序进行复杂性分析。
三.问题分析:一般思路:假设袋中有n 个金块。
可以用函数M a x(程序1 - 3 1)通过n-1次比较找到最重的金块。
找到最重的金块后,可以从余下的n-1个金块中用类似法通过n-2次比较找出最轻的金块。
这样,比较的总次数为2n-3。
分治法:当n很小时,比如说,n≤2,识别出最重和最轻的金块,一次比较就足够了。
当n 较大时(n>2),第一步,把这袋金块平分成两个小袋A和B。
第二步,分别找出在A和B中最重和最轻的金块。
设A中最重和最轻的金块分别为HA 与LA,以此类推,B中最重和最轻的金块分别为HB 和LB。
第三步,通过比较HA 和HB,可以找到所有金块中最重的;通过比较LA 和LB,可以找到所有金块中最轻的。
在第二步中,若n>2,则递归地应用分而治之方法程序设计据上述步骤,可以得出程序1 4 - 1的非递归代码。
该程序用于寻找到数组w [ 0 : n - 1 ]中的最小数和最大数,若n < 1,则程序返回f a l s e,否则返回t r u e。
当n≥1时,程序1 4 - 1给M i n和M a x置初值以使w [ M i n ]是最小的重量,w [ M a x ]为最大的重量。
首先处理n≤1的情况。
若n>1且为奇数,第一个重量w [ 0 ]将成为最小值和最大值的候选值,因此将有偶,数个重量值w [ 1 : n - 1 ]参与f o r循环。
当n 是偶数时,首先将两个重量值放在for 循环外进行比较,较小和较大的重量值分别置为Min和Max,因此也有偶数个重量值w[2:n-1]参与for循环。
分治算法的实验报告

一、实验背景分治算法是一种常用的算法设计方法,其基本思想是将一个复杂问题分解成若干个相互独立的小问题,然后将小问题递归求解,最终将子问题的解合并为原问题的解。
分治算法具有高效性、可扩展性和易于实现等优点,被广泛应用于各个领域。
本实验旨在通过实现分治算法解决实际问题,掌握分治算法的设计思想,并分析其时间复杂度。
二、实验目的1. 理解分治算法的基本思想;2. 掌握分治算法的递归实现方法;3. 分析分治算法的时间复杂度;4. 应用分治算法解决实际问题。
三、实验内容本实验选择两个分治算法:快速排序和合并排序。
1. 快速排序快速排序是一种高效的排序算法,其基本思想是将待排序序列分为两个子序列,其中一个子序列的所有元素均小于另一个子序列的所有元素,然后递归地对两个子序列进行快速排序。
(1)算法描述:① 选择一个基准值(pivot),通常取序列的第一个元素;② 将序列分为两个子序列,一个子序列包含所有小于基准值的元素,另一个子序列包含所有大于基准值的元素;③ 递归地对两个子序列进行快速排序。
(2)代码实现:```cvoid quickSort(int arr[], int left, int right) {if (left < right) {int pivot = arr[left];int i = left;int j = right;while (i < j) {while (i < j && arr[j] >= pivot) {j--;}arr[i] = arr[j];while (i < j && arr[i] <= pivot) {i++;}arr[j] = arr[i];}arr[i] = pivot;quickSort(arr, left, i - 1);quickSort(arr, i + 1, right);}}```2. 合并排序合并排序是一种稳定的排序算法,其基本思想是将待排序序列分为两个子序列,分别对两个子序列进行排序,然后将排序后的子序列合并为一个有序序列。
分治法实验报告

一. 实验目的及实验环境实验目的:熟练掌握运用分治法解决问题。
实验环境:windows下的Ubuntu虚拟机二. 实验内容利用分治法求一个数组的最大值、最小值(要求:数组的大小和数组的长度随机产生)三.方案设计分治法解决问题就是要将原问题分解成小问题,再将小问题分解成更小的问题,以此类推,直到最终分解的问题能够一步解决即可。
代码要求最后要输出数组的最大值、最小值。
所以,在用分治法求最值的函数max_min()中,需要将设置参数int *max,int *min。
即void max_min(int a[],int m,int n,int *max,int *min)。
这样就可以直接得到最大值、最小值。
该函数使用递归来实现,而递归的终止条件是最后分得的数组中只有一个或两个元素,当分得的数组元素个数大于2时,就进行递归调用。
四.测试数据及运行结果正确的3组运行结果:出现的错误:若将代码中的随机数函数返回值的类型改变,则会出现错误结果,甚至编译不通过。
五.总结1.实验过程中遇到的问题及解决办法;实验过程中,用分治法求最大值、最小值时,如果用返回值求最大值和最小值,则需要两个函数。
这样就会导致代码冗余,不会达到代码的复用性功能。
所以要将两个功能用一个函数直接实现就可以使用参数指针的形式。
2.对设计及调试过程的心得体会。
算法设计的课内实验既要实现实验的功能,还要讲究代码中算法的精妙、简单以及它的效率。
不能同其他高级语言的课内实验一样仅仅考虑如何完成该实验的功能,这样就可以真正地体验到算法与设计这门课的意义。
平时做实验时我们可以用不同算法实现,这样不仅可以积累平常上课学到的知识,还可以为以后的算法设计能力奠定基础。
平常更多地进行思考,可以让我们在求职时更受益。
六.附录:源代码(电子版)#include<stdio.h>#include<stdlib.h>#include<time.h>void max_min(int a[],int m,int n,int *max,int *min){int middle,hmax,hmin,gmax,gmin;if(m==n){ *max=a[m];*min=a[m];}else if(m==n-1){if(a[m]>a[n]){*max=a[m];*min=a[n];}else{*max=a[n];*min=a[m];}}else{max_min(a,m,middle,&gmax,&gmin);max_min(a,middle+1,n,&hmax,&hmin);if(gmax>hmax)*max=gmax;else*max=hmax;if(gmin<hmin)*min=gmin;else*min=hmin;}}int main(){int i;int max,min;srand((unsigned)time(NULL));int n=rand()%10+1;printf("数组的个数:%d\n",n);int a[n];for(i=0;i<n;i++){a[i]=rand()%50+1;printf("%d\t",a[i]);}max_min(a,0,n-1,&max,&min);printf("最大数:%d,最小数:%d\n",max,min);retur n 0;}。
分治算法实验报告
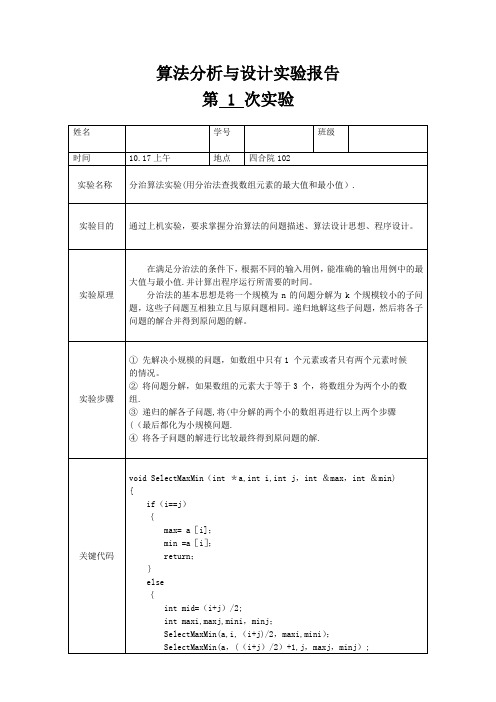
算法分析与设计实验报告第 1 次实验if(maxi>maxj)max=maxi;elsemax=maxj;if(mini<minj)min=mini;elsemin=minj;return;}}srand((unsigned int)time(NULL));cout <〈”随机产生的数据(0—100):”;for(int i=0; i〈m; i++)a[i] = rand()%100;测试结果附录:完整代码SelectMaxMin.cpp:#include <iostream>#include <ctime>#include 〈cstdio>#include <iomanip>#include 〈cstdlib〉using namespace std;void SelectMaxMin(int *a,int i,int j,int &max,int &min) {if(i==j){max= a[i];min =a[i];return;}else{int mid=(i+j)/2;int maxi,maxj,mini,minj;SelectMaxMin(a,i,(i+j)/2,maxi,mini);SelectMaxMin(a,((i+j)/2)+1,j,maxj,minj);if(maxi〉maxj)max=maxi;elsemax=maxj;if(mini<minj)min=mini;elsemin=minj;return;}}int main(){clock_t start,end,over;start=clock();end=clock();over=end—start;start=clock();//freopen("in。
txt",”r",stdin);//freopen(”out。
txt”,”w",stdout);int m;cout 〈<"Please input the number : ”;cin>〉 m;int a[m];srand((unsigned int)time(NULL));cout 〈〈 "随机产生的数据(0-100):";for(int i=0; i〈m; i++)a[i] = rand()%100;for(int i=0; i〈m; i++)cout <〈 a[i] 〈< " ";cout 〈< endl;int max,min;SelectMaxMin(a,0,m-1,max,min);cout 〈< "max = " 〈〈 max 〈〈 endl;cout <〈”min = " <〈 min 〈〈 endl;end=clock();printf(”The time is %6.3f”,(double)(end-start—over)/CLK_TCK); }。
分治算法设计(求第K个最小数)

福建工程学院计算机与信息科学系实验报告2010 – 2011 学年第一学期任课老师:实验题目1.设计程序利用分治策略求n个数的最大值和最小值。
2.利用分治策略,在n个不同元素中找出第k个最小元素。
实验时间实验开始日期:报告提交日期:实验目的、要求一、算法设计技术当我们求解某些问题时,由于这些问题要处理的数据相当多,或求解过程相当复杂,使得直接求解法在时间上相当长,或者根本无法直接求出。
对于这类问题,我们往往先把它分解成几个子问题,找到求出这几个子问题的解法后,再找到合适的方法,把它们组合成求整个问题的解法。
如果这些子问题还较大,难以解决,可以再把它们分成几个更小的子问题,以此类推,直至可以直接求出解为止。
这就是分治策略的基本思想。
下面通过实例加以说明。
【例】在n个元素中找出最大元素和最小元素。
我们可以把这n个元素放在一个数组中,用直接比较法求出。
算法如下:void maxmin1(int A[],int n,int *max,int *min){ int i;*min=*max=A[0];for(i=2;i < n;i++){ if(A[i] > *max) *max= A[i];if(A[i] < *min) *min= A[i];}}上面这个算法需比较2(n-1)次。
能否找到更好的算法呢?我们用分治策略来讨论。
把n个元素分成两组:A1={A[1],...,A[int(n/2)]}和A2={A[int(N/2)+1],...,A[N]}分别求这两组的最大值和最小值,然后分别将这两组的最大值和最小值相比较,求出全部元素的最大值和最小值。
如果A1和A2中的元素多于两个,则再用上述方法各分为两个子集。
直至子集中元素至多两个元素为止。
例如有下面一组元素:-13,13,9,-5,7,23,0,15。
用分治策略比较的过程如下:图中每个方框中,左边是最小值,右边是最大值。
从图中看出,用这种方法一共比较了10次,比直接比较法的14次减少4次,即约减少了1/3。
分治策略算法实验报告

分治策略算法实验报告引言分治策略是一种经典的算法设计策略,也是算法设计中最重要的思想之一。
其基本思想是将大问题划分成小的、相互独立的子问题,再将子问题合并求解,最终得到原问题的解。
本实验将通过实际例子,验证分治策略算法的有效性。
实验内容本实验选择两个经典的算法问题进行实现和验证,分别是二分查找和快速排序。
这两个问题在算法领域都有重要的应用价值,也是实践分治算法的好例子。
问题1:二分查找二分查找是一种在有序数组中查找特定元素的算法,其基本思想是将数组分为两部分,然后判断目标值在哪一部分,并且逐步缩小问题的规模。
具体实现如下:pythondef binary_search(arr, target):low = 0high = len(arr) - 1while low <= high:mid = (low + high) 2if arr[mid] == target:return midelif arr[mid] < target:low = mid + 1else:high = mid - 1return -1问题2:快速排序快速排序是一种高效的排序算法,其基本思想是通过一趟划分将待排序序列分割成两个独立的子序列,然后递归地对子序列进行排序,最终得到有序序列。
具体实现如下:pythondef quicksort(arr):if len(arr) <= 1:return arrpivot = arr[len(arr) 2]left = [x for x in arr if x < pivot]middle = [x for x in arr if x == pivot]right = [x for x in arr if x > pivot]return quicksort(left) + middle + quicksort(right)实验结果为了验证分治策略算法的有效性,我们分别对上述两个问题进行了测试。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分治法实验心得
分治法实验心得
分治法是一种常见的算法设计策略,它将原问题划分成若干个规模较小但结构与原问题相似的子问题,然后递归地求解这些子问题,最终将子问题的解合并得到原问题的解。
在本次实验中,我们实现了两个基于分治法的算法:归并排序和快速排序,并对它们进行了性能测试和比较。
一、归并排序
1. 原理
归并排序是一种典型的分治算法。
它将待排序数组不断地二分为两个子数组,直到每个子数组只剩下一个元素。
然后将相邻的两个子数组合并成一个有序数组,再将相邻的两个有序数组合并成一个更大的有序数组,直到最终合并成整个待排序数组。
2. 实现
我们采用了自顶向下的递归方式实现了归并排序。
具体来说,我们定
义了一个merge函数用于合并两个有序子数组,并定义了一个sort 函数用于递归地对左右两个子数组进行排序和合并。
3. 性能测试与比较
我们使用Python内置的time模块对不同规模(10^2 ~ 10^6)的随机整数列表进行了性能测试,并绘制出了运行时间随数组规模增大的变化曲线。
结果表明,归并排序的时间复杂度为O(nlogn),与理论分析相符。
二、快速排序
1. 原理
快速排序也是一种分治算法。
它选择一个基准元素,将数组中小于等于它的元素放在其左侧,大于它的元素放在其右侧。
然后递归地对左右两个子数组进行同样的操作,直到每个子数组只剩下一个元素。
2. 实现
我们实现了两个版本的快速排序:递归版本和非递归版本。
其中,递归版本采用了经典的Lomuto分区方案,而非递归版本则采用了更高效的Hoare分区方案。
3. 性能测试与比较
我们同样使用Python内置的time模块对不同规模(10^2 ~ 10^6)的随机整数列表进行了性能测试,并绘制出了运行时间随数组规模增
大的变化曲线。
结果表明,快速排序具有很好的平均时间复杂度
(O(nlogn)),但最坏情况下时间复杂度会退化到O(n^2)。
三、总结与思考
通过本次实验,我们深入理解了分治算法设计策略,并学会了如何实
现归并排序和快速排序。
同时,我们也了解到了算法的时间复杂度分
析和性能测试方法,并通过实验数据对两个算法的性能进行了比较。
在实践中,我们还发现了一些问题和思考点。
例如,在快速排序中,
选择哪种分区方案对算法的效率有很大影响;在实际应用中,如何根
据具体问题选择合适的排序算法也是一个值得深入探讨的问题。
希望
通过不断学习和实践,我们能够更好地掌握分治算法的设计与应用。
