您的位置：360文档中心› 【20套精选试卷合集】江苏省南京市南师附中集团新城中学2019-2020学年中考数学模拟试卷含答案

【20套精选试卷合集】江苏省南京市南师附中集团新城中学2019-2020学年中考数学模拟试卷含答案

合集下载

江苏省南京市南师附中集团新城中学2019-2020学年数学《7份试卷合集》八上期中模拟试卷

江苏省南京市南师附中集团新城中学2019-2020学年数学《7份试卷合集》八上期中模拟试卷

∴OF=EF=，6
故答案为： 6．
13．如图，正六边形 ABCDE．F 若 11∥１2，则∠ 1﹣∠ 2=60°
．
【分析】根据多边形的内角和公式，求出每个内角的度数，延长 线的性质把∠ 1 搬到∠ 3 处，利用三角形的外角计算出结果．
【解答】解：延长 DC 交直线 l 1于点 M，如图所示 ∵ABCDEF是正六边形， ∴∠ BCD=∠A=120°， ∴∠ MCB=6°0 ． ∵１1∥１2， ∴∠ 1=∠３ ∵∠ 3=∠2+∠MCB， ∴∠ 1﹣∠ 2=∠MCB=6°0 ． 故答案
∴点 A 关于 y 轴的对称点的坐标是（ 2，﹣ 3），故选： B．
3. 在△ ABC中，∠ A：∠ B：∠ C=3：4： 8，则这个三角形一定是（
A．等腰三角形
B．直角三角形
C．锐角三角形
） D．钝角三角形
【分析】根据三角形的内角和 =180°，列方程即可得到结论．
【解答】解：∵∠ A：∠ B：∠ C=3： 4： 8，
的图形，并写出点 B 关于 AC 的对称点 B′的坐标．
【分析】直接利用轴对称图形的性质得出对应点位置进而得出答案． 【解答】解：如图所示：△ AB′C 即为所求，
7
B′（ 3， 7）．
16．（8 分）如图， CF∥ＡB，过 AC 的中点 E 作一直线交 AB 于 D，交 CF 于 F，则 DE 与 FE 有
C． 5cm， 5cm， 10cm
D． 4cm， 8cm，14cm
【分析】根据三角形任意两边的和大于第三边，进行分析判断．
【解答】解： A、 5+9=14，故不能构成三角形，选项错误；
B、 6+6＞ 11，故能构成三角形，选项正确； C 、

2019-2020学年南京师范大学附属中学新城高级中学高三英语第一次联考试题及参考答案

2019-2020学年南京师范大学附属中学新城高级中学高三英语第一次联考试题及参考答案

2019-2020学年南京师范大学附属中学新城高级中学高三英语第一次联考试题及参考答案第一部分阅读（共两节，满分40分）第一节（共15小题；每小题2分，满分30分）阅读下列短文，从每题所给的A、B、C、D四个选项中选出最佳选项AThe last thing Caitlin Hipp would have expected as she prepared to turn 28 years old was to be living at homewith her parents. But through working as a part-time skating instructor and restaurant server, she isn't able to earn enough to live anywhere other than home.To some degree, multigenerational households have always been a part of American life. However, the number of young adults who have been moving back in with their parents — or never leaving home in the first place — has been growing steadily.UBS Financial Services released a report that even suggests one reason for the growing number of young adultsstill living at home could be that their family doesn't want them to leave.The report shows that 74 percent of millennials (千禧一代)get some kind of financial support from their parents after college. It finds that millennials have redefined the ties that connect parents and children. Millennials see their parents as peers,friends and instructors. Nearly three quarters talked with their parents more than once a week during college. In return, their parents happily provide financial support well into adulthood, helping fund everything for them.Stuart Hoffman, chief economist for the PNC Financial Services Group in theUS, said the number of young adults striking out on their own fell during the Great Recession. Although job growth for millennials since 2014 has improved, that doesn't necessarily mean that millennials are starting to fly the nest. He said, “They may like living at home and being able to save money.“ There's no doubt it has held back household formation and purchases of things people spend money on related to household formation and perhaps related to child-raising," Hoffman explained. "But they are probably traveling more and eating out more if they don't have a house expense or marriage. I don't know if it represents a change in moral values. But it's much more common for adult children to live in their parents’ homes because it's becoming part of the culture.1. What can we learn from the UBS Financial Services' report?A. Millennials are on good terms with their parents.B. Millennials are financially independent after college.C. Parents are unwilling to give their young adults allowance.D. Parents want their kids to stay with them forever.2. What does Hoffman think of young adults' living at home?A. It increases the consumption of household products.B. It may continue despite job growth.C. It is a sign of shift in moral values.D. It is new in American culture.3. What is the author's purpose of writing this passage?A. To introduce millennials' living habits.B. To stress the importance of financial independence.C. To explain why American young adults still live at home.D. To inform people of a social trend in theUS.BHoneybees can’t swim, and when their wings are wet, they can’t fly, either. But Chris Roh and other researchers at the California Institute of Technology found that when bees drop into bodies of water, they can use their wings toproduce little waves and slide toward land-like surfers who create and then ride their own waves.As with many scientific advances-IsaacNewton’s apple or Benjamin Franklin’s lightning bolt-Dr. Roh’s experiment began with a walk. Passing Caltech’s Millikan Pond in 2016, he observed a bee on the water’s surface producing waves. He wondered how an insect known for flight could push itself through water.Dr. Roh and his co-worker, Morteza Gharib, used butterfly nets to collect localPasadenahoneybees and observed their surf-like movements. The researchers used a wire to restrict each bee’s bodily movement, allowing close examination of their wings. They found that the bee bends its wings at a 30-degree angle, pulling up water and producing a forward force. Bees get trapped on the surface because water is roughly three times heavier than air. But that weight helps to push the bee forward when its wings move quickly up and down. It’s a tough exercise for the bees, which the researchers guess could handle about 10 minutes of the activity.The researchers said the surf-like movement hasn’t been documented in other insects and most semiaquatic insects use their legs forpropulsion, which is known as water-walking. It may have evolved in bees, they-predicted.Dr. Roh and Dr. Gharib have imagined many practical applications for bees’ surfing. One plan is to use their observations to design robots able to travel across sky and sea. “This could be useful for search and rescues, or forgetting samples of the surface of the ocean, if you can’t send a boat or helicopter,” Dr. Gharib said.4. What does the author intend to show by mentioningNewtonandFranklin?A. Roh’s admiration for them.B. Roh’s chance discovery about bees.C. Their outstanding talent for science.D. Their similar achievements in discovery.5. What plays the most vital role in a bee’s moving forward on water?A. The air weight.B. Its leg extension.C. The water movement.D. Its continuous wingbeat.6. What does the underlined word “propulsion” in Paragraph 4 mean?A. Fast flightB. Driving force.C. Pulling speed.D. Explosive power.7. What does the text mainly tell us?A. Honeybees can surf to safety.B. Bees help scientists make inventions.C. Insects can adapt to the environment.D. Nature is a helpful guide for discovery.CI don’t think I can recall a time whenI wasn’t aware of the beauty of the ocean. Growing up inAustralia, I had the good fortune of having the sea at my side. The first time I went toHalfmoonBay,I suddenly had the feeling of not being able to feel the ground with my feet anymore.For my 10th birthday, my sister and I were taken out to theGreat Barrier Reef. There were fish in different color1 s, caves and layers of coral. They made such an impression on me. When I learned that only one percent ofAustralia’sCoral Seawas protected, I was shocked. Australian marine (海洋的) life is particularly important because the reefs have more marine species than any other country on earth. But sadly, only 45% of the world’s reefs are considered healthy.This statistic is depressing, so it’s important for usto do everything to protect them. The hope that theCoral Searemains a complete ecosystem has led me to take action. I’ve become involved with the Protect Our Coral Sea activity, which aims to create the largest marine park in the world. It would serve as a place where the ocean’s species will all have a safe place forever.Together, Angus and I created a little video and we hope it will inspire people to be part of the movement. Angus also shares many beautiful childhood memories of the ocean as a young boy, who grew up sailing, admiring the beauty of the ocean, and trying to find the secrets of ocean species.8. What can we learn about the author from the underlined sentence inPara. 1?A. He seldom went surfing at the sea.B. He forgot his experiences about the ocean.C. He never went back to his hometown.D. He had a wonderful impression ofHalfmoonBay.9. What is Australian marine life like according to the second paragraph?A. It is escaping from theCoral Seagradually.B. It depends on reefs for living greatly.C. It may be faced with danger.D. It is protected better than that in other oceans.10. What’s the purpose of The Protect Our Coral Sea activity?A. It is intended to contribute to a complete ecosystem.B. It is intended to prevent more marine species being endangered.C. It is intended to set up a large nature reserve for reefs.D. It is intended to raise more teenagers’ environmental awareness.11. Why do Angus and the author create a little video?A. To urge more people to take action toprotect the marine species.B. To inspire more people to explore the secret of the ocean.C. To share their childhood experiences about the ocean.D. To bring back to people their memory of ocean species.DI started out in life with few advantages. I didn't graduate from high school. I worked at menial (不体面的) jobs. I had limited education, limited skills and a limited future.And then I began asking, "Why are some people more successful than others?" This question changed my life.Over the years, I have read thousands of books and articles on the subjects of success and achievement(成就). It seems that the reasons have been discussed and written about for more than two thousand years, in every possible way. One quality that most philosophers, teachers and experts agree on is the importance of self-discipline (自律). As Al Tomsik summarized it years ago, "Success is tons of discipline."Some years ago, I attended a conference in Washington. It was the lunch break and I was eating at a nearby food fair. The area was crowded and I sat down at the last open table by myself, even though it was a table for four.A few minutes later, an older gentleman and a younger woman who was his assistant came along carrying trays of food, obviously looking for a place to sit. With plenty of room at my table, I immediately invited the oldergentleman to join me. He was hesitant (犹豫), but I insisted. Finally, thanking me as he sat down, we began to chat over lunch.It turned out that his name was Kop Kopmeyer. As it happened, I immediately knew who he was. He was a legend in the field of success and achievement. Kop Kopmeyer had written four large books, each of which contained 250 success principles that he had obtained from more than fifty years of research and study. I had read all four books from cover to cover, more than once.After we had chatted for a while, I asked him the question that many people in this situation would ask, "Of all the one thousand success principles that you have discovered, which do you think is the most important?”He smiled at me, as if he had been asked this question many times, and replied, without hesitating, "The most important success principle of all was stated by Thomas Huxley many years ago. He said, 'Do what you should do, when you should do it, whether you feel like it or not.'"He went on to say, "There are 999 other success principles that I have found in my reading and experience, but without self-discipline, none of them work."12. Why did the writer ask the question in Paragraph 2 ?A. Because he wasn't satisfied with himself.B. Because he was a person of self-discipline.C. Because he dislike those successful people.D. Because he wanted to share his idea on success.13. What made the writer invite the older gentleman to join him ?A. His great kindness.B. The gentleman's fame.C. His eagerness for success.D. The gentleman's habit.14. What are the four large books about ?A. Personal changesB. The secret of successC. Sayings of wisdomD. The gentleman's manners.15. What's the best title for the text ?A. The Magic of ReadingB. An Unexpected ConversationC. A Question that Changed MyLifeD. The Power of Self-discipline第二节（共5小题；每小题2分，满分10分）阅读下面短文，从短文后的选项中选出可以填入空白处的最佳选项。

【40套试卷合集】江苏省南京市南师附中集团新城中学2019-2020学年数学七上期中模拟试卷含答案

【40套试卷合集】江苏省南京市南师附中集团新城中学2019-2020学年数学七上期中模拟试卷含答案

2019-2020学年七上数学期中模拟试卷含答案一、我会选（本题每小题3分，共30分，每题只有一个．．．．选项符合） 10.834，0.83，83.3%中，最大的数是（ ） 2. 小丽坐在教室的第5行第3列用（3，5）表示，小华坐在该教室的第2行第5列，应当表示为（ ）A ．（2，5）B ．（5，3）C ．（5，2） D. (4, 5)3. 圆的位置和大小分别由（ ）决定。

A ．直径和圆心B ．圆心和半径C ．半径和直径 D. 圆心4. a 、b 、c 为自然数，且65521523a ÷=⨯=⨯c b ，则a 、b 、c 中最大的数是（ ）A. aB. bC. cD. 无法确定5. 用一个长5厘米，宽3厘米的长方形纸片剪一个最大的圆，这个圆的周长是（ ）10. 3：8的前项加上6，要使比值不变，比的后项应（ ） A. 加16 B. 乘16 C. 加6 D. 乘6二、我会填（本题共9小题，每空1分，共21分）12. 六（1）班昨天有48人出勤，有2人请病假，昨天该班的出勤率是______．13. 15是20的______%，50米的20%是______米，______吨的40%是10吨, 60吨比______吨多20%，比14. 在○里填上“>”“<”“=”.15. 行同一段路，甲用5小时，乙用4小时，甲乙的速度比是_________,所用时间比是_____________________.19. 画一个周长为12.56cm 的圆，圆规的两脚之间的距离应该是______cm ，所画圆的面积是______2cm ．三、我会判（对的打“√”，错的打“×”，每小题1分，共6分）20. 大圆的圆周率大于小圆的圆周率． （）22. 一种盐水中，盐的质量占盐水质量的3%，盐和水质量比是3∶100。

（ ）23. 一种商品先降价5%，后涨价5%，商品价格不变。

（）25. 半圆的周长就是与它半径相同圆的周长的一半。

【21套精选试卷合集】江苏省南京市南师附中集团新城中学2019-2020学年中考物理模拟试卷含解析

【21套精选试卷合集】江苏省南京市南师附中集团新城中学2019-2020学年中考物理模拟试卷含解析

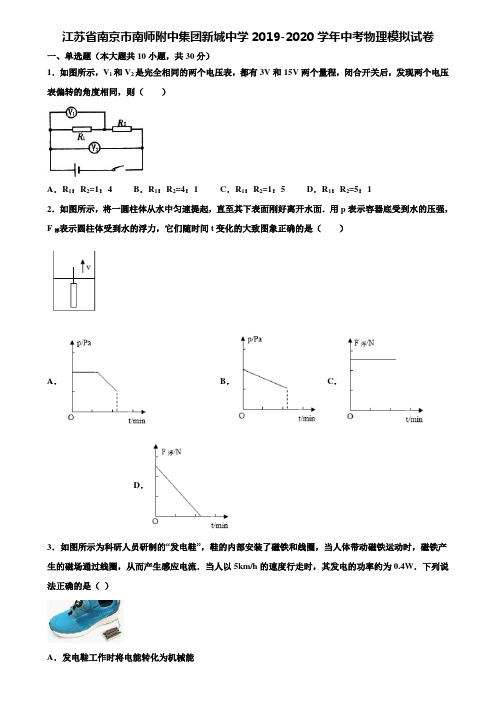
江苏省南京市南师附中集团新城中学2019-2020学年中考物理模拟试卷一、单选题（本大题共10小题，共30分）1．如图所示，V1和V2是完全相同的两个电压表，都有3V和15V两个量程，闭合开关后，发现两个电压表偏转的角度相同，则（）A．R1：R2=1：4 B．R1：R2=4：1 C．R1：R2=1：5 D．R1：R2=5：12．如图所示，将一圆柱体从水中匀速提起，直至其下表面刚好离开水面．用p表示容器底受到水的压强，F浮表示圆柱体受到水的浮力，它们随时间t变化的大致图象正确的是（）A．B． C．D．3．如图所示为科研人员研制的“发电鞋”，鞋的内部安装了磁铁和线圈，当人体带动磁铁运动时，磁铁产生的磁场通过线圈，从而产生感应电流．当人以5km/h的速度行走时，其发电的功率约为0.4W．下列说法正确的是（）A．发电鞋工作时将电能转化为机械能B．发电鞋是利用电磁感应原理工作的C．发电鞋是利用电流磁效应原理工作的D．在人以5km/h的速度行走1h的过程中，发电鞋可以产生约0.4J的电能4．如图两个容器中分别盛有甲、乙两种不同的液体，把体积相同的A、B两个实心小球放入甲液体中，两球沉底如图甲所示；放入乙液体中，两球静止时的情况如图乙所示，两容器中液面刚好相平，则下列说法正确的是A．小球A 的质量大于小球B 的质量B．甲液体的密度大于乙液体的密度C．小球A 在甲液体中受到的浮力大于在乙液体中的浮力D．甲液体对容器底的压强小于乙液体对容器底的压强5．某实验小组分别用如图所示的甲乙两个滑轮组（每个滑轮重相同）匀速提起相同的重物，所用的拉力分别为F1和F2，机械效率分别为η1和η2，不计绳重及摩擦，下列说法正确的是（）A．F1＞F2，η1=η2B．F1＜F2，η1=η2C．F1＜F2，η1＞η2D．F1＞F2，η1＜η26．下列关于图中所示光学现象的描述或解释正确的是A．图甲中，小孔成的是倒立的虚像B．图乙中，人配戴的凹透镜可以矫正近视眼C．图丙中，白光通过三棱镜要分解成红、橙、黄、绿、蓝、灰、紫七色光D．图丁中，漫反射的光线杂乱无章不遵循光的反射定律7．小阳设计一个天然气泄漏检测电路，如图甲所示，R为气敏电阻，其阻值随天然气浓度变化曲线如图乙所示，R0为定值电阻，电源电压恒定不变．则下列说法正确的是（）A．天然气浓度增大，电压表示数变小B．天然气浓度减小，电流表示数变大C．天然气浓度增大，电路消耗的总功率变小D．天然气浓度减小，电压表与电流表示数的比值不变8．有下列几种做法：①用手接触三节串联的铅蓄电池组；②用手去捡落在地上的高压输电线；③用湿布去擦亮着的电灯泡；④站在地上用手碰家庭电路中的火线．其中会发生触电事故的做法是A．②③B．①③C．②③④D．①②③④9．如图甲所示是“探究不同物质吸热升温的现象”实验装置两个相同的易拉罐中分别装有质量和初温都相同的a、b两种液体，用相同的装置加热，根据记录的实验数据绘制的温度与时间的关系图象如图乙所示，下列说法中正确的是（）A．组装器材时，先固定上面铁圈的高度B．升高相同温度，a液体吸收的热量更多C．a液体的比热容小于b液体的比热容D．不添加器材，利用本实验装置还可以比较质量相等的不同燃料燃烧时放出的热量10．导体容易导电是由于A．导体中存在大量的自由电子B．导体中存在大量的自由电荷C．导体中存在大量的自由离子D．导体中存在大量的带电粒子二、多选题（本大题共3小题，共12分）11．弹簧测力计下挂一长方体物体，将物体从盛有适量水的烧杯上方离水面某一高度处缓缓下降，然后将其逐渐浸入水中如图甲；图乙是弹簧测力计示数F与物体下降高度h变化关系的图象，则下列说法中正确的是A．物体的体积是400cm3B．物体受到的最大浮力是8NC．物体的密度是1.5×103kg/m3D．物体刚浸没时下表面受到水的压力是12N12．图所示的是中国科技馆展示的地热发电模型，它模拟了地热发电过程：左侧水管内水位降低，蓝色LED 灯逐渐向下亮起，表示冷水注入地下．随后，红色LED 灯亮起，表示冷水被加热成热水，接着右侧水管下方喷出烟雾，表示高温地热已将热水变为水蒸气．水蒸气进入汽轮发电机，地面上的LED 灯发光表示发电成功．下列说法中正确的是A．右侧水管下方喷出的烟雾是水蒸气B．水蒸气推动汽轮发电机做功，水蒸气的内能减小C．高温地热将热水变为水蒸气的过程中，热水需要放热D．地热发电是将内能转化为机械能再转化为电能的过程13．如图所示，电源电压不变，闭合开关S，将滑动变阻器的滑片P向右移动的过程中，电压表V1、V2的示数变化量分别△U1、△U2，电流表示数的变化量为△I。

江苏省南京市新城中学2019-2020学年中考数学模拟试卷

江苏省南京市新城中学2019-2020学年中考数学模拟试卷

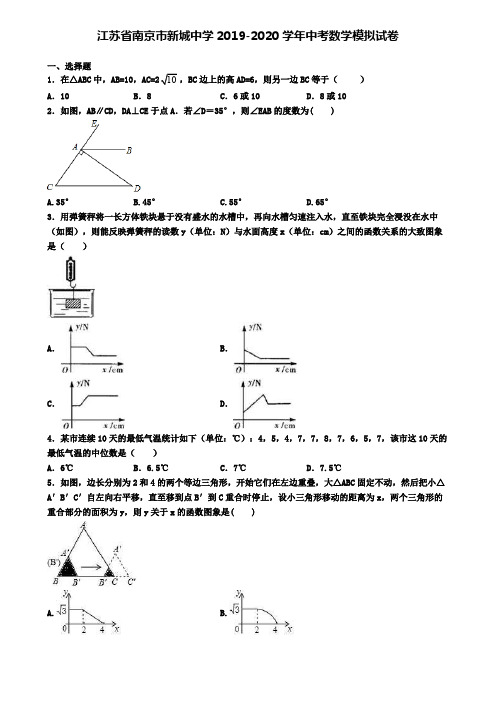
江苏省南京市新城中学2019-2020学年中考数学模拟试卷一、选择题1．在△ABC中，AB=10，AC=2BC边上的高AD=6，则另一边BC等于（）A．10 B．8 C．6或10 D．8或102．如图，AB∥CD，DA⊥CE于点A．若∠D＝35°，则∠EAB的度数为( )A.35°B.45°C.55°D.65°3．用弹簧秤将一长方体铁块悬于没有盛水的水槽中，再向水槽匀速注入水，直至铁块完全浸没在水中（如图），则能反映弹簧秤的读数y（单位：N）与水面高度x（单位：cm）之间的函数关系的大致图象是（）A．B．C．D．4．某市连续10天的最低气温统计如下（单位：℃）：4，5，4，7，7，8，7，6，5，7，该市这10天的最低气温的中位数是（）A．6℃B．6.5℃C．7℃D．7.5℃5．如图，边长分别为2和4的两个等边三角形，开始它们在左边重叠，大△ABC固定不动，然后把小△A′B′C′自左向右平移，直至移到点B′到C重合时停止，设小三角形移动的距离为x，两个三角形的重合部分的面积为y，则y关于x的函数图象是( )A. B.C. D.6．在2015-2016CBA 常规赛季中，易建联罚球投篮的命中率大约是82.3%，下列说法错误的是（ ）A ．易建联罚球投篮2次，一定全部命中B ．易建联罚球投篮2次，不一定全部命中C ．易建联罚球投篮1次，命中的可能性较大D ．易建联罚球投篮1次，不命中的可能性较小7．下列各式的计算中正确的是（ ）A ．325a a a +=B ．236a a a ⋅=C ．632a a a ÷=D ．326()a a -=8．一个两位数，十位数字比个位数字的2倍大1，若将这个两位数减去36恰好等于个位数字与十位数字对调后所得的两位数，则这个两位数是（ ）A ．86B ．68C ．97D ．739．将一幅三角尺如图所示的方式摆放（两条直角边在同一条直线上，且两锐角顶点重合），连接另外两条锐角顶点，并测得147∠=，则2∠的度数为（ ）A ．60°B ．58°C ．45°D ．43°10．如图，平行四边形纸片ABCD ，CD=5，BC=2，∠A=60°，将纸片折叠，使点A 落在射线AD 上（记为点A′），折痕与AB 交于点P ，设AP 的长为x ，折叠后纸片重叠部分的面积为y ，可以表示y 与x 之间关系的大致图象是（ ）A ．B ．C ．D ．11．如图，在四边形AOBC 中，若∠1＝∠2，∠3+∠4＝180°，则下列结论正确的有（ ）（1）A 、O 、B 、C 四点共圆（2）AC ＝BC（3）cos ∠1＝2a b c+ （4）S 四边形AOBC ＝()sin 12a b c +⋅∠A ．1个B ．2个C ．3个D ．4个 12．下列式子值最小的是（ ）A ．﹣1+2019B ．﹣1﹣2019C ．﹣1×2019D ．2019﹣1 二、填空题 13．如图，边长为1的小正方形构成的网格中，半径为1的⊙O 的圆心O 在格点上，则∠BED 的余弦值等于_____．14．一元二次方程x 2﹣3x ﹣4=0与x 2+4x+5=0的所有实数根之和等于_____．15．如图，∠3=40°，直线b 平移后得到直线a ，则∠1+∠2=_____°．16．方程4806002x x-＝45的解是_____． 17．小华用家里的旧纸盒做了一个底面半径为3cm ，高为4cm 的圆锥模型，则此圆锥的侧面积是___cm 2．18．单项式9x m y 3与单项式4x 2y n 是同类项，则m+n 的值是_____．三、解答题19．给定关于x 的二次函数y ＝kx 2﹣4kx+3（k≠0），（1）当该二次函数与x 轴只有一个公共点时，求k 的值；（2）当该二次函数与x 轴有2个公共点时，设这两个公共点为A 、B ，已知AB ＝2，求k 的值；（3）由于k 的变化，该二次函数的图象性质也随之变化，但也有不会变化的性质，某数学学习小组在探究时得出以下结论：①与y 轴的交点不变；②对称轴不变；③一定经过两个定点；请判断以上结论是否正确，并说明理由．20．如图，在△ABC 中，∠BAC ＝90°，以AC 为直径的⊙O 交BC 于点D ，点E 在AB 上，连接DE 并延长交CA 的延长线于点F ，且∠AEF ＝2∠C ．（1）判断直线FD 与⊙O 的位置关系，并说明理由；（2）若AE ＝2，EF ＝4，求⊙O 的半径．21．先化简，再求值：22121111x x x x ⎛⎫++-÷ ⎪--⎝⎭，其中x ． 22．如图，在平面直角坐标系中，Rt △AOC 的直角边OA 在y 轴正半轴上，且顶点O 与坐标原点重合，点C 的坐标为（1，2），直线y ＝﹣x+b 过点C ，与x 轴交于点B ，与y 轴交于点D ．（1）B 点的坐标为 ，D 点的坐标为 ；（2）动点P 从点O 出发，以每秒1个单位长度的速度，沿O→A→C 的路线向点C 运动，同时动点Q 从点B 出发，以相同速度沿BO 的方向向点O 运动，过点Q 作QH ⊥x 轴，交线段BC 或线段CO 于点H ．当点P 到达点C 时，点P 和点Q 都停止运动，在运动过程中，设动点P 运动的时间为t 秒：①设△CPH 的面积为S ，求S 关于t 的函数关系式；②是否存在以Q 、P 、H 为顶点的三角形的面积与S 相等？若存在，直接写出t 的值；若不存在，请说明理由．23．如图，在每个小正方形的边长为1的网格中，点A 、B 、O 、P 均在格点上.I. OB 的长等于______________；Ⅱ.点M 在射线OA 上，点N 在射线OB 上，当PMN 的周长最小时，请在如图所示的网格中，用无刻度的直尺，画出PMN ，并简要说明点M ，N 的位置是如何找到的（不要求证明）____________ .24．已知：如图，在矩形ABCD 中，点E 在边AD 上，点F 在边BC 上，且AE=CF ，作EG ∥FH ，分别与对角线BD 交于点G 、H ，连接EH ，FG ．（1）求证：△BFH ≌△DEG ；（2）连接DF ，若BF=DF ，则四边形EGFH 是什么特殊四边形？证明你的结论．25．如图，在ABC ∆中，4AB AC ==，以AB 为直径的O 交BC 于点D ，交AC 于点E ，点P 是AB 的延长线上一点，且∠PDB=12∠A ，连接DE ，OE ． (1)求证：PD 是O 的切线．(2)填空： ①当P ∠的度数为______时，四边形OBDE 是菱形；②当45BAC ∠=︒时，CDE ∆的面积为_________．【参考答案】***一、选择题13．1214．-115．22016．x ＝417．15π．18．5三、解答题19．（1）32（2）1（3）①②③ 【解析】【分析】（1）由抛物线与x 轴只有一个交点，可知△=0；（2）由抛物线与x 轴有两个交点且AB=2，可知A 、B 坐标，代入解析式，可得k 值；（3）通过解析式求出对称轴，与y 轴交点，并根据系数的关系得出判断．【详解】（1）∵二次函数y＝kx2﹣4kx+3与x轴只有一个公共点，∴关于x的方程kx2﹣4kx+3＝0有两个相等的实数根，∴△＝（﹣4k）2﹣4×3k＝16k2﹣12k＝0，解得：k1＝0，k2＝32，k≠0，∴k＝32；（2）∵AB＝2，抛物线对称轴为x＝2，∴A、B点坐标为（1，0），（3，0），将（1，0）代入解析式，可得k＝1，（3）①∵当x＝0时，y＝3，∴二次函数图象与y轴的交点为（0，3），①正确；②∵抛物线的对称轴为x＝2，∴抛物线的对称轴不变，②正确；③二次函数y＝kx2﹣4kx+3＝k（x2﹣4x）+3，将其看成y关于k的一次函数，令k的系数为0，即x2﹣4x＝0，解得：x1＝0，x2＝4，∴抛物线一定经过两个定点（0，3）和（4，3），③正确．综上可知：正确的结论有①②③．【点睛】本题考查了二次函数的性质，与x、y轴的交点问题，对称轴问题，以及系数与图象的关系问题，是一道很好的综合问题．20．（1）直线FD与⊙O相切，理由详见解析；（2）⊙O的半径为【解析】【分析】（1）连接OD，根据已知条件得到∠AEF＝∠AOD，等量代换得到∠AOD＋∠AED＝180°，求得∠ODF＝90°，于是得到结论；（2）解直角三角形得到∠F＝30°，AF=OF＝2OD，于是得到OD＝FA，即可得到结论．【详解】解：（1）直线FD与⊙O相切；理由：连接OD，∵∠AEF＝2∠C，∠AOD＝2∠C，∴∠AEF＝∠AOD，∵∠AEF+∠AED＝180°，∴∠AOD+∠AED＝180°，∵∠BAC＝90°，∴∠ODF＝90°，∴直线FD与⊙O相切；（2）∵∠BAC＝90°，AE＝2，EF＝4，∴∠F＝30°，AF=，∵∠ODF＝90°，∴OF ＝2OD ，∴OD ＝FA ，∴⊙O的半径为【点睛】本题利用了切线的判定和性质，要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．21．21x x -+,4-【解析】【分析】根据分式的运算法则即可求出答案【详解】 原式＝22(1)(1)1(1)x x x x x -+--+＝21x x -+ ， 当x时，原式＝21x x -==+．【点睛】本题考查分式的运算，解题的关键是熟练运用分式的运算法则，本题属于基础题型． 22．（1）（3，0）；（0，3）；（2）①S ＝ 22153(02)2256(23)t t t t t t ⎧-+<⎪⎨⎪-+-<<⎩…；②存在，t ＝1或73时，以Q 、P 、H 为顶点的三角形的面积与S 相等．【解析】【分析】（1）把点C 坐标代入直线求得b 的值即得到直线解析式，令y ＝0求点B 坐标，令x ＝0求点D 坐标．（2）①由Rt △AOC 中∠OAC ＝90°求得OA+AC ＝OB ＝3，即t 的取值范围为0≤t＜3且t≠2．画图发现有两种情况：当0≤t＜2时，点P 在线段OA 上，点H 在线段BC 上，可证得PH ∥x 轴，故S ＝S △CPH ＝12PH•AP，用t 表示PH 、AP 的值再代入即能用t 表示S ；当2＜t ＜3时，点P 在线段AC 上，点H 在线段OC 上，此时以PC 为底、点H 到CP 距离h 为高来求S ，用t 表示CP 、h 的值再代入即能用t 表示S ．再把两式统一写成S 关于t 的分段函数关系式．②与①类似把点P 、Q 的位置分两种情况讨论计算；其中P 在AC 上、H 在OC 上时，以QH 为底求△QPH 的面积，需对点P 到QH 的距离PE 的表示再进行一次分类．用t 表示△QPH 面积后与S 相等列得方程，解之求得t 的值．【详解】解：（1）∵直线y＝﹣x+b过点C（1，2）∴﹣1+b＝2∴b＝3，即直线为y＝﹣x+3当y＝0时，﹣x+3＝0，得x＝3；当x＝0时，y＝3∴B（3，0），D（0，3）故答案为：（3，0）；（0，3）．（2）①∵Rt△AOC中，∠OAC＝90°，C（1，2）∴A（0，2），OA＝2，AC＝1∵OB＝OD＝3，∠BOD＝90°∴OA+AC＝OB＝3，∠OBD＝45°∴0≤t＜3，且t≠2i）当0≤t＜2时，点P在线段OA上，点H在线段BC上，如图1∴OP＝BQ＝t∴AP＝OA﹣OP＝2﹣t，OQ＝OB﹣BQ＝3﹣t∵HQ⊥x轴于点Q∴∠BQH＝90°∴△BQH是等腰直角三角形∴HQ＝BQ＝t∴HQ∥OP且HQ＝OP∴四边形OPHQ是平行四边形∴PH∥x轴，PH＝OQ＝3﹣t∴S＝S△CPH＝12PH•AP＝12（3﹣t）（2﹣t）＝12t2﹣52t+3ii）当2＜t＜3时，点P在线段AC上，点H在线段OC上，如图2∴CP＝OA+AC﹣t＝3﹣t，x H＝OQ＝3﹣t∵直线OC解析式为：y＝2x∴QH＝y H＝2（3﹣t）＝6﹣2t∴点H 到CP 的距离h ＝2﹣（6﹣2t ）＝2t ﹣4∴S ＝S △CPH ＝12CP•h＝12（3﹣t ）（2t ﹣4）＝﹣t 2+5t ﹣6 综上所述，S 关于t 的函数关系式为S ＝ 22153(02)2256(23)t t t t t t ⎧-+<⎪⎨⎪-+-<<⎩… ②存在以Q 、P 、H 为顶点的三角形的面积与S 相等．i ）当0≤t＜2时，如图3∵S △CPH ＝S △QPH ，两三角形有公共底边为PH∴点C 和点Q 到PH 距离相等，即AP ＝OP∴t ＝2﹣t∴t ＝1ii ）当2＜t≤2.5时，如图4，延长QH 交AC 于点E∴AE ＝OQ ＝3﹣t ，AP ＝t ﹣2，QH ＝6﹣2t∴PE ＝AE ﹣AP ＝（3﹣t ）﹣（t ﹣2）＝5﹣2t∴S △QPH ＝12QH•PE＝12（6﹣2t ）（5﹣2t ）＝2t 2﹣11t+15 ∵S △CPH ＝S △QPH ∴﹣t 2+5t ﹣6＝2t 2﹣11t+15解得：t 1＝3（舍去），t 2＝73iii ）当2.5＜t ＜3时，如图5，延长QH 交AC 于点E∴PE＝AP﹣AE＝（t﹣2）﹣（3﹣t）＝2t﹣5∴S△QPH＝12QH•PE＝12（6﹣2t）（2t﹣5）＝﹣2t2+11t﹣15∴﹣t2+5t﹣6＝﹣2t2+11t﹣15 解得：t1＝t2＝3（舍去）综上所述，t＝1或73时，以Q、P、H为顶点的三角形的面积与S相等．【点睛】本题考查了一次函数的图象与性质，等腰三角形的性质，平行四边形的性质，解一元二次方程．由于点P、Q位置不同导致求三角形的计算不同是解决本题的关键，需画出图形数形结合地进行分类讨论．23图见解析，选取点P关于直线OA的对称点1P；选取点C，连接PC并延长，选取点EF，连接EF与PC延长线交于点2P；连接12P P，分别交OA、OB于M、N，连接PM、PN，则PMN的周长最小.【解析】【分析】I.根据勾股定理求出OB的长.Ⅱ. 如图，选取点P关于直线OA的对称点1P；选取点C，连接PC并延长，选取点EF，连接EF与PC延长线交于点2P；根据直角边长都为2和3，EF和PC为斜边的两个三角形全等，得出∠BCP=∠FEG，再根据EG//PH，所以∠BEG=∠BPH,再根据三角形的内角和定理和等量代换，得出∠EP2P=90︒，再根据两组对边分别相等的四边形是平行四边形得出四边行BEFO为平行四边形，从而得EF//OB，得出PP2⊥OB,再根据BE=BP，从而得出OB垂直平分PP2，连接P2P1与OB、OA分别相交于M点和N点，即可解决问题．【详解】I.在Rt OBD中，OB==Ⅱ.如图，选取点P关于直线OA的对称点1P；选取点C，连接PC并延长，选取点EF，连接EF与PC延长线交于点2P；连接12P P，分别交OA、OB于M、N，连接PM、PN.则点M、N即为所求．证明：由网格图可得，直角边长都为2和3，且EF和PC为斜边的两个三角形全等∠∴BCP=∠FEGEG//PH∠∴BEG=∠BPH在PCH中，∠BCP+∠BPC+∠BPH=90︒∠∴FEG+∠BEG+∠BPC=90︒∠∴EP2P=90︒∴PP2⊥EF根据勾股定理可得，BE=OF，EF=OB,∴四边行BEFO为平行四边形∴EF//OB∴PP2⊥OBBE=BP, EF//OB∴OB垂直平分PP2∴点P与点P关于OB对称2连接P2P1与OB、OA分别相交于M点和N点，则此时PMN的周长最小【点睛】此题考查了应用与设计作图轴对称—最短距离、平行四边形的性质与判定、勾股定理等知识，解题的关键是利用数形结合的思想解决问题．24．(1)见解析；（2）四边形EGFH是菱形，理由见解析【解析】【分析】（1）由平行四边形的性质得出AD∥BC，AD=BC，OB=OD，由平行线的性质得出∠FBH=∠EDG，∠OHF=∠OGE，得出∠BHF=∠DGE，求出BF=DE，由AAS即可得出结论；（2）先证明四边形EGFH是平行四边形，再由等腰三角形的性质得出EF⊥GH，即可得出四边形EGFH是菱形．【详解】（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC，∴∠FBH=∠EDG，∵AE=CF，∴BF=DE，∵EG∥FH，∴∠OHF=∠OGE，∴∠BHF=∠DGE，在△BFH和△DEG中，FBH EDG BHF DGEBF DE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴BFH ≌△DEG （AAS ）；（2）解：四边形EGFH 是菱形；理由如下：连接DF ，设EF 交BD 于O ．如图所示：由（1）得：BFH ≌△DEG ，∴FH=EG ，又∵EG ∥FH ，∴四边形EGFH 是平行四边形，∵DE=BF ，∠EOD=∠BOF ，∠EDO=∠FBO ，∴△EDO ≌△FBO ，∴OB=OD ，∵BF=DF ，OB=OD ，∴EF ⊥BD ，∴EF ⊥GH ，∴四边形EGFH 是菱形．【点睛】此题考查全等三角形的判定与性质，矩形的性质，解题关键在于利用平行四边形的性质求证25．（1）证明见解析；（2）①30°；②2【解析】【分析】（1）要证明切线，按照圆周角定理和已知的2倍角关系，证明∠ODP 为直角（2）当四边形OBDE 为菱形时，△OBD 为等边三角形，则∠P 为30°（3）连接AD ，过点E 作BC 的垂线，通过平行相似得到a 、b 的第一种关系，根据勾股定理得到a 、b 的第二种关系，用a 、b 表示出△CDE 的面积，再代入a 与b 的关系，获得面积值．【详解】（1）如图，连接OD∵OB ＝OD ，∠PDB ＝12∠A ∴∠ODB ＝∠ABD ＝90°﹣12∠A ＝90°﹣∠PDB∴∠ODB+∠PDB ＝90°∴∠ODP ＝90°又∵OD 是⊙O 的半径∴PD 是⊙O 的切线（2）①30°若四边形OBDE 为菱形，则OB ＝BD ＝DE ＝EO ＝OD∴△OBD 为等边三角形∴∠ABD ＝∠A ＝60°∴∠PDB ＝30°∴∠P ＝30°即当∠P 为30°时，四边形OBDE 为菱形②2如图所示∵AO ＝OE ＝2，∠AOE ＝90°∴AE ＝12x x ∴EC ＝4﹣12x x ∵∠BAC ＝45°∴∠EDB ＝135°∴∠EDC ＝45°设DF ＝EF ＝b ，FC ＝a∵△EFC ∽△ADC ∴CF EF EC CD AD AC ==∴a a b =+ ∵a 2+b 2＝（4﹣12x x ）2解得21),4a b b ==-211())222CDE S a b b b b b ∆=+=-+==. 【点睛】本题考查了圆的基本性质，菱形的性质，（3）是本题的难点，需要以相似和勾股的关系建立方程并表示出关于面积的代数式．。

江苏省南京师范大学附属中学2019-2020学年度高一第一学期期末考试数学试卷

江苏省南京师范大学附属中学2019-2020学年度高一第一学期期末考试数学试卷

南京师大附中2019-2020学年度第1学期高一年级期末考试数学试卷一、单项选择题：本小题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 已知集合 U = R ，集合{}2|320A x x x =-+>，则U C A =（ ） A. (1,2) B. [1,2 ] C. (-2，-1 ) D. [ -2，-1]2. 设13331log ,4,log 24a b c ===，则a ，b ，c 的大小关系为（ ）．A. c >a> bB. b> a> cC. c> b> aD. b> c> a3. 如图，已知点 C 为△OAB 边AB 上一点，且AC=2CB ，若存在实数m ，n ，使得OC mOA nOB =+，则m- n 的值为（ ）．A.13-B. 0C.13D.234.已知函数()()2sin 0,2f x x πωϕωϕ⎛⎫=+><⎪⎝⎭的图象如图所示，则ϕ的值为（ ）．A.6π B.6π- C.4π- D.4π5. 函数()21log 1x f x x -=++的定义域是 ( )A. [1,+∞ )B. (0,1)C. (-1,0 ]D. (−∞ −1]6. 设a ，b 是实数，已知角θ的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上有两点A (a ，1 )，B(-2，b )，且1sin 3θ=，则ab的值为（ ）． A. -4 B.-2 C. 4 D. ±47. 函数()2sin2xy x x R =∈的图象大致为（ ）．8. 若函数()()lg 12f x x =-+，则对于任意的()12,1,x x ∈+∞，()()122f x f x +与122x x f +⎛⎫⎪⎝⎭的大小关系是（ ）． A.()()122f x f x +≥122x x f +⎛⎫ ⎪⎝⎭ B. ()()122f x f x +≤122x x f +⎛⎫⎪⎝⎭C.()()122f x f x +=122x x f +⎛⎫⎪⎝⎭D.不确定二、多项选择题：本小题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得3分，有选错的得0分． 9. 下列计算结果为有理数的有（ ）． A.23log 3log 2⋅ B. lg2 +lg5 C.1ln22e - D.5sin6π 10. 对于定义在 R 上的函数()f x ，下列判断错误的有（ ）． A.若()()22f f ->，则函数()f x 是 R 的单调增函数B.若()()22f f -≠，则函数()f x 不是偶函数C.若()00f =，则函数()f x 是奇函数D.函数()f x 在区间 (−∞，0]上是单调增函数，在区间 (0,+∞)上也是单调增函数，则()f x 是 R 上的单调增函数11. 设 a 为实数，则直线y =a 和函数41y x =+的图象的公共点个数可以是（ ）． A. 0 B. 1 C. 2 D. 312. 设函数()f x 的定义域为D ，若对于任意x ∈D ，存在y ∈D 使()()2f x f y C -=（C为常数）成立，则称函数()f x 在D 上的“半差值”为C ．下列四个函数中，满足所在定义域上“半差值”为1的函数是（ ）． A.()31y x x R =+∈ B. ()2xy x R =∈C. ()()ln 0,y x x =∈+∞ D. y=sin2x+1( x ∈R)三、填空题：本小题共4小题，每小题5分，共20分．13. 设m 为实数，若函数()22f x x mx =+-在区间 (−∞,2)上是单调减函数，则m 的取值范围是 ． 14. 把函数sin 23y x π⎛⎫=-⎪⎝⎭图象上每一点的横坐标变为原来的 2 倍（纵坐标不变），得到图象为1C ；再把1C 上每一点的纵坐标变为原来的2倍（横坐标不变），得到图象为2C ，则2C 对应的解析式为 ．15. 若()()cos ,1,2cos ,2sin AB AC θθθ=-=，其中θ∈[0,π]，则BC 的最大值为 ． 16. 已知函数()22,1,1x x f x x x -≥⎧=⎨<⎩，那么()()3ff = ；若存在实数 a ，使得()()()f a f f a =，则a 的个数是 ．四、解答题：本小题共6小题，共70分．解答应写出应写出文字说明、证明过程或演算步骤．17. （10 分）设 t 为实数，已知向量()()1,2,1,.a b t ==-⑴ 若 t = 3，求a b +和a b -的值；⑵ 若向量a b +与3a b -所成角为 135° ，求 t 的值．18. （12 分）设实数 x 满足 sinx+ cos x= c ，其中 c 为常数． ⑴ 当c =时，求44sin cos x x +的数值；⑵ 求值：()33443cos cos 2sin cos x x x xππ⎛⎫+++ ⎪⎝⎭-（用含 c 的式子表示）．19. （12 分）设 a 为正实数．如图，一个水轮的半径为a m ，水轮圆心 O 距离水面2am ，已知水轮每分钟逆时针转动 5 圈．当水轮上的点 P 从水中浮现时（即图中点0P ）开始计算时间． ⑴ 将点 P 距离水面的高度 h(m )表示为时间 t(s)的函数； ⑵ 点 P第一次达到最高点需要多少时间．20. （12 分）设向量()11,a x y =,()22,b x y =，其中0a ≠． ⑴ 若//a b ，求证：12210x y x y -= ； ⑵ 若12210x y x y -= ，求证：//a b ．21. （12 分）⑴ 运用函数单调性定义，证明：函数()31f x x x =-在区间 (0,+∞)上是单调减函数； ⑵ 设 a 为实数， 0 <a < 1 ，若 0 <x < y ，试比较33yx a a -和4334x y x y a a ++-的大小，并说明理由．22. （12 分） ⑴ 已知函数()()11,1x f x x x R x -=≠-∈+，试判断函数()f x 的单调性，并说明理由； ⑵ 已知函数()()1lg1,1x g x x x R x -=≠±∈+. （i ）判断()g x 的奇偶性，并说明理由；（ii ）求证：对于任意的x ,y ∈R ，且x ≠±1 ，y ≠±1，xy ≠−1都有()()1x y g x g y g xy ⎛⎫++= ⎪+⎝⎭①.⑶ 由⑵可知满足①式的函数是存在的，如()()1lg 1,1x g x x x R x -=≠±∈+．问：满足①的函数是否存在无穷多个？说明理由．南京师大附中2019-2020学年度第1学期高一年级期末考试数学试卷答案一、单项选择题：本小题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 已知集合 U = R ，集合{}2|320A x x x =-+>，则U C A =（ ） A. (1,2) B. [1,2 ] C. (-2，-1 ) D. [ -2，-1] 【答案】B ；【解析】因为A ()(),12,=-∞+∞，U = R ,所以U C A =[ 1,2] ．2. 设13331log ,4,log 24a b c ===，则a ，b ，c 的大小关系为（ ）．A. c >a> bB. b> a> cC. c> b> aD. b> c> a 【答案】D ；【解析】0,1,01a b c <><<,所以 b> c> a ．3. 如图，已知点 C 为△OAB 边AB 上一点，且AC=2CB ，若存在实数m ，n ，使得OC mOA nOB =+，则m- n 的值为（ ）．A.13-B. 0C.13D.23【答案】A ；【解析】由等和线定理，易得1233OC OA OB =+，所以m- n =13-.4.已知函数()()2sin 0,2f x x πωϕωϕ⎛⎫=+><⎪⎝⎭的图象如图所示，则ϕ的值为（ ）．A.6π B.6π- C.4π- D.4π【答案】D ； 【解析】由图可知，322T π=，所以223T πω==，所以()22sin 3f x x ϕ⎛⎫=+ ⎪⎝⎭，又因为328f π⎛⎫= ⎪⎝⎭，所以232382k ππϕπ⨯+=+，解得()24k k Z πϕπ=+∈，因为2πϕ<，所以4πϕ=.5. 函数()21log 1x f x x -=++的定义域是 ( )A. [1,+∞ )B. (0,1)C. (-1,0 ]D. (−∞ −1]【答案】C ；【解析】由对数的真数大于 0 ，及二次根式内非负，得101x x ->+且21103x⎛⎫-≥ ⎪⎝⎭，解得11x -<<且x ≤0 ，所以定义域为 (-1,0 ]．6. 设a ，b 是实数，已知角θ的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上有两点A (a ，1 )，B(-2，b )，且1sin 3θ=，则ab的值为（ ）． A. -4 B.-2 C. 4 D. ±4【答案】A ；【解析】由三角函数的定义，13==，且a< 0，解得b a ==-，所以4ab=-. 7. 函数()2sin2xy x x R =∈的图象大致为（ ）．【答案】D ；【解析】由该函数为奇函数，排除选项 A ，B ，由2x π=时，函数值为 0，可排除选项 C ，故选 D ．8. 若函数()()lg 12f x x =-+，则对于任意的()12,1,x x ∈+∞，()()122f x f x +与122x x f +⎛⎫ ⎪⎝⎭的大小关系是（ ）． A.()()122f x f x +≥122x x f +⎛⎫ ⎪⎝⎭ B. ()()122f x f x +≤122x x f +⎛⎫⎪⎝⎭C.()()122f x f x +=122x x f +⎛⎫⎪⎝⎭D.不确定【答案】B ；【解析】观察图象，可得函数“凹凸性”如图，故选 B ．二、多项选择题：本小题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得3分，有选错的得0分． 9. 下列计算结果为有理数的有（ ）． A.23log 3log 2⋅ B. lg2 +lg5 C.1ln22e - D.5sin6π 【答案】ABCD ；【解析】23log 3log 21⋅=；lg2+ lg5=1；1ln220e -=；51sin62π=， 故选 ABCD ．10. 对于定义在 R 上的函数()f x ，下列判断错误的有（ ）． A.若()()22f f ->，则函数()f x 是 R 的单调增函数 B.若()()22f f -≠，则函数()f x 不是偶函数C.若()00f =，则函数()f x 是奇函数D.函数()f x 在区间 (−∞，0]上是单调增函数，在区间 (0,+∞)上也是单调增函数，则()f x 是 R 上的单调增函数 【答案】ACD ；【解析】A 选项，由()()22f f ->，则()f x 在 R 上必定不是增函数； B 选项，正确；C 选项，()2f x x =，满足()00f =，但不是奇函数；D 选项，该函数为分段函数，在 x =0 处，有可能会出现右侧比左侧低的情况，故错误． 11. 设 a 为实数，则直线y =a 和函数41y x =+的图象的公共点个数可以是（ ）． A. 0 B. 1 C. 2 D. 3 【答案】ABC ；【解析】41y x =+是偶函数，且在 [0,+∞ ) 上递增，画出草图，可知y=a 与该函数的交点个数可能为 0，1，2．12. 设函数()f x 的定义域为D ，若对于任意x ∈D ，存在y ∈D 使()()2f x f y C -=（C为常数）成立，则称函数()f x 在D 上的“半差值”为C ．下列四个函数中，满足所在定义域上“半差值”为1的函数是（ ）． A.()31y x x R =+∈ B. ()2xy x R =∈C. ()()ln 0,y x x =∈+∞ D. y=sin2x+1( x ∈R)【答案】AC ；【解析】即对任意定义域中的 x ，存在 y ，使得f(y)=f(x)-2；由于AC 值域为R ，故满足； 对于B ，当x=0时，函数值为1，此时不存在自变量y ，使得函数值为-1，故B 不满足； 对于D ，当2x π=-时，函数值为−1，此时不存在自变量y ，使得函数值为−3 ,故D 不满足，所以选AC ．三、填空题：本小题共4小题，每小题5分，共20分．13. 设m 为实数，若函数()22f x x mx =+-在区间 (−∞,2)上是单调减函数，则m 的取值范围是 ． 【答案】m ≤−4；【解析】()f x 为开口向上的二次函数，对称轴为直线2mx =-,要使得函数在(−∞,2)上递减，则22m-≥，解得4m ≤-. 14. 把函数sin 23y x π⎛⎫=-⎪⎝⎭图象上每一点的横坐标变为原来的 2 倍（纵坐标不变），得到图象为1C ；再把1C 上每一点的纵坐标变为原来的2倍（横坐标不变），得到图象为2C ，则2C 对应的解析式为 ．【答案】2sin 3y x π⎛⎫=-⎪⎝⎭【解析】1C :sin 3y x π⎛⎫=-⎪⎝⎭,2C :2sin 3y x π⎛⎫=-⎪⎝⎭.15. 若()()cos ,1,2cos ,2sin AB AC θθθ=-=，其中θ∈[0,π]，则BC 的最大值为 ． 【答案】3；【解析】()cos ,2sin 1,BC AC AB θθ=-=+ 所以()2222cos 2sin 13sin 4sin 2,BC θθθθ=++=++因为[]0,θπ∈，令[]sin 0,1t θ=∈，所以22342,BC t t =++所以当t=1时，取最大值 9，所以BC 的最大值为 3．16. 已知函数()22,1,1x x f x x x -≥⎧=⎨<⎩，那么()()3f f = ；若存在实数 a ，使得()()()f a f f a =，则a 的个数是 ．【答案】 1 ；4； 【解析】()()()311;ff f =-=令()f a t =，即满足()f t t =，①t=1，即a=±1时，经检验，均满足题意；②t <1，即 −1 <a <1 或 a >1时，()2f t t =，由2t t =，解得t =0或1（舍去）；再由()0t f a ==解得a = 0或 2 ；③t > 1，即a < − 1时，()2f t t =-，由t= 2−t ，解得 t = 1 （舍去）； 综上所述：共有 4 个 a ．四、解答题：本小题共6小题，共70分．解答应写出应写出文字说明、证明过程或演算步骤．17. （10 分）设 t 为实数，已知向量()()1,2,1,.a b t ==- ⑴ 若 t = 3，求a b +和a b -的值；⑵ 若向量a b +与3a b -所成角为 135° ，求 t 的值． 【答案】⑴a b += 5，5a b -=；⑵ t = 2；【解析】⑴ 当 t = 3时，()1,3b =-,()0,5a b +=,()2,1a b -=- 所以a b += 5，5a b -=；⑵ ()0,2a b t +=+,()34,23a b t -=-,()()3223cos13532a b a b t t a b a b+⋅-+-===-+⋅-+, 平方化简得：23440t t --=，解得1222,.3t t ==-经检验，当23t =-时，夹角为 45° 舍去，故 t = 2． 18. （12 分）设实数 x 满足 sinx+ cos x= c ，其中 c 为常数． ⑴ 当c =时，求44sin cos x x +的数值；⑵ 求值：()33443cos cos 2sin cos x x x xππ⎛⎫+++ ⎪⎝⎭-（用含 c 的式子表示）．【答案】⑴12;⑵212c c +;【解析】⑴1+ 2sinx cosx = 2，所以sinx cosx=12; ()24422221sin cos sin cos 2sin cos 2x x x x x x +=+-=; （2）()()()33334422223cos cos sin cos 1sin cos 2sin cos sin cos sin cos sin cos x x x x x x x x x x x x x x ππ⎛⎫+++ ⎪-+⎝⎭==-+-+ 由sinx+ cos x= c ，所以平方得：1+ 2sinx cosx = 2c ，sinx cosx =212c -所以原式=221122c c c c++=. 19. （12 分）设 a 为正实数．如图，一个水轮的半径为a m ，水轮圆心 O 距离水面2am ，已知水轮每分钟逆时针转动 5 圈．当水轮上的点 P 从水中浮现时（即图中点0P ）开始计算时间． ⑴ 将点 P 距离水面的高度 h(m )表示为时间 t(s)的函数； ⑵ 点 P 第一次达到最高点需要多少时间．【答案】⑴sin ,0;662a h a t t ππ⎛⎫=-+≥⎪⎝⎭⑵ 4s ；【解析】⑴ 如图，以水轮圆心 O 为原点，与水面平行的直线为 x 轴建立直角坐标系．当t= 0时，点 P的坐标为,2a ⎫-⎪⎪⎝⎭，角度为6π-;根据水轮每分钟逆时针转动 5 圈，可知水轮转动的角速度为6πrad / s,所以 t 时刻，角度为66t ππ-;根据三角函数定义，可得sin ,0;662a h a t t ππ⎛⎫=-+≥⎪⎝⎭⑵ 当32a h =时，sin 166t ππ⎛⎫-= ⎪⎝⎭，所以2662t k ππππ-=+，解得t=4+12k ()k N ∈，所以当k= 0时， t = 4，即第一次达到最高点时需要 4s ．20. （12 分）设向量()11,a x y =,()22,b x y =，其中0a ≠． ⑴ 若//a b ，求证：12210x y x y -= ； ⑵ 若12210x y x y -= ，求证：//a b ．【解析】()11,a x y =,()22,b x y =，其中0a ≠，所以11,x y 不全为 0，不妨设10x ≠; ⑴ 如果//a b ，则存在实数λ，使得b a λ= ，即()()()221111,,,x y x y x y λλλ==,所以2121x x y y λλ=⎧⎨=⎩,则()()122111110x y x y x y x y λλ-=-=⑵ 反之，如果12210x y x y -=，因为10x ≠，所以()()22221222111111,,,,x xx y y x y x y x y x x x ⎛⎫=== ⎪⎝⎭ ， 令21x x λ=，则b a λ=，所以//a b ． 21. （12 分）⑴ 运用函数单调性定义，证明：函数()31f x x x=-在区间 (0,+∞)上是单调减函数； ⑵ 设 a 为实数， 0 <a < 1 ，若 0 <x < y ，试比较33yx a a -和4334x y x y a a ++-的大小，并说明理由．【答案】⑴ 答案见解析；⑵33yx aa -<4334x y x y a a ++-【解析】⑴ 对任意的()12,0,x x ∈+∞，且12x x <，()()()()()222121211212213333121211x x x x x x f x f x x x x x x x x x -++⎛⎫⎛⎫-=---=+- ⎪ ⎪⎝⎭⎝⎭因为210,x x ->22332121120,0x x x x x x ++>>，所以()()120f x f x ->，即()()12f x f x > ，所以函数()f x 在区间 (0,+∞) 上是单调减函数；⑵ 因为 0<a<1，所以()x g x a =在R 上是单调减函数， 因为 0< x< y ，所以 0<3x<3y ， 0< 4x+ 3y<3x+4y ， 所以()()33330yx g y g x aa <⇒-< ，且()()4334g x y g x y +>+⇒43340x yx y a a ++->，所以33yx aa -<4334x y x y a a ++-.22. （12 分） ⑴ 已知函数()()11,1x f x x x R x -=≠-∈+，试判断函数()f x 的单调性，并说明理由； ⑵ 已知函数()()1lg1,1x g x x x R x -=≠±∈+. （i ）判断()g x 的奇偶性，并说明理由；（ii ）求证：对于任意的x ,y ∈R ，且x ≠±1 ，y ≠±1，xy ≠−1都有()()1x y g x g y g xy ⎛⎫++= ⎪+⎝⎭①.⑶ 由⑵可知满足①式的函数是存在的，如()()1lg 1,1x g x x x R x -=≠±∈+．问：满足①的函数是否存在无穷多个？说明理由．【答案】⑴()f x 在(−∞，−1)和(-1,+∞)上单调递增；⑵答案见解析；⑶存在无穷多个； 【解析】⑴ 对任意的()12,,1x x ∈-∞-，且12x x <，则()()()()()12121212122111111x x x x f x f x x x x x ----=-=++++， 因为()()12120,110x x x x -<++>，所以()()120f x f x -<，即()()12f x f x <，所以函数()f x 在区间(−∞，−1)上是单调递增，同理可得()f x 在区间(-1,+∞)上单调递增； ⑵（i ）()g x 的定义域为()()(),11,11,-∞--+∞，对任意的()()(),11,11,x ∈-∞--+∞，有()()(),11,11,x -∈-∞--+∞，且()()1111lg lg lg lg101111x x x x g x g x x x x x ⎛⎫------+-=+=⋅== ⎪+-++-+⎝⎭， 所以()g x 为奇函数，又()()22g g ≠-，所以()g x 不是偶函数；（ii ）对于任意的x,y ∈R ，且x ≠±1 ，y ≠±1，xy ≠−1， 因为()()111111lglg lg lg111111x y x y x y g x g y x y x y x y ⎛⎫------+=+=⋅=⋅ ⎪++++++⎝⎭， 所以111lg lg lg 1111x yx y x y xy xy g x y xy x y xy xy+-⎛⎫++--+=== ⎪+++++⎝⎭++()()1111x y g x g y x y --⋅=+++； ⑶ 设()lg k g x k =⋅11x x -+()k g x =⋅，则对于任意的x, y ∈R ，且x ≠±1 ，y ≠±1，xy ≠−1，都有即()k g x 满足①，因为 k 有无穷多个，所以这样的()k g x 也有无穷多个．。

2019-2020学年南京师范大学附属中学新城高级中学高三英语第一次联考试卷及参考答案

2019-2020学年南京师范大学附属中学新城高级中学高三英语第一次联考试卷及参考答案

2019-2020学年南京师范大学附属中学新城高级中学高三英语第一次联考试卷及参考答案第一部分阅读（共两节，满分40分）第一节（共15小题；每小题2分，满分30分）阅读下列短文，从每题所给的A、B、C、D四个选项中选出最佳选项AIn the 1994 filmForrest Gump, there’s a famous saying, “Life is like a box of chocolates; you never know what you’re gonna get.” The surprise is part of the fun. Now blind box toys are bringing the magic of surprise to online shopping.A blind box toy is hidden inside uniform packaging but invisible from the outside. You don’t know what will be inside, although the toys typically come from pop culture, ranging from movies to comics and cartoons.Blind boxes have caught on since they were first introduced fromJapantoChinain 2014. According to a 2019 Tmall report, the mini-series of Labubu blind box, designed byHong Kong-born Kasing Lung, was named Champion of Unit Sales with 55,000 sold in just 9 seconds during the Singles Day shopping event. Most customers for blind boxes are young people aged 18 to 35.According to The Paper, blind box toys are popular in part because of their cute appearances. The typically cute cartoon figurines come in miniature sizes, making them suitable for display almost anywhere.Even if blind boxes are not their top choice for decorations, the mystery and uncertainty of the process also attracts people. It’s the main reason why people buy blind boxes one after another.“Fear of the unknown is always a part of the box-opening process,” said Miss Cao, 24, who lives and works inShenyang. Speaking to Sina News, she said: “Until you open all the boxes, you cannot know what it is inside.”Opening a blind box is a delightful little surprise for our mundane daily lives, something small but fun to wait for each day, week or month. When people open this simple little box, they may be disappointed, but the uncertainty is part of the fun. People will open more blind boxes and hope for a better outcome.When someone re-makesForrest Gump, don't be surprised if he says, “Life is like a blind box...”1. Why is the famous saying in the filmForrest Gumpquoted at the beginning?A. To arouse the readers’ interest.B. To present the writer’s view.C. To introduce the topic.D. To highlight the fun of blind boxes.2. Which of the following is the main feature that makes blind box so popular?A. Miniature sizes.B. Cute appearances.C. Fear of the unknown.D. Mystery and uncertainty.3. What can we learn from the passage?A. Blind box became popular in 2019 after being first introduced fromJapantoChina.B. Blind box toys typically originated in pop culture, varying from movies to cartoons.C. Blind box toys was designed and named by Hong Kong-born Kasing Lung.D. When people open this simple little box, they will feel disappointed.BMasks that helped save lives during the Covid-19 pandemic（疫情）are proving a deadly risk for wildlife, with birds and sea creatures trapped in many facial coverings in animal habitats.Single-use masks have been found on the ground, waterways and beaches worldwide since countries required（heir use in public places to slow the pandemic's spread. Worn once, the thin protective materials can take hundreds of years to break down. "Face masks aren't going away any time soon-but when we throw them away, these items can harm the environment and the animals who share our planet," Ashley from anima! rights group PETA said.Monkeys have been found playing with used masks in the hills outsideMalaysia's capitalKuala Lumpur. And in an incident inBritain, a seagull was saved inChelmsfordafter its legs got caught in an abandoned mask for a week.However, the biggest influence is in the water. More than 1.5 billion masks made their way into the world's oceans last year, accounting for around 6200 extra tons of ocean plastic pollution, according to environmental group OceansAsia. “Masks and gloves are particularlyproblematicfor sea creatures," says George Leonard, chief scientist from NGO. "When those plastics break down in the environment, they form smaller and smaller particles （颗粒）.Those particles then enter the food chain and influence the entire ecosystem,“ he added.Campaigners have urged people to deal with masks properly after using them. OceansAsia has also called on governments to increase punishment for littering and encourage the use of washable masks.4. What bring（s）a great danger to wildlife now?A. Waste masks.B. Covid-19.C. Polluted water.D. Damaged habitats.5. What does the underlined word “problematic”in paragraph 4 mean?A. Important.B. Attractive.C. Common.D. Troubling.6. What can we infer from the text?A. Monkeys learned to wear masks from humans.B. Plastics are less harmful after becoming particles.C. Used masks have a worse effect on sea creatures.D. Waste masks arc the main ocean plastic pollution.7. How should we solve the problem from the last paragraph?A. Keep masks after they' re used.B. Call on governments to stop littering.C. Punish those who wear single-use masks.D. Put used masks in the recycling box.CItzhak Perlman was born in Tel Aviv, in whatwas thenPalestine, in 1945. Today he lives inNew York City. But his music has made him a citizen of the world. He has played in almost every major city. He has won many Grammy awards for his recordings. He has also won Emmy Awards for his work on television.Itzhak Perlman suffered from polio (小儿麻痹症) at the age of four. The disease damaged his legs. He uses a wheelchair or walks with the aid of crutches (拐杖) on his arms. But none of this stopped him from playing the violin. He began as a young child. He took his first lessons at the Music Academy of Tel Aviv. Very quickly, his teachers recognized that he had a special gift.At thirteen he went to the United Sates to appear on television. His playing earned him the financial aid to attend theJuilliardSchoolinNew York. In 1964 Itzhak Perlman won the Leventritt Competition in that city. His international fame had begun.His music is full of power and strength. It can be sad or joyful, loud or soft. But critics (评论家) say it is not the music alone that makes his playing so special. They say he is able to communicate the joy he feels in playing, and the emotions that great music can deliver.Anyone who has attended a performance by Itzhak Perlman will tell you thatit is exciting to watch him play. His face changes as the music from his violin changes. He looks sad when the music seems sad. He smiles and closes his eyes when the music is light and happy. He often looks dark and threatening when the music seems dark and threatening.8. According to the passage, what do we know about Itzhak Perlman?A. He is 75 years old today.B. He was born inNew York City.C. He has some achievements in music.D. He was a rich citizen of the world.9. When Itzhak Perlman first learned music, his teachers ________.A. ignored his talentsB. thought he was fit to learn musicC. had pity on himD. didn't want to accept him10. What makes Itzhak Perlman's playing special according to critics?A. The emotions he communicates in his playing.B. The style in which he plays his music.C. The kind of music he plays.D. The power and strength in his music.11. How do people feel when they hear Itzhak Perlman play?A. Moved.B. Calm.C. Funny.D. Excited.DWhen you walk with a backpack, do you know how the things inside move from side to side? Now scientists havefigured out how to tap into that movement to produce electricity.Picture a pendulum (摆锤) fixed to a backpack frame and stabilized with springs on either side. The pack’s weight is attached to the pendulum, so the pendulum swings side to side as you walk.Then a machine is driven by that swinging movement, and spits out electrical current to charge a battery.Volunteers carried the pack while walking on a running machine and wore masks to measure the flow of O2and CO2. Walking with the slightly swinging 20-pound load, the device (设备) did not significantly affect the volunteers’ metabolic (新陈代谢的) rate compared to when they carried the same weight fixed in place. In fact, the energy-harvesting pack reduced the forces of acceleration they’d feel in a regular pack, which might mean greater comfort for a long hike. And the device did produce a steady trickle (涓流) of electricity. If you up the load to 45 pounds, the swing of the pack could fully charge a smart phone only after 12 hours. The details are in the journal Royal Society Open Science.The device produces electricity from human movement and has been identified as a workable solution to providing a renewable energy source for portable electronic devices. It is particularly useful for those who work in remote areas, as these people often carry a lot of weight in a backpack for their exploration.But here’s a realconundrum: the energy-harvesting device currently weighs five pounds. The researchers saythat’s about four pounds too many to be a smart alternative to batteries. So they hope that more research lets them lighten the load, to ensure the pack charges you up without weighing you down.12. What does Paragraph 2 mainly talk about?A. How the device works.B. What the device looks like.C. Who the device is designed for.D. Why scientists designed the device.13. Which of the following describes the device?A. It greatly affected the volunteers metabolic rate.B. It harvested energy as the volunteers walk.C. It failed to produce steady electricity.D. It was useless for a long walk.14. What does the underlined word “conundrum” in the last paragraph mean?A. Problem.B. Method.C. Bond.D. Decision.15. What will the researchers try to do next?A. Increase the charging speed of their device.B. Find smarter alternatives to batteries.C. Reduce the weight of their device.D. Put their device on the market.第二节（共5小题；每小题2分，满分10分）阅读下面短文，从短文后的选项中选出可以填入空白处的最佳选项。

江苏省南京南师附中新城中学2019_2020学年七年级上学期期末数学试卷

江苏省南京南师附中新城中学2019_2020学年七年级上学期期末数学试卷

2019~2020学年江苏南京建邺区南京师范⼤学附属中学新城初级中学初⼀上学期期末数学试卷⼀、选择题（本⼤题共6⼩题，每⼩题2分，共12分。

在每⼩题所给出的四个选项中，恰好有⼀项是符合题⽬要求的）1.A.B.C.D.下列各式中，结果为正数的是（ ）．2.A.的次数是B.与是同类项C.不是单项式D.的系数是下列说法正确的是（ ）．3.A. B. C. D.将如图所示的绕直⻆边旋转⼀周，所得⼏何体的主视图是（ ）．4.A.B.C.D.若直线外⼀点与直线上四点的连线段⻓分别为，，，，则点到直线的距离最接近（ ）．5.有理数在数轴上的位置如图所示，下列各数中，可能在到之间的是（ ）．6.找出以下图形变化的规律，则第个图形中⿊⾊正⽅形的数量是（ ）．A. B. C. D.⼆、填空题（本⼤题共10⼩题，每⼩题2分，共20分）7.⽐较⼤⼩： （选填“”、“”、“”）．8.地球与太阳的平均距离⼤约为，将⽤科学记数法表示为 ．9.已知关于的⽅程的解是，则的值为 ．10.若，则 ．11.若，则的余⻆的度数是 ．12.某种商品的进价为元，出售标价为元，后来由于该商品积压，商店准备打折销售，但要保证利润率不低于，则商店最低可打 折．13.观察下⾯的单项式：，，，，…根据你发现的规律，第个式⼦是 ．14.在时钟上，当分时，时针与分针的夹⻆度数为 ．15.如图，将⼀张⻓⽅形纸条折叠，若，则的度数为 ．16.如图，⻓⽅形中，，，为的中点，动点从点出发，以每秒的速度沿运动，最终到达点．若点运动的时间为秒，则当时，的⾯积等于．三、解答题（本⼤题共10⼩题，共68分）17.（1）（2）计算：．．18.（1）（2）解⽅程．．．19.先化简，再求值：，其中，．20.（1）（2）（3）如图，每个⼩⽅格都是边⻓为个单位的⼩正⽅形，，，三点都是格点（每个⼩⽅格的顶点叫格点）．找出格点，并且满⾜线段所在直线与线段所在直线互相垂直．计算格点的⾯积为 ．标明格点，使得与⾯积相等．21.把⼀些图书分给某班学⽣阅读，如果每⼈分本，则剩余本；如果每⼈分本，则还缺本，请⽤⽅程的知识求出这个班级有多少学⽣．22.已知线段，点在直线上，线段，分别为线段和的中点，请画出示意图，求线段的⻓．23.（1）（2）如图，直线、相交于点，已知，把分成两个⻆，且．求的度数．若平分，问：是的⻆平分线吗？试说明理由．24.（1）（2）（3）在桌⾯上，有个完全相同的⼩正⽅体堆成的⼀个⼏何体，如图所示．左视图俯视图请画出这个⼏何体的左视图和俯视图．若将此⼏何体的表⾯喷上红漆（放在桌⾯上的⼀⾯不喷），则三个⾯是红⾊的⼩正⽅体有 个．若现在你的⼿头上还有⼀些相同的⼩正⽅体可添放在⼏何体上，要保持主视图和左视图不变，则最多可以添加 个⼩正⽅体．25.（1）某物流公司的甲、⼄两辆货⻋分别从相距千⽶的、两地同时出发相向⽽⾏，并以各⾃的速度匀速⾏驶，两⻋⾏驶⼩时时甲⻋先到达配货站地，此时两⻋相距千⽶，甲⻋在地⽤⼩时配货，然后按原速度开往地；两⻋⾏驶⼩时时⼄⻋也经过地，未停留继续开往地．（友情提醒：画出线段图帮助分析）甲⻋的速度是 千⽶⼩时，⼄⻋的速度是 千⽶⼩时，、两地的距离是 千⽶，、两地的距离是 千⽶．（2）这⼀天，⼄⻋出发多⻓时间，两⻋相距千⽶？26.（1）（2）（3）（4）（5）在数学的学习过程中，我们要不断地归纳，思考和迁移，这样才能提⾼我们解决问题的能⼒：规律发现：在学完《数轴》这节课后，⼩明的作业有⼏道⼩题，请你帮他把余下的空完成．点表示的数是，点表示的数是，则线段的中点表示的数为 ．点表示的数是，点表示的数是，则线段的中点表示的数为 ．发现：点表示的数是，点表示的数是，则线段的中点表示的数为 ．直接运⽤：将数轴按如图所示从某⼀点开始折出⼀个等边三⻆形，设点表示的数为，点表示的数为，点表示的数为，则的值为 ，若将从图中位置向右滚动，则数字对应的点将与的顶点 重合．类⽐迁移：如图，，，，若射线绕点每秒的速度顺时针旋转，射线绕点每秒的速度顺时针旋转，射线以每秒的速度逆时针旋转，三线同时旋转，当⼀条射线与射线重合时，三条射线同时停⽌运动，问：运动⼏秒时，其中⼀条射线是另外两条射线夹⻆的平分线？图（）图（）参考答案一、选择题1.B2.B3.D4.A5.C6.D二、填空题7.<8.1.5×109.-510.-211.57°34′12.713.-128a814.105°15.5616.10/3或6三、解答题17.（1）-2（2）518.（1）x=-4/3（2）x=-319.-1120.（1）（2）4.5（3）21.4522.4cm或2cm23.（1）30°（2）是24.（1）（2）2（3）425.（1）120；60；120；180（2）x=5/6或19/626.（1）4（2）6（3）（a+b）/2（4）-3；B（5）t=3/2或15/7或12/5。

【20套试卷合集】江苏省南京市新城中学2019-2020学年物理九上期中模拟试卷含答案

【20套试卷合集】江苏省南京市新城中学2019-2020学年物理九上期中模拟试卷含答案

2019-2020学年九上物理期中模拟试卷含答案本试卷分第I卷（选择题）和第II（非选择题）两部分．共五大题33小题，满分100分．考试用时100分钟．注意事项：1．答题前，考生务必将姓名、考点名称、考场号、座位号、考试号填涂在答题卷相应的位置上．2．答题必须用0.5mm黑色墨水签字笔写在答题卷指定的位置上，不在答题区域内的答案一律无效，不得用其它笔答题．3．考生答题必须在答题卷上，答在试卷和草稿纸上一律无效，第I卷（选择题，共24分）一、选择题（每小题只有一个选项符合题意．每小题2分，共24分）1．“给我一个支点和一根足够长的棍，我就能撬起整个地球．”下列生产和生活中的杠杆与阿基米德设想的杠杆属于同一类型的是2．如果你将掉落在地面的物理课本捡起来放在课桌上，你对课本所做的功最接近于A．0.02J B．0.2J C．2J D．20J3．下列说法正确的是A．功率越大的机械做功越快B．功率越大的机械做功越多C．机械效率越高的机械做功越快D．机械效率越高的机械做功越多4．一物体沿固定的粗糙斜面匀速下滑，物体在下滑的过程中A．动能不变，势能减小，机械能不变 B．动能不变，势能减小．机械能减小C．动能增大，势能减小，机械能不变D．动能增大，势能减小，机械能减小5．一桶汽油用去一半后，剩下的汽油的：A．比热容和热值均不变B．比热容不变，热值为原来的1/2C．比热容和热值都变为原来的1/2 D．比热容为原来的1/2，热值不变6．关于温度、热量和内能，下列说法正确的是A．温度高的物体内能一定大，温度低的物体内能一定小B．物体的内能与温度有关，只要温度不变，物体的内能就一定不变C．内能小的物体也可能将热量传递给内能大的物体D．物体的温度越高，所含热量越多7．如图所示的四种情景中，人对物体做功的是：8．一个滑轮组经改装后提高了机械效率，用它把同一物体匀速提升同样的高度，改进后与改进前相比较A．总功减少，额外功增多B．机械做功加快C．功率变大，机械做功更多D．有用功不变，总功减少9．用两个相同的加热器给质量相同的物质甲和水加热，它们的温度随加热时间的变化关系如图所示，据此判断物质甲的比热容为A．4.2×103J／(kg．℃)B．2.1×103J／(kg．℃)C．1.2×103J／(kg．℃)D．条件不足，不能确定10．保密室有两道门，只有当两道门都关上时（关上一道门相当于闭合一个开关），值班室内的指示灯才会发光，表明门都关上了，下图中符合要求的电路是11．如图所示，杠杆AOB用细绳悬挂起来，当A端挂重物G1，B端挂重物G2时，杠杆平衡，此时OA恰好处于水平位置(AO＝BO，杠杆重力不计)．则A．G1＝G2B．G1>G2C．G1<G2D．无法确定12．如图所示的电路中，当开关闭合时，灯L1、L2均不亮，某同学用一根导线去查找电路的故障．他先将导线接在灯L 1两端，发现灯L2亮，灯L1不亮；再将导线接在灯L2两端，发现两灯均不亮，由此可以判断A．灯L1断路B．灯L1短路C．灯L2断路D．灯L2短路第II卷（非选择题，共76分）二、填空题（每空1分，共24分）13．下列物体：①挂在屋顶上的电灯；②被拉开的弹簧门；③空中飞行的小鸟；④在地面冰场上滑行的运动员；⑤正从斜坡上滚下的石头；⑥在平直公路上行驶的汽车，其中只具有动能的是▲，只具有势能的是▲，既具有动能又具有势能的是▲．14．皮划艇是奥运会的竞赛项目之一，已知比赛中皮划艇船桨的阻力臂是动力臂的3倍，则船桨是▲杠杆；若运动员在划船时对船桨施加的力是360N，则船桨受到水的作用力至少是▲N．15．如图用甲、乙两个不同的滑轮把同一货物提到相同高度，若不计绳重和摩擦，且G动<G物，则使用▲滑轮能够省力，使用▲滑轮机械效率较高．若用乙图匀速提升重为180N的物体，所用拉力为120N，物体升高2m．此过程中，不计绳重和摩擦，动滑轮的机械效率为▲，动滑轮重▲N．16．马用200N的力拉着重为1500N的车子，在水平路面上匀速前进了100m，拉力对车做功▲J，重力对车做的功为▲J．17．中央气象台每天都会发布全国主要城市的大气预报，右表列出的是沿海城市上海和内地城市西安的气温情况，请根据两座城市气温变化情况判断城市名称，甲是▲，你做出如此判断的依据是▲．18．在市政建设中，经常看到工人用切割机切割水泥路面，在切割机工作时需不断地对锯片浇水，否则锯片会很快损坏，这是由于锯片在切割路面时不断做功，使锯片的内能▲，温度升高，对锯片浇水，是通过▲的方式让锯片的内能减少，温度降低．19．质量均为1kg的铜块[C铜＝3.9×102J／(kg．℃)]和铅块[C铅＝1.3×102J／（kg．℃）]，如吸收了相等的热量，则铜块与铅块升高的温度之比为▲；若铜块温度升高了100℃，则它吸收了▲J的热．20．如图所示电路，要使灯L、L2组成串联电路，应闭合开关▲；要使L1、L2组成并联电路应闭合开关▲，同时闭合▲是绝对不允许的．21．一些家用电器的内部结构中常常装有控制开关，这些开关一般与相应的用电器▲联．还有一些家用电器内部又分成好几个不同的工作部分，如双桶洗衣机分洗涤侧和脱水侧，分别由两个电动机来工作，根据你的经验，这两个电动机应该是▲联的；如图所示，是家用电冰箱及其部分电路图．冰箱压缩机由温控开关自动控制，冷藏室照明灯由冰箱门联动开关控制．冰箱门关闭后，联动开关应该处于▲状态，当冰箱里的温度升高到一定程度时，温控开关会自动▲（选填“断开”或“闭合”）三、作图与实验题（第22题每小题2分，第23题6分，第24、25题各5分，第26题3分，第27题7分，共32分）22．按照题目要求作图：(1)如下图所示，用螺丝刀撬起图钉．请在图上画出螺丝刀受到图钉阻力F2的力臂；并画出作用在螺丝刀柄上A点的最小动力F1的示意图．(2)上图中，站在地面上的同学借助滑轮组匀速提升重物，请画出合适的绕线方法．(3)下图是某手电筒的剖面图，请按实物剖面图，在虚线框中画出这种手电筒的电路图．23．在“探究杠杆平衡条件”的实验中，先把杠杆的中点支在支架上，杠杆停在如图甲所示的位置，此时杠杆处于▲_（选填“平衡”或“不平衡”）状态．为了使杠杆在水平位置平衡，可以将右端的平衡螺母向右调节，也可以将左端的平衡螺母向▲调节．（选填“左”或“右”）(1)在杠杆上挂2N的重物，如图乙所示，杠杆静止时弹簧秤的示数为▲N，将所挂的重物往左移1格，杠杆重新平衡后，弹簧秤的示数会▲（填“变大”、“变小”或“不变”)．(2)某同学进行正确的实验操作后，得到的数据为F1＝6N、L1＝20cm、F2＝4N和L2＝30cm．该同学根据这些数据就得出了杠杆平衡条件为：F1L1＝F2L2，请你对该同学的做法进行评价：▲．(3)使杠杆在倾斜的位置做实验，也能得出杠杆平衡条件．这种实验方案与杠杆在水平位置做实验的方案相比较，我们选则在水平位置做实验，理由是▲．24．学习了机械效率知识后，全班同学对“斜面的机械效率跟什么因素有关”这一课题提出了一些值得探究的猜想：A．跟斜面的倾斜程度有关；B．跟斜面的粗糙程度有关；C．跟斜面的长度有关；D．跟物体的重力有关．小刚同学为了证实其中的部分猜想是否正确，设计方案并进行了探究，每次都匀速将物体从斜面底部拉到了斜面顶部，下表记录了他的探究过程和数据．(1)通过对比实验①②数据，可初步验证猜想▲（填写字母）．(2)通过对比实验①③数据，可以初步得出的探究结论是：当其它条件一时，▲．(3)若要验证猜想D，应控制斜面的长、斜面的倾斜程度和▲不改变．(4)小刚同学根据实验数据分析得出：沿同一斜面向上匀速拉动同一物体时，斜面倾角越▲，拉力越小．(5)如果你是一位建筑设计师，需要设计一幢老年人俱乐部的大楼，受上述实验的启发，在设计楼梯时，你会把楼梯设计得较▲（填“缓”或“陡”）．25．为了比较水和沙子吸热本领的大小，小明做了如图所示的实验：在2个相同的烧杯中分别装有质量、初温都相同的水和沙子，用两个相同的酒精灯对其加热，实验数据记录如下表：(1)在此实验中，用加热时间的长短来表示水和沙子▲．(2)在实验中，应不停地用搅拌棒搅动水和沙子，其目的是：▲．(3)分析表中的实验数据可知；质量相同的水和沙子，升高相同的温度，水吸收的热量▲（选填“大于”或“小于”）沙子吸收的热量．(4)可以推想，如果给质量相同的水和沙子加热相同的时间，则▲（选填“沙子”或“水”）升高的温度会更高些．(5)实验中，有些同学发现：刚开始加热时，情况与(4)的结论不符，你认为可能的原因是▲．（写出一点）26．如右图所示，把两个小灯泡串联接入电路研究串联电路特点．(1)开关闭合并且两灯都发光时，取下其中一个灯，可观察到▲现象；(2)在串联的两个小灯电路中再串联一个小灯，闭合开关后可观察到▲现象；(3)以上两个现象都说明了串联电路中▲这一特点．27．小芳想验证重力势能与高度的关系：她在水平地面上铺一张纸，将篮球表面涂黑，使篮球分别从不同高度处自由下落，在纸上留下黑色圆斑A、B，如图所示．球从较高处下落形成的圆斑是图中▲（选填“A”或“B”），判断的依据▲，同时发现，每次篮球落地后反弹的高度也不相同．针对这个问题大家进行了讨论，并提出了不同的猜想．猜想1：篮球反弹的高度可能与球的型号有关；猜想2：篮球反弹的高度可能与下落的高度有关；猜想3：篮球反弹的高度可能与地面材料有关，于是，他们用两只充足气的#7(标准男子)、#6(标准女子)篮球及刻度尺，在水泥地面和木制地板上进行了实验，得到的实验数据如下表：(1)要验证猜想2，需要选用实验序号为▲、▲的两组数据进行分析．(2)通过实验，可得到的结论是：篮球反弹的高度与▲、▲一有关，与▲无关．四、计算题（第28题6分，第29题8分，第30题6分，共20分）28．一列质量为1×103t的火车，以180km/h的速度在平直轨道上匀速行驶，整列火车受到的阻力是9×103N．则(1)火车的牵引力多大？(2)火车行驶1min时间内，机车牵引力做了多少功？(3)牵引力的功率多大？29．某工人用如右图所示的动滑轮将重物匀速提升2m，已知动滑轮重为10N(不计绳重和摩擦)．若拉力所做的功为196 J，求此过程中：(1)工人所做的额外功为多少焦耳？(2)有用功为多少？(3)重物的重力为多少？(4)机械效率是多少？30．某锅炉将水从25℃加热到100℃消耗了6kg无烟煤，已知水的比热容是4.2×103J/(kg．℃)，无烟煤的热值是3.4×107J/kg．求：(1)锅炉内200kg水吸收的热量是多少？(2)完全燃烧6kg无烟煤放出的热量是多少？(3)烧水过程中，锅炉的效率是多少？2019-2020学年九上物理期中模拟试卷含答案一单项选择题（本大题共10小题，每小题3分，共30分）每小题给出的四个选项中，只有一个最符合题意，请将正确答案的序号填写在表格中.1.5月31日是“世界无烟日”，吸烟有损自己和他人的健康，据世卫组织统计，每年因吸烟导致近600万人失去生命，造成他人吸二手烟是由于（）A.烟分子间存在着引力B.烟分子间有空隙C.烟分子在不停地做无规则运动D.烟分子间存在着斥力2.如图所示，取两个相同的验电器A和B,A带负电，B不带电，用带绝缘手柄的金属棒把A和B连接起来，下列说法正确的是（）A.B中正电荷通过金属棒流向A,A金属箔的张角减小B.A中自由电子通过金属棒流向B,B金属箔的张力增大C.A中负电荷通过金属棒流向B,同时B中正电荷通过金属棒流向AD.金属棒中瞬间电流的方向从A流向B,B金属箔的张角增大3.下列有关电阻的说法正确的是（）A.导体的电阻越大，表面道题的导电能力越强，流过的电流越小B.导体的电阻与导体两端的电压成正比与流过的电流成反比C.导体中的电流为零时电阻也为零D.导体的电阻式导体本身的乙种性质，与导体的材料、长度和横截面积等因素有关4.关于物理的内能，下列说法正确的是（）A.在相同物态下，同一物体温度降低，它的内能会减少B.物理内能增加，一定要从外界吸收热量C.温度为0℃的物理没有内能D.温度相等的1kg水和100g水内能相同5.如图所示电路，开关闭合时观察到：L1和L2亮灯均不亮，电流表无示数，电压表有示数，其原因可能是（）A.L1断路B.L2断路C.电流表断路D.电流表短路6.如图所示，用丝线悬挂着A、B、C、D、E、F六个小球，它们之间相互作用的情况如图甲、乙、丙、丁所示，则肯定带电的小球是（）A.A、C小球B.A、D小球C.A、B小球D.E、F小球7.如图所示，与实物一致的电路图是（）8.如图所示的电路，下列判断正确的是（）A.闭合开关S1、S3，断开开关S2时，灯L1、L2串联B.闭合开关S2，断开开关S1、S3时，灯L1、L2并联C.闭合开关S1、S2，断开开关S3时，灯L1亮、L2不亮D.同时闭合开关S1、S2、S3时，电源短路9.在图所示的电路中，闭合开关S后，要使滑动变阻器的滑片P向右移动时，电流表顶点示数减小，则M、N与滑动变阻器连接的是（）A.M接C N接DB.M接A N接BC.M接C N接BD.M接A N接D10.用两个相同的电热器给质量相同的物质甲和谁加热，它们的温度随加热时间的变化关系如果所示，据此判断物质甲的比热容为（）A.2.1×103J/(kg∙℃)B.4.2×103J/(kg∙℃)C.1.2×103J/(kg∙℃)D.条件不足，不能确定二不定项选择题（本大题共3小题，每小题3分，共9分）在给出的四个选项中，均有多个符合题意，全部选对的得3分，选对但不全的得1分，不选或选错的得0分.11.下列现象中，能用分子动理论解释的是（）A.走进花园闻到花香B.放入水中的糖使水变甜C.看到烟雾在空中弥漫D.水和酒精混合总体积变小12.小明根据下表提供的几种物质的比热容得出以下四个结论，其中正确的是（）A.液体的比热容一定比固体的大B.同一物质发生物态变化后，比热容不变C.汽车发动机用水来冷却是因为水的比热容较大D.质量相等的铝块和铜块，升高相同的温度，铝块吸收的热量多13.小敏在爷爷的卧室设计了一个如图的“聪明”电路，方便爷爷，“光控开关”在光弱（晚上）时自动闭合，光强（白天）时自动断开；“声控开关”在有声时自动闭合，两分钟后自动断开，表中开关使用情况，符合电路设计工作要求的是（）A.AB.BC.CD.D三填空题（共6小题，每小题4分，共24分）14.在下面的两句话中，“热”字的含义各指的是什么？（填“温度”、“热量”或“内能”）(1)摩擦生热，这里的“热”是指；(2)物体吸热升温，这里的“热”是指 .15.在我国，家庭电路的电压是 V.有一串节日小彩灯是50只小灯泡串联组成，若测出通过第一只小灯泡的电流是100mA,则通过第5值小灯泡的电路是 A.16.如图所示是电吹风的简化电路图，A是风扇是电动机，B是电热丝，要吹热风应闭合开关 .一台内燃机运行时各种能量损耗大致为：气缸散热损失占25%，废气带走的能力占30%，摩擦等机械损耗占10%，则它的机械效率为 .17.在如图所示的四幅图中，甲、乙时两个演示实验示意图；丙、丁是四冲程汽油机工作过程中的两个冲程示意图，与丙冲程原理相同的是图所示的演示实验；实验与丁冲程原理相同.18.一柴油机的转速是3000r/min，它1秒钟对外做功次；钻木能取火，说明可以改变物体的内能。

【精选5份试卷合集】江苏省南京市南师附中集团新城中学2019年英语八年级上学期期中模拟试卷

【精选5份试卷合集】江苏省南京市南师附中集团新城中学2019年英语八年级上学期期中模拟试卷

2019-2020学年八上语文期中模拟试卷含答案注意事项：1. 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、积累运用与传统文化（共28分）1、根据拼音写出汉字，给加点的字注音（2分）匆忙奔．赴南方的雁阵呼唤你怀抱中的鸟儿，金色的风拖曳着清凉的尾巴，拂过你斑驳的衣襟，你就知道，那朔风凌厉的季节正在逼近，可你只是淡然一笑——你全身心的爱，又一轮结出满树丰硕的梦想；你以宁折勿曲的坚韧，再度 hàn 卫了人格的尊严。

（1）奔（2） hàn2、依次填入下列各句横线上的词语，最恰当的一组是( ) （2分）(1)傍晚时候，上灯了，一点点黄晕的光，______出一片安静而和平的夜。

(2)我一直______于科学世界的优美之中，我所热爱的科学也不断增加它崭新的远景。

(3)云，能够帮助我们______阴晴风雨，预知天气变化。

(4)你把我的______引向远古，描绘出一幅幅生物进化的图画。

A.烘托沉迷识别思念 B．衬托沉醉辨别思绪C.烘托沉醉识别思绪 D．衬托沉迷辨别思念3、下列加点成语使用完全正确的一项是 ( ) (2分)A．随着最后一个隧洞竣工剪彩，这条南北交通大动脉豁然开朗．．．．。

B．为了在科技比赛中体现创新精神，许多同学处心积虑．．．．，设计了各种造型的航空模型。

C．对于叔叔回国这桩十拿九稳．．．．的事，大家还拟定了上千种计划，甚至计划到要用这位叔叔的钱置一所别墅。

D．《敬业与乐业》是把《礼记》里头“敬业乐群”和《老子》里头“安其居，乐其业”那两句话，无．中生有．．．造出来的。

【20套试卷合集】江苏省南京市南师附中集团新城中学2019-2020学年数学七上期中模拟试卷含答案

【20套试卷合集】江苏省南京市南师附中集团新城中学2019-2020学年数学七上期中模拟试卷含答案

2019-2020学年七上数学期中模拟试卷含答案一、精心选一选（本大题共10个小题，每小题3分，共30分） 1. ﹣2的相反数是（ ）A ．﹣2B ．0C ．2D ．42. 下列各组中的两个项不属于．．．同类项的是（ ） A ．3x 2y 和﹣2x 2y B ．﹣xy 和2yx C ．23和32 D ．a 2b 和ab 23. 下列判断错误．．的是（ ） A ．若a=b ，则a-3=b-3 B ．若a=b ，则33-=-ba C ．若ax=bx ，则a=b D ．若x=2，则x 2=2x4. 今年是蒙城六中建校20周年，从六中走出的学子大约有43000人，将43000用科学记数法表示为（ ） A ．43×103 B ．4.3×104 C ．4.3×103 D ．0.43×1055. 若2（a+3）的值与4互为相反数，则a 的值为（ ） A ．﹣1 B ．﹣27 C ．﹣5 D ．21 6. 当1＜a ＜2时，代数式|a ﹣2|+|1﹣a|的值是（ ） A ．﹣1 B ．1 C ．3 D ．﹣37. 已知x ﹣2y=3，那么代数式3﹣2x+4y 的值是（ ） A ．﹣3 B ．0 C ．6 D ．98. 超市店庆促销，某种书包原价每个x 元，第一次降价打“八折”，第二次降价每个又减10元，经两次降价后售价为90元，则得到方程（ ）A ．0.8x ﹣10=90B ．0.08x ﹣10=90C ．90﹣0.8x=10D ．x ﹣0.8x ﹣10=90 9. 点A ，B 在数轴上的位置如图所示，其对应的数分别是a 和b.对于以下结论：甲：b-a<0； 乙：a+b>0； 丙：|a|<|b|； 丁：0ba>. 其中正确的是（ ）A ．甲乙B ．丙丁C ．甲丙D ．乙丁10. 下列图形都是由同样大小的棋子按一定的规律组成，其中第①个图形有1颗棋子，第②个图形一共有6颗棋子，第③个图形一共有16颗棋子，……，则第⑥个图形中棋子的颗数为（ ） A ．51 B ．70 C ．76 D ．81二、细心填一填（本大题共10个小题，每小题3分，共30分） 11. 单项式42ba π-的次数是_________.12. 在-（-8），（-1）2007，-22，-|-1|，-|0|，-3π，-2.113中，负有理数有_________． 13. 计算：﹣3+2=_________.14. 小红要购买珠子串成一条手链，黑色珠子每个a 元，白色珠子每个b 元，要串成如图所示的手链，小红购买珠子应该花费_________元.15. 当a ＝_________时，关于x 的方程x －24－2x ＋a6＝1的解是2.16. 如果13x a+2y 3与-3x 3y 21b -是同类项，那么|3a-2b|的值是_________． 17. 若多项式221231002x kxy y xy x --+--中不含xy 项，则k =_________．18. 若关于x 的方程032=+--m mx m 是一元一次方程，则这个方程的解x=_________．19. 为了改善办学条件，学校购置了笔记本电脑和台式电脑共100台，已知笔记本电脑的台数比台式电脑的台数的14还少5台，则购置的笔记本电脑有_________台． 20. 设[x)表示大于x 的最小整数，如[3)=4，[－1.2)=－1，则下列结论中正确的是_________．(填写所有．．正确结论的序号)① [0) = 0； ②[x) －x 的最小值是0；③[x) －x 的最大值是0； ④存在实数x ，使[x) －x = 0.5成立． 三、认真做一做（共60分） 21. 计算（每小题4分，共8分） （1）()()583.7 1.71313⎛⎫-+++-- ⎪⎝⎭（2）-32×（-2）+42÷（-2）3-5÷21×222. 化简（每小题4分，共8分）（1）3b+5a ﹣（2a ﹣4b ） （2）5（3a 2b ﹣ab 2）﹣4（﹣ab 2+3a 2b ）；23. 解方程（每小题4分，共8分）（1）4x-15=3（x+2） (2)x －x －12＝2－x ＋2524.（本题8分）小马虎在解方程312-x =2ax +-1去分母时，方程右边的-1项没有乘6，因而求得的解是x=10，试求a 的值，并正确地解方程．25.（本题8分）化简并求值：,,x y z 满足： （1）2x =-， （2）222y ab +-与233a b 是同类项，（3）负数z 的平方等于9，求多项式()2222432x y x y xyz x z x z xyz ⎡⎤-----⎣⎦的值．26.（本题9分）一块长、宽、高分别为πcm、3cm、2cm的长方体橡皮泥，要用它来捏一个底面半径为3cm的圆锥，圆锥的高是多少厘米？27.（本题11分）某农户承包果树若干亩，今年投资13800元，收获水果总产量为18000千克．此水果在市场上每千克售a元，在果园直接销售每千克售b元（b＜a）．该农户将水果拉到市场出售平均每天出售1000千克. （1）若这批水果全部在市场上销售，则需要天；（2）用代数式分别表示两种方式出售水果的收入；（3）水果在市场上销售时需2人帮忙，每人每天付工资150元，每天还需缴纳市场管理费100元．两种出售水果方式都在相同的时间内售完全部水果.当a=4.5元，b=4元时，请你计算两种销售方式的利润，并确定哪种出售方式较好．（利润=收入﹣支出）1-5CDCBC 6-10BAACC 11、3 12、（-1）2007，-22，-|-1|，-2.11313、-1 14、（3a+4b ） 15、-10 16、1 17、1418、0 19、16 20、④21. (1)-1 （2）-422. 解：（1）原式=3b+5a-2a+4b=3a+7b （2）原式=15a 2b-5ab 2+4ab 2-12a 2b=3a 2b-ab 223. （1）x=21 (2) x ＝11724.解：把x=10代入4x-2=3x+3a-1得40-2=30+3a-1，3a=9，a=3．故a 的值是3． 方程312-x =23+x -1的解为x=5 25.解：因为222y a b +-与233a b 是同类项 所以y+2=3 y=1 因为负数z 的平方等于9 所以`z=-3()2222432x y x y xyz x z x z xyz ⎡⎤-----⎣⎦= 222243x y x y xyz x z x z ⎡⎤--+-⎣⎦-2xyz = 2222432x y x y xyz x z x z xyz -+-+-= 2232x y xyz x z --+ 当x=-2，y=1，z=-3，原式=-42 26. 2cm 27.（1）18（2）市场上销售：18000a 果园直接销售：18000b（3）市场上销售获利：18000×4.5-（2×150+100）×18-13800=60000元 果园直接销售获利：18000×4-13800=58200元 因为60000＞58200，所以应选择在市场出售.2019-2020学年七上数学期中模拟试卷含答案一、精心选一选(本大题共8小题，每小题3分，共24分) 1．21-的相反数是 A ．2 B ．21C ．2-D ．21-2. 下列计算结果相等的为A ．32和23B ．32－和32－ C ．23－和 ()23－D ．()21－和22(1)n --（n 是大小1的整数）3．两个有理数的差A ．小于被减数B ．大于被减数C ．等于被减数D ．上述情况都有可能4．如图是一个简单的数值运算程序，当输入x 的值为1-时，则输出的值为A ．1B ． －5C ．－1D ．55．一个整式与x 2－y 2的和是x 2＋y 2，则这个整式是A ． 2x 2B ．2y 2C ．－2x 2D ．－2y 26．餐桌边的一蔬一饭，舌尖上的一饮一酌，实属来之不易，舌尖上的浪费让人触目惊心．据统计，中国每年浪费的食物总量折合粮食约500亿千克，这个数据用科学记数法表示为 A ．5×109千克B ． 50×109千克C ．5×1010千克D ． 0.5×1011千克7．若︱a ︱+a=0 则a 是A ．零B ．负数C ．非负数D ．负数或零8．数a ，b ，c 在数轴上对应的点如图所示，则下列式子中正确的是A ． ac ＞bcB ． |a ﹣b|=a ﹣bC ．﹣a ＜﹣b ＜cD ．﹣a ﹣c ＞﹣b ﹣c二、细心填一填(本大题共10小题，每小题3分，共30分)9．如果向北走50米记为是+50米，那么向南走30米记为 ▲ ．10．某超市出售的三种品牌月饼袋上，分别标有质量为（500±5）g ，（500±10）g ，（500±20）g 的字样，从中任意拿出两袋，它们的质量最多．．相差 ▲ g ． 11．已知代数式y x -2的值是5，则代数式1324--y x 的值是 ▲ ．12．已知A 是数轴上表示－3的点，把A 点移动3个单位长度后，A 点表示的数是 ▲ ． 13．若﹣2a m b 6与5a 2b 2m+n 是同类项，则m n 的值是 ▲ ．14．若a,b 互为相反数，c ,d 互为倒数，m 的绝对值为2，则cd m mba -++2的值是 ▲ ． 15．请你把()32113,2,0,,210---这五个数按从小到大用“<”连接起来： ▲ ． 16．某商品先按批发价a 元提高20%零售，后又按零售价降低10%出售，则它最后的单价是 ▲ 元． 17．观察下列各式：221324-=⨯ 222434-=⨯ 223544-=⨯ …请你将猜想到的规律用自然数n （n ≥1）表示出来 ▲ ． 18．定义新运算“*”为：⎩⎨⎧<≥-=*)(3)(b a b b a b a b a，则当3=x 时，计算x x *-*42的结果为 ▲ ．三、认真算一算，答一答(本大题共有7小题，共66分) 19．（本题满分8分）把下列各数分别填入相应的集合里88.1,2012,14.3,722,0,34,4+---，121121112.1-……，2π （1）正数集合：｛ …｝； （2）负数集合：｛ …｝； （3）整数集合：｛ …｝； （4）无理数集合：｛ …｝. 20．计算：(每题4分共24分) （1）2014)2()2014(22+-+-+（2）)131(13)5()105(-÷+-÷-（3）)43()76(22+----a a a a（4）)32(3)23(4)(5n m n m n m ----+（5）)361()12765321(-÷-+-（6）)1615(]8.0)31(3[21422-÷--⨯-⨯21．（本题满分6分）先化简，再求值：)1(3)1()1(2222--+-----a a a a a a ，其中21-=a ．（1）上星期五借出图书是多少册？（2）上星期二比上星期五多借出图书多少册？ （3）上星期平均每天借出图书多少册？23．（本题满分6分）为了能有效地使用电力资源,县城跃进花苑实行居民峰谷用电，居民家庭在峰时段(上午800~晚上2100)用电的电价为0.55元/千瓦时，谷时段(晚上2100~次日晨800)用电的电价为0.35元/千瓦时．若某居民户某月用电100千瓦时，其中峰时段用电x 千瓦时． （1）请用含x 的代数式表示该居民户这个月应缴纳电费； （2）利用上述代数式计算，当x=50时，求应缴纳电费．24．（本题满分8分）已知033)5(2=++-y x ，222y xy x A +--=， 223635y xy x B +--=， （1）求x y -的值。

2019-2020学年南京师范大学附属中学新城高级中学高三英语下学期期末试题及参考答案

2019-2020学年南京师范大学附属中学新城高级中学高三英语下学期期末试题及参考答案

2019-2020学年南京师范大学附属中学新城高级中学高三英语下学期期末试题及参考答案第一部分阅读（共两节，满分40分）第一节（共15小题；每小题2分，满分30分）阅读下列短文，从每题所给的A、B、C、D四个选项中选出最佳选项ADesign a science holiday to win a science holidayIs there a scientific holiday,tour,vacation or experience in your list that you dream of making a reality? We might just be able to help with that! We are the crowd sourcing thoughts and suggestions onnew tours,and the winner will receive two free places on their tour when it's launched.Starting entries 1st May 2020Deadline 31st August 2020ENTER NOW---Write a brief description of your ideal science holiday,tour,vacation or experience.---No matter how big or small,we are looking for brilliant, unique thoughts.It can be a complex multi-location overseas holiday tour,a weekend away deep-diving,or a simple walking tour(and everything in between).---Our current tours are mainly individual-focused but we would love to hear ideas for families and schools.---Creations that have environmentally friendly themes and a low carbon impact are also welcome.---Your entry can be as simple as a great title but writing more specifies will improve the possibility of walking off with the prize.---The competition doesn't close by September,2020,so plenty of time to brainstorm your entry.---We will launch the best idea in late 2020 or at the beginning of 2021. The winner will receive the award once the result is published.If you want to submit more than 3,999 words,include photos/maps with your entry, or submit multiple entries then send it to tours @ . The competition guidelines and other related information are available at .1. When will the winner probably be announced?A. In August,2020.B. In September,2020.C. In January,2021.D. In May,2021.2. What kind of entries might be more likely to win?A. Those producing a low carbon impact.B. Those with a long and unique title.C. Those providing detailed information.D. Those for individual-focused tours.3. What is the purpose of this text?A. To give guidance on a competition.B. To advertise a science holiday.C. To inspire creativity in teenagers.D. To collect the ideas for tours.BWhen my friend suggested going to the op shop (二手商店)，instantly I thought “I hope no one I know sees me”. It was the same when my cousin commented on my new furniture and Japanese, fine-bone-china bowls and asked where I got them. They were from the local op shop but instead I said “from the antique shop”.Many people in my Greek-Cypriot community would look down on me if I said I shopped at the op shop. They may pity me, consider me poor, a failure. Immigrants sacrificed their families and homes for a better life. Buying a house and having enough money to live comfortably, to educate your children and see them also live comfortably, are a big part of the immigrant dream, But has this dream made us materialistic at the cost of our own planet?Our love for purchasing the latest trendy clothes or furniture, then donating them when we are tired of them has become normal. I was once like this. But after watching the documentaryThe True CostI learned donated clothes that don’t get sold are sent to developing nations, many of them ending up in landfills (垃圾填埋地). In addition, your new dress requires electricity and materials to make. But if you buy a second-hand dress, that’s one less dress in a landfill and one less new dress to be made.A friend introduced me to op shopping only a few years ago. My firstitem was a dress she gifted me. It was lovely and I loved it. Nobody could tell it was second-hand. This opened me up to purchasing more second-hand high quality branded clothes. Once I visited a friend and was impressed by how she decorated her apartment. “It’s all second-hand,” she said. I couldn’t believe it. The truth is a lot of things sold at the op shop are in new or almost new condition. That’s when I made the decision to only buy second-hand things.Selling second-hand things isn’t anything new butwhat the planet needs is more buyers. There is so much excess (过量) production in the world. So stop feeling ashamed, and let’s get shopping.4. What kind of feeling is expressed in Paragraph 1?A. Pride.B. Embarrassment.C. Delight.D. Sympathy.5. Whatare many people in the author’s community like?A. They are probably materialistic.B. They care about the environment.C. They think highly of op shopping.D. They look down upon immigrants.6. What was the author encouraged to do after visiting her friend’s apartment?A. Watch the documentaryThe True Cost.B. Donate more to local charities.C. Avoid shopping too much.D. Stop buying new things.7. What’s the purpose of the text?A. To entertain.B. To advertise.C. To persuade.D. To describe.CA student had to get his long hair cut off in a middle school in GuangDong Province. It was talked a lot among teachers and students.In fact, all schools have their own rules. In most schools, boy students are not allowed to have long hair while girls are not allowed to dye their hair. And most school rules say that students should wear their school uniforms at school. And students must obey these rules so that they can get healthy development at school.But some students have disagreements. They think that boy students having long hair doesn't mean that they are not good students. They want to show their own personality. They think that they would look cool too if they had long hair and the hairstyles like their favorite stars.A girl student thought that she would look much more beautiful if she had brown hair. So she had her dark hair dyed brown one day. When she went back to school the next day, the teacher was very angry with her. She said that she worked hard at her lessons and did well in every subject. She just didn't know why the teacher didn't allow her to dye her hair while women teachers can.It is not wrong for teenagers to love stars' hairstyles or wear their favorite clothes. However, a school has its own rules for all the students to obey so that the school can be in good order. Students should not break the rules at school.8. What aren't boy students allowed to do in most middle schools according to this passage?A. To have long hair.B. To wear uniforms.C. To like famous stars.D. To show their own personalities.9. Why did the girl make her hair brown?A. Because she wanted to be cool.B. Because she thought that she would look much more beautiful.C. Because she wanted to make her teacher angry.D Because women teachers dyed their hair.10. What does the writer think of these school rules?A. The students should be against them.B. They are bad for students.C. They can make schools in good order.D. They can't make students grow healthily.11. What is the passage mainly about?A. Hair styles and clothes.B. Schoolboys and schoolgirls.C. Students and famous stars.D. School rules.DA trip to thelibrary was like a great journey to a different country. To get there, we had to walk a mile. But our weekly journeys to the library were a piece of perfection. I had around me at one time all the people I loved best-my father and mother and brothers and sister--and all the things I loved best- quiet, space and books.I read a lot of books about science: not the spaceships my brothers preferred, but the birds and the bees--literally. I brought home a book of birds and searched the trees for anything other than robins (知更鸟). I went through a phrase of loving books with practical science experiments and used up a whole bottle of white vinegar by pouring it on the sides of our apartment building to prove that it was constructed of limestone (石灰石).One Saturday, as I wandered through the young adult section, I saw a title: Little Women, by Lousia May Alcott. I had learned from experience that titles weren’t everything. A book that sounded great on the shelf could be dull once you got it home. So I sat in a chair near the shelves to skim the first paragraphs.I read and read and read Little Women until it was time to walk home, and, except for a few essential interruptions like sleeping and eating, I did not put it down until the end. Even the freedom to watch weekend television held no appeal for me in the wake of Alcott' s story. It was about girls, for one thing, girls who could almost be like me, especially Jo. I had found someone who thought and felt the way I did.12. What can we say about the author’s family?A. They enjoyed traveling abroad.B. They were library frequenters.C. They were very fond of walking.D. They led a perfectly quiet life.13. What does the author mainly want to show in paragraph 2?A. Her different hobbies from her brothers.B. How she conducted science experiments.C. Why she loved books about the birds and the bees.D. Her reading interests during a particular period of time.14. What opinion does the author hold on books?A. Book titles can sometimes be misleading.B. Science books are as interesting as novels.C. The first few paragraphs of a book are attractive.D. Books seem duller when read in libraries than at home.15. How would the author describe Little Women?A. It helped her to discover her true character.B. It made her forget about food and sleep.C. It inspired confidence in her.D. It kept her absorbed.第二节（共5小题；每小题2分，满分10分）阅读下面短文，从短文后的选项中选出可以填入空白处的最佳选项。

江苏省南京市南师附中集团新城中学2019-2020学年中考数学模拟教学质量检测试题

江苏省南京市南师附中集团新城中学2019-2020学年中考数学模拟教学质量检测试题

江苏省南京市南师附中集团新城中学2019-2020学年中考数学模拟教学质量检测试题一、选择题1．某小学为了了解各年级留守儿童的数量，对一到六年级留守儿童数量进行了统计，得到每个年级的留守儿童人数分别为10，15，10，17，18，20．对于这组数据，下列说法错误的是（）A.平均数是15B.众数是10C.中位数是17D.方差是44 32．已知函数：①y＝x；②y＝1x-（x＜0）；③y＝﹣x+3；④y＝x2+x（x≥0），其中，y随x的增大而增大的函数有（）A．1个B．2个C．3个D．4个3．如图，在△ABC中，AB＝AC，在边AB上取点D，使得BD＝BC，连结CD，若∠A＝36°，则∠BDC等于（）A．36°B．54°C．72°D．126°4．计算﹣6+1的结果为（）A．﹣5 B．5 C．﹣7 D．75．下列事件是必然事件的是A．抛掷一次硬币，正面向上B．13名同学中，至少有两名同学出生的月份相同C．射击运动员射击一次，命中9环D．买一张电影票，座位号是奇数6．若函数，则当函数值y＝8时，自变量x的值是（）A.±B.4C.±或4D.4或－7．一蓄水池有水40m3,按一定的速度放水，水池里的水量y (m3)与放水时间t(分)有如下关系：A．y随t的增加而增大B．放水时间为15分钟时，水池中水量为8m3C．每分钟的放水量是2m3D．y与t之间的关系式为y=38-2t8．在我们的生活中，常见到很多美丽的图案，下列图案中，既是中心对称，又是轴对称图形的是( )A．B．C．D．9．若a＝2e，向量b和向量a方向相反，且|b|＝2|a|，则下列结论中不正确的是（）A．|a|＝2 B．|b|＝4 C．b＝4e D．a＝1 2b -10．如图是根据我市某天七个整点时的气温绘制成的统计图，则这七个整点时气温的中位数和众数分别是（ ）A ．中位数31，众数是22B ．中位数是22，众数是31C ．中位数是26，众数是22D ．中位数是22，众数是2611．如图，小山岗的斜坡AC 的坡度是tan α＝34，在与山脚C 距离200米的D 处，测得山顶A 的仰角为26.6°，则小山岗的高AB 是（ ）（结果取整数，参考数据：sin26.6°＝0.45，cos26.6°＝0.89，tan26.6°＝0.50）A.300米B.250米C.400米D.100米12．已知点A （t ，y 1），B （t+2，y 2）在抛物线212y x =的图象上，且﹣2≤t≤2，则线段AB 长的最大值、最小值分别是（ ）A ． 2B ．C ．，2D ．， 二、填空题13．如图，点是等边的边上的一个动点，连结，将射线绕点顺时针旋转交于点，若，则的最小值是 ___________.14．如图，⊙O 的半径为2，AB ，CD 是互相垂直的两条直径，点P 是⊙O 上任意一点（P 与A ，B ，C ，D 不重合），过点P 作PM ⊥AB 于点M ，PN ⊥CD 于点N ，点Q 是MN 的中点，当点P 沿着圆周转过45°时，点Q 走过的路径长为________．15．如图，点P 是第一象限内一点，OP=4，经过点P 的直线l 分别与x 轴、y 轴的正半轴交于点A 、点B ，若OP 平分∠AOB ，则11OA OB+=______．16．使得关于x 的分式方程111x k kx x +-=+-的解为负整数，且使得关于x 的不等式组322144x x x k +≥-⎧⎨-≤⎩有且仅有5个整数解的所有k 的和为_____．17．如图，正方形ABCD 的边长为4，M 、N 分别是BC 、CD 上的两个动点，且始终保持AM ⊥MN ，当BM= ，四边形ABCN 的面积最大。

2019-2020学年南京市建邺区新城中学七年级下学期期末数学试卷(含解析)

2019-2020学年南京市建邺区新城中学七年级下学期期末数学试卷(含解析)

2019-2020学年南京市建邺区新城中学七年级下学期期末数学试卷一、选择题（本大题共5小题，共10.0分）1.下列图形中，直线a与直线b平行的是()A. B.C. D.2.如下图，已知圆心角∠AOB的度数为100°，则圆周角∠ACB的度数是()A. 80°B. 100°C. 120°D. 130°3.下列运算正确的是()A. (−x2)3=−x5B. x2⋅x4=x8C. x3+x3=2x3D. (x−y)2=x2−y24.如图，在△ABC与△BAD中，AC=BD，若使△ABC≌△BAD，下列添加的条件错误的是()A. ∠C=∠DB. ∠BAC=∠ABDC. AE=BED. CE=DE5.某校七(2)班42名同学为“希望工程”捐款，共捐款320元，捐款情况如下表：表格中捐款6元和8元的人数不小心被墨水污染已看不清楚.若设捐款6元的有x名同学，捐款8元的有y名同学，根据题意，可得方程组()A. {x+y=298x+6y=226B. {x+y=296x+8y=226C. {x+y=296x+8y=320D. {x+y=298x+6y=320二、填空题（本大题共10小题，共20.0分）6.某种计算机完成一次基本运算的时间约为0.0000000001s，把0.0000000001用科学记数法可以表示为______．7.写出“角平分线上任意一点到角的两边距离相等”的逆命题______．8.如图，在△ABC和△DCB中，AB=DC，若不添加任何字母与辅助线，要使△ABC≌△DCB，则还需增加的一个条件是______．9.如图，AB//CD，直线EF分别交AB、CD于点E、F，EH平分∠BEF，若∠1=70°，∠2=______°.10.若16x2+mxy+9y2是完全平方式，那么m的值是______ ．11.在平面直角坐标系中，如果一个点的横、纵坐标均为整数，那么我们称该点是格点．若格点P(2m−1,m+2)在第二象限，则m的值为______．12.如图，已知AB//CD，∠1=115°，∠2=65°，则∠C=______°.13.如图Rt△ABC中，CD是斜边AB上的中线，已知CD=2，AC=3，则cosA=______．14. 通信市场竞争日益激列，某通信公司的手机市话费标准按原标准每分钟降低a 元后，再次下调了20％，现在收费标准是每分钟b 元，则原收费标准每分钟是________．15. 若x +y =7，则x 2+y 22+xy = ______ ．三、计算题（本大题共1小题，共6.0分）16. 先化简：3(3x 4y 2+xy 2−2)−(−3x 2y)2−14(x 2y +4)，再代入求值，其中x =2，y =−2．四、解答题（本大题共9小题，共64.0分）17. 因式分解：(1)a 2x 2y −axy 2；(2)x 3−2x 2y +xy 2．18. 解不等式组并写出非负整数解．{x −3(x −2)≥4 ①1+2x 3>x −1 ②19. 如图，在平行四边形ABCD 中，E ，F ，G ，H 分别是边AB ，BC ，CD ，DA 上的点，且AE =CG ，BF =DH ，求证：EG 与FH 互相平分(提示：可连接EF ，FG ，GH ，HE ，证四边形EFGH 为平行四边形即可)．20. 解方程组(1){x −y =52x +y =4(2){23x +12y =6x −3y =4(3){2x −3y =12x −z =5x +3y +z =421. 补全下列推理过程：如图，已知△ABC中，AB=AC点D、E分别在AB、AC上，且BD=CE，如何说明BE=CD呢？解：因为AB=AC______所以∠ABC=∠ACB______又因为BD=CE______BC=CB______所以△BCD≌△CBE______所以BE=CD______22.用方程解答下列问题：(1)x与4之和的1.2倍等于x与14只差的3.6倍，求x；(2)y的3倍与1.5之和的二分之一等于y与1之差的四分之一，求y．23.为了鼓励市民节约用水，某市居民生活用水按阶梯式水价计费．下表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息：(说明：①每户产生的污水量等于该户的用水量，②水费=自来水费+污水处理费)已知小明家2014年4月份用水20吨，交水费66元；5月份用水35吨，交水费150元．(1)求a、b的值．(2)实行“阶梯水价”收费之后，该市一户居民6月用水27吨，其当月交水费多少元？24. 如图所示，在△ABC中，∠ABC与∠ACB的平分线交于点O，根据下列条件，求出∠BOC的度数．(1)如图1，已知∠ABC+∠ACB=100°，则∠BOC=______．(2)如图2，已知∠A=90°，求∠BOC的度数．(3)从上述计算中，你能发现∠BOC与∠A的关系吗？请直接写出∠BOC与∠A的关系．25. 某智能手机越来越受到大众的喜爱，各种款式相继投放市场，某店经营的A款手机去年销售总额为50000元，今年每部销售价比去年降低400元，若卖出的数量相同，销售总额将比去年减少20%．(1)今年A款手机每部售价多少元？(2)该店计划新进一批A款手机和B款手机共90部，且B款手机的进货数量不超过A款手机数量的两倍，应如何进货才能使这批手机获利最多？已知A，B两款手机的进货和销售价格如下表：A款手机B款手机进货价格(元)11001400销售价格(元)今年的销售价格2000【答案与解析】1.答案：B解析：解：A.∵117°+73°=190°≠180°，∴不能得到直线a与直线b平行；B.∵122°+58°=180°，∴能得到直线a与直线b平行；C.∵85°≠75°，∴不能得到直线a与直线b平行；D.∵125°+45°=170°≠180°，∴不能得到直线a与直线b平行；故选：B．根据同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行进行判断即可．本题主要考查了平行线的判定，解题时注意：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．2.答案：D解析：解：∵∠AOB=100°，∴它所对的是100°，设D为优弧上任一点为360°−100°=260°；∴∠ACB=130°．故选D．3.答案：C解析：此题主要考查了幂的乘方和积的乘方，同底数幂的乘法法则，合并同类项以及完全平方公式．A：根据幂的乘方和积的乘方的运算法则计算即可．B：根据同底数幂的乘法法则计算即可．C ：根据合并同类项的方法计算即可．D ：根据完全平方公式判断即可．解：∵(−x 2)3=−x 6，∴选项A 错误；∵x 2⋅x 4=x 6，∴选项B 错误；∵x 3+x 3=2x 3，∴选项C 正确；∵(x −y)2=x 2−2xy +y 2，∴选项D 错误．故选：C ．4.答案：A解析：解：∵AC =BD ，而AB 为公共边，∴当∠BAC =∠ABD 时，根据“SAS ”可判断△ABC≌△BAD ，当AE =BE 时，则∠BAC =∠ABD ，根据“SAS ”可判断△ABC≌△BAD ，当DE =CE ，则AE =BE ，所以∠BAC =∠ABD ，根据“SAS ”可判断△ABC≌△BAD ．故选：A ．利用全等三角形的判定方法对各选项进行判断．本题考查了全等三角形的判定：灵活运用全等三角形的5种判定方法．5.答案：B解析：本题考查了二元一次方程组的应用，根据实际问题中的条件列方程组时，要注意抓住题目中的一些关键性词语，找出等量关系，列出方程组．根据捐款学生42名，捐款金额是320元，即可得出方程组．解：设捐款6元的有x 名同学，捐款8元的有y 名同学，由题意得，{x +y +6+7=4224+6x +8y +70=320，即{x +y =296x +8y =226． 故选：B ．6.答案：1×10−10解析：解：0.0000000001=1×10−10．故选：1×10−10．绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10−n，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数n由原数左边起第一个不为零的数字前面的0的个数所决定．本题考查了科学记数法．解题的关键是掌握用科学记数法表示较小的数，一般形式为a×10−n，其中1≤|a|<10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．7.答案：到角两边距离相等的点在角的角平分线上解析：解：将原命题题设与结论对调，得到逆命题：到角两边距离相等的点在角的角平分线上．故答案为：到角两边距离相等的点在角的角平分线上首先要分清原命题的题设与结论，题设是角平分线上的点，可改为点在角平分线上，结论是该点到角的两边距离相等，然后将结论与题设对调即可．本题考查了角平分线的性质及命题的改写问题．找准原命题的题设与结论是正确解答本题的关键．8.答案：∠ABC=∠DCB或AC=DB解析：解：∵AB=DC，BC=BC，∴当∠ABC=∠DCB(SAS)或AC=DB(SSS)时，△ABC≌△DCB．故填∠ABC=∠DCB或AC=DB．本题是三角形全等知识点常见考题，应注意的一点是“不添加任何字母与辅助线”，已知条件中已经具备一对应边相等和一公共边，所以只能加的是已知两边的夹角相等或第3边对应相等．判定两个三角形全等的一般方法有：SSS、SAS、AAS、ASA、HL，不论是哪个判定定理，都必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．9.答案：125解析：解：∵EH平分∠BEF，∴∠BEH=∠HEF，∵AB//CD，∠1=70°，∴∠1+∠BEF=180°，即∠BEF=110°，∴∠FEH=55°，∴∠2=∠1+∠FEH=70°+55°=125°．故答案为：125．根据平行线的性质和角平分线定义求出∠FEH，再根据三角形外角性质计算即可．本题主要考查了平行线的性质以及三角形外角性质，解题时注意：三角形的一个外角等于和它不相邻的两个内角的和．10.答案：±24解析：解：∵16x2+mxy+9y2=(4x)2+mxy+(3y)2，∴m=±2×4×3=±24，故答案为：±24．根据已知算式得出m=±2×4×3，求出即可．本题考查了完全平方式，能熟记完全平方式的特点是解此题的关键，注意：完全平方式有两个：a2+ 2ab+b2和a2−2ab+b2．11.答案：−1或0解析：解：∵格点P(2m−1,m+2)在第二象限，∴{2m−1<0 ①m+2>0 ②，解不等式①得，m<12，解不等式②得，m>−2，∴不等式的解集为−2<m<12，∵点的横、纵坐标均为整数，∴m是整数，∴m的值为−1或0．故答案为：−1或0．根据第二象限内点的横坐标是负数，纵坐标是正数列出不等式组，然后求解即可．本题考查了各象限内点的坐标的符号特征以及解不等式，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限(+,+)；第二象限(−,+)；第三象限(−,−)；第四象限(+,−)．12.答案：50解析：此题主要考查了平行线的性质、三角形的内角和定理，正确得出∠FGD=∠1=115°是解题关键．直接利用平行线的性质结合三角形内角和定理分析得出答案．解：∵AB//CD，∠1=115°，∴∠FGD=∠1=115°，∴∠FGC=180°−115°=65°，∵∠C+∠2+∠FGC=180°，∠2=65°，∴∠C=180°−65°−65°=50°．故答案为50．13.答案：34解析：解：∵直角△ABC中，CD是斜边AB上的中线，∴AB=2CD=2×2=4，则cosA=ACAB =34．故答案是：34．首先根据直角三角形斜边上的中线等于斜边的一半，即可求得AB的长，然后利用余弦函数的定义求解．本题考查了直角三角形的性质：直角三角形斜边上的中线等于斜边的一半，以及三角函数的定义，求得AB的长是关键．14.答案：a+1.25b解析：此题考查了列代数式及方程思想的应用，可设原收费标准是x元/分，根据降价a元后，再次下调了20%后是b元/分作为相等关系列出方程，用含a，b的代数式表示x即可求解．解：设原收费标准每分钟是x元，则(x−a)(1−20%)=b，解得x=a+1.25b．故填a+1.25b．15.答案：492解析：解：∵x+y=7，∴(x+y)2=49，∴x2+y22+xy=x2+y22+2xy2=(x+y)22=492，故答案为492．根据x+y=7，可得出(x+y)2=49，再整理原式代入即可．本题考查了完全平方公式，熟练掌握完全平方公式是解题的关键．16.答案：解：原式=9x4y2+3xy2−6−9x4y2−14x2y−1=3xy2−14x2y−7，当x=2，y=−2时，原式=24+2−7=19．解析：此题考查了整式的混合运算−化简求值，熟练掌握运算法则是解本题的关键．原式去括号合并得到最简结果，把x与y的值代入计算即可求出值．17.答案：解：(1)a2x2y−axy2=axy(ax−y)；(2)x3−2x2y+xy2，=x(x2−2xy+y2)，=x(x−y)2．解析：(1)提取公因式axy即可；(2)先提取公因式x，再对余下的多项式利用完全平方公式继续分解．本题考查了提公因式法与公式法分解因式，要求灵活使用各种方法对多项式进行因式分解，一般来说，如果可以先提取公因式的要先提取公因式，再考虑运用公式法分解．18.答案：解：解不等式①得：x≤1，解不等式②得：x<4，在数轴上表示不等式①、②的解集，如图所示：这两个不等式解集的公共部分是x≤1．∴不等式组的解集是x≤1，非负整数解有0、1．解析：先解不等式，再利用数轴找出解集的公共部分，求出不等式组的解集，最后在其解集中找出非负整数．19.答案：证明：连接EF，FG，GH，HE，∵四边形ABCD是平行四边形，∴∠A=∠C，∠B=∠D，AB=CD，AD=BC，∵AE=CG，BF=DH，∴AH=CF，BE=DG，在△AEH和△CFG中，{AE =CG ∠A =∠C AH =CF，∴△AEH≌△CGF(SAS)，∴EH =GF ，同理：GH =EF ，∴四边形EFGH 为平行四边形，∴EG 与FH 互相平分．解析：首先连接EF ，FG ，GH ，HE ，由在平行四边形ABCD 中，E ，F ，G ，H 分别是边AB ，BC ，CD ，DA 上的点，且AE =CG ，BF =DH ，易证得△AEH≌△CFG ，即可得FG =EH ，继而可得HG =EF ，即可证得四边形EFGH 为平行四边形，继而证得EG 与FH 互相平分．此题考查了平行四边形的判定与性质以及全等三角形的判定与性质．此题比较适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．20.答案：解：(1){x −y =5 ①2x +y =4 ②， ①+②，得：3x =9，解得：x =3，把x =3代入①得：3−y =5，解得：y =−2，则方程组的解为{x =3y =−2； (2)方程组整理得：{4x +3y =36 ①x −3y =4 ②， ①+②，得：5x =40，解得：x =8，把 x =8代入②得：y =43，则方程组的解为{x =8y =43．(3){2x −3y =1①2x −z =5②x +3y +z =4③，②+③得：3x +3y =9④，①+④得：5x =10，解得：x =2，把x =2代入①得：y =1，把x =2代入②得：z =−1，则方程组的解为{x =2y =1z =−1．解析：(1)方程组利用加减消元法求出解即可；(2)方程组整理后，利用加减消元法求出解即可；(3)方程组利用加减消元法求出解即可．此题考查了解三元一次方程组，解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．21.答案：已知 等边对等角 已知 公共边 SAS 全等三角形的对应边相等解析：解：∵AB =AC(已知)∴∠ABC =∠ACB(等边对等角)又∵BD =CE(已知)，BC =CB(公共边)∴△BCD≌△CBE(SAS)∴BE =CD(全等三角形的对应边相等)故答案为：已知，等边对等角，已知，公共边，SAS ，全等三角形的对应边相等．由“SAS ”可证△BCD≌△CBE ，可得BE =CD ．本题考查了全等三角形的判定和性质，熟练运用全等三角形的判定是本题的关键．22.答案：解：(1)根据题意得：1.2(x +4)=3.6(x −14)，解得：x =23；(2)根据题意得：12(3y +1.5)=14(y −1)，解得：y =−45．解析：(1)首先列出一元一次方程，然后去括号，移项、合并同类项即可求解；(2)首先列出一元一次方程，然后去括号，移项、合并同类项即可求解．本题考查了一元一次方程的解法，正确列出方程是关键． 23.答案：解：(1)由题意可得：{17a +3b +0.8×20=6617a +13b +6×5+0.8×35=150，解得{a =2.2b =4.2； 答：a =2.2，b =4.2；(2)(27−17)×4.2+17×2.2+27×0.8=101元．答：当月交水费101元．解析：(1)根据4月份用水20吨，交水费66元；5月份用水35吨，交水费150元列出a 和b 的二元一次方程组，求出a 和b 的值即可；(2)根据阶梯水价计费模式求出当月水费即可．本题主要考查了列二元一次方程解实际问题的运用，解答时由水费=自来水费+污水处理费建立方程是关键．24.答案：(1)130°；(2)∵在三角形ABC 中∠A =90°，∴∠ABC +∠ACB =180°−90°=90°，又∵∠OBC +∠BCO =12(∠ABC +∠ACB)=45°，∴∠BOC =180°−45°=135°；(3)在三角形ABC 中中∠ABC +∠ACB =180°−∠A ，又∵∠OBC +∠BCO =12(∠ABC +∠ACB)，∴∠BOC =90°+12∠A ．解析：解：(1)∵在△ABC 中，∠ABC 与∠ACB 的平分线交于点O ，如图1，已知∠ABC +∠ACB =100°， ∴∠OBC =12∠ABC ，∠BCO =12∠ACB ，∴∠OBC +∠BCO =12(∠ABC +∠ACB)=12×100°=50°，∵在三角形BOA 中有∠BOA =180°−∠OBC −∠BCO =180°−50°=130°，故答案为：130°；(2)见答案(3)见答案(1)(2)根据题意可知∠OBC +∠BCO =12(∠ABC +∠ACB)，然后在三角形BOC 中利用三角形内角和即可求得∠BOC 的度数；(3)利用三角形内角和定理分别在三角形ABC和三角形BOC中：∠BOC=180°−∠OBC−∠OCB即可得出结论．本题考查的是三角形内角和定理，能求出∠OBC+∠OCB的度数是解答此题的关键．25.答案：解：(1)设今年A款手机每部售价x元，则去年售价每部为(x+400)元，由题意，得，50000x+400=50000(1−20%)x，解得：x=1600．经检验，x=1600是原方程的根，且符合题意．答：今年A款手机每部售价1600元；(2)设今年新进A款手机a部，则B款手机(60−a)部，获利y元，由题意，得y=(1600−1100)a+(2000−1400)(60−a)=−100a+36000．∵B款手机的进货数量不超过A款手机数量的两倍，∴60−a≤2a，∴a≥20，∵y=−100a+36000．∴k=−100<0，∴y随a的增大而减小．∴a=20时，y最大=34000元．∴B款手机的数量为：60−20=40部．答：当新进A款手机20部，B款手机40部时，这批手机获利最大．解析：(1)设今年A款手机的每部售价x元，则去年售价每部为(x+400)元，由卖出的数量相同建立方程求出其解即可；(2)设今年新进A款手机a部，则B款手机(60−a)部，获利y元，由条件表示出y与a之间的关系式，由a的取值范围就可以求出y的最大值．本题考查了列分式方程解实际问题的运用，分式方程的解法的运用，一次函数的解析式的运用，解答时由销售问题的数量关系求出一次函数的解析式是关健．。

2019-2020学年南京师范大学附属中学新城高级中学高三英语期中考试试卷及答案

2019-2020学年南京师范大学附属中学新城高级中学高三英语期中考试试卷及答案

2019-2020学年南京师范大学附属中学新城高级中学高三英语期中考试试卷及答案第一部分阅读（共两节，满分40分）第一节（共15小题；每小题2分，满分30分）阅读下列短文，从每题所给的A、B、C、D四个选项中选出最佳选项APlan Your Visit to the British MuseumWe've made a few changes to ensure you can safely enjoy your visit:How to book tickets·Tickets for the permanent collection can only be hooked online in advance.·To book tickets for exhibitions, visit our exhibition pages. If you want to guarantee your visit to the permanent collection as well as the exhibition on your visit, you will need to book a separate ticket.·We are limiting numbers of people in the museum to ensure there is room for you to safely enjoy your visit. Everyone, including members and volunteers, will therefore need to book a free, timed ticket in advance.Important information about your ticket booking·You can book up to six tickets for people who live in the same family.·We will email yourticket to you, and you will need to show it either printed out or on your device (设备) when you arrive.·Please arrive at the time stated on your ticket-we cannot guarantee admission before or after it.Following the routeWe have created a new one-way route through the museum which will allow you to safely explore world cultures from the Mediterranean to the Middle East and from the Americas to Africa.·View a map of the route (Open in a new window).·Our audio guides (音频指南) are not available. However, youcan pay to download the audio introductions from iTunes (Open in a new window) or Google Play (Open in a new window) to each of the galleries and listen on your own device. Please remember to bring along your own headphones.1.Why does the museum offer timed tickets?A.To earn more money.B.To hire more volunteers.C.To save room for collections.D.To control the number of visitors.2.How can a visitor learn about the new route in advance?A.View an online map.B.Buy a new headphone.C.Buy audio guides from the museum.D.Download video introductions from iTunes.3.Where can you probably find the text?A.In a newspaper.B.In a magazine.C.On a website.D.In a report.BAfter years of releasing e-readers that compete directly with Amazon’s Kindle, Rakuten Kobo’s latest device offers something totally different: theability to draw and write directly on the screen.With a large 10.3-inch E-ink display, the Kobo Elipsa looks more like an electronic clipboard than the standard paperpack-sized e-reader. Although the ability to write on the screen is no big deal — especially given its high price tag of $ 600 — the overall package is impressively functional.In terms of reading, the Elipsa packs just about everything you’d expect in a Kobo. You can purchase and download books from the store, read web articles you’ve saved online via Pocket, and connect to your local library to borrow e-books and magazines. It’s known that Kindle basically requires you to buy books from Amazon. Unlike Kindles, Kobos are pretty open with the formats they support; you can connect the Elipsa to a computer and transfer over any PDF books you have bought or downloaded from stores like Booktopia or Google Books.You can fill your virtual notepads with notes using brush and pen types, and export them as PDFs or images to a PC. There’s also an “advanced” notebook that can turn your writing into typed and editable text for exporting to Microsoft Word format. You can also write directly onto documents themselves, with all your word circling and underlining saved as you go to review later. This is especially handy when it comes to PDFs, as changes you make are synced（同步）automatically when you have Wi-Fi, so you can move between your Elipsa, PC and phone and keep your notes.With all that said, we can see it really appealing to e-reader fans who also tend to do a lot of work on paper. If you ever print things out to mark them up, fill notepads with writing or drawing that you later have to transcribe or scan, or just wish you could write all over your library books, this could be the device for you.4. Which of the following best describes the Elipsa?A. Automatic.B. Traditional.C. Useful.D. Standard.5. How is a Kobo different from a Kindle in reading?A. A Kindle has a larger screen.B. A Kindle can support more formats.C. A Kobo supports books from various sources.D. A Kobo should be connected to local libraries.6. What does paragraph 4 mainly tell us about Kobos?A Their function in syncing. B. Their function in typing.C. Their function in writing.D. Their function in reading.7. In which section of a newspaper can the text probably be found?A. Education.B. Technology.C. Lifestyle.D. Business.COlder adults with a better sense of smell may live longer than thosewho have a poor sense of smell, a new study suggests. The study was a project of researchers in theUnited Statesthat was ongoing for over 13 years. They asked nearly 2,300 men and women to identify 12 common smells. All the subjects were from 71 to 82 years of age. The researchers gave the adults scores, from 0 to as high as 12, based on how many smells they identified correctly.During the years of follow-up investigation, over 1,200 of the subjects died. When the study was launched, none of the adults were weak. They could walk a little under half a kilometer, climb 10 steps and independently complete daily activities. In the latest findings, the researchers noted that those with a weak nose were 30 percent more likely to die than people with a good sense of smell. The findings were reported last month in the scientific publication Annals of Internal Medicine.Honglei Chen, a doctor withMichiganStateUniversityinEast Lansing,Michigan, was the lead writer of a report on the study. He said the connection between a poor sense of smell and an increased risk of dying was limited to adults who first reported good-to-excellent health. This suggests that a poor sense of smell is an early and sensitive sign for worsening health before it is recognizable in medical tests. With a poor sense of smell, people are more likely to die of brain and heart diseases, but not of cancer or breathing disorders.The results also suggest that a poor sense of smell may be an early warning for poor health in older age that goesbeyond dementia or other neurodegenerative(神经变性的) diseases. These often signal the beginning of a weakening of the mind or body.8. What do you know about the study mentioned?A. The study involved researchers from the world.B. All the participants were of different ages.C. The study began to be performed about 13 years ago.D. 2 ,300 men and women were young and healthy.9. What was the situation like at the beginning of the study?A. More than 1,200 of the participants passed away.B. Many of the subjects were found with health problems.C. All the subjects were independent of others when walking.D. One third of the participants had a poor smell sense.10. What can be inferred from the last two paragraphs?A. People with a poor sense of smell have heart disease.B. You should be careful with your health if you smell poorly.C. People with a poor sense of smell won't suffer from cancer.D. Most of the elder people may have the dementia disease.11. Which is the best title for the passage?A. Strong Sense of Smell May Be Linked to Longer LifeB. Old People Tend to Have a Poor Sense of SmellC. A Number of Factors Result in Longer LifeD. Being Ill Means Losing the Sense of SmellDWhen I was 13, I lost my sight. Since then, I had learned to get about with a walking stick, but had to stay at home because my parents thought I would get lost or robbed, even get hit by a car.I, however, believed I could regain my way if I lost it. A neighbor told me that a public library was offering a free course designed for the blind. That's an important opportunity for me to kill two birds with one stone: I could practice my getting — about skills on my way to learning practical technology. My parentssettled forit.But how would I plan my course? I knew that the blind singer Ray Charles, get around without a walking stick by counting steps. But I couldn't seem to do that the way he had. I developed the power of my imagination, catching the layout（布局）of places I visited and taking note of landmarks in my mind. Every time I visited a place, the mental map I'd drawn would turn up and helped me with the direction. But that doesn't mean I didn't lose my way in the process of acquiring this skill. I'd have to swallow（吞下）my pride to ask kind strangersfor help.On those days I lost my way, I'd go to bed feeling down. But my desires to beat blindness and further my education were usually enough to get me out of bed the next day and try again. Today, I'm a published reporterand audio producer.Yes, I've lost my way at times and found it again. And when people ask me,"Aren't you afraid to be out on your own?” the answer to me is clear：I'd rather risk and find happiness than stick to safety and be painful.Now, impressed by my progress, my father told my mother, "Our boy can see!".12. What does the underlined phrases “settled for" in the second paragraph mean?A. Talked about.B. Stuckto.C. Agreed to.D. Cared about.13. How did the author go around on his own after losing his sight?A.He created pictures of places in his mind.B. He drew a map on the paper to help him.C. He was always asking strangers for directions.D.He threw away the walking stick and counted steps.14. Which of the following can best describe the author?A. Determined and adventurous.B. Patient and intelligent.C. Warm-hearted and positive.D. Adventurous and outgoing.15. How did the author's parents feel about his progress?A.Concerned.B. Surprised.C. Confident.D. Proud.第二节（共5小题；每小题2分，满分10分）阅读下面短文，从短文后的选项中选出可以填入空白处的最佳选项。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

中考模拟数学试卷一、选择题（每题3分，共30分）1．的倒数是（）A．﹣B．C．D．2．改革开放以来，我国国内生产总值由2006年的3645亿元增长到2016年的300 670亿元．将300 670用科学记数法表示应为（）A．0.30067×106B．3.0067×105C．3.0067×104D．30.067×1043．如图是婴儿车的平面示意图，其中AB∥CD，∠1=120°，∠3=40°，那么∠2的度数为（）A．80° B．90° C．100°D．102°4．小明因流感在医院观察，要掌握他在一周内的体温是否稳定，则医生需了解小明7天体温的（）A．众数 B．方差 C．平均数D．频数5．几个棱长为1的正方体组成的几何体的三视图如图所示，则这个几何体的体积是（）A．4 B．5 C．6 D．76．若关于x的一元二次方程（k﹣1）x2+2x﹣2=0有不相等实数根，则k的取值范围是（）A．k＞B．k≥C．k＞且k≠1 D．k≥且k≠17．一个袋子中装有3个红球和2个黄球，这些球的形状、大小、质地完全相同，在看不到球的条件下，随机从袋中摸出2个球，其中2个球颜色不相同的概率是（）A．B．C．D．8．如图，已知OP平分∠AOB，∠AOB=60°，CP=2，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．如果点M是OP的中点，则DM的长是（）A．2 B．C．D．9．如图所示，⊙O是以坐标原点O为圆心，4为半径的圆，点P的坐标为（，），弦AB经过点P，则图中阴影部分面积的最小值等于（）A．2π﹣4 B．4π﹣8 C．D．10．二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法：①2a+b=0，②当﹣1≤x≤3时，y＜0；③3a+c=0；④若（x1，y1）（x2、y2）在函数图象上，当0＜x1＜x2时，y1＜y2，其中正确的是（）A．①②④B．①③ C．①②③D．①③④二、填空题（每题3分，共15分）11．如果代数式有意义，那么字母x的取值范围是．12．如图，⊙O的半径为4，△ABC是⊙O的内接三角形，连接OB、OC，若∠BAC和∠BOC互补，则弦BC 的长度为．13．如图所示，AB∥CD∥EF，AC与BD相交于点E，若CE=4，CF=3，AE=BC，则的值是．14．如图，矩形OABC的边OA、OC分别在x轴、y轴上，点B的坐标为（7，3），点E在边AB上，且AE=1，已知点P为y轴上一动点，连接EP，过点O作直线EP的垂线段，垂足为点H，在点P从点F（0，）运动到原点O的过程中，点H的运动路径长为．15．如图，在Rt△ABC中，∠ACB=90°，AB=5，AC=3，点D是BC上一动点，连结AD，将△ACD沿AD折叠，点C落在点C′，连结C′D交AB于点E，连结BC′．当△BC′D是直角三角形时，DE的长为．三、解答题（共8个小题，满分75分）16．先化简，再求值：（）÷（﹣1），其中a是满足不等组的整数解．17．小明在学习了数据的收集、整理与描述后，为妈妈整理记录了10月份的家庭支出情况，并绘制成如下尚不完整的统计图表，请你根据图表信息完成下列各题：项目物业费伙食费服装费其他费金额/元800 400（1）10月份小明家共支出多少元？（2）在扇形统计图中，表示“其他费”的扇形圆心角为多少度？（3）请将表格补充完整；（4）请将条形统计图补充完整．18．如图所示，某工程队准备在山坡（山坡视为直线l）上修一条路，需要测量山坡的坡度，即tanα的值．测量员在山坡P处（不计此人身高）观察对面山顶上的一座铁塔，测得塔尖C的仰角为31°，塔底B 的仰角为26.6°．已知塔高BC=40米，塔所在的山高OB=240米，OA=300米，图中的点O、B、C、A、P在同一平面内．求：（1）P到OC的距离．（2）山坡的坡度tanα．（参考数据sin26.6°≈0.45，tan26.6°≈0.50；sin31°≈0.52，ta n31°≈0.60）19．随着柴静纪录片《穹顶之下》的播出，全社会对空气污染问题越来越重视，空气净化器的销量也大增，商社电器从厂家购进了A，B两种型号的空气净化器，已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元，用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同．（1）求一台A型空气净化器和一台B型空气净化器的进价各为多少元？（2）在销售过程中，A型空气净化器因为净化能力强，噪音小而更受消费者的欢迎．为了增大B型空气净化器的销量，商社电器决定对B型空气净化器进行降价销售，经市场调查，当B型空气净化器的售价为1800元时，每天可卖出4台，在此基础上，售价每降低50元，每天将多售出1台，如果每天商社电器销售B型空气净化器的利润为3200元，请问商社电器应将B型空气净化器的售价定为多少元？20．在平面直角坐标系中，一次函数y=ax+b（a≠0）的图形与反比例函数y=（k≠0）的图象交于第二、四象限内的A、B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH=3，tan∠AOH=，点B的坐标为（m，﹣2）．（1）求△AHO的周长；（2）求该反比例函数和一次函数的解析式．21．如图，在Rt△ABC中，∠BAC=90°，O是AB边上的一点，以OA为半径的⊙O与边BC相切于点E．（1）若AC=6，BC=10，求⊙O的半径．（2）过点E作弦EF⊥AB于M，连接AF，若∠AFE=2∠ABC，求证：四边形ACEF是菱形．22．在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B、C重合），以AD为边在AD 的右侧作正方形ADEF，连接CF．（1）观察猜想：如图（1），当点D在线段BC上时，①BC与CF的位置关系是：；②BC、CD、CF之间的数量关系为：（将结论直接写在横线上）（2）数学思考：如图（2），当点D在线段CB的延长线上时，上述①、②中的结论是否仍然成立？若成立，请给予证明，若不成立，请你写出正确结论再给予证明．23．如图，抛物线y=ax2﹣2ax+c（a≠0）与y轴交于点C（0，4），与x轴交于点A、B，点A坐标为（4，0）．（1）求该抛物线的解析式；（2）抛物线的顶点为N，在x轴上找一点，使C+N最小，并求出点的坐标；（3）点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ．当△CQE的面积最大时，求点Q的坐标；（4）若平行于x轴的动直线l与该抛物线交于点P，与直线AC交于点F，点D的坐标为（2，0）．问：是否存在这样的直线l，使得△ODF是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．2017年河南省三门峡市中考数学一模试卷参考答案与试题解析一、选择题（每题3分，共30分）1．的倒数是（）A．﹣B．C．D．【考点】28：实数的性质．【分析】根据倒数的定义求解即可．【解答】解：的倒数是，故选：C．2．改革开放以来，我国国内生产总值由2006年的3645亿元增长到2016年的300 670亿元．将300 670用科学记数法表示应为（）A．0.30067×106B．3.0067×105C．3.0067×104D．30.067×104【考点】1I：科学记数法—表示较大的数．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：将300 670用科学记数法表示应为3.0067×105，故选：B．3．如图是婴儿车的平面示意图，其中AB∥CD，∠1=120°，∠3=40°，那么∠2的度数为（）A．80° B．90° C．100°D．102°【考点】JA：平行线的性质．【分析】根据平行线性质求出∠A，根据三角形外角性质得出∠2=∠1﹣∠A，代入求出即可．【解答】解：∵AB∥CD，∴∠A=∠3=40°，∵∠1=120°，∴∠2=∠1﹣∠A=80°，故选A．4．小明因流感在医院观察，要掌握他在一周内的体温是否稳定，则医生需了解小明7天体温的（）A．众数 B．方差 C．平均数D．频数【考点】WA：统计量的选择．【分析】根据方差的含义和求法，可得：小明因流感在医院观察，要掌握他在一周内的体温是否稳定，则医生需了解小明7天体温的方差．【解答】解：小明因流感在医院观察，要掌握他在一周内的体温是否稳定，则医生需了解小明7天体温的方差．故选：B．5．几个棱长为1的正方体组成的几何体的三视图如图所示，则这个几何体的体积是（）A．4 B．5 C．6 D．7【考点】U3：由三视图判断几何体．【分析】根据三视图，该几何体的主视图以及俯视图可确定该几何体共有两行三列，故可得出该几何体的小正方体的个数，即可得出这个几何体的体积．【解答】解：综合三视图可知，这个几何体的底层应该有3+1=4个小正方体，第二层应该有1个小正方体，因此搭成这个几何体所用小正方体的个数是4+1=5个，所以这个几何体的体积是5．故选：B．6．若关于x的一元二次方程（k﹣1）x2+2x﹣2=0有不相等实数根，则k的取值范围是（）A．k＞B．k≥C．k＞且k≠1 D．k≥且k≠1【考点】AA：根的判别式；A1：一元二次方程的定义．【分析】根据判别式的意义得到△=22﹣4（k﹣1）×（﹣2）＞0，然后解不等式即可．【解答】解：∵关于x的一元二次方程（k﹣1）x2+2x﹣2=0有不相等实数根，∴△=22﹣4（k﹣1）×（﹣2）＞0，解得k＞；且k﹣1≠0，即k≠1．故选：C．7．一个袋子中装有3个红球和2个黄球，这些球的形状、大小、质地完全相同，在看不到球的条件下，随机从袋中摸出2个球，其中2个球颜色不相同的概率是（）A．B．C．D．【考点】6：列表法与树状图法．【分析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与其中2个球的颜色不相同的情况，再利用概率公式求解即可求得答案．【解答】解：画树形图得：∵共有20种等可能的结果，其中2个球的颜色不相同的有12种情况，∴其中2个球的颜色不相同的概率是=；故选D．8．如图，已知OP平分∠AOB，∠AOB=60°，CP=2，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．如果点M是OP的中点，则DM的长是（）A．2 B．C．D．【考点】F：角平分线的性质；O：含30度角的直角三角形；P：直角三角形斜边上的中线；Q：勾股定理．【分析】由OP平分∠AOB，∠AOB=60°，CP=2，CP∥OA，易得△OCP是等腰三角形，∠COP=30°，又由含30°角的直角三角形的性质，即可求得PE的值，继而求得OP的长，然后由直角三角形斜边上的中线等于斜边的一半，即可求得DM的长．【解答】解：∵OP平分∠AOB，∠AOB=60°，∴∠AOP=∠COP=30°，∵CP∥OA，∴∠AOP=∠CPO，∴∠COP=∠CPO，∴OC=CP=2，∵∠PCE=∠AOB=60°，PE⊥OB，∴∠CPE=30°，∴CE=CP=1，∴PE==，∴OP=2PE=2，∵PD⊥OA，点M是OP的中点，∴DM=OP=．故选：C．9．如图所示，⊙O是以坐标原点O为圆心，4为半径的圆，点P的坐标为（，），弦AB经过点P，则图中阴影部分面积的最小值等于（）A．2π﹣4 B．4π﹣8 C．D．【考点】MO：扇形面积的计算；D5：坐标与图形性质．【分析】由题意当OP⊥AB时，阴影部分的面积最小，求出AB的长，∠AOB的大小即可解决问题．【解答】解：由题意当OP⊥AB时，阴影部分的面积最小，∵P（，），∴OP=2，∵OA=OB=4，∴PA=PB=2，∴tan∠AOP=tan∠BOP=，∴∠AOP=∠BOP=60°，∴∠AOB=120°，∴S阴=S扇形OAB﹣S△AOB=﹣•2=，故选D．10．二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法：①2a+b=0，②当﹣1≤x≤3时，y＜0；③3a+c=0；④若（x1，y1）（x2、y2）在函数图象上，当0＜x1＜x2时，y1＜y2，其中正确的是（）A．①②④B．①③ C．①②③D．①③④【考点】H4：二次函数图象与系数的关系．【分析】由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．【解答】解：∵函数图象的对称轴为：x=﹣==1，∴b=﹣2a，即2a+b=0，①正确；由图象可知，当﹣1＜x＜3时，y＜0，②错误；由图象可知，当x=1时，y=0，∴a﹣b+c=0，∵b=﹣2a，∴3a+c=0，③正确；∵抛物线的对称轴为x=1，开口方向向上，∴若（x1，y1）、（x2，y2）在函数图象上，当1＜x1＜x2时，y1＜y2；当x1＜x2＜1时，y1＞y2；故④错误；故选：B．二、填空题（每题3分，共15分）11．如果代数式有意义，那么字母x的取值范围是x≥﹣1且x≠2 ．【考点】72：二次根式有意义的条件；62：分式有意义的条件．【分析】先根据分式及二次根式有意义的条件列出关于x的不等式组，求出x的取值范围即可．【解答】解：∵代数式有意义，∴，解得x≥﹣1且x≠2．故答案为：x≥﹣1且x≠2．12．如图，⊙O的半径为4，△ABC是⊙O的内接三角形，连接OB、OC，若∠BAC和∠BOC互补，则弦BC 的长度为4．【考点】MA：三角形的外接圆与外心；M2：垂径定理．【分析】首先过点O作OD⊥BC于D，由垂径定理可得BC=2BD，又由圆周角定理，可求得∠BOC的度数，然后根据等腰三角形的性质，求得∠OBC的度数，利用余弦函数，即可求得答案．【解答】解：过点O作OD⊥BC于D，则BC=2BD，∵△ABC内接于⊙O，∠BAC与∠BOC互补，∴∠BOC=2∠A，∠BOC+∠A=180°，∴∠BOC=120°，∵OB=OC，∴∠OBC=∠OCB==30°，∵⊙O的半径为4，∴BD=OB•cos∠OBC=4×=2，∴BC=4．故答案为：4．13．如图所示，AB∥CD∥EF，AC与BD相交于点E，若CE=4，CF=3，AE=BC，则的值是．【考点】S4：平行线分线段成比例．【分析】先利用AB∥EF得到=，则可求出解得AE=12，然后利用AB∥CD，根据平行线分线段成比例定理可求出的值．【解答】解：∵AB∥EF，∴=，∵CE=4，CF=3，AE=BC，∴=，解得AE=12，∵AB∥CD，∴===．故答案为．14．如图，矩形OABC的边OA、OC分别在x轴、y轴上，点B的坐标为（7，3），点E在边AB上，且AE=1，已知点P为y轴上一动点，连接EP，过点O作直线EP的垂线段，垂足为点H，在点P从点F（0，）运动到原点O的过程中，点H的运动路径长为．【考点】O4：轨迹；D5：坐标与图形性质．【分析】H经过的路径是以OE为直径的弧，连接OE，首先求得△OPE的面积，然后利用三角形面积公式求得OH的长，然后在直角△OEH中，利用三角函数求得∠OEH的度数，然后利用长公式即可求解．【解答】解：连接OE．S△OPE=××7=，在直角△OEA中，OE====5，PE==，∵S△OPE=PE•OH，即×OH=，∴OH=5，∴在直角△OEH中，sin∠OEH===，∴∠OEH=45°，点H的运动路径长是： =．故答案是：．15．如图，在Rt△ABC中，∠ACB=90°，AB=5，AC=3，点D是BC上一动点，连结AD，将△ACD沿AD折叠，点C落在点C′，连结C′D交AB于点E，连结BC′．当△BC′D是直角三角形时，DE的长为或．【考点】PB：翻折变换（折叠问题）．【分析】点E与点C′重合时．在Rt△ABC中，由勾股定理可求得BC=4，由翻折的性质可知：AE=AC=3、DC=DE．则EB=2．设DC=ED=x，则BD=4﹣x．在Rt△DBE中，依据勾股定理列方程求解即可；当∠EDB=90时．由翻折的性质可知：AC=AC′，∠C=∠C′=90°，然后证明四边形ACDC′为正方形，从而求得DB=1，然后证明DE∥AC，△BDE∽△BCA，依据相似三角形的性质可求得DE=．【解答】解：如图1所示；点E与点C′重合时．在Rt△ABC中，BC==4．由翻折的性质可知；AE=AC=3、DC=DE．则EB=2．设DC=ED=x，则BD=4﹣x．在Rt△DBE中，DE2+BE2=DB2，即x2+22=（4﹣x）2．解得：x=．∴DE=．如图2所示：∠EDB=90时．由翻折的性质可知：AC=AC′，∠C=∠C′=90°．∵∠C=∠C′=∠CDC′=90°，∴四边形ACDC′为矩形．又∵AC=AC′，∴四边形ACDC′为正方形．∴CD=AC=3．∴DB=BC﹣DC=4﹣3=1．∵DE∥AC，∴△BDE∽△BCA．∴，即．解得：DE=．点D在CB上运动，∠DBC′＜90°，故∠DBC′不可能为直角．故答案为：或．三、解答题（共8个小题，满分75分）16．先化简，再求值：（）÷（﹣1），其中a是满足不等组的整数解．【考点】6D：分式的化简求值；CC：一元一次不等式组的整数解．【分析】先算括号内的减法（通分后化成同分母的分式，再按同分母的分式相加减法则计算），同时把除法变成乘法，再根据分式的乘法法则进行计算，求出不等式组的整数解，取使分式有意义的数代入求出即可．【解答】解：（）÷（﹣1）=•=•=，∵解不等式组得＜a＜5，∴a=2，3，4，∵原式中a≠0，2，4，∴a=3，∴当a=3时，原式==1．17．小明在学习了数据的收集、整理与描述后，为妈妈整理记录了10月份的家庭支出情况，并绘制成如下尚不完整的统计图表，请你根据图表信息完成下列各题：项目物业费伙食费服装费其他费金额/元800 400（1）10月份小明家共支出多少元？（2）在扇形统计图中，表示“其他费”的扇形圆心角为多少度？（3）请将表格补充完整；（4）请将条形统计图补充完整．【考点】VC：条形统计图；VA：统计表；VB：扇形统计图．【分析】（1）根据题意列式计算即可；（2）“其他费”的扇形圆心角为用360°去乘以“其他费”所占的百分比即可得到结论；（3）小明家共支出的费用乘以伙食费、服装费所占的百分数即可得到结论；（4）根据题意补充条形统计图即可；【解答】解：（1）10月份小明家共支出800÷16%=5000（元）；（2）“其他费”的扇形圆心角为360°×（1﹣40%﹣36%﹣16%）=28.8°；（3）伙食费=5000×36%=1800元；服装费=5000×40%=2000元；故答案为：1800，2000；（4）补充条形统计图如图所示；18．如图所示，某工程队准备在山坡（山坡视为直线l）上修一条路，需要测量山坡的坡度，即tanα的值．测量员在山坡P处（不计此人身高）观察对面山顶上的一座铁塔，测得塔尖C的仰角为31°，塔底B的仰角为26.6°．已知塔高BC=40米，塔所在的山高OB=240米，OA=300米，图中的点O、B、C、A、P在同一平面内．求：（1）P到OC的距离．（2）山坡的坡度tanα．（参考数据sin26.6°≈0.45，tan26.6°≈0.50；sin31°≈0.52，tan31°≈0.60）【考点】TA：解直角三角形的应用﹣仰角俯角问题；T9：解直角三角形的应用﹣坡度坡角问题．（1）过点P作PD⊥OC于D，PE⊥OA于E，则四边形ODPE为矩形，先解Rt△PBD，得出BD=PD•tan26.6°；【分析】解Rt△CPD，得出CD=PD•tan31°；再根据CD﹣BD=BC，列出方程，求出PD=400即可求得点P到OC的距离；（2）利用求得的线段PD的长求出PE=40，AE=100，然后在△APE中利用三角函数的定义即可求解．【解答】解：（1）如图，过点P作PD⊥OC于D，PE⊥OA于E，则四边形ODPE为矩形．在Rt△PBD中，∵∠BDP=90°，∠BPD=26.6°，∴BD=PD•tan∠BPD=PD•tan26.6°；在Rt△CPD中，∵∠CDP=90°，∠CPD=31°，∴CD=PD•tan∠CPD=PD•tan31°；∵CD﹣BD=BC，∴PD•tan31°﹣PD•tan26.6°=40，∴0.60PD﹣0.50PD=40，解得PD=400（米），∴P到OC的距离为400米；（2）在Rt△PBD中，BD=PD•tan26.6°≈400×0.50=200（米），∵OB=240米，∴PE=OD=OB﹣BD=40米，∵OE=PD=400米，∴AE=OE﹣OA=400﹣300=100（米），∴tanα===0.4，∴坡度为0.4．19．随着柴静纪录片《穹顶之下》的播出，全社会对空气污染问题越来越重视，空气净化器的销量也大增，商社电器从厂家购进了A，B两种型号的空气净化器，已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元，用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同．（1）求一台A型空气净化器和一台B型空气净化器的进价各为多少元？（2）在销售过程中，A型空气净化器因为净化能力强，噪音小而更受消费者的欢迎．为了增大B型空气净化器的销量，商社电器决定对B型空气净化器进行降价销售，经市场调查，当B型空气净化器的售价为1800元时，每天可卖出4台，在此基础上，售价每降低50元，每天将多售出1台，如果每天商社电器销售B型空气净化器的利润为3200元，请问商社电器应将B型空气净化器的售价定为多少元？【考点】AD：一元二次方程的应用；B7：分式方程的应用．【分析】（1）设每台B种空气净化器为x元，A种净化器为（x+300）元，根据用6000元购进B种空气净化器的数量与用7500元购进A种空气净化器的数量相同，列方程求解；（2）根据总利润=单件利润×销量列出一元二次方程求解即可．【解答】解：（1）设每台B型空气净化器为x元，A型净化器为（x+300）元，由题意得， =，解得：x=1200，经检验x=1200是原方程的根，则x+300=1500，答：每B型空气净化器、每台A型空气净化器的进价分别为1200元，1500元；（2）设B型空气净化器的售价为x元，根据题意得；（x﹣1200）（4+）=3200，解得：x=1600，答：如果每天商社电器销售B型空气净化器的利润为3200元，请问商社电器应将B型空气净化器的售价定为1600元．20．在平面直角坐标系中，一次函数y=ax+b（a≠0）的图形与反比例函数y=（k≠0）的图象交于第二、四象限内的A、B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH=3，tan∠AOH=，点B的坐标为（m，﹣2）．（1）求△AHO的周长；（2）求该反比例函数和一次函数的解析式．【考点】G8：反比例函数与一次函数的交点问题．【分析】（1）根据正切函数，可得AH的长，根据勾股定理，可得AO的长，根据三角形的周长，可得答案；（2）根据待定系数法，可得函数解析式．【解答】解：（1）由OH=3，tan∠AOH=，得AH=4．即A（﹣4，3）．由勾股定理，得AO==5，△AHO的周长=AO+AH+OH=3+4+5=12；（2）将A点坐标代入y=（k≠0），得k=﹣4×3=﹣12，反比例函数的解析式为y=；当y=﹣2时，﹣2=，解得x=6，即B（6，﹣2）．将A、B点坐标代入y=ax+b，得，解得，一次函数的解析式为y=﹣x+1．21．如图，在Rt△ABC中，∠BAC=90°，O是AB边上的一点，以OA为半径的⊙O与边BC相切于点E．（1）若AC=6，BC=10，求⊙O的半径．（2）过点E作弦EF⊥AB于M，连接AF，若∠AFE=2∠ABC，求证：四边形ACEF是菱形．【考点】MC：切线的性质；Q：勾股定理；L9：菱形的判定．【分析】（1）连接OE，设圆的半径为r，在直角三角形ABC中，利用勾股定理求出AB的长，根据BC与圆相切，得到OE垂直于BC，进而得到一对直角相等，再由一对公共角，利用两角相等的三角形相似得到△BOE与△ABC相似，由相似得比例求出r的值即可；（2）利用同弧所对的圆周角相等，得到∠AOE=4∠B，进而求出∠B与∠F的度数，根据EF与AD垂直，得到一对直角相等，确定出∠MEB=∠F=60°，CA与EF平行，进而得到CB与AF平行，确定出四边形ACEF 为平行四边形，再由∠CAB为直角，得到CA为圆的切线，利用切线长定理得到CA=CE，利用邻边相等的平行四边形为菱形即可得证．【解答】（1）解：连接OE，设圆O半径为r，在Rt△ABC中，AC=6，BC=10，根据勾股定理得：AB==8，∵BC与圆O相切，∴OE⊥BC，∴∠OEB=∠BAC=90°，∵∠B=∠B，∴△BOE∽△BCA，∴=，即=，解得：r=3；（2）∵=，∠AFE=2∠ABC，∴∠AOE=2∠AFE=4∠ABC，∵∠AOE=∠OEB+∠ABC，∴∠ABC=30°，∠F=60°，∵EF⊥AD，∴∠EMB=∠CAB=90°，∴∠MEB=∠F=60°，CA∥EF，∴CB∥AF，∴四边形ACEF为平行四边形，∵∠CAB=90°，OA为半径，∴CA为圆O的切线，∵BC为圆O的切线，∴CA=CE，∴平行四边形ACEF为菱形．22．在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B、C重合），以AD为边在AD 的右侧作正方形ADEF，连接CF．（1）观察猜想：如图（1），当点D在线段BC上时，①BC与CF的位置关系是：BC⊥CF ；②BC、CD、CF之间的数量关系为：BC=CF+CD （将结论直接写在横线上）（2）数学思考：如图（2），当点D在线段CB的延长线上时，上述①、②中的结论是否仍然成立？若成立，请给予证明，若不成立，请你写出正确结论再给予证明．【考点】LO：四边形综合题．【分析】（1）①根据正方形的性质得到∠BAC=∠DAF=90°，推出△DAB≌△FAC，根据全等三角形的性质即可得到结论；②由正方形ADEF的性质可推出△DAB≌△FAC，根据全等三角形的性质得到CF=BD，∠ACF=∠ABD，根据余角的性质即可得到结论；（2）根据正方形的性质得到∠BAC=∠DAF=90°，推出△DAB≌△FAC，根据全等三角形的性质以及等腰直角三角形的角的性质可得到结论．【解答】解：（1）①正方形ADEF中，AD=AF，∵∠BAC=∠DAF=90°，∴∠BAD=∠CAF，在△DAB与△FAC中，∵，∴△DAB≌△FAC，∴∠B=∠ACF，∴∠ACB+∠ACF=90°，即BC⊥CF；故答案为：BC⊥CF；②△DAB≌△FAC，∴CF=BD，∵BC=BD+CD，∴BC=CF+CD；故答案为：BC=CF+CD；（2）CF⊥BC成立；BC=CD+CF不成立，CD=CF+BC．∵正方形ADEF中，AD=AF，∵∠BAC=∠DAF=90°，∴∠BAD=∠CAF，在△DAB与△FAC中，∵，∴△DAB≌△FAC，∴∠ABD=∠ACF，∵∠BAC=90°，AB=AC，∴∠ACB=∠ABC=45°．∴∠ABD=180°﹣45°=135°，∴∠BCF=∠ACF﹣∠ACB=135°﹣45°=90°，∴CF⊥BC．∵CD=DB+BC，DB=CF，∴CD=CF+BC．23．如图，抛物线y=ax2﹣2ax+c（a≠0）与y轴交于点C（0，4），与x轴交于点A、B，点A坐标为（4，0）．（1）求该抛物线的解析式；（2）抛物线的顶点为N，在x轴上找一点，使C+N最小，并求出点的坐标；（3）点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ．当△CQE的面积最大时，求点Q的坐标；（4）若平行于x轴的动直线l与该抛物线交于点P，与直线AC交于点F，点D的坐标为（2，0）．问：是否存在这样的直线l，使得△ODF是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．【考点】HF：二次函数综合题．【分析】（1）把A、C两点坐标代入抛物线解析式可求得a、c的值，可求得抛物线解析；（2）可求得点C关于x轴的对称点C′的坐标，连接C′N交x轴于点，再求得直线C′的解析式，可求得点坐标；（3）过点E作EG⊥x轴于点G，设Q（m，0），可表示出AB、BQ，再证明△BQE≌△BAC，可表示出EG，可得出△CQE关于m的解析式，再根据二次函数的性质可求得Q点的坐标；（4）分DO=DF、FO=FD和OD=OF三种情况，分别根据等腰三角形的性质求得F点的坐标，进一步求得P点坐标即可．【解答】解：（1）∵抛物线经过点C（0，4），A（4，0），∴，解得，∴抛物线解析式为y=﹣；（2）由（1）可求得抛物线顶点为N（1，），如图1，作点C关于x轴的对称点C′（0，﹣4），连接C′N交x轴于点，则点即为所求，设直线C′N的解析式为y=kx+b，把C′、N点坐标代入可得，解得，∴直线C′N的解析式为y=，令y=0，解得x=，∴点的坐标为（，0）；（3）设点Q（m，0），过点E作EG⊥x轴于点G，如图2，由﹣=0，得x1=﹣2，x2=4，∴点B的坐标为（﹣2，0），AB=6，BQ=m+2，又∵QE∥AC，∴△BQE≌△BAC，∴，即，解得EG=；∴S△CQE=S△CBQ﹣S△EBQ===．又∵﹣2≤m≤4，∴当m=1时，S△CQE有最大值3，此时Q（1，0）；（4）存在．在△ODF中，（ⅰ）若DO=DF，∵A（4，0），D（2，0），∴AD=OD=DF=2．又在Rt△AOC中，OA=OC=4，∴∠OAC=45°．∴∠DFA=∠OAC=45°．∴∠ADF=90°．此时，点F的坐标为（2，2）．由﹣=2，得x1=1+，x2=1﹣．此时，点P的坐标为：P1（1+，2）或P2（1﹣，2）；（ⅱ）若FO=FD，过点F作FM⊥x轴于点M．由等腰三角形的性质得：OM=OD=1，∴AM=3．∴在等腰直角△AMF中，MF=AM=3．∴F（1，3）．由﹣=3，得x1=1+，x2=1﹣．此时，点P的坐标为：P3（1+，3）或P4（1﹣，3）；（ⅲ）若OD=OF，∵OA=OC=4，且∠AOC=90°．∴AC=4．∴点O到AC的距离为2．而OF=OD=2＜2，与OF≥2矛盾．∴在AC上不存在点使得OF=OD=2．此时，不存在这样的直线l，使得△ODF是等腰三角形．综上所述，存在这样的直线l，使得△ODF是等腰三角形．所求点P的坐标为：（1+，2）或（1﹣，2）或（1+，3）或（1﹣，3）．中考模拟数学试卷满分120分, 考试时间100分钟.一、仔细选一选（本题有10个小题，每小题3分，共30分） 1．下列计算正确的是（ ） A ．347a a a +=B ．347a a a ⋅=C ．347()a a =D ．632a a a ÷=2．温家宝总理强调，“十二五”期间，将新建保障性住房36 000 000套，用于解决中低收入和新参加工作的大学生住房的需求．把36 000 000用科学记数法表示应是（ ） A. 3.6×107B. 3.6×106C. 36×106D. 0.36×1083. 如图，已知△ABC 中，∠ABC=45°，F 是高AD 和BE 的交点，CD=4，则线段DF 的长度为（ ） A ．22B ． 4C ．32D ．424.如图，一束光线从y 轴上点A （0，1）发出，经过x 轴上点C 反射后，经过点B （6，2），则光线从A 点到B 点经过的路线长度为（ ）A ．6B ．37C ．35D ．85．用四个全等的矩形和一个小正方形拼成如图所示的大正方形，已知大正方形的面积是144，小正方形的面积是4,若用x ，y 表示矩形的长和宽(x ＞y)，则下列关系式中不正确的是（ ） A. x+y=12 B. x －y=2． C. xy=35 D. x 2＋y 2=1446．已知1212,1212+--=+-=--xx x x N M ，x 为整数，则N M ,的大小关系是（ ） A. N M > B. N M = C. N M < D. 无法确定7．如图，△MBC 中，∠B=90°，∠C=60°，MB=23，点A 在MB 上，以AB 为直径作⊙O 与MC 相切于点D ，则CD 的长为（ ）A. 2B. 3C. 2D. 3 8．如图，A 、B 是双曲线 y ＝kx (k ＞0) 上的点， A 、B 两点的横坐标分别是a 、2a ，线段AB 的延长线交x 轴于点C ，若S △AOC ＝6．则k 的值为( ) A.1 B.2 C.4 D.无法确定9．Rt △ABC 中，∠C=90°，c b a 、、分别是∠A 、∠B 、∠C 的对边，那么c 等于 （ ） A.cos sin a A b B + B.sin sin a A b B + C.B b A a sin sin + D.BbA a sin cos + yxO BCA第7题第8题图第15题图10.如图，P 是菱形ABCD 的对角线AC 上一动点，过P 垂直于AC 的直线交菱形ABCD 的边于M 、N 两点，设AC=2，BD=1，AP=x ，则△AMN 的面积为y ，则y 关于x 的函数图象的大致形状是（ ）A. B. C. D. 二、认真填一填（本题有6小题，每小题4分，共24分）11.多项式324x x -+在实数范围进行因式分解可得 .12.如图，已知△ABC 是等边三角形，点B 、C 、D 、E 在同一直线上，且CG=CD ，DF=DE ，则∠E ＝ 度． 13.用一张半径为24cm 的扇形纸片做一个如图所示的圆锥形小丑帽子侧面（接缝忽略不计），如果做成的圆锥形小丑帽子的底面半径为10cm ，那么这张扇形纸片的面积是 ． 14.线段a x y +-=21（1≤x ≤3），当a 的值由-1增加到2时，该线段运动所经过的平面区域的面积为 ．15.如图，若干全等正五边形排成环状．图中所示的是前3个五边形，要完成这一圆环还需要 个五边形．16.如图，有n+1个等腰梯形，上底、两腰长皆为1，下底长为2，且下底均在同一直线上，设四边形P 1M 1N 1N 2面积为S 1，四边形P 2M 2N 2N 3的面积为S 2，……，四边形P n M n N n N n+1的面积记为S n ，则S n = .三、全面答一答（本题有7小题，共66分） 17．计算（本小题满分6分） （1） 计算：－(1-)2012－(3.14－π)0×2sin30º＋2-1×4（2）先化简，再求值：（2-a ）（211--a a ）,其中2=a18．（本小题满分8分）如图在8×8的正方形格中建立直角坐标系，已知A （2，4），B （4，2）．C 是第一象限内的一个格点，由点C 与线段AB 组成一个以AB 为底，且腰长为无理数的等腰三角形．（1）填空：C 点的坐标是_ _____，△ABC 的面积是___________；（2）在图上将△ABC 绕点C 旋转180º得到△A 1B 1C 1，写出点A 1、B 1的坐标，以及在旋转过程中线段AB 所扫过的面积.第12题图第16题图M 4M 3M 2M 1第10题图yxO AB第13题图。

相关文档
最新文档