第二章控制系统的动态数学模型
合集下载
《控制工程基础》课程作业习题(含解答)
第一章概论本章要求学生了解控制系统的基本概念、研究对象及任务，了解系统的信息传递、反馈和反馈控制的概念及控制系统的分类，开环控制与闭环控制的区别；闭环控制系统的基本原理和组成环节。
学会将简单系统原理图抽象成职能方块图。
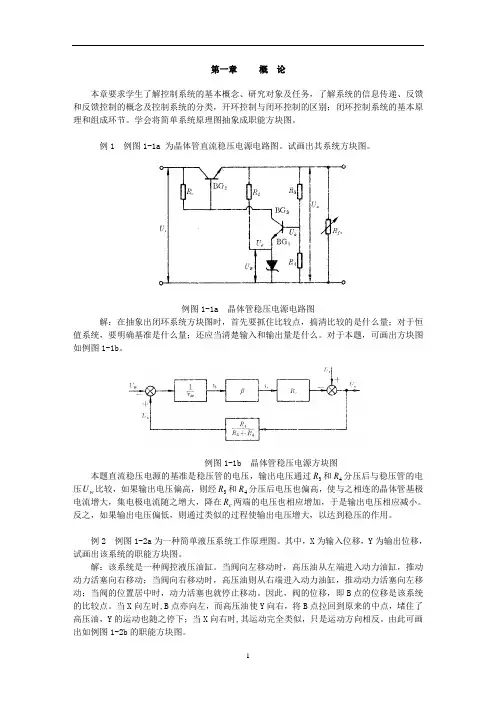
例1 例图1-1a 为晶体管直流稳压电源电路图。
试画出其系统方块图。
例图1-1a 晶体管稳压电源电路图解：在抽象出闭环系统方块图时，首先要抓住比较点，搞清比较的是什么量；对于恒值系统，要明确基准是什么量；还应当清楚输入和输出量是什么。
对于本题，可画出方块图如例图1-1b。
例图1-1b 晶体管稳压电源方块图本题直流稳压电源的基准是稳压管的电压，输出电压通过R和4R分压后与稳压管的电3压U比较，如果输出电压偏高，则经3R和4R分压后电压也偏高，使与之相连的晶体管基极w电流增大，集电极电流随之增大，降在R两端的电压也相应增加，于是输出电压相应减小。
c反之，如果输出电压偏低，则通过类似的过程使输出电压增大，以达到稳压的作用。
例2 例图1-2a为一种简单液压系统工作原理图。
其中，X为输入位移，Y为输出位移，试画出该系统的职能方块图。
解：该系统是一种阀控液压油缸。
当阀向左移动时，高压油从左端进入动力油缸，推动动力活塞向右移动；当阀向右移动时，高压油则从右端进入动力油缸，推动动力活塞向左移动；当阀的位置居中时，动力活塞也就停止移动。
因此，阀的位移，即B点的位移是该系统的比较点。
当X向左时,B点亦向左，而高压油使Y向右，将B点拉回到原来的中点，堵住了高压油，Y的运动也随之停下；当X向右时,其运动完全类似，只是运动方向相反。
由此可画出如例图1-2b的职能方块图。
例图1-2a 简单液压系统例图1-2b 职能方块图1．在给出的几种答案里，选择出正确的答案。
（1）以同等精度元件组成的开环系统和闭环系统，其精度比较为_______ （A ）开环高； （B ）闭环高； （C ）相差不多； （D ）一样高。
（2）系统的输出信号对控制作用的影响 （A ）开环有； （B ）闭环有； (C ）都没有； （D ）都有。
第2章_控制系统的动态数学模型_2.4传递函数以及典型环节的传递函数
X o ( s) 1 G( s) Fi ( s ) Ms 2 Ds K
【例】R-L-C无源电路网络的传递函数
已知系统的微分方程为：
d2 d LC 2 uc (t ) RC uc (t ) uc (t ) ur (t ) dt dt
所有初始条件均为零时，其拉氏变换为：
LCs 2U c (s) RCsU c (s) U c (s) U r (s)
n
m n bm K =K * (-Zi ) / ( p j ) an i 1 j 1
为传递函数的增益
b0 K a0
*
为根轨迹增益
Ti和 i 为时间常数
零、极点分布图：
G ( s) b0 (s z1 )(s z2 )(s zm ) M (s) a0 (s p1 )(s p2 )(s pn ) D(s)
r (t ) 1(t )
零状态响应分别为： c1 (t ) 1 2et 3e2t
c2 (t ) 1 0.5et 0.5e2t
各个模态在两个系统输出响应中所占的比重不同，
取决于零点相对于极点的距离。
j
z2
z1
0
（5）关于传递函数的几点说明
传递函数是一种以系统参数表示的线性定常系统输 入量与输出量之间的关系式。传递函数的概念通常只 适用于线性定常系统。 传递函数是复数自变量s的复变函数。传递函数中 的各项系数和相应微分方程中的各项系数对应相等， 完全取决于系统结构参数。
D(s)=0 称为系统的特征方程，其根称为系统的 特征根。特征方程决定着系统的动态特性。
D(s) 中s 的最高阶次等于系统的阶次。
将传递函数的分子和分母多项式进行因式分解可得
【例】R-L-C无源电路网络的传递函数
已知系统的微分方程为：
d2 d LC 2 uc (t ) RC uc (t ) uc (t ) ur (t ) dt dt
所有初始条件均为零时，其拉氏变换为：
LCs 2U c (s) RCsU c (s) U c (s) U r (s)
n
m n bm K =K * (-Zi ) / ( p j ) an i 1 j 1
为传递函数的增益
b0 K a0
*
为根轨迹增益
Ti和 i 为时间常数
零、极点分布图：
G ( s) b0 (s z1 )(s z2 )(s zm ) M (s) a0 (s p1 )(s p2 )(s pn ) D(s)
r (t ) 1(t )
零状态响应分别为： c1 (t ) 1 2et 3e2t
c2 (t ) 1 0.5et 0.5e2t
各个模态在两个系统输出响应中所占的比重不同，
取决于零点相对于极点的距离。
j
z2
z1
0
（5）关于传递函数的几点说明
传递函数是一种以系统参数表示的线性定常系统输 入量与输出量之间的关系式。传递函数的概念通常只 适用于线性定常系统。 传递函数是复数自变量s的复变函数。传递函数中 的各项系数和相应微分方程中的各项系数对应相等， 完全取决于系统结构参数。
D(s)=0 称为系统的特征方程，其根称为系统的 特征根。特征方程决定着系统的动态特性。
D(s) 中s 的最高阶次等于系统的阶次。
将传递函数的分子和分母多项式进行因式分解可得
第二章控制系统的数学模型.
2.2.1传递函数的定义和性质
⑴ 定义 线性定常系统的传递函数,定义为初始条件为零时,输出 量的拉氏变换与输入量的拉氏变换之比,记为G(S),即:
C ( s) G( s) R( s)
(2-4)
注：所有初始条件为零，指的是原系统处于静止状态. 设线性定常系统的n阶线性常微分方程为
dn d n 1 d a0 n c(t ) a1 n 1 c(t ) an 1 c(t ) an c(t ) dt dt dt dm d m1 d b0 m r (t ) b1 m 1 r (t ) bm1 r (t ) bm r (t ) dt dt dt
F(t)
K
F(t) F2(t)
m
f
m
x(t)
F1(t) b)
x(t)
根据牛顿第二运动定律有：
d 2 x (t ) F (t ) F1 (t ) F2 (t ) m dt2
a)
图2-2 机械位移系统
（2-2） 7
式中:
F1 (t ) ——阻尼器阻力。其大小与运动速度成正比，方向 与运动方向相反，阻尼系数为f，即： dx (t ) F1 (t ) f dt F2 (t ) ——弹簧力。设为线性弹簧，根据虎克定律有：
F2 (t ) Kx(t )
K——弹簧刚度 联立以上三式并整理得：
d 2 x (t ) dx(t ) m f Kx (t ) F (t ) 2 dt dt
（2-3） 8
综上所述,列写元件微分方程的步骤可归纳如下: ① 根据元件的工作原理及其在控制系统中的作用,确定其 输入量和输出量; ② 分析元件工作中所遵循的物理规律或化学规律,列写相 应的微分方程; ③ 消去中间变量,得到输出量与输入量之间关系的微分方 程,便是元件时域的数学模型. 9
基本要求-控制系统数学模型
航空工程学院航空工程实验中心
自动控制原理
第二章控制系统的数学模型
线性连续系统微分方程的一般形式
d c (t ) d c (t ) dc (t ) an an 1 ... a1 a0 c ( t ) n n 1 dt dt dt d m r (t ) d m 1r (t ) dr (t ) bm bm 1 ... b1 b0 r (t ) m m 1 dt dt dt
航空工程学院航空工程实验中心
自动控制原理
第二章控制系统的数学模型
• 3.表示形式 a.时域:微分﹑差分﹑状态方程 b.复域:传递函数﹑结构图 c.频域:频率特性
三种数学模型之间的关系 线性系统
拉氏 傅氏 传递函数 微分方程 频率特性 变换 变换
航空工程学院航空工程实验中心
自动控制原理
第二章控制系统的数学模型
自动控制原理
第二章控制系统的数学模型
题目变种3，寻求新解法
1 R1 cs I ( s) U ( s) U r ( s) c 1 R1 cs
Uc( s ) I (s) R2
联立，可解得： 微分方程为:
U c ( s) R2 (1 R1Cs) U r (s) R1 R2 R1 R2 Cs
微分方程的标准形式: 1、与输入量有关的项写在方程的右端； 2、与输出量有关的项写在方程的左端； 3、方成两端变量的导数项均按降幂排列
mx(t ) fx(t ) kx(t ) F (t )
航空
第二章控制系统的数学模型
电气系统三元件（知识补充）
电阻
航空工程学院航空工程实验中心
自动控制原理
第二章控制系统的数学模型
2.为什么要建立数学模型： 只是定性地了解系统的工作原理和大致的 运动过程是不够的，还要从理论上对系统 性能进行定量的分析和计算。 另一个原因：许多表面上看毫无共同之处 的控制系统，其运动规律具有相似性，可 以用相同形式的数学模型表示。
自动控制原理
第二章控制系统的数学模型
线性连续系统微分方程的一般形式
d c (t ) d c (t ) dc (t ) an an 1 ... a1 a0 c ( t ) n n 1 dt dt dt d m r (t ) d m 1r (t ) dr (t ) bm bm 1 ... b1 b0 r (t ) m m 1 dt dt dt
航空工程学院航空工程实验中心
自动控制原理
第二章控制系统的数学模型
• 3.表示形式 a.时域:微分﹑差分﹑状态方程 b.复域:传递函数﹑结构图 c.频域:频率特性
三种数学模型之间的关系 线性系统
拉氏 傅氏 传递函数 微分方程 频率特性 变换 变换
航空工程学院航空工程实验中心
自动控制原理
第二章控制系统的数学模型
自动控制原理
第二章控制系统的数学模型
题目变种3，寻求新解法
1 R1 cs I ( s) U ( s) U r ( s) c 1 R1 cs
Uc( s ) I (s) R2
联立，可解得： 微分方程为:
U c ( s) R2 (1 R1Cs) U r (s) R1 R2 R1 R2 Cs
微分方程的标准形式: 1、与输入量有关的项写在方程的右端； 2、与输出量有关的项写在方程的左端； 3、方成两端变量的导数项均按降幂排列
mx(t ) fx(t ) kx(t ) F (t )
航空
第二章控制系统的数学模型
电气系统三元件（知识补充）
电阻
航空工程学院航空工程实验中心
自动控制原理
第二章控制系统的数学模型
2.为什么要建立数学模型： 只是定性地了解系统的工作原理和大致的 运动过程是不够的，还要从理论上对系统 性能进行定量的分析和计算。 另一个原因：许多表面上看毫无共同之处 的控制系统，其运动规律具有相似性，可 以用相同形式的数学模型表示。
自动控制原理：第二章--控制系统数学模型全
TaTLma KJe K
dMdML m dtdt
L
Tm
Ra J K eKm
——机电时间常数(秒)；
Ta
La Ra
—电动机电枢回路时间常数 (秒)
若输出为电动机的转角q ，则有
TaTm
d 3q
dt 3
Tm
d 2q
dt 2
dq
dt
1 Ke
ua
Tm J
ML
TaTm J
dM L dt
—— 三阶线性定常微分方程 9
（1）根据克希霍夫定律可写出原始方程式
（（23））式消LuLCcdd中去(titd)i中2d是utRc间2(中Cti1)变间C1量iR变dCti量idd后udt，ct，(t它)u输r与u(入tc输)(输t)出出uu微rc((tt)分)有方如程下式关系
或
T1T2
d 2uc (t) dt 2
T2
duc (t) dt
扰动输入为负载转矩ML。 （1）列各元件方程式。电动机方程式为：
TaTm
d 2w
dt 2
测输T速Km出发td为d电wt电测压机速w 反 K馈1e系ua数
Tm J
M反L馈 电TaJT压m
dM L dt
ua Kae ut Ktw e ur ut 12
（2）消去中间变量。从以上各式中消去中间变
量ua，e，ut，最后得到系统的微分方程式
线性(或线性化)定常系统在零初始条件下， 输出量的拉氏变换与输入量的拉氏变换之比 称为传递函数。
令线C性(s定)=常L[c系(t统)]，由R下(s)述=Ln阶[r(微t)]分，方在程初描始述条：件为零
时[[aab，nnmbssdmdn进mt+ndn+dt行acmmbn(tm拉-r1)-(s1t氏ns)-am1变n+-1b1+…m换dd…1t+，nndd+1a1t得mm1bcs1(11到+ts)r+a关(t0b)]于0C]的RD(sM的s的a(()分s1s(分))=代sdbd为母)t1子为数cd传d多(tt多传方)r递项(项t程递函)式a式0函数c。b(0数tr) (t)
第二章_控制系统的数学模型
+
R
a
La
Ea
+
if -
i a (t ) U a (t )
m Mm
Jm fm
MC
dia ( t ) R a i a (t) E a dt E a C e m ( t ) u a La M m (t) M c (t) J m M m (t) C mi a (t) dm ( t ) f m m ( t ) dt
2.2 控制系统的复数域数学模型
1、传递函数的定义
在零初始条件下，线性定常系统输出量的拉普拉斯变 换与输入量的拉普拉斯变换之比，定义为线性定常系统 的传递函数。 即，
传递函数与输入、输出之间的关系，可用结构图表示:
若已知线性定常系统的微分方程为 dnc(t ) dn 1c(t ) dc(t ) a0 a1 a n 1 anc(t ) n n 1 dt dt dt m m 1 d r(t ) d r(t ) dr (t ) b0 b1 b m 1 b mr(t ) m m 1 dt dt dt
设 c(t)和r(t)及其各阶导数初始值均为零，对上 式取拉氏变换，得
(a0s a1s
n m
n 1
an 1s an )C(s)
(b 0s b1s
m 1
bm 1s bm )R(s)
则系统的传递函数为
C(s) b 0sm b1sm 1 bm 1s bm G (s ) R(s) a0sn a1sn 1 an 1s an
L[f (t )] e sF(s)
F ( s ) f ( 1 ) ( 0 ) ( 1 ) L[ f (t )dt ] , f (0) f (t )dt t 0 s s
R
a
La
Ea
+
if -
i a (t ) U a (t )
m Mm
Jm fm
MC
dia ( t ) R a i a (t) E a dt E a C e m ( t ) u a La M m (t) M c (t) J m M m (t) C mi a (t) dm ( t ) f m m ( t ) dt
2.2 控制系统的复数域数学模型
1、传递函数的定义
在零初始条件下，线性定常系统输出量的拉普拉斯变 换与输入量的拉普拉斯变换之比，定义为线性定常系统 的传递函数。 即，
传递函数与输入、输出之间的关系，可用结构图表示:
若已知线性定常系统的微分方程为 dnc(t ) dn 1c(t ) dc(t ) a0 a1 a n 1 anc(t ) n n 1 dt dt dt m m 1 d r(t ) d r(t ) dr (t ) b0 b1 b m 1 b mr(t ) m m 1 dt dt dt
设 c(t)和r(t)及其各阶导数初始值均为零，对上 式取拉氏变换，得
(a0s a1s
n m
n 1
an 1s an )C(s)
(b 0s b1s
m 1
bm 1s bm )R(s)
则系统的传递函数为
C(s) b 0sm b1sm 1 bm 1s bm G (s ) R(s) a0sn a1sn 1 an 1s an
L[f (t )] e sF(s)
F ( s ) f ( 1 ) ( 0 ) ( 1 ) L[ f (t )dt ] , f (0) f (t )dt t 0 s s
控制工程基础 清华大学 董景新 第二章 控制系统的动态数学模型
2.1 基本环节数学模型
数学模型是描述物理系统的运动规律、特性 和输入输出关系的一个或一组方程式。 系统的数学模型可分为静态和动态数学模型。 静态数学模型：反映系统处于平衡点（稳态） 时，系统状态有关属性变量之间关系的数学模型。 即只考虑同一时刻实际系统各物理量之间的数学 关系，不管各变量随时间的演化，输出信号与过 去的工作状态（历史）无关。因此静态模型都是 代数式，数学表达式中不含有时间变量。
控制工程基础
（第二章）
清华大学
第二章
2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9
控制系统的动态数学模型
基本环节数学模型 数学模型的线性化 拉氏变换及反变换 传递函数以及典型环节的传递函数 系统函数方块图及其简化 系统信号流图及梅逊公式 受控机械对象数学模型 绘制实际机电系统的函数方块图 状态空间方程
式中， a1 , a2 是常值，可由以下步骤求得 将上式两边乘 s j s j , 两边同 时令s j（或同时令s j ）， 得
a1s a2 s j X s s j s j s j
s3 例 试求 X s 2 s 3s 2
的拉氏反变换。
s 3 解： X s 2 s 3s 2 s3 s 1s 2 a1 a2 s 1 s 2
s3 a1 s 1 2 s 1s 2 s 1 s3 a2 s 2 1 s 1s 2 s 2 2 1 X s s 1 s 2 t 2t xt 2e e 1t
T st
2T T
xt e
st
n 1T dt
第二章 自动控制系统原理的数学模型分析
c(t ) a n1
d n1
c(t ) ... a1
d c (t ) a 0 c (t ) dt d r (t ) ... b1 r (t ) b0 r (t ) dt
在初始条件为零时，对方程两边进行拉氏变换并整理得
C ( s) bm s m bm 1 s m 1 b1 s b0 M ( s) G ( s) （2-25） n n 1 R( s ) N ( s) a n s a n 1 s a1 s a 0
一阶常系数线性微分方程
RC
duc uc ur dt
(2-4)
微分方程建立举例(2)
【例2-2】机械位移系统 （1）确定输入、输出量
设外作用力F (t ) 为输入量，质量 物体的位移 y (t )为输出量。
（2）建立微分方程组
根据牛顿第二定律可得:
F (t ) FB (t ) FK (t ) ma
初始条件为零，一般是指输入量在t=0时刻以后才 作用于系统，系统的输入量和输出量及其各阶导数在 t≤时的值也均为零。
传递函数的一般表达式
如果系统的输入量为 r (t ) ，输出量为 c(t ) ，并 由下列微分方程描述
an
bm
dn dt n dm
dt m
dt n1 d m 1 r (t ) bm 1d m 1 dt
c (t ) 1
式中
<1时
(2-44)
1 2
e n t 1 2
4.应用实例 例2-2机械位 移系统等。
sin( d t )
，
arctan
d n 1 2
R 将 R1 1 K 、 2 1 K 代入上式得： 2 1
第二章 控制系统的数学模型
= Ur (s)
传递函数为: di + u ur= R · + L i c dt Uc (s) 1 = duc G (s) = i = C dt Ur (s) LCs2 + RCs + 1
电气系统三要素：电阻、电容、电感
+ ί(t) R –
u(t)= ί(t)· R
u (t )
ί(t) C
–
u(t) ί(t)= R
图2-9 速度控制系统
+
R1 R2 R2 R1 k2
ui
R1
k1 u 1
c
u2
功 ua 放
m
SM
ω
负 载
ut
TG
运算放大器
uu+ ii+
_ +
+
Add
uo
差模输入电压等于零
u+= u-
运放同相输入端与反向输入端两点的电压相等，如同该 两点短路一样，称为虚短。
i+=i-=0
运放同相输入端与反向输入端的电流都等于零，如同该 两点被断开一样，称为虚断。
Tm s m ( s ) m (t ) K1U a ( s )
Tm s 1 m ( s) K1U a ( s)
m ( s) K1 G ( s) U a ( s) Tm s 1
m ( s) K2 G ( s) M c ( s) Tm s 1
传递函数的性质（续）
（5）传递函数与微分方程有相通性;
b1s b2 C (s) G ( s) R( s ) a0 s 2 a1s a2
对角线相乘
a0 s 2 a1s a2 C ( s ) b1s b2 R ( s )
控制工程基础 第二章 控制系统的数学模型
R1 ui C1 K
R2 C2 uc
U c ( s) K U i ( s ) ( R1C1s 1)( R2C2 s 1)
有源网络：
Ur R0
R1
C1 +12V
+
-12V
Uc
U c ( s) R1C1s 1 U r ( s) R0C1s
2-3 典型环节及其传递函数
环节：具有某种确定信息传递关系的元 件、元件组或元件的一部分称为一个环 节。 系统传递函数可写为：
例2 电学系统： 其中：电阻为R，电感为L，电容为C。
＋ ur(t) － i
＋ uc(t) －
解：系统的微分方程如下
d U c (t ) dUc (t ) LC RC U c (t ) U r (t ) 2 dt dt
2
拉氏变换后（零初始条件下）
U c ( s) 1 2 U r ( s ) LCs RCs 1
2 2
1 1 1 , 2 2 s Ts 1, T s 2Ts 1
各典型环节名称：
比例环节：K 一阶微分环节：s 1 2 2 s 二阶微分环节： 2 s 1 1 积分环节： s 1 惯性环节： 1 Ts 1 二阶振荡环节：2 s 2 2Ts 1 T
传递函数的性质： （1）传递函数只取决于系统或元件的结构和 参数，与输入输出无关； （2）传递函数概念仅适用于线性定常系统， 具有复变函数的所有性质； （3）传递函数是复变量s 的有理真分式， 即n≥m； （4）传递函数是系统冲激响应的拉氏变换；
传递函数的性质： （5）传递函数与真正的物理系统不存在一 一对应关系； （6）由于传递函数的分子多项式和分母多 项式的系数均为实数，故零点和极点可以是 实数，也可以是成对的共轭复数。
控制系统的动态数学模型
控制工程基础
2.1 系统的数学模型
数学模型是描述系统输入、输出量以及 内部各变量之间关系的数学表达式，它 揭示了系统结构及其参数与其性能之间 的内在关系。
静态数学模型 : 静态条件（变量各阶导
数为零）下描述变量之间关系的代数方 程。反映系统处于稳态时，系统状态有 关属性变量之间关系的数学模型。
控制工程基础
2.2 数学模型的线性化
线性化的提出： 线性系统是有条件存在的，只在一定的范围内 具有线性特性； 非线性系统的分析和综合是非常复杂的； 对于实际系统而言，在一定条件下，采用线性 化模型近似代替非线性模型进行处理，能够满 足实际。
控制工程基础
非线性系统数学模型的线性化
控制工程基础
非线性系统数学模型的线性化
增量方程的数学含义就是将参考坐标的原点移
到系统或元件的平衡工作点上，对于实际系统就是
以正常工作状态为研究系统运动的起始点，这时，
系统所有的初始条件均为零。 对多变量系统，如：y=f(x1,x2)，同样可采用 泰勒级数展开获得线性化的增量方程：数的拉式变换
幂函数(Power Function)：
函数的拉氏变换及反变换通常可以由拉氏变 换表直接或通过一定的转换得到。
控制工程基础
控制工程基础
拉氏变换积分下限的说明: 在某些情况下，函数 在t＝0处有一个脉冲函数。 这时必须明确拉氏变换的积分下限是0-还是0+， 并相应记为：
控制工程基础
拉普拉斯变换的定义
（1）当t<0时， ； t>0时， 区间上分段连续。 （2）存在一正实常数σ，使得： 为指数级的； 则函数 在任一有限
的拉普拉氏变换存在，并定义为： F (s) L f (t ) f (t )e st dt 0 s：拉普拉斯算子；Res> ；量纲为时间的倒数 f(t)：原函数（时间域）F(s)：象函数（复数域） L为拉氏变换的符号;
第二章 控制系统的数学模型
输出转速ω 既受ua控制，又受到ML 的影响。相当于具有
两个输人一个输出的线性系统，可以应用叠加原理进行分析。
如果忽略电枢电阻R 和电动机转动惯量J ，则Tm = 0 。
上式可变为 ω = cd ua 此时，电动机转速与电枢电压成正比。
2．1 控制系统微分方程的建立
三、系统的稳态数学模型
由直流电机例分析 如果电机处于平衡状态，则方程中各阶导数均为零。 此时微分方程变成代数方程，即
3.积分定理
若f(t) n重积分，各重积分在t=0 的值为0时，
2．2拉普拉斯变换及其应用——拉氏变换的几个重要运算定理
4．位移定理 ⑴实位移定理（时间坐标中有一个位移）
该定理又称延迟定理。 ⑵复位移定理（在复数s坐标中有一位移）
2．2拉普拉斯变换及其应用——拉氏变换的几个重要运算定理
5．终值定理 6．初值定理 Nhomakorabea2．1 控制系统微分方程的建立——例3
解 ua为给定输人，ML为干扰输人，ω 为输出。
据KVL 电枢回路方程：
据牛顿转动定律，电机转子的运动方程（动力学方程）：
当激磁磁通不变时，M与ia 成正比:
2．1 控制系统微分方程的建立——例3
将各式联立，消去中间变量M、ed、ia可得：
Ta ：电磁时间常数 Tm ：机电时间常数
4．整理微分方程，使其规范化，
将输出项放到方程左侧， 输人项放到方程右侧， 各阶导数项按阶次从高到低的顺序排列。
2．1 控制系统微分方程的建立
二、举例
例1：已知RLC 电路系
统如图所示，试列写其 输入—输出之间的微分 方程。
2．1 控制系统微分方程的建立
例2：带阻尼的弹簧系统( k-m-f )， 输入力x,输出位移y ， 试列写系统的微分方程。
两个输人一个输出的线性系统，可以应用叠加原理进行分析。
如果忽略电枢电阻R 和电动机转动惯量J ，则Tm = 0 。
上式可变为 ω = cd ua 此时，电动机转速与电枢电压成正比。
2．1 控制系统微分方程的建立
三、系统的稳态数学模型
由直流电机例分析 如果电机处于平衡状态，则方程中各阶导数均为零。 此时微分方程变成代数方程，即
3.积分定理
若f(t) n重积分，各重积分在t=0 的值为0时，
2．2拉普拉斯变换及其应用——拉氏变换的几个重要运算定理
4．位移定理 ⑴实位移定理（时间坐标中有一个位移）
该定理又称延迟定理。 ⑵复位移定理（在复数s坐标中有一位移）
2．2拉普拉斯变换及其应用——拉氏变换的几个重要运算定理
5．终值定理 6．初值定理 Nhomakorabea2．1 控制系统微分方程的建立——例3
解 ua为给定输人，ML为干扰输人，ω 为输出。
据KVL 电枢回路方程：
据牛顿转动定律，电机转子的运动方程（动力学方程）：
当激磁磁通不变时，M与ia 成正比:
2．1 控制系统微分方程的建立——例3
将各式联立，消去中间变量M、ed、ia可得：
Ta ：电磁时间常数 Tm ：机电时间常数
4．整理微分方程，使其规范化，
将输出项放到方程左侧， 输人项放到方程右侧， 各阶导数项按阶次从高到低的顺序排列。
2．1 控制系统微分方程的建立
二、举例
例1：已知RLC 电路系
统如图所示，试列写其 输入—输出之间的微分 方程。
2．1 控制系统微分方程的建立
例2：带阻尼的弹簧系统( k-m-f )， 输入力x,输出位移y ， 试列写系统的微分方程。
自动控制原理与应用第2章自动控制系统的数学模型
自动控制原理与应用第2章自动控制系统的数学模型自动控制是现代工业和科学技术的重要组成部分，它在各种自动化系统中起着关键作用。
通过对自动控制系统的数学建模，我们可以对系统的行为进行分析和预测，并设计合适的控制策略来实现系统的稳定性和性能要求。
本章主要介绍自动控制系统的数学模型及其应用。
自动控制系统的数学模型主要包括线性时不变系统和非线性时变系统两类。
1.线性时不变系统线性时不变系统是指系统的输出与输入之间存在线性关系，并且系统的性质不随时间的推移而变化。
线性时不变系统的数学模型可以用常微分方程或差分方程来表示，其中常微分方程适用于连续系统，差分方程适用于离散系统。
常见的线性时不变系统包括电路、机械系统等。
2.非线性时变系统非线性时变系统是指系统的输出与输入之间存在非线性关系，并且系统的性质随时间的推移而变化。
非线性时变系统的数学模型可以用偏微分方程、泛函方程等形式来表示。
非线性时变系统由于具有更复杂的动力学特性，通常需要借助数值方法来求解。
二、数学模型的建立方法建立自动控制系统的数学模型有多种方法，常用的方法包括物理模型法、数据模型法和状态空间法。
1.物理模型法物理模型法主要通过物理规律来建立系统的数学模型。
它基于系统的物理特性及其输入输出关系，通过建立微分方程或差分方程来描述系统的动态行为。
物理模型法适用于那些具有明确的物理意义和物理规律的系统。
例如，对机械系统可以利用牛顿定律建立系统的动力学方程。
2.数据模型法数据模型法是通过分析实验数据来建立系统的数学模型。
它基于系统的输入输出数据，借助统计方法和系统辨识技术来进行模型识别和参数估计。
数据模型法适用于那些难以建立明确物理模型的系统。
例如，对于生物系统或经验性系统，可以通过数据模型法来建立系统的数学模型。
3.状态空间法状态空间法是一种以状态变量和输出变量为基础的建模方法。
它将系统的动态行为表示为一组一阶微分方程或差分方程的形式。
状态空间法对于较复杂的系统具有较好的描述能力，能够反映系统的内部结构和动态特性。
自动控制理论-第二章
2-1 控制系统的时域数学模型
1、控制系统微分方程的建立 （1）举例 例1：电路无源网络 试列写以 u (t ) 为输入量，以 u (t )为 输出量的网络微分方程
i
o
解：设回路电流为 i(t ) ，由基尔霍夫 定律可写出回路方程为
di ( t ) 1 + i ( t ) dt + Ri ( t ) = u i ( t ) dt C ∫ 1 u o (t ) = i ( t ) dt C ∫ L
f 2 (t )
c(t ) = c1 (t )
作用时， c(t ) = c2 (t ) 叠加性：当 f (t ) 、 f (t ) 同时作用时，c(t ) = c1 (t ) + c2 (t ) 均匀性：当 f (t ) = A ⋅ f1 (t ) 时， c(t ) = A ⋅ c1 (t ) 线性系统的叠加原理表明：两个外作用同时加于系统所产生的 总输出，为各个外作用单独作用时分别产生的输出之和。
[
]
1 1 1 F ( s ) + n f ( −1) (0) + L + f ( − n ) (0) n s s s
式中
f
( −1)
f ( −1) (0)、f ( −2) (0) L f ( − n ) (0)
(−n)
为
f (t )
的各重积分在 t = 0 时的值。如果
(0) = f ( −2 ) (0) = L = f
(0) = 0 ，则有
L ∫ L ∫ f (t )(dt ) n =
[
]
1 F (s) sn
（4）初值定理 若函数 f (t ) 及其一阶导数都是可拉氏变换的，则
f (0 + ) = lim f (t ) = lim sF ( s)
第2章_控制系统的动态数学模型_2.6系统信号流图及梅逊公式
支路
混合节点
输入节点（源点）：只有输出的节点，表示系统的 输入变量。 输出节点（阱点、汇点） :只有输入的节点，表示 系统的输出变量。 混合节点：既有输入又有输出的节点，表示系统的 中间变量。如果从混合节点引出一条具有单位增益 的支路，则可以将混合节点变为输出节点，即成为 系统的输出变量。
支路
前向通路P1的特征式的余因子为： 1 1 将上述结果代入梅逊公式，计算该系统的传递 函数，化简后为：
1 1 P Pk k P 1 k k 1 = R1 R2C2C2 s 2 ( R1C 1 R2C2 R1C 2 ) s 1
【例3】用梅逊公式求系统传递函数 （说明：与教材P.45例2-21比较，去掉了G8、G9和-H3 等三个环节。）
信号流图 的特征式 系统的闭环传递 函数（也称为系 统总增益）
信号流图的特征式Δ的计算公式： 1 La Lb Lc Ld Le L f L 其中： a b ,c d ,e , f
a a
L 为所有不同回路的传递函数（增益）之和。
b c
L L 为每两个互不接触回路的传递函数（增益）
信号流图起源于梅逊（S. J. Mason）利用图 示法来描述一个或一组线性代数方程式，是由节点 和支路组成的一种信号传递网络。 节点：表示信号或变量，其值等于所有进入该节点 的信号之和。节点用小圆圈“ο”表示。 支路：连接两个节点的定向线段，用支路增益（即 传递函数）表示方程式中两个变量的因果关系。支 路相当于乘法器。信号在支路上沿箭头单向传递。
【例2】基于系统的信号流图，采用梅逊公式计算上例 系统的传递函数。
系统输入信号Ui(s)与输出信号Uo(s)之间只有一条 前向通路P1，即k=1，而且其传递函数（增益）为：
混合节点
输入节点（源点）：只有输出的节点，表示系统的 输入变量。 输出节点（阱点、汇点） :只有输入的节点，表示 系统的输出变量。 混合节点：既有输入又有输出的节点，表示系统的 中间变量。如果从混合节点引出一条具有单位增益 的支路，则可以将混合节点变为输出节点，即成为 系统的输出变量。
支路
前向通路P1的特征式的余因子为： 1 1 将上述结果代入梅逊公式，计算该系统的传递 函数，化简后为：
1 1 P Pk k P 1 k k 1 = R1 R2C2C2 s 2 ( R1C 1 R2C2 R1C 2 ) s 1
【例3】用梅逊公式求系统传递函数 （说明：与教材P.45例2-21比较，去掉了G8、G9和-H3 等三个环节。）
信号流图 的特征式 系统的闭环传递 函数（也称为系 统总增益）
信号流图的特征式Δ的计算公式： 1 La Lb Lc Ld Le L f L 其中： a b ,c d ,e , f
a a
L 为所有不同回路的传递函数（增益）之和。
b c
L L 为每两个互不接触回路的传递函数（增益）
信号流图起源于梅逊（S. J. Mason）利用图 示法来描述一个或一组线性代数方程式，是由节点 和支路组成的一种信号传递网络。 节点：表示信号或变量，其值等于所有进入该节点 的信号之和。节点用小圆圈“ο”表示。 支路：连接两个节点的定向线段，用支路增益（即 传递函数）表示方程式中两个变量的因果关系。支 路相当于乘法器。信号在支路上沿箭头单向传递。
【例2】基于系统的信号流图，采用梅逊公式计算上例 系统的传递函数。
系统输入信号Ui(s)与输出信号Uo(s)之间只有一条 前向通路P1，即k=1，而且其传递函数（增益）为：
第2章 控制系统动态数学模型1
25
2.1基本环节数学模型
2.1.3 直流电动机
电枢控制式直流电动机
+
绕组电阻
-
-
+
输入：ei(t) 输出：θo(t)
2.1基本环节学模型
26
直流电动机电枢绕组中的电枢电流Ia与磁通相互作用，产生电磁转矩 线圈在磁场中旋转，将在线圈中产生感应电动势
2.1基本环节数学模型
27
2.1.3 电动机
2.1基本环节数学模型
19
2.1.2 电气系统 电气系统三个基本元件
电阻 电容 电感
电阻
耗能元件
2.1基本环节数学模型
20
2.1.2 电气系统 电容
电感
2.1基本环节数学模型
21
2.1.2 RLC无源电路网络
不依靠外加电源的存在，就能独 立表现出其外特性的器件就是无 源器件
输入：ui(t) 输出：uO(t)
举例
一阵大风过后摇晃的树会慢慢停下 用手拨一下吉他的弦后声音会越来越小
2.1基本环节数学模型
14
2.1.1 机械运动系统的三要素 在机械系统中，多数阻尼以阻力形式出现
两物体表面的摩擦阻力 加入润滑剂后油膜的粘性阻力 物体在流体中运动受到的介质阻力 振荡电路中的电阻、材料和结构的内阻引起的结构阻尼
产生阻尼作用的原因有以下几种：
d (y ) d (y ) pL A M D 2 dt dt
2
联立方程，消去中间变量，得到线性方程
K c M d 2 (y ) K c D d (y ) A K q (x) 2 A dt A dt
K cM KcD (t ) K q x (t ) y( t ) Ay A A
2.1基本环节数学模型
2.1.3 直流电动机
电枢控制式直流电动机
+
绕组电阻
-
-
+
输入：ei(t) 输出：θo(t)
2.1基本环节学模型
26
直流电动机电枢绕组中的电枢电流Ia与磁通相互作用，产生电磁转矩 线圈在磁场中旋转，将在线圈中产生感应电动势
2.1基本环节数学模型
27
2.1.3 电动机
2.1基本环节数学模型
19
2.1.2 电气系统 电气系统三个基本元件
电阻 电容 电感
电阻
耗能元件
2.1基本环节数学模型
20
2.1.2 电气系统 电容
电感
2.1基本环节数学模型
21
2.1.2 RLC无源电路网络
不依靠外加电源的存在，就能独 立表现出其外特性的器件就是无 源器件
输入：ui(t) 输出：uO(t)
举例
一阵大风过后摇晃的树会慢慢停下 用手拨一下吉他的弦后声音会越来越小
2.1基本环节数学模型
14
2.1.1 机械运动系统的三要素 在机械系统中，多数阻尼以阻力形式出现
两物体表面的摩擦阻力 加入润滑剂后油膜的粘性阻力 物体在流体中运动受到的介质阻力 振荡电路中的电阻、材料和结构的内阻引起的结构阻尼
产生阻尼作用的原因有以下几种：
d (y ) d (y ) pL A M D 2 dt dt
2
联立方程，消去中间变量，得到线性方程
K c M d 2 (y ) K c D d (y ) A K q (x) 2 A dt A dt
K cM KcD (t ) K q x (t ) y( t ) Ay A A
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
微分方程 （时间域）
拉氏变换
拉氏反变换
代数方程 （复数域）
方块图 传递函数 信号流图
数学模型的形式 ➢ 时间域：微分方程（连续系统）
差分方程（离散系统） 状态方程
➢ 复数域：传递函数（连续系统） 脉冲传递函数（离散系统）
➢ 频率域：频率特性
§2-1 基本环节数学模型
例1 质量-弹簧-阻尼系统
牛顿 yo(t) 第二定 F律 M： a工件
其 — 正 中实
则 可 定 xt的 义拉 氏 变 XS换
XSLxt
e xt stdt 0
象函数
原函数
复变量 量纲 t 1
二、简单函数的拉氏变换
1. 单位阶跃函数 1t
1
1t
0 1
t0 t 0
0
t
L1t0 1tesd t t1 sest 01 s
动 力滑 台FitkyotfyotFM i(t) y ot
即： M y otfyotkyotFit
yo(t)
k
M
Fi(t)
f
例2 电路网络
ui
u C i1t
R1
i 2 t
it R 2
根 据 基 尔 霍 夫 定 律 和 欧姆 定 律 ， 有
o
i1t i2 t it
1
ui t uo t R1i2 t 2
对于一个控制系统，在一定的输 入作用下有些什么运动规律，我们不 仅希望了解其稳态情况，更重要的是 了解其动态过程。如果能将物理系统 在信号传递过程中的这一动态特性用 数学表达式描述出来，就得到了组成 物理系统的数学模型。
建立控制系统的数学模型，并
在此基础上对控制系统进行分析、 综合，是控制工程的基本方法。
当 o很小时，可忽略高阶小 量，则
sin o o 可近似为线性方程 :
m 2d l2 d o 2 tt m og t lT it
线性化步骤：
1. 找出静态工作点（工作点不同， 所得方程系数也不同）
2. 在工作点附近展开成台劳级数 3. 略去高阶项，得到关于增量的线
性化方程
§2-3 拉氏变换及反变换
机械控制工程基础
主讲教师：王国荣
第二章 控制系统的动态数学模型
2-1、基本环节数学模型 2-2、数学模型的线性化 2-3、拉氏变换和拉氏反变换 2-4、传递函数以及典型环节的传递函数 2-5、系统函数方框图及其简化 2-6、系统信号流图及梅逊公式 2-8、绘制实际物理系统的函数方框图
第二章 控制系统的数学模型
过切线法进行线性化，求其增量 方程
根据牛顿第： 二定律，有
Titmsginotlm2ld2do 2tt
这是一个非线性微分方 程，
o ( t ) 将 sin o在 o 0 附近用
l
台劳级数展开，得：
m T i( t )
P 1 5 单图 摆2 - 5 单 摆
sin o
o
o3
3!
o5
5!
—一种解线性微分方程的简便方法
是分析工程控制系统的基本数学方法
微分方程 （时间域）
拉氏变换 拉氏反变换
代数方程 （复数域）
传递函数
复习复变量和复变函数
复数有实部和虚部，两部分都是常数。
如： 2 j5 复变量指复数的实部或虚部中含有变量。
如： s j
复变函数 Fs 是 s 的函数，也有实部和虚 部。如：F s F x jF y F s F s
即：
RCduo(t) dt
ui(t)
例3 电枢控制式直流电动机
Ra
La
f
ei(t)
em
o (t)
T
J
ia if= 常 数
根据电磁感应定律，有
其中根 其 根，eKP中 据 据 m1e3e—TtK图根 i， 磁 — 2基 t-tT4— 电K反 据 场 枢— 尔 KR Te电 控d牛 制对 aTt电 势霍 idio直ata顿 常 载 tt流机 ft夫 电数d第 流 动力 Ld机o作 定 at二 t线 d矩 d用 a律 i定 圈 ttJ常 ， 定 d律 ， 的 2ed数 有 律 m to定 2有 tt， 律有
e it R a ia t L a d d a ti te m t T t K T ia t emtKeddott
Ttfdd ottJd2 d o 2 tt
将上面四个方程联立，可得
L a J d 3 d o 3 t tL a f R a J d 2 d o 2 t tR a f K T K e d d o t K tT e i t
1 c
i1 t
dt
R1i2
t
3
uo t R2it
4
将2、 3、 4分 别 代 1， 入并 整 理 得
R1CdduottR1R 2R2 uotR1Cdduittuit
i2(t)
ui(t) i1(t)
C
a
uo(t)
R
+
u i1
a (t (t)
)0 i2 (t
)
ui(t) Cduo(t)
R
dt
其中：Fs
F F 2 2
xyFs源自arctan FFxy例如：
G ss2 其:中 sjr s2r2 2
j
S平面
jGy G(s)平面
2
4
0
0
Gx
一、拉氏变换定义：
对于函数 xt ，满足下列条件
1、当 t 0时， xt0; 当t 0时， xt在每个有限区 续间
e 2、 xt td t ， 0
3. 将各环节方程式联立，消去中间变量， 最后得到只含有输入、输出变量以及 参量的系统方程式。
单输入、单输出系统微分方程的
一般形式：
ax ax a a 0 ont 1 on1t n1x ot nxot
bx bx b b 0
imt 1
im1t m1x it mxit
其中n： m
§2-2 数学模型的线性化
若 忽 略 电化 枢为 电： 感 ， 可 简
RaJd2 do 2ttRafKTKeddottKTeit
若电枢电感、都 电忽 枢略 电， 阻可进为 一： 步简化
Keddotteit
列写系统微分方程的一般步骤：
1. 将系统划分环节，确定各环节的输入 及输出信号，每个环节列写一个方程；
2. 根据物理定律或通过实验得出的物理 规律列写各环节的原始方程，并适当 简化，线性化；
严格讲： 所有系统都是非线性的
尽管线性系统的理论已经相当 成熟，但非线性系统的理论还远不 完善。另外，迭加原理不适用于非 线性系统，这给解非线性系统带来 很大不便。故我们尽量对所研究的 系统进行线性化处理，然后用线性 理论进行分析。
线性化条件：
1. 非线性因素对系统影响很小 2. 系统变量只发生微小偏移，可通