典型例题
典型例题(22套)典型例题20

典型例题(22套)典型例题20
把一个装满水的酒瓶倒立在装着水的盘子里,使瓶颈浸没在盘内水面下,如下图,就做成了一个简便自动家禽喂水器.试讲明它的工作原理.
选题目的:通过此题扩展学生知识,提高分析能力.
解答:这一简便自动家禽喂水器是利用大气压强工作的.由于瓶内水柱产生的压强远小于外界大气压强,当瓶口浸入水中时,瓶口外水受大气压强作用,使瓶内外的压强相等,水可不能流出.当家禽饮水使盘子里的水面下降而瓶口刚露出水面时,空气能够从瓶口进人瓶内,使瓶内压强大于不处大气压强,瓶内的水就会流出来,升高盘里的水位.使瓶口重新没入水中.瓶中的水连续流出,使瓶中气体体积增大,压强减小,直至瓶口内外压强相等时,水就停止流出.因此只要瓶内有水,盘里的水就能不断得到补充.实现家禽自动喂水.。
典型例题

第七节 功率典型例题例1一个质量为m 的物体沿倾角a=30°的光滑斜面由静止滑下.当它竖直方向下落h 高时,重力的即时功率为 ( ) A.gh mg 2 B.gh mg 2sin30° C.gh mg 2cos30° D.0[说明]本题用到即时功率的表达式。
例2汽车发动机的额定功率为60kw ,汽车质量为5×103kg ,汽车在水平路面上行驶时,阻力是车重的0.1倍,求:(1)汽车保持额定功率,从静止起动后能达到的最大速度是多少?(2)汽车从静止开始,保持0.5m /s 2的加速度作匀加速直线运动,这一过程能维持多长时间?[说明]要能解好该题,我们首先应知道机车功率的含义,机车功率即为发动机的功率,而发动机是产生牵引力的。
故机车功率P 只能与牵引力F 联系在一起,不能和机车所受的阻力或者机车的合外力联系在一起。
也即 P=F ·v ≠f ·v ≠F 合·v 基础练习1.关于功率,下列说法中正确的是 ( ) A .由P=w/t 可知.P 与W 成正比 B .由P=W/t 可知,P 与t 成反比C .由P=W/t 可知,只要知道W 和t 的值就可以计算出任一时刻的功率D .由P=Fv 可知,汽车的输出功率恒定时,牵引力一定与其速度成反比2.有一水平恒力F 先后两次作用在同一物体上,使物体由静止开始沿着力的方向发生相同的位移s ,第一次是在光滑的平面上运动;第二次是在粗糙的平面上运动。
比较这两次力F 所做的功W 1和W 2以及力F 做功的平均功率P 1和P 2的大小 ( )A. W 1=W 2 ,P 1>P 2B. W 1=W 2,P 1=P 2C. W 1>W 2,P 1>P 2D. W 1<W 2,P 1<P 23.雨滴在空中运动时所受阻力与其速度的平方成正比。
若有两个雨滴从高空中落下,其质量为m 1、m 2,落至地面前均已做匀速直线运动,则其匀速运动时重力的功率之比为 ( )A.21:m mB.21:m mC.12:m mD.3231:m m4.质量为m 的物体沿倾角为θ的斜面滑至底端时的速度大小为v 0,此时重力对物体做功的功率是 ( ) A. mgv B. mgvsin θ C.mgvcos θ D. 05一位高三年级的男生在平直的公路上以最快速度骑自行车,该车所受阻力为车和人总重力的0.05倍,则该男生的功率最接近于 ( )A .40WB .l00WC .250WD .500W6.起重机的钢绳吊着物体由静止开始竖直向上运动,先以加速度a(a<g)加速运动,接着匀速运动,最后减速到静止。
典型例题

若要以带符号 数形式显示, 应如何处理?
9
2、字符串处理
例5
例6
输入小写字母,显示其前导和后继;
输入字符串,显示最后4个字符;
例7 输入字符串,并逆序显示; 例8 输入字符串str1和str2,若str2是str1的子串,则输出Y, 否则输出N; 例9 删除串首尾空格,压缩串内空格;
从str1串首开始,至str1中能够截取与str2相同长度串的字符结束;
str1子串与str2的比较; str1长度范围内,匹配不成功,则继续循环; 匹配成功,则显示Y; 循环次数达到,则显示N;
17
循环体
循环控制
2019年2月2日星期六
开始
例8流程图 (方法2)
Str2是空串? Y
19
串中,则保留一个空格;若是串尾,设置串尾标志0;
2019年2月2日星期六
开始
例9 流程图
串扫描初始化 DI、CX(最大值)、AL(空格)、DF 设置新串指针BX,起始位置同DI 在原串中扫描非空格
Y
最后扫描字符为0?
Y
N
是串首?
在新串中保留 串尾标志0 结束
2019年2月2日星期六
清除串首标志
Y 从当前位置之后开始匹配str1和str2 Y 匹配成功? N str1搜索完毕? 显示Y
2019年2月2日星期六
N
Y
显示N
16
结束
例8(方法2 ) 输入字符串str1和str2,若str2是str1的子串, 则输出Y,否则输出N。
方法2:直接进行str1的子串与str2的比较;
具体的处理方法 从str1不同位置截取长度与str2相同子串,进行比较;
典型例题(有答案)
典型例题
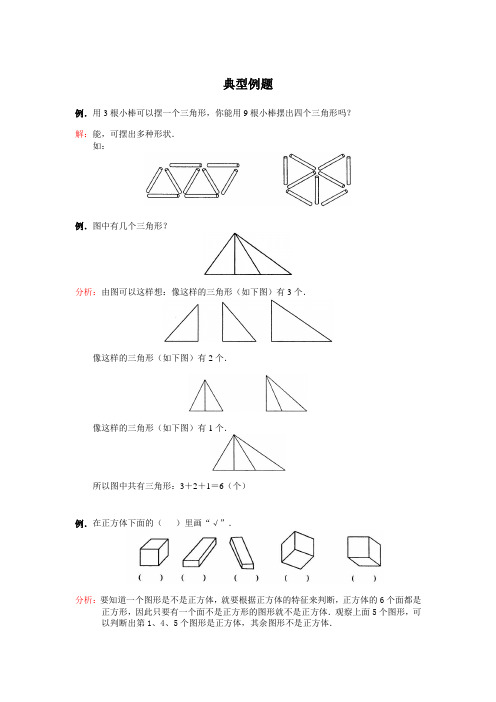
例.用3根小棒可以摆一个三角形,你能用9根小棒摆出四个三角形吗?
解:能,可摆出多种形状.
如:
例.图中有几个三角形?
分析:由图可以这样想:像这样的三角形(如下图)有3个.
像这样的三角形(如下图)有2个.
像这样的三角形(如下图)有1个.
所以图中共有三角形:3+2+1=6(个)
例.在正方体下面的()里画“√”.
分析:要知道一个图形是不是正方体,就要根据正方体的特征来判断,正方体的6个面都是正方形,因此只要有一个面不是正方形的图形就不是正方体.观察上面5个图形,可以判断出第1、4、5个图形是正方体,其余图形不是正方体.
解:
例.数一数下面的图(1)中有多少个三角形?
分析:先观察图,从图中很容易看出上面有1个三角形,中间有1个三角形,下面左、右两边各有一个三角形,合起来共有4个小三角形,如图(2)所示.
假如把中间三角形的三条边去掉,那么图形就变成了一个大三角形,如图(3)所示.因此,图中就有小三角形4个,大三角形1个,合起来是5个三角形.
解:此图形中有5个三角形.
例.仔细观察小松鼠在几个长方形中.
分析:这样想:小松鼠所在的长方形有以下几种形状:
所以:小松鼠在4个长方形中.
解:小松鼠在4个长方形中.
例.先剪三张正方形纸片,如图所示,再用这三张正方形纸片拼出不同的图形.
分析与参考答案:可以拼出的图形很多,下面是其中的几种:。
典型例题

典型例题-G-方差分析-2某企业准备用三种方法组装一种新的产品,为确定哪种方法每小时生产的产品数量最多,随机抽取了30名工人,并指定每个人使用其中的一种方法。
通过对每个工人生产的产品数进行方差分析,得到如下表所示的结果。
每个工人生产产品数量的方差分析表(2)若显著性水平为α=0.05,检验三种方法组装的产品数量之间是否有显著差异。
解:(1)完成方差分析表,以表格中所标的①、②、③、④、⑤、⑥为顺序,来完成表格,具体步骤如下: ①求k -1根据题目中“该企业准备用三种方法组装一种新的产品”可知,因素水平(总体)的个数k =3,所以第一自由度df 1=k -1=3-1=2,即SSA 的自由度。
②求n -k由“随机抽取了30名工人”可知,全部观测值的个数n =30,因此可以推出第二自由度df 2=n -k =30-3=27,即SSE 的自由度。
③求组间平方和SSA已知第一自由度df 1=k -1=3-1=2,MSA =210 根据公式1-==k SSAMSA 自由度组间平方和所以,SSA =MSA ×(k -1)=210×2=420④求总误差平方和SST由上面③中可以知道SSA =420;此外从表格中可以知道:组内平方和SSE =3836,根据公式SST =SSA +SSE 可以得出SST =420+3836=4256,即总误差平方和SST=4256 ⑤求SSE 的均方MSE已知组内平方和SSE =3836,SSE 的自由度n -k =30-3=27 根据公式0741.142273836==-==k n SSE MSE 自由度组内平方和所以组内均方MSE =142.0741⑥求检验统计量F已知MSA =210,MSE =142.0741 根据4781.10741.142210===MSE MSA F所以F=1.4781(2)题目中假设α=0.05,根据第一自由度df 1=k -1=3-1=2和第二自由度df 2=n -k =30-3=27,查F 分布表得到临界值F 0.05(2,27)=3.354131,所以F =1.4781<F α=3.354131,所以接受原假设,即μ1=μ2=μ3成立,表明μ1、μ2、μ3之间没有显著差异,也就是说,用三种方法组装的产品数量之间没有显著差异。
牛吃草经典例题

牛吃草经典例题
牛吃草问题是著名的趣味数学问题,典型例题有:
例1:牧场上一片青草,每天牧草都匀速生长。
这片牧草可供10头牛吃20天,或者供15头牛吃10天。
问可供25头牛吃几天?
例2:某块草地,假设每天匀速生长出青草正好够10头牛吃,这块草地可以放牧24头牛,则可以放牧多少头牛?
例3:有一片牧场,已知养牛60头,10天可以把草吃完;如果养牛45头,15天可以把草吃完;那么如果养牛20头,多少天可以把草吃完?
例4:有一块牧场,如果养25只羊,8天可以把草吃没,如果养21只羊,12天可以把草吃没,如果养16只羊,几天能把牧场上的一片牧草吃没?。
典型例题(有答案).DOC

典型例题
例 如图1,请你根据格子中的数,从1开始横着数或者竖着数,按照1,2,3,4,5,6,7,8,9,10的顺序数到10,如图2是其中的一种数法,你还有其他的吗?请你试一试.
分析与参考答案:
有以下几种不同的数法:
例.填空.
54)(=- 8)(10=- 分析:解答这组题可以想数的组成与分解.如54)(=-,想4和5组成几,4和5组成9,
所以括号里填9.8)(10=-,想10可以分成几和8,10可以分成2和8,所以括号里填2.根据加减法算式中各数的关系(即整体与部分的关系)来计算未知数也是
可以的,如
5
4
)
(=
-,想4加5等于几,4加5等9,所以括号里填9.8
)
(
10=
-,
想10减8等于几,10减8等于2,所以括号里填2.
答案:
5
4
)9(=
-8
)2(
10=
-
例.连线.
分析:第(1)题的意思是:左边算式的结果是几就应该和右边相应的数连起来.如:左边7+2=9,应该和右边的9连起来.
第(2)题是把左边和右边的结果相同的算式连起来,如:左边7+3=10,右边5+5=10,应该把这两个算式连起来.
例.在□里填上合适的数.
分析:做这道题要对数的组成比较熟悉.另外还要掌握解题技巧,按一定的顺序做,如:可以按从左往右,即10的分解来想.由于10的分解中右边的数又是7的组成中的一部分,因此所填的数必须比7小,即1、2、3、4、5、6,那么在7的组成中,右边的□所填的数相应是6、5、4、3、2、1.也可以按从右往左或从下往上,方法同上.
答案:略.。
函数的图像经典例题

函数的图象一、典型例题例1 设函数2()45f x x x =-- (1)在区间[2,6]-上画出函数()f x 的图像;(2)设集合{}()5,(,2][0,4][6,)A x f x B =≥=-∞-+∞ ,试判断集合A 和B 之间的关系,并给出证明;(3)当2k >时,求证:在区间[1,5]-上,3y kx k =+的图像位于函数()f x 图像的上方。
例2(1)若把函数()y f x =的图像作平移,可以使图像上的点()1,0P 变换成点()2,2Q ,则函数()y f x =的图像经此变换后所得图像对应的函数为 ( )A .(1)2y f x =-+ B.(1)2y f x =--C . (1)2y f x =++D . (1)2y f x =+-(2)己知函数33(),()232x f x x x -=≠-,若(1)y f x =+的图像是1C ,它关于直线y x =对称图像是22,C C 关于原点对称的图像为33,C C 则对应的函数解析式是__________(3)作出下列函数的大致图象: ①()21y x x =-+;② 21x y x -=+; ③ lg 1y x =-④ 11xy x -=-例3 (1)设函数()x f 的定义域为R ,它的图像关于直线1x =对称,且当1≥x 时()13-=x x f 则( ) ⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛322331A.f f f ⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛312332B.f f f ⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛233132C.f f f ⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛313223D.f f f (2)已知()f x 是定义域为(-∞,0)∪(0,+∞)的奇函数,在区间(0,+∞)上单调递增, ()f x 的图象如图所示,若[]()()0x f x f x --<,则x 的取值范围是__________________例3 已知函数()()()()1212()211xx f x x x x ⎧⎛⎫-≤-⎪ ⎪=⎝⎭⎨⎪-->-⎩,如果方程()f x a =有四个不同的实根,求实数a 的取值范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数串为空?
Y
N 累加和乘以基数
获取数串的一位,并累加
修改
N
循环结束?
Y
保存结果
2020年2月29日星期六
结束
5
例2 将字变量BUF的值当作无符号数,以十进 制形式输出。
➢ BUF中的数据为十六进制,程序的主要任务为数制转换;
✓ 除基取余法:不断地除以基数10,余数倒序排列即可;
➢ 循环结构程序
✓ 初始化:基数CX、数据指针、被除数(DX:AX)
开始 计数值清0
➢ 方法2:利用堆栈逆序; ✓ 注意:入出栈数据不
输入一个字符
能为8位;
输入的是回车? N
入栈该字符 计数加1
Y Y
结束
计数值为0? N
出栈字符
计数值减1
2020年2月29日星期六
14
例8(方法1 ) 输入字符串str1和str2,若str2是str1的子串, 则输出Y,否则输出N。
字符加1,求后继
N 后继是小写字母?
Y 保存后继
显示前导和后继
结束
11
例6 从键盘输入一个字符串(长度<80),显示其 最后4个字符。
开始 输入一个字符串
在串尾设置显示用的结束标志“$”
N
显示整个 输入串
串长度大于4?
Y
显示输入串的最 后4个字符
结束
2020年键盘输入一个字符串(长度<80),再逆 序显示该字符串。
利用一个0/1标志区分串首与串中;
2020年2月29日星期六
19
例9 流程图
开始 串扫描初始化 DI、CX(最大值)、AL(空格)、DF
设置新串指针BX,起始位置同DI
在原串中扫描非空格
Y
在新串中保留 串尾标志0 结束
2020年2月29日星期六
最后扫描字符为0?
N
清除串首标志
Y 是串首?
N
新串中保留一个空格
Y
N 匹配成功?
str1搜索完毕?
显示Y
Y
2020年2月29日星期六
结束
N
N 显示N
16
例8(方法2 )
输入字符串str1和str2,若str2是str1的子串, 则输出Y,否则输出N。
➢ 方法2:直接进行str1的子串与str2的比较;
➢ 具体的处理方法
✓ 从str1不同位置截取长度与str2相同子串,进行比较;
计算出十进制数值,为BUF赋值即可;
➢程序的主要任务
✓ 将字节数据计算出数值;
数值=[(01*10+02)*10+03]*10+04 循环结构程序实现——a1*10+a2;
2020年2月29日星期六
3
十进制数串转化为数值的方法
➢ 初始化 ✓ 数据指针SI、累加和AX、基数BX(10)、循环次数CX
➢ 该程序的主要任务是:删除空格;
✓ 删除后,新串的长度一定小于原串;
设置两个指针,分别指向原串和新串;
➢ 删除的方法:
✓ 遇到空格,跳过,直接向后扫描;
✓ 遇到非空格,将其后的所有非空格的保存位置向前移动, 覆盖之前的空格;
移动到空格位置,再重复之前的扫描;
✓ 串中,则保留一个空格;若是串尾,设置串尾标志0;
➢ 除法采用32位被除数, 16位除数(10);
✓ 商在AX中,可作为下 次除法的被除数;
被除数扩展 AXDX:AX
执行一次除法,余数转换为字符 保存于SI指定单元
✓ 无符号数扩展,采用 0扩展;
➢ 显示结果时,注意串要 以“$”结束;
减量修改SI指针
N
商为0?
Y
✓ 可直接定义,也可程 序中写入;
✓ 循环次数:与数组元素个数相同;
2020年2月29日星期六
21
例10流程 图
插入数据X 结束
开始
循环初始化
Y
空数组?
N
从后向前获取数组的一个元素
Y
X大于该元素?
N 后移该元素
修改数组指针
2020年2月29日星期六
22
累加和为小于16位的数据;循环次数与数串位数相同;
➢ 循环体 ✓ 累加和乘以10,再加数串的一位;
从高位开始处理数串;
➢ 修改:数据指针 ➢ 循环控制:计数控制 ➢ 结束处理:保存结果值
2020年2月29日星期六
4
开始
例1流程图
输入十进制字符串 循环初始化
➢注意事项 ✓ 寄存器的使用; ✓ 数串位使用时应将字符转 换为数值; ✓ 数串处理从最高位开始;
开始
➢ 方法1:输入字符串, 原地首尾相交换;
✓ 交换次数为串长度 的一半;
✓ 可用指针判断;
Y
输入一个字符串 在串尾设置显示用的结束标志“$”
设置串首和串尾的两个指针
首指针大于尾指针?
显示逆序后的字符串
N 首尾字符相交换
结束
2020年2月29日星期六
首尾指针向串中间位置移动
13
例7 (方法2) 从键盘输入一个字符串(长度<80),再逆 序显示该字符串。
将扫描到非空格字符及其后 的非空格字符保留在原串中
20
3、数据排序
➢ 例10. 已知无符号字数组LIST的第一个字数据为其元素个数。 试将某无符号字数据X插入数组LIST的正确位置,并修改元素 个数。 ✓ 要向数组插入数据,则数据段定义时,应预留一个字空间; ✓ 插入位置的确定,可从后向前扫描;
若数组元素大于插入数据X,则数组元素向后移动; 若数组元素小于插入数据X,则在该数组元素之后插入X;
(方法2)
Str1长度大于str2?
N
Y
Str2是空串?
N
循环初始化
Y
str1指针、循环次数(两串长度之差)
串比较(str1的子串与str2)
Y
显示Y
2020年2月29日星期六
匹配成功?
N
循环次数达到?
Y
结束
N
显示N
18
例9 将以0为结束符的字符串string的首尾空格 删除,并将串中的多个空格压缩成1个。
➢ 在实际搜索字符之前,要先排除两种情况
✓ str1的长度小于str2的长度 显示N;
✓ Str2是空串
显示Y;
2020年2月29日星期六
15
例8流程图 (方法1)
开始 输入字符串str1和str2
Str1长度大于str2? Y
Str2是空串? Y
N
在str1中搜索str2的首字符
找到?
N
Y 从当前位置之后开始匹配str1和str2
数据指针指向保存余数的单元,从尾单元到首单元逐次减量;
✓ 循环体:
采用除法指令,不断地除以10;注意避免除法溢出;
✓ 修改:数据指针
✓ 循环控制:条件控制——商为0;
✓ 结束处理:显示各位余数;注意转换为字符;
2020年2月29日星期六
6
开始
例2流程图
初始化 10CX,BUFAX,EA(string+4)SI
否则输出N; ➢ 例9 删除串首尾空格,压缩串内空格;
2020年2月29日星期六
10
例5 从键盘输入一
个小写字母,
显示该字母的
前导与后继。
是否小写 字母的判 断,可使 用过程调 用的方式
实现!
2020年2月29日星期六
开始
输入一个字符
N
是小写字母?
Y 字符减1,求前导
N
前导是小写字母?
Y 保存前导
2020年2月29日星期六
2
例1 从键盘输入一个无符号的十进制数(0~65535), 将其值存入变量BUF中。
➢输入数据为字符串,要转换成数值
✓ 例如,输入‘1234’,得到31H、32H、33H、34H字符串;
✓ 转换为数值为01、02、03、04四个字节的数据;
✓ 实际的数值为01*1000+02*100+03*10+04;
从str1串首开始,至str1中能够截取与str2相同长度串的字符结束;
✓ 循环体
str1子串与str2的比较;
✓ 循环控制
str1长度范围内,匹配不成功,则继续循环;
匹配成功,则显示Y;
循环次数达到,则显示N;
2020年2月29日星期六
17
开始
例8流程图
输入字符串str1和str2
算法同5-6
输入数据范围为 0~65535
以十进制数据的形式显示和与差
算法同5-7
结束
可使用过程调用 的方式实现!
若要以带符号 数形式显示, 应如何处理?
2020年2月29日星期六
9
2、字符串处理
➢ 例5 输入小写字母,显示其前导和后继; ➢ 例6 输入字符串,显示最后4个字符; ➢ 例7 输入字符串,并逆序显示; ➢ 例8 输入字符串str1和str2,若str2是str1的子串,则输出Y,
ROL BX , CL
每次取BX不同的4位,使用移位和逻辑操作得到;
MOV AND
DL , BL DL , 0FH
注意:若使用16位系统指令,与课本代码有所区别;
2020年2月29日星期六
8
例4 从键盘读入两个两位的十进制数,显示其 和与差。
开始 输入两个十进制数串,并转换为数值
求两个数值的和与差
典型例题
数据输入输出及转换 字符串处理 数据排序
1、数据输入输出及转换
➢ 理解数据的形式 ✓ 输入/输出的数据:字符串(‘0’~‘9’的ASCII码) ✓ 存储的数据:十六进制数据
