人口增长模型
人口增长模型有哪些【中国人口模型】

表二
而平均相对误差=0.009587
(2)求出原始数据平均值,残差平均值:
其中,
运用Excel求得:,
(3)求出原始数据方差与残差方差的均方差比值C和小误差概率p:
其中,
,
计算可得:,,,p=0.96
通常、、C值越小,p值越大,则模型的精度越好。若
0.95,则模型精度为一级.观察数据可知该模型为一级模型。有很高的信任度。Ⅱ模型二的结果的分析:
.分别令,
, .那么有
. (式七)
(式八)
(式九)
式十)
(式十一)
(
在社会稳定的前提下,生育率和死亡率都比较稳定,从而可以视A(t),B(t)为常矩阵A,B,则上式可化为
.
为了便于处理数据,我们采常矩阵的改进莱斯利模型,但由于矩阵A,B的维数过大,所以将具体的
--以及
--置于附录,相应的A(t)和B(t)也同样在附录。
人口指数:(1)人口总数
(2)平均年龄
(3)平均寿命
(4)老龄化指数
Байду номын сангаас依据这个模型不仅可以求出人口总数,还可以求出平均年龄、平均寿命及老龄化指数等众多量。子模型一:生育模型
若k(r,t)p(r,t)个妇女中t年代平均每年生育孩子数为整个育龄期间的妇女单位时间(t年代)生育孩子数为
毕设之人口增长模型讲解(可编辑修改word版)

毕业设计——第一章绪论1.研究背景2.国内外研究现状3.人口概念介绍人口增长模型及其应用孙建锋第二章人口增长模型的概述1.马尔萨斯模型(人口指数增长模型)2.Logistic 模型(人口阻滞增长模型)3.年龄移算法模型4.L eslie 人口增长模型5.灰色 GM(1,1)预测模型6.人口发展方程7.各模型的优缺点对比第三章基本人口预测1.出生人数的预测2.死亡人数的预测3.分年龄分性别人口数预测4.人口总数预测第四章人口实例预测1.数据准备2.模型应用与求解3.结果分析4.结论及相关建议第一章绪论1.1研究背景人口问题是联系社会经济发展最基本、最复杂问题,受到世界各国诸多领域的关注.就人口规模的发展而言存在极大地差异,如,某些发展中国家人口生育率过高;而某些发达国家的生育率过低,甚至为负増长,这些现象会引发一系列社会经济问题,如,失业、老龄化,进而影响社会稳定.人口问题事关国计民生,是影响经济社会发展全局的重大问题。
以人为本的科学发展观必然要求我们在一切发展序列中首先关注人口发展,中国人口发展在中国经济社会发展框架中具有绝对优先的工具价值和目的意义。
人口发展对一个国家经济、社会协调和可持续发展具有重要影响。
发现人口问题、制定相应政策、采取合适措施对人口发展进行调节,是政府保证经济社会协调和可持续发展的重要内容。
众所周知,人口众多是我国基本的国情,人口问题一直以来就是中国经济发展的绊脚石,中国是人口第一大国,固然有地大物博,资源丰富的美誉,但按人口数量平均下来,也就成了人均占有量不足的基本国情。
中国在世纪之交的2000 年进行了全国第五次人口普查,国家许多重大社会、政治,经济问题的研究都要依据人口的数量。
为此,进行人口预测是有效地控制人口发展与资源关系不可缺少的手段之一,同时也是人口决策的重要依据.对人口进行预测,做到人口有计划地发展不仅能有效地处理好人类与资源的关系,而且对于经济发展的预测,各个生态专项规划及制定建设决策都有重要的借鉴意义,也是我国经济稳定、高效、协调发展的保证。
人口增长模型例题

人口增长模型例题1.某地区初始人口为1000人,年增长率为2%,求10年后的人口数量。
2.一个城市的人口初始为5000,按照每年1.5%的速度增长,5年后人口是多少?3.若某村庄人口起始为800,人口增长率为3%,8年后人口达到多少?4.有一个小镇,最初人口是2000,年增长率为2.5%,计算12年后的人口。
5.某国人口初始为10000,年增长比例为1.8%,求15年后人口数量。
6.一片区域初始人口600,每年人口增长4%,3年后人口为多少?7.一个岛屿的初始人口为1200,人口以每年2.2%的速度增长,10年后人口是多少?8.某社区人口开始为900,年增长率为3.5%,7年后人口达到多少?9.若某部落人口起始为550,人口增长率为2.8%,9年后人口为多少?10.有一个聚居地,最初人口是1500,年增长率为2.3%,计算11年后的人口。
11.某地区人口初始为3000,年增长比例为1.9%,求20年后人口数量。
12.一个小县城初始人口800,每年人口增长3.2%,4年后人口为多少?13.一个地区的初始人口为1800,人口以每年2.6%的速度增长,13年后人口是多少?14.某城镇人口开始为1100,年增长率为3.8%,6年后人口达到多少?15.若某村落人口起始为700,人口增长率为2.1%,14年后人口为多少?16.有一个村落最初人口是1300,年增长率为2.7%,计算16年后的人口。
17.某省人口初始为50000,年增长比例为1.2%,求25年后人口数量。
18.一个区域初始人口1000,每年人口增长3.6%,5年后人口为多少?19.一个国家的初始人口为2500,人口以每年2.4%的速度增长,18年后人口是多少?20.某城市区人口开始为1600,年增长率为3.3%,9年后人口达到多少?21.若某县人口起始为1400,人口增长率为2.9%,17年后人口为多少?22.有一个城市最初人口是3500,年增长率为1.7%,计算22年后的人口。
中国人口增长预测模型

中国人口增长预测模型摘要本文针对我国人口增长中出现的新特点,建立了两个符合实际情况的预测模型,对中国人口增长的中短期和长期趋势做出预测。
模型一:建立时间序列分析法中的ARMA 模型, 对中国人口总数进行预测。
根据处理后的数据的自相关函数和偏相关函数的拖尾性,估计出ARMA 的参数p和q,并对估计的参数进行检验和调节,最终确定参数,建立出ARMA(p ,q)模型。
用此模型预测出2020 年和2030 年的人口分别为138135.3 万人和143352.6 万人。
模型二:建立阻滞增长模型,把出生率和死亡率考虑进去,对人口进行预测,并用Matlab软件编程进行求解。
通过此模型预测出2020年和2030年的人口分别为142108.3万人和146768.4万人,并且人口在2036年左右达到峰值。
模型三:建立人口发展方程,模型一需要的原始数据少,操作简单,适合于中短期预测,但长期预测效果不佳;模型二和模型三综合考虑了各因素,对中短期和长期均有较好的预测效果,但所需数据量大,操作较为复杂。
关键字时间序列模型Eviews 人口发展模型微分方程1.问题重述近年来中国的人口发展出现了一些新的特点,例如,老龄化进程加速、出生人口性别比持续升高,以及乡村人口城镇化等因素,这些都影响着中国人口的增长。
关于中国人口问题已有多方面的研究,并积累了大量数据资料。
试从中国的实际情况和人口增长的上述特点出发,参考相关数据资料,建立中国人口增长的数学模型,并由此对中国人口增长的中短期和长期趋势做出预测;并指出模型中的优点与不足之处。
2.问题的分析一个国家人口的变化和随时间的发展过程,是由很多因素决定的,社会制度、自然环境、生活水平、科学文化水平、战争、自然灾害和移民等等,都能严重地影响社会人口的发展过程。
要预测人口发展的总趋势,首先要预测的是人口总数。
在当代中国社会,环境稳定,如果没有大规模传染病和战争等的影响,每年的死亡率应该相对稳定,出生率也一直在国家政策的控制中,所以人口总数的预测可以看成一个平稳序列的预测,这样我们考虑用时间序列来进行预测。
数学应用典型案例模型1马尔萨斯人口增长(指数增长)模型

xc e hx
C
其中 C 为任意常数,可由初始条件确定。
捕食----被捕食模型有着广泛的应用。当一个包含两个群体的系统中,只要
两个群体相互依存、相互制约,均可用捕食----被捕食模型来描述。例如,鲨鱼
与食用鱼、寄生虫与其宿主、害虫与其天敌、肿瘤细胞与正常细胞等都可用该模
型来描述。下图表明了狐狸----野兔(数量)随着时间 t 所发生的周而复始的变
化,正是这种变化维持着该系统的生态平衡。
在狐狸----野兔生态系统中,生态系统的平衡点就是使 dx 0, dy 0 的点。 dt dt
即
a byx 0 c hxy 0
(3-2)
只求非零解,可知平衡点为: x c , y a 。也就是说,当野兔数量保持在 c ,
设人类生存空间及可利用资源(食物、水、空气)等环境因素所能容纳的最 大人口容量为 K(称为饱和系数).人口数量 N(t)的增长速率不仅与现有人口 数量成正比,而且还与人口尚未实现的部分(相对最大容量 K 而言)所占比例 K N 成比例,比例系数为固有增长率 r.于是,修改后的模型为
K
dN
hb
h
狐狸数量保持在 a 时,就能维持狐狸----野兔生态系统的平衡。 b
图 3-2
例 狐狸----野兔模型为
dx dt
0.03x
0.001xy
dy dt
0.9 y 0.002xy
(3-3)
试问:狐狸、野兔的数目各为多少时,该系统才达到平衡?
解:由 dx 0 ,得 y狐狸 0.03 3(0 只);
模型 3 捕食——被捕食模型 所用知识:微分方程组 内容介绍:
人口指数增长模型和Logistic模型
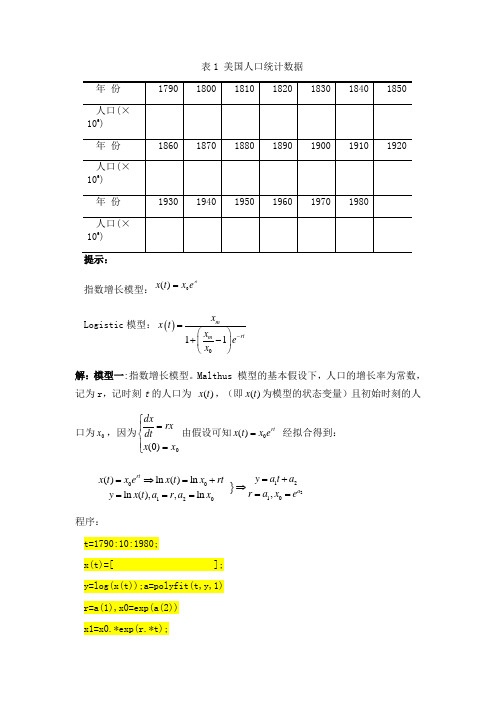
表1 美国人口统计数据指数增长模型:rt e x t x 0)(=Logistic 模型:()011mrtm x x t x e x -=⎛⎫+- ⎪⎝⎭解:模型一:指数增长模型。
Malthus 模型的基本假设下,人口的增长率为常数,记为r ,记时刻t 的人口为 )(t x ,(即)(t x 为模型的状态变量)且初始时刻的人口为0x ,因为⎪⎩⎪⎨⎧==0)0(x x rxdt dx由假设可知0()rt x t x e = 经拟合得到:}2120010120()ln ()ln ,ln (),,ln rt a y a t a x t x e x t x rt r a x ey x t a r a x =+=⇒=+⇒=====程序:t=1790:10:1980;x(t)=[ ]; y=log(x(t));a=polyfit(t,y,1) r=a(1),x0=exp(a(2)) x1=x0.*exp(r.*t);plot(t,x(t),'r',t,x1,'b') 结果:a =r= x0=所以得到人口关于时间的函数为:0.02140()t x t x e =,其中x0 = , 输入:t=2010;x0 = ;x(t)=x0*exp*t)得到x(t)= 。
即在此模型下到2010年人口大约为 610⨯。
模型二:阻滞增长模型(或 Logistic 模型) 由于资源、环境等因素对人口增长的阻滞作用,人口增长到一定数量后,增长率会下降,假设人口的增长率为 x 的减函数,如设)/1()(m x x r x r -=,其中 r 为固有增长率 (x 很小时 ) ,m x 为人口容量(资源、环境能容纳的最大数量), 于是得到如下微分方程:⎪⎩⎪⎨⎧=-=0)0()1(xx x x rx dt dxm 建立函数文件function f=curvefit_fun2 (a,t)f=a(1)./(1+(a(1)/*exp(-a(2)*(t-1790))); 在命令文件中调用函数文件 % 定义向量(数组) x=1790:10:1990; y=[ 76 ... 92 204 ];plot(x,y,'*',x,y); % 画点,并且画一直线把各点连起来 hold on;a0=[,1]; % 初值% 最重要的函数,第1个参数是函数名(一个同名的m 文件定义),第2个参数是初值,第3、4个参数是已知数据点 a=lsqcurvefit('curvefit_fun2',a0,x,y); disp(['a=' num2str(a)]); % 显示结果 % 画图检验结果 xi=1790:5:2020; yi=curvefit_fun2(a,xi); plot(xi,yi,'r'); % 预测2010年的数据 x1=2010;y1=curvefit_fun2(a,x1) hold off 运行结果: a= y1 =其中a(1)、a(2)分别表示()011mrtm x x t x e x -=⎛⎫+- ⎪⎝⎭中的m x 和r ,y1则是对美国美国2010年的人口的估计。
(完整版)毕设之人口增长模型讲解

毕业设计——人口增长模型及其应用孙建锋第一章绪论1.研究背景2.国内外研究现状3.人口概念介绍第二章人口增长模型的概述1.马尔萨斯模型(人口指数增长模型)2.Logistic模型(人口阻滞增长模型)3.年龄移算法模型4.Leslie人口增长模型5.灰色GM(1,1)预测模型6.人口发展方程7.各模型的优缺点对比第三章基本人口预测1.出生人数的预测2.死亡人数的预测3.分年龄分性别人口数预测4.人口总数预测第四章人口实例预测1.数据准备2.模型应用与求解3.结果分析4.结论及相关建议第一章绪论1.1研究背景人口问题是联系社会经济发展最基本、最复杂问题,受到世界各国诸多领域的关注.就人口规模的发展而言存在极大地差异,如,某些发展中国家人口生育率过高;而某些发达国家的生育率过低,甚至为负増长,这些现象会引发一系列社会经济问题,如,失业、老龄化,进而影响社会稳定.人口问题事关国计民生,是影响经济社会发展全局的重大问题。
以人为本的科学发展观必然要求我们在一切发展序列中首先关注人口发展,中国人口发展在中国经济社会发展框架中具有绝对优先的工具价值和目的意义。
人口发展对一个国家经济、社会协调和可持续发展具有重要影响。
发现人口问题、制定相应政策、采取合适措施对人口发展进行调节,是政府保证经济社会协调和可持续发展的重要内容。
众所周知,人口众多是我国基本的国情,人口问题一直以来就是中国经济发展的绊脚石,中国是人口第一大国,固然有地大物博,资源丰富的美誉,但按人口数量平均下来,也就成了人均占有量不足的基本国情。
中国在世纪之交的2000年进行了全国第五次人口普查,国家许多重大社会、政治,经济问题的研究都要依据人口的数量。
为此,进行人口预测是有效地控制人口发展与资源关系不可缺少的手段之一,同时也是人口决策的重要依据.对人口进行预测,做到人口有计划地发展不仅能有效地处理好人类与资源的关系,而且对于经济发展的预测,各个生态专项规划及制定建设决策都有重要的借鉴意义,也是我国经济稳定、高效、协调发展的保证。
人口增长模型

一、 人口增长模型: 1. 问题下表列出了中国1982—1998年的人口统计数据,取1982年为起始年(t=0),…人口自然增长率14%,以36亿作为我国的人口容纳量,是建立一个较好的数学模型并给出相从图中我们可以看到人口数在1982—1998年是呈增长趋势的,而且我们很容易发现上述图像和我们学过指数函数的图像有很大的相似性,所以我们很自然想到建立指数模型,但是指数模型有个不妥之处就是没有考虑社会因素的,即资源的有限性,也就是人口不可能无限制的增长,所以有必要改进模型,这里我们假设人口增长率随人口增加而呈线性递减,从而建立起比较优越阻滞增长模型 模型一:指数增长模型(马尔萨斯模型)1.假设:人口增长率r 是常数.2.建立模型:记时刻t=0时人口数为0X ,时刻t 的人口为X (t ),由于量大,X (t )可以视为连续、可微函数,t 到t+t ∆时间段人口的增量为:)()()(t rX tt X t t X =∆-∆+于是X (t )满足微分方程:)1()0(0⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧==X X rX dt dx3.模型求解:解得微分方程(1)得: X (t )=0X )(0t t r e- (2)表明:t ∞−→−时,t X )0.(>∞−→−r . 4.模型的参数估计要用模型2对人口进行预报,必须对其中的参数r 进行估计,这可以用表1通过Matlab 拟合: 程序:x=[1982 1983 1984 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 19971998]';X=[ones(17,1),x]Y=[101654 103008 104357 105851 107507 109300 111026 112704 114333 115823 117171 118517 119850 121121 122389 123626 124810]';[b,bint,r,rint,stats]=regress(Y,X); %回归分析b,bint,stats%输出这些值rcoplot(r,rint);%画出残差及其置信区间z=b(1)+b(2)*x;plot(x,Y,'k+',x,z,'r'),%预测及作图运行结果:b =1.0e+006 *-2.84470.0015bint =1.0e+006 *-2.9381 -2.75130.0014 0.0015stats =1.0e+005 *0.0000 0.0455 0 1.9800图1各数据点及回归方程的图形 即回归模型为:y=-2844700+1500x从上图可用看出拟和得效果比较好。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
lim
t
P0
e
r
(
t
t0
)
,我们的地球是有限的,故
指数增长模型(Malthus模型)对未来人口总数预测非
常荒谬,不合常理,应该予以修正。
2021/4/14
5
模型II:阻滞增长模型(Logistic)
模型假设
1. 地球上的资源有限,不妨设为1;而一个人的正常生存
需要占用资源1/ P*(t) ;
2. 在时刻t,人口增长的速率与当时人口数成正比,为简
2021/4/14
10
P* P(t)
1 ( P * 1) e r*(tt0 ) P0
1600 1400 1200 1000
800 600 400 200
20
40
60
80 100 120 140
称为阻滞增长模型(或Logistic模型)
2021/4/14
8
模型检验
当人口数的初始值P0>P*时,人口曲线(虚线)单调 递减; 当人口数的初始值P0<P*时,人口曲线(实线)单调 递增;无论人口初值如何,当t,它们皆趋于极 限值。
2021/4/14
1
模型I:
人口指数增长模型(马尔萨斯Malthus,1766--1834)
模型假设
1)时刻t人口增长的速率与当时人口数成正比, 增长率为常数r。 2)以P(t)表示时刻t某地区(或国家)的人口数, 设人口数P(t)足够大,可以视做连续函数处理, 且P(t)关于t连续可微
2021/4/14
还有比指数增长模型、阻滞增长模型更好的人口预测方法吗? 事实上,人口的预测是一个相当复杂的问题,影响人口增长的因素 除了人口基数与可利用资源量外,还和医药卫生条件的改善、人们生 育观念的变化等因素有关,特别在做中短期预测时,我们希望得到满 足一定预测精度的结果,比如在刚刚经历过战争或是由于在特定的历 史条件下采纳了特殊的人口政策等,这些因素本身以及由此而引起的 人口年龄结构的变动就会变的相当重要,进而需要必须予以考虑。
2
模型建立及求解
据模型假设,在t到 t + t 时间内人口数的增长量为
P(t t) P(t) r P(t) t
P(t t) P(t) r P(t) t
dP r P dt
2021/4/14
3
如果设 t = t0时刻的人口数为,则P(t)满足初值问题:
ቤተ መጻሕፍቲ ባይዱP
dt
rP
P(t0 ) P0
P(t) P0 er(t t0 )
30 25 20 15 10
5
5
10
15
20
25
30
35
称为指数增长模型(或Malthus模型)。
2021/4/14
4
模型检验
• 19世纪以前欧洲一些地区的人口统计数据可以很好的吻 合。19世纪以后的许多国家,模型遇到了很大的挑战。
•
注意到lim P(t) t
2021/4/14
9
模型讨论
阻滞增长模型从一定程度上克服了指数增长模型的不足,可以被 用来做相对较长时期的人口预测,而指数增长模型在做人口的短期预 测时因为其形式的相对简单性也常被采用。 不论是指数增长模型曲线,还是阻滞增长模型曲线,它们有一个共同 的特点,即均为单调曲线。但我们可以从一些有关我国人口预测的资 料发现这样的预测结果:在直到2030年这一段时期内,我国的人口一 直将保持增加的势头,到2030年前后我国人口将达到最大峰值16亿, 之后,将进入缓慢减少的过程——这是一条非单调的曲线,即说明其 预测方法不是本节提到的两种方法的任何一种。
单起见也假设与当时剩余资s 源1 P / P
成正比;比例
系数表示人口的固有增长率;
3. 设人口数P(t)足够大,可以视做连续变量处理,且P(t)关
于t连续可微。
2021/4/14
7
模型建立及求解
r(P) r * s r * (1 P / P )
dP
r
P
(1
P
/
P
)
dt
P(t0 ) P0
