《结构力学教程》
哈工大结构力学教材

哈工大结构力学教材
哈尔滨工业大学的结构力学教材有多个版本,包括:
1. 《结构力学教程》(上册、下册),由哈尔滨工业大学工程力学系编写组编写,高等教育出版社出版,1981年8月第一版,1990年6月第二版。
2. 《结构力学》(上册、下册),由戴鸿哲、盛兴、朱耀臻、李建中、王焕定等编写,哈尔滨工业大学出版社出版,2000年12月第一版。
3. 《结构力学》(上册、下册),由王焕定、祁皑主编,高等教育出版社和哈尔滨工业大学出版社出版,2007年5月第一版。
4. 《结构力学》(上册、下册),由唐锦春主编,高等教育出版社出版,2010年2月第二版。
这些教材在哈尔滨工业大学结构力学课程中被广泛使用。
如需了解更多版本,建议登陆学校官网或相关论坛查询。
结构力学教程——第10章 力法

系数和自由项 ➢ 梁、刚架:
ii
M i 2 ds
EI
Ai yi EI
ij
M i M j ds EI
Aj yi EI
iP
M i M P ds EI
➢ 桁架:
2
ii
Ni l EA
ij
Ni N jl EA
iP
Ni N Pl EA
知识点
10.3 超静定刚架和排架
1. 刚架
20kN/m
11
M12 EI
ds
FN21 EA
ds
y2
cos2
EI ds EA ds
1P
M1 M P EI
ds
M0y ds
EI
(4)求多余未知力,即水平推力FH
M0y
X1
FH
1P 11
y2 EI
EI ds
cos2
ds EA
ds
(5)内力计算
M M 0 FH y
FQ FQ0cos FHsin FN FQ0sin FHcos
1P 11X1 0
P
2P 0
P
0
a
11
2 2
1
1
1
P
a
N1
NP
(3)求系数
11
2
Ni l 2( EA
2)2 EA
2a 4 12 a EA
4a (1 EA
2)
1P
Ni N jl 1 Pa 2 EA EA
(
2 )( EA
2P)
2a 2Pa (1 EA
2)
(4)解方程
X1
1P
11
P 2
当结构框格数目为 f , 则 n=3f 。
结构力学(全套课件131P) ppt课件
的两根链杆的杆轴可以平行、交叉,或延长线交于
一点。
当两个刚片是由有交汇点的虚铰相连时,两个刚
片绕该交点(瞬时中心,简称瞬心)作相对转动。
从微小运动角度考虑,虚铰的作用相当于在瞬时
中心的一个实铰的作用。
19
20
规则二 (三刚片规则): 三个刚片用不全在一条直线上的三个单铰(可以
是虚铰)两两相连,组成无多余约束的几何不变体 系。
两个平行链杆构成沿平行方向上的无穷远虚铰。
三个刚片由三个单铰两两相连,若三个铰都有交 点,容易由三个铰的位置得出体系几何组成的结论 。当三个单铰中有或者全部为无穷远虚铰时,可由 分析得出以下依据和结论:
1、当有一个无穷远虚铰时,若另两个铰心的连 线与该无穷远虚铰方向不平行,体系几何不变;若 平行,体系瞬变。
3、通过依次从外部拆除二元体或从内部(基础、 基本三角形)加二元体的方法,简化体系后再作分 析。
41
第一部分 静定结构内力计算
静定结构的特性: 1、几何组成特性 2、静力特性 静定结构的内力计算依据静力平衡原理。
第三章 静定梁和静定刚架
§3-1 单 跨 静 定 梁
单跨静定梁的类型:简支梁、伸臂梁、悬臂梁 一、截面法求某一指定截面的内力
15
1、单约束(见图2-2-2) 连接两个物体(刚片或点)的约束叫单约束。
1)单链杆(链杆)(上图) 一根单链杆或一个可动铰(一根支座链杆)具
有1个约束。 2)单铰(下图)
一个单铰或一个固定铰支座(两个支座链杆) 具有两个约束。 3)单刚结点
一个单刚结点或一个固定支座具有3个约束。
16
2、复约束 连接3个(含3个)以上物体的约束叫复约束。
三、对体系作几何组成分析的一般途径
《新版结构力学教程》

2-1(a)
2-2(a)
2-2(b)
2-1(b)
彭怀林-4
2-2(c)
2-3(a)
2-3(b)
2-3(c)
2-3(d)
2-4(a)
2-4(b)
2-4(c)
2-4(d)
2-4(e)
2-5(a)
2-5(b)
2-5(c)
彭怀林-5
2-6(a)
2-7(b)
1A
2
35 B 6
7
C 8
9
D 10 11
4
I
E
II 12
刚结) h---单铰个数 b---单链杆根数(支座链杆数)
②W=2j-b j--结点个数 b—单链杆个数
(支座链杆数+结点之间的杆件数) 由以上两个公式计算出来W的可能为正、 为负为零。
2-1(c)
定性结论: 若W>0,则s>0,则体系为几何可变体系。 若W=0,则s=n,如无多余约束则为几何不 变;如有多余约束则为几何可变。 若W<0,则n>0,体系有多余约束。 我们把:无多余约束的几何不变体系称为 静定结构,有多余约束的几何不变体系称 为超静定结构。
房屋建筑中的梁、板、柱体系;交通土建 中的公路、铁路上的桥梁和隧洞;水工建 筑物中的闸门和水坝。
彭怀ቤተ መጻሕፍቲ ባይዱ-1
☻结构的分类☻
从几何外形角度: ①杆件结构(杆系结构) 由若干杆件组成,杆件的横截面尺寸要比 长度小得多。梁、拱、刚架、桁架属于杆 件结构。
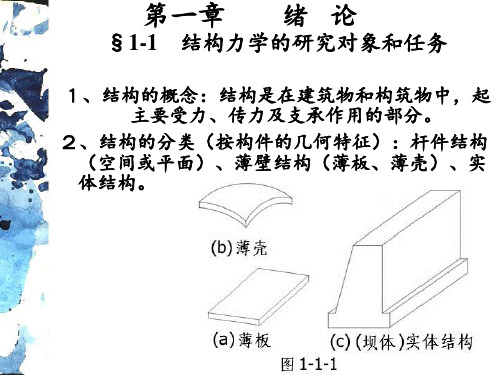
②板壳结构(薄壁结构):它的 厚度要比长度和宽度小得多。 如:楼板、壳体屋盖。
c.组合结点:特征是汇交于结点 的各杆均不能移动,但其中一部分 杆件为刚性联结,各杆端不允许 相对转动,其余杆件为铰接,允许 绕结点转动。
结构力学教程——第12章 渐进法和超静定结构的影响线

性质,可得到柱子两端弯矩。
知识点 12.5-3
柱间有水平荷载作用时的计算
I=∞
A
C
q
i1 h1
B
i2 h2 D
I=∞
A
C
q
i1 h1
i2 h2
B
+
D
A
i1 h1 B
I=∞ C
i2 h2 D
P 单跨梁计算
P 力矩分配法
知识点
12.6 用机动法绘制连续梁的影响线
力法基本方程
11 Z1 1P 0
SBA 1 5
CBA 1
例2:作图示刚架的弯矩图
解 (1)固端弯矩
M
F AB
M
F BA
1 4 kN 3.3m 2
= 6.6kN m
M
F BC
M
F CB
1 (4 8.5)kN 3.6m 2
= 22.5kN m
(2)分配系数
SBA iBA 3.5 SBC iBC 5 SBE 3iBE 162
(http://structuremechanics/index1.htm)
1. 课程导入
连续梁桥
q
多跨连续梁
2. 结点力矩下单结点力矩分配
2.1 力矩分配法概念的提出 回顾位移法
例1:若梁线刚度 i 相同,求梁各杆端弯矩。
M
M
B
A
MBA MBC
M BA 4iB
B
θB
C
M AB 2iB
M BC 3iB
SCB 4 SCF 2 SCD 3
CB 0.445 CD 0.333 CF 0.222
解(1)转动刚度和分配系数
EI0=1
结构力学教程1

4)、几何组成分析举例 例1:用基本规律分析图示体系的几何构造。 解Ⅰ:用固定一个点的装配方式。 从基础出发:基础A、B→C、D→E、F→G 解Ⅱ:因为基础可视为几何不变的刚片,可用减二元体 的方法进行分析。 注:二元体遇到,可以先去掉。
例2:分析图示体系 解: 两刚片装配方式。从内部出发, 1)、支座杆为3,可先不考虑基础, 分析体系本身。 2)、几何不变部分,可视为一刚片。 ADC→Ⅰ,CBE→Ⅱ,ⅠⅡ用铰C和链杆 DE联结满足规律2,组成一大刚片。 上部体系与基础用3根链杆联结。
6、钢结构建筑的结构形式:
桁架、框架、悬索结构、杂交结构、张拉集成结构、索膜结构、拱或拱架。
我国钢结构在各个领域都在飞速发展,特别近几年出现了许多具有国 际水平的钢结构。希望同学们能刻苦钻研,为我国的钢结构事业的发展 做出自己的一份贡献。
第十一章 平面体系的几何组成分析
本章学习目标: 1、掌握几何不变体系的组成规律。 2、会判断几何不变体系和几何可变体系。 3、能正确分析静定结构和超静定结构。 4、能进行静定梁和平面刚架的内力计算。 5、明确几何组成分析的目的。 一、基本概念 1、几何不变体系——在不考虑材料 应变的条件下,体系的位置和形状 不能改变。只有几何不变体系才能作为结构来使用。
5)材料的性质的简化 对组成结构的建筑材料,一般都假定为均匀连续、各向同性、完全弹性 (或弹塑性)。 6)荷载的简化 体力和面力均简化为作用在轴线上的分布荷载和集中荷载。 7)结构的计算简图举例: 例 1:
例 3:
4、钢结构在我国的发展与应用 (1)钢结构:由钢材筑成,能承受荷载而起骨架作用的构筑物称为钢结构。 1)国外钢结构:
埃菲尔铁塔(法国巴黎)1889年建成
旧金山金门大桥
结构力学教程——第8章 影响线

P1 P2 Pk
PN
C
a
b
dx dy1
y1 y2 yk h
yN
MC影响线
dyk+1 dx
MC (x) =P1y1 + P2y2 + Pkyk +…+ PNyN
dMC (x) =P1dy1 + P2dy2 + Pkdyk +…+ PNdyN
dMC (x) =dy1 (P1+ P2 +…+ Pk)+dyk+1 (Pk+1+ Pk+2 +…+ PN)
横坐标以 下的图形,影响线系数取负号。
例:机动法作简支梁C点弯矩和剪力的影响线。 x P=1
A
C
B
a
b
l
解:弯矩的影响线
ab/l
1
b
A
C
B
MC
x P=1
A
C
B
a
b
l
解:剪力的影响线
b/l
1
A
C
B
QC
a/l
小结
机动法作影响线的步骤
撤去与Z相应的约束,代以未知力Z。 使体系沿Z的正方向发生位移,作出δP图, 既为Z的影响线的轮廓。 令δz=1,可定出影响线的竖距。 横坐标以上的图形,影响线系数取正号;
P1
RL Pk RR
a
b
RL Pk RR
a
b
R L Pk 7 2 > R R 4.5
求QC
q
A
C
B
dx
b
l
QC
a
y
l
QC
结构力学实用教程讲解

2.1 几何可变系统和几何不变系统工程结构是用来承受和传递外载荷的系统。
一个工程结构通常是由若干个构件用某种方法联结而成的。
它在承受载荷作用时,各构件只允许发生材料的弹性变形,而不应发生构件间相对的机械运动。
如图2.1(a)所示的系统,如果不考虑弹性变形,系统也未发生破坏,则其几何形状与位置均保持不变,这样的系统,我们称之为几何不变系统。
但是,对如图2.1(b)所示的系统,在载荷作用下,即使不考虑弹性变形,它的形状和位置也将改变,这样的系统,我们称之为几何可变系统,它是不能用来承受和传递外载荷的。
所以,凡是工程结构必须是几何不变系统。
图2.1对系统进行几何组成分析的目的在于:判断该系统是否为几何不变系统,以决定其能否作为工程结构使用;研究并掌握几何不变系统的组成规则,以便合理安排构件,设计出合理的结构;根据系统的组成规则,确定结构的性质(静定系统还是静不定系统),以便选用相应的计算方法。
3.2 静定桁架的内力桁架是由某些杆系结构经过简化而得到的计算模型,其特点是:(1)各元件均为直杆;(2)各杆两端均用没有摩擦的理想铰链相连接;(3)杆的轴线通过铰心,称铰心为桁架的结点;(4)载荷和支座反力仅作用在各结点上。
由于理想铰链没有摩擦力,故不能传递力矩。
显然,在载荷仅作用在结点上时,若不计杆的自重,各杆都只受到两端结点的作用力,且在此二力作用下处于平衡。
因此,桁架的杆件均为“二力杆”,即杆两端受到大小相等、方向相反、沿着杆轴线的两个力作用。
杆子横截面上只有轴力,这些轴力就是所要计算的桁架内力。
静定桁架是一种没有多余约束的结构,它的内力计算原则上,只要把桁架分解为若干自由体(结点)和约束(杆),用未知力代替约束的作用,对所有的自由体列出全部静力平衡方程式,所得方程式数与包含的未知力数相等。
由于结构是几何不变的,方程组有唯一解。
解这联立方程组就可得到静定桁架的内力。
但在工程实际中,往往可以运用下述两种方法:结点法和截面法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§8-3
杆端力与杆端位移的关系
为此,我们要把各种单跨超静定梁在支座位移及 荷载作用下的杆端弯矩用力法求出,然后列出表格, 以供查用。
弯矩正负号的规定与原来不同了,现在是以使杆 端顺时针转为正。剪力和轴力的规定与原来相同。
正弯矩:对杆端是顺 时针转的,对结点是 逆时针转的。
下面开始对单跨超静定梁在支座位移及荷载作用 下的杆端弯矩用力法进行逐个求解。
§8-4
例:
B q EI A L/2
利用平衡条件建立位移法方程
FP
2EI C
BA杆:杆端弯矩表达式:
M
BA
4 2
EI L EI L
B B
6EI L
2
BC BC
qL
2
L
M
AB
12 qL
2
6EI L
2
12
L/2
BC杆:端弯矩表达式:
M
BC
未知量2个: B B C 建立位移法方程:
F
§8-3
杆端力与杆端位移的关系
一端固定一端铰结单元在荷载、支座位移共同作用下 的杆端弯矩表达式:
M M
AB
BA
3 i A 3 i M A B L 0
F
一端固定一端滑动单元在荷载、支座位移共同作用下 的杆端弯矩表达式:
M M
AB
BA
F i A M B A
§8-1
位移法概述
总结一下位移法解题的步骤: ① 确定结点位移的数量; ② 写出杆端力与杆端位移的关系式; ③ 由结点平衡或截面平衡,建立方程; ④ 解方程,得到结点位移; ⑤ 结点位移回代,得到杆端力。
B
§8-2
位移法未知量的确定
● 位移法是以结点的位移作为的未知量的。 ● 结点:指杆件与杆件的交结处,不包括支座结点 (初学时)。 ● 杆件:等截面的直杆,不能是折杆或曲杆。 例1: 例2:
● 为了减少未知量,忽略轴向变形,即认为杆件的EA=∞。
B C
B
C
A
只有一个刚结点B,由于忽 略轴向变形,B结点只有 B
A
只有一个刚结点B, 由于忽略轴向变形及C 结点的约束形式,B结 点有一个转角和水平位 移 B BH
§8-2
例3:
B
位移法未知量的确定
C
有两个刚结点B、C,由于忽略轴向 变形,B、C点的竖向位移为零,B、C 点的水平位移相等,因此该结构的未 知量为: B C B C
A
45o D
△
B 45o
C
结点位移与杆端位移分析 BD伸长:
2
D结点有 一向下的 位移
DA伸长: 2 DC伸长:
FP
EA L
2 2
由材料力学可知:
FNDB FN D A FN D C
EA 2L 2 2
杆 端 位 移 分 析 杆端力与杆端 位移的关系
§8-1
NDB NDA D Fp
F AB
i A M
§8-3
杆端力与杆端位移的关系
利用前面得到的单跨超静定梁的杆端弯矩表达式, 就可写出结构中每根杆件的杆端力与杆端位移的表达式。
例:
q B EI A
EI
C 杆长为:L 未知量为: B
BA杆: 可看作两端固定的梁,但是在B端 支座发生了转角 B ,方向假设 为顺时针,杆端弯矩表达式:
M
BA
4
EI L
B
M
AB
2
EI L
B
BC杆: 可看作一端固定,一端铰结的梁, 在B端发生了转角 B 以及在均布 M B c 荷载作用下,杆端弯矩表达式:
3
EI L
B
qL 8
2
M
AB
0
§8-3
例:
B
q 2EI
杆端力与杆端位移的关系
FP C L L/2
EI
A L/2
BA杆: 可看作两端固定的梁,在B端支座发 生了转角 B 水平位移 B C ,还有均 布荷载作用下,杆端弯矩表达式:
6EI
M CB 0
§8-4
利用平衡条件建立位移法方程
基本思路 ——先拆、后装,即: 1)化整为零——逐杆写出杆端弯矩式表达式;
2)拼零为整——汇交于刚结点的各杆端弯矩 应满足 M 0 ,对于任意 的脱离体都应满足 X 0 或 Y 0 。
§8-4
例:
B
EI EI
利用平衡条件建立位移法方程
C
杆长为:L 未知量为: B
q
B
EI
C
BC杆
§8-3
杆端力与杆端位移的关系
B
B
对于BA杆 :其变形与受力情况相
当于:一根两端固定的单跨超静定 梁,在B端发生了角位移 B 的结果, 其杆端力也可以用力法求解。
A
BA杆
结论: 在杆端力与杆端位移分析时,可以把结构中的杆件,看作 一根根单跨的超静定梁,其杆端力可以由力法求解。
《结构力学教程》(I)
第8章 位移法
主要内容
§8-1 位移法概述
§8-2 位移法未知量的确定
§8-3 杆端力与杆端位移的关系 §8-4 利用平衡条件建立位移法方程 §8-5 位移法举例 §8-6 基本体系和典型方程法
§8-7 对称性的利用
§8-8 其它各种情况的处理
§8-1
位移法概述
内力 产生 变形 内力与变形间存在关系
§8-2
例10: △
B’ B
位移法未知量的确定
C’
C D
结论: 该题有两个未知量: B 其中BA杆的线位移为:△ BC杆的线位移为:
S in
A
分析方法:
该题有一个刚结点,因此有一个转角位移。水平线位移 的分析方法:假设B结点向左有一个水平位移△,BC杆平 移至B’C’,然后它绕B’转至D点。
§8-3
杆端力与杆端位移的关系
EI L 2 EI L
1、两端固定单元,在A端 发生一个顺时针的转角 A 。
A
M
AB
4
A 4 i A A 2 i A
MAB A
EI,L
由力法求得:
B MBA
M
BA
2、两端固定单元,在B端 发生一个顺时针的转角 B 。
B
M
BA
4 2
F
例4:
E
A
D
D
C
有两个刚结点E、F、D、C,由于忽 略轴向变形, E、F、D、C 点的竖向 位移为零, E、F 点及D、C 点的水平 位移相等,因此该结构的未知量为:
E F C D EF CD
A
B
§8-2
结论:
位移法未知量的确定
刚架(不带斜杆的)一个结点一个转角,一层一个侧移。
EI L EI L
B 4 i B B 2 i B
由力法求得:
M
AB
MAB A
EI,L
B MBA§ຫໍສະໝຸດ -3杆端力与杆端位移的关系
3、两端固定单元,在B端 发生一个向下的位移 。
A MAB EI,L
B
△
MBA
M M
由力法求得:
AB
6 EI L L
2
6i L 6i L
MBA FQBA q B
求FQBA,取BA杆,由
M
A
0
FQ B A
M
BA
M L
AB
qL 2 qL 2
A
MAB FQAB
6i L
把FQBA代入②式,得:
6i L
B
12i L
2
B
12i L
2
qL 2
0
----位移法方程②
§8-5
例1:
位移法举例
q
EI
q C
BA杆:杆端弯矩表达式:
M
BA
4
EI L
B
M
AB
2
EI L
B
杆长为:L A 未知量为: B
BC杆:杆端弯矩表达式:
M
Bc
3
EI L
B
qL 8
2
M
AB
0
0
建立位移法方程:取B结点,应该满足:
B MBC
M
B
M
BC
M
BA
2
0
0
MBA
7 i B
qL 8
——位移法方程
6 EI
2
BA
4、一端固定一端铰结单元,在A端 发生一个顺时针的转角 A 。
A
MAB
A
EI,L
B
由力法求得:
MBA
M M
AB
3 0
EI L
B 3 i B
BA
§8-3
杆端力与杆端位移的关系
5、一端固定一端铰结单元,在B端 发生一个向下的位移 。
MAB
A
EI,L
B
△ 由力法求得:
M
BA
4
EI L EI
B
6EI L
2
BC
qL
2
12 qL
2
M AB 2 B 2 BC 未知量2个: B B C L L 12 BC杆: 可看作一端固定,一端铰结的梁, 3 FP L 2EI 在B端发生了转角 B 、以及在集 M B C 3 L B 1 6 中力作用下,杆端弯矩表达式:
位移法概述
