湘一芙蓉中学2019-2020学年高一上学期入学考试数学试卷
【精品高一数学试卷】2019-2020学年湖南省高一(上)期中数学试卷+答案

2019-2020学年湖南省高一(上)期中数学试卷一、选择题(共12小题,每小题5分,共60分) 1.(5分)设集合{|21A x x k ==+,}k Z ∈,则( ) A .3A ∉B .3A ∈C .3A ⊆D .3A Ü2.(5分)下列函数既是偶函数又有零点的是( ) A .21y x =+B .||2x y =C .2y x x =+D .1||y lg x =+3.(5分)函数()f x ,()g x 由下列表格给出,则(f g (3))(= )A .4B .3C .2D .14.(5分)函数()f x 为定义在R 上的奇函数,当0x …时,()4x f x m =+,则1()(2f -=) A .1B .2-C .1-D .32-5.(5分)函数()f x 与()x g x a =互为反函数,且()g x 过点(2,4)-,则f (1)f +(2)(=) A .1-B .0C .1D .146.(5分)根据表格中的数据,可以判定方程20x e x --=的一个根所在的区间为( )A .(1,0)-B .(0,1)C .(1,2)D .(2,3)7.(5分)如图,在直三棱柱111ABC A B C -(侧棱1AA 垂直于底面)ABC 中,D 为11A B 的中点,12AB BC BB ===,AC =BD 与AC 所成的角为( )A .30︒B .45︒C .60︒D .90︒8.(5分)我们处在一个有声世界里,不同场合,人们对声音的音量会有不同要求.音量大小的单位是分贝()dB ,对于一个强度为I 的声波,其音量的大小η可由如下公式计算:10IlgI η=(其中0I 是人耳能听到的声音的最低声波强度),则70dB 的声音强度1I 是60dB 的声音强度2I 的( )A .76倍B .7610倍C .10倍D .76ln 倍9.(5分)下列不等式中不成立的是( ) A .0.50.556< B .22log 3log 5<C .0.23log 0.83-<D .0.30.40.10.1<10.(5分)若三棱锥P ABC -中,PA PB ⊥,PB PC ⊥,PC PA ⊥,且1PA =,2PB =,3PC =,则该三棱锥外接球的表面积为( ) A .72πB .14πC .28πD .56π11.(5分)已知函数2,1()1,1x ax x f x ax x ⎧-+=⎨->⎩…,若1x ∃,2x R ∈,12x x ≠,使得12()()f x f x =成立,则实数a 的取值范围是( ) A .2a <B .2a >C .22a -<<D .2a >或2a <-12.(5分)已知[]x 表示不超过x 的最大整数,例如[2.3]2=,[ 1.8]2-=-,方程[1|1|]3x +-=的解集为A ,集合22{|211150}B x x kx k =-+-<,且A B R =U ,则实数k 的取值范围是()A .6446[,)(,]5335--⋃B .6422(,][,)5335--UC .6422[,][,]5335--UD .6422[,)(,]5335--⋃二、填空题(本大题共4个小题,每小题5分,共20分)13.(5分)已知幂函数()f x 经过点1(4,)2,则f (9)= .14.(5分)不等式12log (1)1x ->-的解集为 .15.(5分)碳14的衰变极有规律,其精确性可以称为自然界的“标准时钟”.碳14的“半衰期”是5730年,即碳14大约每经过5730年就衰变为原来的一半.科学研究表明,宇宙射线在大气中能够产生放射性碳14.动植物在生长过程中衰变的碳14,可以通过与大气的相互作用得到补充,所以活着的动植物每克组织中的碳14含量保持不变.死亡后的动植物,停止了与外界环境的相互作用,机体中原有的碳14就按其确定的规律衰变.经探测,一块鸟化石中碳14的残留量约为原始含量的37.5%.设这只鸟是距探测时t 年前死亡的,则t 满足的等式为 .16.(5分)已知,若定义域为[0,1]的函数()f x 同时满足以下三条:①对任意的[0x ∈,1],总有()0f x …;②f (1)1=;③当10x …,20x …,121x x +…时,1212()()()f x x f x f x ++…成立,则称函数()f x 为Z 函数.以下说法: (1)若函数()f x 为Z 函数,则(0)0f =; (2)函数()21([0,1])x g x x =-∈是一个Z 函数;(3)若函数()f x 为Z 函数,则函数在区间[0,1]上单调递增;(4)若函数()f x 、()g x 均为Z 函数,则函数()()(0mf x ng x m +>,0n >,且1)n n +=必为Z 函数.正确的有 (填写序号).三、解答题(本大题共6个小题,共70分) 17.(10分)若函数2x y +的定义域为集合A ,集合21|log ,[,4]2B y y x x ⎧⎫==∈⎨⎬⎩⎭.(1)求R A ð,A B I ;(2)若集合{|24}x m C x -=…,且()C A B U Ü,求实数m 的取值范围. 18.(12分)如图所示的圆锥SO 中,母线长为4,且其侧面积为8π. (1)求该圆锥的体积;(2)若AB 为底面直径,点P 为SA 的中点,求圆锥面上P 点到B 点的最短距离.19.(12分)如图,正方形1111ABCD A B C D -的棱长为2,E ,F 分别为1A B ,AC 的中点. (1)证明://EF 平面11A C D ; (2)求三棱锥11F AC D -的体积.20.(12分)渔场中鱼群的最大养殖量为m 吨,为保证鱼群的生长空间,实际养殖量不能达到最大养殖量,必须留也适当的空闲量.已知鱼群的年增长量y 吨和实际养殖量x 吨与空闲率的乘积成正比,比例系数为(0)k k >.(空闲率为空闲量与最大养殖量的比值). (1)写出y 关于x 的函数关系式,并指出这个函数的定义域; (2)求鱼群年增长量的最大值;(3)当鱼群的年增长量达到最大值值时,求k 的取值范围. 21.(12分)已知二次函数2()224f x x mx m =+++.(1)若函数()f x 有两个零点,且一个小于1,一个大于4,求实数m 的取值范围; (2)若关于x 的方程(2)40x f +=有实数解,求实数m 的取值范围. 22.(12分)已知函数2()||1(af x x a x=+-为常数). (1)当1a =-时,判断()f x 在(0,)+∞的单调性,并说明理由; (2)若存在x R ∈,使不等式(2)0x f <成立,求a 的取值范围; (3)讨论()f x 零点的个数.2019-2020学年湖南省高一(上)期中数学试卷参考答案与试题解析一、选择题(共12小题,每小题5分,共60分) 【解答】解:由213k +=,得1k Z =∈,所以3A ∈. 故选:B .【解答】解:由偶函数定义再定义内满足()()f x f x -=,是偶函数的是A ,B ,D ; 且A ,B 没有零点;D 由零点1x e=, 故选:D .【解答】解:由表格可知,g (3)2=, (f g ∴(3))f =(2)4=.故选:A .【解答】解:函数是奇函数, (0)0f ∴=,即(0)10f m =+=,得1m =-,则1211()()(41)(21)122f f -=-=--=--=-,故选:C .【解答】解:由题意指数函数()x g x a =的图象过点(2,4)-, 故可得24a -=,解得12a =或,故函数1()()2x g x =, 故其反函数12()log f x x =,故f (1)f +(2)1122log 1log 2011=+=-=-故选:A .【解答】解:令()2x f x e x =--,由图表知,f (1) 2.7230.280=-=-<,f (2)7.394 3.390=-=>,方程20x e x --=的一个根所在的区间为 (1,2), 故选:C .【解答】解:根据题意,1BB AC ⊥,111BB A B ⊥,Q 2,AB BC AC ===22()AC BC BA =-u u u r u u u r u u u r, ∴20442BC BA =+-u u u r u u u rg , ∴6BC BA =-u u u r u u u rg ,又D 为11A B 的中点,∴2111111()()32522222BD AC BB BA AC BA AC BA BC BA BA BC BA =+==-=-=--=-u u u r u u u r u u u ru u u r u u u r u u u r u u u r u u u r u u u r u u u r u uu r u u u r u u u r g g g g g , 又12BB =,∴BD =AC =∴1cos ,2||||BD AC BD AC BD AC <>===-u u u r u u u ru u u r u u u r g u u ur u u u r ,且0,180BD AC ︒<>︒u u u r u u u r 剟, ∴,120BD AC <>=︒u u u r u u u r,∴异面直线BD 与AC 所成的角为60︒.故选:C .【解答】解:由题意,令107010I lg I =,解得,71010I I =⨯,令206010I lg I =,解得,62010I I =⨯, 所以1210I I = 故选:C .【解答】解:A .Q 函数0.5()f x x =在(0,)+∞上单调递增,f ∴(5)f <(6),即0.50.556<,故A 正确;B .2()log f x x =Q 在(0,)+∞上单调递增,f ∴(3)f <(5),即22log 3log 5<,故B 正确; C .3log 0.80<Q ,0.230->,∴0.23log 0.83-<,故C 正确;D .Q 函数0.1x y =在R 上单调递减,(0.3)(0.4)f f ∴>,即0.30.40.10.1>,故D 错误.故选:D . 【解答】解:如图,把三棱锥P ABC -补形为长方体,则长方体的对角线即为该三棱锥外接球的直径. 设三棱锥外接球的半径为R ,则2222(2)12314R =++=,∴该三棱锥外接球的表面积为2414R ππ=.故选:B .【解答】解:若1x ∃,2x R ∈,12x x ≠,使得12()()f x f x =成立,则说明()f x 在R 上不单调 ①当0a =时,2,1()1,1x x f x x ⎧-=⎨->⎩…,其图象如图所示,满足题意②当0a <时,函数2y x ax =-+的对称轴02ax =<,其图象如图所示,满足题意③当0a >时,函数2y x ax =-+的对称轴02ax =>,其图象如图所示, 要使得()f x 在R 上不单调 则只要二次函数的对称轴12a x =< 2a ∴<综上可得,2a <故选:A .【解答】解:由题意,31|1|4x +-<…,即2|1|3x -<…,解得21x -<-…或34x <…,即(2A =-,1][3-U ,4),22{|211150}B x x kx k =-+>,设22()21115f x x kx k =-+,显然函数()f x 为开口向上,对称轴为114kx =且与x 轴有两个交点的二次函数, A B R =Q U ,∴函数()f x 的两个零点在区间(2-,1]-内或在区间[3,4)内,∴22(2)152280(1)15112011214f k k f k k k⎧⎪-=++>⎪-=++⎨⎪⎪-<<-⎩…或22(3)1533180(4)154432011344f k k f k k k ⎧⎪=-+⎪=-+>⎨⎪⎪<<⎩…, 解得6453k <…或2235k -<-….故选:D .二、填空题(本大题共4个小题,每小题5分,共20分) 【解答】解:设幂函数为()a f x x =, 代入点1(4,)\2,142a =,解之得12a =-, ∴121(9)93f -==. 故答案为:13【解答】解:不等式12log (1)1x ->-,即1122log (1)log 2x ->,012x ∴<-<,求得13x <<, 故答案为:(1,3).【解答】解:根据题意可设原来量为1,则经过t 年后变成了0.375,∴573011()0.3752t ⨯=,0.50.3755730tln ln =, 即57300.3750.5ln t ln =.故答案为:57300.3750.5ln t ln =.【解答】解:若函数()f x 为Z 函数,则令10x =,20x =,得(0)(0)(0)f f f +…,即(0)0f …,又由①对任意的[0x ∈,1],总有()0f x …,(0)0f ∴=,故(1)正确; 函数()21([0,1])x g x x =-∈满足()0g x …,g (1)1=, 若10x …,20x …,121x x +…, 则_1_2_1_2_1_2_1_2_1_21212()[()()]21[(21)(21)2221(21)(21)0x x x x x x x x x x g x x g x g x +++-+=---+-=--+=--…,即1212()()()g x x g x g x ++…,则函数()21([0,1])x g x x =-∈是Z 函数,故(2)正确; 设1201x x <剟,则2101x x <-<,22112111()()()()()f x f x x x f x x f x f x ∴=-+-+厖,即有12()()f x f x …,∴函数()f x 在区间[0,1]上单调递增,故(3)正确;若函数()f x 、()g x 均为Z 函数,则对任意的[0x ∈,1],总有()0f x …,()0g x …, 又0m >,0n >,()()0mf x ng x ∴+….f (1)1=,g (1)1=,则mf (1)ng +(1)1m n =+=.当10x …,20x …,121x x +…时,1212()()()f x x f x f x ++…成立,1212()()()g x x g x g x ++…成立, 0m >Q ,0n >,12121212()()()()()()mf x x ng x x mf x mf x ng x ng x ∴++++++…成立,∴函数()()(0mf x ng x m +>,0n >,且1)n n +=必为Z 函数,故(4)正确. ∴正确命题的序号是:(1)(2)(3)(4).故答案为:(1)(2)(3)(4).三、解答题(本大题共6个小题,共70分)【解答】解:(1){|1}A x x =>,{|1}R C A x x =…,[1B =-,2],(1A B =I ,2];(2)24x m -…,2x m -…,2x m +…,[1A B =-U ,)+∞; ()C A B Q U Ü,21m ∴+-…,3m -…,[3m ∴∈-,)+∞.【解答】解:(1)设底面圆半径为r ,周长为l ,2l r π=, 11424822S l r ππ=⋅=⋅⋅=侧,2r =,||SO ==211||433V r SO ππ=⨯=g g g (2)设圆锥展开为扇形时,圆心角为θ,则22224r l ππθπ⨯===, 故展开图中SP SB ⊥,则圆锥面上P 点到B =【解答】解:(1)证明:连结BD ,E Q 、F 分别为AB ,BD 的中点,1//EF A D ∴, EF ⊂/Q 面11A C D ,1A D ⊂面11A C D ,//EF ∴面11A C D .(2)解:FD AC ⊥Q ,1FD CC ⊥,FD ∴⊥平面11ACC A ,∴三棱锥11F AC D -的体积:11111142222323F A C D D A C F V V --===g g g .【解答】解:(1)由题意,空闲率为1x m-, (1)x y kx m ∴=-,定义域为(0,)m ; (2)由(1)得2(1)()24x k m km y kx x m m =-=--+, 因为(0,)x m ∈,0k >; 所以当2m x =时,4max km y = (3)由题意有0x y m <+< 即:024m km m <+< 因为0m >,解得22k -<<又0k >故k 的取取值范围为(0,2).【解答】解:(1)f (1)12240m m =+++<,解得54m <-, f (4)168240m m =+++<,解得2m <-, 2m ∴<-;(2)令2x t =,(0,)t ∈+∞22(2)()22442280x f f t t mt m t mt m ==++++=+++=, ∴2281(1)2(1)919[(1)2]2222121t t t m t t t t ++-++=-=-=-++--+++g …,当且仅当911t t +=+,即2t =时等号成立,(m ∴∈-∞,2]-.【解答】解:(1)2()||1f x x x =--,0x >时,2()1f x x x=--, 令21212121220()()11x x f x f x x x x x >>-=---++ 2121212()x x x x x x -=-+ 20122()(1)0x x x x =-+>, ()f x ∴在(0,)+∞上单调递增.(2)由(2)0x f >,得2(2)102x xa +->, 22(2)2202(2)2x x x x a a +->>-+,令2(0,)x t =∈+∞,2y t t =-+,11244max y a =>,∴18a >. (3)2()||10a f x x x =+-=, 2||a x x x ∴=-+,0x ≠,作出||y x x x =-+,0x ≠的图象如图;ⅰ1)24a <-或124a >即18a <-或18a >时,1个零点; ⅱ1)24a =-或124a =或0a =即18a =±或0a =时,2个零点; ⅲ1)204a -<<或1024a <<, 即108a -<<或108a <<时,函数有3个零点.。
2019-2020年高一上学期新生入学考试数学试题含答案
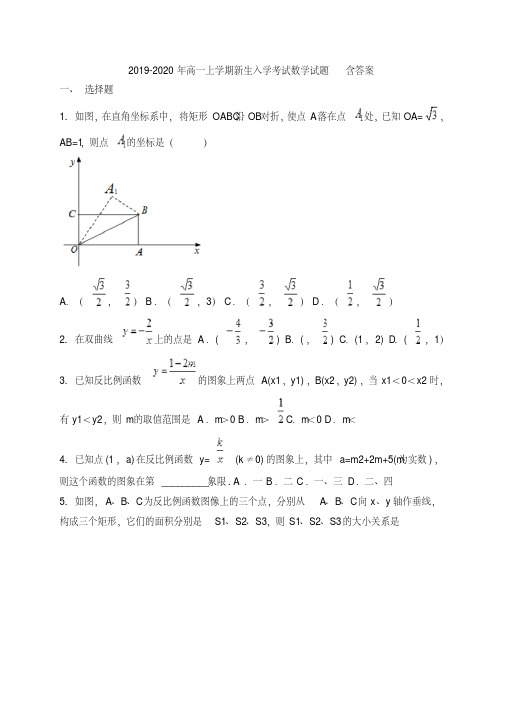
21. 已知 Rt△ABC中,∠ C= 90°,根据下列条件解直角三角形. ( 1)∠ B= 60°, a =4; ( 2) a = - 1, b =3- ; ( 3)∠ A= 60°, c =2+ .
22. 如图 17-2-12 ,正比例函数 y=k 1 x 的图象与反比例函数 y= 的图象相交于 A,B
B : S1<S2<S3 D: S1=S2=S3
6. 函数
是反比例函数 , 则( )
A. m ≠0 B . m ≠0 且 m ≠ 1 C. m =2 D. m =1 或 2
7. 某水坝的坡度 i =1∶ A.10 m B .20 m
,坡长 AB= 20 m,则坝的高度为 ( )
C.40 m D. 2 m 8. sin30 °的值是 ( )
A.1 B . C. D.
9. 若点 (-2 ,y 1 ) 、 (1 ,y 2 ) 、 (3 ,y 3 ) 都在反比例函数 y= y 3 的大小关系是 ( )
的图象上,则 y 1 、y 2 、
A.y 1 3 2
B.y 2 1 3 C.y 1 2 3
D.y 2 3 1
10. 在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积
3. 已知反比例函数
的图象上两点 A(x1 ,y1) ,B(x2 ,y2) ,当 x1<0<x2 时,
有 y1<y2,则 m的取值范围是 A .m>0 B .m> C.m<0 D. m<
4. 已知点 (1 , a) 在反比例函数 y=
(k ≠0) 的图象上,其中 a=m2+2m+5(m为实数 ) ,
表格中空缺的数值可能是多少?请你给出合理的数值。
20. 如图,将一副直角三角形拼放在一起得到四边形 ABCD,其中∠ BAC=4°5 ,∠
【开学考试】湖南2020年高一新生开学考试复习卷-数学 一(含答案)

2020年高一新生开学考试复习卷-数学一一、选择题1.下列说法正确的有()①所有的有理数都能用数轴上的点表示;②符号不同的两个数互为相反数;③有理数分为正数和负数;④两数相减,差一定小于被减数;⑤两数相加,和一定大于任何一个加数.A.1个B.2个C.3个D.4个2.下列剪纸图形中,既是轴对称图形又是中心对称图形的有()A.1个B.2个C.3个D.4个3.一根铁丝正好围成一个长方形,一边长为2a+b,另一边比它长a﹣b,则长方形的周长为( )A.6aB.10a+3bC.10a+2bD.10a+6b4.下列实数中,是无理数的是()A. B.﹣0.3 C. D.5.如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为()A. B. C D.6.如图所示,一辆汽车,经过两次转弯后,行驶的方向与原来保持平行,如果第一次转过的角度为α,第二次转过的角度为β,则β等于()A.αB.90°﹣αC.180°﹣αD.90°+α7.如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则( )A.40°B.30°C.20°D.10°8.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为()A.20°B.30°C.35°D.40°9.如图,已知矩形OABC,A(4,0),C(0,3),动点P从点A出发,沿A﹣B﹣C﹣O的路线勻速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是()A. B. C. D.10.如图,在△ABC中,∠C=90°,AB=4,以C点为圆心, 2为半径作⊙C,则AB的中点O与⊙C的位置关系是()A.点O在⊙C外B.点O在⊙C上C.点O在⊙C内D.不能确定11.某中学准备建一个面积为375 m2的矩形游泳池,且游泳池的宽比长短10m.设游泳池的长为x m,则可列方程( )A.x(x-10)=375B.x(x+10)=375C.2x(2x-10)=375D.2x(2x+10)=37512.大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是103,则m的值是()A.9B.12C.11D.10二、填空题13.如果实数x、y满足方程组,那么x2– y2= .14.某企业对应聘人员进行英语考试,试题由50道选择题组成,评分标准规定:每道题的答案选对得3分,不选得0分,选错倒扣1分。
湖南省湘南中学2019_2020学年高一数学入学考试试题

湖南省湘南中学2019-2020学年高一数学入学考试试题一、选择题(本大题共10小题,共40.0分)aa可以是(中的元素,但不是集合1.若中的元素,则)是集合D.B.A. 3.14 C.,则等于(已知 2.)D. A. C. B.函数的值域是()3.D.A. C.B.设函数4.在区间上都是增函数,则下列说法中:②是增函数;①是增函数;.④是增函数是增函数;③)所有正确说法的个数是(D. 4B. 2C. 3A. 1)下列函数在上是增函数的是(5.C.A. D.B.6.),则已知集合中(,至多有一个元素仅有一个元素 B. A.D. 可能有两个元素C. 至少有一个元素7.下列六个关系式中正确的个数是())(3(1)(2 ) 6)5()((4 )D. 4A. 1B. 2C. 3)的子集,且,,则与的关系是(8.设,,为非空集合A. D.B.C.- 1 -能表示集合到9.,那么下面的四个图形中,设集合)集合的函数关系的有(D. ② C. ②③ A. ①②③④ B. ①②③10.)成立的已知(,则使得C. A. B.D.分)5小题,共20.0二、填空题(本大题共________. 的最大值为若则11.有最小值,已知函数,135°的两面墙(如图),另两边植物园要建形状为直角梯形的苗圃,两邻边借用夹角为12.mm的函数解析式为关于的总长为30,则苗圃面积,设垂直于底边的腰长为__________.,则已知13.__________.xxAx,则={________|≤1或.>3}, 14.已知,15.已知集合.,且,则实数____- 2 -三、解答题(本大题共5小题,共40.0分)分)用列举法表示集合.(616.,求实数的值., 17.8(,若分)设集合,求:(8,分)设,18.);(1)(2..的定义域,并用区间表示(8分)求函数19.- 3 -(10分)如图,该曲线表示一人骑自行车离家的距离与时间的关系.骑车者20.9时离开家,15时回家.根据这个曲线图,请你回答下列问题:(1)最初到达离家最远的地方是什么时间?离家多远?(2)何时开始第一次休息?休息多长时间?(3)第一次休息时,离家多远?(4)11:00到12:00他骑了多少千米?(5)他在9:00~10:00和10:00~10:30的平均速度分别是多少?- 4 -答案和解析D B D A B B C B CC 5.8.6.1. 10.2.3.7.4. 9.13.11.1 )(12.)(14.15.【答案】1解:由. 16.【答案】可得满足方程的解有,故方程的解集为.,所以.因为17.【答案】解:因为,或.所以无解,此时.时,方程当时,此时,当,得..所以,即有则或.综上,得解:由题意可知.18.【答案】)因为,(1所以;)又因为,(2所以.所以.19.【答案】解:要使函数解析式有意义,且. 需满足解得或}. 所以函数的定义域是 {(用区间表示为)[].20.【答案】解:(1)最初到达离家最远的地方的时间是12时,离家30千米.(2)10:30开始第一次休息,休息了半小时.(3)第一次休息时,离家17千米.(4)11:00至12:00他骑了13千米.(5)9:00~10:00的平均速度10千米/时;10:00~10:30的平均速度是14千米/时. - 5 -- 6 -。
湖南高一上学期入学摸底考试数学试题

湘南高一入学摸底考试数学试卷时间:120分钟 分值:100分一、选择题(每小题3分,共30分)每小题有四个答案,其中有且只有一个答案是正确的, 请在答题卡上相应题目的答题区域内作答,答对的得3分,答错或不答的一律得0分.1.计算(﹣3)+(﹣9)的结果是( )A .12-B . 6-C .6+D .12 2..函数1-=x y 中,自变量x 的取值范围是( )A . 1>xB .1≥xC .1<xD .1≤x 3. 下列各式计算不正确...的是( ) A .(3)3--= B2= C .()3339x x = D .2121=- 4.中国的领水面积约为370000km 2,将数370000用科学记数法表示为( ) A .37×104 B . 3.7×104 C . 0.37×106 D . 3.7×105 5.点(35)p ,-关于x 轴对称的点的坐标为( )A . (3,5)--B . (5,3)C .(3,5)-D . (3,5) 6.下列事件中,必然事件是( ) A . 掷一枚硬币,正面朝上B . 任意三条线段可以组成一个三角形C . 投掷一枚质地均匀的骰子,掷得的点数是奇数D . 抛出的篮球会下落7.设21,x x 是一元二次方程0322=--x x 的两根,则21x x +=( )A .2B . 2-C .3-D . 38. 如图1,已知扇形AOB 的半径为6cm ,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的侧面积为( )A . 24πcmB . 26πcmC . 29πcmD . 212πcm图1120︒BOA6cm9. 一元二次方程2350x x --=中的一次项系数和常数项分别是( ) A 、1,-5 B 、1,5 C 、-3,-5 D 、-3,5 10.如图所示的几何体的俯视图是( )A .B .C .D .二、填空题(本题满分24分,共8小题,每小题3分)11.2015的相反数是___________. 12.因式分解:=-42m _________ 13.方程063=-x 解是_________14.如图3,在四边形ABCD 中,已知AB CD =,再添加一个条件___________(写出一个即可),则四边形ABCD 是平行四边形.(图形中不再添加辅助线)15.将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是__________ 16.抛物线5)1(32+--=x y 的顶点坐标为__________.17.不透明的袋中装有2个红球和3个黑球,它们除颜色外没有任何其它区别,搅匀后小红从中随机摸出一球,则摸出红球的概率是__________.18、下列方程:①012=+x ;②02=+x x ;③012=-+x x ;④02=-x x , 其中,没有实数根的方程是 。
2019-2020年高一上学期开学数学试卷含解析

2019-2020年高一上学期开学数学试卷含解析一、选择题:1.下列各式中,表达错误的是()A.∅⊆{x|x<4}B. C.∅∈{∅,{0},{1}} D.2.已知集合A={x∈Z|x2﹣3x﹣18<0},B={x|2﹣x>0},则A∩B等于()A.{3,4,5}B.{﹣2,﹣1,0,1}C.{﹣5,﹣4,﹣3,﹣2,﹣1,0,1}D.{﹣5,﹣4,﹣3}3.已知U=R,A={x|﹣1≤x≤2},B={x|x<a},且B⊆∁R A,则实数a的取值范围是()A.a<﹣1 B.a≤﹣1 C.a>2 D.a≥24.设全集U=M∪N=﹛1,2,3,4,5﹜,M∩∁U N=﹛2,4﹜,则N=()A.{1,2,3}B.{1,3,5}C.{1,4,5}D.{2,3,4}5.如图中阴影部分所表示的集合是()A.B∩[∁U(A∪C)]B.(A∪B)∪(B∪C)C.(A∪B)∩(∁U B)D.B∪[∁U(A∩C)]6.设U为全集,集合M、N⊊U,若M∪N=N,则()A.∁U M⊇(∁U N)B.M⊆(∁U N)C.(∁U M)⊆(∁U N)D.M⊇(∁U N)7.定义集合运算:A⊙B={z︳z=xy(x+y),x∈A,y∈B},设集合A={0,1},B={2,3},则集合A⊙B的所有元素之和为()A.0 B.6 C.12 D.188.设M和P是两个非空集合,定义M与P的差集为M﹣P={x|x∈M,且x∉P},则M﹣(M ﹣P)=()A.P B.M∩P C.M∪P D.M9.若函数f(x)=的定义域为R,则实数m的取值范围是()A.(0,3)B.[0,3)C.[0,2)∪(2,3)D.[0,2)∪(2,3]10.下列各组函数表示同一函数的是()A.与y=x+3 B.与y=x﹣1C.y=x0(x≠0)与y=1(x≠0)D.y=x+1,x∈Z与y=x﹣1,x∈Z11.已知函数f(x)=,则不等式(x+1)f(x)>2的解集是()A.(﹣3,1)B.(﹣∞,﹣3)C.(﹣∞,﹣3)∪(1,+∞)D.(﹣∞,﹣3)∪[1,+∞)二、填空题:12.设全集U={a2﹣2,2,1},A={a,1},则∁U A=.13.设集合M={x|x>1,x∈R},N={y|y=2x2,x∈R},P={(x,y)|y=x﹣1,x∈R,y∈R},则(∁R M)∩N=,M∩P=.14.已知集合A={y|y>a2+1或y<a},B={y|2≤y≤4},若A∩B≠∅,则实数a的取值范围是.三、解答题:解答应写出文字说明、证明过程或演算步骤.15.已知集合A={x|2<x<7},B={x|2<x<10},C={x|5﹣a<x<a}.(Ⅰ)求A∪B,(∁R A)∩B;(Ⅱ)若C⊆B,求实数a的取值范围.16.已知全集U=R,A={x∈R|x2﹣3x+b=0},B={x∈R|(x﹣2)(x2+3x﹣4=0)}.(1)若b=4时,存在集合M使得A是M的真子集,M是B的真子集,求出所有这样的集合M;(2)集合A,B是否能满足(∁U B)∩A=∅?若能,求实数b的取值范围;若不能,请说明理由.17.已知f(x)=﹣4x2+4ax﹣4a﹣a2在区间[0,1]内有一最大值﹣5,求a的值.2016-2017学年山东省烟台二中高一(上)开学数学试卷参考答案与试题解析一、选择题:1.下列各式中,表达错误的是()A.∅⊆{x|x<4}B. C.∅∈{∅,{0},{1}} D.【考点】集合的包含关系判断及应用.【分析】直接利用元素与集合的关系,集合与集合的包含关系判断选项即可.【解答】解:∅⊆{x|x<4},满足集合的包含关系,正确;∅∈{∅,{0},{1}}满足元素与集合的关系,正确;{x|x<4},满足元素与集合的关系,{2}∈{x|x<4},不满足集合与集合的包含关系,错误.故选:D.2.已知集合A={x∈Z|x2﹣3x﹣18<0},B={x|2﹣x>0},则A∩B等于()A.{3,4,5}B.{﹣2,﹣1,0,1}C.{﹣5,﹣4,﹣3,﹣2,﹣1,0,1}D.{﹣5,﹣4,﹣3}【考点】交集及其运算.【分析】求出集合A,集合B,然后求解交集即可.【解答】解:集合A={x∈Z|x2﹣3x﹣18<0}={﹣2,﹣1,0,1,2,3,4,5},B={x|2﹣x >0}={x|x<2},∴A∩B={﹣2,﹣1,0,1}.故选:B.3.已知U=R,A={x|﹣1≤x≤2},B={x|x<a},且B⊆∁R A,则实数a的取值范围是()A.a<﹣1 B.a≤﹣1 C.a>2 D.a≥2【考点】集合的包含关系判断及应用.【分析】由U=R,A={x|﹣1≤x≤2},可得∁R A={x|x<﹣1,或x>2}.再根据B={x|x<a},且B⊆∁R A,即可得出.【解答】解:∵U=R,A={x|﹣1≤x≤2},∴∁R A={x|x<﹣1,或x>2}.又B={x|x<a},且B⊆∁R A,∴a≤﹣1.故选:B.4.设全集U=M∪N=﹛1,2,3,4,5﹜,M∩∁U N=﹛2,4﹜,则N=()A.{1,2,3}B.{1,3,5}C.{1,4,5}D.{2,3,4}【考点】交、并、补集的混合运算.【分析】利用集合间的关系,画出两个集合的韦恩图,结合韦恩图求出集合N.【解答】解:∵全集U=M∪N=﹛1,2,3,4,5﹜,M∩C u N=﹛2,4﹜,∴集合M,N对应的韦恩图为所以N={1,3,5}故选B5.如图中阴影部分所表示的集合是()A.B∩[∁U(A∪C)]B.(A∪B)∪(B∪C)C.(A∪B)∩(∁U B)D.B∪[∁U(A∩C)]【考点】Venn图表达集合的关系及运算.【分析】由韦恩图可以看出,阴影部分是B中且不在A、C内部分所得,由韦恩图与集合之间的关系易得答案.【解答】解:由韦恩图可以看出,阴影部分是B中且不在A、C内部分所得,即B与[C U(A∪C)]的交集组成的集合,即:B∩[C U(A∪C)].故选A.6.设U为全集,集合M、N⊊U,若M∪N=N,则()A.∁U M⊇(∁U N)B.M⊆(∁U N)C.(∁U M)⊆(∁U N)D.M⊇(∁U N)【考点】集合的包含关系判断及应用.【分析】根据集合交并补的运算,结合文恩图即可【解答】解:∵M∪N=N,∴M⊆N,又∵U为全集,∴∁U M⊇∁U N.故答案选:A7.定义集合运算:A⊙B={z︳z=xy(x+y),x∈A,y∈B},设集合A={0,1},B={2,3},则集合A⊙B的所有元素之和为()A.0 B.6 C.12 D.18【考点】进行简单的合情推理.【分析】根据定义的集合运算:A⊙B={z︳z=xy(x+y),x∈A,y∈B},将集合A={0,1},B={2,3}的元素代入求出集合A⊙B后,易得答案.【解答】解:当x=0时,z=0,当x=1,y=2时,z=6,当x=1,y=3时,z=12,故所有元素之和为18,故选D8.设M和P是两个非空集合,定义M与P的差集为M﹣P={x|x∈M,且x∉P},则M﹣(M ﹣P)=()A.P B.M∩P C.M∪P D.M【考点】交、并、补集的混合运算.【分析】由条件中差集的定义便可表示M﹣(M﹣P)={x|x∈M,且x∉(M﹣P)},然后用venn图表示集合M,P,由图形即可得出答案.【解答】解:根据差集的定义,M﹣(M﹣P)={x|x∈M,且x∉(M﹣P)},用venn图表示集合M,P的关系如下图:阴影部分表示M﹣P;∴M﹣(M﹣P)=M∩P.故选:B.9.若函数f(x)=的定义域为R,则实数m的取值范围是()A.(0,3)B.[0,3)C.[0,2)∪(2,3)D.[0,2)∪(2,3]【考点】函数的定义域及其求法;二次函数的性质.【分析】利用函数的定义域为R,推出分母不为0,求解即可.【解答】解:函数f(x)=的定义域为R,可得mx2+2mx+3≠0,m=0显然成立,m≠0时,判别式△=4m2﹣12m<0解得0<m<3,综上:m∈[0,3).故选:B.10.下列各组函数表示同一函数的是()A.与y=x+3 B.与y=x﹣1C.y=x0(x≠0)与y=1(x≠0)D.y=x+1,x∈Z与y=x﹣1,x∈Z【考点】判断两个函数是否为同一函数.【分析】根据函数的三要素,观察定义域和对应法则是否相同,相同者就是同一个函数.【解答】解:对于选项A,定义域为{x|x≠3},y=x+3的定义域为R,故定义域不同,故不是同一个函数;对于选项B,函数的定义域均为R,但是对应法则不同,故不是同一个函数;对于选项C,函数的定义域相同,对应法也相同,故是同一个函数;对于选项D,函数的定义域均为R,但是对应法则不同,故不是同一个函数;故选:C11.已知函数f(x)=,则不等式(x+1)f(x)>2的解集是()A.(﹣3,1)B.(﹣∞,﹣3)C.(﹣∞,﹣3)∪(1,+∞)D.(﹣∞,﹣3)∪[1,+∞)【考点】其他不等式的解法.【分析】通过讨论x的范围,求出f(x)的值,从而解关于x的不等式,取并集即可.【解答】解:x≥0时,f(x)=1,故x+1>2,解得:x>1,x<0时,f(x)=﹣1,故﹣(x+1)>2,解得:x<﹣3,故选:C.二、填空题:12.设全集U={a2﹣2,2,1},A={a,1},则∁U A={2} .【考点】补集及其运算.【分析】利用全集,求出a,然后求解补集即可.【解答】解:全集U={a2﹣2,2,1},A={a,1},可得a2﹣2=a,解得a=﹣1,a=2(舍去),全集U={﹣1,2,1},A={﹣1,1},则∁U A={2}.故答案为:{2}.13.设集合M={x|x>1,x∈R},N={y|y=2x2,x∈R},P={(x,y)|y=x﹣1,x∈R,y∈R},则(∁R M)∩N={x|0≤x≤1} ,M∩P=∅.【考点】交、并、补集的混合运算.【分析】根据集合的基本运算进行求解即可.【解答】解:N={y|y=2x2,x∈R}={y|y≥0},则∁R M={x|x≤1},则(∁R M)∩N={x|0≤x≤1},M∩P=∅,故答案为:{x|0≤x≤1},∅14.已知集合A={y|y>a2+1或y<a},B={y|2≤y≤4},若A∩B≠∅,则实数a的取值范围是a或a>2.【考点】交集及其运算.【分析】通过解不等式化简集合A,B;先算A∩B=∅,再取其补集即可求出a的范围.【解答】解:集合A={y|y>a2+1或y<a},B={y|2≤y≤4},若A∩B=∅,,可得a或,则A∩B≠∅,则实数a的取值范围是:a或a>2.故答案为:a或a>2.三、解答题:解答应写出文字说明、证明过程或演算步骤.15.已知集合A={x|2<x<7},B={x|2<x<10},C={x|5﹣a<x<a}.(Ⅰ)求A∪B,(∁R A)∩B;(Ⅱ)若C⊆B,求实数a的取值范围.【考点】交、并、补集的混合运算;集合的包含关系判断及应用.【分析】(Ⅰ)由A与B求出A∪B,由A求出A的补集,求出(∁R A)∩B即可;(Ⅱ)根据C为B的子集,分C为空集与不为空集两种情况,求出a的范围即可.【解答】解:(Ⅰ)∵A={x|2<x<7},B={x|2<x<10},∴A∪B={x|2<x<7},∁R A={x|x≤2或x≥7},则(∁R A)∩B={x|7≤x<10};(Ⅱ)∵B={x|2<x<10},C={x|5﹣a<x<a},且C⊆B,∴当C=∅时,则有5﹣a≥a,即a≤2.5时,满足题意;当C≠∅时,5﹣a<a,即a>2.5,则有,解得:2.5<a≤3,综上,a的范围为a≤3.16.已知全集U=R,A={x∈R|x2﹣3x+b=0},B={x∈R|(x﹣2)(x2+3x﹣4=0)}.(1)若b=4时,存在集合M使得A是M的真子集,M是B的真子集,求出所有这样的集合M;(2)集合A,B是否能满足(∁U B)∩A=∅?若能,求实数b的取值范围;若不能,请说明理由.【考点】交、并、补集的混合运算;子集与真子集.【分析】(1)由条件易知M应该是Q的一个非空子集,用列举法可得这样的M个数.(2)由(C U Q)∩P=∅可得P⊆Q,当P=∅时求出b的范围.当P≠∅时,由Q={﹣4,1,2},分﹣4∈P、1∈P、2∈P,分别求出b的范围,再把b的范围取并集,即得所求.【解答】解:(1)由条件易知b=4时,P=∅,且Q={﹣4,1,2},由已知P⊊M⊆Q可得,M 应该是一个非空集合,且是Q的一个子集,用列举法可得这样的M共有如下7个:{﹣4}、{1}、{2}、{﹣4,1}、{﹣4,2}、{1,2}、{﹣4,1,2}.(2)由(C U Q)∩P=∅可得P⊆Q,当P=∅时,P是Q的一个子集,此时△=9﹣4b<0,∴b>.当P≠∅时,∵Q={﹣4,1,2},若﹣4∈P,解得b=﹣28,此时,P={﹣4,7},不满足P⊆Q.若1∈P,解得b=2,此时,P={1,2},满足P⊆Q.若2∈P,解得b=2,此时,P={1,2},满足P⊆Q.综上可得,当P=∅或P={1,2}时,满足P⊆Q,(C U Q)∩P=∅.故实数b的取值范围为{b|b>,或b=2 }.17.已知f(x)=﹣4x2+4ax﹣4a﹣a2在区间[0,1]内有一最大值﹣5,求a的值.【考点】二次函数的性质.【分析】先求对称轴,比较对称轴和区间的关系,利用二次函数的图象与性质来解答本题.【解答】解:∵f(x)=﹣4x2+4ax﹣4a﹣a2=﹣4(x﹣)2﹣4a,对称轴为x=,当a<0时,<0,∴f(x)在区间[0,1]上是减函数,它的最大值为f(0)=﹣a2﹣4a=﹣5,∴a=﹣5,或a=1(不合题意,舍去),∴a=﹣5;当a=0时,f(x)=﹣4x2,不合题意,舍去;当0<a<2时,0<<1,f(x)在区间[0,1]上的最大值是f()=﹣4a=﹣5,∴a=;当a≥2时,≥1,f(x)在区间[0,1]上是增函数,它的最大值为f(1)=﹣4+4a﹣4a﹣a2=﹣5,∴a=±1,(不合题意,舍去);综上,a的值是或﹣5.2016年10月29日。
2019-2020学年湖南省长沙一中高一(上)第一次段考数学试卷

(x≠0),
2
∴f(1﹣2x) =
1 ― 2
,
2
1
1
令 1﹣2x = ,得 x = ,
2
4
1 2
15
1―( )
1
4
16
= 1 = 15.
∴f( ) =
1
2
( )2
4
16
故选:C.
12.【分析】由已知可得 f(x) +
2
1
= a 恒成立,且 f(a) = ,求出 a=1 后,将 x=log23
17,
则 f(7)=a•73+7b+7=﹣(﹣a•73﹣7b+7)+14=17+14=31.
故选:A.
9.【分析】对任意 x1,x2∈R 有 f(x1+x2)=f(x1)+f(x2)+1,考察四个选项,本题要研
究函数的奇偶性,故对所给的 x1,x2∈R 有 f(x1+x2)=f(x1)+f(x2)+1 进行赋值研究
A.{2}
B.{2,﹣2}
C.{2,0}
D.{2,﹣2,0}
5.(3 分)函数 f(x)=ax﹣2+1(a>0,a≠1)的图象恒过定点( )
A.(0,1)
B.(0,2)
C.
(2,1)
D.(2,2)
6.(3 分)已知函数 f(x)=x2﹣2x+3 在区间[0,t]上的最大值为 3,最小值为 2,则实数 t
或者直接使用子集的公式,
因为集合元素个数有 2 个,所以子集的个数为 22=4 个.
故选:D.
2.【分析】求函数的定义域化简集合 P,求函数的值域化简集合 Q,再根据补集与交集的定
湖南省长沙市湘一芙蓉中学2018-2019学年初三第一学期入学考试数学试卷(无答案)

湖南省长沙市湘一芙蓉中学2018-2019学年初三第一学期入学考试数学试卷(无答案)湘一芙蓉中学2018 -2019学年上学期入学考试初三数学试卷时量:110 分钟总分:120 分命题人:刘舒娜审核人:文莺洁一、选择题(在下列各题的四个选项中,只有一项是符合题意的。
请在答题卡中填涂符合题意的选项,本题共12 个小题,每小题3 分,共36 分)1.若 O 的半径为5cm,点A 到圆心O 的距离为4cm,则点A 与 O 的位置关系是()A. 点A 在圆上B. 点A 在圆内C. 点A 在圆外D. 不能确定2.在下图中,既是中心对称图形又是轴对称图形的是()A. B. C. D.3.下列计算正确的是()A. a2 +a2 = 2a4B.(2a)2 =4aC. 3 ⨯= 3D. ÷3= 24.小伟5 次引体向上的测试成绩(单位:个)分别为16、18、20、18、18,对此成绩描述错误的是()A. 平均数为18B. 众数为18C. 方差为0D. 极差为45.把多项式x3 - 2x2 +x 分解因式结果正确的是()A.x(x2 -2x)B. x2 (x - 2)C. x (x+1)(x -1)D.x(x-1)26.下列命题是真命题的是()A.相等的圆心角所对的弧相等B. 平分弦的直径垂直于弦C. 长度相等的两条弧是等弧D. 经过圆心的每一条直线都是圆的对称轴x2 - 1的值为0,则x 的值为()7.若分式x -1A. -1B. 1C. 0D. ±18.如右图,在 O 中,已知∠OAB = 22.5︒,则∠C 的度数为()A. 135︒B. 122.5︒C. 115.5︒D. 112.5︒9.二次函数y=2x2 的图象可由y=2(x-1)2 +2的图象()A.向左平移1 个单位,再向下平移2 个单位得到B.向左平移1 个单位,再向上平移2 个单位得到C.向右平移1 个单位,再向下平移2 个单位得到D.向右平移1 个单位,再向上平移2 个单位得到10.在某次聚会上,每两人都握了一次手,所有人共握手10 次,设有x 人参加这次聚会,则列出方程正确的是()A. x (x-1)=10B. 1 x (x-1)=102 C. x (x+1)=10 D. 1 x (x+1)=10211.连接一个几何图形上任意两点间的线段中,最长的线段称为这个几何图形的直径,根据此定义,图(扇形、菱形、直角梯形、结十字图标)中“直径”最小的是()A. B. C. D.12.如右图,边长为1 的正方形ABCD 绕点A 逆时针旋转30︒到正方形AB'C'D',图中阴影部分的面积为()A.1 2B.3 3C. 1 -33D. 1 -34二、填空题(本大题 6 个小题,每小题 3 分,共18 分)13.等边三角形至少要旋转度,才能与自身重合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湘一芙蓉中学2019-2020学年上学期高一入学考试
注意事项:
1.本试卷分试题卷和答题卡两部分,请将答案写在答题卡上每题对应的答题区域内,写在试题卷上无效.
2.考试结束,请将本试题卷和答题卡一并上交. 3.参考公式:二次函数
图象的顶点坐标是(
,
).
一、选择题(下列各小题中,只有一个选项是符合题目要求的,请在答题卡上指定的位置填涂符合要求的选项前面的字母代号.每小题3分,共15题,共45分)
1.下列计算准确的是( ) A. B.
C.
D.
=
2. 函数x
x y +=的图象是( )
A B C
D
3. 如图是某几何体的三视图,则这个几何体是( ) A. 圆柱 B. 球 C. 圆锥 D. 棱柱
4.已知点
)在平面直角坐标系的第二象限内,则的取值范围在数轴上
可表示为(阴影部分)( )
A. B.
C. D.
5.实数
在数轴上的位置如图所示,则下列结论准确的是( )
A. a+b >0
B. a ﹣b >0
C. a•b >0
D. >0
O y
x
O
y
x
O y
x
O
y
x
-1
1 1
-1
-1
-1
1
1
6.某同学在用描点法画二次函数的图象时,列出了下面的表格:
x …-2 -1 0 1 2 …
y …-11 -2 1 -2 -5 …
因为粗心,他算错了其中一个值,则这个错误的数值是( )
A. -11
B. -2
C. 1
D. -5
7.如图,均匀地向此容器注水,直到把容器注满.在注水的过程中,下列图象能大致反映水面高度随时间变化规律的是()
A. B. C. D.
8.如图,是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点,恰好能使△ABC的面积为1的概率是()
A. B. C. D.
9.若等腰三角形中有两边长分别为2和5,则这个三角形的周长为()
A. 9
B. 12
C. 7或9
D. 9或12
10.设函数,的定义域为,且是奇函数,是偶函数,则下列结论中一定准确的是()
A. 是偶函数
B. 是奇函数
C. 是奇函数
D. 是奇函数
11.如图,正方形ABCD中,E是BC边上一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则sin∠EAB的值为().
A. B. C. D.
12.下列命题:①三角形的内心到三角形三个顶点的距离相等;②如果
,那么;③若关于x的方程的解是负数,则m
的取值范围为m<-4;④相等的圆周角所对的弧相等;⑤对于反比例函数,当x﹥-1时,y随着x的增大而增大其中假命题有
A. 1个
B. 2个
C. 3个
D. 4个
13.设则的最大值是()
A. B. 18 C. 20 D. 不存有
14.在下列四个图案中,不是中心对称图形的是()
A. B. C. D.
15.出售某种文具盒,若每个可获利元,一天可售出()个.当一天出售该种文具盒的总利润最大时,的值为( )
A. 1
B. 2
C. 3
D. 4
二、解答题(将解答过程写在答题卡上指定的位置.本大题共有6小题,计55分.)
16.(8分)先化简,再求值:,其中是方程的根。
17.(8分)已知集合,,
(1)求A∪B,(2)求.
18.(9分)解关于x的方程:
19.(10分)如图所示,已知直线与双曲线交于A,B两点,且点A的横坐标为4.
(1)求的值及B点坐标;(2)结合图形,直接写出一次函数的函数值大于反比例函数的函数值时x的取
值范围.
20.(10分)如图所示,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到,抛物线经过B、D两点.
(1)求二次函数的解析式;
(2)连接BD,点P是抛物线上一点,直线OP把△BOD的周长分成相等的两部分,
求点P的坐标.
21.(10分(1)问题发现
如右图,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE。
填空:①∠AEB的度数为____________;
②线段AD、BE之间的数量关系是_________。
(2)拓展探究
如右图,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=900, 点A、D、E
在同一直线上,CM为△DCE中DE边上的高,连接BE。
请判断∠AEB的度数及
线段CM、AE、BE之间的数量关系,并说明理由。
(3)解决问题
如右图,在正方形ABCD中,CD=。
若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离。
参考答案:
一、选择题15*3=45分
题号 1 2 3 4 5 6 7 8
答案 A C A C A D A A
题号9 10 11 12 13 14 15 --------- 答案 B C B D B D C
16.解:∵m是方程x2+3x-1=0的根,
∴m2+3m-1=0,即m2+3m=1,…………2分
∴=……….4分
=………….6分
===……….8分
17. 解:(1)由,可得,所以,…………1分
又因为…………2分所以;…………4分
(2)由可得或,…………5分
由可得. …………6分
所以.…………8分
18.解由题意,关于的方程:+=,
则得或,…………4分,而是原方程的增根,
所以是原方程的根.…………9分
19.解(1)因为直线与双曲线交于A,B两点,且点A的横坐标为4,
将代入直线解析式得:,
所以A点的坐标为,
将代入反比例解析式得:,解得,
所以反比例函数的解析式为,并根据图像的对称性可得.…………5分
(2 )因为,由图像可知:当-4<x<0或x>4时,
一次函数的值大于反比例函数的值.…………10分
20解(1)∵Rt△AOB绕点O逆时针旋转90°得到Rt△COD,
∴CD=AB=1,OA=OC=2,则点B(2,1),D(﹣1,2),代入解析式,
得,解得,∴二次函数的解析式为y=﹣x2+x+.
…………5分
(2)如图:∵OA=2,AB=1,∴B(2,1).
∵直线OP把△BOD的周长分成相等的两部分,且OB=OD,∴DQ=BQ,即点Q为BD的中点,D(﹣1,2),
∴点Q坐标为(,).设直线OP解析式为y=kx,将点Q坐标代入,得k=,解得k=3,
∴直线OP的解析式为y=3x,代入y=﹣x2+x+,得﹣x2+x+=3x,解得x=1或x=﹣4.当x=1时,y=3;当x=﹣4时,y=﹣12.∴点P坐标为(1,3)或(﹣4,﹣12).………10分
21.解(1)因为,所以,
在和中,,CD=CE,
所以和全等,所以AD=BE, ,所以
.…………4分
(2)(2)∠AEB=900;AE=2CM+BE.
理由:∵△ACB和△DCE均为等腰直角三角形,∠ACB =∠DCE= 900,
∴AC=BC, CD=CE, ∠ACB=∠DCB=∠DCE-∠DCB,
即∠ACD= ∠BCE,∴△ACD≌△BCE,∴AD = BE, ∠BEC=∠ADC=1350.
∴∠AEB=∠BEC-∠CED=1350-450=900.
在等腰直角三角形DCE中,CM为斜边DE上的高,∴CM= DM= ME,∴DE=2CM,∴AE=DE+AD=2CM+BE.…………8分
(3)或.…………10分。
