学而思杯六年级数学真题上课讲义
2010 学而思杯 6年级 数学 真题及答案
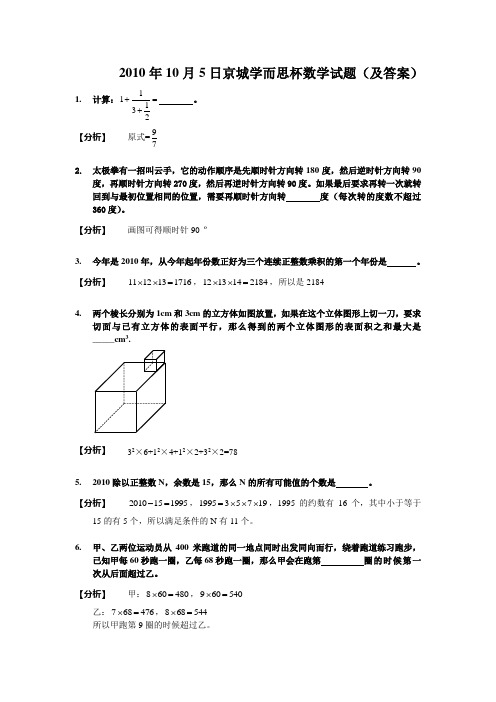
2010年10月5日京城学而思杯数学试题（及答案）1.计算：11132+=+。
【分析】原式=9 72.太极拳有一招叫云手，它的动作顺序是先顺时针方向转180度，然后逆时针方向转90度，再顺时针方向转270度，然后再逆时针方向转90度。
如果最后要求再转一次就转回到与最初位置相同的位置，需要再顺时针方向转度（每次转的度数不超过360度）。
【分析】画图可得顺时针90 º3.今年是2010年，从今年起年份数正好为三个连续正整数乘积的第一个年份是。
【分析】1112131716⨯⨯=，1213142184⨯⨯=，所以是21844.两个棱长分别为1cm和3cm的立方体如图放置，如果在这个立体图形上切一刀，要求切面与已有立方体的表面平行，那么得到的两个立体图形的表面积之和最大是_____cm3.【分析】32×6+12×4+12×2+32×2=785.2010除以正整数N，余数是15，那么N的所有可能值的个数是。
【分析】2010151995-=，199535719=⨯⨯⨯，1995的约数有16个，其中小于等于15的有5个，所以满足条件的N有11个。
6.甲、乙两位运动员从400米跑道的同一地点同时出发同向而行，绕着跑道练习跑步，已知甲每60秒跑一圈，乙每68秒跑一圈，那么甲会在跑第圈的时候第一次从后面超过乙。
【分析】甲：860480⨯=，960540⨯=乙：768476⨯=，868544⨯=所以甲跑第9圈的时候超过乙。
7.将100个5分硬币排成一排，每次操作都从第一个开始。
第一次操作将硬币按顺序1，2，1，2……数，然后将数到2的硬币全部用1角硬币替换；第二次操作将硬币按顺序1，2，3，1，2，3……数，然后将数到3的硬币全部用5角硬币替换；第三次操作将硬币按顺序1，2，3，4，1，2，3，4……数，然后将数到4的硬币全部用1元硬币替换，那么经过上述操作后这100个硬币的总值是元。
学而思六年级数学讲义
学而思六年级数学讲义第一章：整数的运算1. 整数的概念整数是由正整数、零、负整数组成的数集，用于表示有方向的量和相反的数。
2. 整数的加法与减法•整数的加法：同号相加，异号相减。
例如，(2) + (3) = 5，(-2) + (-3) = -5，(-2) + 3 = 1。
•整数的减法：加上相反数。
例如，(5) - (2) = 3，(-5) - (-2) = -3，(-5) - 2 = -7。
3. 整数的乘法与除法•整数的乘法：规律同整数的加法，同号相乘为正，异号相乘为负。
例如，(2) × (3) = 6，(-2) × (-3) = 6，(-2) × 3 = -6。
•整数的除法：除数与被除数同号时为正，异号时为负。
例如，(6) ÷(3) = 2，(-6) ÷ (-3) = 2，(-6) ÷ 3 = -2。
4. 混合运算整数的加减乘除可以进行混合运算，按照运算顺序进行计算，并注意运算符的优先级。
例题：计算：(4 + 6) × (-2) ÷ (-2) - 5解答：首先计算括号内的加法，得到10。
然后进行乘法，得到-20。
接下来进行除法，答案为10。
最后减去5，最终得到5。
第二章：小数的运算1. 小数的概念小数是由整数部分和小数部分组成的数，小数部分用十进制表示。
小数可以表示较小或无法用整数表示的数。
2. 小数的加法与减法•小数的加法：对齐小数点，逐位相加。
例如，1.2 + 3.4 = 4.6，5.8 +0.7 = 6.5。
•小数的减法：转换成加法，被减数加上减数的相反数。
例如，5.2 -1.3可以转换为5.2 + (-1.3)。
3. 小数的乘法与除法•小数的乘法：按照小学乘法的规则进行计算，然后确定小数点的位置。
例如，1.2 × 3 = 3.6，0.5 × 0.4 = 0.2。
•小数的除法：先将除法转化为乘法，然后确定小数点的位置。
学而思-六年级奥数-第七讲.行程问题(一).刘--用-教师版综述
第一讲行程问题学习目标：1、比例的基本性质2、熟练掌握比例式的恒等变形及连比问题3、能够进行各种条件下比例的转化，有目的的转化；4、单位“1”变化的比例问题5、方程解比例应用题知识点拨：发车问题（1）、一般间隔发车问题。
用3个公式迅速作答；汽车间距=（汽车速度+行人速度）×相遇事件时间间隔汽车间距=（汽车速度-行人速度）×追及事件时间间隔汽车间距=汽车速度×汽车发车时间间隔（2）、求到达目的地后相遇和追及的公共汽车的辆数。
标准方法是：画图——尽可能多的列3个好使公式——结合s全程＝v×t-结合植树问题数数。
（3）当出现多次相遇和追及问题——柳卡火车过桥火车过桥问题常用方法⑴火车过桥时间是指从车头上桥起到车尾离桥所用的时间，因此火车的路程是桥长与车身长度之和.⑵火车与人错身时，忽略人本身的长度，两者路程和为火车本身长度；火车与火车错身时，两者路程和则为两车身长度之和.⑶火车与火车上的人错身时，只要认为人具备所在火车的速度，而忽略本身的长度，那么他所看到的错车的相应路程仍只是对面火车的长度.对于火车过桥、火车和人相遇、火车追及人、以及火车和火车之间的相遇、追及等等这几种类型的题目，在分析题目的时候一定得结合着图来进行.接送问题根据校车速度（来回不同）、班级速度（不同班不同速）、班数是否变化分类为四种常见题型：（1）车速不变-班速不变-班数2个（最常见）（2）车速不变-班速不变-班数多个（3）车速不变-班速变-班数2个（4）车速变-班速不变-班数2个标准解法：画图＋列3个式子1、总时间=一个队伍坐车的时间+这个队伍步行的时间；2、班车走的总路程；3、一个队伍步行的时间=班车同时出发后回来接它的时间。
时钟问题：时钟问题可以看做是一个特殊的圆形轨道上2人追及问题，不过这里的两个“人”分别是时钟的分针和时针。
时钟问题有别于其他行程问题是因为它的速度和总路程的度量方式不再是常规的米每秒或者千米每小时，而是2个指针“每分钟走多少角度”或者“每分钟走多少小格”。
2019学而思被六年级数学真题解析(上)
2019学而思被六年级数学真题解析(上)试卷名称：XX 年六年级学而思杯数学考试年级：六年级科目：数学试卷满分：150分答题时间：90分钟试题形式：全部为填空题能力分值：全部为0开放时间：XX 年10月6日9:30－11:00一、填空题(每题4分，共40分)1．XX －201.1＋20.11－2.011＋0.001＝________(4分)2．(..)÷+⨯÷254138512311854＝________(4分)3．已知N *等于N 的因数个数，比如4*＝3，则(2011*10*6*)*++＝_______(4分)4．一个非等腰三角形，一边长为6，一边长为7，还有一边长为6k ，已知k 是自然数，则三角形的周长为________(4分)5．红光大队用拖拉机耕地，2台3小时耕地75亩，照这样计算，4台5小时耕地________亩。
(4分)6．一个骗子到商店买了5元的东西，他付给店员50元钱，然后店员把剩下的钱找给了他；这时他又说自己有零钱，于是给店员5元的零钱，并且要回了开始给出的50元。
那么这个骗子一共骗了______元钱？(4分)7．已知A 、B 两数的最小公倍数是120，B 、C 两数的最小公倍数是180，A 、C 两数的最小公倍数是72，则A 、B 、C 三数的最小公倍数是_______(4分)8．XX 年8月14日，伦敦羽毛球世锦赛进入最后一个比赛日。
在女单决赛中，中国选手王仪涵2比0完胜中华台北选手郑韶婕，首次夺得世锦赛冠军，中国队也实现了女单项目的八连冠。
已知二人共得到67分，其中第二局，王仪涵竟然赢了整整11分，请问，第一局郑韶婕得了_______分。
(羽毛球为21分制)(4分)9．下图为面积100的平行四边形，则阴影部分的面积和是_______(4分)10．AB 间的路被平均分成三段，王先生驾车从A 地开往B 地，已知他这三段路上的平均速度分别为30 km /h ，40 km /h 和60km /h ，则王先生在AB 间的平均速度为_______km /h 。
六年级学而思数学内部讲义pdf
六年级学而思数学内部讲义pdf毕业季作文六年级1初中的三年结束！回眸这三年，我们有多少起伏，又有多少的辛酸往事！三年，我们一起度过了三年！三年的生活说长不长，记得那时初一的我还处于一个懵懂的时期，那时，我们满怀青春，带着对未来的憧憬走进初中的大门！三年，老师陪我们三年！三年来我们调皮过，捣蛋过！但我们也给了老师和家长们满意的答案，他们在这个毕业季为我们付出了很多！我们以优异的成绩回报给了母校一张合格的答卷！当我们迈出集宁七中的大门，回想起刚来这里时，我们用一颗炙热的心来迎接这所学校！但，当我们离去时，我们用不安的心面对未来的生活！当我们聚会那天，忽然觉得我们都以长大，长大成人！聚会，无意就是散火饭！一说吃散火饭，眼泪就回像决坝的洪水流下！相处三年的朋友忽然离去，面对我们的将是新面孔。
我们害怕，害怕那些崭新的面孔，害怕那些崭新的人！毕业啦，我希望和我在一起三年的朋友们不会忘记我；在这个毕业季，我们光荣的分手；在这个毕业季，我们光荣的离去；在这个毕业季，我们骄傲的迎接未来！毕业季作文六年级2说实话，还真舍不得离开同学们，舍不得上司，舍不得睿睿，舍不得小岳……六年来，他们陪我学习，陪我打闹，六年的同学友谊换来了最后那句话“别了，朋友！”是啊，别了朋友；别了同学；别了我讨厌的人；别了我的老师；别了帮助过我和我帮助过的人；那些我不知道名字却整天跟我说话的人……离开学校后，我们也就各奔东西，我不知道再次团聚会是什么感觉？什么样的身份？离别＝再见毕业＝代表增长同学＝见证了我一生中最快乐的时光也许只有分开后，才会知道同学在自已心中的重要性，也许我讨厌的学生是他们离开后我最想念的学生。
从今以后，也许就再也没有人在我身边吵闹……不知道，多年以后，再次走过熟悉的街道，迈入熟悉的大门，见到熟悉的操场、老师们会有什么样的心情，悲伤还是怀念？多年后，我不知道老师是否记得教过我这个学生，不知道那个陪我打闹的胡老师，还会不会记得有个女孩说他穿西装不帅，给他扮免耳朵……也许长大后，我也许会忘记老师，忘记同学，但我忘不了有多少人曾经和我一起玩。
(小学教育)2019学而思被六年级数学真题解析(上)
2019学而思被六年级数学真题解析(上)试卷名称：XX年六年级学而思杯数学考试年级：六年级科目：数学试卷满分：150分答题时间：90分钟试题形式：全部为填空题能力分值：全部为0开放时间：XX年10月6日9:30－11:00一、填空题(每题4分，共40分)1．XX－201.1＋20.11－2.011＋0.001＝________(4分)2．＝________(4分)3．已知N*等于N的因数个数，比如4*＝3，则＝_______(4分)4．一个非等腰三角形，一边长为6，一边长为7，还有一边长为6k，已知k是自然数，则三角形的周长为________(4分)5．红光大队用拖拉机耕地，2台3小时耕地75亩，照这样计算，4台5小时耕地________亩。
(4分)6．一个骗子到商店买了5元的东西，他付给店员50元钱，然后店员把剩下的钱找给了他；这时他又说自己有零钱，于是给店员5元的零钱，并且要回了开始给出的50元。
那么这个骗子一共骗了______元钱？(4分)7．已知A、B两数的最小公倍数是120，B、C两数的最小公倍数是180，A、C两数的最小公倍数是72，则A、B、C三数的最小公倍数是_______(4分)8．XX年8月14日，伦敦羽毛球世锦赛进入最后一个比赛日。
在女单决赛中，中国选手王仪涵2比0完胜中华台北选手郑韶婕，首次夺得世锦赛冠军，中国队也实现了女单项目的八连冠。
已知二人共得到67分，其中第二局，王仪涵竟然赢了整整11分，请问，第一局郑韶婕得了_______分。
(羽毛球为21分制)(4分)9．下图为面积100的平行四边形，则阴影部分的面积和是_______(4分)10．AB间的路被平均分成三段，王先生驾车从A地开往B地，已知他这三段路上的平均速度分别为30 km/h，40 km/h和60km/h，则王先生在AB间的平均速度为_______km/h。
(4分)二、填空题(每题5分，共50分)11．＝________(5分)12．111113572011113572011++⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯＝________(5分)13．解一元一次方程，则＝_______(5分) 14．解一元一次方程，则＝_______(5分)15．解方程组292232202a bca cbb ca+⎧+=⎪⎪+⎪+=⎨⎪+⎪+=⎪⎩，则＝_______(5分)16．分别先后掷2次骰子，点数之积为8的概率为三十六分之______(5分)17．小明看一本书，计划每天看全书的九分之一。
学而思数学2020秋六年级14讲加油站解析
学而思数学2020秋六年级14讲加油站解析在学而思2020年秋季学期的数学课程中，第14讲探讨了加油站问题，并给出了相应的解析。
本文将对该问题进行详细的讲解和解析，帮助同学们更好地理解。
加油站问题是一个常见的数学问题，用来训练学生在实际情境中运用数学知识进行推理和解决问题的能力。
在这个问题中，我们需要考虑一个加油站的位置以及从家到加油站再到目的地的最短路径等相关因素。
在解析这个问题时，首先我们需要确定的是加油站的位置。
我们可以通过题目中给出的信息来确定加油站在整个路径中的位置。
例如，题目可能提到加油站是在起点和终点之间的某个位置，或者是在距离起点和终点相等的位置等。
接下来，我们需要计算从家到加油站再到目的地的最短路径。
这里我们可以运用一些数学工具和方法，比如图论中的最短路径算法。
最常用的最短路径算法是迪杰斯特拉算法和弗洛伊德算法。
根据具体情况，我们可以选择其中一个算法来计算最短路径。
假设我们选择了迪杰斯特拉算法来解决这个问题。
我们需要创建一个图，其中节点表示路段，边表示相邻路段之间的距离。
然后，我们可以运行迪杰斯特拉算法，从起点出发，逐步更新最短路径，直到到达目的地。
在更新路径时，我们需要考虑加油站所在的位置。
当我们计算出最短路径之后，我们还可以进一步研究一些相关问题。
例如，如果题目中给出了不同的加油站，我们可以计算每个加油站到目的地的最短路径，并比较它们之间的差异。
这样，我们就可以找到最佳的加油站位置，使得整个行程的距离最短。
除了最短路径的计算，我们还可以对其他一些因素进行分析。
例如，如果加油站的价格不同，我们可以计算不同加油站的加油成本，并比较它们之间的差异。
如果题目给出了每个加油站能够加满油箱的容量，我们还可以计算从加油站到目的地的最大行驶距离。
这些额外的分析可以帮助我们做出更明智的选择。
总结起来，学而思2020秋季学期的数学课程中的加油站问题是一个实践应用数学知识的经典问题。
通过运用合适的数学工具和方法，我们可以解决该问题并得出最优解。
奥数 六年级 千份讲义 25 1[1].学而思杯考前辅导
![奥数 六年级 千份讲义 25 1[1].学而思杯考前辅导](https://img.taocdn.com/s3/m/49ed10cabb4cf7ec4afed0e8.png)
模块一、计算【例 1】（2008年学而思杯6年级1试第1题）计算：11111200820092010201120121854108180270++++= 。
【例 2】（2009年学而思杯6年级第6题）计算：1122426153577++++=____。
【例 3】（2008年学而思杯6年级第1题）计算：3413441344413444444441344444444412389275277527775277777777527777777775+⨯+⨯++⨯+⨯=。
【巩固】(第五届《小数报》数学竞赛初赛计算题第3题)计算：11111 123420 261220420 +++++学而思杯考前辅导【巩固】 计算：1111111315356399143195++++++【巩固】 111111212312100++++++++++【巩固】234501(12)(12)(123)(123)(1234)(12349)(12350)++++⨯++⨯++++⨯+++++++⨯++++【巩固】 111111212312100++++++++++【巩固】234501(12)(12)(123)(123)(1234)(12349)(12350)++++⨯++⨯++++⨯+++++++⨯++++【巩固】 (仁华学校入学测试题) 22222211111131517191111131+++++=------ .【巩固】 计算：222222223571512233478++++⨯⨯⨯⨯【巩固】 计算：222222222231517119931199513151711993119951++++++++++=----- ．【巩固】计算：222212350133********++++=⨯⨯⨯⨯．【巩固】11111 (......) 1200722006(2008)200622007120071111 (......) 20081200622005(2007)20061n nn n+++++-⨯⨯⨯-⨯⨯+++++⨯⨯⨯-⨯【巩固】1 2【例 4】（2009年学而思杯6年级第1题）a=10.8+10.98+10.998+10.9998+10.99998，的整数部分是。
2019学而思被六年级数学真题解析(上)
2019学而思被六年级数学真题解析(上)试卷名称：XX年六年级学而思杯数学考试年级：六年级科目：数学试卷满分：150分答题时间：90分钟试题形式：全部为填空题能力分值：全部为0开放时间：XX年10月6日9:30－11:00一、填空题(每题4分，共40分)1．XX－201.1＋20.11－2.011＋0.001＝________(4分)2．＝________(4分)3．已知N*等于N的因数个数，比如4*＝3，则＝_______(4分)4．一个非等腰三角形，一边长为6，一边长为7，还有一边长为6k，已知k是自然数，则三角形的周长为________(4分)5．红光大队用拖拉机耕地，2台3小时耕地75亩，照这样计算，4台5小时耕地________亩。
(4分)6．一个骗子到商店买了5元的东西，他付给店员50元钱，然后店员把剩下的钱找给了他；这时他又说自己有零钱，于是给店员5元的零钱，并且要回了开始给出的50元。
那么这个骗子一共骗了______元钱？(4分)7．已知A、B两数的最小公倍数是120，B、C两数的最小公倍数是180，A、C两数的最小公倍数是72，则A、B、C三数的最小公倍数是_______(4分)8．XX年8月14日，伦敦羽毛球世锦赛进入最后一个比赛日。
在女单决赛中，中国选手王仪涵2比0完胜中华台北选手郑韶婕，首次夺得世锦赛冠军，中国队也实现了女单项目的八连冠。
已知二人共得到67分，其中第二局，王仪涵竟然赢了整整11分，请问，第一局郑韶婕得了_______分。
(羽毛球为21分制)(4分)9．下图为面积100的平行四边形，则阴影部分的面积和是_______(4分)10．AB间的路被平均分成三段，王先生驾车从A地开往B地，已知他这三段路上的平均速度分别为30 km/h，40 km/h和60km/h，则王先生在AB间的平均速度为_______km/h。
(4分)二、填空题(每题5分，共50分)11．＝________(5分)12．111113572011113572011++⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯＝________(5分)13．解一元一次方程，则＝_______(5分) 14．解一元一次方程，则＝_______(5分)15．解方程组292232202a bca cbb ca+⎧+=⎪⎪+⎪+=⎨⎪+⎪+=⎪⎩，则＝_______(5分)16．分别先后掷2次骰子，点数之积为8的概率为三十六分之______(5分)17．小明看一本书，计划每天看全书的九分之一。
奥数 六年级 千份讲义 25 1[1].学而思杯考前辅导精编版
![奥数 六年级 千份讲义 25 1[1].学而思杯考前辅导精编版](https://img.taocdn.com/s3/m/d83bdf821a37f111f1855b96.png)
模块一、计算【例 1】（2008年学而思杯6年级1试第1题）计算：11111200820092010201120121854108180270++++= 。
【例 2】（2009年学而思杯6年级第6题）计算：1122426153577++++=____。
【例 3】（2008年学而思杯6年级第1题）计算：3413441344413444444441344444444412389275277527775277777777527777777775+⨯+⨯++⨯+⨯=。
【巩固】(第五届《小数报》数学竞赛初赛计算题第3题)计算：11111 123420 261220420 +++++【巩固】计算：1111111++++++学而思杯考前辅导【巩固】 111111212312100++++++++++【巩固】 234501(12)(12)(123)(123)(1234)(12349)(12350)++++⨯++⨯++++⨯+++++++⨯++++【巩固】 111111212312100++++++++++【巩固】 234501(12)(12)(123)(123)(1234)(12349)(12350)++++⨯++⨯++++⨯+++++++⨯++++【巩固】 (仁华学校入学测试题) 22222211111131517191111131+++++=------ .【巩固】 计算：222222223571512233478++++⨯⨯⨯⨯【巩固】 计算：222222222231517119931199513151711993119951++++++++++=----- ．【巩固】计算：222212350133********++++=⨯⨯⨯⨯．【巩固】11111 (......) 1200722006(2008)200622007120071111 (......) 20081200622005(2007)20061n nn n+++++-⨯⨯⨯-⨯⨯+++++⨯⨯⨯-⨯【巩固】1 2【例 4】（2009年学而思杯6年级第1题）a=10.8+10.98+10.998+10.9998+10.99998，的整数部分是。
小学六年级学而思奥数讲解
某科室有 12 人，其中 6 人会英语， 5 人会俄语， 5 人会日语， 3 人既会英语又会俄语， 2 人 既会俄语又会日语， 2 人既会英语又会日语， 1 人三种语言全会。只会 1 种外语的人比 1 种 外语也不会的人多 ______个。
2006 盏亮着的电灯，各有一个拉线开关控制，按顺序编号为
1、 2、， 2006。将编号为 2 的
第 2008 次截去剩余长度的 米？
1 20092 ，此时该铁丝还剩
2010 厘米，那么该铁丝原长为
______厘
【附加练习】
1 1
13
1 1
24
1 1
35
1 1
2007 2009
4
已知
1 A＝
3
5
24 6
97 99
246
， B＝
98 100
357
试求 A、B、 C 三者大小关系。
96 98
1
， C＝ 。
97 99
10
【开裆裤的课堂笔记总结】 1．整体约分：
被除数、除数中的分母对应相等： 要么带化假、 要么假化带， 考虑提取公因数后整体约分； 2．连锁约分：
多分数连乘，将分子、分母都化成乘积形式，伺机约分。
测试题
例 1 测： 计算： 3 2 2 1 35
2 2 13 35
11 A．1
8
11 B．
8
1 C． 1
11
【举一反三】 还是用数字 0、1、2、3、4、5 六个数字可组成 _____个没有重复数字且能被 5 整除的四位数？
(2010 年北大附中小升初试题 ) 一个三位数，若它的中间数字恰好为首尾数字的平均值，则称它为“好数” 共有 ______个。
2014学而思杯数学解析(6年级)
形的面积）是
平方厘米．（ π 3 ）
B
O
A
【考点】几何，圆与扇形，勾股定理 【难度】☆☆☆ 【答案】225 【分析】如图所示，所求面积即为大扇形的面积加上小扇形的面积：
B
O
A
根据勾股定理， AB2 102 102 200 ，故大扇形的面积是 200π 90 360
π 102 90 25π ，故总面积是 50π 25π 75π 225 . 360
图a
图b
图c
4. 甲要完成一批零件，原计划 10 天完成．实际上甲每天比原计划多做 16 个，结果 8 天完成．这批
零件共
个．
ቤተ መጻሕፍቲ ባይዱ
【考点】应用题，工程问题
【难度】☆☆
【答案】640
【分析】量率对应求总量，16 1 1 640 个. 8 10
5. 如右图，正六边形 ABCDEF 面积是 2014 平方厘米，在 AB、BC、DE、EF 上分别取中点 G、H、I、
【难度】☆☆
【答案】10 【分析】依题意，语、数、英的诊断日期分别是 2 的倍数、3 的倍数、4 的倍数，可见进行英语诊断时
也一定在进行语文诊断，故只考虑语文和数学即可，可见每[2,3] 6 天一周期. 方法一（周期法）：从 1 号开始，每一周期 6 天中只有第 1 天和第 5 天没有任何诊断，30 6 5 ，
语每隔 3 天进行一次，3 月 31 日晚上他们同时在进行诊断，以后则按上述规定进行，从不间断．4
月一共有
天是没有进行过任何科目诊断的．
2014 年 4 月 日一二三四五六
12345 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 【考点】组合，周期问题，容斥原理
学而思 小学六年级数学奥数刘 第二讲 _比和比例
第二讲比和比例学习目标：1、比例的基本性质2、熟练掌握比例式的恒等变形及连比问题3、能够进行各种条件下比例的转化，有目的的转化；4、单位“1”变化的比例问题5、方程解比例应用题知识点拨：比例与百分数作为一种数学工具在人们日常生活中处理多组数量关系非常有用，这一部分内容也是小升初考试的重要内容.通过本讲需要学生掌握的内容有：一、比和比例的性质性质1：若a: b=c：d，则(a + c)：(b + d)= a：b=c：d；性质2：若a: b=c：d，则(a - c)：(b - d)= a：b=c：d；性质3：若a: b=c：d，则(a +x c)：(b +x d)=a：b=c：d；(x为常数)性质4：若a: b=c：d，则a×d = b×c；(即外项积等于内项积)正比例：如果a÷b=k(k为常数)，则称a、b成正比；反比例：如果a×b=k(k为常数)，则称a、b成反比．二、主要比例转化实例①x ay b=⇒y bx a=；x ya b=；a bx y=；②x ay b=⇒mx amy b=；x may mb=(其中0m≠)；③x ay b=⇒x ax y a b=++；x y a bx a--=；x y a bx y a b++=--；④x ay b=，y cz d=⇒x acz bd=；::::x y z ac bc bd=；⑤x的ca等于y的db，则x是y的adbc，y是x的bcad．三、按比例分配与和差关系⑴按比例分配例如：将x个物体按照:a b的比例分配给甲、乙两个人，那么实际上甲、乙两个人各自分配到的物体数量与x的比分别为():a a b+和():b a b+，所以甲分配到axa b+个，乙分配到bxa b+个.⑵已知两组物体的数量比和数量差，求各个类别数量的问题例如：两个类别A、B，元素的数量比为:a b(这里a b>)，数量差为x，那么A的元素数量为axa b-，B的元素数量为bxa b-，所以解题的关键是求出()a b-与a或b的比值．四、比例题目常用解题方式和思路解答分数应用题关键是正确理解、运用单位“l”。
2011年“六年级学而思杯排位赛”数学真题讲解与分析(一)
1 22011年“六年级学而思杯排位赛”数学真题讲解与分析㈠考试时间：2011年2月20日 13:00～14:30 科目：数学 满分：120分1．今年是2011年，请计算(2011)2－2009×2013＝_______。
2．如果一个六位数52188□能被9整除，□里的数是 。
3．一件工程有甲乙两人可以做，甲单独做8天完成，两人合作6天完成，则乙单独做需要 天。
4．从2瓶不同的纯净水，3瓶不同的可乐和4瓶不同的果汁中，拿出2瓶不同类型的饮料，共有____种不同的选法。
5．某种商品按定价卖出可得利润60元，若按定价的80%出售，则亏损12元。
问：商品的购入价是 元。
6．已知两数最大公因数为8，最小公倍数为64，那么这两个数的乘积为 。
7．通过下列各式找规律：32＋42＝52； 52＋122＝132； 72＋242＝252； 92＋402＝412； □2＋□2＝□2。
则三个方框所填的数的和为_____。
8．甲、乙二人以均匀的速度分别从A 、B 两地同时出发，相向而行，他们第一次相遇地点离A 地4千米，相遇后二人继续前进，走到对方出发点后立即返回，在距B 地3千米处第二次相遇，A 、B 两地的距离为 千米。
3 49．如图，已知梯形ABCD 中，AD 平行于BC ，而且BC ＝2AD 三角形AOB 面积为6，那么梯形ABCD的面积为 。
10．如图，ABCD 是正方形。
阴影部分的面积为_____。
(π取3)答 案1．4 2．3 3．244．265．3006．512 7．132 8．9 9．27 10．25。
【学而思】六年级春季第二讲知识概述
第二讲 几何模块之立体几何一、长方体与正方体1. 长方体与正方体的基础概念与表面积、体积公式：正方体：3V a =，26S a =长方体：V abc =，2()S ab bc ac =++对于立体图形来说，每切一刀，表面积增加2个切面对应题目：例1、B1、B7、补充1补充1（强调计算出的面数，不是具体表面积）一个正方体木块，棱长是5米，沿着水平方向将它锯成2片，每片又锯成3长条，每条又锯成4小块，共得到大大小小的长方体24块，那么新得到的这24块长方体的表面积之和是多少？【解析】锯一次增加两个面，锯的总次数转化为增加的面数的公式为：锯的总次数⨯2=增加的面数．原正方体表面积：5×5×6=150(平方米)，一共锯了(2-1)+(3-1)+(4-1)=6次， 所以表面积为150×5×5×2×6=450(平方米)．2. 三视图法求表面积（注意凹槽）对于由若干个小正方体组成的堆积体来说，它的表面积为：（正视、俯视、侧视三个方向看见的面数之和 + 凹槽数）× 2 × 每个面的面积对应题目：例2、B2、补充2补充2（注意底面涂不到）将15个棱长为1的正方体堆放在桌子上，喷上红色后再将它们分开。
涂上红色的部分，面积是（ ）。
【解析】注意底面放在桌子上，不能被染到。
从上向下看有10个：从左向右看有6个；从前向后看有7个。
因此被染色的面有()1067236++⨯=个面，染上红色的面积为36。
3. 染色问题（了解即可）当长宽高都大于等于2时（分别设为a 、b 、c ）：三面染色的有：8个 （角上）；两面染色的有：4【（a -2）+（b -2）+（c -2）】个 （棱上）；一面染色的有：2【（a -2）（b -2）+（a -2）（c -2）+（b -2）（c -2）】个 （面上）； 没有染色的有：（a -2）（b -2）（c -2）个 （内部）；对应题目：例3、练一练二、圆与扇形（圆柱和圆锥的铺垫知识）1. 圆与扇形的概念与公式：圆：2S r π=，2C d r ππ== 扇形：2360n S r π=，222360n C l r r r π=+=⨯+ 对应题目：B3、例42. 曲线图形中求面积的常用方法：1、几何变换（割补、平移、旋转、对称）：例5、补充32、阴影面积 = 整体 – 空白（核心方法）：练一练、B4、B93、差不变：补充4补充3如图，正方形边长为1，正方形的4个顶点和4条边分别为4个圆的圆心和半径，求阴影部分面积．(π取3.14)【解析】把中间正方形里面的4个小阴影向外平移，得到如右图所示的图形，可见，阴影部分的面积等于四个正方形面积与四个90︒的扇形的面积之和，所以221444441π14π7.14S S S S S =⨯+⨯=⨯+=⨯+⨯=+=圆阴影圆．补充4下图中以AB 为直径的半圆与直角三角形ABC 重叠在一起，AB =20，并且上方的阴影部分面积比下方的阴影部分面积大17，求BC 的长度．(π取3.14)【解析】两块阴影都加上空白部分差不变，半圆面积为π×10×10÷2=157，所以三角形ABC面积为157 – 17 = 140，所以BC = 140×2 ÷ 20 = 14．Cba 三、圆柱与圆锥1. 圆柱与圆锥的表面积、体积公式：圆柱：222S r rh ππ=+，2V r h π=圆锥：213V r h π=，圆锥的表面积小学阶段不要求掌握 对应题目：例6、B5、练一练（注意“增加”与“增加到”的区别）2. 旋转问题① 以a 为轴旋转得到圆柱，底面半径为b ，高为a ：2V b a π=，222S b ba ππ=+② 以b 为轴旋转得到圆柱，底面半径为a ，高为b ：2V a b π=，222S a ab ππ=+③ 将边长a 卷成圆柱，底面周长为a ，高为b ： 24a b V π=，22a S ab π=+ ④ 将边长b 卷成圆柱，底面周长为b ，高为a ： 24b a V π=，22b S ab π=+① 以a 为轴旋转得到圆锥，底面半径为b ，高为a ：213V b a π= ② 以b 为轴旋转得到圆锥，底面半径为a ，高为b ：213V a b π= ③ 以c 为轴旋转得到两个圆锥，底面半径为h ，高的和为c ： 21133V h c abh ππ==所以一个直角三角形沿着斜边为轴旋转一周，得到的立体图形体积最小。
2015年六年级学而思杯 数学卷详解 (1)
7. 有 A、B、C 三种溶液，浓度分别为 28%、32%、36%，小明准备用这三种溶液配出浓 度 33%的溶液，但配的时候不小心把 28%和 36%的瓶子弄反了，则小明实际配出的的 溶液浓度是__________. 【答案】31% 【考点】浓度问题、整体法 【解析】根据题意，假设 x 克 A 溶液、 y 克 B 溶液、 z 克 C 溶液混合，得到浓度为 33% 的溶液，但实际却是 z 克 A 溶液、 y 克 B 溶液、 x 克 C 溶液进行混合. 我们从整体考虑，把两次合起来看，即将（ x z ）克 A 溶液、 2 y 克 B 溶液、 （ x z ）克 C 溶液进行混合： 显然， （ x z ）克 28%的溶液和（ x z ）克 36%的溶液混合，得到的溶液浓 度为 32%，而 32%的溶液不管按什么比例混合，浓度还是 32%. 所以题目相当于（ x y z ）克 33%的溶液和（ x y z ）克浓度未知的 D 溶 液混合，得到 32%的溶液. 显然 D 溶液的浓度为 31%.
1 2V2 2 V12 2
4V2 2 V12
2V2 V1 V1 : V2 2 : 1
S1 学学 V1
S2 思思 V2
5. 下面竖式中，相同的汉字代表相同的数字，不同的汉字代表不同的数字，则三位数 学而思 = __________. 【答案】218 【考点】数字谜 【解析】显然“而”= 1 先看个位： “学”+“思”= 10， 再看百位：1 +“思”+ 1（十位的进位）= 10， 所以“思”= 8， “学”= 2. 所以学而思 = 218.
第二届六年级学而思杯
数学卷详解
1. 英文字母中的 A~Z， 正好对应着 1~26 这 26 个数， 例如 A 对应着 1， B 对应着 2， ……， Z 对应着 26. 请在下面方框中填入合适的英文大写字母 使得算式成立. 答： □ 内应该填 ．．．．．． __________.
2011 学而思被六年级数学真题解析(上)
12011学而思杯六年级数学真题解析(上)试卷名称：2011年六年级学而思杯数学考试年级：六年级科目：数学试卷满分：150分答题时间：90分钟试题形式：全部为填空题能力分值：全部为0开放时间：2011年10月6日9:30－11:00一、填空题(每题4分，共40分)1．2011－201.1＋20.11－2.011＋0.001＝________(4分)2．(..)÷+⨯÷254138512311854＝________(4分)3．已知N *等于N 的因数个数，比如4*＝3，则(2011*10*6*)*++＝_______(4分)4．一个非等腰三角形，一边长为6，一边长为7，还有一边长为6k ，已知k 是自然数，则三角形的周长为________(4分)5．红光大队用拖拉机耕地，2台3小时耕地75亩，照这样计算，4台5小时耕地________亩。
(4分)6．一个骗子到商店买了5元的东西，他付给店员50元钱，然后店员把剩下的钱找给了他；这时他又说自己有零钱，于是给店员5元的零钱，并且要回了开始给出的50元。
那么这个骗子一共骗了______元钱？(4分)7．已知A 、B 两数的最小公倍数是120，B 、C 两数的最小公倍数是180，A 、C 两数的最小公倍数是72，则A 、B 、C 三数的最小公倍数是_______(4分)8．2011年8月14日，伦敦羽毛球世锦赛进入最后一个比赛日。
在女单决赛中，中国选手王仪涵2比0完胜中华台北选手郑韶婕，首次夺得世锦赛冠军，中国队也实现了女单项目的八连冠。
已知二人共得到67分，其中第二局，王仪涵竟然赢了整整11分，请问，第一局郑韶婕得了_______分。
(羽毛球为21分制)(4分)9．下图为面积100的平行四边形，则阴影部分的面积和是_______(4分)10．AB 间的路被平均分成三段，王先生驾车从A 地开往B 地，已知他这三段路上的平均速度分别为30 km /h ，40 km /h 和60km /h ，则王先生在AB 间的平均速度为_______km /h 。
奥数六年级千份讲义439第二讲.竞赛班.学生版
【例 1】 某仿古钱币直径为4厘米，钱币内孔边缘恰好是圆心在钱币外缘均匀分布的等弧(如图)．求钱币在桌面上能覆盖的面积为多少？【例 2】 (祖冲之杯邀请赛试题、仁华入学测试题)如图，ABC 是等腰直角三角形，D 是半圆周的中点，BC是半圆的直径．已知10AB BC ==，那么阴影部分的面积是多少？(圆周率取3.14)D第 2讲几何之圆与扇形【例 3】 如图，ABCD 是平行四边形，8AD cm =，10AB cm =，30DAB ∠=︒,高4CH cm =，弧BE 、DF分别以AB 、CD 为半径，弧DM 、BN 分别以AD 、CB 为半径，则阴影部分的面积为多少？(精确到0.01)FEA【例 4】 (迎春杯竞赛试题)如图中三个圆的半径都是5cm ，三个圆两两相交于圆心．求阴影部分的面积和．(圆周率取3.14)【例 5】 (华校2005～2006年度第一学期期中测试第6题)大圆半径为R ，小圆半径为r ，两个同心圆构成一个环形．以圆心O 为顶点，半径R 为边长作一个正方形：再以O 为顶点，以r 为边长作一个小正方形．图中阴影部分的面积为50平方厘米，求环形面积．(圆周率取3.14)【例 6】 (2006年小学生数学报竞赛)传说古老的天竺国有一座钟楼，钟楼上有一座大钟，这座大钟的钟面有10平方米．每当太阳西下，钟面就会出现奇妙的阴影(如右图)．那么，阴影部分的面积是 平方米．96312【例 7】 草场上有一个长20米、宽10米的关闭着的羊圈，在羊圈的一角用长30米的绳子拴着一只羊(见如图)．问：这只羊能够活动的范围有多大？(圆周率取3.14)【例 8】 (祖冲之杯竞赛试题)如图，ABCD 是一个长为4，宽为3，对角线长为5的正方形，他绕C 点按顺时针方向旋转90 ，分别求出四边扫过图形的面积．CBD A【例9】如图，15枚相同的硬币排成一个长方形，一个同样大小的硬币沿着外圈滚动一周，回到起始位置．问：这枚硬币自身转动了多少圈?【例10】一枚半径为1cm的圆形硬币相互紧靠着平放在桌面上，让一枚硬币沿着它们的外轮廓滚过后回到原来的位置，那么与原A点重合的点是______．硬币自己转动______，硬币圆心的运动轨迹周长为_______．1.求下列各图中阴影部分的面积(图中长度单位为cm，圆周率按3计算)：⑴3⑵4⑶111⑷2⑸2⑹2.用一块面积为36平方厘米的圆形铝板下料，从中裁出了7个同样大小的圆铝板．问：所余下的边角料的总面积是多少平方厘米？3. 如图是一个等腰直角三角形ABC ，直角边长度为1，将整个三角形绕C 点顺时针旋转90︒，求斜边扫过图形的面积．CBA4.一只狗被拴在底座为边长3m的等边三角形建筑物的墙角上(如图)，绳长是4m，求狗所能到的地方的总面积．你赢她输阿凡提专与巴依做对，有一位自认为聪明的巴依为了报复阿凡提，雇他为长工。
学而思杯六年级真题及详解数学
2014年六年级学而思综合能力测评（学而思杯）解析一、填空题A（本大题共10小题．每个小题5分，共50分）1.下面四个图形中，阴影面积占总面积一半的图形有个．①②③④【考点】计算，分数定义【难度】☆【答案】2【分析】图形①和④.2.杨老师按零售价买了6本相同的练习本，用了24元．如果按批发价购买，每本将便宜2元，这样可以多买．．本．【考点】应用题，基础应用题【难度】☆【答案】6【分析】零售6本24元，则每本4元，即批发价为422-=元，可以买24212÷=本，多买6本. 3.用2、0、1、4这四个数字可以组成个没有重复数字的四位数．【考点】计数，乘法原理【难度】☆【答案】18【分析】乘法原理，332118⨯⨯⨯=.4.下面的竖式中，被除数是．16□□□□□□□□□【考点】数字谜，除法数字谜【难度】☆【答案】116【分析】由第三行是10得出除数只能是2或5，又由于第五行尾数是6，那么除数只能是2，第五行是16，则商是58，被除数是116.5. 下图中，大长方形的长是40厘米，长是宽的2倍．那么阴影面积是 平方厘米．（π取3.14）【考点】几何，圆与扇形，图形的分割与剪拼 【难度】☆ 【答案】400【分析】图形中小正方形边长是10厘米，阴影部分正好可以拼成四个小正方形. 41010400⨯⨯=.6. 甲、乙两所小学，甲校的人数是乙校人数的25，甲校的女生人数占全校人数的40%，乙校男生人数占全校人数的60%．如果将甲、乙两校合并，女生人数占总人数的 %． 【考点】应用题，分百应用题 【难度】☆ 【答案】40%【分析】设甲乙两校人数分别为2份和5份，则女生共240%5(160%) 2.8⨯+⨯-=，占2.8(25)40%÷+=.另外，实际上，从甲乙两校女生都占各自的40%即可得出结论.7. 下图中，长方形ABCD 的长为16厘米，宽为10厘米，E 、F 分别是AB 、BC 的中点，那么，三角形DEF 的面积是 平方厘米．FE DCBA【考点】几何，三角形面积 【难度】☆☆ 【答案】60【分析】用总面积减去三个白色三角形的面积，11116101658108560222⨯-⨯⨯-⨯⨯-⨯⨯=.8. 某项工程，如果甲单独做，12天完成；如果乙单独做，24天完成；如果要求10天完成任务，并且要求甲、乙两人合作的时间尽可能少，那么甲、乙合作 天． 【考点】应用题，工程问题 【难度】☆☆ 【答案】4【分析】设工总24份，则甲每天做2份，乙每天做1份，尽量不合作的话则尽量让做得多的甲做，即全程只有两种状态：甲做、甲乙合作，则甲10天都在做，共做20份，乙需要做4份，即合作4天.9. 将8个相同的球分给甲、乙、丙、丁、戊五个小朋友，每人得到1个球或2个球，那么共有 种分法．【考点】计数，排列组合 【难度】☆☆ 【答案】10【分析】有2人得到1个球，3人得到2个球，25C 10=.10. 将5个自然数排成一列，从第三个数开始，每个数等于前面两个数的和，那么这5个数中，最多有 个质数．【考点】数论，质数与合数，数论中的最值 【难度】☆☆☆ 【答案】4【分析】注意到2、3、5、8、13中有4个质数，接下来论证不可能有5个质数.由于第三个数加第四个数等于第五个，这三个数不能都是奇数，必有一偶，这个偶数如果是2的话则它前面的数必然不能都是质数，所以这5个数不可能都是质数.二、填空题B （本大题共5小题．每个小题8分，共40分） 11. 两位数ab 比一位数a 少1个约数，那么ab 最大是 ． 【考点】数论，数论中的最值 【难度】☆☆ 【答案】97【分析】极端分析，9a =有三个因数，则ab 有两个因数，只能是个质数，97.12.将10个棱长为1厘米的立方体如下图摆放，那么，这个立体图形的表面积是平方厘米．【考点】几何，立体图形三视图【难度】☆☆【答案】36【分析】画出三视图，三个方向的面积都是1236++⨯=.++=，(666)23613.甲乙两车分别从A、B两地同时出发，相向而行．出发时，甲、乙两车的速度之比是5:4，相遇后，甲的速度增加20%，乙的速度增加50%，他们到达目的地后都立即返回，再次相遇的地点距离第一次相遇地点20千米．那么，A、B两地的距离是千米．【考点】行程，比例法解行程，多次相遇【难度】☆☆☆【答案】180【分析】相遇后两人的速度比变为[5(120%)]:[4(150%)]6:61:1⨯+⨯+==，将全程分为9份，则第一次相遇两人共走9份，其中甲走了5份，第二次相遇两人共走18份，其中甲走了9份，即第二次相遇时甲共走5914⨯=千米.+=份，两次相遇地点相距1份，所以全程距离为29018014.有一个三位数abc，满足如下性质：由a、b、c所组成的没有重复数字的三位数中，最大的三位数与最小的三位数之差恰好等于abc．那么，这个三位数abc是．【考点】数论，位值原理【难度】☆☆☆☆【答案】495【分析】如果a、b、c中没有0，设最大三位数M xyz=，99()=，则最小三位数N zyx-=-，M N x z 即99()=-是99的倍数，注意其中x是a、b、c最大的一个，而z是a、b、c中最小的一个，abc x z枚举99的倍数，有49599(94)=⨯-满足条件；如果a、b、c中有一个0，设最大三位数0=，9990N y xM xy=，则最小三位数0-=-，M N x y 即9990=-，注意其中a、b、c中有一个0，另外两个分别为x和y（x y abc x y>），通过枚举x 来算出c，发现没有符合条件的三位数；如果a、b、c中有一个0，则只能组成一个三位数，显然不满足条件.综上，只有一个三位数495满足条件.15. 将一张正方形纸片，按下图方式进行操作：将正方形的四个顶点向内折叠至正方形中心，然后将新得到的图形的四个顶点再次向内折叠至中心．最后将纸片完全展开，原正方形四条边与所有折痕所组成的新图形中，共有 个正方形．．．．第二次向内折：第一次向内折：？展开【考点】计数，几何计数 【难度】☆☆☆☆ 【答案】11【分析】展开后的图形如图所示：计数其中正方形的个数，共有11个.第II 卷（解答题 共60分）三、解答题（本大题共5题. 解答过程请写在答题纸上、试卷作答无效） 16. 计算及解方程（每题4分、共16分）：（1）3343 4.41624815⨯+⨯+÷（2）22222222246810121416+++++++ （3）11916122030-+-（4）1291212x x+--= 【考点】计算，分数计算，公式类计算，裂项计算，分数方程 【难度】☆☆ 【答案】30、816、12、5x = 【分析】（1）3341515323 4.4162(4.42)66246304815445⨯+⨯+÷=⨯++=⨯+=+=（2）2222222221246810121416289178166+++++++=⨯⨯⨯⨯=或222222222468101214164163664100144196256816 +++++++=+++++++=（3）1191111111111111111 6122030233445562443362⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-+-=---++--=++-+-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭或1191191111111111 6122030122030344556362⎛⎫⎛⎫⎛⎫-+-=+-=-++--=+=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭或11911052721 6122030606060602 -+-=-+-=（4）12916(1)(29)127355 212x xx x x x+--=⇒+--=⇒=⇒=17.列方程（组）解应用题（6分）小英的玩具个数是小丽的5倍，如果小英把6个玩具送给小丽，那么小丽的玩具个数就是小英的2倍了．请问：小英、小丽原来各有玩具多少个？【考点】应用题，列方程（组）解应用题【难度】☆☆【答案】10、2【分析】标准格式如下解：设小丽原有x个玩具，则小英原有5x个玩具，根据题意，得62(56)x x+=-解得2x=55210x=⨯=答：小英原有10个玩具，小丽原有2个玩具.18.如果一个数能被它前两位数字按序组成的两位数整除，则称这个数为“好数”．例如：120的前两位数字按序组成的两位数是12，120能被12整除，所以120是“好数”．请问：（1）四位数中，最小的“好数”是多少？（4分）（2）若存在连续98个自然数都不是“好数”，那么这98个数中，最小的那个数最小可能是多少？（6分）【考点】数论，数论中的最值【难度】☆☆☆【答案】1000、9901【分析】（1）极端分析，1000能被10整除.（2）注意到0xy、00xy都是好数，所以这连续98个数至少是4位数，由于连续n个自然数中必然有一个数能被n整除，所以这些数的前两位不能是10~98，所以最小的情况只可能是9901~9998.19.请回答下列问题：（1）是否能将1～8排成一个圈，使得相邻两个数字的和都是一位数？如果能，请写出一种，如果不能，请说明理由．（3分）（2）请将1～8从左到右排成一行，使得相邻两个数字的和都是一位数．写出1种即可．（3分）（3）第2问中，将1～8从左到右排成一行，相邻两数字之和都是一位数，那么共有多少种不同的排法？（6分）【考点】组合，计数，构造与论证【难度】☆☆☆【答案】不能、81634527、16【分析】（1）不能，因为8要和两个数相邻，而8只有和1相邻才能得出一位数的和.（2）所有情况如下：81634527 81635427 81453627 8154362772634518 72635418 72453618 7254361881726345 81726354 81724536 8172543663452718 63542718 45362718 54362718（3）81一定在一侧，即81（左右可颠倒，2种情况），剩余的6个格中，7一定在最左或最右，且只能与2相邻，2种情况，剩余的4个格中，6一定在最左或最右，且只能与3相邻，2种情况，最后4和5随意排，2种情况，共222216⨯⨯⨯=种.20.如图，大正方形格板是由64个1平方厘米的小正方形铺成的，A、B、C、D是其中四个格点．AD与BC相交于点E．（1）三角形ACD的面积是多少平方厘米？（4分）（2）在其它格点中标出一点F，使得三角形ABF的面积恰等于2平方厘米，这样的点F共有几个？（4分）（3）:CE EB是多少？（4分）（4）三角形ABE的面积是多少平方厘米？（4分）【考点】几何，格点，比例模型【难度】☆☆☆【答案】6、9、4:3、12 7.【分析】（1）直接套公式计算，14362⨯⨯=平方厘米.（2）如图所示，9个点分布在两条与AB平行的直线上.（3）通过数格点利用毕克公式算出593122 ABDS=+-=，或者通过整体减空白来算1119361215112222 ABDS=⨯⨯-⨯⨯-⨯⨯-⨯=.利用风筝模型，9::6:4:32ACD ABDCE EB S S===.（4）14242ABCS=⨯⨯=，3124347ABES=⨯=+.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2011学而思杯六年级
数学真题
2011学而思杯六年级数学真题
一、填空题(每题4分，共40分)
1．2011－201.1＋20.11－2.011＋0.001＝________(4分)
2．(..)÷+⨯÷254138512311854
＝________(4分)
3．已知N *等于N 的因数个数，比如4*＝3，则(2011*10*6*)*++＝_______(4分)
4．一个非等腰三角形，一边长为6，一边长为7，还有一边长为6k ，已知k 是自
然数，则三角形的周长为________(4分)
5．红光大队用拖拉机耕地，2台3小时耕地75亩，照这样计算，4台5小时耕地
________亩。
(4分)
6．一个骗子到商店买了5元的东西，他付给店员50元钱，然后店员把剩下的钱找
给了他；这时他又说自己有零钱，于是给店员5元的零钱，并且要回了开始给出的50元。
那么这个骗子一共骗了______元钱？(4分)
7．已知A 、B 两数的最小公倍数是120，B 、C 两数的最小公倍数是180，A 、C 两
数的最小公倍数是72，则A 、B 、C 三数的最小公倍数是_______(4分)
8．2011年8月14日，伦敦羽毛球世锦赛进入最后一个比赛日。
在女单决赛中，
中国选手王仪涵2比0完胜中华台北选手郑韶婕，首次夺得世锦赛冠军，中国队也实现了女单项目的八连冠。
已知二人共得到67分，其中第二局，王仪涵竟然赢了整整11分，请问，第一局郑韶婕得了_______分。
(羽毛球为21分制)(4分)
9．下图为面积100的平行四边形，则阴影部分的面积和是_______(4分)
10．AB 间的路被平均分成三段，王先生驾车从A 地开往B 地，已知他这三段路上
的平均速度分别为30 km /h ，40 km /h 和60km /h ，则王先生在AB 间的平均速度为_______km /h 。
(4分)
二、填空题(每题5分，共50分)
11．15191113()142612203042+-
-+-⨯＝________(5分)
12．111113572011113572011++⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯＝________(5分) 13．解一元一次方程 [(8)88]88x +⨯-÷=，则x ＝_______(5分)
14．解一元一次方程 ()x x ⎡⎤⨯⨯++-=⎢⎥⎣⎦321321223423
，则x ＝_______(5分)
15．解方程组29
2232
202a b c a c b b c a +⎧+=⎪⎪+⎪+=⎨⎪+⎪+=⎪⎩ ，则b ＝_______(5分)
16．分别先后掷2次骰子，点数之积为8的概率为三十六分之______(5分)
17．小明看一本书，计划每天看全书的九分之一。
按计划看了3天后，由于急于知
道结局，于是跳过了200页，并将看书速度提高了一倍，又看了1天，把书看完。
已知小明计划每天看书的页数相同，则这本书共______页。
(5分)
18．一次超难的数学考试，某班前五名同学共得20分(得分是任意正整数)，并且
分数各不相同，也没有得0分的，则有_______种得分的情况。
(5分)
19．用1、2、3、4、5这几个数字组成一个5位数，要求每个数字均出现1次，且
3必须在2前面(但它们不一定相邻)，2必须在1前面，则共能组成_____个不同的五位数。
(5分)
20．如图所示，直角三角形PQR的短直角边长为5厘米．正方形EFRQ的面积是89平方厘米，则正方形PQDC的面积为______(5分)
三、填空题(每题6分，共60分)
21．今天是2011年10月6日，已知六位数2011□□能被106整除，则该六位数的末两位是______(6分)
22．1000千克青菜早晨测得它的含水量为90%，这些菜到了下午测得含水量为80%，那么这些菜的重量减少了______千克。
(6分)
23．一项工程，乙单独做要12.5天完成．如果第一天甲做，第二天乙做，第三天一起做，这样交替轮流做，那么恰好用整数天完成；如果第一天乙做，第二天一起做，第三天甲做，这样交替轮流做，那么比上次轮流的做法少用半天完工。
已知甲乙工效不相等，则甲单独做需要______天。
(6分)
24．用0、1、2、3、4这5个数字(可以重复)，共能组成______个比2011小，比1006大的偶数。
(6分)
25．有一个三位数，它们除以2、4、6、7所得到的余数互不相同(不能余0)。
这样的三位数中最大的是______(6分)
26．小偷与警察相隔30秒先后逆向跑上一自动扶梯，小偷每秒可跨越3级阶梯，警察每秒可跨越4级阶梯。
已知该自动扶梯每秒运行1.5级阶梯，警察要想在自动扶梯上抓住小偷的话，自动扶梯至少要有_______级。
(6分)
27．如图，有一座圆柱塔，在地面到塔顶要通过塔内部的螺旋形通道上去，已知塔内底面圆周长为30米，塔高140米，通道共转了三圈半。
问：通道共长
______米。
(6分)
28．如图，以直角三角形ABC 的两条直角边为直径作两个半圆，已知这两段半圆
弧的长度之和是75.36厘米，那么三角形ABC 的面积最大是______平方厘米。
( 取3.14) (6分)
C
B A
29．学而思杯数学考试时间为8：00－9：30，请问在考试时间内分针与秒针共重
合了______次。
(8点为第一次)(6分)
30．B 地在A ，C 两地之间．甲从B 地到A 地去送信，甲出发10分后，乙从B 地
出发到C 地去送另一封信，乙出发后10分，丙发现甲、乙刚好把两封信拿颠倒了，于是他从B 地出发骑车去追赶甲和乙，以便把信调过来。
已知甲、乙的速度相等，丙的速度是甲、乙速度的3倍，丙出发把甲乙二人的信调过来后自己返回B 地至少要用_____分钟。
(注：甲、乙出发后不停留也不转向，忽略丙调换信件和转向的时间)(6分)。