材料力学_图乘法
合集下载
材料力学图乘法
材料力学图乘法材料力学图乘法是材料力学中的一种重要计算方法，它可以帮助工程师和科研人员快速准确地计算材料的性能参数，为材料的设计和应用提供重要参考。
在材料力学图乘法中，我们需要了解一些基本概念和计算步骤，下面将对材料力学图乘法进行详细介绍。
首先，我们需要了解什么是材料力学图。
材料力学图是用来描述材料在外力作用下的性能变化规律的图表，通常包括应力-应变曲线、拉伸性能曲线、压缩性能曲线等。
通过材料力学图，我们可以直观地了解材料在不同应力下的应变变化情况，从而评估材料的力学性能。
接下来，我们来介绍材料力学图乘法的计算步骤。
首先，我们需要准备两个材料的力学图，分别记为A和B。
然后，我们将这两个力学图进行叠加，即将A图的应力-应变曲线与B图的应力-应变曲线进行对应相乘。
这样，我们就可以得到一个新的力学图，用来描述两种材料叠加后的性能。
在进行材料力学图乘法计算时，我们需要注意一些细节。
首先，要保证A图和B图的坐标轴尺度一致，这样才能进行准确的叠加计算。
其次，要注意叠加计算的顺序，通常是先进行应力的叠加，然后再进行应变的叠加。
最后，要对叠加后的新力学图进行分析，得出叠加后材料的性能参数，如弹性模量、屈服强度、断裂强度等。
通过材料力学图乘法，我们可以更加深入地了解材料的性能特点。
例如，当我们需要设计一个复合材料结构时，可以通过材料力学图乘法来评估不同材料叠加后的性能，从而选择合适的材料组合方案。
另外，材料力学图乘法还可以帮助我们预测材料在复杂加载条件下的性能表现，为工程实践提供重要参考。
总之，材料力学图乘法是材料力学中一种重要的计算方法，它可以帮助我们快速准确地评估材料的性能参数，为材料的设计和应用提供重要参考。
通过深入学习和应用材料力学图乘法，我们可以更好地理解材料的性能特点，为工程实践和科研工作提供有力支持。
希望本文的介绍能够帮助大家更好地掌握材料力学图乘法的基本原理和计算方法，为相关领域的工作提供帮助。
结构力学(第三章)-图乘法
( M x tan ) 1 x tan M P dx EI tan
xM P dx
图乘法求位移公式为:
图乘法的 适用条件是 什么?
EI tan 1 xc yc EI EI
ip
yc
EI
例. 试求图示梁B端转角.
A
P
B B
MP
A
M 1 B 1
B
c
y c
ql 2 / 2
ql 2 / 8
例 4. 图示梁 EI 为常数，求C点竖向位移 。 q ql 2 / 8 ql 2 / 2
MP
A
l/2 C
1
q q
l/2
B
l/2
Mi
c
y c
C ql / 2 ql 2 / 8
ql 2 / 8 ql 2 / 4 ql 2 / 8
ql / 2
§3.4 图乘法及其应用
(Graphic Multiplication Method and its Applications)
刚架与梁的位移计算公式为：
iP MM P ds EI
在杆件数量多的情况下,不方便. 下面介绍 计算位移的图乘法.
一、图乘法
MM P ds EI 1 图乘法是Vereshagin于 M M P ds (对于等 截面杆) EI 1925年提出的，他当时 1 为莫斯科铁路运输学院 MM P dx (对于直杆) EI 的学生。
1 1
B
Mi
l
ql / 4
2
l
ql 2 / 4
1/ l
0 解：作荷载弯矩图和单位荷载弯矩图
q
MP
5结构力学图乘法.
（1）常见图形面积和形心：
矩 形
a
l
A al
xc 1 l 2 xc 1 3l
xc 1 4l
3 xc 8 l
三角形
a
l
A 1 2 al A 1 3 al A 2 3 al
l
a
l
标准二次 抛物线
a
l
a
A 2 3 al
xc 1 l 2
（2） 梯形相乘
A1
A2
M M
i
K
dx A1 y1 A2 y 2
1 M M P dx EI
(M x tanα)
yc
xc x
M
x
图乘法是Vereshagin于1925年 提出的，他当时为莫斯科铁路 运输学院的学生。
4、 注意事项
KP AP yc EI
还记得 吗？
（1）必须符合图乘法的适用条件； （2） 必须取自直线图形； （3）同侧弯矩图相乘为正，反之为负； （4）拱、曲杆结构和连续变截面的结构只能通过积 分的方式求解； （5）应用图乘法首先熟练掌握常用图形面积及形心 位置。
如果将AC段的 M P图如下图那样分块，就比 16 较麻烦。 4kN 4 2kN/m 8 M P图 4 A C C A 2m 4kN.m 例2 求 B, EI等于常数。 12kN.m 4kN C 4m
2kN/m
4kN.m 4m B 7kN
A
5kN
解： 作 M 图 M P 图，如下页图所示。
12
c
y2
d
M图
（3）一般形式的二次抛物线图形相乘 （4）曲线图形与折线图形相乘
M M
i
K
矩 形
a
l
A al
xc 1 l 2 xc 1 3l
xc 1 4l
3 xc 8 l
三角形
a
l
A 1 2 al A 1 3 al A 2 3 al
l
a
l
标准二次 抛物线
a
l
a
A 2 3 al
xc 1 l 2
（2） 梯形相乘
A1
A2
M M
i
K
dx A1 y1 A2 y 2
1 M M P dx EI
(M x tanα)
yc
xc x
M
x
图乘法是Vereshagin于1925年 提出的，他当时为莫斯科铁路 运输学院的学生。
4、 注意事项
KP AP yc EI
还记得 吗？
（1）必须符合图乘法的适用条件； （2） 必须取自直线图形； （3）同侧弯矩图相乘为正，反之为负； （4）拱、曲杆结构和连续变截面的结构只能通过积 分的方式求解； （5）应用图乘法首先熟练掌握常用图形面积及形心 位置。
如果将AC段的 M P图如下图那样分块，就比 16 较麻烦。 4kN 4 2kN/m 8 M P图 4 A C C A 2m 4kN.m 例2 求 B, EI等于常数。 12kN.m 4kN C 4m
2kN/m
4kN.m 4m B 7kN
A
5kN
解： 作 M 图 M P 图，如下页图所示。
12
c
y2
d
M图
（3）一般形式的二次抛物线图形相乘 （4）曲线图形与折线图形相乘
M M
i
K
材料力学-图乘法
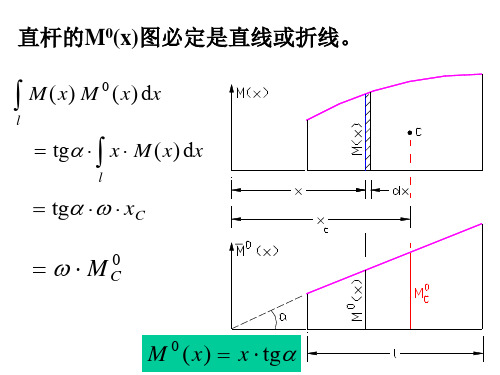
例：图示刚架，EI=const。求A截面的水 平位移 ΔAH 和转角θA 。
CL12TU41
解： AH
qa 4 EI
1 4
2 3
1 3
85
3qa 4 8E I
qa 2
qa qa 2 qa / 2
2
CL12TU31
解：
M(x) M 0(x)
vB
l
EIdxM Nhomakorabea0 C
EI
1 Pl 2 2l
EI 2 3
Pl 3
3E I
B
1 EI
Pl 2 2
1
Pl 2
顺时针
2EI
例：试用图乘法求所示简支梁的最大挠度 和最大转角。
CL12TU32
顶点 顶点
2lh
3
1lh
3
二次抛物线
解：
ml 2
2 3
ml 逆时针
3E I
例：试用图乘法求所示悬臂梁自由端B的 挠度和转角。
CL12TU35
解：
ql 2
vB
1 EI
l
3
ql 2 2
3l
4
2
ql4 8E I
ql 2
B
1 EI
l
3
ql 2 2
1
2
ql 3
顺时针
6E I
例：试用图乘法求图示悬臂梁中点C处的 铅垂位移。
ql 3 12
a
2
0
X ql 3 8a(l a)
C
1 EI
Xal 2
2 3
Xa 2 2
1
ql 3 12
1
2
0
X ql 3 4a(2l 3a)
第五节图乘法
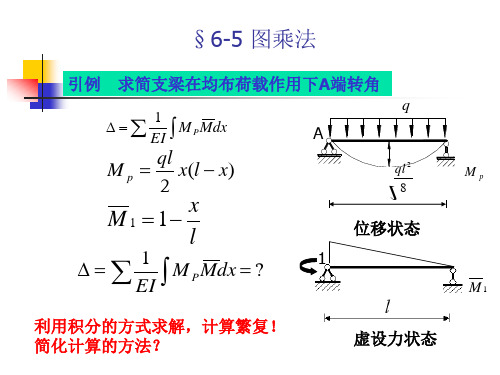
4m C 4m
MP图(kN·m)
须注意两点：一是对于斜杆CD， 解：求解本题∆DV时，须注意两点：一是对于斜杆 ，应以杆 轴为基线计算；二是对于阶形住AC，应按EI不同分段图乘 不同分段图乘。 轴为基线计算；二是对于阶形住 ，应按 不同分段图乘。 (1)作MP图 作
A1 = 2 × 12.65 × 45 = 379.5 3
§6-5 图乘法
求简支梁在均布荷载作用下A端转角 引例 求简支梁在均布荷载作用下 端转角
1 ∆=∑ ∫ M P Mdx EI
q
A
ql 2 8
ql M p = x(l − x) 2
Mp
x M 1 = 1− l
1 ∆=∑ ∫ M P Mdx = ? EI
利用积分的方式求解，计算繁复！ 利用积分的方式求解，计算繁复！ 简化计算的方法？ 简化计算的方法？ 1
2.5kN/m D 2EI (12.65m) 3EI B 8m 4EI A 12m
20kN 100 A2 C A3 20 B A4 A A5
(45)
A1
D
4m C 4m
140
MP图(kN·m)
1 A2 = × 12.65 × 100 = 632.5 2
A4 =
A5 =
1 × 8 × 20 = 80 2
A q B l/2 l
ql 2 ( ) 32
ql
C l/2
并按A 作MP图，并按 1、A2、A3、A4四部 分划分，如图6-22b所示 分划分，如图 所示
∆CV 1 = ( A1 y01 + A2 y02 + A3 y03 − A4 y04 ) EI 1 = EI 1 l ql 2 l l ql 2 3 )× + ( × )× l ( × × 3 2 2 4 2 2 2
0404图乘法(力学)
例：求图示梁B端转角。
A
P
l/2
B B
MP
A
M 1
EI
B 1
Mi
l/2 Pl / 4
解:
Ayc B EI 1 1 Pl 1 1 Pl 2 l ( EI 2 4 2 16 EI
)
60
求 B
A
MP
20
40 B
20
20kN m
EI
40kN m 10 m
Pl
P
P
MP
l
AB
l
l
1
l
1
Mi
1
1
Ay c ABY EI 1 1 2 ( l Pl l 4 l有什么发 Pl l 2) EI 2 3 现？ 3 10 Pl () 3 EI Ayc Ayc ABX 0 AB 0 EI EI
1 x tan α M P dx EI tan α tan α xdA xM P dx EI EI tan α 1 A xc Ayc EI EI
yc
xc x x
2. 注意事项
KP Ayc EI
还记得 吗？
（1）必须符合图乘法的适用条件； （2）yc 必须取自直线图形； （3）同侧弯矩图相乘为正，反之为负； （4）拱、曲杆结构和连续变截面的结构只能通过积 分的方式求解； （5）应用图乘法首先熟练掌握常用图形面积及形心 位置。
求 B
q
MP
A
q
B
ql / 8
2
EI
l
ql 2 / 4
ql 2 / 8
1
Mi
ql 2 4
工程力学-图乘法
顶点
标准抛物线:
2 A lh 3
C
h
5l/8 l
3l/8
图形顶点的斜率必须平行于杆轴线
河南理工大学
结构力学
图乘法
例
计算下图所示简支梁的跨中挠度
q
EI 常数
真实系统
A
l 2
A C
B
l 2
MP 图
ql 2 8
虚设系统
P 1
A
5 l 8 4
C
B
l 4
ቤተ መጻሕፍቲ ባይዱ
M 图
C点竖向位移
1 ql 5l 5ql 1 MM P dx 2 () EI EI 24 32 384EI
Ay0
河南理工大学
结构力学
图乘法
MMP 1 ds Ay0 EI EI
一个弯矩图的图形面积 面积A形心处的另一直线弯矩图上的纵标
!!切莫丢掉 此项
注意: 适用条件: 直杆; EI=C; 一个弯矩图为直线
y0必须取自直线弯矩图 符号规定: 两弯矩图位于杆件的同侧，Ay0 为正；反之，为负
河南理工大学
结构力学
第十一章 能量法
虚功原理
线弹性结构，各种基本变形情况下微段的变形为
则
河南理工大学
结构力学
图乘法（Graph-multiplication Method）
补充条件:
L
MM p EI
o
ds
杆件为直杆
抗弯刚度EI常数
其中一个弯矩图为直线图形
河南理工大学
结构力学
图乘法
河南理工大学
结构力学
图乘法
常用图形的面积和形心 三角形
6.5 图形相乘法 结构力学
=
MA
MB
+
MA B A dx a qa2/8 MB
MA MA A MB a q B MB
=
+
qa2/8
All Rights Reserved
重庆大学土木工程学院
四、应用图乘法的计算步骤
1）作实际荷载弯矩图MP图； ）作实际荷载弯矩图 图 2）加相应单位荷载，作单位弯矩图图； ）加相应单位荷载，作单位弯矩图图； 3）用图乘法公式（6-17）求位移。 ）用图乘法公式（ ）求位移。 所示简支梁跨中截面C的挠度 例6-7】试求图 】试求图6-21a所示简支梁跨中截面 的挠度CV和B端的 所示简支梁跨中截面 端的 已知EI=常数。 常数。 转角θB。已知 常数
O
M =xtanα
α
x A x0
M
M图
x
式中， 式中，dA=MPdx为MP图中有阴影线的微分面积，而 xdA即为 为 图中有阴影线的微分面积， 整个M 图的面积对y轴的静矩 轴的静矩。 表示M 的形心至y轴的距 整个 P图的面积对 轴的静矩。用x0表示 P的形心至 轴的距 离，则有 xdA = Ax (b)
1
20kN 100 A2 C A3 20 B A4 A A5 140 (45) A1 D
y02 y01 12 y03
C
4m C 4m
D
y04 y05
A
MP图(kNm)
M 图(m)
y 01
1 = ×12 = 6 2
2 y02 = × 12 = 8 3
y 03 = y 04 = y 05 = 12
MP图 l y03 y 04 y01
A
1
B
y02
C
M图
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
4
2
ql4 8E I
ql 2
B
1 EI
l
3
ql 2 2
1
2
ql 3
顺时针
6E I
例：试用图乘法求图示悬臂梁中点C处的 铅垂位移。
CL12TU36
解：
vC
1 EI
l2 8
m
ml2 8E I
例：图示梁，抗弯刚度为EI，承受均布载 荷q及集中力X作用。用图乘法求：
(1)集中力作用端挠度为零时的X值； (2)集中力作用端转角为零时的X值。
3E I
B
1 EI
Pl 2 2
1
Pl 2
顺时针
2EI
例：试用图乘法求所示简支梁的最大挠度 和最大转角。
CL12TU32
顶点 顶点
2lh
3
1lh
3
二次抛物线
解：
vmax
2 EI
2
3
l 2
ql 2 8
5l
32
5ql 4
384E I
ql 2 / 8
l/4
max
1 EI
图乘法求位移
虚功原理（虚力原理） 单位荷载法
M(x) M 0 (x)
l
EI
dx
对于等直杆，EI=const，可以提到积分号外， 故只需计算积分
M (x) M 0 (x) dx
l
直杆的M0(x)图必定是直线或折线。
M (x) M 0 (x) dx
l
tg x M (x) dx
l
tg xC
1 4
2 3
1 3
3qa 4 8E I
qa 2
qa qa 2 qa / 2
2
谢谢观看！ 2020
M
0 C
M 0 (x) x tg
M(x) M 0 (x)
dx
l
EI
M
0 C
EI
顶点 顶点
2lh
3
1lh
3
二次抛物线
例：试用图乘法求所示悬臂梁自由端B的 挠度和转角。
CL12TU31
解：
M(x) M 0(x)
vB
l
EI
dx
M
0 C
EI
1 Pl 2 2l
EI 2 3
Pl 3
CL12TU40
解：
A
Pa 2 EI
1 2
5 6
1 2
16
Pa 2 2E I
2
21
Pa 2 EI
vE
Pa 3 EI
1 2
1 3
2
Pa 2E
3
I
3 2
1
13Pa 3 12EI
例：图示刚架，EI=const。求A截面的水 平位移 ΔAH 和转角θA 。
CL12TU41
解： AH
qa 4 EI
CL12TU34
解：
vC
1 EI
l2 8
m 2
ml 2
16E I
l/4
A
1 EI
ml 2
1 3
ml 顺时针
6E I
B
1 EI
ml 2
2 3
ml 逆时针
3E I
例：试用图乘法求所示悬臂梁自由端B的 挠度和转角。
CL12TU35
解：
ql 2
vB
1 EI
l
3
ql 2 2
3l
2
l
3
ql 2 8
1 2
ql 3
24E I
ql 2 / 8
例：试用图乘法求所示简支梁的最大挠度 和最大转角。
CL12TU33
解：
v max
2 EI
1 2
l 2
Pl 4
6l
Pl 3
48E I
Pl / 4 l/4
max
1 EI
1 2
l
Pl 4
1 2
Pl 2
16E I
Pl / 4
例：试用图乘法求所示简支梁C截面的挠 度和A、B截面的转角。
Pa 2 2
2a
3
Pa 3 EI
CL12TU38
例：图示开口刚架，EI=const。求A、B两 截面的相对角位移 θAB 和沿P力作用线方向的 相对线位移 ΔAB 。(结构对称，取一半)
AB
2 Pa3 EI
1 8
12 3
1 2
21
2 Pa 3 3EI
AB 0
例：用图乘法求图示阶梯状梁A截面的转 角及E截面的挠度。
CL12TU37
解：(1)
vC
1 EI
Xal 2
2a 3
Xa 2 2
2a 3
ql 3 12
a
2
0
X ql 3 8a(l a)
C
1 EI
Xal 2
2 3
Xa 2 2
1
ql 3 12
1
2
0
X ql 3 4a(2l 3a)
例：图示梁的抗弯刚度为EI，试求D点的
铅垂位移。
vC
3 EI