高中数学几何证明选讲过关模拟卷(十三)含答案
高中数学几何证明选讲过关模拟卷(12)含答案
高中数学几何证明选讲过关模拟卷（12）题号 一 二 三 总分 得分一、选择题（本大题共10小题，每小题4分，共40分）1.以点(2,1)为圆心，且与直线21y x =+相切的圆的方程为( )A ．2216(2)(1)5x y +++=B ．2245(2)(1)5x y +++=C ．2216(2)(1)5x y -+-=D ．2245(2)(1)5x y -+-=2.如图，AB 是半圆O 的直径，C 、D 是半圆上两点，半圆O 的切线PC 交AB 的延长线于点P ，︒=∠25PCB ，则=∠ADC （ ）A ．︒105B ．︒115C ．︒120D ．︒1253.正方形ABCD 的边长为1，点E 在边AB 上，点F 在边BC 上，AE ＝BF ＝73.动点P 从E 出发沿直线喜爱那个F 运动，每当碰到正方形的方向的边时反弹，反弹时反射等于入射角，当点P 第一次碰到E 时，P 与正方形的边碰撞的次数为 （A ）16（B ）14（C ）12(D)10【解析】结合已知中的点E,F 的位置，进行作图，推理可知，在反射的过程中，直线是平行的，那么利用平行关系，作图，可以得到回到EA 点时，需要碰撞14次即可.4.若从n 边形的同一个顶点出发的对角线恰好把这个多边形分割成5个三角形，则n 的值为A ．5B ．6C ．7D ．85.过点()11,2A 作圆22241640x y x y ++--=，其中弦长为整数的弦共有（ ）A ．16条B ．17条C ．32条D ．34条6.已知圆C: 2210x y my m ++--=,则圆C 必过定点的坐标是()A (1,1)- ()B (1,0)- ()C (1,1)-- ()D (0,1)7.若三角形三边上的高为a b c 、、，这三边长分别为6、4、3，则::a b c =（ ）A. 1:2:3B. 6:4:3C. 2:3:4D. 3:4:68.直角三角形ABC 的直角边AB 在平面α内，顶点C 在α外，且C 在α内的射影为C 1（C 1不在AB 上），则△ABC 1是A ．直角三角形B ．锐角三角形C ．钝角三角形D ．以上都有可能9.如图甲,四边形ABCD 是等腰梯形,//AB CD .由4个这样的等腰梯形可以拼出图乙所示的平行四边形，则四边形ABCD 中A ∠度数为 ( )A ．30︒B ．45︒C ．60︒D ．75︒10.已知直线:210l x y k +++=被圆22:4C x y +=所截得的弦长为4，则k 是（ ） A ．－1 B ．－2 C ． 0 D ．2二、填空题（本大题共10小题，每小题2分，共20分）11.已知：如下图，⊙O 与⊙P 相交于A 、B 两点，点P 在⊙O 上，⊙O 的弦BC 切⊙P于点B ，CP 及其延长线交⊙P 于D 、E 两点，过点E 作EF ⊥CD 交CB 延长线于点F ，若CD=2，CB=22，则CE= ，EF= 。
精选2019年高中数学单元测试《平面几何的证明》专题模拟考核题库(含答案)
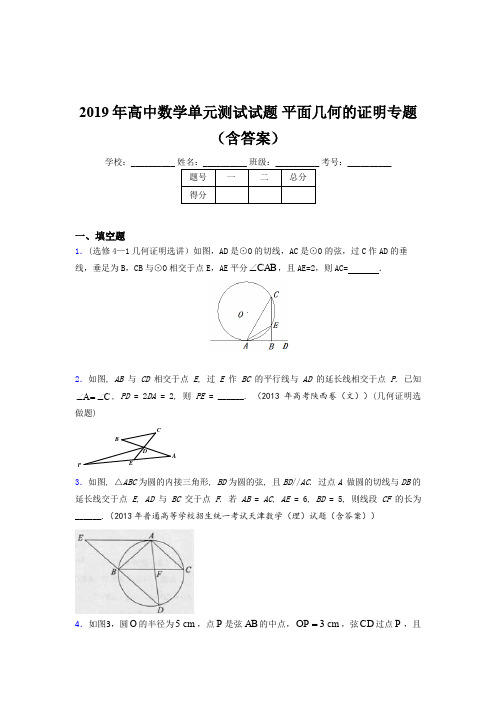
2019年高中数学单元测试试题平面几何的证明专题（含答案）学校：__________ 考号：__________一、填空题1．(选修4—1几何证明选讲）如图，AD是⊙O的切线，AC是⊙O的弦，过C作AD的垂∠，且AE=2，则AC= ．线，垂足为B，CB与⊙O相交于点E，AE平分CAB2．如图, AB与CD相交于点E, 过E作BC的平行线与AD的延长线相交于点P. 已知∠=∠, PD = 2DA = 2, 则PE = ______. （2013年高考陕西卷（文））(几何证明选A C做题)P3．如图, △ABC为圆的内接三角形, BD为圆的弦, 且BD//AC. 过点A做圆的切线与DB的延长线交于点E, AD与BC交于点F. 若AB = AC, AE = 6, BD = 5, 则线段CF的长为______.（2013年普通高等学校招生统一考试天津数学（理）试题（含答案））OP=cm，弦CD过点P，且4．如图3，圆O的半径为5cm，点P是弦AB的中点，3FABC13CP CD =，则CD 的长为 cm ．（几何证明选讲选做题）二、解答题5．如图，PAQ ∠是直角，圆Ｏ与AP 相切于点T ，与AQ 相交于两点B ，C 。
求证：BT 平分OBA ∠6．如图，在△ABC 中，D 是AC 的中点，E 是BD 的中点，AE 的延长线交BC 于F . (1）求FCBF的值； (2）若△BEF 的面积为1S ，四边形CDEF 的面积为2S ，求21:S S 的值．图3Q CBATPO（第1题）7．如图，⊙O 1与⊙O 2交于M 、N 两点，直线AE 与这两个圆及MN 依次交于A 、B 、C 、D 、E ．求证：AB ·CD ＝BC ·DE ．8．自圆O 外一点P 引切线与圆切于点A ，M 为PA 中点，过M 引割线交圆于B ,C 两点． 求证:MCP MPB ∠=∠．1．（几何证明选讲选做题） 证明：∵PA 与圆相切于A ，∴2MA MB MC =⋅， ………………2分 ∵M 为PA 中点，∴PM MA =， ………………3分 ∴2PM MB MC =⋅， ∴PM MBMC PM=． ………………5分 ∵BMP PMC ∠=∠， ………………6分 ∴△BMP ∽△PMC ，………………8分 ∴MCP MPB ∠=∠． ………………10分9．如图，ABC △是圆O 的内接三角形，AC BC =，D 为圆O 中AB 上一点，延长DA 至点E ，使得CE CD =． (Ⅰ)求证：AE BD =；(6分) (Ⅱ)若AC BC ⊥，求证：AD BD +=．(4分)10．如图，已知D 为△ABC 的BC 边上一点，⊙O 1经过点B ，D ，交AB 于另一点E ，⊙O 2经过点C ，D ，交AC 于另一点F ，⊙O 1与⊙O 2交于点G. (1)求证：∠EAG=∠EFG ；(5分)(2)若⊙O 2的半径为5，圆心O 2到直线AC 的距离为3，AC=l0，AG 切⊙O 2于G ，求线段AG的长．(5分)11．过平行四边形ABCD 的顶点B 、C 、D 的圆与直线AD 相切，与直线AB 相交于点E ，已知AD=4，CE=5。
高中数学几何证明选讲详解
【命题立意】本题考查几何证明选做题的解法，属送分题
【思路点拨】条件
【规范解答】因为以AC为直径的圆与AB交于点D,所以
A. B. C. D.
【解析】设半径为 ,则 ,由 得 ,从而 ,故 ,选A.
7.在 中, 分别为 上的点,且 , 的面积是 ,梯形 的面积为 ,则 的值为( )
A. B. C. D.
【解析】 ,利用面积比等于相似比的平方可得答案B.
8.半径分别为1和2的两圆外切,作半径为3的圆与这两圆均相切,一共可作( )个.
5． （2010·天津高考理科·Ｔ１4）如图，四边形ABCD是圆O的内接四边形，延长AB和DC相交于点P，若 ,则 的值为
【命题立意】考查三角形的相似性质的应用。
【思路点拨】利用相似三角形的性质进行转化。
【规范解答】由题意可知 ∽ 相似，
所以 ,由 及已知条件
可得 ,又 , 。
【答案】
6．（2010·广东高考文科·Ｔ14）如图3，在直角梯形ABCD中，DC∥AB，CB⊥AB，AB=AD=a，CD= ，点E，F分别为线段AB，CD的中点，则EF=.
【答案】
7.（2010·广东高考理科·Ｔ14）如图3，AB，CD是半径为a的圆O的两条弦，它们相交于AB的中点P，PD= ，∠OAP=30°，则CP＝______.
【命题立意】本题考察垂径定理及相交弦定理.
【思路点拨】由垂径定理得 ，算出 ，再由相交弦定理求出
【规范解答】因为 为 的中点，由垂径定理得 ，在 中， ，由相交弦定理得： ，即 ，
高中数学几何证明选讲过关模拟卷(五)含答案
第14题 高中数学几何证明选讲过关模拟卷（五）高中数学题号 一 二 三 总分 得分一、选择题（本大题共10小题，每小题4分，共40分）1.圆内接三角形ABC 角平分线CE 延长后交外接圆于F ，若2,FB =1EF =，则CE =（ ）A. 3B. 2C. 4D. 12.对于a ∈R，直线(a －1)x －y ＋a ＋1＝0恒过定点C ，则以C 为圆心，以5为半径的圆的方程为( )A ．x 2＋y 2－2x ＋4y ＝0B ．x 2＋y 2＋2x ＋4y ＝0C ．x 2＋y 2＋2x －4y ＝0D ．x 2＋y 2－2x －4y ＝0 3.在等腰三角形ABC 中，=4AB AC =，点P 是边AB 上异于,A B 的一点，光线从点P 出发，经,BC CA 反射后又回到原点P （如图1）.若光线QR 经过ABC ∆的中心，则AP 等于A ．2B ．1C ．83D ．434.圆内接四边形ABCD 中，A ∠、B ∠、C ∠的度数比是2:3:6，则D ∠=（ ）．A ．67.5B ．135C ．112.5D ．1105.如图甲,四边形ABCD 是等腰梯形,//AB CD .由4个这样的等腰梯形可以拼出图乙所示的平行四边形，则四边形ABCD 中A ∠度数为 ( )A ．30︒B ．45︒C ．60︒D ．75︒6.如图，设P 为ABC ∆内一点，且AC AB AP 5152+=，则ABP ∆的面积与ABC ∆的面积之比等于（ ）．A ．15B ．25C ．35D ．127.圆22(2)5x y ++=关于原点(0,0)P 对称的圆的方程为 ( )A 22(2)5x y -+= B 22(2)5x y +-= C 22(2)(2)5x y +++= D 22(2)5x y ++=8.圆x 2+y 2-4x-4y-10=0上的点到直线x+y-14=0的最大距离与最小距离的差是（ ）A ．36B ． 18C ．26D ． 25 9.圆1C ：22(1)(2)16x y -++=与圆2C ：22(2)1x y -+=的位置关系是( )（A ）内含 （B ）内切 （C ）相交 （D ）外切10.过点()11,2A 作圆22241640x y x y ++--=，其中弦长为整数的弦共有（ ）A ．16条B ．17条C ．32条D ．34条二、填空题（本大题共10小题，每小题2分，共20分） 11. (二)选做题(14-15题,考生只能从中选做一题)14.(坐标系与参数方程选做题) 圆C 的极坐标方程2cos ρθ=化为直角坐标方程为 ，该圆的面积为 ．15.(几何证明选讲选做题) 如图，圆 O 的割线 PBA 过圆心 O ，弦 CD 交 P A 于点F ，且△COF ∽△PDF ，PB = OA = 2，则PF = 。
高中数学几何证明选讲过关模拟卷(十五)含答案
BCD O AP高中数学几何证明选讲过关模拟卷（十五）高中数学题号 一 二 三 总分 得分一、选择题（本大题共10小题，每小题4分，共40分）1.对于a ∈R，直线(a －1)x －y ＋a ＋1＝0恒过定点C ，则以C 为圆心，以5为半径的圆的方程为( )A ．x 2＋y 2－2x ＋4y ＝0B ．x 2＋y 2＋2x ＋4y ＝0C ．x 2＋y 2＋2x －4y ＝0D ．x 2＋y 2－2x －4y ＝02.如图5，锐角三角形ABC 中，以BC 为直径的半圆分别交AB 、AC 于点D 、E ，则△ADE 与△ABC 的面积之比为（ ）A ．cosAB ．sinAC ．sin 2A D ．cos 2A3.一个圆的两弦相交,一条弦被分为12cm 和18cm 两段,另一弦被分为3:8,则另一弦的长为( )A.11cmB.33cmC.66cmD.99cm4.如图，CD 是⊙O 的直径，AE 切⊙O 于点B ，连接DB ，若20D ∠=︒，则DBE ∠的大小为A. 20︒B. 40︒C. 60︒D. 70︒5.已知圆C: 2210x y my m ++--=,则圆C 必过定点的坐标是()A (1,1)- ()B (1,0)- ()C (1,1)-- ()D (0,1)6.Rt △ABC 中,CD 是斜边AB 上的高,该图中只有x 个三角形与△ABC 相似,则x 的值为( )Ａ.1 Ｂ.2 Ｃ.3 Ｄ.47.在⊙O 中,弦 1.8AB cm =,圆周角30ACB ∠=,则⊙O 的直径等于( )Ａ.3.2cm Ｂ.3.4cm Ｃ.3.6cm Ｄ.4.0cm8.已知直线)0)(2(>+=k x k y 与抛物线x y C 8:2=相交于A ，B 两点，F 为C 的焦点，若|FA|=2|FB|，则实数k 的值为（ ） A ．31B ．32C ．32D ．3229.如图,在梯形ABCD 中,AB//DC,AB=,a )(b a b CD >=。
高二数学几何选讲试题答案及解析
高二数学几何选讲试题答案及解析于点，过点作两1.如图，已知⊙与⊙相交于、两点，过点A作⊙的切线交⊙O2圆的割线，分别交⊙、⊙于点、，与相交于点.（1）求证：；（2）若是⊙的切线，且，，求的长．【答案】（1）证明见解析；（2）【解析】（1）圆的切线的性质定理圆的切线垂直于过切点的半径，推论1经过圆心且垂直于切线的直线必过切点，推论2经过切点且垂直于切线的直线必过圆心；（2）圆的切线的性质定理经过半径的外端并且垂直于这条半径的直径是圆的切线；若已知条件中直线与圆的公共点不明确，则应过圆心作直线的垂线，得到垂线段，设法证明这条垂线段的长等于圆的半径；（3）掌握与圆有关的比例线段，如相交弦定理，割线定理，切割线定理，切线长定理.试题解析：解：（I）∵AC是⊙O的切线，∴∠BAC＝∠D，1又∵∠BAC＝∠E，∴∠D＝∠E，∴AD∥EC. 5分（II）设BP＝x，PE＝y，∵PA＝6，PC＝2，∴＝12 ①∵AD∥EC，∴，∴②由①、②解得（∵x>0，y>0）∴DE＝9＋x＋y＝16，∵AD是⊙O的切线，∴AD2＝DB·DE＝9×16，∴AD＝12. 11分2【考点】（1）证明直线与直线平行；（2）求切线长.2.如图，在△ABC中，AB=8，AC=7，BC=6，D是AB的中点，∠ADE=∠ACB，则DE=_________．【答案】.【解析】首先由知，∽，所以.然后因为AB=8，D是AB的中点，所以.又AC=7，BC=6，所以，即.【考点】相似三角形的性质.3.如图，AC为⊙O的直径，OB⊥AC，弦BN交AC于点M．若OC=，OM=1，则MN=_________．【答案】1.【解析】因为AC为⊙O的直径，OB⊥AC，且OC=，OM=1，所以，. 设，由相交弦定理知，即，所以，即.【考点】与圆有关的比例线段.4.如图，四边形是圆的内接四边形，延长和相交于点，若，，则的值为（）A．B．C．D．【答案】B【解析】四边形是圆的内接四边形，它的两对对角互补，进而得到∽，因而有，故选择B.【考点】平面几何中的圆与四边形.5.如图在△中,∥,,交于点,则图中相似三角形的对数为( ).A．1B．2C．3D．4【答案】B【解析】,;又,,故选B.【考点】相似三角形.6.如图所示，△ABC内接于⊙O，AB＝AC，直线XY切⊙O于点C，BD∥XY，AC、BD相交于E.(1)求证：△ABE≌△ACD；(2)若AB＝6 cm，BC＝4 cm，求AE的长．【答案】（1）见解析；（2）.【解析】（1）欲证三角形全等，需牢牢掌握这种证明方法和所需要的条件.本小题,(已知)，下寻找另外的边和角，考虑到这里有圆，所以运用同弧所对应的圆周角相等可得(弧所对)，接着证明(其他角和边不好证，同时这里有弦切角可以利用).（2）欲求,因,则可转化为求,考虑到，需将联系起来就得考虑三角形相似.注意到,.试题解析：(1)证明因为XY是⊙O的切线，所以.因为，所以，∴. 2分因为，所以. 4分因为，又因为，所以. 5分(2)解因为，，所以， 7分所以，即 8分因为，，所以.所以AE. 10分【考点】（1）三角形全等的证明；（2）三角形相似的证明与应用；（3）圆性质的应用.7.如图，已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF＝CF＝，AF∶FB∶BE＝4∶2∶1，若CE与圆相切，求线段CE的长.【答案】【解析】利用相交弦定理可得到的等量关系，并结合已知条件可计算出,利用切割线定理可得到的等量关系，并结合前面所得可得结果.试题解析：由相交弦定理得，由于，可解得，所以.由切割线定理得，即.【考点】相交弦定理，切割线定理.8.若一个直角三角形的一条直角边为3 cm，斜边上的高为2.4 cm，则这个直角三角形的面积为A．7.2 cm2B．6 cm2C．12 cm2D．24 cm2【答案】B【解析】长为3 cm的直角边在斜边上的射影为＝1.8 (cm)，故由射影定理知斜边长为＝5 (cm)，∴三角形的面积为×5×2.4＝6 (cm2)．9.如图，在直角梯形ABCD中，DC∥AB，CB⊥AB，AB＝AD＝a，CD＝，点E，F分别为线段AB，AD的中点，则EF＝________.【答案】【解析】连接BD、DE，由题意可知DE⊥AB，DE＝a，即BC＝DE＝a，∴BD＝＝a，∴EF＝BD＝.10.如图所示，圆内的两条弦AB、CD相交于圆内一点P，已知PA＝PB＝4，PC＝PD.求CD 的长．【答案】10【解析】解设CD＝x，则PD＝x，PC＝x.由相交弦定理，得PA·PB＝PC·PD，∴4×4＝x·x，x＝10.∴CD＝10.11.如图所示，PA是⊙O的切线，切点为A，PA＝2.AC是⊙O的直径，PC与⊙O交于点B，PB＝1，则⊙O的半径r＝________.【答案】【解析】依题意，△PBA∽△ABC，所以＝，即r＝＝＝.12.如图所示，P、Q分别在BC和AC上，BP∶CP＝2∶5，CQ∶QA＝3∶4，则等于A．3∶14B．14∶3C．17∶3D．17∶14【答案】B【解析】过Q点作QM∥AP交BC于M，则＝＝，又∵＝，∴＝.又＝＝，＝＝，∴＝，∴＝.13.如图所示，点D、E分别在AB、AC上，下列条件能判定△ADE与△ACB相似的有①∠AED＝∠B②＝③＝④DE∥BCA．1个 B．2个 C．3个 D．4个【答案】C【解析】由判定定理1知①正确，由判定定理2知②正确，由预备定理1知④正确，③不符合相似三角形的判定定理，故不正确，从而选C.14.如图所示，在直角梯形ABCD中，AB＝7，AD＝2，BC＝3.设边AB上的一点P，使得以P、A、D为顶点的三角形和以P、B、C为顶点的三角形相似，那么这样的点P有A．1个 B．2个C．3个 D．4个【答案】C【解析】设AP＝x，则PB＝7－x.(1)若△PAD∽△PBC，则＝，即＝，得x＝<7，符合条件．(2)若△PAD∽△CBP，即＝，x2－7x＋6＝0，解得x1＝1，x2＝6也符合条件，故满足条件的点P 有3个．15. 在四边形ABCD 中，∠A ＝135°，∠B ＝∠D ＝90°，BC ＝2，AD ＝2，则四边形ABCD 的面积是______． 【答案】4【解析】因∠B ＝∠D ＝90°，于是设想构造直角三角形，延长BA 与CD 的延长线交于E ，则得到Rt △BCE 和Rt △ADE ，由题目条件知，△ADE 为等腰直角三角形，所以DE ＝AD ＝2，所以S △ADE ＝×2×2＝2. 又可证Rt △EBC ∽Rt △EDA ， 所以＝2＝2＝3.∴S △EBC ＝3S △EDA ，∴S 四边形ABCD ＝S △EBC －S △ADE ＝4.16. 如图所示，D 为△ABC 中BC 边上的一点，∠CAD ＝∠B ，若AD ＝6，AB ＝8，BD ＝7，求DC 的长．【答案】9【解析】解 ∵∠CAD ＝∠B ，∠C ＝∠C ， ∴△CAD ∽△CBA.∴＝＝.∴AC ＝，AC ＝.∴＝.设CD ＝x ， 则＝，解得x ＝9.故DC ＝9.17. 如图所示，已知⊙O 的两条弦AB 、CD 相交于AB 的中点E ，且AB ＝4，DE ＝CE ＋3，则CD 的长为________．【答案】5【解析】由相交弦定理知 EA·EB ＝EC·ED. (*)又∵E 为AB 中点，AB ＝4，DE ＝CE ＋3， ∴(*)式可化为22＝EC(CE ＋3)＝CE 2＋3CE ， ∴CE ＝－4(舍去)或CE ＝1.∴CD ＝DE ＋CE ＝2CE ＋3＝2＋3＝5.18. 如图所示，已知BC 是⊙O 的弦，P 是BC 延长线上一点，PA 与⊙O 相切于点A ，∠ABC ＝25°，∠ACB＝80°，求∠P的度数．【答案】55°【解析】解因为PA与⊙O相切于点A，所以∠PAC＝∠ABP＝25°.又因为∠ACB＝80°，所以∠ACP＝100°.又因为∠PAC＋∠PCA＋∠P＝180°，所以∠P＝180°－100°－25°＝55°.19.(拓展深化)如图所示，△ABC内接于⊙O，AB＝AC，直线XY切⊙O于点C，BD∥XY，AC、BD相交于E.(1)求证：△ABE≌△ACD；(2)若AB＝6 cm，BC＝4 cm，求AE的长．【答案】(1)见解析 (2)cm【解析】(1)证明因为XY是⊙O的切线，所以∠1＝∠2.因为BD∥XY，所以∠1＝∠3，∴∠2＝∠3.因为∠3＝∠4，所以∠2＝∠4.因为∠ABD＝∠ACD，又因为AB＝AC，所以△ABE≌△ACD.(2)解因为∠3＝∠2，∠ABC＝∠ACB，所以△BCE∽△ACB，＝，AC·CE＝BC2.因为AB＝AC＝6 cm，BC＝4 cm，所以6·(6－AE)＝16.所以AE＝cm.20.如图所示，在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，以BC上一点O为圆心作⊙O与AB相切于E，与AC相切于C，又⊙O与BC的另一个交点为D，则线段BD的长为A．1B．C．D．【答案】C【解析】⊙O与AC相切于C，则∠ACB＝90°，又AC＝4，BC＝3，∴AB＝5，连接OE，且设⊙O的半径为R，则由△OEB∽△ACB，∴OB＝＝R，∴BC＝OC＋OB＝R＋R＝R＝3，∴R＝，∴BD＝BC－2R＝3－＝.21.若两条直线(a＋2)x＋(1－a)y－3＝0，(a－1)x＋(2a＋3)y＋2＝0与两坐标轴围成的四边形有一个外接圆，则实数a＝________.【答案】1或－1【解析】由圆内接四边形的性质，知(a＋2)(a－1)＋(1－a)·(2a＋3)＝0，整理得a2＝1，∴a＝±1. 22.(拓展深化)如图，已知△ABC中的两条角平分线AD和CE相交于H，∠B＝60°，F在AC上，且AE＝AF.(1)证明：B、D、H、E四点共圆；(2)证明：CE平分∠DEF.【答案】见解析【解析】证明(1)在△ABC中，因为∠B＝60°，所以∠BAC＋∠BCA＝120°.因为AD，CE是角平分线，所以∠HAC＋∠HCA＝60°，故∠AHC＝120°.于是∠EHD＝∠AHC＝120°.因为∠EBD＋∠EHD＝180°，所以B、D、H、E四点共圆．(2)连接BH，则BH为∠ABC的平分线，得∠HBD＝30°.由(1)知B、D、H、E四点共圆．所以∠CED＝∠HBD＝30°.又∵∠AHE＝∠EBD＝60°，由已知可得EF⊥AD，可得∠CEF＝30°，所以CE平分∠DEF.23.如图，点A、B、C是圆O上的点，且AB＝4，∠ACB＝30°，则圆O的面积等于A．4π B．8πC．12π D．16π【答案】D【解析】连接OA、OB，∵∠ACB＝30°，∴∠AOB＝60°，又∵OA＝OB，∴△AOB为等边三角形，又AB＝4，∴OA＝OB＝4，∴S＝π·42＝16π.⊙O24.在Rt△ABC中，∠BAC＝90°，AD⊥BC，垂足为D.若BC＝m，∠B＝α，则AD的长为A．m sin2α B．m cos2αC．m sin αcos α D．m sin αtan α【答案】C【解析】由射影定理，得AB2＝BD·BC，AC2＝CD·BC，即m2cos2α＝BD·m，m2sin2α＝CD·m，即BD＝mcos2α，CD＝msin2α.又∵AD2＝BD·DC＝m2cos2αsin2α，∴AD＝mcos αsin α.故选C.25.如图，在正方形ABCD中，E为AB的中点，AF⊥DE于点O，则等于________．【答案】【解析】在Rt△DAO及Rt△DEA中，∠ADO为公共角，∴Rt△DAO∽Rt△DEA，∴＝，即＝.∵E为AB的中点，∴＝＝，∴＝.26. (拓展深化)如图，M为线段AB的中点，AE与BD交于点C，∠DME＝∠A＝∠B＝α.且DM交AC于F，ME交BC于G，(1)写出图中三对相似三角形，并证明其中的一对；(2)连接FG，如果α＝45°，AB＝4，AF＝3，求FG的长．【答案】(1)△AMF∽△BGM，△DMG∽△DBM，△EMF∽EAM，证明见解析 (2)【解析】解(1)△AMF∽△BGM，△DMG∽△DBM，△EMF∽EAM.以下证明：△AMF∽△BGM.∵∠AFM＝∠DME＋∠E＝∠A＋∠E＝∠BMG，∠A＝∠B，∴△AMF∽△BGM.(2)当α＝45°时，可得AC⊥BC且AC＝BC.∵M为AB的中点，∴AM＝BM＝2.又∵△AMF∽△BGM，∴＝∴BG＝＝＝.又AC＝BC＝4×sin 45°＝4，∴CG＝4－＝.∵CF＝4－3＝1，∴FG＝＝＝.27.如图所示，已知DE∥BC，BF∶EF＝3∶2，则AC∶AE＝________，AD∶DB＝________.【答案】3∶22∶1【解析】∵DE∥BC，∴＝＝.∵BF∶EF＝3∶2，∴＝＝.∴AC∶AE＝3∶2.又DE∥BC，得AB∶AD＝3∶2，即＝.∴＝.即＝＝2，即＝2.∴AD∶BD＝2∶1.28.如图，以梯形ABCD的对角线AC及腰AD为邻边作平行四边形ACED，DC的延长线交BE于点F，求证：EF＝BF.【答案】见解析【解析】证明如图所示，连接AE交DC于O.∵四边形ACED是平行四边形．∴O是AE的中点．∵在梯形ABCD中，DC∥AB，在△EAB中，OF∥AB，又∵O是AE的中点，∴F是EB的中点，∴EF＝BF.29.如图甲,四边形是等腰梯形,.由4个这样的等腰梯形可以拼出图乙所示的平行四边形,则四边形中度数为 ( )A．B．C．D．【答案】C【解析】由于上底和两腰长已知，故要求梯形面积，关键是要找出底边上和高，由于图形中无法再分析出边与边的关系，所以我们可以从角的方向入手，求梯形的内角。
高中数学几何证明选讲过关模拟卷(11)含答案
第20题高中数学几何证明选讲过关模拟卷（11）题号 一 二 三 总分 得分一、选择题（本大题共10小题，每小题4分，共40分）1.若圆C 的半径为1，圆心在第一象限，且与直线430x y x -=和轴都相切，则该圆的标准方程是（ ）A ．327(3)()13x y -+== B ．22(2)(1)1x y -+-= C ．22(1)(3)1x y -+-= D ．223()(1)12x y -+-=2.如图,四边形ABCD 是等腰梯形,//AB CD .由4个这样的等腰梯形可以拼出图乙所示的平行四边形, 则四边形ABCD 中A ∠度数为 ( ) A.30︒ B.45︒ C.60︒ D.75︒3.如图，点P 为⊙O 的弦AB 上一点，且AP ＝16，BP ＝4，连接OP ，作PC ⊥OP 交圆于C ，则PC 的长为( )A ．9B ．8C ．6D ．44.如图5，锐角三角形ABC 中，以BC 为直径的半圆分别交AB 、AC 于点D 、E ，则△ADE 与△ABC 的面积之比为（ ）A ．cosAB ．sinAC ．sin 2A D ．cos 2A5.．直线y ＝kx ＋3与圆(x －3)2＋(y －2)2＝4相交于M ，N 两点，若|MN |≥23，则k 的取值范围是 ( )A.⎣⎢⎡⎦⎥⎤－34，0B.⎝ ⎛⎦⎥⎤－∞，－34∪[0，＋∞)C.⎣⎢⎡⎦⎥⎤－33，33 D.⎣⎢⎡⎦⎥⎤－23，06.如图，090ACB ∠=，CD AB ⊥于点D ，以BD 为直径的圆与BC 交于点E.则( )A. CE CB AD DB •=•B. CE CB AD AB •=•C. 2AD AB CD •=D. 2CE EB CD •=o 20D ∠=，则7.如图，CD 是O 的直径，AE 切O 于点B ，连接DB 。
若DBE ∠的大小为A ．20°B ．40°C ．60°D ．70°8.在空间直角坐标系Oxyz 中，已知()2,0,0A ，()2,2,0B ，()0,2,0C ，()1,1,2D ，若1S ，2S ，3S 分别表示三棱锥D ABC -在xOy ，yOz ，zOx 坐标平面上的正投影图形的面积，则（ ）A.123S S S ==B.12S S =且 31S S ≠C.13S S =且 32S S ≠D.23S S =且 13S S ≠9.在ABC ∆中,,D E 分别为,AB AC 上的点,且//DE BC ,ADE ∆的面积是22cm ,梯形DBCE 的面积为26cm ,则:DE BC 的值为( )A.1:3B.1:2C.1:3D.1:410.如图,在ABC ∆和DBE ∆中,53AB BC AC DB BE DE ===,若ABC ∆与DBE ∆的周长之差为10cm ,则ABC ∆的周长为( )A DBCE 姓名：__________班级：__________考号：__________ ●-------------------------密--------------封--------------线--------------内--------------请--------------不--------------要--------------答--------------题-------------------------●BODACA ．20cmB ．254cm C ．503cm D ．25cm二、填空题（本大题共10小题，每小题2分，共20分）11.（几何证明选讲选做题）如图，已知EB 是半圆O 的直径，A 是BE 延长线上一点，AC 切半圆O 于点D ，BC AC ⊥于点C ，若6BC =，8AC =，则AE = ，AD =12.如图，AB 是半圆O 的直径，P 在AB 的延长线上，PD 与半圆O 相切于点C ，AD ⊥PD.若PC=4， PB=2，则CD=____________.13.（几何证明选讲选做题）已知PA 是圆O 的切线，切点为A ，2PA =．AC 是圆O 的直径，PC 与圆O交于点B ，1PB =，则圆O 的半径R = ．14.三角形中有一个角为60度，夹这个角的两边长分别为8和5，则这个三角形内切圆的面积为1.15.由直线1y x =+上的点向圆22(3)(2)1x y -++=引切线，则直线1y x =+上的点与切点之间的线段长的最小值为 .16.如图，AB 是半圆D 的直径，P 在AB 的延长线上，PD 与半圆O 相切于点C ，AD ⊥PD.若PC=4，PB=2，则CD=____________.圆的切线AD 和割线ABC ，已知23AD =，17.（几何证明选讲）如图，从圆O 外一点A 引6AC =，圆O 的半径为3，则圆心O 到AC 的距离为 ．18. (几何证明选讲选做题) 已知圆O 的半径为3，从圆O 外一点A引切线AD 和割线ABC ，圆心O 到AC 的距离为22，3AB =， 则切线AD 的长为 ．OCBD19.如图4, CD 是圆O 的切线, 切点为C , 点A 、B 在圆O 上,1,30BC BCD ︒=∠=，则圆O 的面积为OCDBA20.如图，已知圆O 的半径为3，从圆O 外一点A 引切线AD 和割线ABC ，圆心O 到AC 的距离为22，3AB =，则切线AD 的长为三、解答题（本大题共4小题，共40分） 21.（10分）已知直线的极坐标方程为224sin =⎪⎭⎫⎝⎛+πθρ，圆M 的参数方程为⎩⎨⎧+-==θθsin 22cos 2y x （其中θ为参数）（1）将直线的极坐标方程化为直角坐标方程；（2）求圆M 上的点到直线的距离的最小值22.（08年中卫一中三模） 如图所示，AB 为圆O 的直径，BC ，CD 为 圆O 的切线，B ，D 为切点。
高中数学几何证明选讲过关模拟卷(20)含答案
高中数学几何证明选讲过关模拟卷（20）题号 一 二 三 总分 得分一、选择题（本大题共10小题，每小题4分，共40分）1.如图，设P 为ABC ∆内一点，且AC AB AP 5152+=，则ABP ∆的面积与ABC ∆的面积之比等于（ ）．A ．15B ．25 C ．35D ．122.一个圆的两弦相交,一条弦被分为12cm 和18cm 两段,另一弦被分为3:8,则另一弦的长为( )A.11cm B .33cm C.66cm D.99cm 3.过点()11,2A 作圆22241640x y x y ++--=，其中弦长为整数的弦共有（ ）A ．16条B ．17条C ．32条D ．34条4.()220,210m x y m x y m >+++=+=设则直线与圆的位置关系为（ ）A ．相切B ．相交C ．相切或相离D ．相交或相切5.方程2222210x y ax ay a a +++++-=表示圆，则a 的取值范围是 （ ）A 2a <- Ｂ203a -<< Ｃ20a -<< Ｄ223a -<<6.已知角α的终边与单位圆的交点为36(,)33-，则tan α= （A ）33 （B ）63- （C ）2- （D ）22-7.在直角三角形中，斜边上的高为6cm ，且把斜边分成3︰2两段，则斜边上的中线的长为（ ）A ．265cm B ．64cm C ．65cm D ．235cm8.如图4，正方形ABCD 中，E 是AB 上任一点，作EF ⊥BD 于F ，则EF ︰BE=（ ）A ．21B ．22C ．23D ．29.若直线01243=+-y x 与两坐标轴的交点分别为A 、B ，则以线段AB 为直径的圆的标准方程为（ ）A.()42523222=⎪⎭⎫ ⎝⎛++-y xB.()42523222=⎪⎭⎫ ⎝⎛-++y xC.()2523222=⎪⎭⎫ ⎝⎛-++y xD. ()2523222=⎪⎭⎫ ⎝⎛++-y x10.在⊙O 中,弦 1.8AB cm =,圆周角30ACB ∠=,则⊙O 的直径等于( ) Ａ.3.2cm Ｂ.3.4cm Ｃ.3.6cm Ｄ.4.0cm二、填空题（本大题共10小题，每小题2分，共20分）13.11.斜率为1的直线l 被圆422=+y x 截得的弦长为2，则直线l 的方程为____________________________12.如图，已知O 的直径6AB =，C 为O 上一点，且2BC =B 的O 的切线交AC 延长线于点D ，则DA =________;ABC P姓名：__________班级：__________考号：__________ ●-------------------------密--------------封--------------线--------------内--------------请--------------不--------------要--------------答--------------题-------------------------●13.（几何证明选讲选做题）如图，已知AB 是⊙O 的直径，AB =2，AC 和AD 是⊙O 的两条弦，AC =2,AD =3,则∠CAD 的弧度数为 .14.如右图，点,,A B C 是圆O 上的点，且04,45AB ACB =∠=，则圆O 的面积等于 ．15.如图，在圆内接四边形中，对角线，相交于点。
高中数学几何证明选讲过关模拟卷(13)含答案
高中数学几何证明选讲过关模拟卷（13）题号 一 二 三 总分 得分一、选择题（本大题共10小题，每小题4分，共40分）1.圆222650x y x y a +-++=关于直线2y x b =+成轴对称图形，则b a -的取值范围是（ ）A ．(,4)-∞B ．()-∞，0C ．(4,)-+∞D ．(4,)+∞2.两个圆C 1：x 2＋y 2＋2x ＋2y －2＝0，C 2：x 2＋y 2－4x －2y ＋1＝0的公切线条数（ )A ．1条B ．2条C ．3条D ．4条3.如图,在梯形ABCD 中,AB//DC,AB=,a )(b a b CD >=。
若,//AB EF EF 到CD 与AB 的距离之比为n m :,则可推算出:nm nbma EF ++=,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD 中,延长梯形的两腰AD 和BC 交于O 点,设OAB ∆,OCD ∆的面积分别为21,S S ,EF//AB,且EF 到CD 与AB 的距离之比为n m :,则OEF ∆的面积0S 与21,S S 的关系是( )A nm nS mS S ++=210 B n m mS nS S ++=210C n m S n S m S ++=210D n m S m S n S ++=2104.圆x 2+y 2-4x-4y-10=0上的点到直线x+y-14=0的最大距离与最小距离的差是（ ）A ．36B ． 18C ．26D ． 255.已知圆的方程为086222=++-+y x y x ，那么下列直线中经过圆心的直线方程为( )A ．012=+-y xB ．012=++y xC ．012=--y xD ．012=-+y x6.对任意实数K ,直线()011=--+Ky x K 与圆022222=---+y x y x 的位置关系是 ( )A.相交B.相切C.相离D.与K 的值有关7.对于a ∈R，直线(a －1)x －y ＋a ＋1＝0恒过定点C ，则以C 为圆心，以5为半径的圆的方程为( )A ．x 2＋y 2－2x ＋4y ＝0B ．x 2＋y 2＋2x ＋4y ＝0C ．x 2＋y 2＋2x －4y ＝0D ．x 2＋y 2－2x －4y ＝0 8.圆内接四边形ABCD 中，A ∠、B ∠、C ∠的度数比是2:3:6，则D ∠=（ ）．A ．67.5B ．135C ．112.5D ．1109.如图，设P 为ABC ∆内一点，且AC AB AP 5152+=，则ABP ∆的面积与ABC ∆的面积之比等于（ ）．A ．15B ．25 C ．35D ．1210.如图，在正方形ABCD 中，E 为AB 中点，BF⊥CE 于F ，那么S △BFC :S 正方形ABCD =（ ）．A ．1：3B ．1：4C ．1：5D ．1：6二、填空题（本大题共10小题，每小题2分，共20分）11.已知点是△的外心，是三个单位向量，且2，，如图所示，△的顶点分别在轴和轴的非负半轴上移动，是坐标原点，则的最大值为 。
几何证明选讲知识点汇总与练习（内含答案）
⼏何证明选讲知识点汇总与练习（内含答案）《⼏何证明选讲》知识点归纳与练习(含答案)⼀、相似三⾓形的判定及有关性质平⾏线等分线段定理平⾏线等分线段定理：如果⼀组平⾏线在⼀条直线上截得的线段相等，那么在其他直线上截得的线段也相等。
推理1：经过三⾓形⼀边的中点与另⼀边平⾏的直线必平分第三边。
推理2：经过梯形⼀腰的中点，且与底边平⾏的直线平分另⼀腰。
平分线分线段成⽐例定理平分线分线段成⽐例定理：三条平⾏线截两条直线，所得的对应线段成⽐例。
推论：平⾏于三⾓形⼀边的直线截其他两边（或两边的延长线）所得的对应线段成⽐例。
相似三⾓形的判定及性质相似三⾓形的判定：定义：对应⾓相等，对应边成⽐例的两个三⾓形叫做相似三⾓形。
相似三⾓形对应边的⽐值叫做相似⽐（或相似系数）。
由于从定义出发判断两个三⾓形是否相似，需考虑6个元素，即三组对应⾓是否分别相等，三组对应边是否分别成⽐例，显然⽐较⿇烦。
所以我们曾经给出过如下⼏个判定两个三⾓形相似的简单⽅法：（1）两⾓对应相等，两三⾓形相似；（2）两边对应成⽐例且夹⾓相等，两三⾓形相似；（3）三边对应成⽐例，两三⾓形相似。
预备定理：平⾏于三⾓形⼀边的直线和其他两边（或两边的延长线）相交，所构成的三⾓形与三⾓形相似。
判定定理1：对于任意两个三⾓形，如果⼀个三⾓形的两个⾓与另⼀个三⾓形的两个⾓对应相等，那么这两个三⾓形相似。
简述为：两⾓对应相等，两三⾓形相似。
判定定理2：对于任意两个三⾓形，如果⼀个三⾓形的两边和另⼀个三⾓形的两边对应成⽐例，并且夹⾓相等，那么这两个三⾓形相似。
简述为：两边对应成⽐例且夹⾓相等，两三⾓形相似。
判定定理3：对于任意两个三⾓形，如果⼀个三⾓形的三条边和另⼀个三⾓形的三条边对应成⽐例，那么这两个三⾓形相似。
简述为：三边对应成⽐例，两三⾓形相似。
引理：如果⼀条直线截三⾓形的两边（或两边的延长线）所得的对应线段成⽐例，那么这条直线平⾏于三⾓形的第三边。
定理：（1）如果两个直⾓三⾓形有⼀个锐⾓对应相等，那么它们相似；（2）如果两个直⾓三⾓形的两条直⾓边对应成⽐例，那么它们相似。
高中几何证明选讲课后练习及答案解析
高中几何证明选讲课后练习及答案解析1、[选修4-1：几何证明选讲]如图，P是⊙O外一点，PA是切线，A为切点，割线PBC与⊙O相交于点B，C，PC=2PA，D为PC的中点，AD的延长线交⊙O于点E.证明：①BE=EC;②AD·DE=2PB2.证明：①∵PC=2PA，PD=DC，∴PA=PD，△PAD为等腰三角形.连接AB，那么∠PAB=∠DEB=β，∠BCE=∠BAE=α，∵∠PAB+∠BCE=∠PAB+∠BAD=∠PAD=∠PDA=∠DEB+∠DBE，∴β+α=β+∠DBE，即α=∠DBE，即∠BCE=∠DBE，所以BE=EC.②∵AD·DE=BD·DC，PA2=PB·PC，PD=DC=PA，BD·DC=(PA-PB)PA=PB·PC-PB·PA=PB·(PC-PA)，PB·PA=PB·2PB=2PB2.2、[选修4-4：坐标系与参数方程]在直角坐标系xOy中，曲线C1的参数方程为y=2+2sinα(x=2cosα)(α为参数)，M为C1上的动点，P点满足→(OP)=2→(OM)，点P的轨迹为曲线C2.①求C2的参数方程;②在以O为极点，x轴的正半轴为极轴的极坐标系中，射线θ=3(π)与C1的异于极点的交点为A，与C2的异于极点的交点为B，求|AB|.解：①设P(x，y)，那么由条件知M2(y).由于M点在C1上，所以=2+2sinα(y)，即y=4+4sinα(x=4cosα).从而C2的参数方程为y=4+4sinα(x=4cosα)(α为参数).②曲线C1的极坐标方程为=4sinθ，曲线C2的极坐标方程为=8sinθ.射线θ=3(π)与C1的交点A的极径为1=4s in3(π)，射线θ=3(π)与C2的交点B的极径为2=8sin3(π).所以|AB|=|2-1|=2.3、 [选修4-5：不等式选讲]函数f(x)=|x-m|+|x+6|(m∈R).①当m=5时，求不等式f(x)≤12的解集;②假设不等式f(x)≥7对任意实数x恒成立，求m的取值范围.解：①当m=5时，f(x)≤12即|x-5|+|x+6|≤12，当x<-6时，得-2x≤13，即x≥-2(13)，所以-2(13)≤x<-6;当-6≤x≤5时，得11≤12成立，所以-6≤x≤5;当x>5时，得2x≤11，即x≤2(11)，所以5故不等式f(x)≤12的解集为2(11).②f(x)=|x-m|+|x+6|≥|(x-m)-(x+6)|=|m+6|，由题意得|m+6|≥7，那么m+6≥7或m+6≤-7，解得m≥1或m≤-13，故m的取值范围是(-∞，-13]∪[1，+∞).三道题让你快速“吃透”几何选讲，你还在等什么呢?更多数学资讯，尽在数学网。
「精选」人教版最新高中数学高考总复习几何证明选讲习题及详解及参考答案-精选文档
高中数学高考总复习几何证明选讲习题(附参考答案)一、选择题1．已知矩形ABCD ，R 、P 分别在边CD 、BC 上，E 、F 分别为AP 、PR 的中点，当P 在BC 上由B 向C 运动时，点R 在CD 上固定不变，设BP ＝x ，EF ＝y ，那么下列结论中正确的是( )A ．y 是x 的增函数B ．y 是x 的减函数C ．y 随x 的增大先增大再减小D ．无论x 怎样变化，y 为常数 [答案] D[解析] ∵E 、F 分别为AP 、PR 中点，∴EF 是△P AR 的中位线，∴EF ＝12AR ，∵R 固定，∴AR 是常数，即y 为常数．2．(2010·湖南考试院)如图，四边形ABCD 中，DF ⊥AB ，垂足为F ，DF ＝3，AF ＝2FB ＝2，延长FB 到E ，使BE ＝FB ，连结BD ，EC .若BD ∥EC ，则四边形ABCD 的面积为( )A ．4B ．5C ．6D ．7 [答案] C[解析] 由条件知AF ＝2，BF ＝BE ＝1， ∴S △ADE ＝12AE ×DF ＝12×4×3＝6，∵CE ∥DB ，∴S △DBC ＝S △DBE ，∴S 四边形ABCD ＝S △ADE ＝6.3．(2010·广东中山)如图，⊙O 与⊙O ′相交于A 和B ，PQ 切⊙O 于P ，交⊙O ′于Q 和M ，交AB 的延长线于N ，MN ＝3，NQ ＝15，则PN ＝( )A ．3 B.15 C ．3 2 D ．3 5 [答案] D[解析] 由切割线定理知：PN 2＝NB ·NA ＝MN ·NQ ＝3×15＝45， ∴PN ＝3 5.4．如图，Rt △ABC 中，CD 为斜边AB 上的高，CD ＝6，且AD BD ＝，则斜边AB 上的中线CE 的长为( )A ．5 6 B.562 C.15 D.3102[答案] B[解析] 设AD ＝3x ，则DB ＝2x ，由射影定理得CD 2＝AD ·BD ，∴36＝6x 2，∴x ＝6，∴AB ＝56，∴CE ＝12AB ＝562.5．已知f (x )＝(x －2010)(x ＋2009)的图象与x 轴、y 轴有三个不同的交点，有一个圆恰好经过这三个点，则此圆与坐标轴的另一个交点的坐标是( )A ．(0,1)B ．(0,2)C ．(0，20102009) D ．(0，20092010) [答案] A[解析] 由题意知圆与x 轴交点为A (2010,0)，B (－2009,0)，与y 轴交点为C (0，－2010×2009)，D (0，y 2)．设圆的方程为：x 2＋y 2＋Dx ＋Ey ＋F ＝0令y ＝0得x 2＋Dx ＋F ＝0，此方程两根为2010和－2009，∴F ＝－2010×2009 令x ＝0得y 2＋Ey －2010×2009＝0 ∴－2010×2009×y 2＝－2010×2009 ∴y 2＝1，故选A.[点评] 圆与x 轴交点A (2010,0)，B (－2009,0)与y 轴交点C (0，－2010×2009)，D (0，y 2)，∵A 、C 、B 、D 四点共圆，∴AO ·OB ＝OC ·OD ， ∴OD ＝1，∴y 2＝1.6．设平面π与圆柱的轴的夹角为β (0°<β<90°)，现放入Dandelin 双球使之与圆柱面和平面π都相切，若已知Dandelin 双球与平面π的两切点的距离恰好等于圆柱的底面直径，则截线椭圆的离心率为( )A.12B.22C.33D.32[答案] B[解析] ∵Dandelin 双球与平面π的两切点是椭圆的焦点，圆柱的底面直径恰好等于椭圆的短轴长，∴2b ＝2c ，∴e ＝c a ＝c b 2＋c 2＝c 2c ＝22.二、填空题7．如图，PT 切⊙O 于点T ，P A 交⊙O 于A 、B 两点，且与直径CT 交于点D ，CD ＝2，AD ＝3，BD ＝6，则PB ＝________.[答案] 15[解析] 由相交弦定理得DC ·DT ＝DA ·DB ，则DT ＝9.由切割线定理得PT 2＝PB ·P A ，即(PB ＋BD )2－DT 2＝PB (PB ＋AB )．又BD ＝6，AB ＝AD ＋BD ＝9，∴(PB ＋6)2－92＝PB (PB ＋9)，得PB ＝15.8．(09·天津)如图，AA 1与BB 1相交于点O ，AB ∥A 1B 1且AB ＝12A 1B 1.若△AOB 的外接圆的直径为1，则△A 1OB 1的外接圆的直径为______________．[答案] 2[解析] ∵AB ∥A 1B 1且AB ＝12A 1B 1，∴△AOB ∽△A 1OB 1，∴两三角形外接圆的直径之比等于相似比，∴△A 1OB 1的外接圆直径为2.9．如图，EB 、EC 是⊙O 的两条切线，B 、C 是切点，A 、D 是⊙O 上两点，如果∠E ＝46°，∠DCF ＝32°，则∠A 的度数是________．[答案] 99°[解析] 连接OB 、OC 、AC ，根据弦切角定理得， ∠EBC ＝∠BAC ，∠CAD ＝∠DCF ，可得∠A ＝∠BAC ＋∠CAD ＝12(180°－∠E )＋∠DCF ＝67°＋32°＝99°.[点评] 可由EB ＝EC 及∠E 求得∠ECB ，由∠ECB 和∠DCF 求得∠BCD ，由圆内接四边形对角互补求得∠A .10．PC 是⊙O 的切线，C 为切点，P AB 为割线，PC ＝4，PB ＝8，∠B ＝30°，则BC ＝________.[答案] 4 3[解析] (1)由切割线定理 PC 2＝P A ·PB ， ∴P A ＝2，∠ACP ＝∠B ＝30°，在△P AC 中，由正弦定理2sin30°＝4sin ∠P AC ，∴sin ∠P AC ＝1，∴∠P AC ＝90°，从而∠P ＝60°，∠PCB ＝90°， ∴BC ＝PB 2－PC 2＝82－42＝4 3.11．(2010·重庆文)如图中实线是由三段圆弧连接而成的一条封闭曲线C ，各段弧所在的圆经过同一点P (点P 不在C 上)且半径相等，设第i 段弧所对的圆心角为αi (i ＝1,2,3)，则cosα13cos α2＋α33－sin α13sin α2＋α33＝____________.[答案] －12[解析] 如图，O 1、O 2、O 3为三个圆的圆心，A 1、A 2、A 3分别是每两个圆的交点，则∠A 1P A 2＋∠A 2P A 3＋∠A 3P A 1＝12(α1＋α2＋α3)＝2π，∴α1＋α2＋α3＝4π，∴cos α13cos α2＋α33－sin α13sin α2＋α33＝cos α1＋α2＋α33＝cos 4π3＝cos ⎝⎛⎭⎫π＋π3 ＝－cos π3＝－12.12．(2010·广东中山市四校联考)如图，P A 切圆O 于点A ，割线PBC 经过圆心O ，OB ＝PB ＝1，OA 绕点O 逆时针旋转60°到OD ，则PD 的长为________．[答案]7[解析] 由图可知，P A 2＝PB ·PC ＝PB ·(PB ＋BC )＝3，∴P A ＝3，∴∠AOP ＝60°， 又∠AOD ＝60°，∴∠POD ＝120°，∵PO ＝2，OD ＝1， ∴cos ∠POD ＝22＋12－PD 22×2×1＝－12，∴PD ＝7.三、解答题13．(2010·南京市调研)如图，AB 是⊙O 的直径，点P 在AB 的延长线上，PC 与⊙O 相切于点C ，PC ＝AC ＝1，求⊙O 的半径．[解析] 连接OC .设∠P AC ＝θ.因为PC ＝AC ，所以∠CP A ＝θ，∠COP ＝2θ. 又因为PC 与⊙O 相切于点C ，所以OC ⊥PC . 所以3θ＝90°.所以θ＝30°.设⊙O 的半径为r ，在Rt △POC 中， r ＝CP ·tan30°＝1×33＝33. 14．(2010·江苏盐城调研)如图，圆O 的直径AB ＝8，C 为圆周上一点，BC ＝4，过C 作圆的切线l ，过A 作直线l 的垂线AD ，D 为垂足，AD 与圆O 交于点E ，求线段AE 的长．[解析] 连结OC 、BE 、AC ，则BE ⊥AE .∵BC ＝4，∴OB ＝OC ＝BC ＝4，即△OBC 为正三角形，∴∠CBO ＝∠COB ＝60°， 又直线l 切⊙O 于C ， ∴∠DCA ＝∠CBO ＝60°，∵AD ⊥l ，∴∠DAC ＝90°－60°＝30°，而∠OAC ＝∠ACO ＝12∠COB ＝30°，∴∠EAB ＝60°，在Rt △BAE 中，∠EBA ＝30°，∴AE ＝12AB ＝4.15．(2010·辽宁实验中学)如图，⊙O 的直径AB 的延长线与弦CD 的延长线相交于点P ，E 为⊙O 上一点，AE ＝AC ，DE 交AB 于点F ，且AB ＝2BP ＝4，(1)求PF 的长度．(2)若圆F 与圆O 内切，直线PT 与圆F 切于点T ，求线段PT 的长度． [解析] (1)连结OC ，OD ，OE ，由同弧对应的圆周角与圆心角之间的关系， 结合题中条件弧长AE 等于弧长AC 可得∠CDE ＝∠AOC ，又∠CDE ＝∠P ＋∠PFD ，∠AOC ＝∠P ＋∠OCP ， 从而∠PFD ＝∠OCP ，故△PFD ∽△PCO ， ∴PF PC ＝PDPO， 由割线定理知PC ·PD ＝P A ·PB ＝12， 故PF ＝PC ·PD PO ＝124＝3.(2)若圆F 与圆O 内切，设圆F 的半径为r ， 因为OF ＝2－r ＝1，即r ＝1，所以OB 是圆F 的直径，且过P 点的圆F 的切线为PT ， 则PT 2＝PB ·PO ＝2×4＝8，即PT ＝2 2.。
备战高考数学(精讲+精练+精析)专题13.1几何证明选讲试题文(含解析)
专题1 几何证明选讲（文科）【三年高考】1. 【2016高考天津】如图，AB是圆的直径，弦CD与AB相交于点E，BE=2AE=2，BD=ED，则线段CE的长为__________.【答案】2.【2016高考新课标1卷】如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心,OA为半径作圆.(I)证明：直线AB与O相切；(II)点C,D在⊙O上,且A,B,C,D四点共圆,证明：AB∥CD.【解析】（Ⅰ）设是的中点,连结,因为,所以,．在中,,即到直线的距离等于圆的半径,所以直线与⊙相切．（Ⅱ）因为,所以不是四点所在圆的圆心,设是四点所在圆的圆心,作直线．由已知得在线段的垂直平分线上,又在线段的垂直平分线上,所以．同理可证,．所以．3．【2016高考新课标2】如图，在正方形中，分别在边上（不与端点重合），且，过点作，垂足为．(Ⅰ) 证明：四点共圆；(Ⅱ)若，为的中点，求四边形的面积．4．【2016高考新课标3】如图，中的中点为，弦分别交于两点．（I）若，求的大小；（II）若的垂直平分线与的垂直平分线交于点，证明．【解析】（Ⅰ）连结，则.因为，所以，又，所以.又，所以，因此.（Ⅱ）因为，所以，由此知四点共圆，其圆心既在的垂直平分线上，又在的垂直平分线上，故就是过四点的圆的圆心，所以在的垂直平分线上，又也在的垂直平分线上，因此．5.【2015高考新课标2，】如图，为等腰三角形内一点，圆与的底边交于、两点与底边上的高交于点，与、分别相切于、两点．（Ⅰ）证明：；（Ⅱ）若等于的半径，且，求四边形的面积．【解析】（Ⅰ）由于是等腰三角形，，所以是的平分线．又因为分别与、相切于、两点，所以，故．从而．（Ⅱ）由（Ⅰ）知，,，故是的垂直平分线，又是的弦，所以在上．连接，，则．由等于的半径得，所以．所以和都是等边三角形．因为，所以，．因为，，所以．于是，．所以四边形的面积．6．【2015高考陕西，】如图，切于点，直线交于，两点，，垂足为．（I ）证明：；（II ）若，，求的直径．7.【2015高考新课标1】如图，AB是O的直径，AC是O的切线，BC交O于E.（Ⅰ）若D为AC的中点，证明：DE是O的切线；（Ⅱ）若，求∠ACB的大小.【解析】（Ⅰ）连结AE，由已知得，AE⊥BC，AC⊥AB，在Rt△AEC中，由已知得DE=DC，∴∠DEC=∠DCE，连结OE，∠OBE=∠OEB，∵∠ACB+∠ABC=90°，∴∠DEC+∠OEB=90°，∴∠OED=90°，∴DE是圆O的切线. （Ⅱ）设CE=1，AE=,由已知得AB=，，由射影定理可得，，∴，解得=，∴∠ACB=60°.8.【2015高考湖南】如图，在圆中，相交于点的两弦，的中点分别是，，直线与直线相交于点，证明：（1）；（2）【解析】（1）如图所示，∵，分别是弦，的中点，∴，，即，，，又四边形的内角和等于，故；（2）由（I）知，，，，四点共圆，故由割线定理即得9. 【2014高考辽宁第22题】如图，EP交圆于E、C两点，PD切圆于D，G为CE上一点且，连接DG并延长交圆于点A，作弦AB垂直EP，垂足为F.（Ⅰ）求证：AB为圆的直径；（Ⅱ）若AC=BD，求证：AB=ED.【解析】（Ⅰ）因为PD=PG,所以∠PDG=∠PGD. 由于PD为切线，故∠PDA=∠DBA, 又由于∠PGD=∠EGA,故∠DBA=∠EGA,所以∠DBA+∠BAD=∠EGA+∠BAD,从而∠BDA=∠PFA.由于AF垂直EP，所以∠PFA=90°，于是∠BDA=90°，故AB是直径.(Ⅱ)连接BC，DC.由于AB是直径，故∠BDA=∠ACB=90°，在Rt△BDA与Rt△ACB中，AB=BA,AC=BD，从而Rt△BDA≌Rt△ACB，于是Rt△BDA与∠DAB=∠CBA.又因为∠DCB=∠DAB,所以∠DCB=∠CBA，故DC∥AB. 由于ED是直径，由（Ⅰ）得ED=AB.10. 【2014高考全国2第22题】如图，P是O外一点，PA是切线，A为切点，割线PBC与O相交于点B，C，PC=2PA，D为PC的中点，AD的延长线交O于点E.证明：（Ⅰ）BE=EC；（Ⅱ）AD DE=2【解析】（Ⅰ）连结AB，AC，由题意知PA=PD，故，因为，，，所以，从而，因此BE=EC. （Ⅱ）由切割线定理得：，因为，所以，，由相交弦定理得：===，所以等式成立.11. 【2014高考全国1第22题】如图，四边形是的内接四边形，的延长线与的延长线交于点，且.（Ⅰ）证明：；（Ⅱ）设不是的直径，的中点为，且，证明：为等边三角形.【三年高考命题回顾】纵观前三年各地高考试题, 高考对几何证明的考查，主要考查有关三角形相似、全等、面积、线段长度及角相等的求解及证明，以平行线等分线段定理，平行线截割定理，相似三角形的判定与性质定理，直角三角形射影定理，圆心角、圆周角定理，圆内接四边形的性质定理及判定定理，圆的割线定理，切割线定理，弦切角定理，相交弦定理等为主要考查内容，题目难度一般为中、低档，备考中应严格控制训练题的难度．【2017年高考复习建议与高考命题预测】由前三年的高考命题形式可以看出, 高考对这部分要求不是太高，要求会以圆为几何背景，利用直角三角形射影定理，圆周角定理、圆的切线的判定定理及性质定理，相交弦定理、圆内接四边形的性质定理与判定定理、切割线定理证明三角形相似，全等，求线段长等，预测2017年高考还会以圆为几何背景，考查相交线定理，切割线定理，以及圆内接四边形的性质定理与判定定理，考查学生的数形结合的能力.“几何证明选讲”是选修系列4的一个专题,该专题在高考中只考查“相似三角形”和“圆”这两部分平面几何内容,且与另三个选修4的专题一起命题,供考生选择作答.其核心内容为:线段成比例与相似三角形,圆的切线及其性质,与圆有关的相似三角形等.对同学们来说,“几何证明选讲”是初中所学知识的深化,因而倍感亲切.试题题型为解答题,且难度不大.题型以比例问题为主，平行线分线段成比例定理、相似形、角平分线定理、直角三角形中的射影定理、圆中的割线定理、切割线定理和相交弦定理等,都涉及线段成比例,因此比例问题是本专题中所占比重最大的题型.解决这类问题,主要方法就是设法利用上述定理,并灵活变形.复习建议：圆内接四边形的重要结论：内接于圆的平行四边形是矩形；内接于圆的菱形是正方形；内接于圆的梯形是等腰梯形.应用这些性质可以大大简化证明有关几何题的推证过程.与圆有关的比例线段的证明要诀：相交弦、切割线定理是法宝，相似三角形中找诀窍，联想射影定理分角线，辅助线来搭桥，第三比作介绍，代数方法不可少，分析综合要记牢，十有八九能见效.【2017年高考考点定位】几何证明选讲的内容涉及的考点可归纳为:①相似三角形的定义与性质;②平行线截割定理;③直角三角形射影定理;④圆周角与圆心角定理;⑤圆的切线的判定定理及性质定理;⑥弦切角的性质;⑦相交弦定理;⑧圆内接四边形的性质定理和判定定理;⑨切割线定理.【考点1】相似三角形的判定与性质【备考知识梳理】1．平行线等分线段定理如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等．推论1：经过三角形一边的中点与另一边平行的直线必平分第三边．推论2：经过梯形一腰的中点，且与底边平行的直线平分另一腰．2．平行线分线段成比例定理三条平行线截两条直线，所得的对应线段成比例．推论：平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例．3．相似三角形的判定与性质(1)判定定理：结论相似三角形外接圆的直径比、周长比等于相似比，外接圆的面积比等于相似比的平方射影定理直角三角形中，每一条直角边是这条直角边在斜边上的射影和斜边的比例中项；斜边上的高是两条直角边在斜边上的射影的比例中项【规律方法技巧】1．判定两个三角形相似的常规思路(1)先找两对对应角相等；(2)若只能找到一对对应角相等，则判断相等的角的两夹边是否对应成比例；(3)若找不到角相等，就判断三边是否对应成比例，否则考虑平行线分线段成比例定理及相似三角形的“传递性”．2．借助图形判断三角形相似的方法(1)有平行线的可围绕平行线找相似；(2)有公共角或相等角的可围绕角做文章，再找其他相等的角或对应边成比例；(3)有公共边的可将图形旋转，观察其特征，找出相等的角或成比例的对应边．3.比例线段常用平行线产生，利用平行线转移比例是常用的证题技巧，当题中没有平行线条件而有必要转移比例时，也常添加辅助平行线，从而达到转移比例的目的.4.判定两个三角形相似要注意结合图形特征灵活选择判定定理，特别要注意对应角和对应边．在一个题目中，相似三角形的判定定理和性质定理可能多次用到．相似三角形的性质可用来证明线段成比例、角相等；也可间接证明线段相等．5.．在使用直角三角形射影定理时，要学会将“乘积式”转化为相似三角形中的“比例式”．证题时，要注意作垂线构造直角三角形是解直角三角形时常用的方法．6.相似关系的证明中，经常要应用比例的性质：若，则①；②；③；④；⑤；⑥.7.辅助线作法：几何证明题的一个重要问题就是作出恰当的辅助线，相似关系的基础就是平行截割定理，故作辅助线的主要方法就是作平行线，见中点取中点连线利用中位线定理，见比例点取等比的分点构造平行关系，截取等长线段构造全等关系，立体几何中通过作平行线或连结异面直线上的点化异为共等等都是常用的作辅助线方法．【考点针对训练】1.【2016届河南省郑州一中高三考前冲刺四】如图所示，已知圆O外有一点P，作圆O的切线PM，M为切点，过PM的中点N作割线NAB，交圆O于A，B两点，连接PA并延长，交圆O于点C，连接PB交圆O于点D，若MC=BC.（1）求证：△APM△ABP；（2）求证：四边形PMCD是平行四边形.2.【2016年山西省右玉一中高考冲刺压轴卷三】如图，已知⊙和⊙相交于两点，为⊙的直径，直线交⊙于点，点为弧中点，连结分别交⊙、于点，连结.（Ⅰ）求证：；（Ⅱ）求证：.【解析】（Ⅰ）连结，∵为⊙的直径，∴，∵为⊙的直径，∴，∵，∴，∵为弧中点，∴，∵，∴，∴，∴，∴.（Ⅱ）由（Ⅰ）知，，∴，∴，由（Ⅰ）知，∴.【考点2】圆的有关问题【备考知识梳理】1．圆周角定理(1)圆周角：顶点在圆周上且两边都与圆相交的角．(2)圆周角定理：圆上一条弧所对的圆周角等于它所对的圆心角的一半．(3)圆心角定理：圆心角的度数等于它所对弧的度数．推论1：同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等．推论2：半圆(或直径)所对的圆周角是直角；90°的圆周角所对的弦是直径．2．圆内接四边形的性质与判定定理(1)性质：定理1：圆内接四边形的对角互补．定理2：圆内接四边形的外角等于它的内角的对角．(2)判定：判定定理：如果一个四边形的对角互补，那么这个四边形的四个顶点共圆．推论：如果四边形的一个外角等于它的内角的对角，那么这个四边形的四个顶点共圆．另外：若两点在一条线段同侧且对该线段张角相等，则此两点与线段两个端点共圆，特别的，对定线段张角为直角的点共圆．3.圆的切线(1)直线与圆的位置关系直线与圆交点的个数直线到圆心的距离d与圆的半径r的关系相交两个d＜r相切一个d＝r相离无d＞r性质定理：圆的切线垂直于经过切点的半径．推论1：经过圆心且垂直于切线的直线必经过切点．推论2：经过切点且垂直于切线的直线必经过圆心．判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线．(3)切线长定理：从圆外一点引圆的两条切线长相等．3．弦切角(1)弦切角：顶点在圆上，一边与圆相切，另一边与圆相交的角．(2)弦切角定理及推论①定理：弦切角的度数等于所夹弧的度数的一半．②推论：同弧(或等弧)上的弦切角相等，同弧(或等弧)上的弦切角等于它所夹的弧所对的圆周角． 4．与圆有关的比例线段定理名称基本图形条件结论应用相交弦定理弦AB、CD相交于圆内点P(1)PA·PB＝PC·PD；(2)△ACP∽△DBP(1)在PA、PB、PC、PD四线段中知三求一；(2)求弦长及角切割线定理PA切⊙O于A，PBC是⊙O的割线(1)PA2＝PB·PC；(2)△PAB∽△PCA(1)已知PA、PB、PC知二可求一；(2)求解AB、AC割线定理PAB、PCD是⊙O的割线(1)PA·PB＝PC·PD；(2)△PAC∽△PDB(1)求线段PA、PB、PC、PD及AB、CD；(2)应用相似求AC、BD(1)(2)割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等．(3)切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项．(4)切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角．【规律方法技巧】1. 与圆有关的比例线段： (1)应用相交弦定理、切割线定理要抓住几个关键内容：如线段成比例与相似三角形、圆的切线及其性质、与圆有关的相似三角形等．(2)相交弦定理、切割线定理主要是用于与圆有关的比例线段的计算与证明．解决问题时要注意相似三角形知识及圆周角、弦切角、圆的切线等相关知识的综合应用．(3)相交弦定理、切割线定理、割线定理、切线长定理统称为圆幂定理：圆的两条弦或其延长线若相交，各弦被交点分成的两条线段长的积相等.当两交点在圆内时为相交弦定理，当两交点在圆外时为割线定理，两交点重合时为切线，一条上两点重合时为切割线定理，两条都重合时为切线长定理，应用此定理一定要分清两条线段是指哪两条．2. 弦切角定理及推论的应用(1)圆周角定理及其推论与弦切角定理及其推论多用于推出角的关系，从而证明三角形全等或相似，可求线段或角的大小．(2)涉及圆的切线问题时要注意弦切角的转化；关于圆周上的点，常作直线(或半径)或向弦(弧)两端画圆周角或作弦切角．3. 证明多点共圆，当两点在一条线段同侧时，可证它们对此线段张角相等，也可以证明它们与某一定点距离相等；如两点在一条线段异侧，则证明它们与线段两端点连成的凸四边形对角互补．4.涉及圆的切线问题时要注意弦切角的转化；关于圆周上的点，常作直径(或半径)或向弦(弧)两端画圆周角或作弦切角．5.一般地，涉及圆内两条相交弦时首先要考虑相交弦定理，涉及两条割线时要想到割线定理，涉及切线和割线时要注意应用切割线定理，要注意相交弦定理中线段之间的关系与切割线定理线段关系之间的区别．6.在平面几何的有关计算中往往要使用比例线段，产生比例线段的一个主要根据是两三角形相似．在涉及两圆的公共弦时，通常是作出两圆的公共弦．如果有过公共点的切线就可以使用弦切角定理．在两个圆内实现角的等量代换，这是解决两个圆相交且在交点处有圆的切线问题的基本思考方向．【考点针对训练】1.【2016届湖北七市教研协作体高三4月联考】已知中，，是外接圆劣弧上的点（不与点重合），延长至，延长至.（1）求证：；（2）若，中边上的高为，求外接圆的面积.2.【2016届陕西省高三下学期教学质检二】如图，已知圆与相交于两点，过点作圆的切线交圆于点，过点作两圆的割线，分别交圆、圆于点、，与相交于点. （Ⅰ）求证：；（Ⅱ）若是圆的切线，且，求的长.【解析】（Ⅰ）连接．∵是圆的切线，∴.又∵，∴，∴.（Ⅱ）证明：设，∵，∴.又∵，∴，∴.又∵，联立上述方程得到，∴.∵是圆的切线，∴.∴.【应试技巧点拨】1．辅助线作法：几何证明题的一个重要问题就是作出恰当的辅助线，相似关系的基础就是平行截割定理，故作辅助线的主要方法就是作平行线，见中点取中点连线利用中位线定理，见比例点取等比的分点构造平行关系，截取等长线段构造全等关系，立体几何中通过作平行线或连结异面直线上的点化异为共等等都是常用的作辅助线方法．2．比例的性质的应用相似关系的证明中，经常要应用比例的性质：若，则①；②；③；④；⑤；⑥.3．同一法：先作出一个满足命题结论的图形，然后证明图形符合命题已知条件，确定所作图形与题设条件所指的图形相同，从而证明命题成立．4.证明多点共圆，当两点在一条线段同侧时，可证它们对此线段张角相等，也可以证明它们与某一定点距离相等；如两点在一条线段异侧，则证明它们与线段两端点连成的凸四边形对角互补．5.与圆有关的比例线段(1)应用相交弦定理、切割线定理要抓住几个关键内容：如线段成比例与相似三角形、圆的切线及其性质、与圆有关的相似三角形等．(2)相交弦定理、切割线定理主要是用于与圆有关的比例线段的计算与证明．解决问题时要注意相似三角形知识及圆周角、弦切角、圆的切线等相关知识的综合应用．二年模拟1. 【2016年山西榆林高三二次模考】如图所示，在中，是的平分线，的外接圆交于点，.（1）求证：；（2）当时，求的长.2. 【2016年湖北八校高三四次联考】如图，在锐角三角形中，，以为直径的圆与边另外的交点分别为，且于．（Ⅰ）求证：是的切线；（Ⅱ）若，，求的长．【解析】（Ⅰ）连结则又，∴为的中点，而为中点，∴，又，∴，而是半径，∴是的切线.（Ⅱ）连，则，则，∴，设，则，由切割线定理得：，即，解得：（舍），∴EFDOC BA3. 【2016年安徽安庆二模】如图,以的边为直径作圆,圆与边的交点恰为边的中点,过点作于点．（I ）求证：是圆的切线；（II ）若,求的值．【解析】（Ⅰ）如图,连接.因为是的中点,是的中点,所以//.因为,所以,所以是⊙的切线. （Ⅱ）因为是⊙的直径,点在⊙上,所以. 又是的中点,所以. 故.因为,所以. 在直角三角形中,；在直角三角形中,. 于是.4.【2016年江西高三九校联考】如图所示，为的直径，为的中点，为的中点．（1）求证：；（2）求证：．5. 【2016年安徽淮北一中高三模考】如图，是圆上的两点，为圆外一点，连结分别交圆于点，且，连结并延长至，使．（1）求证：；（2）若，且，求．【解析】（1）连结，因为，又因为，所以，所以，由已知，所以，且，所以，所以．（2）因为，所以，则，所以，又因为，所以，所以，所以．6. 【2016年江西南昌高三一模】如图，圆M与圆N交于A， B两点，以A为切点作两圆的切线分别交圆M和圆N于C、D两点，延长DB交圆M于点E，延长CB交圆N于点F．已知BC=5， DB=10. (I)求AB的长；（II）求.【解析】（Ⅰ）根据弦切角定理，知，，∴△∽△，则，故.（Ⅱ）根据切割线定理，知，，两式相除，得（*）.由△∽△，得，，又，由（*）得．7. 【2016年河南八市高三三模】已知，内接于圆，延长到点，使得交圆于点.（1）求证：；（2）若，求证：.【解析】(1）如图，连结．．又（2）8.【2016届河北省石家庄市高三二模】如图，内接于⊙，，弦交线段于，为的中点，在点处作圆的切线与线段的延长线交于，连接.（I）求证：；（II）若，⊙的半径为，求切线的长.【解析】（I）证明：在中，弦相交于E，，又E为AC的中点，所以，又因为,，根据射影定理可得,;（II）因为为直径，所以，又因为，所以为等腰直角三角形．，根据勾股定理得，解得，所以，由（I）得所以，所以．9.【2016届陕西省高三高考全真模拟四】如下图,是圆的两条互相垂直的直径,是圆上的点,过点作圆的切线交的延长线于.连结交于点.（1）求证：；（2）若圆的半径为,求的长.【解析】（1）证明：连接,由弦切角定理知，又,即.由切割线定理得,所以.（2）由知，.在中，由得，.在中，由得，于是.10.【2016届山西右玉一中高三下学期模拟】已知如图，四边形是圆的内接四边形，对角线交于点，直线是圆的切线，切点为，.（1）若，求的长；（2）在上取一点，若，求的大小.11. 【2015届陕西西安西北工大附中高三下学期5月模拟】如图，和相交于A，B两点，过A 作两圆的切线分别交两圆于两点，连结并延长交于点．证明：（Ⅰ）；（Ⅱ）．【解析】（1）由与相切于，得，同理，所以从而，即（2）由与相切于，得，又，得从而，即，综合（1）的结论，12.【2015届陕西省西工大附中高三下学期模拟考试一】如图,⊙的直径的延长线与弦的延长线相交于点,为⊙上一点,AE＝AC ,交于点,且,（Ⅰ）求的长度．（Ⅱ）若圆F 与圆内切，直线PT与圆F切于点T，求线段PT的长度【解析】（Ⅰ）连结,由同弧对应的圆周角与圆心角之间的关系结合题中条件弧长等于弧长可得,又,,从而,故∽,∴, 由割线定理知,故．（Ⅱ）若圆F 与圆内切，设圆的半径为，因为即，所以是圆的直径，且过点圆的切线为，则，即.13.【2015届吉林省吉林市高三第三次模拟考试】如图，在△ABC 中，，以为直径的⊙O 交于，过点作⊙O 的切线交于，交⊙O 于点．（Ⅰ）证明：是的中点；（Ⅱ）证明：.【解析】（Ⅰ）证明：连接，因为为⊙O 的直径，所以，又，所以CB切⊙O于点B ，且ED 切于⊙O 于点E ，因此，，所以，得，因此，即是的中点（Ⅱ）证明：连接BF ，可知BF 是△ABE 斜边上的高，可得△ABE ∽△AFB ，于是有，即，同理可证，所以.14.【2015届辽宁省师大附中高三模拟考试】如图，圆周角的平分线与圆交于点，过点的切线与弦的延长线交于点，交于点．（1）求证：;（2）若四点共圆，且弧与弧相等，求【解析】（1）因为与圆相切，，平方，所以，，所以（2）弧与弧相等，设，，，.15.【2015届陕西省西安市第一中学高三下学期自主命题二】如图，在中，是的角平分线，的外接圆交于点，．EDCA B（Ⅰ）求证：； （Ⅱ）当，时，求的长．【解析】（Ⅰ）连接，因为是圆内接四边形，所以又∽，即有，又因为，可得因为是的平分线，所以，从而（Ⅱ）由条件知，设，则，根据割线定理得，即即，解得或（舍去），则．EDCA B拓展试题以及解析 1. 如图，内接于⊙，弦AE 交BC 于点D ，已知，，OD =1,. （Ⅰ）求；（Ⅱ）求中BC 边上的高．【入选理由】本题主要考查平面几何的相关知识，同时考查考生的逻辑推理能力.高考对平面几何的考查主要是通过三角形全等或三角形相似进行边角转化，并综合运用圆的切割线定理、相交弦定理等 进行证明计算．以圆为背景是基本不变的，因而灵活应用圆的几何性质，找准有关的对应三角形、对应边和对应角是解题的关键.本题构思巧妙，难度不大，故选此题.2．如图，过圆外一点作圆的切线，切点为，割线、割线分别交圆于与、与．已知的垂直平分线与圆相切．（1）求证：；（2）若，，求的长．【解析】（1）证明：连结，∵与圆相切，∴．又为的垂直平分线，∴，∴，∴．（2）由（1）知且为的中点，∴为的中点，且，∴．∵为圆的切线，∴，∴，∴，∴．【入选理由】本题考查圆的切割线定理，弦切角定理等基础知识，意在考查逻辑思维能力和推理论证能力. 切割线定理、三角形相似、四点共圆的性质，是高考重点考查知识点，本题难度不大，故选此题.3.如图，直线AB过圆心O，交圆O于A、B，直线AF交圆O于F（不与B重合），直线与圆O相切于C，交AB于E，且与AF垂直，垂足为G，连接AC．求证：（Ⅰ）；（Ⅱ）．【证明】（Ⅰ）连接，是直径，，．切圆于，．．（Ⅱ）连接，切圆于，．又∽．．【入选理由】本题考查圆的弦切角定理、三角形相似等基础知识，意在考查逻辑思维能力和推理论证能力.本题由弦切角定理入手，得出三角形相似，从而可证，本题难度不大，故选此题.4.如图，是⊙的直径，是圆上两点，交于点，若，．（Ⅰ）求证：；（Ⅱ）求线段的长度．【入选理由】本题考查平面几何的证明，具体涉及圆的性质，四点共圆，割线定理等基础知识，意在考察学生推理证明和逻辑思维能力.本题考查知识基础，综合性强，是高考出题方向，故选此题.5.如图，圆内接四边形满足∥，在的延长线上，且. 若，.（Ⅰ）证明：；（Ⅱ）求的长.【解析】（Ⅰ）由知是圆的切线. ∴由弦切线角定理得，又，∴，∴；（Ⅱ）由（Ⅰ）知，又，∴∽，∴，又，，∴，∵，∴. 【入选理由】本题考查圆的切线的性质，圆內接四边形的性质，三角形相似等基础知识，意在考察学生推理证明和逻辑思维能力.本题考查知识基础，难度不大，故选此题.6.如图，点P是△ABC的外接圆O在C点的切线与直线AB的交点．（Ⅰ）若∠ACB＝∠APC，证明：BC⊥PC；（Ⅱ）若D是圆O上一点，∠BPC=∠DAC，AC=，AB=，PC＝4，求CD的长．【证明】（Ⅰ）由弦切角定理知，∠ABC=∠ACP，∵∠ACB＝∠APC，∴△ACB∽△APC，∴∠BAC=∠CAP，∵∠BAC+∠CAP=，∴∠BAC=∠CAP=90°，∴BC是圆O的直径，又PC是圆O的切线，∴BC⊥PC. （Ⅱ）由切割线定理知，，即，即，解得（负值舍去），由弦切角定理及同弧所对的圆周角相等知，∠ACP=∠ABC=∠CDA，∵∠BPC=∠DAC，∴△CAD∽△APC，∴，∴=.【入选理由】本题考查三角形相似的判定与性质、弦切角定理、切割线定理等基础知识，意在考查学生推理证明和逻辑思维能力.本题第一问由弦切角入手，得三角形相似，从而得结论，第二问由切割线定理入手，结合弦切角定理及同弧所对的圆周角相等，得三角形相似，像这种题型考查知识基础，综合性强，是高考出题方向，故选此题.7.如图所示，在四边形中，交于点，.（Ⅰ）求证：、、、四点共圆;（Ⅱ）过作四边形外接圆的切线交的延长线于，,求证：平分.【证明】（Ⅰ）∵,∴,,∵,, ∴,,∴=,=,=,=,∴=+++=+++==,∴、、、四点共圆；（Ⅱ）由弦切角定理可知：∠=∠，∵,∴∽,∴=，∵，∴=,∴=,∴=,∴=,∴=∠,∴平分.。
高考数学 课后作业 121 几何证明选讲 新人教A版
2013高考数学人教A 版课后作业：12-1 几何证明选讲1.如图，CD 是圆O 的切线，切点为C ，点A ，B 在圆O 上，BC ＝1，∠BCD ＝30°，则圆O 的面积为( )A.π2 B ．π C.3π2D ．2π[答案] B[解析] ∠A ＝∠BCD ＝30°，由BC sin A＝2R ，得R ＝1，所以圆O 的面积为πR 2＝π. 2．(文)如图所示，在▱ABCD 中，BC ＝24，E 、F 为BD 的三等分点，则BM －DN ＝( )A ．6B ．3C ．2D ．4 [答案] A[解析] ∵E 、F 为BD 的三等分点，四边形为平行四边形，∴M 为BC 的中点，连CF 交AD 于P ，则P 为AD 的中点，由△BCF ∽△DPF 及M 为BC 中点知，N 为DP 的中点，∴BM －DN ＝12－6＝6，故选A.(理)如图，E 是▱ABCD 边BC 上一点，BE EC ＝4，AE 交BD 于F ，BF FD等于( )A.45B.49C.59D.410[答案] A[解析]在AD上取点G，使AG:GD＝1:4，连结CG交BD于H，则CG∥AE，∴BFFH＝BECE＝4，DHFH＝DGGA＝4，∴BFFD＝45.3．如图，Rt△ABC中，CD为斜边AB上的高，CD＝6，且AD:BD＝3:2，则斜边AB上的中线CE的长为( )A．5 6 B.56 2C.15D.310 2[答案] B[解析]设AD＝3x，则DB＝2x，由射影定理得CD2＝AD·BD，∴36＝6x2，∴x＝6，∴AB＝56，∴CE＝12AB＝562.4．(文)(2010·湖南考试院)如图，四边形ABCD中，DF⊥AB，垂足为F，DF＝3，AF＝2FB ＝2，延长FB到E，使BE＝FB，连结BD，EC.若BD∥EC，则四边形ABCD的面积为( )A ．4B ．5C ．6D ．7[答案] C[解析] 由条件知AF ＝2，BF ＝BE ＝1， ∴S △ADE ＝12AE ×DF ＝12×4×3＝6，∵CE ∥DB ，∴S △DBC ＝S △DBE ，∴S 四边形ABCD ＝S △ADE ＝6.(理)已知矩形ABCD ，R 、P 分别在边CD 、BC 上，E 、F 分别为AP 、PR 的中点，当P 在BC 上由B 向C 运动时，点R 在CD 上固定不变，设BP ＝x ，EF ＝y ，那么下列结论中正确的是( )A ．y 是x 的增函数B ．y 是x 的减函数C ．y 随x 的增大先增大再减小D ．无论x 怎样变化，y 为常数 [答案] D[解析] ∵E 、F 分别为AP 、PR 中点，∴EF 是△PAR 的中位线，∴EF ＝12AR ，∵R 固定，∴AR是常数，即y为常数．5．(2011·海淀期末)如图，半径为2的⊙O中，∠AOB＝90°，D为OB的中点，AD的延长线交⊙O于点E，则线段DE的长为( )A.55B.255C.355D.32[答案] C[解析]延长BO交圆O于点F，由D为OB的中点，知DF＝3，DB＝1，又∠AOB＝90°，所以AD＝5，由相交弦定理知AD·DE＝DF·DB，即5DE＝3×1，解得DE＝355.6．(2010·广东中山)如图，⊙O与⊙O′相交于A和B，PQ切⊙O于P，交⊙O′于Q和M，交AB的延长线于N，MN＝3，NQ＝15，则PN＝( )A．3 B.15 C．3 2 D．3 5[答案] D[解析]由切割线定理知：PN2＝NB·NA＝MN·NQ＝3×15＝45，∴PN＝3 5.7．(2011·深圳调研)如图，割线PBC经过圆心O，OB＝PB＝1，OB绕点O逆时针旋转120°到OD，连PD交圆O于点E，则PE＝________.[答案]37 7[解析]∵∠POD＝120°，OD＝OB＝1，PO＝2，∴PD＝PO2＋OD2－2OD·PO·cos120°＝7，由相交弦定理得，PE·PD＝PB·PC，∴PE＝PB·PCPD＝1×37＝377.8．(文)(2011·北京西城区模拟)如图，从圆O外一点P引圆O的切线PA和割线PBC，已知PA＝22，PC＝4，圆心O到BC的距离为3，则圆O的半径为________．[答案] 2[解析]设圆O的半径为R.依题意得PA2＝PB·PC，∴PB＝PA2PC＝2，BC＝PC－PB＝2，∴R＝12BC2＋32＝2，即圆O的半径为2.(理)(2010·广东中山市四校联考)如图，PA切圆O于点A，割线PBC经过圆心O，OB＝PB ＝1，OA绕点O逆时针旋转60°到OD，则PD的长为________．[答案]7[解析]由图可知，PA2＝PB·PC＝PB·(PB＋BC)＝3，∴PA＝3，∴∠AOP＝60°，又∠AOD＝60°，∴∠POD＝120°，∵PO＝2，OD＝1，∴cos∠POD＝22＋12－PD22×2×1＝－12，∴PD＝7.1.(文)(2011·广东湛江高考调研)如图，圆O上一点C在直径AB上的射影为D，AD＝2，AC＝25，则AB＝________.[答案]10[解析]由射影定理知，AC2＝AD·AB，所以AB＝2522＝10.(理)(2010·茂名市模考)如图所示，已知圆O直径为6，AB是圆O的直径，C为圆O上一点，且BC＝2，过点B的圆O的切线交AC延长线于点D，则DA＝________.[答案] 3[解析]∵AB为直径，∴∠ACB为直角，∵BC＝2，AB＝6，∴AC＝2，∵DB与⊙O相切，∴∠DBA为直角，由射影定理BC2＝AC·CD，∴CD＝1，∴AD＝3.2．(文)如图，BD为⊙O的直径，AB＝AC，AD交BC于E，AE＝2，ED＝4.则AB的长为________．[答案]2 3[解析]∵∠ABC＝∠C，∠C＝∠D，∴∠ABC＝∠D，又∠BAE＝∠DAB，∴△ABE∽△ADB，∴AB2＝AE·AD，∴AB＝2 3.(理)已知EB是半圆O的直径，A是BE延长线上一点，AC切半圆O于点D，BC⊥AC于点C，若BC＝6，AC＝8，则AE＝______，AD＝________.[答案]52，5[解析]∵OD⊥AC，BC⊥AC，∴△ADO∽△ACB，∴ODBC ＝AO AB，∵BC＝6，AC＝8，∴AB＝10，设OD＝R，则AO＝53R，∴R＋53R＝10，∴R＝154，AE＝AB－2R＝52，ADOD＝ACBC＝43，∴AD＝5.3．(文)(2011·广东汕头测试)如图，正△ABC的边长为2，点M，N分别是边AB，AC的中点，直线MN与△ABC的外接圆的交点为P，Q，则线段PM＝________.[答案]5－1 2[解析]设PM＝x，则QN＝x，由相交弦定理可得PM·MQ＝BM·MA即x·(x＋1)＝1，解得x＝5－1 2.(理)(2011·佛山质检)如图，AB，CD是半径为a的圆O的两条弦，它们相交于AB的中点P，PD＝23a，∠OAP＝30°，则CP＝________.[答案]9a 8[解析] 因为点P 是AB 的中点，由垂径定理知，OP ⊥AB .在Rt △OPA 中，BP ＝AP ＝a cos30°＝32a .由相交弦定理知，BP ·AP ＝CP ·DP ，即32a ·32a ＝CP ·23a ，所以CP ＝98a . 4．(文)(2011·惠州市模拟)如图，⊙O 的割线PAB 交⊙O 于A 、B 两点，割线PCD 经过圆心O ，已知PA ＝6，AB ＝223，PO ＝12，则⊙O 的半径是________．[答案] 8[解析] 设⊙O 的半径是R ，∵PA ·PB ＝PC ·PD ＝(PO －R )(PO ＋R )＝PO 2－R 2， ∴PA (PA ＋AB )＝PO 2－R 2， 将PA ＝6，AB ＝223，PO ＝12代入得R ＝8. (理)(2010·天津理)如下图，四边形ABCD 是圆O 的内接四边形，延长AB 和DC 相交于点P ，若PB PA ＝12，PC PD ＝13，则BCAD的值为__________．[答案]66[解析] 由割线定理知：PB ·PA ＝PC ·PD ， 又∵PA ＝2PB ，PD ＝3PC ，∴PB ·2PB ＝13PD ·PD ，∴PB 2＝16PD 2，∴PB ＝66PD ，又∵△PBC ∽△PDA ，∴BC AD ＝PB PD ＝66. 5．如图，EB 、EC 是⊙O 的两条切线，B 、C 是切点，A 、D 是⊙O 上两点，如果∠E ＝46°，∠DCF ＝32°，则∠A 的度数是________．[答案] 99°[解析] 连接OB 、OC 、AC ，根据弦切角定理得， ∠EBC ＝∠BAC ，∠CAD ＝∠DCF ，可得∠A ＝∠BAC ＋∠CAD ＝12(180°－∠E )＋∠DCF ＝67°＋32°＝99°.[点评] 可由EB ＝EC 及∠E 求得∠ECB ，由∠ECB 和∠DCF 求得∠BCD ，由圆内接四边形对角互补求得∠A .6．(文)(2010·南京市调研)如图，AB 是⊙O 的直径，点P 在AB 的延长线上，PC 与⊙O 相切于点C ，PC ＝AC ＝1，求⊙O 的半径．[解析]连接OC.设∠PAC＝θ.因为PC＝AC，所以∠CPA＝θ，∠COP＝2θ. 又因为PC与⊙O相切于点C，所以OC⊥PC.所以3θ＝90°.所以θ＝30°.设⊙O的半径为r，在Rt△POC中，r＝CP·tan30°＝1×33＝33.(理)(2010·江苏盐城调研)如图，圆O的直径AB＝8，C为圆周上一点，BC＝4，过C作圆的切线l，过A作直线l的垂线AD，D为垂足，AD与圆O交于点E，求线段AE的长．[解析]连结OC 、BE 、AC ，则BE ⊥AE .∵BC ＝4，∴OB ＝OC ＝BC ＝4，即△OBC 为正三角形， ∴∠CBO ＝∠COB ＝60°， 又直线l 切⊙O 于C ， ∴∠DCA ＝∠CBO ＝60°，∵AD ⊥l ，∴∠DAC ＝90°－60°＝30°，而∠OAC ＝∠ACO ＝12∠COB ＝30°，∴∠EAB ＝60°，在Rt △BAE 中，∠EBA ＝30°，∴AE ＝12AB ＝4.7．(文)(2010·辽宁)如图，△ABC 的角平分线AD 的延长线交它的外接圆于点E .(1)证明：△ABE ∽△ADC ；(2)若△ABC 的面积S ＝12AD ·AE ，求∠BAC 的大小．[解析] (1)∵AD 为∠BAC 的角平分线 ∴∠BAE ＝∠CAD又∵∠AEB 与∠ACB 为AB 所对的圆周角 ∴∠AEB ＝∠ACD ，∴△ABE ∽△ADC . (2)由(1)可知△ABE ∽△ADC 故AB AE ＝AD AC， 即AB ·AC ＝AD ·AE ① 又S ＝12AB ·AC sin ∠BAC且S ＝12AD ·AE∴12AB ·AC sin ∠BAC ＝12AD ·AE ② 由①②式得 sin ∠BAC ＝1∵∠BAC 为三角形内角，∴∠BAC ＝90°(理)(2010·辽宁实验中学)如图，⊙O 的直径AB 的延长线与弦CD 的延长线相交于点P ，E 为⊙O 上一点，AE ＝AC ，DE 交AB 于点F ，且AB ＝2BP ＝4，(1)求PF 的长度．(2)若圆F 与圆O 内切，直线PT 与圆F 切于点T ，求线段PT 的长度． [解析] (1)连结OC ，OD ，OE ，由同弧对应的圆周角与圆心角之间的关系，结合题中条件弧长AE 等于弧长AC 可得∠CDE ＝∠AOC ， 又∠CDE ＝∠P ＋∠PFD ，∠AOC ＝∠P ＋∠OCP ， 从而∠PFD ＝∠OCP ，故△PFD ∽△PCO ， ∴PF PC ＝PD PO， 由割线定理知PC ·PD ＝PA ·PB ＝12， 故PF ＝PC ·PD PO ＝124＝3. (2)若圆F 与圆O 内切，设圆F 的半径为r ， 因为OF ＝2－r ＝1，即r ＝1，所以OB是圆F的直径，且过P点的圆F的切线为PT，则PT2＝PB·PO＝2×4＝8，即PT＝2 2.1.如图所示，矩形ABCD中，AB＝12，AD＝10，将此矩形折叠使点B落在AD边的中点E 处，则折痕FG的长为( )A．13 B.63 5C.656D.636[答案] C[解析]过点A作AH∥FG交DG于H，则四边形AFGH为平行四边形．∴AH＝FG. ∵折叠后B点与E点重合，折痕为FG，∴B与E关于FG对称．∴BE⊥FG，∴BE⊥AH.∴∠ABE＝∠DAH，∴Rt△ABE∽Rt△DAH.∴BEAB＝AHAD.∵AB＝12，AD＝10，AE＝12AD＝5，∴BE＝122＋52＝13，∴FG＝AH＝BE·ADAB＝656.2．如图所示，在矩形ABCD中，AE⊥BD于E，S矩形＝40cm2，S△ABE:S△DBA＝1:5，则AE的长为________．[答案] 4cm[解析] ∵∠BAD ＝90°，AE ⊥BD ，∴△ABE ∽△DBA ， ∴S △ABE :S △DBA ＝AB 2:DB 2.∵S △ABE :S △DBA ＝1:5，∴AB 2:DB 2＝1:5， ∴AB :DB ＝1: 5.设AB ＝k ，则DB ＝5k ，AD ＝2k ，∵S 矩形＝40cm 2，∴k ·2k ＝40，∴k ＝25， ∴BD ＝5k ＝10，AD ＝45，S △A BD ＝12BD ·AE ＝20，∴12×10×AE ＝20，∴AE ＝4cm. 3．(2011·北京朝阳区统考)如图，AB 是⊙O 的直径，CB 切⊙O 于点B ，CD 切⊙O 于点D ，直线CD 交AB 于点E .若AB ＝3，ED ＝2，则CB 的长为________．[答案] 3[解析] 由切割线定理得，ED 2＝EA ·EB ， ∴4＝EA (EA ＋3)，∴EA ＝1，∵CB 是⊙O 的切线，∴EB ⊥CB ， ∴EB 2＋CB 2＝CE 2，又∵CD是⊙O的切线，∴CD＝CB，∴42＋CB2＝(CB＋2)2，∴CB＝3.4.(2011·北京西域区期末)如图所示，过圆C外一点P做一条直线与圆C交于A，B两点，AB＝2AP，PT与圆C相切于T点．已知圆C的半径为2，∠CAB＝30°，则PT＝________.[答案] 3[解析]∵AC＝2，∠CAB＝30°，∴AB＝2AC cos30°＝2×2×32＝23，∴AP＝12AB＝3，∴PB＝AP＋AB＝33，∵PT是⊙C的切线，∴PT2＝AP·PB＝9，∴PT＝3.5．(2011·广东理，15)如下图，过圆O外作一点P分别作圆的切线和割线交圆于A，B，且PB＝7，C是圆上一点使得BC＝5，∠BAC＝∠APB，则AB＝________.[答案]35[解析]由圆的切线性质可知∠PAB＝∠ACB，又∠APB＝∠BAC，所以△PAB∽△ACB，所以ABBC＝PBAB，而BC＝5，PB＝7，∴AB5＝7AB，∴AB2＝35，AB＝35.6．(2011·湖南理，11)如下图，A，E是半圆周上的两个三等分点，直径BC＝4，AD⊥BC，垂足为D，BE与AD相交于点F，则AF的长为________．[答案]23 3[解析]如图，连结CE，OA，AB，∵A、E是半圆周上的两个三等分点，BC为直径，∴∠CEB＝90°，∠CBE＝30°，∠AOB＝60°，又OA＝2，∴AD＝3，OD＝BD＝1，∴DF＝33，∴AF＝AD－DF＝233.7．(2011·天津文，13)如图，已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF＝CF＝2，AF:FB:BE＝4:2:1.若CE与圆相切，则线段CE的长为________．[答案]72[解析] 由题意：⎩⎪⎨⎪⎧AF ·FB ＝DF ·FC ＝2AFFB＝2∴A F ＝2，FB ＝1，∴BE ＝12，AE ＝AF ＋BF ＋BE ＝72.由切割线定理得：CE 2＝BE ·AE ＝12×72＝74.∴CE ＝72. 8．(2011·辽宁文，22)如图，A 、B 、C 、D 四点在同一圆上，AD 的延长线与BC 的延长线交于E 点，且EC ＝ED .(1)证明：CD ∥AB;(2)延长CD 到F ，延长DC 到G ，使得EF ＝EG ，证明：A 、B 、G 、F 四点共圆．[解析](1)因为EC＝ED，所以∠EDC＝∠ECD.因为A，B，C，D四点在同一圆上，所以∠EDC＝∠EBA.故∠ECD＝∠EBA.所以CD∥AB.(2)由(1)知，AE＝BE，因为EF＝EG，故∠EFD＝∠EGC，从而∠FED＝∠GEC.连接AF，BG，则△EFA≌△EGB，故∠FAE＝∠GBE.又CD∥AB，∠EDC＝∠ECD，所以∠FAB＝∠GBA.所以∠AFG＋∠GBA＝180°.故A、B、G、F四点共圆．9．(2011·新课标全国文，22)如图，D，E分别为△ABC的边AB，AC上的点，且不与△ABC的顶点重合，已知AE的长为m，AC的长为n，AD，AB的长是关于x的方程x2－14x＋mn ＝0的两个根．(1)证明：C，B，D，E四点共圆；(2)若∠A＝90°，且m＝4，n＝6，求C，B，D，E所在圆的半径．[解析](1)连结DE，根据题意在△ADE和△ACB中，AD×AB＝mn＝AE×AC，即ADAC＝AEAB.又∠DAE＝∠CAB，从而△ADE∽△ACB.因此∠ADE＝∠ACB.所以C，B，D，E四点共圆。
高中数学几何证明选讲过关模拟卷(十二)含答案
D CA E B高中数学几何证明选讲过关模拟卷（十二）高中数学题号 一 二 三 总分 得分一、选择题（本大题共10小题，每小题4分，共40分）1.半径分别为1和2的两圆外切,作半径为3的圆与这两圆均相切,一共可作( )个.A.2B.3C.4D.5 2.直线02=--y x 被圆4)(22=+-y a x 截得的弦长为22，则实数a 的值为A .1-或3B .1或3C .2-或6D .0或43.对于a ∈R，直线(a －1)x －y ＋a ＋1＝0恒过定点C ，则以C 为圆心，以5为半径的圆的方程为( )A ．x 2＋y 2－2x ＋4y ＝0B ．x 2＋y 2＋2x ＋4y ＝0C ．x 2＋y 2＋2x －4y ＝0D ．x 2＋y 2－2x －4y ＝0 4.已知直线:210l x y k +++=被圆22:4C x y +=所截得的弦长为4，则k 是（ ）A ．－1B ．－2C ． 0D ．25.（2012年高考（四川理））如图,正方形ABCD 的边长为1,延长BA 至E ,使1AE =,连接EC 、ED 则sin CED ∠=（ ）A ．31010 B ．1010C ．510D ．5156.若三角形三边上的高为a b c 、、，这三边长分别为6、4、3，则::a b c =（ ）A. 1:2:3B. 6:4:3C. 2:3:4D. 3:4:6 7.在⊙O 中,弦 1.8AB cm =,圆周角30ACB ∠=,则⊙O 的直径等于( )Ａ.3.2cm Ｂ.3.4cm Ｃ.3.6cm Ｄ.4.0cm8.圆222650x y x y a +-++=关于直线2y x b =+成轴对称图形，则b a -的取值范围是（ ）A ．(,4)-∞B ．()-∞，0C ．(4,)-+∞D ．(4,)+∞9.如右图，以半圆的一条弦AN 为对称轴将折叠过来和直径MN 交于点B ，如果MB ：BN=2：3，且MN=10，则弦AN 的长为（ ）A ．B ．C ．D ．10.如图，点P 为⊙O 的弦AB 上一点，且AP ＝16，BP ＝4，连接OP ，作PC ⊥OP 交圆于C ，则PC 的长为( )A ．9B ．8C ．6D ．4二、填空题（本大题共10小题，每小题2分，共20分） 11.（08年山东十模） 如图，，于，是的中点，交于于，。
高中数学几何证明选讲过关模拟卷(十九)含答案
高中数学几何证明选讲过关模拟卷（十九）高中数学题号 一 二 三 总分 得分一、选择题（本大题共10小题，每小题4分，共40分） 1.如图，已知AD//BE//CF ，下列比例式成立的是A ．BE AD DEAB = B.DF EF AC BC = C.EF DF AB AC = D.BC DEEF AB =2.两个圆C 1：x 2＋y 2＋2x ＋2y －2＝0，C 2：x 2＋y 2－4x －2y ＋1＝0的公切线条数（ )A ．4条B ．1条C ．2条D ．3条3.半径分别为1和2的两圆外切,作半径为3的圆与这两圆均相切,一共可作( )个.A.2B.3C.4D.54.已知直线)0)(2(>+=k x k y 与抛物线x y C 8:2=相交于A ，B 两点，F 为C 的焦点，若|FA|=2|FB|，则实数k 的值为（ ）A ．31B ．32C ．32D ．3225.如图：线段AF 中，e EF d DE c CD b BC a AB =====,,,,.则以A,B,C,D,E,F 为端点的所有线段长度的和为:A ．e d c b a 58985++++B ．e d c b a 581085++++C ．e d c b a 59995++++D ．e d c b a 1016181610++++ 6.()220,210m x y m x y m >+++=+=设则直线与圆的位置关系为（ ）A ．相切B ．相交C ．相切或相离D ．相交或相切7.圆内接三角形ABC 角平分线CE 延长后交外接圆于F ，若2,FB =1EF =，则CE =（ ）A. 3B. 2C. 4D. 18.一个圆的两弦相交,一条弦被分为12cm 和18cm 两段,另一弦被分为3:8,则另一弦的长为( )A.11cmB.33cmC.66cmD.99cm9.如图，CD 是⊙O 的直径，AE 切⊙O 于点B ，连接DB ，若20D ∠=︒，则DBE ∠的大小为A. 20︒B. 40︒C. 60︒D. 70︒10.过直线y x =上的一点作圆22(5)(1)2x y -+-=的两条切线12,l l ，当直线12,l l 关于y x =对称时,它们之间的夹角为( )A ．30°B ．45°C ．60°D ．90°二、填空题（本大题共10小题，每小题2分，共20分）11.选做题（请考生在以下三个小题中任选一题做答，如果多做，则按所做的第一题评阅记分）（1）．（选修4—4坐标系与参数方程）已知直线的极坐标方程为242sin()πρθ+=，则极点到该直线的距离是 .（2）．（选修4—5 不等式选讲）已知lg lg 0a b +=，则满足不等式2211a b a b λ+++≤的实数λ的范围是 .⊙'O 外切，过（3）．(选修4—1 几何证明选讲）如图，两个等圆⊙O 与O 作⊙'O 的两条切线,,OA OB ,A B 是切点，点C 在圆'O 上且不与点,A B 重合，则ACB ∠= .12.（选修4-1：几何证明选讲）如图，点D 在O 的弦AB 上移动，4AB =，连接OD ，过点D 作OD 的垂线交O 于点C ，则CD 的最大值为 .13.（几何证明选讲）如图，已知EB 是半圆O 的直径，A 是BE 延长线上一点，AC 是半圆O 的切线，BC ⊥ACCB AD O.第15题图姓名：__________班级：__________考号：__________ ●-------------------------密--------------封--------------线--------------内--------------请--------------不--------------要--------------答--------------题-------------------------●于C ，若BC =6，AC =8，则AE = ．14.若E 、F 、G 、H 顺次为空间四边形ABCD 四条边AB 、BC 、CD 、DA 的中点，且EG=3，FH=4，则AC 2+BD 2=_____ .15..已知圆04222=+-++a y x y x 关于直线b x y +=2成轴对称，则b a -的取值范围是________.16.圆内接四边形ABCD 中，cos cos cos cos A B C D +++= .17.如图，已知AB 和AC 是圆的两条弦，过点B 作圆的切线与AC 的延长线相交于点D. 过点C 作BD 的平行线与圆相交于点E ，与AB 相交于点F ，AF=3，FB=1，EF=23，则线段CD 的长为____________. F CDBA18.已知，如图，在梯形ABCD 中，AD//BC ，AD=3，BC=7，点M ，N 分别是对角线BD ，AC 的中点，则MN 等于19.曲线()142≤--=x x y 的长度是 .20.直线30x y a +-=与圆3cos ,(1sin ,x y θθθ⎧=+⎪⎨=+⎪⎩为参数)没有公共点,则a 的取值范围是 ．三、解答题（本大题共4小题，共40分）21.如图，⊙O 和⊙/O 相交于,A B 两点，过A 作两圆的切线分别交两圆于C ，D 两点，连接DB 并延长交⊙O于点E 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高中数学几何证明选讲过关模拟卷（十三）高中数学题号 一 二 三 总分 得分一、选择题（本大题共10小题，每小题4分，共40分） o 20D ∠=，则1.如图，CD 是O 的直径，AE 切O 于点B ，连接DB 。
若DBE ∠的大小为A ．20°B ．40°C ．60°D ．70°2.如图,AB 是半圆O 的直径,点C 在半圆上,CD AB ⊥于点D ,且DB AD 3=,设COD θ∠=,则2tan 2θ＝( )A ．13B ．14C ．423-D ．33.已知圆C 与圆(x －1)2＋y 2＝1关于直线y ＝－x 对称，则圆C 的方程为（ ）A ．(x ＋1)2＋y 2＝1B ．x 2＋y 2＝1C ．x 2＋(y ＋1)2＝1D ．x 2＋(y －1)2＝14.已知直线kx y =与圆⎩⎨⎧=+=t y t x sin 2cos 24（t 为参数）相切，则直线的倾斜角为A 6πB 3πC 323ππ或 D656ππ或5.如图，AB 是圆O 的直径，C 、D 是圆上的点，20=∠BAC ，弧和弧的长相等，DE 是圆O 的切线，则=∠EDCA ．70 B ．40 C ．20 D ．356.如图4所示,圆O 的直径AB=6,C 为圆周上一点,BC=3过C 作圆的切线l,过A 作l 的垂线AD,垂足为D,则∠DAC =A.15︒B.30︒C.45︒D.60︒7.在Rt ABC ∆中,CD 、CE 分别是斜边AB 上的高和中线,则该图中共有x 个三角形与ABC ∆相似,则x =( )A.0B.1C.2D.3 8.正方形ABCD 的边长为1，点E 在边AB 上，点F 在边BC 上，13AE BF ==。
动点P 从E 出发沿直线向F 运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角，当点P 第一次碰到E 时，P 与正方形的边碰撞的次数为（A ）8 （B ）6 （C ）4 （D ）39.若圆C 的半径为1，圆心在第一象限，且与直线430x y x -=和轴都相切，则该圆的标准方程是（ ） A ．327(3)()13x y -+== B ．22(2)(1)1x y -+-= C ．22(1)(3)1x y -+-= D ．223()(1)12x y -+-=10.如图，在正方形ABCD 中，E 为AB 中点，BF⊥CE 于F ，那么S △BFC :S 正方形ABCD =（ ）．姓名：__________班级：__________考号：__________ ●-------------------------密--------------封--------------线--------------内--------------请--------------不--------------要--------------答--------------题-------------------------●A ．1：3B ．1：4C ．1：5D ．1：6二、填空题（本大题共10小题，每小题2分，共20分）11.设,0,0>>b a 称ba ab+2为a 、b 的调和平均数，如图，C 为线段AB 上的点，且AC=a ，CB=b ，O 为AB 的中点，以AB 为直径作半圆，过点C 作AB 的垂线交半圆于D ，连结OD ，AD ，BD ，过点C 做OD 的垂线，垂足为E ，则图中线段OD 的长度是a ，b 的算术平均数，线段 的长度是a ，b 的几何平均数，线段的长度是a ，b 的调和平均数.12.如图，已知⊙O 的割线PAB 交⊙O 于A ，B 两点，割线PCD 经过圆心，若PA=3，AB=4，PO=5，则⊙O 的半径为______________．13.（几何证明选讲选做题）如图2所示AB 与CD 是O 的直径，AB ⊥CD ，P 是AB 延长线上一点，连PC 交O 于点E ，连DE 交AB 于点F ，若42==BP AB ，则=PF ．14.（2012年高考（广东理））(几何证明选讲)如图3,圆O 的半径为1,A 、B 、C 是圆周上的三点,满足30ABC ∠=︒,过点A 作圆O 的切线与OC 的延长线交于点P ,则PA =__________.15.如图所示，圆的直径，为圆周上一点，，过作圆的切线，过作的垂线，垂足为，则．16.选做题（请考生在以下三个小题中任选一题做答，如果多做，则按所做的第一题评阅记分）（1）．（选修4—4坐标系与参数方程）已知直线的极坐标方程为242sin()πρθ+=，则极点到该直线的距离是 .（2）．（选修4—5 不等式选讲）已知lg lg 0a b +=，则满足不等式2211aba b λ+++≤的实数λ的范围是 .⊙'O 外切，过（3）．(选修4—1 几何证明选讲）如图，两个等圆⊙O 与O 作⊙'O 的两条切线,,OA OB ,A B 是切点，点C 在圆'O 上且不与点,A B 重合，则ACB ∠= .17. (几何证明选讲选做题）如图5,⊙O 的直径cm AD 2=，四边形ABCD 内接于⊙O ，直线MN 切⊙O 于点B ，030=∠MBA ，则AB 的长是 .cm18. (几何证明选讲选做题)如图，BD 为⊙O 的直径，AB AC =，AD 交BC 于E ，2AE =，4ED =．则AB 的长为 ．19.如图，已知10与20相交于A ，B 两点，直线PQ 切10于P ，与20交于N 、Q 两点，直线AB 交PQ于M ，若MN=2，PQ=12，则PM=________________。
ADCO图5AD PC OEBF 图220.如图，在直角梯形ABCD 中，DC ∥AB,CB AB ⊥,AB=AD=a,CD=2a,点E,F 分别为线段AB,AD 的中点，则EF=三、解答题（本大题共4小题，共40分）21.已知AB 为半圆O 的直径，4AB =，C 为半圆上一点，过点C 作半圆的切线CD ，过A 点作AD CD⊥于D ，交半圆于点E ，1DE =．（1）证明：AC 平分BAD ∠；（2）求BC 的长．22.已知：如图正方形ABCD 的边长为a ，P ，Q 分别为AB ，DA 上的点，当△PAQ的周长为2a 时，求∠PCQ 。
23.已知直线:l 415315x t y t⎧=+⎪⎪⎨⎪=--⎪⎩（为参数t ）与曲线C 的极坐标方程:2cos()4πρθ=+。
（1）求直线l 与曲线C 的直角坐标方程（极点与坐标原点重合，极轴与x 轴重合） （2）求直线l 被曲线C 截得的弦长。
24.（本小题满分10分）如图，、是圆的两条平行弦，∥，交于交圆于，过点的切线交的延长线于，，.（1）求的长；（2）求证：.QCBAD高中数学几何证明选讲过关模拟卷（十三）答案解析一、选择题1.D2.A【解析】略3.C【解析】略4.D【解析】略5.D【解析】略6.B【解析】略7.B【解析】结合已知中的点E,F的位置，进行作图，推理可知，在反射的过程中，直线是平行的，那么利用平行关系，作图，可以得到回到EA点时，需要碰撞6次即可.8.B【解析】略9.C【解析】略二、填空题10.【答案】CD DE【解析】在Rt△ADB中DC为高，则由射影定理可得2CD AC CB=⋅，故CD ab=，即CD长度为a,b的几何平均数，将OC=, ,222a b a b a ba CD ab OD+-+-==代入OD CE OC CD⋅=⋅可得a bCE aba b-+故222()2()a bOE OC CEa b-=-=+，所以ED=OD-OE=2aba b+，故DE的长度为a,b的调和平均数．11.2【解析】试题分析：由于PAB与PCD是圆的两条割线，且PA=3，AB=4，PO=5，我们可以设圆的半径为R，然后根据切割线定理构造一个关于R的方程，解方程即可求解解：设⊙O的半径为R，则PC=PO-OC=5-R，PD=PO+OD=5+R，又∵PA=3，AB=4，，∴PB=PA+AB=7，由切割线定理易得：，PA?PB=PC?PD，即3×7=（5-R）×（5+R），解得R=2，故答案：2考点：圆相关的比例线段点评：本题考查的知识点是与圆相关的比例线段，设出未知的线段根据圆幂定理列出满足条件的方程是解答的关键12.3【解析】略13.解析3连接OA,则60AOC∠=︒,90OAP∠=︒,因为1OA=,所以3PA=14.30º【解析】试题分析：根据所给的圆的直径和BC的长，得到三角形的一个锐角是30°，根据同弧所对的圆周角等于弦切角，得到另一个直角三角形的角的度数，即为所求。
∵圆O的直径AB=6，C为圆周上一点，BC=3∴∠BAC=30°，∠B=60°，∵过C作圆的切线l，∠B=∠ACD=60°，∵过A作l的垂线AD，垂足为D∴∠DAC=30°，故填写30º。
考点：几何证明点评：题解题的关键是同弧所对的圆周角和弦切角相等和含有30°角的直角三角形的应用，本题是一个基础题．15. (选做题2； (2) [)1,+∞； (3) 60或12016.1【解析】略17.32【解析】 18.419.2a 【解析】解：连结DE ，可知AED ∆为直角三角形。
则EF 是DEA Rt ∆斜边上的中线，等于斜边的一半，为2a .三、解答题20.（1）参考解析；（2）2【解析】试题分析：（1）需证明AC 平分∠BAD ，通过连接OC,EC.由题意可得直线AD ∥OC.从而可得角DAC 等于角ACO.又由于三角形AOC 是等腰三角形.即可得到结论.（2）由（1）的结论∠DAC=∠CAB.以及再根据弦切角与所夹的弧对的圆周角相等即可得到三角形DEC 相似三角形CBA.（1）连接OC ，因为OA OC =， 所以 OAC OCA ∠=∠．CD 为半圆的切线，∴CD OC ⊥． ∵CD AD ⊥，//OC AD ∴．OCA CAD OAC CAD ∴∠=∠∴∠=∠，． AC ∴平分BAD ∠． 5分（2）连接CE ，由（1）得CAD OAC ∠=∠，∴CE BC =． ∵A B C E 、、、四点共圆．∴ABC CED ∠=∠．∵AB 是圆O 的直径，∴ACB ∠是直角．∴CDE Rt ∆∽ACB Rt ∆， DE CB CE AB ∴=．∴41BCBC =2BC ∴=． 10分 考点：1.弦切角与圆周角.2.圆的切线.3.等腰三角形.21.解：设PB =ma ，DQ =na ,则AP ＝(1)m a -，AQ ＝(1)n a -则PQ=22222()2AP AQ a m n m n +=+-++…………………………………(3分)由题意AP ＋AQ ＋PQ ＝2a ＝(1)m a -＋(1)n a -＋222()2a m n m n +-++化简得 1m n mn ++=，……………………………………………………… (6分)tan ,tan DCQ n PCB m ∠=∠=………………………………………………… (8分)所以1cot tan()111m n mn PCQ PCQ BCP mn mn +-∠=∠+∠===--，………………… (11分)又PCQ ∠为锐角，所以PCQ ∠=4π。