高中数学几何证明题

合集下载

高中数学几何证明题

高中数学几何证明题高中数学几何证明题一、如图，AB∩α=P，CD∩α=P，点A，D与点B，C分别在平面α的两侧，且AC∩α=Q，BD∩α=R，求证：P，Q,R三点在同一条直线上∵AB∩α=PCD∩α=P∴AB∩CD=P即AB与CD在同一个面β上(假设为该平面为β)由此得:β与α相交即有一条交线而A、B、C、D四点均属于平面α∴AC属于平面α，DB属于平面α而AC∩α=Q，BD∩α=R则有Q、R均属于平面β，同时Q、R又是平面α上的两点由上述得：P、Q、R共线二、如图，四棱锥P-ABCD的底面ABCD是矩形，点E，F分别是AB，PC的中点，求证：EF‖平面PAD找DC中点G 连接EG FG那么因为底面是个矩形所以EG平行等于ADF点和G点的连线就是三角形的中位线所以FG平行DP在因为DP属于平面PAD DA也属于平面PAD且DP交DA于D在因为EG属于平面EFG FG也属于平面EFG所以平面EFG平行于平面PAD又因为EF属于平面EFG 所以EF平行于PAD三、怎样才能一步步学会证明几何题呢??我实在是不懂啊!!证明几何题的步骤是怎样呢>?有什么方法吗?其实证明几何题关键是要把一些定理公式的用法搞清楚。

学数学最重要的是多做题，其实数学题就是反复的那几中类型的，做的题多了，就自然的会了，还要注意多总结，做好数学笔记，告诉你数学笔记是很重要的。

然后就是要有耐心，可能一开始你感觉没有效果，但是漫漫效果会出来的，相信自己一定可以的。

我是以我的高考经验来说的，我得数学以前一直是我的弱项，但我最后高考得了131，虽然不是很高，但是对我来说很不错的了。

希望你高考可以取得好的成绩。

在正方形ABCD-A'B'C'D'中，证明：平面ACC'A'⊥平面A'BD各位帮忙写下这题的证明过程啊因为CC'垂直于面ABCD所以CC'垂直于AC又AC垂直于BDAC交CC'于C所以DB垂直于面AA'C'C即两面垂直四、AB为圆O所在平面为a，PA⊥a于A，C为圆O上一点，求证：平面PAC⊥平面PBCAB是圆O的直径吧解:圆O所在平面是a,AB是圆O的直径,PA⊥a于A,C为圆O上一点所以PA⊥BC AC⊥BC PA与AC交于点A所以BC⊥平面PAC BC属于平面PBC所以平面PAC⊥平面PBC。

高中数学立体几何10道大题

高中数学立体几何10道大题1.在四棱锥S-ABCD中，底面ABCD为平行四边形，侧面SBC垂直于面ABCD，已知∠ABC=45°，AB=2，BC=22，SB=SC=3.1) 证明平面SCD与平面SAB的交线l平行于AB；2) 证明SA垂直于BC；3) 求直线SD与面SAB所成角的正弦值。

2.在四棱锥P-ABCD中，底面ABCD是平行四边形，P为其顶点，O为其中心，PO平行于AB且PO=2，M为PD的中点，AD=AC=1，O为AC的中点。

1) 证明PB平行于平面ACM；2) 证明AD在平面PAC上；3) 求直线AM与平面ABCD所成角的正切值。

3.在四棱锥P-ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB与△PAD均为等边三角形。

1) 证明CD垂直于平面PBD；2) 求二面角CPBD的平面角的余弦值。

4.在四棱锥P-ABCD中，PA垂直于底面ABCD，AC垂直于AD，ABCD为梯形，AB平行于DC，AB垂直于BC，PA=AB=BC=3，点E在棱PB上，且PE=2EB。

Ⅰ) 证明平面PAB垂直于平面PCB；Ⅱ) 证明PD平行于平面EAC；Ⅲ) 求平面AEC和平面PBC所成锐二面角的余弦值。

5.在图中，矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直线AB，平面ABCD与平面ABPE的交线为AB，且AB=BP=2，AD=AE=1，AE垂直于AB，且AE平行于BP。

1) 在面ABCD内是否存在点N，使得MN垂直于平面ABCD？若存在，请证明；若不存在，请说明理由；2) 求二面角D-PE-A的余弦值。

6.在直三棱柱ABC-A1B1C1中，平面A1BC垂直于侧面A1BB1，且AA1=AB=2.1) 证明AB垂直于BC；2) 若直线AC与平面A1BC所成角为α，求锐二面角AAC1B的大小。

7.在四棱锥V-ABCD中，底面ABCD为正方形，侧面VAD 为正三角形，平面VAD垂直于底面ABCD。

高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)

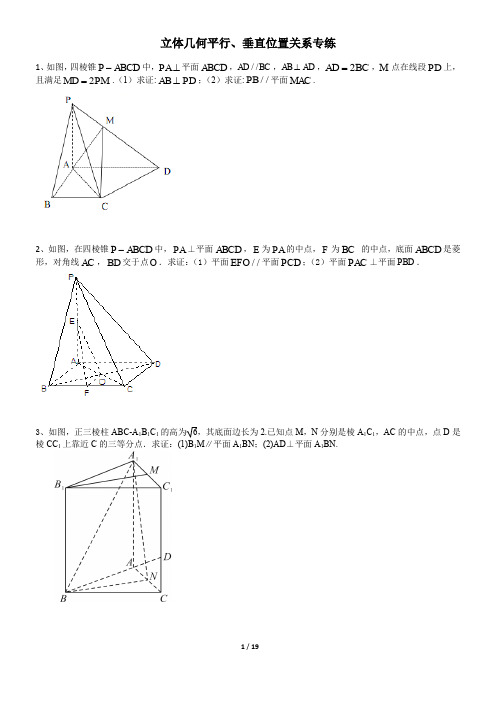
立体几何平行、垂直位置关系专练1、如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .2、如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ．3、如图，正三棱柱ABC-A 1B 1C 1的高为6，其底面边长为2.已知点M ，N 分别是棱A 1C 1，AC 的中点，点D 是棱CC 1上靠近C 的三等分点．求证：(1)B 1M ∥平面A 1BN ；(2)AD ⊥平面A 1BN.4、如图，等边三角形ABC与直角梯形ABDE所在平面垂直，BD∥AE，BD＝2AE，AE⊥AB，M为AB的中点．(1)证明：CM⊥DE；(2)在边AC上找一点N，使CD∥平面BEN.5、如图，矩形ABCD所在平面与三角形ABE所在平面互相垂直，AE＝AB，M，N，H分别为DE，AB，BE 的中点．求证：(1)MN∥平面BEC；(2)AH⊥CE.6、如图，在三棱台ABCDEF中，CF⊥平面DEF，AB⊥BC.(1)设平面ACE∩平面DEF＝a，求证：DF∥a；(2)若EF＝CF＝2BC，试问在线段BE上是否存在点G，使得平面DFG⊥平面CDE？若存在请确定点G的位置；若不存在，请说明理由．7、在三棱锥S ABC -中，平面SAB ⊥平面SBC ，AB BC ⊥，AS AB =，过A 作AF SB ⊥，垂足为F ，点E ，G 分别是棱SA ，SC 的中点．（1）求证：平面EFG ∥平面ABC ．（2）求证：BC SA ⊥．8、如图，在直三棱柱111ABC A B C -中，AB BC ⊥，点D 为棱1C C 的中点，1AC 与1A D 交于点E ，1BC 与1B D 交于点F ，连结EF .求证：（1）//AB EF ；（2）平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A 1B 1∥平面DEC 1；（2）BE ⊥C 1E ．点，平面PAB ⊥底面ABCD ，90PAB ∠= ．求证：（1）//PB 平面AEC ；（2）平面PAC ⊥平面ABCD ．11、2.（2020·江苏省镇江高三二模）如图，三棱锥P ABC -中，点D ，E 分别为AB ，BC 的中点，且平面PDE ⊥平面ABC ．()1求证：//AC 平面PDE ；()2若2PD AC ==，PE =PBC ⊥平面ABC .12、（2020·江苏省建湖高级中学高三月考）如图，在四面体ABCD 中，,90AD BD ABC =∠= ，点,E F 分别为棱,AB AC 上的点，点G 为棱AD 的中点，且平面//EFG 平面BCD ．（1）求证：12EF BC =；（2）求证：平面EFD ⊥平面ABC ．点，PA ⊥平面ABCD .（1）求证：//PB 平面AEC ；（2）若四边形ABCD 是矩形且PA AD =，求证：AE ⊥平面PCD .14、（2020·江苏省高三二模）如图，在三棱柱111ABC A B C -中，侧面11ABB A ⊥底面ABC ，AB AC ⊥，E ，F 分别是棱AB ，BC 的中点.求证：（1）11AC ∥平面1B EF ；（2）1AC B E ⊥.15、（2020·江苏省连云港高三）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =，E 、F 分别为AD 、PB 的中点.（Ⅰ）求证：PE BC ⊥；（Ⅱ）求证：平面PAB ⊥平面PCD ；（Ⅲ）求证：//EF 平面PCD .16、（2020·江苏省苏州高三）如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A1B 1∥平面DEC 1；（2）BE ⊥C 1E ．17、（2020·江苏省通州高三）如图，在三棱柱111ABC A B C -中，侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点．（1）求证: 平面ABE ⊥平面11B BCC ；（2）求证:1C F ∥平面ABE ；18、（2020·江苏省高三三模）如图，三棱柱111ABC A B C -中，1BC B C =，O 为四边形11ACC A 对角线交点，F 为棱1BB 的中点，且AF ⊥平面11BCC B .（1）证明：//OF 平面ABC ；（2）证明：四边形11ACC A 为矩形.参考答案1．如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .【解析】（1）∵四棱锥P ABCD -中，PA ⊥平面ABCD ，AB 平面ABCD ， ∴AB PA ⊥，又AB AD ⊥，,PA AD ⊂平面PAD ，PA AD A ⋂=， ∴AB ⊥面PAD .PD ⊂面PAD ，∴AB PD ⊥. （2）连结BD AC O ⋂=，连结MO ， ∵//AD BC ，2AD BC =，2DO BO ∴=,∵在PBD ∆中，2DM MP =，2DO BO =∴//PB MO ，又PB ⊄面MAC ，MO ⊂面MAC ，∴//PB 面MAC .2．如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ．【详解】（1）因为在ΔPAC 中，E 为PA 的中点，O 为AC 的中点，所以//EO PC又EO ⊄平面PCD ，PC ⊂平面PCD ，所以//EO 平面PCD同理可证，//FO 平面PCD ，又EO FO O = ，EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD ．（2）因为PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以PA BD ⊥因为底面ABCD 是菱形，所以AC BD ⊥，又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。

高中数学立体几何证明题汇总

高中数学立体几何证明题汇总立体几何常考证明题1.已知四边形ABCD是空间四边形，E,F,G,H分别是边AB,BC,CD,DA的中点。

1）证明EFGH是平行四边形。

2）已知BD=23，AC=2，EG=2，求异面直线AC、BD所成的角和EG、BD所成的角。

2.如图，已知空间四边形ABCD中，BC=AC,AD=BD，E 是AB的中点。

1）证明AB垂直于平面CDE。

2）证明平面CDE垂直于平面ABC。

3.如图，在正方体ABCD-A1B1C1D1中，E是AA1的中点。

证明A1C平行于平面BDE。

4.已知三角形ABC中∠ACB=90，SA垂直于面ABC，AD垂直于SC。

证明AD垂直于面SBC。

5.已知正方体ABCD-A1B1C1D1，O是底面ABCD对角线的交点。

1）证明C1O平行于面AB1D1.2）证明AC1垂直于面AB1D1.6.正方体ABCD-A1B1C1D1中。

1）证明AC垂直于平面B1D1D。

2）证明BD1垂直于平面ACB1.7.正方体ABCD-A1B1C1D1中。

1）证明平面A1BD平行于平面B1DC。

2）已知E、F分别是AA1、CC1的中点，证明平面EB1D1平行于平面FBD。

8.四面体ABCD中，AC=BD，E、F分别为AD、BC的中点，且EF=AC/2，∠XXX。

证明BD垂直于平面ACD。

9.如图P是△ABC所在平面外一点，PA=PB，CB垂直于平面PAB，M是PC的中点，N是AB上的点，AN=3NB。

1）证明XXX垂直于AB。

2）当∠APB=90，AB=2BC=4时，求MN的长度。

10.如图，在正方体ABCD-A1B1C1D1中，E、F、G分别是AB、AD、C1D1的中点。

证明平面D1EF平行于平面BDG。

11.如图，在正方体ABCD-A1B1C1D1中，E是AA1的中点。

1）证明A1C平行于平面BDE。

2）证明平面A1AC垂直于平面BDE。

12、已知矩形ABCD，PA垂直于平面ABCD，AB=2，PA=AD=4，E为BC的中点。

高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)

高中立体几何典型50题及解析

高中立体几何典型500题及解析(一)1、二面角βα--l 是直二面角，βα∈∈B A ，，设直线AB 与βα、所成的角分别为∠1和∠2，则（A ）∠1+∠2=900 （B ）∠1+∠2≥900 （C ）∠1+∠2≤900 （D ）∠1+∠2＜900 解析：C分别作两条与二面角的交线垂直的线，则∠1和∠2分别为直线AB 与平面,αβ所成的角。

根据最小角定理：斜线和平面所成的角，是这条斜线和平面内经过斜足的直线所成的一切角中最小的角2ABO ∴∠>∠1902190ABO ∠+∠=∴∠+∠≤2. 下列各图是正方体或正四面体，P ，Q ，R ，S 分别是所在棱的中点，这四个点中不共．．面．的一个图是PPQQRSSPPPQQRR RSSSPP PQQQ R RS SS PP Q QR RRSS（A ）（B ）（C ）（D ） D解析： A 项：PS 底面对应的中线，中线平行QS ，PQRS 是个梯形B 项：如图C 项：是个平行四边形D 项：是异面直线。

3. 有三个平面α，β，γ，下列命题中正确的是（A ）若α，β，γ两两相交，则有三条交线（B ）若α⊥β，α⊥γ，则β∥γ（C ）若α⊥γ，β∩α=a ，β∩γ=b ，则a ⊥b （D ）若α∥β，β∩γ=∅，则α∩γ=∅ D解析：A 项：如正方体的一个角，三个平面相交，只有一条交线。

B 项：如正方体的一个角，三个平面互相垂直，却两两相交。

C 项：如图4. 如图所示，在正方体ABCD －A 1B 1C 1D 1的侧面AB 1内有一动点P到直线AB 与直线B 1C 1的距离相等，则动点P 所在曲线的形状为1111C解析：11B C ⊥平面AB 111,B C PB ∴⊥，如图：点到定点B 的距离与到定直线AB 的距离相等，建立坐标系画图时可以以点B 1B 的中点为原点建立坐标系。

5. 在正方体ABCD －A 1B 1C 1D 1中与AD 1成600角的面对角线的条数是（A ）4条（B ）6条（C ）8条（D ）10条C解析：如图这样的直线有4条，另外，这样的直线也有4条，共8条。

(完整版)高中数学立体几何经典常考题型

高中数学立体几何经典常考题型题型一:空间点、线、面的位置关系及空间角的计算空间点、线、面的位置关系通常考查平行、垂直关系的证明，一般出现在解答题的第(1)问，解答题的第(2)问常考查求空间角，求空间角一般都可以建立空间直角坐标系，用空间向量的坐标运算求解.【例1】如图，在△ABC中，∠ABC＝，O为AB边上一点，且3OB＝3OC＝2AB，已知PO⊥平面ABC，2DA＝2AO＝PO，且DA∥PO.(1)求证：平面PBD⊥平面COD；(2)求直线PD与平面BDC所成角的正弦值.(1)证明　∵OB＝OC，又∵∠ABC＝，∴∠OCB＝，∴∠BOC＝.⊥∴CO AB.又PO⊥平面ABC，⊥OC⊂平面ABC，∴PO OC.又∵PO，AB⊂平面PAB，PO∩AB＝O，∴CO⊥平面PAB，即CO⊥平面PDB.又CO⊂平面COD，∴平面PDB⊥平面COD.(2)解　以OC，OB，OP所在射线分别为x，y，z轴，建立空间直角坐标系，如图所示.设OA＝1，则PO＝OB＝OC＝2，DA＝1.则C(2，0，0)，B(0，2，0)，P(0，0，2)，D(0，－1，1)，∴PD＝(0，－1，－1)，BC＝(2，－2，0)，BD＝(0，－3，1).设平面BDC的一个法向量为n＝(x，y，z)，∴∴令y＝1，则x＝1，z＝3，∴n＝(1，1，3).设PD与平面BDC所成的角为θ，则sin θ＝＝＝.即直线PD与平面BDC所成角的正弦值为.【类题通法】利用向量求空间角的步骤间标.第一步：建立空直角坐系第二步：确定点的坐标.线)坐标.第三步：求向量(直的方向向量、平面的法向量计夹(或函数值).第四步：算向量的角将夹转为间.第五步：向量角化所求的空角查关键错题规.第六步：反思回顾.看点、易点和答范【变式训练】如图所示，在多面体A1B1D1DCBA中，四边形AA1B1B，ADD1A1，ABCD均为正方形，E为B1D1的中点，过A1，D，E的平面交CD1于F.(1)证明：EF∥B1C.(2)求二面角EA1DB1的余弦值.(1)证明　由正方形的性质可知A1B1AB DC∥∥，且A1B1＝AB＝DC，所以四边形A1B1CD为平行四边形，从而B1C A∥1D，又A1D⊂面A1DE，B1C⊄面A1DE，于是B1C∥面A1DE.又B1C⊂面B1CD1，面A1DE∩面B1CD1＝EF，所以EF∥B1C.(2)解　因为四边形AA1B1B，ADD1A1，ABCD均为正方形，所以AA1⊥AB，AA1⊥AD，AB⊥AD且AA1＝AB＝AD.以A为原点，分别以AB，AD，AA1为x轴，y轴和z轴单位正向量建立如图所示的空间直角坐标系，可得点的坐标A(0，0，0)，B(1，0，0)，D(0，1，0)，A1(0，0，1)，B1(1，0，1)，D1(0，1，1)，而E点为B1D1的中点，所以E点的坐标为.设平面A1DE的一个法向量n1＝(r1，s1，t1)，而该面上向量A1E＝，A1D＝(0，1，－1)，由n1⊥A1E，n1⊥A1D得r1，s1，t1应满足的方程组(－1，1，1)为其一组解，所以可取n1＝(－1，1，1).设平面A1B1CD的一个法向量n2＝(r2，s2，t2)，而该面上向量A1B1＝(1，0，0)，A1D＝(0，1，－1)，由此同理可得n2＝(0，1，1).所以结合图形知二面角EA1DB1的余弦值为＝＝.题型二:立体几何中的探索性问题此类试题一般以解答题形式呈现，常涉及线、面平行、垂直位置关系的探究或空间角的计算问题，是高考命题的热点，一般有两种解决方式：(1)根据条件作出判断，再进一步论证；(2)利用空间向量，先假设存在点的坐标，再根据条件判断该点的坐标是否存在.【例2】如图，在四棱锥P－ABCD中，平面PAD⊥平面ABCD，PA⊥PD，PA＝PD，AB⊥AD，AB＝1，AD＝2，AC＝CD＝.(1)求证：PD⊥平面PAB；(2)求直线PB与平面PCD所成角的正弦值；(3)在棱PA上是否存在点M，使得BM∥平面PCD？若存在，求的值；若不存在，说明理由.(1)证明　因为平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，AB⊥AD，所以AB⊥平面PAD，所以AB⊥PD.又PA⊥PD，AB∩PA＝A，所以PD⊥平面PAB.(2)解　取AD的中点O，连接PO，CO.因为PA＝PD，所以PO⊥AD.因为PO⊂平面PAD，平面PAD⊥平面ABCD，所以PO⊥平面ABCD.因为CO⊂平面ABCD，所以PO⊥CO.因为AC＝CD，所以CO⊥AD.如图，建立空间直角坐标系O－xyz.由题意得，A(0，1，0)，B(1，1，0)，C(2，0，0)，D(0，－1，0)，P(0，0，1).设平面PCD的一个法向量为n＝(x，y，z)，则即令z＝2，则x＝1，y＝－2.所以n＝(1，－2，2).又PB＝(1，1，－1)，所以cos〈n，PB〉＝＝－.所以直线PB与平面PCD所成角的正弦值为.(3)解　设M是棱P A上一点，则存在λ∈0，1]，使得AM＝λAP.因此点M(0，1－λ，λ)，BM＝(－1，－λ，λ).因为BM⊄平面PCD，所以要使BM∥平面PCD，则BM·n＝0，即(－1，－λ，λ)·(1，－2，2)＝0，解得λ＝.所以在棱P A上存在点M，使得BM∥平面PCD，此时＝.应设，把要成立的作件结论当条，据此列方对断问题，先假存在【类题通法】(1)于存在判型的求解规围内”等.标，是否有定范的解程或方程组，把“是否存在”化问题转为“点的坐是否有解对问题，通常借助向量，引进参数，合已知和列出等式综结论，解出参数.(2)于位置探究型【变式训练】如图，在四棱锥P－ABCD中，PD⊥平面ABCD，AB∥DC，AB⊥AD，DC＝6，AD＝8，BC＝10，∠P AD＝45°，E为P A的中点.(1)求证：DE∥平面BPC；(2)线段AB上是否存在一点F，满足CF⊥DB？若存在，试求出二面角F－PC－D的余弦值；若不存在，请说明理由.(1)证明　取PB的中点M，连接EM和CM，过点C作CN⊥AB，垂足为点N.∵CN⊥AB，DA⊥AB，∴CN∥DA，又AB∥CD，∴四边形CDAN为平行四边形，∴CN＝AD＝8，DC＝AN＝6，在Rt△BNC中，BN＝＝＝6，∴AB＝12，而E，M分别为P A，PB的中点，∴EM∥AB且EM＝6，又DC∥AB，∥且EM＝CD，四边形CDEM为平行四边形，∴EM CD∥∵⊂平面PBC，DE⊄平面PBC，∴DE CM.CM∴DE∥平面BPC.(2)解　由题意可得DA，DC，DP两两互相垂直，如图，以D为原点，DA，DC，DP分别为x，y，z轴建立空间直角坐标系D－xyz，则A(8，0，0)，B(8，12，0)，C(0，6，0)，P(0，0，8).假设AB上存在一点F使CF⊥BD，设点F坐标为(8，t，0)，则CF＝(8，t－6，0)，DB＝(8，12，0)，由CF·DB＝0得t＝.又平面DPC的一个法向量为m＝(1，0，0)，设平面FPC的法向量为n＝(x，y，z).又PC＝(0，6，－8)，FC＝.由得即不妨令y＝12，有n＝(8，12，9).则cos〈n，m〉＝＝＝.又由图可知，该二面角为锐二面角，故二面角F－PC－D的余弦值为.题型三:立体几何中的折叠问题将平面图形沿其中一条或几条线段折起，使其成为空间图形，这类问题称为立体几何中的折叠问题，折叠问题常与空间中的平行、垂直以及空间角相结合命题，考查学生的空间想象力和分析问题的能力.【例3】如图，菱形ABCD的对角线AC与BD交于点O，AB＝5，AC＝6，点E，F分别在AD，CD 上，AE＝CF＝，EF交BD于点H.将△DEF沿EF折到△D′EF的位置，OD′＝.(1)证明：D′H⊥平面ABCD；(2)求二面角B－D′A－C的正弦值.(1)证明　由已知得AC ⊥BD ，AD ＝CD .又由AE ＝CF 得＝，故AC ∥EF .因此EF ⊥HD ，从而EF ⊥D ′H .由AB ＝5，AC ＝6得DO ＝BO ＝＝4.由EF ∥AC 得＝＝.所以OH ＝1，D ′H ＝DH ＝3.于是D ′H 2＋OH 2＝32＋12＝10＝D ′O 2，故D ′H ⊥OH .又D ′H ⊥EF ，而OH ∩EF ＝H ，所以D ′H ⊥平面ABCD .(2)解　如图，以H 为坐标原点，HF 的方向为x 轴正方向，建立空间直角坐标系H －xyz .则H (0，0，0)，A (－3，－1，0)，B (0，－5，0)，C (3，－1，0)，D ′(0，0，3)，AB ＝(3，－4，0)，AC ＝(6，0，0)，AD′＝(3，1，3).设m ＝(x 1，y 1，z 1)是平面ABD ′的一个法向量，则即所以可取m ＝(4，3，－5).设n ＝(x 2，y 2，z 2)是平面ACD ′的一个法向量，则即所以可取n ＝(0，－3，1).于是cos 〈m ，n 〉＝＝＝－.sin 〈m ，n 〉＝.因此二面角B －D ′A －C 的正弦值是.【类题通法】立体几何中的折叠问题，是翻折前后形中面位置系和度量系的化关键搞清图线关关变情况，一般地翻折后在同一平面上的性不生化还个质发变，不在同一平面上的性生化个质发变.【变式训练】如图1，在直角梯形ABCD 中，AD ∥BC ，∠BAD ＝，AB ＝BC ＝1，AD ＝2，E 是AD 的中点，O 是AC 与BE 的交点.将△ABE 沿BE 折起到△A 1BE 的位置，如图2.(1)证明：CD⊥平面A1OC；(2)若平面A1BE⊥平面BCDE，求平面A1BC与平面A1CD夹角的余弦值.(1)证明　在题图1中，因为AB＝BC＝1，AD＝2，E是AD的中点，∠BAD＝，所以BE⊥AC.即在题图2中，BE⊥OA1，BE⊥OC，从而BE⊥平面A1OC.又CD∥BE，所以CD⊥平面A1OC.(2)解　由已知，平面A1BE⊥平面BCDE，又由(1)知，BE⊥OA1，BE⊥OC，所以∠A1OC为二面角A1－BE－C的平面角，所以∠A1OC＝.如图，以O为原点，OB，OC，OA1分别为x轴、y轴、z轴正方向建立空间直角坐标系，因为A1B＝A1E＝BC＝ED＝1，BC∥ED，所以B，E，A1，C，得BC＝，A1C＝，CD＝BE＝(－，0，0).设平面A1BC的一个法向量n1＝(x1，y1，z1)，平面A1CD的一个法向量n2＝(x2，y2，z2)，平面A1BC与平面A1CD的夹角为θ，则得取n1＝(1，1，1)；得取n2＝(0，1，1)，从而cos θ＝|cos〈n1，n2〉|＝＝，即平面A1BC与平面A1CD夹角的余弦值为.。

高中数学几何证明题解题方法总结

高中数学几何证明题解题方法总结数学几何证明题是高中数学中的一大难点，需要学生具备较强的逻辑思维能力和几何直观的想象力。

在解决这类问题时，我们可以采用以下方法：一、直接法直接法是最常用的证明方法之一，它通过直接给出证明结论的过程，从而得出结论。

在使用直接法时，我们需要根据题目的要求，利用已知条件和几何定理，一步步推导出结论。

这种方法常用于证明一些基本的几何定理，如垂直定理、平行定理等。

例如，对于证明两条直线平行的问题，我们可以利用平行线的定义和垂直线的性质进行证明。

首先，我们可以假设两条直线不平行，然后根据垂直线的性质推导出矛盾，从而得出两条直线平行的结论。

二、间接法间接法是通过反证法来证明结论的方法。

它假设结论不成立，然后通过推理和推导，得出矛盾的结论，从而推翻假设，证明结论成立。

间接法常用于证明一些几何性质的逆命题或矛盾命题。

例如，对于证明一个角的两边平分另一个角的问题，我们可以采用间接法。

假设一个角的两边不平分另一个角，然后通过推理和推导，得出两边平分另一个角的结论，与假设矛盾，从而证明结论成立。

三、反证法反证法是通过假设结论不成立，然后通过推理和推导，得出矛盾的结论，从而推翻假设，证明结论成立。

反证法常用于证明一些几何性质的逆命题或矛盾命题。

例如，对于证明一个三角形的三个内角和为180度的问题，我们可以采用反证法。

假设三角形的三个内角和不为180度，然后通过推理和推导，得出三个内角和为180度的结论，与假设矛盾，从而证明结论成立。

四、类比法类比法是通过将一个问题转化为另一个已知的问题进行证明的方法。

它常用于证明一些几何性质的相似性或等价性。

例如，对于证明两个三角形相似的问题，我们可以采用类比法。

我们可以找到一个已知相似的三角形，然后通过类比和推理，得出两个三角形相似的结论。

综上所述，高中数学几何证明题的解题方法有直接法、间接法、反证法和类比法。

在解决这类问题时，我们可以根据题目的要求，选择合适的方法进行推导和证明。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

新课标立体几何常考证明题汇总1、已知四边形 ABCD 是空间四边形，E,F,G,H 分别是边AB, BC,CD, DA 的中点 (1) 求证：EFGH 是平行四边形(2) 若BD=2√3，AC=2 EG=2求异面直线 AG BD 所成的角和EG BD 所成的角。

1证明：在 ABD 中，∙∙∙ E, H 分别是AB, AD 的中点二EH //BD ,EH BD21同理，FG // BD , FG BD ∕∙ EH // FG ,EH = FG .∙.四边形 EFGH 是平行四边形。

2⑵ 90 ° 30 °考点：证平行(利用三角形中位线)，异面直线所成的角2、如图，已知空间四边形 ABCD 中，BC =AC, AD =BD ,E 是AB 的中点。

同理，AD一BD=DE _ AB AE =BE,又∙.∙ CE DE=E.∙. AB _ 平面 CDE(2)由(1)有AB _平面CDE 又∙.∙ A B-平面ABC ,.∙.平面CDE _平面ABC 考点：线面垂直，面面垂直的判定求证：(1) AB _ 平面 CDE;(2) 平面CDE _平面ABC 。

证明：BC=AC [— (1) ⅛ CE 丄 ABAE=BEAC3、如图，在正方体ABCD-A1B1C1D1中，E是AA l的中点,求证：AC//平面BDE 。

证明：连接AC交BD于O ,连接EO ,∙∙∙ E为AA1的中点，O为AC的中点∙∙∙ EO为三角形A1AC的中位线∙∙∙ EO//AC又EO在平面BDE内，AC在平面BDE夕卜∙A I C // 平面BDE。

考点：线面平行的判定4、已知ABC 中.ACB =90〔SA_ 面ABC, AD _ SC,求证：AD _ 面SBC.证明：T ACB =90 ° BC _ AC又SA_面ABC . SA_ BC.BC _ 面SAC.BC _ AD又SC — AD, SC「BC =C AD_ 面SBC考点：线面垂直的判定5、已知正方体ABCD -A I BIGD I , O是底ABCD对角线的交点•求证：（1 ）C I O // 面AB1D1 ; （2）AC-面AB1D1 .证明：（1）连结A1C1,设AICλ BID^O I,连结AO1∙∙∙ ABCD -^B1C1D1是正方体.A l ACC I是平行四边形∙ A1C1 // AC 且A I C^AC又O1,O 分别是A1C1,AC 的中点，∙∙∙ O1C1∕/ AO 且O1C1 =AO AOC1O1是平行四边形Ca AOI, AOI面AB1D1, C1O 二面AB1D1∙ C1O// 面AB1D1（2）'* CC1丄面A1B1C1D1 =CC 丄BD又T AG 丄BIDI, ΛB1 D1丄面 A1C1C 即 AC丄BD同理可证AIC—AD I ,又D I B I AD1 = D IAC -面AB1D1考点：线面平行的判定（利用平行四边形），线面垂直的判定B CCBC1C6、正方体 ABCD —A'B'C'D'中，求证：（1）AC 丄平面 B'D'DB ；（ 2）BD'丄平面 ACB'7、正方体 ABCD — A I B I C I D I 中.⑴求证：平面 A i BD //平面B i D i C;⑵若E 、F 分别是AA i ，CC i 的中点，求证：平面 EB i D i /平面FBD . 证明：⑴由B i B/ DDi ,得四边形BB i D i D 是平行四边形，二B i D i / BD , 又 BD 二平面 B i D i C, B i D i 平面 B i D i C,∙∙∙ BD //平面 B i D i C . 同理 A i D //平面 B i D i C .而 A i D ∩ BD = D ,∙平面 A i BD //平面 B i CD .⑵由 BD/ B i D i ,得 BD //平面 EB i D i •取 BB i 中点 G,∙ AE // B i G .从而得 B i E // AG ,同理 GF // AD . ∙ AG // DF . ∙ B i E/ DF . ∙ DF //平面 EB i D i考点：线面平行的判定（利用平行四边形） 8、如图P 是 ABC 所在平面外一点，PA = PB,CB _平面PAB , M 是PC 的中点，N 是AB 上的点,AN =3NB(i)求证：MN _ AB ; (2)当.APB =90 , AB =2BC =4 时，求 MN 的长。

证明：(i)取PA 的中点Q ,连结MQ,NQ , V M 是PB 的中点，∙ MQ // BC , V CB _ 平面 PAB , ∙ MQ _ 平面 PAB∙ QN 是MN 在平面PAB 内的射影，取 AB 的中点D ,连结 PD , V PxPB , PD- AB ,又 AN = 3NB , ∙ BN = ND W源学§科§H ]∙ QN //PD ,∙ QN _ AB ,由三垂线定理得 MN _ ABr i(2) V -APB = 90" , PA = PB, ∙ PD AB = 2 ,∙ QN = i , V MQ _ 平面 PAB . ∙ MQ _ NQ ,且2 MQ =i BC =i, ∙ MN =、22考点：三垂线定理i0、如图，在正方体 ABCD-A 1B i C i D i 中，E 、F 、G 分别是AB 、AD 、C i D i 的中点.求证：平面D i EF //考点：线面垂直的判定D'∙平面EB i D i /平面FBD . F CDPA平面BDG .证明：V E、F分别是AB、AD的中点，∙ EF // BD又EF二平面BDG , BD 平面BDG EF //平面BDGD i G- EB •四边形D i GBE为平行四边形，D iE // GB 又D i E二平面BDG , GB 平面BDG D i E //平面BDGEF - D 1E = E ,平面DEF //平面BDGI考点：线面平行的判定(利用三角形中位线)11、如图，在正方体ABCD-ABC i D i中，E是AA的中点.(1)求证：AC//平面BDE ；(2)求证：平面A1AC _平面BDE .证明：(1)设ACrBD=O ,∙∙∙ E、Q 分别是AA1、AC 的中点，.A1C // EQ又AC -平面BDE , EQ二平面BDE , AQ //平面BDE(2)∙∙∙ AA^ _ 平面ABCD , BD 平面ABCD , AA _ BD又BD _ AC , A C-AA=A , BD _平面A1AC , BD 平面BDE , 平面BDE _ 平面AAC考点：线面平行的判定(利用三角形中位线) ，面面垂直的判定12、已知ABCD 是矩形，PA _ 平面ABCD , AB = 2 , PA = AD= 4 , E 为BC的中点•(1)求证：DE _平面PAE ; (2)求直线DP与平面PAE所成的角.证明：在ADE 中，AD2=AE2DE2, . AE _ DE∙.∙ PA _ 平面ABCD , DE 平面ABCD , PA_ DED 又PA-AE=A , DE _ 平面PAE(2)DPE为DP与平面PAE所成的角在Rt PAD , PD=4、、2 ,在Rt DCE 中，DE =2,2 在Rt DEP 中，PD =2DE , -ZDPE =30°考点：线面垂直的判定，构造直角三角形13、如图，在四棱锥P-ABCD中，底面ABCD是.DAB =60°且边长为且平面PAD垂直于底面ABCD •(1)若G为AD的中点，求证：BG _平面PAD ;(2)求证：AD _ PB ;(3)求二面角A-BC-P的大小.证明：(1) ABD为等边三角形且G为AD的中点，.BG_AD又平面PAD _平面ABCD , BG _平面PAD(2)PAD是等边三角形且G为AD的中点，.AD _ PG且AD _ BG , PG-BG=G , AD _ 平面PBG ,PB 平面PBG , ■ AD _ PB(3)由AD _ PB , AD // BC , BC _ PB又BG _ AD , AD // BC , BG _ BC-PBG为二面角A-BC-P的平面角在Rt PBG 中，PG=BG , PBG =45°考点：线面垂直的判定，构造直角三角形，面面垂直的性质定理，二面角的求法(定义法)14、如图1,在正方体ABCD -AB 1C 1D 1中，M 为CC I 的中点，AC 交BD 于点0,求证：AP _平面MBD .证明：连结 MO, A 1M , V DB 丄 A 1A , DB 丄 AC,A IA AC=∙∙∙ DB 丄平面 A ACC 1 ,而 AO 平面 A 1ACC 1 ∙∙∙ DB 丄 A 1O .33设正方体棱长为a ,贝U A 1O 2= 3a 2, MO 2=3a 2.2 4在 Rt△ A 1C 1M 中，AM2=9a 2. V A 1O 2MO 2-A 1∣M , ∙ AO 4V OM ∩ DB=0,∙∙∙ A 1O 丄平面 MBD .考点：线面垂直的判定，运用勾股定理寻求线线垂直 15、如图2,在三棱锥 A -BCD K BC= AC AD= BD作BEICD E 为垂足，作 AHL BE 于H .求证：AHL 平面BCD证明：取AB 的中点F ,连结CF DFV AC= BC , ∙ CF _ AB . V AD=BD , ∙ DF _ AB .又 CF n DF =F , ∙ AB _ 平面 CDFV CD 二平面 CDF ∙ CD _ AB .又 CD _ BE , BE-AB=B ,∙ CD _ 平面 ABE CD _ AH .V AH _ CD , AH _ BE , CD-BE=E ,∙ AH —平面 BCD考点：线面垂直的判定16、证明：在正方体 ABCD — A 1B 1C 1D 1中，AQ 丄平面BC 1D证明：连结ACV BDLA C. AC 为AQ 在平面AC 上的射影■ BD -A 1C同理可证AoBC 厂心平面BC I D考点：线面垂直的判定，三垂线定理17、如图，过 S 引三条长度相等但不共面的线段 SA 、SB 、SC,且∠ ASB= ∠ ASC=60 °平面ABC 丄平面BSC.证明V SB=SA=SC , ∠ ASB= ∠ ASC=60 ° ∙ AB=SA=AC 取 BC 的中点 O,连 AO 、SO, 则 AO 丄CCBC , SO 丄 BC,√2∙∙∙∠ AoS 为二面角的平面角，设 SA=SB=SC=a ,又∠ BSC=90 °,二 BC= , 2 a, So= 2 a,1 1AO 2=AC 2— OC2=a2- 2 a2= 2 a2, ∙ SA2=AO 2+OS2,∙∠ AOS=90 °,从而平面 ABC 丄平面 BSC. 考点：面面垂直的判定（证二面角是直二面角）。