直角三角形的射影定理限时练

合集下载

射影定理复习题

定义：射影定理的内容是在直角三角形中，每条直角边是这条直角边在斜边的射影和斜边的比例中项，斜边上的高线是两条直角边在斜边射影的比例中项例如：公式Rt△ABC 中,∠BAC=90°,AD 是斜边BC 上的高,则有射影定理如下(1)(AD)^2;=BD·DC,(2)(AB)^2;=BD·BC ,(3)(AC)^2;=CD·BC 。

例题1：1、ABC 中，90A ∠=，AD BC ⊥于点D ，AD=6，BD=12，则CD=，AC= ，22:AB AC = 。

2、如图1-1，在Rt ABC 中，CD 是斜别AB 上的高，在图中六条线段中，你认为只要知道（）线段的长，就可以求其他线段的长3、如图2-1，在Rt ABC 中，90ACB ∠=，CD AB ⊥，AC=6，AD=3.6，则BC= ．3、已知CD 是ABC 的高，,DE CA DF CB ⊥⊥，如图3-1，求证：CEF CBA ∽变式训练：图1—4—3，已知：BD 、CE 是△ABC 的两条高，过点D 的直线交BC 和BA 的延长线于G 、H ，交CE 于F ，且∠H=∠BCF 。

求证：GD 2=GF ·GH 。

中考链接：如图3-2，矩形ABCD 中，AB=a ，BC=b ，M 是BC 的中点，DE AM ⊥，E 是垂足，求证：DE =创新训练：如图1-2，在矩形ABCD 中，1,3DE AC ADE CDE ⊥∠=∠，则EDB ∠=大家都来到荷塘，挖莲藕抓鱼虾，捉泥鳅捡螃蟹，人声鼎沸，笑语欢声，相互谈说着要如何弄出一顿顿可口的美味。

光是莲藕的吃法就有很多：熬汤炖肉八宝酿、清炒生吃蜜饯糖，还可以磨成藕粉，加入砂糖或蜂蜜，在温水里一泡，就是一杯清凉清甜的解暑饮料。

用鲜莲叶来熬粥，蒸饭蒸鸡，或蒸其它肉类味道都是极鲜美的，做出来的食物均带着一股淡淡的莲叶清香。

人们那么喜欢荷花，不单单是因为它的芳香美丽洁净高雅，更因为它全身是宝，每一处都可食可药可用。

射影定理复习题.doc

例题1：1、ABC 中，90A ∠=，AD BC ⊥于点D ，AD=6，BD=12，则CD=，AC= ，22:AB AC = 。

求证：GD 2=GF ·GH 。

中考链接：如图3-2，矩形ABCD 中，AB=a ，BC=b ，M 是BC 的中点，DE AM ⊥，E 是垂足，求证：224DE a b =+创新训练：如图1-2，在矩形ABCD 中，1,3DE AC ADE CDE ⊥∠=∠，则EDB ∠=赠送以下资料考试知识点技巧大全一、考试中途应饮葡萄糖水大脑是记忆的场所，脑中有数亿个神经细胞在不停地进行着繁重的活动,大脑细胞活动需要大量能量。

科学研究证实,虽然大脑的重量只占人体重量的2%-3%,但大脑消耗的能量却占食物所产生的总能量的20%,它的能量来源靠葡萄糖氧化过程产生。

据医学文献记载,一个健康的青少年学生30分钟用脑,血糖浓度在120毫克/100毫升,大脑反应快,记忆力强；90分钟用脑，血糖浓度降至80毫克/100毫升，大脑功能尚正常；连续120分钟用脑，血糖浓度降至60毫克/100毫升，大脑反应迟钝，思维能力较差。

课时作业4：四　直角三角形的射影定理

四直角三角形的射影定理一、基础达标1．如图，在△ABC中，∠BAC＝90°，AD是BC边上的高，则图中共有相似三角形()A．0对B．1对C．2对D．3对解析△ACD∽△BAD，△ACD∽△BCA，△ABD∽△CBA，共有3对相似三角形．答案 D2.如图所示，在Rt△MNP中，MN⊥MP，MQ⊥PN于点Q，NQ＝3，则MN等于()A.3PNB.13PNC.3PND.9PN解析∵MN⊥MP，MQ⊥PN，∴MN2＝NQ·PN，又NQ＝3，∴MN＝NQ·PN ＝3PN.答案 C3.在Rt△ABC中，∠BAC＝90°，AD⊥BC于点D，若ACAB＝34，则BDCD＝()A.34 B.43 C.169 D.916解析如图，由射影定理得AC2＝CD·BC，AB2＝BD·BC∴AC2AB2＝CDBD＝⎝⎛⎭⎪⎫342，即CDBD＝916，∴BDCD＝169.答案 C4.已知在Rt△ABC中，CD是斜边上的高，若AD＝p，BD＝q，则tan A的值是()A.p∶qB.pq∶qC.pq∶pD.p∶q解析由已知可利用射影定理得：CD＝pq，在Rt△ACD中，tan A＝CD AD＝pqp.答案 C5.如图，在矩形ABCD中，AB＝3，BC＝3，BE⊥AC，垂足为E，则ED＝________.解析∵AB⊥BC，BE⊥AC，∴AC＝AB2＋BC2＝23，由射影定理得：BC2＝CE·AC，∴CE＝3223＝332.又在Rt△BEC中，cos∠BCE＝CEBC＝32，∴∠BCE＝30°，∴∠ECD＝60°，由余弦定理可求DE2＝214.∴DE＝212.答案21 26.如图，在Rt△ABC中，CD是斜边AB上的高，DE是Rt△BCD斜边BC上的高，若BE＝6，CE＝2，求AD的长.解∵CD⊥AB，即∠CDB＝90°，∵DE⊥BC.由射影定理可知：DE2＝CE·BE＝12，∴DE＝23，CD2＝CE·BC＝16，∴CD＝4，∵BD2＝BE·BC＝48，∴BD＝43，在Rt△ABC中，由射影定理可得：CD2＝AD·BD，∴AD＝CD2BD＝1643＝433.二、能力提升7.如图所示，在△ABC 中，CD ⊥AB ，BD ＝AB －12AC ，则∠BAC 等于( ) A.60° B.30° C.45°D.75°解析 ∵BD ＝AB －12AC ，∴AB －BD ＝12AC ＝AD ，又∵CD ⊥AB ，∴∠CDA ＝90°，在Rt △ADC 中，由AD ＝12AC ，则∠BAC ＝60°. 答案 A8．在Rt △ABC 中，∠C ＝90°，a －b ＝1，tan A ＝32，其中a ，b 分别是∠A 和∠B 的对边，则斜边上的高h ＝________．解析由tan A ＝a b ＝32和a －b ＝1， ∴a ＝3，b ＝2，故c ＝13， ∴h ＝ab c ＝61313.答案613139.在△ABC 中，∠ACB ＝90°，CD ⊥AB 于D ，AD ∶BD ＝2∶3，则△ACD 与△CBD 的面积比为________.解析由已知可设AD ＝2x ，则BD ＝3x ， ∵∠ACB ＝90°，CD ⊥AB ，由射影定理得：CD 2＝AD ·BD ＝6x 2，∴CD ＝6x ，∴S △ACD ∶S △CBD ＝⎝ ⎛⎭⎪⎫CD BD 2＝⎝ ⎛⎭⎪⎫632＝23.答案 2310.如图所示，在△ABC 中，∠BAC ＝90°，AD ⊥BC 于D ，DF ⊥AC 于F ，DE ⊥AB 于E . 求证：(1)AB ·AC ＝AD ·BC ； (2)AD 3＝BC ·BE ·CF ；(3)AB3AC3＝BECF.证明(1)在Rt△ABC中，AD⊥BC，∴S△ABC ＝12AB·AC＝12BC·AD，∴AB·AC＝BC·AD.(2)在Rt△ADB中，DE⊥AB，由射影定理得BD2＝BE·AB.同理，在Rt△ADC中，DF⊥AC，∴CD2＝CF·AC，∴BD2·CD2＝BE·AB·CF·AC.又在Rt△ABC中，AD⊥BC，∴AD2＝BD·DC，∴AD4＝BD2·DC2，即AD4＝BE·AB·CF·AC.由(1)知AB·AC＝BC·AD，∴AD4＝BE·CF·BC·AD，∴AD3＝BE·CF·BC.(3)由射影定理得BD2＝BE·AB，∴BE＝BD2 AB.①又CD2＝CF·AC，∴CF＝CD2 AC，②由①÷②得BECF＝BD2AB·ACCD2＝⎝⎛⎭⎪⎫BDCD2·ACAB.③又∵AB2＝BD·BC，∴BD＝AB2 BC，同理，AC2＝CD·BC，∴CD＝AC2 BC，∴BDCD＝AB2AC2.④将④代入③得BECF＝⎝⎛⎭⎪⎫AB2AC22·ACAB＝AB3AC3，即AB3AC3＝BECF.11.如图，在△ABC中，D，F分别在AC，BC上，且AB⊥AC，AF⊥BC，BD＝DC＝FC＝1，求AC.解在△ABC中，设AC为x，∵AB⊥AC，AF⊥BC.又FC＝1，根据射影定理，得AC 2＝FC ·BC ，即BC ＝x 2.再由射影定理，得AF 2＝BF ·FC ＝(BC －FC )·FC ，即AF 2＝x 2－1，∴AF ＝x 2－1.在△BDC 中，过D 作DE ⊥BC 于E . ∵BD ＝DC ＝1，∴BE ＝EC ＝12x 2. 又∵AF ⊥BC ，∴DE ∥AF ，∴DE AF ＝DCAC ， ∴DE ＝DC ·AF AC ＝x 2－1x.在Rt △DEC 中，∵DE 2＋EC 2＝DC 2，即⎝⎛⎭⎪⎫x 2－1x 2＋⎝ ⎛⎭⎪⎫12x 22＝12， ∴x 2－1x 2＋x 44＝1.整理得x 6＝4，∴x ＝32，即AC ＝32. 三、探究与创新12.在Rt △ABC 中，∠ACB ＝90°，CD ⊥AB 于D ，S 2△BCD ＝S △ABC ·S △ADC .求证：BD ＝AC .证明如图，∵S 2△BCD ＝S △ABC ·S △ADC ，即S △ABC S △BCD ＝S △BCD S △ADC，∴AB ·CD BD ·CD ＝BD ·CDAD ·CD，即AB BD ＝BDAD ，∴BD 2＝AB ·AD . 由射影定理，得AC 2＝AD ·AB ， ∴AC 2＝BD 2，即AC ＝BD .讲末复习1.平行线等分线段定理(1)定理：如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等推论1：经过三角形一边的中点且与另一边平行的直线必平分第三边.推论2：经过梯形一腰的中点且与底边平行的直线必平分另一腰.(2)中位线定理三角形中位线定理：三角形的中位线平行于第三边，并且等于它的一半.梯形中位线定理：梯形的中位线平行于两底，并且等于两底和的一半.2.平行线分线段成比例定理(1)定理：三条平行线截两条直线，所得的对应线段成比例.推论1：平行于三角形一边的直线截其他两边的直线(或两边的延长线)所得的对应线段成比例.推论2：用平行于三角形一边且和其他两边相交的直线截三角形，所得的三角形三边与原三角形的三边对应成比例.推论1的逆定理：如果一条直线截三角形两边或两边的延长线所得的对应线段成比例，那么这条直线平行于三角形的第三边.(2)三角形内角平分线定理定理：三角形的内角平分线分对边所得的两条线段比等于夹这个角的两边比. 3.相似三角形的判定(1)相似三角形的概念定义：对应角相等，对应边成比例的两个三角形叫做相似三角形.对应边的比值称为相似比.(2)预备定理定理1：平行于三角形一边的直线和其他两边(或两边的延长线)相交，所构成的三角形与原三角形相似.利用本定理可以证明相似三角形的判定定理.(3)相似三角形判定定理判定定理1：对于任意两个三角形，如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似.即：两角对应相等，两三角形相似.判定定理2：对于任意两个三角形，如果一个三角形的两边和另一个三角形的两边对应成比例，并且夹角相等，那么，这两个三角形相似.即：两对应边成比例且夹角相等，两三角形相似.判定定理3：对于任意两个三角形，如果一个三角形的三条边和另一个三角形的三条边对应成比例，那么这两个三角形相似.即：三边对应成比例，两三角形相似.(4)直角三角形相似的判定定理定理1：如果两个直角三角形有一个锐角相等，那么它们相似.定理2：如果两个直角三角形的两条直角边对应成比例，那么它们相似.定理3：如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．4．相似三角形的性质性质定理1：相似三角形对应角相等，对应边成比例．性质定理2：相似三角形对应边上的高、中线、对应角平分线和它们的周长的比都等于相似比．性质定理3：相似三角形的面积比等于相似比的平方．性质定理4：相似三角形外接圆或内切圆的直径比、周长比等于相似比，外接圆或内切圆的面积比等于相似比的平方．5．直角三角形的射影定理(1)射影的概念从一点向一条直线所引垂线的垂足，叫做这点在这条直线上的正射影，简称射影．一般地，一个点集(如线段或其他几何图形)中所有的点在某条直线上的射影集合，称这个点集在这条直线上的射影．如一条线段在一条直线上的射影就是线段的两个端点在这条直线上的射影间的线段．(2)直角三角形的射影定理和逆定理定理：直角三角形斜边上的高是两条直角边在斜边上射影的比例中项；两条直角边分别是它们在斜边上射影与斜边的比例中项．逆定理：如果一个三角形一边上的高是另两边在这条边上的射影的比例中项，那么这个三角形是直角三角形．勾股定理：直角三角形两条直角边的平方和等于斜边的平方．题型一构造法添加辅助线是平面几何解决问题最常用的手段，添加辅助线的目的是构造平行线、或三角形、或三角形的相似等结构.例1 如图，梯形ABCD 中，AB ∥CD ，CE 平分∠BCD ，CE ⊥AD 于E ，DE ＝2AE ，若△CED 的面积为1，求四边形ABCE 的面积.解延长CB ，DA 交于点F ，又CE 平分∠BCD ，CE ⊥AD . ∴△FCD 为等腰三角形，E 为FD 的中点.∴S △FCD ＝12FD ·CE ＝12×2ED ×CE ＝2S △CED ＝2，EF ＝2AE . ∴FA ＝AE ＝14FD . 又∵AB ∥CD ， ∴△FBA ∽△FCD .∴S △FBA S △FCD ＝⎝ ⎛⎭⎪⎫FA FD 2＝⎝ ⎛⎭⎪⎫142＝116， ∴S △FBA ＝116×S △FCD ＝18.∴S 四边形ABCE ＝S △FCD －S △CED －S △FBA ＝2－1－18＝78.规律方法多边形的问题常转化为三角形问题去解决，本题从已知条件出发，构造了等腰三角形，使求四边形的面积问题转化为求三角形的面积.跟踪演练1 如图，在△ABC 中，AB >AC ，在边AB 上取一点D ，在边AC 上取一点E ，使AD ＝AE ，直线DE 和BC 的延长线交于点P .求证：BP CP ＝BDCE .证明过点C 作CM ∥AB 交PD 于点M . ∵AD ＝AE ， ∴∠ADE ＝∠AED .∵AD ∥CM ，∴∠ADE ＝∠CME . 又∵∠AED ＝∠CEM ，∴∠CEM ＝∠CME ，∴CE ＝CM . 又∵CM ∥BD ，∴△CPM ∽△BPD . ∴BP CP ＝BD CM ，即BP CP ＝BD CE . 题型二化归法转化化归思想方法是解决数学问题的灵魂，平面几何在证明一些等积式时，往往将其转化为比例式，当证明的比例式中的线段在同一直线上时，常转化为用相等的线段、相等的比、相等的等积式来代换相应的量，证明比例式成立也常用中间比来转化证明.例2 如图，在△ABC 中，∠A ，∠B ，∠C 的对边分别是a ，b ，c ，点P 是AB 上与A ，B 不重合的一个动点，连接PC ，过点P 作PQ ∥AC 交BC 于点Q .(1)如果a ，b 满足关系式a 2＋b 2－12a －16b ＋100＝0，c 是不等式组⎩⎪⎨⎪⎧2x －13>x －4，2x ＋3<6x ＋12的最大整数解，试说明△ABC 的形状. (2)在(1)的条件下，设AP ＝x ，S △PCQ ＝y ，求y 与x 的函数关系式，并注明自变量x 的取值范围.解 (1)a 2＋b 2－12a －16b ＋100＝0，即(a －6)2＋(b －8)2＝0，∴a ＝6，b ＝8.解不等式组⎩⎪⎨⎪⎧2x －13>x －4，2x ＋3<6x ＋12，得52<x <11.∴c ＝10，∴a 2＋b 2＝c 2，∴△ABC 是直角三角形. (2)由(1)得S △ABC ＝12ab ＝24，S △PBC ∶S △ABC ＝PB ∶AB ， ∴S △PBC ＝125(10－x )＝24－125x . ∵PQ ∥AC ，∴△PBQ ∽△ABC ， ∴S △PBQ S △ABC ＝⎝ ⎛⎭⎪⎫PB AB 2，即S △PBQ 24＝⎝⎛⎭⎪⎫10－x 102， ∴S △PBQ ＝24100(10－x )2＝625x 2－245x ＋24， ∴S △PCQ ＝S △PBC －S △PBQ ＝－625x 2＋125x ，即y ＝－625x 2＋125x (0<x <10).规律方法对于(1)，判断△ABC 的形状，由题意转化为解不等式组.对于(2)，由于△PCQ 的面积无法直接利用面积公式求解，但可通过S △PQC ＝S △BPC －S △PBQ ，将问题转化为求S △PBQ 、S △BPC .跟踪演练2 如图，在锐角△ABC 中，AD ，CE 分别是BC ，AB 边上的高，△ABC 和△BDE 的面积分别等于18和2，且DE ＝22，求点B 到直线AC 的距离. 解 ∵AD ⊥BC ，CE ⊥AB ， ∴∠ADB ＝∠CEB ＝90°. 又∵∠B ＝∠B ， ∴△ADB ∽△CEB ， ∴BD BE ＝AB BC ，∴BD AB ＝BE BC . 又∵∠B ＝∠B ， ∴△BED ∽△BCA ，∴S △BED S △BCA ＝ED 2AC 2＝218. ∵DE ＝22，∴DE 2AC 2＝（22）2AC 2＝218， ∴AC ＝6 2.设点B 到直线AC 的距离为h ，则S △ABC ＝12AC ·h ，即18＝12×62h ，∴h ＝3 2. 题型三分类讨论法当点、线的位置关系不确定时常常需分类讨论.例3 要做两个形状相同的三角形框架，其中一个框架的三边长分别是4,5, 6，另一个框架的一边长是2，怎样选料可使这两个三角形相似？解 (1)若2为最长边，设其他两边长分别为x ，y ，根据相似三角形性质有： 4x ＝5y ＝62，解得x ＝43，y ＝53；(2)若2为中间边，设其他两边长分别为x ，y ，根据相似三角形性质有： 4x ＝52＝6y ，解得x ＝85，y ＝125；(3)若2为最短边，设其他两边长分别为x ，y ，根据相似三角形性质有： 42＝5x ＝6y ，解得x ＝52，y ＝3.综上，另一个三角形的另两边长分别为43和53或85和125或52和3.规律方法这是一道开放性试题，由于边长为2的三角形三边关系不明确，边长为2的边可以是最长边、中间边或最短边，因此应分三种情况进行讨论. 跟踪演练3 在△ABC 中，AB >BC >AC ，D 是AC 的中点，过点D 作直线l ，使截得的三角形与原三角形相似，这样的直线有________条. 解析如图，过点D 作DE 1∥BC ，此时∠AE 1D ＝∠B ，所以△ABC ∽△AE 1D ；过点D 作∠ADE 2＝∠B ，此时△ADE 2∽△ABC .同理，过点D 可以作DE 3∥AB ，使∠DE 3C ＝∠B ；过点D作DE 4与BC 相交于E 4，使∠E 4DC ＝∠B ，都能使截得的三角形与原三角形相似，因此共有4条直线符合要求. 答案 4题型四方程法方程思想是从问题的数量关系(相等，成比例等)入手，将问题转化为方程或比例式或不等式问题来求解.例4 如图，在Rt △ABC 中，E 为斜边AB 上一点，AE ＝2，EB ＝1，四边形DEFC 为正方形，则阴影部分的面积为________. 解析设正方形DEFC 的边长为x ，则根据△ADE ∽△EFB ，得AD ＝2x ， BF ＝12x ，从而AC ＝3x ，BC ＝32x .在Rt △ADE 中，(2x )2＋x 2＝22，解得x 2＝45. 故S 阴影＝S △ABC －S 正方形DEFC ＝12·3x ·32x －x 2＝54x 2＝1. 答案 1规律方法将几何图形的比例相等关系转化为方程，是解决平面几何问题常用路子.体验高考1.(2014·广东高考)如图，在平行四边形ABCD 中，点E 在AB 上且EB ＝2AE ，AC 与DE 交于点F ，则△CDF 的周长△AEF 的周长＝________.解析由CD ∥AE ，得△CDF ∽△AEF . 于是△CDF 的周长△AEF 的周长＝CD AE ＝AB AE ＝3.答案 32.(2013·陕西高考)如图，AB 与CD 相交于点E ，过点E 作BC 的平行线与AD 的延长线交于点P ，已知∠A ＝∠C ，PD ＝2DA ＝2，则PE ＝________.解析由PE ∥BC ，∠A ＝∠C 知，∠A ＝∠C ＝∠PED ，在△PDE 和△PEA 中，∠DPE ＝∠EPA ，∠A ＝∠PED ，故△PDE ∽△PEA ，则PD ∶PE ＝PE ∶PA .于是PE 2＝PA ·PD ＝3×2＝6，则PE ＝ 6.答案 63.(2014·重庆高考)过圆外一点P作圆的切线PA(A为切点)，再作割线PBC依次交圆于点B，C.若PA＝6，AC＝8，BC＝9，则AB＝________.解析依题意得△PAC∽△PBA，则PAPC＝ABAC＝PBPA，即6PB＋9＝AB8＝PB6，解得PB＝3，AB＝4.答案 44．(2016·江苏高考)如图，在△ABC中，∠ABC＝90°，BD⊥AC，D为垂足，E是BC的中点，求证：∠EDC＝∠ABD.证明由BD⊥AC.可得∠BDC＝90°，由E为BC中点，可得DE＝CE＝12BC，则∠EDC＝∠C，由∠BDC＝90°，得∠C＋∠DBC＝90°，又∠ABC＝90°，则∠ABD＋∠DBC＝90°，∴∠ABD＝∠C，又∵∠EDC＝∠C，∴∠EDC＝∠ABD.讲末检测一、选择题1.在△ABC中，DE∥BC，若AE∶EC＝1∶2，且AD＝4 cm，则DB等于()A.2 cmB.6 cmC.4 cmD.8 cm解析如图，∵DE∥BC，∴AEEC＝ADDB＝12.又∵AD＝4 cm，∴DB＝8 cm.答案 D2.两个相似三角形对应边上的中线之比为3∶4，周长之和是35，那么这两个三角形的周长分别是()A.13和22B.14和21C.15和20D.16和19解析由相似三角形周长之比，中线之比均等于相似比可得周长之比C1C2＝34.又∵C1＋C2＝35，∴C1＝15，C2＝20，即两个三角形周长分别为15，20. 答案 C3.如图所示，在△ABC中，P，Q分别在BC和AC上，BP∶CP＝2∶5，CQ∶QA＝3∶4，则AR∶RP等于()A.3∶14B.14∶3C.17∶3D.17∶14解析如图，过点Q作QM∥AP交PC于M，则CMMP＝CQQA＝34.又∵BPPC＝25，∴BPPM＝710.又RPQM＝BPBM＝717，QMAP＝CQAC＝37，∴RPAP＝3 17，∴ARRP＝143.答案 B4.如图所示，在△ABC中，M是BC的中点，AN平分∠BAC，BN⊥AN于N，若AB＝14，AC＝19，则MN的长为()A.2B.2.5C.3D.3.5解析延长BN交AC于D，则△ABD为等腰三角形，∴AD＝AB＝14，∴CD＝5.又M，N分别是BC，BD的中点，故MN＝12CD＝2.5.答案 B5.若三角形的三条边长之比为3∶5∶7，与它相似的三角形的最长边为21 cm，则其余两边的长度之和为()A.24 cmB.21 cmC.19 cmD.9 cm解析设其余两边的长度分别为x cm，y cm，则217＝x5＝y3，解得x＝15，y＝9，故x＋y＝24. 答案 A6.如图所示，在梯形ABCD中，AB∥DC，对角线AC与BD交于点O，有下列结论：①△AOB∽△COD；②△AOD∽△ACB；③S△DOC∶S△AOB＝DC∶AB；④S△AOD＝S△BOC，其中始终正确的有()A.1个B.2个C.3个D.4个解析①④正确，②③错误.答案 B7.如图所示，在▱ABCD中，AE∶EB＝1∶2，若S△AEF＝6 cm2，则S△CDF等于()A.54 cm2B.24 cm2C.18 cm2D.12 cm2解析由题意知△AEF∽△CDF，∴S△AEFS△CDF＝⎝⎛⎭⎪⎫AECD2＝⎝⎛⎭⎪⎫AEAB2＝⎝⎛⎭⎪⎫132＝19，∴S△CDF＝9S△AEF＝54 cm2.答案 A8.如图所示，身高为1.6 m的某同学想测量学校旗杆的高度，当他站在C处时，他的影子的顶端正好与旗杆影子的顶端重合，并测得AC＝2 m，BC＝8 m，则旗杆的高度是()A.6.4 mB.7 mC.8 mD.9 m解析∵CD∥BE，∴△ACD∽△ABE，∴CDBE＝ACAB，∵AC＝2 m，BC＝8 m，∴AB＝10 m，又∵CD＝1.6 m，∴1.6BE＝210，∴BE＝8(m).答案 C9.如图所示，AD⊥BC于D，CE⊥AB于E交AD于F，则图中相似三角形的对数是()A.3对B.4对C.5对D.6对解析△ABD∽△CBE∽△AFE∽△CFD，共有6对.答案 D10.如图，在△ABC中，AE∶EB＝1∶3，BD∶DC＝2∶1，AD与CE相交于F，则EFFC＋AFFD的值为()A.12 B.1C.32 D.2解析如图，过D作DG∥CE交AB于G，则BGGE＝BDDC＝21.又AEEB＝13，∴AE＝EG，∴AFFD＝AEEG＝1.又DGCE＝BDBC＝23，EF＝12DG，∴EFCE＝13，∴EFFC＝12，∴EFFC＋AFFD＝32.答案 C二、填空题11.如图，在直角梯形ABCD中，DC∥AB，CB⊥AB，AB＝AD＝a，CD＝a2，点E，F分别为线段AB，AD的中点，则EF＝________.解析如图，连接DE，DB.∵点E，F分别为线段AB，AD的中点，∴EF＝12BD，AE＝EB＝a2.又∵CD＝a2＝BE，CB⊥AB，DC∥AB，∴DE垂直平分线段AB.∴BD＝AD＝a，∴EF＝a 2.答案a 212.如图，在△ABC中，E是AB的中点，EF∥BD，EG∥AC交BD于G，CD＝12AD，若EG＝2 cm，则AC＝________；若BD＝10 cm，则EF＝________.解析由E是AB的中点，EF∥BD，得EG＝12AD＝FD＝2 cm，结合CD＝12AD，可以得到F，D是AC的三等分点，则AC＝3EG＝6(cm).由EF∥BD，得EF＝12BD＝5(cm).答案 6 cm 5 cm13.已知在△ABC中，∠ACB＝90°，CD⊥AB于D，AC＝6，DB＝5，则AD的长为________.解析在Rt△ABC中，∠ACB＝90°，CD⊥AB，∴AC2＝AD·AB.设AD＝x，则AB＝5＋x，又AC＝6，∴62＝x(x＋5)，解得x＝4或x＝－9(舍).∴AD＝4.答案 414.在△ABC中，直线DE与直线AB，AC分别交于点D，E，且DE∥BC.若AD＝1，DB＝2，则DE＋BCDE＝________.解析(1)若点D，E分别在边AB，AC上，则由DE∥BC知ADAB＝DEBC＝13，故DE＋BCDE＝1＋3＝4.(2)若点D，E分别在BA，CA的延长线上，则由DE∥BC知ADAB＝DEBC＝1，故DE＋BCDE＝2.综上，DE＋BCDE＝4或2.答案4或2 三、解答题15.如图，已知ABAD＝BCDE＝ACAE.求证：△ABD∽△ACE.证明因为ABAD＝BCDE＝ACAE，所以△ABC∽△ADE，所以∠BAC＝∠DAE，∠BAC－∠DAC＝∠DAE－∠DAC，即∠DAB＝∠EAC.又ABAD＝ACAE，即ABAC＝ADAE，所以△ABD∽△ACE.16.如图，在△ABC中，D，E，F分别是BC，AB，AC上的点，AD，EF交于P，若BD＝DC，AE＝AF.求证：ABAC＝PF PE.证明如图，过F作MN∥AD交BA的延长线，DC于M，N.对△MEF有PF PE＝AM AE，因为AE＝AF，所以PFPE＝AM AF.对△MBN有ABAM＝BDDN，因为BD＝DC，所以ABAM＝DCDN.对△ADC有ACAF＝DCDN，所以ABAM＝ACAF.所以ABAC＝AMAF，所以ABAC＝PFPE.17.如图所示，AD，CF是△ABC的两条高线，在AB上取一点P，使AP＝AD，再从P点引BC的平行线与AC交于点Q.求证：PQ＝CF.证明∵AD，CF是△ABC的两条高线，∴∠ADB＝∠BFC＝90°.又∠B＝∠B，∴△ABD∽△CBF.∴ADCF＝ABCB.又∵PQ∥BC，∴△APQ∽△ABC.∴PQBC＝APAB，∴APPQ＝ABBC，∴ADCF＝APPQ.又∵AP ＝AD ，∴CF ＝PQ .18.如图所示，CD 为Rt △ABC 斜边上的中线，CE ⊥CD ，CE ＝103，连接DE 交BC 于点F ，AC ＝4，BC ＝3，求证：(1)△ABC ∽△EDC ； (2)DF ＝EF .证明 (1)在Rt △ABC 中，AC ＝4，BC ＝3，则AB ＝5.∵D 为斜边AB 的中点， ∴AD ＝BD ＝CD ＝12AB ＝2.5， ∴CD CE ＝2.5103＝34＝BC AC ，∴△ABC ∽△EDC .(2)由(1)知∠B ＝∠CDF .∵BD ＝CD ， ∴∠B ＝∠DCF ，∴∠CDF ＝∠DCF ， ∴DF ＝CF .① 由(1)知∠A ＝∠CEF ，∠ACD ＋∠DCF ＝90°，∠ECF ＋∠DCF ＝90°， ∴∠ACD ＝∠ECF ，由AD ＝CD 得∠A ＝∠ACD ， ∴∠ECF ＝∠CEF ，∴CF ＝EF .② 由①②可知DF ＝EF.。

数学人教A版选修4-1课后训练：第一讲四直角三角形的射影定理含解析精品

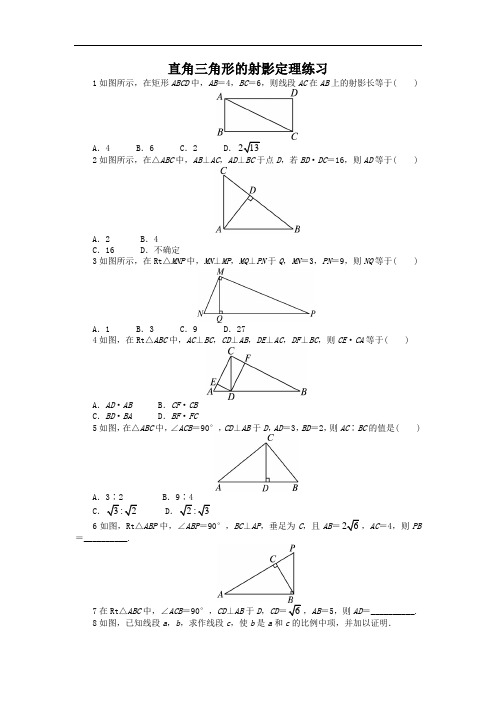
直角三角形的射影定理练习1如图所示，在矩形ABCD中，AB＝4，BC＝6，则线段AC在AB上的射影长等于( )A．4 B．6 C．2 D．2如图所示，在△ABC中，AB⊥AC，AD⊥BC于点D，若BD·DC＝16，则AD等于( )A．2 B．4C．16 D．不确定3如图所示，在Rt△MNP中，MN⊥MP，MQ⊥PN于Q，MN＝3，PN＝9，则NQ等于( )A．1 B．3 C．9 D．274如图，在Rt△ABC中，AC⊥BC，CD⊥AB，DE⊥AC，DF⊥BC，则CE·CA等于( )A．AD·AB B．CF·CBC．BD·BA D．BF·FC5如图，在△ABC中，∠ACB＝90°，CD⊥AB于D，AD＝3，BD＝2，则AC∶BC的值是( )A．3∶2 B．9∶4C D6如图，Rt△ABP中，∠ABP＝90°，BC⊥AP，垂足为C，且AB＝AC＝4，则PB ＝__________.7在Rt△ABC中，∠ACB＝90°，CD⊥AB于D，CD AB＝5，则AD＝__________.8如图，已知线段a，b，求作线段c，使b是a和c的比例中项，并加以证明．9在△ABC中，∠BAC是直角，AD是斜边BC上的高，AB＝2A C．求证：5AD＝2B C．参考答案1 答案：A ∵BC ⊥AB ，∴AC 在AB 上的射影是AB .2 答案：B 由题意知，AD 2＝BD ·DC ＝16，故AD ＝4.3 答案：A ∵MN 2＝NQ ·NP ， ∴32＝NQ ×9.∴NQ ＝1.4答案：B ∵CD ⊥AB ，DE ⊥AC ，∴CD 2＝CE ·CA ，同理可得CD 2＝CF ·CB ， ∴CE ·CA ＝CF ·CB .5 答案：C 在Rt△ABC 中，∠ACB ＝90°，CD ⊥AB ，由射影定理知，AC 2＝AD ·AB ，BC 2＝BD ·AB .又∵AD ＝3，BD ＝2， ∴AB ＝AD ＋BD ＝5，∴AC 2＝3×5＝15，BC 2＝2×5＝10.∴AC BC ==AC ∶BC6答案：∵在Rt△ABP 中，∠ABP ＝90°，BC ⊥AP ，∴AB 2＝AC ·AP ，即2＝4AP ，解得AP ＝6. 在Rt△ABP 中，由勾股定理，得BP ===7答案：2或3 ∵∠ACB ＝90°，CD ⊥AB ，∴CD 2＝AD ·DB .∵CD AD ·DB ＝6.又AB ＝5， ∴DB ＝5－AD .∴AD (5－AD )＝6，解得AD ＝2或3. 8答案：作法：如图所示.(1)作线段AB ＝a ，过B 作AB 的垂线l ，在l 上取一点C ，使BC ＝b ；(2)连接AC ，过C 作AC 的垂线l ′，l ′交AB 的延长线于D ，则线段BD 为所求作线段c .证明：∵AC ⊥CD ，CB ⊥AD ，∴CB 2＝AB ·BD . ∴b 2＝ac ，即线段c 使得b 是a 和c 的比例中项.9 答案：证明：在Rt△ABC 中，设AC ＝k ，则AB ＝2AC ＝2k ，∴BC =，AC 2＝BC ·CD ·CD ＝k 2，则CD ＝5k .∵AD2＝CD·BD，BD＝BC－CD，∴AD2，∴AD.∴AD∶BC＝25.即5AD＝2BC.。

高中同步数学课时训练：1.4直角三角形的射影定理(人教

知能巩固提升(五)/课后巩固作业(五)（时间：45分钟满分：100分）一、选择题(每小题6分，共36分)1.如图，在Rt△ABC中，∠ACB=90°,CD⊥AB,D为垂足，若CD=6，AD∶DB=1∶2，则AD的值是( )(A)6 (B) (C)18 (D)2.如图所示，在Rt△ABC中，∠ACB=90°，CD⊥AB于D，CD=2，BD=3，则AC=( )(A) (B) (C) (D)3.(2012·长沙模拟)如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D.若AD∶DB＝1∶4，则tan ∠ACD的值是( )(A) (B) (C) (D)24.(2012·汕头模拟)一个直角三角形的两条直角边的比是1∶3，则它们在斜边上射影的比是( )(A)1∶3 (B)1∶6 (C)1∶9 (D)2∶95.一个直角三角形的一条直角边为3 cm，斜边上的高为2.4 cm，则这个直角三角形的面积为( )(A)6 cm2 (B)7.2 cm2(C)12 cm2 (D)24 cm26.已知：在△ABC中，AD是高，且AD2=BD·DC,则∠BAC( )(A)大于90°(B)等于90°(C)小于90°(D)不能确定二、填空题(每小题6分，共18分)7.如图，在Rt△ABC中，∠ACB＝90°，AB⊥CD，AD＝4 cm，AC＝5 cm.则CD＝_____cm，BC＝____cm.8.如图，AB是半圆O的直径，点C在半圆上，CD⊥AB于点D，且AD=3DB，设∠COD=θ，则tan2 =______.9.如图，在△ABC中，D、F分别在AC、BC上，且AB⊥AC，AF⊥BC，BD=DC=FC=1，则AC=______.三、解答题(每小题14分，共28分)10.如图，在△ABC中，CD⊥AB于点D，DE⊥AC于点E，DF⊥BC于点F.求证：△ABC∽△FEC.11.(易错题)如图，已知BD，CE是△ABC的两条高，过点D的直线交BC和BA的延长线于G，H，交CE于F，且∠H=∠BCF.求证：GD2=GF·GH.【挑战能力】(18分)在△ABC中，∠ACB=90°，CD⊥AB,AE平分∠BAC交BC于E，CE∶EB=4∶5,CD=24，求AD∶DB及S△ABC.答案解析1.【解析】选B.设AD=x,则DB=2x,∴36=2x2,∴x2=18,x=,即AD=.2.【解析】选C.由射影定理知，CD2=BD·AD,∴AD=，∴AB=AD+BD=,∴AC2=AD·AB=×=,∴AC==.3.【解题指南】解答本题的关键是根据射影定理与已知的线段比，求出Rt △ACD中的的值.【解析】选C.在Rt△ABC中，∵CD⊥AB，∴由射影定理，得CD2＝AD·DB.由AD∶DB＝1∶4，设AD＝m，则DB＝4m，∴CD2＝4m2.∵m＞0，∴CD＝2m.在Rt△ACD中，tan ∠ACD＝=.4.【解析】选C.如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，且BC∶AC＝1∶3.由射影定理，得BC2＝BD·AB，AC2＝AD·AB，∴=，∴==()2=()2=.所以它们在斜边上射影的比是1∶9.【变式训练】在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D.若AC＝12，BC＝15，则S△ACD∶S△BCD＝( )(A)4∶5 (B)5∶12 (C)16∶25 (D)25∶16【解析】选C.在Rt△ABC中，由射影定理，得BC2＝BD·AB，AC2＝AD·AB，∴AD∶BD=AC2∶BC2.又∵S△ACD=·AD·CD,S△BCD=·BD·CD，∴S△ACD∶S△BCD=AD∶BD=AC2∶BC2.又∵AC=12,BC=15,∴S△ACD∶S△BCD=144∶225=16∶25.5.【解析】选A.如图，在Rt△ABC中，CD⊥AB，AC＝3 cm，CD＝2.4 cm.由勾股定理，得AD=＝1.8(cm).由射影定理，得AC2＝AD·AB，即32＝1.8×AB，∴AB＝5 cm.∴S△ABC＝AB·CD＝×5×2.4＝6(cm2).6.【解析】选D.如图(1)，由AD2=BD·CD，有AB2+AC2=BD2+CD2+2AD2=BD2+CD2+2BD·CD=(BD+CD)2，即AB2+AC2=BC2，可得∠BAC=90°，如图(2)，显然AD2=BD·CD，D点在△ABC外，则∠ACB＞90°，∴△ABC是直角或钝角三角形，故选D.7.【解析】由勾股定理，得CD3(cm).由射影定理，得AC2＝AD·AB，∴AB＝=.∴BD＝AB－AD＝－4＝.∵BC2＝BD·AB＝×，∴BC＝(cm).答案：38.【解析】设半径为R，由AD=3DB,得3DB+DB=2R ，∴DB=，AD=2R-=R.连接AC ，BC ，则CD 2=AD ·DB=R ·=R 2，∴tan 2 =tan 2∠CAB=CD 2∶AD 2=R 2∶(R)2=1∶3.答案：9.【解析】在△ABC 中，设AC=x,∵AB ⊥AC,AF ⊥BC,FC=1，根据射影定理，得AC 2=FC ·BC ，即BC=x 2.再由射影定理，得AF 2=BF ·FC=(BC-FC)·FC ，即AF 2=x 2-1.∴AF=.在△BDC 中,过D 作DE ⊥BC 于E,∵BD=DC=1,∴BE=EC.又∵AF ⊥BC ，∴DE ∥AF ， ∴2DE DC DC AF x DE AF AC AC =∴==，在Rt △DEC 中，∵DE 2+EC 2=DC 2,即()2+()2=12,∴=1.整理得x 6=4.∴x=.∴AC=.答案：【方法技巧】射影定理的妙用直角三角形中的射影定理在研究三角形相似、求线段的长度、三角形的面积、周长等方面有广泛的应用.应用时要注意是否是直角三角形，如果不是直角三角形，适当添加辅助线，构造直角三角形，做好问题的转化，使问题迎刃而解.10.【解题指南】在△ABC与△FEC中已具备条件∠ACB＝∠FCE(公共角)，由于题图中具备射影定理的基本图形，只要通过射影定理证明即可.【证明】∵CD⊥AB，∴∠ADC＝90°.在Rt△ACD中，DE⊥AC，由射影定理，得CD2＝EC·AC.同理CD2＝FC·BC.∴EC·AC＝FC·BC，∴.又∵∠ACB＝∠FCE(公共角)，∴△ABC∽△FEC.11.【证明】∵∠H=∠BCF，∠EBC=∠GBH，CE⊥BH，∴△BCE∽△BHG，∴∠BGH=90°，∴HG⊥BC.在Rt△BCD中，∵BD⊥DC，∴GD2=GB·GC. ①在△FCG和△FHE中，∵∠GFC=∠EFH，∠BCF=∠H，∴△FCG ∽△FHE ，∴∠FGC=∠FEH=90°.∴∠FGC=∠HGB=90°,∴△FCG ∽△BHG∴,即GB ·GC=GH ·GF, ②由①②得，GD 2=GH ·GF.【误区警示】证明比例中项问题，通常证明以比例中项的线段为公共边，且包含其他两条线段的两个三角形相似.而本题结论中的三条线段在同一条直线上，要注意借助三角形相似进行线段的转移.中间比或等积式是常见的方法之一.【挑战能力】【解析】∵∠ACB=90°,CD ⊥AB,∴AC 2=AD ·AB,BC 2=DB ·AB,∴.而AC 2+BC 2=AB 2, ∴2222AD AC 1AB DB AB AC ()1AC==--, 又AE 平分∠BAC,∴, ∴2AD 1165DB 9()14==-. 设AD=16a,DB=9a,∴CD 2=AD ·DB,即242=16a ·9a,解得a=2,∴AB=16a+9a=50.∴S△ABC=AB·CD=×50×24=600.。

高一数学直角三角形的射影定理试题

高一数学直角三角形的射影定理试题1.（2011•安徽模拟）如图，AB是半圆O的直径，点C在半圆上，CD⊥AB于点D，且AD=3DB，设∠COD=θ，则tan2=（）A．B．C．4﹣2D．3【答案】A【解析】由已知中AB是半圆O的直径，点C在半圆上，CD⊥AB于点D，且AD=3DB，我们可以设出圆的半径为R，进而根据射影定理求出CD的长，解三角形COD即可求出θ角，进而得到答案．解：设半径为R，则AD=R，BD=，由射影定理得：CD2=AD•BD则CD=R，从而θ=，故tan2=，故选A．点评：本题考查的知识点是直角三角形的射影定理，其中根据射影定理求出CD的长，解三角形COD即可求出θ角，是解答本题的关键2.如图所示，圆O上一点C在直径AB上的射影为D，CD=4，BD=8，则AD的长等于（）A．2B．4C．6D．8【答案】A【解析】直径所对的圆周角为直角，所以在Rt△ABC中CD是斜边AB上的高，可得△ADC∽△CDB，得到比例线段AD：DC=DC：DB，从而得到CD是AD、BD的比例中项，可算出AB的长．解：∵AB是圆O的直径∴AC⊥BC∴∠B+∠A=90°∵CD⊥AB∴∠B+∠DCB=90°∴∠DCB=∠A∴Rt△ADC∽Rt△CDB∴⇒DC2=AD•DB∵CD=4，BD=8∴AD=故选A点评：本题以圆中的直角三角形为例，考查了直角三角形的射影定理，属于基础题．找到题中的相似三角形，利用比例线段求长度，是此类问题的常用方法．3. Rt△ABC中，∠BAC=90°，AD⊥BC于点D，若，则=（）A．B．C．D．【答案】C【解析】在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，由射影定理可得AB2=BD•BC，AC2=CD•BC，即可得出．解：如图所示，∵Rt△ABC中，∠BAC=90°，AD⊥BC于点D，∴AB2=BD•BC，AC2=CD•BC，又．∴=．故选：C．点评：本题考查了直角三角形中的射影定理，属于基础题．4.如图，在矩形ABCD中，BD为对角线，AE⊥BD，，AD=1，则BE=（）A．1B．C．D．【答案】B【解析】矩形各内角为直角，在直角△ABD中，已知AB、AD，根据勾股定理即可求BD的值，根据直角三角形的射影定理，即可求解BE．解：矩形各内角为直角，∴△ABD为直角三角形在直角△ABD中，，AD=1，则BD==，再由射影定理，得AB2=BE×BD∴故选B．点评：本题考查了勾股定理在直角三角形中的运用，考查了直角三角形的射影定理，本题中根据勾股定理求BD的值是解题的关键．5.如图，已知在△ABC中，∠ACB=90°，CD⊥AB于D，AC=6，DB=5，则AD的长为（）A．3B．4C．5D．6【答案】B【解析】设AD长为x，由直角三角形的射影定理，构造关于x的方程，解方程可得答案．解：设AD长为x，∵在△ABC中，∠ACB=90°，CD⊥AB于D，由直角三角形的射影定理得：AC2=AD•AB，∵36=x（x+5），解得x=4，或x=﹣9（舍去），即AD的长为4，故选：B点评：本题考查的知识点是直角三角形的射影定理，熟练掌握直角三角形的射影定理，并由此构造关于x的方程，是解答的关键．6.（2010•湖北）设a＞0，b＞0，称为a，b的调和平均数．如图，C为线段AB上的点，且AC=a，CB=b，O为AB中点，以AB为直径做半圆．过点C作AB的垂线交半圆于D．连接OD，AD，BD．过点C作OD的垂线，垂足为E．则图中线段OD的长度是a，b的算术平均数，线段的长度是a，b的几何平均数，线段的长度是a，b的调和平均数．【答案】CD；DE【解析】在直角三角形中，由DC为高，根据射影定理可得CD2=AC•CB，变形两边开方，得到CD长度为a，b的几何平均数；根据a，b与OC之间的关系，表示出OC的长度，根据直角三角形OCE和直角三角形CDE之间边的关系得到CE的长，得到OE进而ED，得到结果．解：在Rt△ADB中DC为高，则由射影定理可得CD2=AC•CB，∴，即CD长度为a，b的几何平均数，将OC=代入OD•CE=OC•CD可得故，∴ED=OD﹣OE=，∴DE的长度为a，b的调和平均数．故选CD；DE点评：本题是一个新定义问题，解题过程中主要应用直角三角形边之间的比例关系，得到比例式，本题是一个平面几何与代数中的平均数结合的问题，是一个综合题．7.（2004•上海模拟）如图，Rt△ABC中，∠C=90°，CD⊥AB于D，BC=，AC=3，则BD=．【答案】【解析】应用勾股定理先求出AB，再由直角三角形射影定理，BC2="BD×BA" 代入数据求出BD．解：由勾股定理得AB===2．由直角三角形射影定理，BC2=BD×BA，3=2×BD，BD=故答案为：点评：本题考查直角三角形射影定理，牢记公式是前提．8.（2011•天津模拟）如图，已知Rt△ABC的两条直角边AC，BC的长分别为3cm，4cm，以AC为直径的圆与AB交于点D，则BD=cm．【答案】【解析】由已知Rt△ABC的两条直角边AC，BC的长分别为3cm，4cm，利用勾股定理，我们易求出AB的长，再由切割线定理，易得BD的长度．解：∵易知AB==5，又由切割线定理得BC2=BD•AB，∴42=BD•5∴BD=．故答案为：点评：本题是考查同学们推理能力、逻辑思维能力的好资料，题目以证明题为主，特别是一些定理的证明和用多个定理证明一个问题的题目，我们注意熟练掌握：1．射影定理的内容及其证明；2．圆周角与弦切角定理的内容及其证明；3．圆幂定理的内容及其证明；4．圆内接四边形的性质与判定．9.在△ABC外作正方形ABDE和正方形ACFG，已知BC=13，CA=8，AB=15，则△AEG的面积为．【答案】30．【解析】画出图形，在△ABC中，由三边求出cos∠BAC的值，从而得sin∠BAC的值，即得sin∠EAG的值，从而求出△AEG的面积．解：如图，△ABC中，cos∠BAC==；∴sin∠BAC=，∴sin∠EAG=sin∠BAC=；∴△AEG的面积为S△AEG=•AE•AG•sin∠EAG=×15×8×=30；故答案为：30．点评：本题考查了三角形面积公式的应用问题，解题时应画出图形，结合图形，寻找解答问题的思路与方法，是基础题．10.如图，在正方体ABCD﹣A1B1C1D1中，P为BD1的中点，则△PAC在该正方体各个面上的射影可能是．【答案】①④【解析】根据点的投影的做法，做出△PAC在该正方体各个面上的射影，这里应该有三种情况，做出在前后面上的投影，在上下面上的投影，在左右面上的投影，得到结果．解：由所给的正方体知，△PAC在该正方体上下面上的射影是①，△PAC在该正方体左右面上的射影是④，△PAC在该正方体前后面上的射影是④故答案为：①④点评：本题考查平行投影，考查在正方体内的一个三角形在正方体的各个面上的投影情况，要检验全面，做到不重不漏．。

人教新课标版数学高二-练习数学直角三角形的射影定理课时作业新人教A版选修4-1

【全程复习方略】高中数学第一讲四直角三角形的射影定理课时作业（含解析）新人教A 版选修4-11．一个直角三角形的一条直角边为3 cm ，斜边上的高为2.4 cm ，则这个直角三角形的面积为( )A ．7.2 cm2B ．6 cm2C ．12 cm2D ．24 cm2解析：选B.长为3 cm 的直角边在斜边上的射影为32－2.42＝1.8(cm)，故由射影定理知斜边长为321.8＝5(cm)．∴三角形的面积为12×5×2.4＝6(cm2)．2．如图，在Rt △ABC 中，∠ACB ＝90°，CD ⊥AB 于点D ，CD ＝2，BD ＝3，则AC ＝( ) A.2133B.133C.3133D.13解析：选A.由射影定理知CD2＝AD·BD，∴AD ＝CD2BD ＝43. ∴AC ＝ CD2＋AD2＝ 22＋432＝2133. 3．在Rt △ABC 中，∠BAC ＝90°，AD ⊥BC 于点D ，若AC AB ＝34，则BD CD ＝( ) A.34 B.43C.169D.916解析：选C.如图，由射影定理得，AC2＝CD·BC，AB2＝BD·BC，∴AC2AB2＝CD BD ＝(34)2，即CD BD＝916，∴BD CD ＝169.4．如图，在Rt △ABC 中，CD 是斜边AB 上的高，在图中的六条线段中，你认为只要知道几条线段的长，就可以求其他的线段的长( )A ．1B ．2C ．3D ．4解析：选B.由射影定理知CD2＝BD·AD，AB2＝AC2＋BC2，由此可以看出只要知道其中的两条就可以求出第三条线段．5．如图，在△ABC 中，CD ⊥AB 于D ，下列条件中，一定能确定△ABC 为直角三角形的个数为( )①∠1＝∠A ； ②CD AD ＝DB CD； ③∠B ＋∠2＝90°；④BC ∶AC ∶AB ＝3∶4∶5.A ．1B ．2C ．3D ．4解析：选C.①能．∵∠1＋∠B ＝90°，若∠1＝∠A ，则∠A ＋∠B ＝90°，∴△ABC 为直角三角形．②能．若CD AD ＝DB CD，则CD2＝AD·BD， ∴AB2＝(AD ＋BD)2＝AD2＋BD2＋2AD·BD＝AD2＋BD2＋2CD2＝(AD2＋CD2)＋(BD2＋CD2)＝AC2＋BC2，∴△ABC 为直角三角形．③不能．∠B ＋∠2＝90°，又∠B ＋∠1＝90°，则∠1＝∠2，并不能得到△ABC 为直角三角形．④能．设BC ＝3x ，AC ＝4x ，AB ＝5x ，则AB2＝BC2＋AC2，∴△ABC 为直角三角形．6．在△ABC 中，AC ⊥BC ，CD ⊥AB 于点D ，若AD ＝27，BD ＝3，则AC ＝________，BC ＝________，CD ＝________.解析：由射影定理，得CD2＝AD·BD，则CD ＝9.根据勾股定理，得AC ＝AD2＋CD2＝910，BC ＝BD2＋CD2＝310.答案：910 310 97．如图所示，四边形ABCD 是矩形，∠BEF ＝90°，①②③④这四个三角形能相似的是________．解析：因为四边形ABCD 为矩形，所以∠A ＝∠D ＝90°.因为∠BEF ＝90°，所以∠1＋∠2＝90°.因为∠2＋∠3＝90°，所以∠1＝∠3.又因为∠A ＝∠D ＝90°，所以△ABE ∽△DEF.答案：①③8．已知在梯形ABCD 中，DC ∥AB ，∠D ＝90°，AC ⊥BC ，AB ＝10 cm ，AC ＝6 cm ，则此梯形的面积为________．解析：如图，过C 点作CE ⊥AB 于E.在Rt △ACB 中，∵AB ＝10 cm ，AC ＝6 cm ，∴BC ＝8 cm.在Rt △ABC 中，由射影定理易得BE ＝6.4 cm ，AE ＝3.6 cm. ∴CE ＝ 6.4×3.6＝4.8(cm)，∴AD ＝4.8 cm.又∵在梯形ABCD 中，CE ⊥AB ，∴DC ＝AE ＝3.6 cm.∴S 梯形ABCD ＝10＋3.6×4.82＝32.64(cm2)．答案：32.64 cm29．如图，在△ABC 中，∠ACB ＝90°，CD ⊥AB ，AD ＝6 cm ，CD ＝2 3 cm ，求：(1)∠A 的度数；(2)△ABC 的面积．解：(1)在Rt △ACD 中，∵CD ＝2 3 cm ，AD ＝6 cm ，∴tan A ＝CD AD ＝236＝33，∴∠A ＝30°. (2)∵CD2＝AD·BD，∴BD ＝CD2AD ＝2326＝2(cm)． ∴AB ＝6＋2＝8 (cm)．∴S △AB C ＝12×AB×CD＝12×8×23＝8 3(cm2)．10．如图，在△ABC 中，AD 为BC 边上的高，过D 作DE ⊥AB ，DF ⊥AC ，E ，F 为垂足．求证：(1)AE·AB＝AF·AC；(2)△AEF ∽△ACB.证明：(1)∵AD ⊥BC ，DE ⊥AB ，DF ⊥AC ，在Rt △ABD 中，由射影定理得AD2＝AE·AB，在Rt △ADC 中，由射影定理得AD2＝AF·AC，∴AE·AB＝AF·AC.(2)∵AE·AB＝AF·AC，∴AE AC ＝AF AB . 又∵∠EA F ＝∠CAB ，∴△AEF ∽△ACB.11．已知直角三角形的周长为48 cm ，一锐角平分线分对边为3∶5两部分．(1)求直角三角形的三边长；(2)求两直角边在斜边上的射影的长．解：(1)如图，设CD ＝3x ，BD ＝5x ，则BC ＝8x ，过D 作DE ⊥AB ，由题意可得，DE ＝3x ，BE ＝4x ，∴AE ＋AC ＋12x ＝48.又AE ＝AC ，∴AC ＝24－6x ，AB ＝24－2x ，∴(24－6x)2＋(8x)2＝(24－2x)2，解得：x1＝0(舍去)，x2＝2，∴AB ＝20，AC ＝12，B C ＝16，∴三边长分别为：20 cm,12 cm,16 cm.(2)作CF ⊥AB 于F ，∴AC2＝AF·AB，∴AF ＝AC2AB ＝12220＝365(cm)；同理：BF ＝BC2AB ＝16220＝645(cm)．∴两直角边在斜边上的射影长分别为365 cm ，645 cm.。

射影定理练习

相似三角形之射影定理1、已知直角三角形ABC中，斜边AB=5cm,BC=2cm，D为AC上的一点，DE AB⊥交AB于E，且AD=3.2cm，则DE= （）A、1.24cmB、1.26cmC、1.28cmD、1.3cm2、如图1-1，在Rt ABC中，CD是斜别AB 上的高，在图中六条线段中，你认为只要知道（）线段的长，就可以求其他线段的长A、1B、2C、3D、43、在Rt ABC中，90BAC∠=，AD BC⊥于点D，若34ACAB=，则BDCD=（）A、34 B、43 C、169D、9164、如图1-2，在矩形ABCD中，1,3DE AC ADE CDE⊥∠=∠，则EDB∠=（）A、22.5B、30C、45D、60【填空题】5、ABC中，90A∠=，AD BC⊥于点D，AD=6，BD=12，则CD=，AC= ，22:AB AC= 。

6、如图2-1，在Rt ABC中，90ACB∠=，CD AB⊥，AC=6，AD=3.6，则BC= ．【解答题】7.如图,圆O 上一点C 在直径AB 上的射影为 D. AD=2,DB=8,求CD,AC 和BC 的长.8、已知CD 是ABC 的高，,DE CA DF CB ⊥⊥，如图3-1，求证：CEF CBA ∽9、已知90CAB ∠=，AD CB ⊥，ACE ，ABF 是正三角形，求证：DE DF ⊥10、△ABC 中，顶点C 在AB 边上的射影为D ，且CD ²=AD ·DB 求证： △ABC 是直角三角形。

ABDCABDCO如图3-2，矩形ABCD 中，AB=a ，BC=b ，M 是BC 的中点，DE AM ⊥，E 是垂足，求证：224DE a b =+参考答案1、C2、B3、C4、C5、3,35,4:1 6、 87、证明：在Rt ADC 中，由射影定律得，2CD CE AC =，在Rt BCD 中，2CD CF BC =,CE BCCE AC CF BC CF AC ∴=∴=又ECF BCA ∠=∠，CEF CBA ∴8、证明：如图所示，在Rt BAC 中，22,AC CD CB AB BD BC == 222AC CD CD CD CD ADAB BD CD BD AD AD BD ∴=====,,AE ADAC AE AB AF BF BD ==∴=60,60,FBD ABD EAD CAD ABD CAD ∠=+∠∠=+∠∠=∠又FBD EAD ∴∠=∠，,EAD FBD BDF ADE ∴∴∠=∠90FDE FDA ADE FDA BDF ∴∠=∠+∠=∠+∠=DE DF ∴⊥9、证明：在Rt AMB 和Rt ADE 中，AMB DAE ∠=∠，90ABM AED ∠=∠=所以Rt AMB ～Rt ADE所以AB AMDEAD =，因为AB=a ，BC=b ，所以224AB ADDE AMb a ===+（注：专业文档是经验性极强的领域，无法思考和涵盖全面，素材和资料部分来自网络，供参考。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2012-2013学年下学期高二文数限时练习（第1周）
满分：80分时间：40分钟 2013.02.23
1．如图1，∠ACB=90°，CD ⊥AB 于D ，AD=3，BD=2，
则AC ：BC 的值是( )
A ．3：2
B ．9：4
C ． 3：2
D ．2：3 2．在Rt △ACB 中，∠C=90°，CD ⊥AB 于D ，
若BD ：AD=1：4，则tan ∠BCD 的值是( ) A.
4
1 B. 3
1
C.
2
1 D. 2
3．下列命题中，正确的有( )
①两个直角三角形是相似三角形；②等边三角形都是相似三角形；
③锐角三角形都是相似三角形； ④两个等腰直角三角形是相似三角形． A ．1个 B. 2个 C. 3个 D ．4个
4．已知直角△ABC 中，斜边AB=5cm ，BC=2 cm ，D 为AC 上一点，DE ⊥AB 交AB
于E ，且AD=3.2cm ，则DE=( )
A ．1.24 cm
B ．1.26 cm
C ．1.28cm
D ．1.3 cm
5．在△ABC 中，∠ACB=90°，CD ⊥AB 于D ，AD ：BD=2：3，则△ACD 与
△CBD 的相似比为( )
A ．2：3
B ．4：9
C ．6：3
D ．不确定
6．在Rt △ABC 中，∠BAC=90°，AD ⊥BC 于点D ，若
4
3AB
AC =，则
=
CD
BD ( )
A.
4
3 B.
3
4 C.
9
16 D. 16
9
8．Rt △ABC 中，AC ⊥BC ，CD ⊥AB 于点D ，AD=4，sin ∠ACD=5
4，
则BC=_____，CD=_______。

9.如图1—4—2，在△ABC 中，∠BAC=90°，AD ⊥BC 于D ，DF ⊥AC 于F ，DE ⊥AB 于E 。

求证：(1)AB ·AC=AD ·BC ；(2)AD 3=BC ·BE ·CF
10．如图1—4—3，已知：BD 、CE 是△ABC 的两条高，
过点D 的直线交BC 和BA 的延长线于G 、H ，交CE 于F ，
且∠H=∠BCF 。

求证：GD 2=GF ·GH
图1—4—2
11.如图1—4—4，在△ABC中，AD⊥BC于D，DE⊥AB于E，
DF⊥AC于F。

求证：AE·AB=AF·AC
12．如图1—4—6，在梯形ABCD中，AD//BC，AC⊥BD，垂足为E，∠ABC=45°，过E作AD的垂线交AD于F，交BC于G，过E作AD的平行线交AB于H。

求证：FG2=AF·DF+BG·CG+AH·BH。

第 3 页共 3 页。