渐开线直齿轮啮合传动
标准渐开线齿轮直齿圆柱齿轮啮合传动
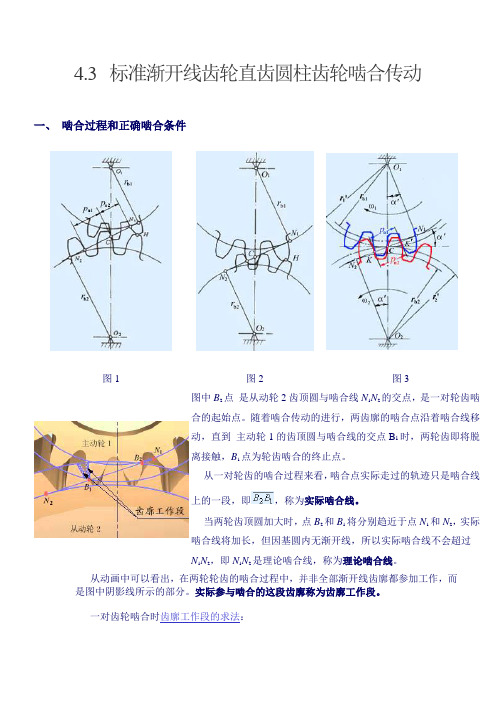
4.3 标准渐开线齿轮直齿圆柱齿轮啮合传动一、啮合过程和正确啮合条件图1 图2 图3图中B2点是从动轮2齿顶圆与啮合线N1N2的交点,是一对轮齿啮合的起始点。
随着啮合传动的进行,两齿廓的啮合点沿着啮合线移动,直到主动轮1的齿顶圆与啮合线的交点B1时,两轮齿即将脱离接触,B1点为轮齿啮合的终止点。
从一对轮齿的啮合过程来看,啮合点实际走过的轨迹只是啮合线上的一段,即,称为实际啮合线。
当两轮齿顶圆加大时,点B2和B1将分别趋近于点N1和N2,实际啮合线将加长,但因基圆内无渐开线,所以实际啮合线不会超过N1N2,即N1N2是理论啮合线,称为理论啮合线。
从动画中可以看出,在两轮轮齿的啮合过程中,并非全部渐开线齿廓都参加工作,而是图中阴影线所示的部分。
实际参与啮合的这段齿廓称为齿廓工作段。
一对齿轮啮合时齿廓工作段的求法:三个图中的齿轮都是渐开线齿轮,但图1和图2中的主动轮只能带动从动轮转过一个小角度就卡死不能动了,而图3中的主动轮可以带动从动轮整周转动,看来并不是任意两个渐开线齿轮都能正确地进行啮合,而是必须满足一定的条件,即正确啮合条件。
那么,这个条件是什么?从图3中可以看出:两个渐开线齿轮在啮合过程中,参加啮合的轮齿的工作一侧齿廓的啮合点都在啮合线N1N2上。
而在图1和图2中,工作一侧齿廓的啮合点H不在啮合线N1N2上,这就是两轮卡死的原因。
从图3中可以看出是齿轮1的法向齿矩,是齿轮2的法向齿矩,亦即:这个式子就是一对相啮合齿轮的轮齿分布要满足的几何条件,称为正确啮合条件。
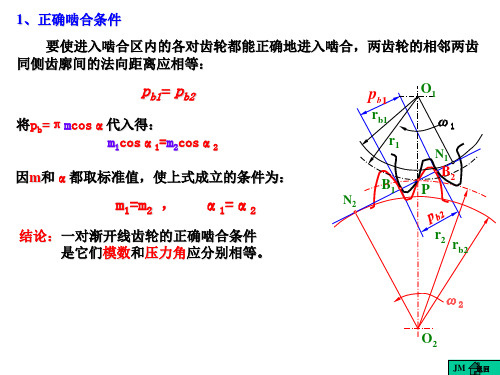
由渐开线性质可知,法向齿距与基圆齿距相等,故上式也可写成将和代入式中得:由于模数m和压力角均已标准化,不能任意选取,所以要满足上式必须使:结论:一对渐开线齿轮,在模数和压力角取标准值的情况下,只要它们分度圆上的模数和压力角分别相等,就能正确啮合。
二、齿轮传动的正确安装条件1、齿侧间隙为了避免齿轮在正转和反转两个方向的传动中齿轮发生撞击,要求相啮合的轮齿的齿侧没有间隙。
第三十九讲渐开线直齿圆柱齿轮的啮合传动
在主动轮顶圆与N1N2 线交点处B1脱离啮合。
B1B2 -实际啮合线
NN22
N1N2 :理论上可能的最长啮合线段 ——理论啮合线段
N1、N 2 ——啮合极限点
阴影线部分——齿廓的实际工作段。
O1 ω1 ra1
B2 NN11 P B1
ra2 rb2
ω2
O2
JM 返回
4、连续传动条件 为保证连续传动,要求: 实际啮合线段B1B2≥pb (齿轮的法向齿距),
r1’ = r1 α’=α
节线与分度线不重合
ra1
r1
rf1
O1
ω1
1
N1
B2 N2 B1P v2
α’=α
2
ra1
r1
rf1
O1
ω1
1
B2 N1 α’=α
N2
P
B1
v2
2
JM 返回
3、一对轮齿的啮合过程
轮齿在从动轮顶圆与N1N2 线交点B2处进入啮合,
主动轮齿根推动从动轮齿顶。
rb1
随着传动的进行,啮合点沿N1N2 线移动。
∴εα =[z1(tgαa1-tgα’) + z2(tgαa2-tgα’)]/2π
O1
ra1 B1
α’ rb1
αa1
P B2N1
N2 ra2
rb2 αa2
α’
O2
JM 返回
②齿轮齿条传动:
εα= B1B2/pb =(PB1+P B2)/πmcosα PB1 =z1mcosα(tgαa1-tgα’)/2 PB2=h*am/sinα
1、正确啮合条件
要使进入啮合区内的各对齿轮都能正确地进入啮合,两齿轮的相邻两齿 同侧齿廓间的法向距离应相等:
知识点渐开线直齿圆柱齿轮的啮合传动1正确啮合条件2渐开线齿轮

1 正确啮合条件
两齿轮的正确啮合条件为
m1 m2 m
1 2
即啮合条件为:Βιβλιοθήκη 轮的 模数和压力角必须分别 相等。
渐开线直齿圆柱齿轮的啮合传动
2 渐开线齿轮传动的重合度
齿轮传动是依靠两轮 的轮齿依次啮合而实 现的。
具体啮合及重合度的 概念观看右图演示。
r'
rb1
cos1'
rb 2
cos
' 2
(r1
r2
)
cos cos '
a
cos cos '
渐开线直齿圆柱齿轮的啮合传动
3.2.齿轮齿条啮合
齿轮齿条啮合时,相当于齿轮的分度圆与齿条的节圆作纯 滚动。标准安装时,齿条的节线与齿轮的分度圆相切。
此时, ' 当齿条圆离或靠近齿轮时,啮合线位置不 变,
啮合角不变,节点位置不变,齿轮与齿条啮合时齿轮的分度圆 永远与节圆重合,啮合角等于压力角。但只有标准安装时,齿 条的分度线才与节线重合。
渐开线直齿圆柱齿轮的啮合传动
渐开线直齿圆柱齿轮的啮合传动
3 渐开线齿轮的无侧隙啮合
3.1.外啮合传动 标准中心距
a r1' r' r1 r2 m(z1 z2 ) / 2
径向方向上留有间隙c
c (ha* c* )m ha*m c*m
非标安装时,中心距
a'
r1'
渐开线标准齿轮的啮合

r’1 = r1 r’2 = r2
定义:N1N2 线与Vc 之间的夹角,称为啮合角α’, O1 即节圆压力角。 标准安装时节圆与分度圆重合。 因此有:α’=α 且: rb1+rb2= a cosα
ω1 rb1 N1
C rb2 a
α’
N2
ω2 O2
小结(4-2—4-5中易混淆的内容)
一.注意: 就单个齿轮而言 就一对齿轮而言 有 分度园d 节圆d' 压力角 啮合角' 当标准齿轮正确安装时,才有: d'=d '= 二.齿轮的主要参数及几何尺寸计算
O1 ra1
c=c*m
ω1 rb1 r1 N1
P r2 rf2
ra1
c a rf2
N2 此时有: a=ra1+ c +rf2 rb2 *m =r1+ha*m +c + r2-(ha*m+c*m) =r1+ r2 =m(z1+z2)/2
a =r1+ r2
标准中心距
O2
ω2
标准安装
两轮节圆总相切: a=r’1+ r’2 =r1+ r2 两轮的传动比: i12 = r’2 / r’1 = r2 / r1
pb
2
O2
O1
1
N1 B2 B1 N2 C 法向齿距pn
基圆齿距pb
2
pn = pb
O2
1 B1B2= pb,正好满足连续传动。 实际啮合线 B1 N2 N1 B2 C
O1
pb
O2
2 2
B1B2> pb,前对轮齿在终止
实际啮合线B1 B2 O1 1 N1 B1 N2 C pb 2 O2 基圆齿距 (法向齿距) B2
渐开线齿轮传动

渐开线齿轮传动摘要:21世纪工业与制造业日新月异,齿轮由于其能实现定传动比、传动可靠性高、传动平稳等优点因此无论是工业还是制造业中齿轮都是极其重要的,早在2400多年前的东周时期,我国就已经出现了铜质的齿轮,我国古代的指南车中就大量运用了齿轮和齿轮系,由此可见我国使用齿轮的历史已经十分悠久,哪怕到了科学技术日新月异的今天齿轮在工业上的作用依旧是不可替代的,本文将就多种不同形式的渐开线齿轮的传动进行浅谈,同时对于齿轮中的一些基本参数进行了简单介绍。
关键词:渐开线、齿轮、啮合、传动1.渐开线直齿圆柱齿轮的啮合传动1.1.渐开线的形成当一直线BK沿一圆周作纯滚动运动时,直线上任意一点K的轨迹AK就是该圆的渐开线,该圆就叫做齿轮的基圆(base circle),其半径用r表示,任意b直线BK就称为渐开线的发生线(generating line),在发生线做纯滚动时会在表示,过K 点做基圆的切线该切基圆上形成一个展角(evolving angle),用θk线与基圆交于一点B,连接基圆圆心O与B点,OB与OK两直线的夹角称为渐开表示,压力角是表示齿轮传动性能的一个极其重要的参数,我线压力角,用αk们将在后文进行介绍。
根据渐开线形成的过程我们不难发现渐开线有以下重要性质:(1)发生线上在基圆上被滚过的弧长AB等于BK线段的长度。
(2)渐开线的曲率半径取决于基圆的大小,当基圆半径趋于无穷大时,此时齿轮将演化为齿条。
(3)基圆内部没有渐开线。
以上的性质在研究渐开线传动过程中十分重要,正因为渐开线具有这些重要性质,渐开线齿轮才在今天任是使用最普遍的齿轮形式,可以说对于渐开线齿轮的研究极大地推动了工业和制造业的发展。
1.2 渐开线直齿圆柱齿轮的啮合渐开线齿廓最大的优点就是能够满足定传动比传动。
但是两齿轮要想正确啮合还必须满足正确啮合条件。
一对渐开线齿轮在传动时,它们的齿廓啮合点都应位于啮合线N1,N2上,因此要使齿轮能正确啮合传动,应使处于啮合线上的各对轮齿都能同时进入啮合,为此两齿轮的法向齿距用pb表示,两齿轮法向齿距应相等,即式中,m1、m2及α1,α2分别为两齿轮的模数和压力角。
26渐开线直齿圆柱齿轮及啮合传动的特点和应用

《机械基础》教案(2009~ 2010学年第二学期)学院山西省工贸学校系(部)机电系教研室教师梁少宁山西省工贸学校③学生学案课题名称:渐开线直齿圆柱齿轮及啮合传动的特点和应用班级:姓名:(一)、工作任务:通过让学生观察齿轮的模型和圆柱齿轮的齿形,然后讨论圆柱齿轮的齿形特点和齿形在齿轮传动过程中能起什么作用。
(二)、学习目标:1、掌握渐开线的形成及性质2、了解齿廓的啮合的特点3、熟悉渐开线标准直齿圆柱齿轮基本参数、几何尺寸计算4、明了渐开线齿廓的啮合的特点(三)、回答问题1、齿轮传动对齿廓曲线的基本要求是什么?2、渐开线齿廓的啮合特点有那些?(四)、分析该资料,完成项目任务:一、齿轮传动对齿廓曲线的基本要求一是传动要平稳,二是承载能力要强二、渐开线的形成、性质1、渐开线的形成当一条动直线(发生线),沿着一个固定的圆(基圆)作纯滚动时,动直线上任意一点K的轨迹称为该圆的渐开线。
2、渐开线的性质由渐开线的形成可知:(1)发生线在基圆上滚过的线段KB,等于基圆上被滚过的圆弧长AB。
(2)渐开线上的任意一点K的法线必与基圆相切。
点离基圆越远,其曲率半径越大,渐开线越平直。
反之亦然。
(4)渐开线的形状决定与基圆的大小。
基圆相同,渐开线的形状完全相同。
基圆半径无穷大时,渐开线将变成直线,齿轮就变成齿条。
(5)基圆内无渐开线。
二、渐开线齿廓啮合基本定律齿轮传动要满足瞬时传动比保持不变,则两轮的齿廓不论在何处接触,过接触点的公法线必须与两轮的连心线交于固定的一点。
三、渐开线齿廓的啮合特点1、传动比恒定2、两齿轮的传动比与两节圆半径成反比,同时与两基圆半径成反比。
由于两啮合齿轮的节圆半径、基圆半径是定值,所以能保证传动比恒定3、传动的可分性当两轮的中心距稍有变化时,其瞬时传动比仍将保持不变,这个特点称为渐开线齿轮传动的可分性。
4、由于齿轮制造和安装误差等原因,常使渐开线齿轮的实际中心距与设计中心距之间产生一定误差,但因有可分性的特点,其传动比仍能保持不变。
渐开线标准直齿圆柱齿轮的啮合传动

渐开线直齿圆柱齿轮
图10-5 渐开线齿轮传动的啮合特性
返回
机械设计基础
Machine Design Foundation
渐开线直齿圆柱齿轮的啮合传动
1.传动比的恒定性 由图10-5,可推得齿轮传动的瞬时传动比
i12
1 2
vK1 / O1K vK 2 / O2 K
O1和O2为圆心,过节点P作两个相切的圆,称为节圆。节圆半径r'1=
O1P,r'2= O2P。所以
i12
1 2
rb 2 rb1
r2 ' r1 '
(10-11)
即一对渐开线齿轮传动的瞬时传动比也等于两节圆半径的反比。
2.啮合角的不变性
一对齿轮通过齿廓的直接接触来传递运动和动力,所有啮合点
都在啮合线上。当不计摩擦时,其齿廓间的正压力将沿接触点的公
B2 B1 1
(10-15)
pb
返回
机械设计基础
Machine Design Foundation
渐开线直齿圆柱齿轮的啮合传动
1.4 安装中心距和标准安装中心距
一对外啮合渐开线标准齿轮传动的安装中心距a'是两齿轮节圆
半径之和,即a'=r1'+ r2'。由式(10-1)可得 r'= rb/cosα',式中α'是节
1.2 渐开线齿轮的正确啮合条件
如图10-6a所示,设相邻两齿同侧齿廓与啮合线(也是公法线)
N1N2的交点分别为K1和K2,线段K1K2的长度称为齿轮的法向齿距。 要使两轮正确啮合,它们的法向齿距必须相等。由渐开线的性质可
知,法向齿距等于两轮基圆上的齿距。因此,要使两轮正确啮合,
§10—5渐开线直齿圆柱齿轮的啮合传动

△=e2′-s1′= e1′-s2′ 但为了使齿轮在正转和反转 时避免轮齿间的冲击,这种齿侧 间隙一般都很小,通常是由制造 公差来保证的。而在设计、计算 齿轮的公称尺寸时,都按无侧隙 来考虑,即△=0。 由图10-13可见,侧隙的大小 与中心距的大小有关。
2)保证两轮的顶隙c为标准值,即c=c*m。 在一轮的齿顶圆 与另一轮的齿根圆之 间应留有一定的间隙, 称为顶隙。顶隙的标 准值为c=c*m。 由图可见,顶隙 的大小也与中心距大 小有关。
图10-17
2、重合度(Contact 、
Ratio)
通常把B1B2与pb的比值εα称为齿轮传动的重合度 重合度。其 重合度 大小反映了齿轮连续传动的程度。则: εα= B1B2 / pb≥1——连续传动条件 在实际的工程中,应要求εα≥[εα](许用重合度 许用重合度)。 [εα] 许用重合度 随齿轮机构的使用要求和制造精度而定,常用的推荐值见 P184表10-3。
∵ a= r1 +r2= r1′+r2′ 且i12= r2′/ r1′= r2 / r1 ∴ r1= r1′, r2= r2′即分度圆 与节圆重合,两个分度圆 相切。 这种按标准中心距 (即分度圆与节圆重合) 的安装,称为标准安装 标准安装。 标准安装
在标准安装时: ∵ 标准齿轮分度圆上:s1= e1= s2=e2=πm/2,且分度圆与 节圆重合 ∴ s1′= e1′= s2′=e2′=πm/2 ∴ △=e2′-s1′= e1′-s2′=0 ——无侧隙条件 ∴ 标准齿轮在标准安装时,能满足无侧隙啮合的要求。
图10-13 a
2、标准中心距和标准安装 、 当顶隙为标准值c=c*m 时,设中心距为a,则 a = ra1+ c + rf2 =r1+ha*m+c*m+r2-( ha*+c*)m = r1 +r2 = m ( z1 + z2 ) / 2 即两轮的中心距a等 于两轮的分度圆半径之和。 我们把这种中心距称为标 标 准中心距。 准中心距
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§10-7 渐开线直齿圆柱齿轮的啮合传动
①正确地啮合传动条件
②正确安装条件
③连续传动条件
m1
m2
一、正确地啮合的条件P.310
应:B 11B 21 = B 12B 22
N 1N 2 :
接触点处公法线
基圆内公切线
啮合线
∴p b 1= B 11B 21=p b 2= B 12B 22
πm 1cos α1= πm 2 cos α2
∴一对标准齿轮正确啮合条件:
α1= α2 m 1= m 2= 200标准系列
中心距与啮合角图
二、中心距及啮合角
1.外啮合
⑴中心距
设:实际中心距为a’;标准中心距为a;
正确安装即是使a保证侧隙和顶隙满足要求:
无侧隙
顶隙为标准值c* m
①无侧隙
可以推出无侧隙时应满足的几何条件是:
节圆上:e
1’= s
2
’
s1’= e2’而:p
1
’=e
1
’+ s1’
p2’= e2’+ s2’
∴p
1’= p
2
’
②. 标准顶隙c = c* m
a ’= r f1 + c* m + r a2= m ( z 1+ z 2 ) / 2 = r 1 + r 2 = a 称为标准中心距
∴当中心距a ’按标准中心距a 安装时可保证标准顶隙c* m
这时又知:a ’= r 2’+ r 1’
∴r 2’+ r 1’= r 1 + r 2
又:i 12= r 2/ r
1
可知:r 1’= r 1;r 2’= r
2
结论:两个标准齿轮按标准中心距安装时,两轮分度圆
分别与其节圆重合。
但a ’≠ a 时,则不重合。
图标准安装令
中心距按标准中心距安装是否满足无侧隙要求?对于标准齿轮:e = s = p / 2= m π / 2
正确啮合时:m 1= m 2 = m
∴e 1= s 1= s 2 =e 2 = m π / 2
满足:e 1’= s 2’
s 1’= e 2’标准中心距时:e 1= s 1= s 2 =e 2 = e 1’= s 1’= s 2 ’=e 2 ’
无侧隙条件
结论:中心距按标准中心距安装,既可满足无侧隙又可
满足标准顶隙。
⑵啮合角α’
定义:一对齿轮传动时,节点p的线速度方向与啮合线所夹的锐角α’-----实际上是啮合线的倾斜角,故称啮合角。
由定义可知:α’= 节圆上压力角,∴α’小好
当a’= a = r
2+ r1时,节圆与分度圆重合,有α’=
α
当a’≠ a = r
2
+ r1时,节圆与分度圆不重合,有:α’≠ αr b1= r1’cosα’= r b1= r1cosα
r b2= r2’cosα’= r b2= r2cosα
∴(r
1’+ r
2
’)cosα’= (r
1
+ r2 )
cosα
a’cosα’= a
cosα
可见当a’= a = r
+ r1时:
2
①满足无侧隙
②满足标准顶隙
③分度圆与节圆重合:r’= r
④α’= α
2.齿轮与齿条啮合
xm
分度线
无论齿轮与齿条是否按标准安装、分度圆与分度线距离xm 为多少,均有特点:
①α’= α∵齿条廓为直线
②齿轮的节圆恒与分度圆重合
三、一对轮齿的传动过程
1. 一对轮齿开始啮合:
起始啮合点啮合点B 2----在从动轮的齿顶圆ra2上
同一对轮齿退出啮合:终止啮合点啮合点B 1----在主动轮的齿顶圆ra1上
B 2
2. 实际啮合线段
啮合点轨迹B 2→B 1 ,实际啮合线段是N 1 N 2上B 1 B 2段可见,B 1 B 2实际上是两齿顶圆与N 1 N 2 的交点要了解:①一对轮齿何处开始和何处退出啮合
②实际啮合点的轨迹----即实际啮合线段在N 1N 2 的哪一部分
又可见,若使r a 1 、r a 2↑ →B 1 B 2↑
故,B 1 B 2 最大只能与N 1 N 2相等----难以做到r a 2 ↑至r a 2’,也不能超过N 1 点
故N 1 N 2称为理论啮合线段
而N 1、N 2 称为啮合极限点若r a 1 ↑至r a 1’,但B 1不能超过点N 2
N 2N 1B 1
B 2
r a 1r a 1’
r a 2r b2r b1O 1O 2
ω1
B1B2 =p b
B1B2 > p b
B1B2 <p b
连续传动:一对齿轮的啮合传动不仅不能中断,且要保持传动比不变。
即:
四、渐开线齿轮连续传动的条件
一对轮齿啮合已到终止啮合点,即要“交班”→为
保证连续→相邻下一对轮齿必须已“接班”(或正好接
班)极限情况极限时:B 1B 2 = p b
若r a 2 ↓使B 1B 2 ﹤p b ---未能及时“接班”→传动不连续
故要实现连续传动,必须B 1B 2 ≥p b
或B 1B 2 / p b ≥1令εa = B 1
B 2 / p b
称为重合度显然,要能实现连续传动,则须:εa ≥ 1
εa 表示了B 1B 2上有几个基节,即表示了有几对齿同时啮合。
如:εa =1.45 表示有1.45 对齿同时啮合,实际上表示:1 -0.45 = 0.55→ 在B 1B 2上有0.55p b 长度的区段为一对齿轮啮合,其余区段为两对齿轮啮合
εa = B 1B 2 / p b =1.45 ↑→传动平稳
εa = 1 →无双齿啮合区→ 危险
∴要验算:εa ≥ [ εa ](见P.317表10-3)
εa 计算式见P.317式10-16
由公式可见,εa 与下列参数关系:
①εa 与m 无关
②i 一定时,z ↑, →εa ↑
③α’↓, αa2 ↑h a * ↑, →εa ↑
⑴. i = w 1/ w 2= n 1 / n 2 = r 2’/ r 1’= r b2 / r b1= r 2 / r 1 = z 2 / z 1标准渐开线直齿圆柱齿轮公式
⑵. a ’= O 1O 2= r 2’+ r 1’标准中心距:a = r 2’+ r 1’= r 2+ r 1⑶. r k = r b /cos αk r b =r k cos αk r b = rcos α d b =d cos= mzcos α ⑷.d = mz
⑸p = m π
⑹. h a = h a * ×m
⑺. h f * = h a * m + c* m
⑻. d a = d + 2 h a = d + 2 h a * m
⑼. d f = d -2 h f = d -2 h a * m -2 c* m
⑽. p b = p cos α = m π cos α
⑾. 标准齿轮:e = s = p / 2 = m π / 2 一②⑿a ’cos α’= a cos
α。
