最新回归分析练习题(有答案)
统计学:相关回归分析习题与答案

一、单选题1、下列哪种关系属于相关关系而非函数关系?()A.销售总额与销售量B.价格与销售量C.工资总额与人均工资D.圆的面积与半径正确答案:B解析: B、函数关系是指现象之间存在的确定性的数量依存关系。
2、若两个变量之间的线性相关系数为0.9,则()。
A.回归系数为0.81B.判定系数为0.81C.回归估计标准误为0.81D.判定系数为0.95正确答案:B3、下列指标一定非负的是()。
A.回归系数bB.相关系数rC.回归估计标准误S yxD.回归常数a正确答案:C4、在回归直线方程中y c=a+bx,b 是直线的斜率,表明()。
A.当x 增加一个单位时,y 增加a的数量B.当y 增加一个单位时,x 的平均增加量C.当y 增加一个单位时,x 增加b的数量D.当x 增加一个单位时,y 的平均增加量正确答案:D5、相关系数r与回归系数b的关系是()。
A. b=r×S x/S yB. b=r×S y/S xC. r=b×S y/S xD. 以上都不对正确答案:B6、当所有的观察值y都落在直线y c=a+bx上时,x与y之间的相关系数是()。
A. r=1B.r=-1C. |r|=1D.r=0正确答案:C解析:当r=1或r=-1时,表示变量之间为完全相关7、相关系数r=0表示()。
A.不存在相关关系B.两变量独立C.不存在线性相关关系D.存在平衡关系正确答案:C8、对相关系数的显著性检验,通常采用的是()。
A.Z检验B.F检验C.χ2检验D.T检验正确答案:D9、线性回归的检验中,检验整个方程显著性的是()。
A.F检验B.DW检验C.t检验D.R检验正确答案:A10、下列现象的相关密切程度高的是A.商品销售额与商业利润率之间的相关系数是0.62B.商品销售额与流通费用率之间的相关系数为-0.76C.某商店职工人数与商品销售额之间的相关系数为0.79D.流通费用率与商业利润率之间的相关系数是-0.89正确答案:D二、多选题1、下列属于负相关的现象是()。
回归分析练习试题和参考答案解析

1 下面是7个地区2000年的人均国内生产总值(GDP)和人均消费水平的统计数据:求:(1)人均GDP作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
α=)。
(5)检验回归方程线性关系的显著性(0.05(6)如果某地区的人均GDP为5000元,预测其人均消费水平。
(7)求人均GDP为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:系数a模型非标准化系数标准系数t Sig.相关性B标准误差试用版零阶偏部分1(常量).003人均GDP.309.008.998.000.998.998.998 a. 因变量: 人均消费水平有很强的线性关系。
(3)回归方程:734.6930.309y x=+系数a模型非标准化系数标准系数t Sig.相关性回归系数的含义:人均GDP没增加1元,人均消费增加元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型非标准化系数标准化系数t显著性B标准误Beta1(常量)人均GDP(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(4)模型汇总模型R R 方调整 R 方标准估计的误差1.998a.996.996a. 预测变量: (常量), 人均GDP。
人均GDP对人均消费的影响达到%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
模型摘要模型R R 方调整的 R 方估计的标准差1.998(a)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(5)F检验:Anova b模型平方和df均方F Sig.1回归.6801.680.000a 残差5总计.7146a. 预测变量: (常量), 人均GDP。
最新应用回归分析-第6章课后习题参考答案

第6章多重共线性的情形及其处理思考与练习参考答案6.1 试举一个产生多重共线性的经济实例。
答:例如有人建立某地区粮食产量回归模型,以粮食产量为因变量Y,化肥用量为X1,水浇地面积为X2,农业投入资金为X3。
由于农业投入资金X3与化肥用量X1,水浇地面积X2有很强的相关性,所以回归方程效果会很差。
再例如根据某行业企业数据资料拟合此行业的生产函数时,资本投入、劳动力投入、资金投入与能源供应都与企业的生产规模有关,往往出现高度相关情况,大企业二者都大,小企业都小。
6.2多重共线性对回归参数的估计有何影响?答:1、完全共线性下参数估计量不存在;2、近似共线性下OLS估计量非有效;3、参数估计量经济含义不合理;4、变量的显著性检验失去意义;5、模型的预测功能失效。
6.3 具有严重多重共线性的回归方程能不能用来做经济预测?答:虽然参数估计值方差的变大容易使区间预测的“区间”变大,使预测失去意义。
但如果利用模型去做经济预测,只要保证自变量的相关类型在未来期中一直保持不变,即使回归模型中包含严重多重共线性的变量,也可以得到较好预测结果;否则会对经济预测产生严重的影响。
6.4多重共线性的产生于样本容量的个数n、自变量的个数p有无关系?答:有关系,增加样本容量不能消除模型中的多重共线性,但能适当消除多重共线性造成的后果。
当自变量的个数p较大时,一般多重共线性容易发生,所以自变量应选择少而精。
6.5 自己找一个经济问题来建立多元线性回归模型,怎样选择变量和构造设计矩阵X才可能避免多重共线性的出现?答:请参考第三次上机实验题——机场吞吐量的多元线性回归模型,注意利用二手数据很难避免多重共线性的出现,所以一般利用逐步回归和主成分回归消除多重共线性。
如果进行自己进行试验设计如正交试验设计,并收集数据,选择向量使设计矩阵X 的列向量(即X 1,X 2, X p )不相关。
6.6对第5章习题9财政收入的数据分析多重共线性,并根据多重共线性剔除变量。
(完整版)数学必修三回归分析经典题型(带答案)

数学必修三回归分析经典题型1.一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归模型为93.7319.7ˆ+=x y用这个模型预测这个孩子10岁时的身高,则正确的叙述是( ) A.身高一定是145.83cm B.身高在145.83cm 以上 C.身高在145.83cm 以下 D.身高在145.83cm 左右 【答案】D【解析】解:把x=10代入可以得到预测值为145.83,由于回归模型是针对3-9岁的孩子的,因此这个仅仅是估计值,只能说左右,不能说在上或者下,没有标准。
选D2.对有线性相关关系的两个变量建立的线性回归方程$y =$a+b $x ,关于回归系数b $,下面叙述正确的是________.①可以小于0;②大于0;③能等于0;④只能小于0. 【答案】①【解析】由b$和r 的公式可知,当r =0时,这两变量不具有线性相关关系,但b 能大于0也能小于0.3.对具有线性相关关系的变量x 、y 有观测数据(x i ,y i )(i =1,2,…,10),它们之间的线性回归方程是$y =3x +20,若101i i x =∑=18,则101i i y =∑=________.【答案】254【解析】由101i i x =∑=18 1.8.因为点在直线$y =3x +2025.4. 所以101i i y =∑=25.4×10=254.4.下表是某厂1~4由散点图可知,用水量其线性回归直线方程是y =-0.7x +a ,则a 等于________. 【答案】5.252.53.5,∵回归直线方程过定点, ∴3.5=-0.7×2.5+a. ∴a =5.25.5.由一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )得到线性回归方程$y =b$x +$a ,那么下列说法正确的是________.①直线$y =b$x +$a 必经过点(x ,y ); ②直线$y =b$x +$a 至少经过点(x 1,y 1),(x 2,y 2),…,(x n ,y n )中的一个点; ③直线$y =b$x +$a 的斜率为1221ni ii nii x ynx y xnx==--∑∑;④直线$y =b $x +$a 和各点(x 1,y 1),(x 2,y 2),…,(x n ,y n )的偏差$21()ni i i b a y x =⎡⎤⎣⎦∑$-+是该坐标平面上的直线与这些点的最小偏差.【答案】①③④【解析】回归直线的斜率为b ,故③正确,回归直线不一定经过样本点,但一定经过样本中心,故①正确,②不正确.6.某数学老师身高176 cm ,他爷爷、父亲和儿子的身高分别是173 cm 、170 cm 和182 cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为________cm. 【答案】185【解析】设父亲身高为173176,b$= $a=-b $ 176-1×173=3, ∴$y =x +3,当x =182时,$y =185.7.下表是关于宿州市服装机械厂某设备的使用年限(年)和所需要的维修费用y (万元)的几组统计数据:)请根据上表提供的数据,用最小二乘法求出y 关于的线性回归方程;(2)估计使用年限为10年时,维修费用为多少?【答案】解:(1)0.08 1.23yx =+线性回归方程为 (2)估计使用年限为10年时,维修费用为12.38万元. 【解析】(1)先求然后利用公可求出回归直线y ax b =+方程.(2)把x=10代入回归直线方程可得y 的值,就可得所求的值.解:(1906543222222512=++++=∑=i ixΘ又x y 23.108.0+=∴线性回归方程为 (2)把10=x 代入回归方程得到:38.121023.108.0=⨯+=y∴估计使用年限为10年时,维修费用为12.38万元.。
回归分析练习题及参考答案
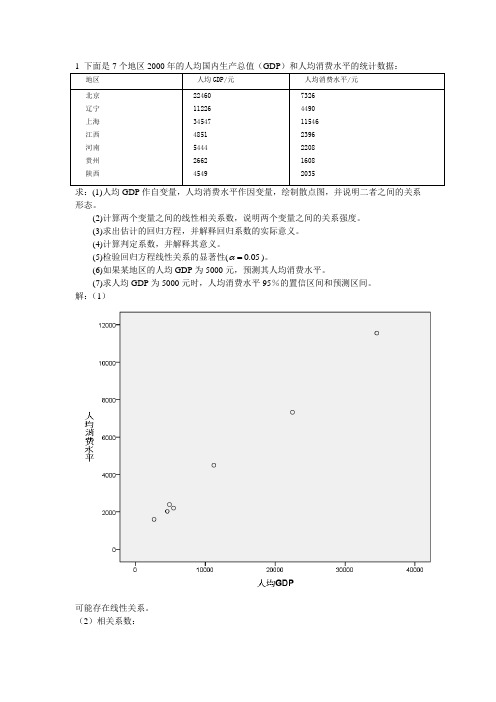
求:(1)人均GDP 作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
(5)检验回归方程线性关系的显著性(0.05α=)。
(6)如果某地区的人均GDP 为5000元,预测其人均消费水平。
(7)求人均GDP 为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:(3)回归方程:734.6930.309y x=+回归系数的含义:人均GDP没增加1元,人均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 (常量)734.693 139.540 5.265 0.003人均GDP(元)0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%人均GDP对人均消费的影响达到99.6%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
模型摘要模型R R 方调整的R 方估计的标准差1 .998(a) 0.996 0.996 247.303a. 预测变量:(常量), 人均GDP(元)。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(5)F 检验:回归系数的检验:t 检验注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型 非标准化系数标准化系数t 显著性B 标准误 Beta1(常量) 734.693 139.540 5.2650.003 人均GDP (元)0.3090.0080.99836.4920.000a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(6)某地区的人均GDP 为5000元,预测其人均消费水平为 734.6930.30950002278.693y =+⨯=(元)。
回归分析练习题

1. 从20的样本中得到的有关回归结果是:SSR=60,SSE=40。
要检验x 与y 之间的线性关系是否显著,即检验假设:01:0H β=。
(1)线性关系检验的统计量F 值是多少? (2)给定显著性水平a =0.05,F a 是多少? (3)是拒绝原假设还是不拒绝原假设?(4)假定x 与y 之间是负相关,计算相关系数r 。
(5)检验x 与y 之间的线性关系是否显著?解:(1)SSR 的自由度为k=1;SSE 的自由度为n-k-1=18;因此:F=1SSR k SSE n k --=6014018=27 (2)()1,18F α=()0.051,18F =4.41 (3)拒绝原假设,线性关系显著。
(4),由于是负相关,因此r=-0.7746(5)从F 检验看线性关系显著。
2. 某汽车生产商欲了解广告费用(x)对销售量(y)的影响,收集了过去12年的有关数据。
通过计算得到下面的有关结果:(1)完成上面的方差分析表。
(2)汽车销售量的变差中有多少是由于广告费用的变动引起的?(3)销售量与广告费用之间的相关系数是多少?(4)写出估计的回归方程并解释回归系数的实际意义。
(5)检验线性关系的显著性(a=0.05)。
(2)R2=0.9756,汽车销售量的变差中有97.56%是由于广告费用的变动引起的。
(3)r=0.9877。
(4)回归系数的意义:广告费用每增加一个单位,汽车销量就增加1.42个单位。
(5)回归系数的检验:p=2.17E—09<α,回归系数不等于0,显著。
回归直线的检验:p=2.17E—09<α,回归直线显著。
3. 根据两个自变量得到的多元回归方程为12ˆ18.4 2.014.74yx x =-++,并且已知n =10,SST =6 724.125,SSR =6 216.375,1ˆ0.0813s β=,2ˆs β=0.056 7。
要求:(1)在a=0.05的显著性水平下,12,x x 与y 的线性关系是否显著? (2)在a =0.05的显著性水平下,1β是否显著?(3)在a =0.05的显著性水平下,2β是否显著?解(1)回归方程的显著性检验:假设:H 0:1β=2β=0 H 1:1β,2β不全等于0 SSE=SST-SSR=6 724.125-6 216.375=507.75 F=1SSR p SSE n p --=6724.1252507.751021--=42.85()2,7F α=4.74,F>()2,7F α,认为线性关系显著。
最新回归分析练习题(有答案)

最新回归分析练习题(有答案)1.1回归分析的基本思想及其初步应⽤⼀、选择题 1. 某同学由x 与y 之间的⼀组数据求得两个变量间的线性回归⽅程为y bx a =+,已知:数据x 的平均值为2,数据y 的平均值为3,则 ( )A .回归直线必过点(2,3)B .回归直线⼀定不过点(2,3)C .点(2,3)在回归直线上⽅D .点(2,3)在回归直线下⽅2. 在⼀次试验中,测得(x,y)的四组值分别是A(1,2),B(2,3),C(3,4),D(4,5),则Y 与X 之间的回归直线⽅程为()A .$yx 1=+B .$y x 2=+C .$y 2x 1=+ D.$yx 1=-3. 在对两个变量x ,y 进⾏线性回归分析时,有下列步骤:①对所求出的回归直线⽅程作出解释;②收集数据(i x 、i y ),1,2i =,…,n ;③求线性回归⽅程;④求未知参数;⑤根据所搜集的数据绘制散点图如果根据可⾏性要求能够作出变量,x y 具有线性相关结论,则在下列操作中正确的是() A .①②⑤③④ B .③②④⑤① C .②④③①⑤ D .②⑤④③①4. 下列说法中正确的是()A .任何两个变量都具有相关关系B .⼈的知识与其年龄具有相关关系C .散点图中的各点是分散的没有规律D .根据散点图求得的回归直线⽅程都是有意义的5. 给出下列结论:(1)在回归分析中,可⽤指数系数2R 的值判断模型的拟合效果,2R 越⼤,模型的拟合效果越好;(2)在回归分析中,可⽤残差平⽅和判断模型的拟合效果,残差平⽅和越⼤,模型的拟合效果越好;(3)在回归分析中,可⽤相关系数r 的值判断模型的拟合效果,r 越⼩,模型的拟合效果越好;(4)在回归分析中,可⽤残差图判断模型的拟合效果,残差点⽐较均匀地落在⽔平的带状区域中,说明这样的模型⽐较合适.带状区域的宽度越窄,说明模型的拟合精度越⾼.以上结论中,正确的有()个.A .1B .2C .3D .4 6. 已知直线回归⽅程为2 1.5y x =-,则变量x 增加⼀个单位时(A.y 平均增加1.5个单位B.y 平均增加2个单位C.y 平均减少1.5个单位D.y 平均减少2个单位7. 下⾯的各图中,散点图与相关系数r 不符合的是()8. ⼀位母亲记录了⼉⼦3~9岁的⾝⾼,由此建⽴的⾝⾼与年龄的回归直线⽅程为?7.1973.93yx =+,据此可以预测这个孩⼦10岁时的⾝⾼,则正确的叙述是()A .⾝⾼⼀定是145.83cmB .⾝⾼超过146.00cmC .⾝⾼低于145.00cmD .⾝⾼在145.83cm 左右9. 在画两个变量的散点图时,下⾯哪个叙述是正确的( ) (A)预报变量在x 轴上,解释变量在y 轴上 (B)解释变量在x 轴上,预报变量在y 轴上 (C)可以选择两个变量中任意⼀个变量在x 轴上 (D)可以选择两个变量中任意⼀个变量在y 轴上10. 两个变量y 与x 的回归模型中,通常⽤2R 来刻画回归的效果,则正确的叙述是()A. 2R 越⼩,残差平⽅和⼩B. 2R 越⼤,残差平⽅和⼤C. 2R 于残差平⽅和⽆关 D. 2R 越⼩,残差平⽅和⼤ 11. 两个变量y 与x 的回归模型中,分别选择了4个不同模型,它们的相关指数2R 如下,其中拟合效果最好的模型是( )A.模型1的相关指数2R 为0.98B.模型2的相关指数2R 为0.80C.模型3的相关指数2R 为0.50 D.模型4的相关指数2R 为0.2512. 在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是( ) A.总偏差平⽅和 B.残差平⽅和 C.回归平⽅和 D.相关指数R 2产率为1000元时,⼯资为90元14. 下列结论正确的是()①函数关系是⼀种确定性关系;②相关关系是⼀种⾮确定性关系;③回归分析是对具有函数关系的两个变量进⾏统计分析的⼀种⽅法;④回归分析是对具有相关关系的两个变量进⾏统计分析的⼀种常⽤⽅法.A.①②B.①②③C.①②④D.①②③④15. 已知回归直线的斜率的估计值为1.23,样本点的中⼼为(4,5),则回归直线⽅程为()A.$1.234y x =+B.$1.235y x =+ C.$1.230.08y x =+ D.$0.08 1.23y x =+ ⼆、填空题16. 在⽐较两个模型的拟合效果时,甲、⼄两个模型的相关指数2R 的值分别约为0.96和0.85,则拟合效果好的模型是.17. 在回归分析中残差的计算公式为.18. 线性回归模型y bx a e =++(a 和b 为模型的未知参数)中,e 称为.19. 若⼀组观测值(x 1,y 1)(x 2,y 2)…(x n ,y n )之间满⾜y i =bx i +a+e i (i=1、2.…n)若e i 恒为0,则R 2为_____三、解答题20. 调查某市出租车使⽤年限x和该年⽀出维修费⽤y(万元),得到数据如下:使⽤年限x 2 3 4 5 6维修费⽤y2.2 3.8 5.5 6.5 7.0(2)由(1)中结论预测第10年所⽀出的维修费⽤.(121()()()ni iiniix x y yb==-?-=-=-∑∑)21. 以下是某地搜集到的新房屋的销售价格y和房屋的⾯积x的数据:(1)画出数据对应的散点图;(2)求线性回归⽅程,并在散点图中加上回归直线;(3)据(2)的结果估计当房屋⾯积为2150m时的销售价格.(4)求第2个点的残差。
回归分析习题及答案.doc

1.1回归分析的基本思想及其初步应用例题:1.在画两个变量的散点图时,下面哪个叙述是正确的()(A)预报变量在x轴上,解释变量在y轴上(B)解释变量在X轴上,预报变量在y轴上(0可以选择两个变量中任意一个变量在x轴上(D)可以选择两个变量中任意一个变量在y轴上解析:通常把自变量X称为解析变量,因变量y称为预报变量.选B2,若一组观测值(xi, yi) (x2, y2) ••- (x…, y n)之间满足 y-bxi+a+e;(i=l> 2. •••!!)若巳恒为0,则仁为_____________解析:e』亘为0,说明随机误差对方贡献为0.答案:1.3.假设关于某设备的使用年限x和所支出的维修费用y (万兀),有如下的统计资料:X 2 3 4 5 6y 22 38 55 65 70若由资料可知y对x呈线性相关关系试求:(1)线性回归方程;(2)估计使用年限为10年时,维修费用是多少?解:(1)列表如下:i 1 2 3 4 5X] 2 3 4 5 622 38 55 65 70时•44 114 220 325 420X; 4 9 16 25 36_ _ 5 5x = 4, y = 5,»;=9o, »,北=112.3z'=l z'=l5 ___况一5xy干旱,仃112.3-5x4x5 …c十正方= ------------- = ------------ -- = 1.23,S,厂2 90 —5x42小「- 5x<=|a = y -bx = 5-1.23x4 = 0.08线性回归方程为:y =bx + a = 1.23x + Q.QS ( 2 )当 x=10 时,y = 1.23x10 + 0.08 = 12.38 (万兀)即估计使用10年时维修费用是1238万元课后练习:1.一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归模型为y=7. 19x+73.93 用这个模型预测这个孩子10岁时的身高,则正确的叙述是()A.身高一定是145. 83cm;B.身高在145. 83cm以上;C.身高在145. 83cm以下;D.身I W J在 145. 83cm 左右.2.两个变量y与x的回归模型中,分别选择了 4个不同模型,它们的相关指数人2如下,其中拟合效果最好的模型是()A.模型1的相关指数人2为0. 98B.模型2的相关指数R2为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1回归分析的基本思想及其初步应用
一、选择题 1. 某同学由x 与y 之间的一组数据求得两个变量间的线性回归方程为y bx a =+,已知:数据x 的平
均值为2,数据
y 的平均值为3,则 ( )
A .回归直线必过点(2,3)
B .回归直线一定不过点(2,3)
C .点(2,3)在回归直线上方
D .点(2,3)在回归直线下方
2. 在一次试验中,测得(x,y)的四组值分别是A(1,2),B(2,3),C(3,4),D(4,5),则Y 与X 之间的回归直线方程为( )A .$y
x 1=+
B .$y x 2=+
C .$y 2x 1=+ D.$y
x 1=-3. 在对两个变量x ,y 进行线性回归分析时,有下列步骤:
①对所求出的回归直线方程作出解释; ②收集数据(i x 、
i y ),1,2i =,…,n ;
③求线性回归方程; ④求未知参数; ⑤根据所搜集的数据绘制散点图
如果根据可行性要求能够作出变量,x y 具有线性相关结论,则在下列操作中正确的是( ) A .①②⑤③④ B .③②④⑤① C .②④③①⑤ D .②⑤④③①
4. 下列说法中正确的是( )
A .任何两个变量都具有相关关系
B .人的知识与其年龄具有相关关系
C .散点图中的各点是分散的没有规律
D .根据散点图求得的回归直线方程都是有意义的
5. 给出下列结论:
(1)在回归分析中,可用指数系数2
R 的值判断模型的拟合效果,2
R 越大,模型的拟合效果越好; (2)在回归分析中,可用残差平方和判断模型的拟合效果,残差平方和越大,模型的拟合效果越好; (3)在回归分析中,可用相关系数r 的值判断模型的拟合效果,r 越小,模型的拟合效果越好;
(4)在回归分析中,可用残差图判断模型的拟合效果,残差点比较均匀地落在水平的带状区域中,说明这样的模型比较合适.带状区域的宽度越窄,说明模型的拟合精度越高. 以上结论中,正确的有( )个.
A .1
B .2
C .3
D .4 6. 已知直线回归方程为2 1.5y x =-,则变量x 增加一个单位时(
)
A.y 平均增加1.5个单位
B.y 平均增加2个单位
C.y 平均减少1.5个单位
D.
y 平均减少2个单位
7. 下面的各图中,散点图与相关系数r 不符合的是( )
8. 一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归直线方程为ˆ7.1973.93y
x =+,据此可以预测这个孩子10岁时的身高,则正确的叙述是( )
A .身高一定是145.83cm
B .身高超过146.00cm
C .身高低于145.00cm
D .身高在145.83cm 左右
9. 在画两个变量的散点图时,下面哪个叙述是正确的( ) (A)预报变量在x 轴上,解释变量在
y 轴上 (B)解释变量在x 轴上,预报变量在y 轴上 (C)可以选择两个变量中任意一个变量在x 轴上 (D)可以选择两个变量中任意一个变量在y 轴上
10. 两个变量
y 与x 的回归模型中,通常用2R 来刻画回归的效果,则正确的叙述是( )
A. 2R 越小,残差平方和小
B. 2R 越大,残差平方和大
C. 2
R 于残差平方和无关 D. 2
R 越小,残差平方和大 11. 两个变量
y 与x 的回归模型中,分别选择了4个不同模型,它们的相关指数2R 如下 ,其中拟合效果
最好的模型是( )
A.模型1的相关指数2R 为0.98
B.模型2的相关指数2R 为0.80
C.模型3的相关指数2
R 为0.50 D.模型4的相关指数2
R 为0.25
12. 在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是( ) A.总偏差平方和 B.残差平方和 C.回归平方和 D.相关指数R 2
13.工人月工资(元)依劳动生产率(千元)变化的回归直线方程为ˆ6090y x =+,下列判断正确的是( ) A.劳动生产率为1000元时,工资为50元 B.劳动生产率提高1000元时,工资提高150元 C.劳动生产率提高1000元时,工资提高90元 D.劳动生产率为1000元时,工资为90元
14. 下列结论正确的是( )
①函数关系是一种确定性关系;②相关关系是一种非确定性关系;③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法. A.①② B.①②③
C.①②④
D.①②③④
15. 已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为( )
A.$1.234y x =+
B.$1.235y x =+ C.$1.230.08y x =+ D.$0.08 1.23y x =+ 二、填空题
16. 在比较两个模型的拟合效果时,甲、乙两个模型的相关指数2
R 的值分别约为0.96和0.85,则拟合效果好的模型是 .
17. 在回归分析中残差的计算公式为 .
18. 线性回归模型y bx a e =++(a 和b 为模型的未知参数)中,e 称为 .
19. 若一组观测值(x 1,y 1)(x 2,y 2)…(x n ,y n )之间满足y i =bx i +a+e i (i=1、2.…n)若e i 恒为0,则R 2
为_____
三、解答题
20. 调查某市出租车使用年限x和该年支出维修费用y(万元),得到数据如下:
使用年限x 2 3 4 5 6
维修费用y2.2 3.8 5.5 6.5 7.0
(2)由(1)中结论预测第10年所支出的维修费用.(1
2
1
()()
()
n
i i
i
n
i
i
x x y y
b
x x
a y bx
=
=
⎧
-⋅-
⎪
⎪=
⎨-
⎪
⎪
=-
⎪⎩
∑
∑
)
21. 以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据:
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线;
(3)据(2)的结果估计当房屋面积为2
150m时的销售价格.
(4)求第2个点的残差。
答案
一、选择题
1. A
2. A
3. D
4. B
5. B
6. C
7. B
8. D
9. 解析:通常把自变量x称为解析变量,因变量y称为预报变量.选B
10. D
11. A
12. B
13. C
14. C
15. C
二、填空题
16. 甲
17. 列联表、三维柱形图、二维条形图
18. 随机误差
19. 解析: e i恒为0,说明随机误差对y i贡献为0.
答案:1.
三、解答题
20. 解析:(1
4=x , 5=y ,
9051
2=∑=i i x , 3.1125
1
=∑=i i i y x
于是23.14
5905
453.112552
2
51
25
1=⨯-⨯⨯-=
--=
∑∑==x
x y
x y
x b i i i i
i , 08.0423.15=⨯-=-=bx y a
∴线性回归方程为:08
.023.1^
+=+=x a bx y (2)当x=10时,
38.1208.01023.1^=+⨯=y (万元)
即估计使用10年时维修费用是1238万元 回归方程为: 1.230.08y x =+
(2) 预计第10年需要支出维修费用12.38 万元.
21. 解析:(1)数据对应的散点图如图所示:
(2)1095151==∑=i i x x ,1570)(2
5
1
=-=∑=x x l i i xx ,
308))((,2.235
1
=--==∑=y y x x l y i i i xy
设所求回归直线方程为a bx y +=)
,
则1962.01570
308
≈=
=
xx
xy l l b 8166.11570
308
1092.23≈⨯
-=-=x b y a 故所求回归直线方程为8166.11962.0+=x y )
(3)据(2),当2
150x m =时,销售价格的估计值为:
2466.318166.11501962.0=+⨯=y )
(万元)。
