2010年中考模拟试卷 数学参考答案及评分标准doc
2010年初中数学中考模拟试卷.doc
2010年初三中考模拟(一)数学试卷时间：120分钟 总分：120一、选择题（本大题共有5小题，每小题3分，共15分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号涂在答题卡相应位置．．．．．．．上） 1、平面直角坐标系内，点A （-2，-3）在（ ）A.第一象限 B 第二象限 C.第三象限 D 。
第四象限 2．下列图形中，既是．．轴对称图形又是．．中心对称图形的是( )3．下列事件中最适合使用普查方式收集数据的是（ ）A ．了解某班同学的身高情况B ．了解全国每天丢弃的废旧电池数C ．了解一批炮弹的杀伤半径D ．了解我国农民的年人均收入情况 4.下面右边的图形是由8个棱长为1个单位的小立方体组成的立体图形，这个立体图形的左视图是( )5、如图，平面直角坐标系中，在边长为1的正方形ABCD 的边上有一动点P 沿A B C D A →→→→运动一周，则P 的纵坐标y 与点P 走过的路程s 之间的函数关系用图象表示大致是（ ）二、填空题（共12小题，每小题2分，共24分。
请将答案写在答题卡相应位置．．．．．．．上）1 2 3 412ys O 1 2 3 4 1 2 y s O s 1 2 3 4 1 2 y sO 1 2 3 4 1 2 y O A B .C .D . DC B A A B C DABC DE 第16题图6计算：2332x x ∙ ，()322x。
7、分解因式：228x -= 。
8、已知数据：2，1-，3，5，6，5，则这组数据的众数是 ，极差是 。
9 函数21+=x y 中，自变量x 的取值范围是 ．10．如图5，∠1，∠2，∠3，∠4是五边形ABCDE 的外角，且∠1=∠2=∠3=∠4=070，则∠AED 的度数是_________________ .第10题 第12题 第13题 11、已知双曲线xky =过点（-2，3），则k = 。
12、AB ∥CD ，AC ⊥BC ，∠BAC ＝65°，则∠BCD ＝______________度。
2010年中考模拟数学试卷和答案
2010年中考模拟试卷数 学考生须知：1.本试卷分试题卷和答题卷两部分，满分120分，考试时间100分钟 .2.答题时，应该在答题卷指定位置内写明校名，姓名和准考证号 .3.所有答案都必须做在答题卷标定的位置上，请务必注意试题序号和答题序号相对应 .4.考试结束后，上交试题卷和答题卷试题卷一、仔细选一选（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的 .注意可以用多种不同的方法来选取正确答案 .1. 如果0=+b a ，那么a ，b 两个实数一定是（ ）A.都等于0B.一正一负C.互为相反数D.互为倒数2. 要了解全校学生的课外作业负担情况，你认为以下抽样方法中比较合理的是（ ）A.调查全体女生B.调查全体男生C.调查九年级全体学生D.调查七、八、九年级各100名学生 3. 直四棱柱，长方体和正方体之间的包含关系是（ ）4. 有以下三个说法：①坐标的思想是法国数学家笛卡儿首先建立的；②除了平面直角坐标系，我们也可以用方向和距离来确定物体的位置；③平面直角坐标系内的所有点都属于四个象限 .其中错误的是（ ）A.只有①B.只有②C.只有③D.①②③ 5. 已知点P （x ，y ）在函数x xy -+=21的图象上，那么点P 应在平面直角坐标系中的（ ）A.第一象限B. 第二象限C. 第三象限D. 第四象限6. 在一张边长为4cm 的正方形纸上做扎针随机试验，纸上有一个半径为1cm 的圆形阴影区域，则针头扎在阴影区域内的概率为（ ）A.161 B.41 C.16π D.4π 7. 如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3和4及x ，那么x 的值（ ） A.只有1个 B.可以有2个 C.有2个以上，但有限 D.有无数个8. 如图，在菱形ABCD 中，∠A=110°，E ，F 分别是边AB 和BC的中点，EP ⊥CD 于点P ，则∠FPC=（ ） A.35° B.45° C.50° D.55°9. 两个不相等的正数满足2=+b a ，1-=t ab ，设2)(b a S -=，则S 关于t 的函数图象是（ ）A.射线（不含端点）B.线段（不含端点）C.直线D.抛物线的一部分10. 某校数学课外小组，在坐标纸上为学校的一块空地设计植树方案如下：第k 棵树种植在点)(k k k y x P ，处，其中11=x ，11=y ，当k≥2时，⎪⎪⎩⎪⎪⎨⎧---+=----+=--]52[]51[])52[]51([5111k k y y k k x x k k k k ，[a ]表示非负实数a 的整数部分，例如[2.6]=2，[0.2]=0 .按此方案，第2009棵树种植点的坐标为（ ）A.（5，2009）B.（6，2010）C.（3，401） D （4，402）二. 认真填一填（本题有6个小题，每小题4分，共24分）要注意认真看清楚题目的条件和要填写的内容，尽量完整地填写答案 11. 如图，镜子中号码的实际号码是___________ .12. 在实数范围内因式分解44-x = _____________________ . 13. 给出一组数据：23，22，25，23，27，25，23，则这组数据的中位数是___________；方差（精确到0.1）是_______________ .14. 如果用4个相同的长为3宽为1的长方形，拼成一个大的长方形，那么这个大的长方形的周长可以是______________ .15. 已知关于x 的方程322=-+x mx 的解是正数，则m 的取值范围为______________ . 16. 如图，AB 为半圆的直径，C 是半圆弧上一点，正方形DEFG 的一边DG 在直径AB 上，另一边DE 过ΔABC 的内切圆圆心O ，且点E 在半圆弧上 .①若正方形的顶点F 也在半圆弧上，则半圆的半径与正方形边长的比是______________；②若正方形DEFG 的面积为100，且ΔABC 的内切圆半径r =4，则半圆的直径AB = __________ .三. 全面答一答（本题有8个小题，共66分）解答应写出文字说明、证明过程或推演步骤 .如果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以 . 17. （本小题满分6分）如果a ，b ，c 是三个任意的整数，那么在2b a +，2c b +，2ac +这三个数中至少会有几个整数？请利用整数的奇偶性简单说明理由 .18. （本小题满分6分）如图，，有一个圆O 和两个正六边形1T ，2T .1T 的6个顶点都在圆周上，2T 的6条边都和圆O 相切（我们称1T ，2T 分别为圆O 的内接正六边形和外切正六边形） . （1）设1T ，2T 的边长分别为a ，b ，圆O 的半径为r ，求a r :及b r :的值； （2）求正六边形1T ，2T 的面积比21:S S 的值 .如图是一个几何体的三视图 . （1）写出这个几何体的名称；（2）根据所示数据计算这个几何体的表面积；（3）如果一只蚂蚁要从这个几何体中的点B 出发，沿表面爬到AC 的中点D ，请你求出这个线路的最短路程 .20. （本小题满分8分）如图，已知线段a .（1）只用直尺（没有刻度的尺）和圆规，求作一个直角三角形ABC ，以AB 和BC 分别为两条直角边，使AB=a ，BC=a 21（要求保留作图痕迹，不必写出作法）； （2）若在（1）作出的RtΔABC 中，AB=4cm ，求AC 边上的高 .学校医务室对九年级的用眼习惯所作的调查结果如表1所示，表中空缺的部分反映在表2的扇形图和表3的条形图中.（1）请把三个表中的空缺部分补充完整；（2）请提出一个保护视力的口号（15个字以内）.22. （本小题满分10分）如图，在等腰梯形ABCD中，∠C=60°，AD∥BC，且AD=DC，E、F分别在AD、DC的延长线上，且DE=CF，AF、BE交于点P .（1）求证：AF=BE；（2）请你猜测∠BPF的度数，并证明你的结论.在杭州市中学生篮球赛中，小方共打了10场球 .他在第6，7，8，9场比赛中分别得了22，15，12和19分，他的前9场比赛的平均得分y 比前5场比赛的平均得分x 要高 .如果他所参加的10场比赛的平均得分超过18分 （1）用含x 的代数式表示y ；（2）小方在前5场比赛中，总分可达到的最大值是多少？ （3）小方在第10场比赛中，得分可达到的最小值是多少？24. （本小题满分12分）已知平行于x 轴的直线)0(≠=a a y 与函数x y =和函数xy 1=的图象分别交于点A 和点B ，又有定点P （2，0） . （1）若0>a ，且tan ∠POB=91，求线段AB 的长； （2）在过A ，B 两点且顶点在直线x y =上的抛物线中，已知线段AB=38，且在它的对称轴左边时，y 随着x 的增大而增大，试求出满足条件的抛物线的解析式； （3）已知经过A ，B ，P 三点的抛物线，平移后能得到259x y =的图象，求点P 到直线AB 的距离 .2010年中考模拟试卷数学参考答案一、仔细选一选（每小题3分，芬30分）二. 认真填一填（本题有6个小题，每小题4分，共24分） 11、326512.)2)(2)(2(2-++x x x 13、23；2.614、14或16或2615、46-≠->m m 或16、①5∶2 ；②21三. 全面答一答（本题有8个小题，共66分） 17、（本题6分）至少会有一个整数 .因为三个任意的整数a,b,c 中，至少会有2个数的奇偶性相同，不妨设其为a ，b ， 那么2ba +就一定是整数 . 18、（本题4分）（1）连接圆心O 和T 1的6个顶点可得6个全等的正三角形 . 所以r ∶a=1∶1;连接圆心O 和T 2相邻的两个顶点，得以圆O 半径为高的正三角形， 所以r ∶b=3∶2;（2） T 1∶T 2的连长比是3∶2，所以S 1∶S 2=4:3):(2=b a .19、（本题6分）（1） 圆锥； （2） 表面积S=πππππ164122=+=+=+r rl S S 圆扇形（平方厘米）（3） 如图将圆锥侧面展开，线段BD 为所求的最短路程 . 由条件得，∠BAB ′=120°，C 为弧BB ′中点，所以BD =33 .20、（本题8分）（1）作图如右，ABC ∆即为所求的直角三角形；（2）由勾股定理得，AC =52cm ， 设斜边AC 上的高为h, ABC ∆面积等于h ⨯⨯=⨯⨯52212421，所以554=h 21、（本题8分）（1）补全的三张表如下：（表一）（2）例如：“象爱护生命一样地爱护眼睛！”等 . 22、（本题10分）（1）∵BA=AD ，∠BAE=∠ADF ，AE=DF ， ∴△BAE ≌△ADF ，∴BE=AF ； （2）猜想∠BPF=120° .∵由（1）知△BAE ≌△ADF ，∴∠ABE=∠DAF .∴∠BPF=∠ABE+∠BAP=∠BAE ，而AD ∥BC ，∠C=∠ABC=60°， ∴∠BPF=120° . 23、（本题10分）（1）9191215225++++=x y ；（2）由题意有x x >++++9191215225，解得x ＜17，所以小方在前5场比赛中总分的最大值应为17×5－1=84分；（3）又由题意，小方在这10场比赛中得分至少为18×10 + 1=181分， 设他在第10场比赛中的得分为S ，则有81+（22+15+12+19）+ S ≥181 .解得S≥29，所以小方在第10场比赛中得分的最小值应为29分 .24、（本题12分）（1）设第一象限内的点B （m,n ），则tan ∠POB 91==m n ，得m=9n ，又点B 在函数xy 1=的图象上，得m n 1=，所以m =3（－3舍去），点B 为)31,3(，而AB ∥x 轴，所以点A （31，31），所以38313=-=AB ；（2）由条件可知所求抛物线开口向下，设点A （a , a ），B （a 1，a ），则AB =a1－ a =38, 所以03832=-+a a ，解得313=-=a a 或 .当a = －3时，点A （―3，―3），B （―31，―3），因为顶点在y = x 上，所以顶点为（－35，－35），所以可设二次函数为35)35(2-+=x k y ，点A 代入，解得k= －43,所以所求函数解析式为35)35(432-+-=x y .同理，当a = 31时，所求函数解析式为35)35(432+--=x y ；（3）设A （a , a ），B （a 1，a ），由条件可知抛物线的对称轴为aa x 212+= .设所求二次函数解析式为：)2)1()(2(59++--=aa x x y .点A （a , a ）代入，解得31=a ，1362=a ，所以点P 到直线AB 的距离为3或136.。
2010年初中数学中考模拟试题答案
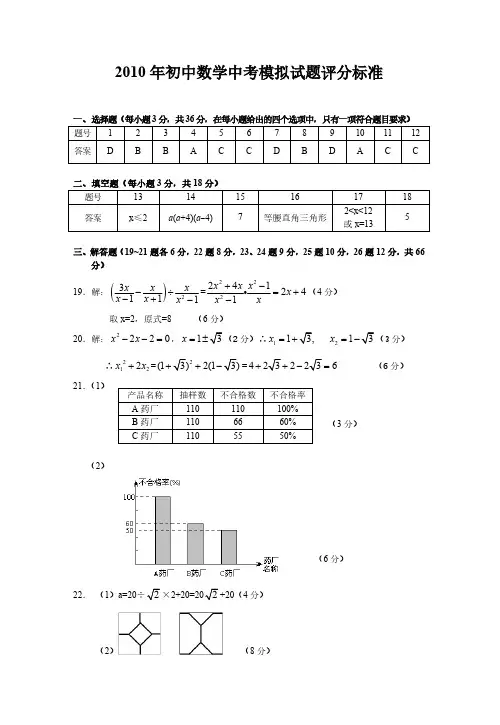
在 R t △ADE 中, EA =ｒ, DE=6-ｒ, AD=x,
∴ x 2 6 r 2 r 2 ，ｒ＝ 1 x 2 ＋３，
∵ EF= EA, ∴AF=2DE,
即 y ＝2(6－ｒ)＝－ 1 x 2 ＋6, （6 分） 6
D
E
C
∵AB∥CD,
∴∠AFE=∠CEF,
G
∴∠AEF=∠AFE, ∴AE=AF, ∵AE=EF,
A
B
F
（ 图3 ）
∴AE=AF=CE=CF, ∴△AEF 和△CEF 都是正三角形，
∴四边形 AECF 是菱形,且∠CEF=60°,
∴∠BCF=30°,
1
∴BF=
1
CF=
AF= 1 AB=2,
BC= 2 3 ．（12 分）
223
②点 F 是 AB 的中点时, y =3，
图 D
E
C
H
G
A
( 图 1)
D
E
B F
C
G
A
B F
（ 图2 ）
1
即-
x 2 ＋6=3，∴ x = 3
2 ．（8 分）
6
(3)（如图 3）．
当x=2
3 时,
︵图 F 是AC的中点。此时，四边形 AECF 菱形．（9 分）
理由如下：
︵ ∵点 F 是AC的中点，∴∠AEF=∠CEF, AF=CF,
2.85×20+2.85×1.5×10+2.85×2×（x-30）=128.25，x=35（5 分）
∴调整后水费是：3.3×20+3.3×1.5×10+3.3×2×5=148.5（元）（6 分）
2010年中考模拟试卷 数学参考答案及评分标准
2010年中考模拟试卷 数学参考答案及评分标准一. 仔细选一选 (本题有10个小题, 每小题3分, 共30分)二. 认真填一填 (本题有6个小题, 每小题4分, 共24分)11、36b a 12、 2.5 13、a=0或a=2 14、1：5 15、（3，2）；（55，358） 16、①②④三. 全面答一答 (本题有8个小题, 共66分) 17.（本小题满分6分）212(2212010））（-+-----π=221211+--+…………………分=227-……………………………2分18.（本小题满分6分）解：原式=x-1 …………………………………4分（从33x -<<的范围内选取一个合适的整数x 代入求值。
其中x ≠±1，0）……2分 19.（本小题满分6分）解：（1）如图所示：……………………………………4分（注：每正确画出1个图且痕迹清晰得2分，）（2）规律：若三角形为锐角三角形，则其最小覆盖圆为该三角形的 外接圆；……………1分 若三角形为直角或钝角三角形， 则其最小覆盖圆是以三角形 最长边（直角或钝角所对的边） 为直径的圆．……………1分20.（本小题满分8分）（1）如图（1）．连结AC ，由∠1＝∠2，∠APC ＝∠DPE∴△ACP ∽△DEP ．…………………………………2分DEAC DP =∴P A 又AP 25=，∴DE=25221÷⨯＝52………………2分（2）如图（2）．当Rt Rt ADP QCP △∽△时有得：1QC =．∴Q 与B 重合，0BQ ∴=……………2分 如图（3），当Rt Rt ADP PCQ △∽△时，有QCPD PCAD =，得=QC 41，即43=BQ ………………………2分∴当0BQ =或43=BQ 时，三角形AD P 与以点Q C P ，，为顶点的三角形相似．21.（本小题满分8分）解：（1）1(10%15%30%15%5%)25%a =-++++=． ······································ 1分初一学生总数：2010%200÷=（人）． ······················································ 1分 （2）活动时间为5天的学生数：20025%50⨯=（人）．活动时间为7天的学生数：2005%10⨯=（人）． ········································· 2分频数分布直方图（如图）······················ 1分（3）活动时间为4天的扇形所对的圆心角是36030%108⨯=°°． ························· 1分（4）该市活动时间不少于4天的人数约是6000(30%25%15%5%)4500⨯+++=（人）． ························································ 2分（第21题图）人数22.（本小题满分10分） （1）27……………..2分（2）△ABC 如图②所示 ……………2分S △ABC=2a ·4a-21a ·2a-21a ·4a-21×2a ·2a=23a……………….2分（3）构造△ABC 如图③所示（图没有但面积算对不扣分） S △ABC=3m ·4n-21m ·4n-213m ·2n-21×2m ·2n=5mn …………….2分23.（本小题满分10分）⑴ 图略。
2010年中考摸拟试卷数学参考答案及评分标准
2010年中考摸拟试卷数学参考答案及评分标准一. 选择题(每小题3分, 共30分)二．认真填一填(本题有6个小题，每小题4分，共24分) 11. (a-1)(a+1) ， x 2+y 2 12. 20 和560 13.52 14.3315.3421或、 16. (3,3);；(3,-2) ；（11，－26）三、解答题（本题有8小题，共66分） 17、（本题6分） (以下给出三种选择方案，其他方案从略) 解答一： Y + Z =(3a 2+3ab )+ (a 2+ab ) =4a 2+4ab ……3分 =4a (a +b )．…………3分 解答二： X- Z = (2a 2＋3ab ＋b 2)-(a 2+ab ) =a 2+2ab +b 2…………3分=(a +b )2 ………3分解答三：Y- X =(3a 2+3ab )- (2a 2＋3ab ＋b 2)=a 2- b 2 …………3分=(a +b )(a -b )……………3分说明：整式计算正确得3分，因式分解正确得3分． 18. （本题6分） 解：（1）设A 市投资“改水工程”年平均增长率是x ，则2600(1)1176x +=．（2分）解得0.4x = 或 2.4x =-（不合题意，舍去）（2分）． 所以，A 市投资“改水工程”年平均增长率为40%． （2）600＋600×1.4＋1176＝2616（万元）． A 市三年共投资“改水工程”2616万元．（2分）19. （本题6分） 解： 如图：（1）画出△A 1B 1C 1…………..2分 （2）画出△A 2B 2C 2………………………………..2分连结OA ，OA 2，OA ＝.点A 旋转到A 2所经过的路线长为l＝1802……2………….2分20. (本题8分)（1）作图如右---------------------- 4分（2）证明：根据作图知，PQ 是A C的垂直平分线， 所以AO C O =，且E F A C ⊥．因为A B C D是平行四边形，所以O A E O C F ∠=∠ 所以O A E O C F △≌△． 所以A E C F =---------------------- 4分21．（本小题满分8分）解：在R t AD B △中，30A B =米 60ABC ∠=°sin 30sin 6025.9826.0AD AB ABC =∠=⨯=≈≈·°（米） ……2分15D B =米连接BE ，过E 作EN BC ⊥于NAE BC∵∥ ∴四边形AEN D是矩形26N E AD =≈米 ……2分在R t EN B △中，由已知45EBN ∠°≤， 当45EBN ∠=°时26.0BN EN ==米 ……2分26.01511AE AD BN BD ==-=-=∴米 ……1分 答：AE 至少是11米． ……………… 1分22.（本小题满分10分）（1）60306060=-FC，30=FC ；……3分（2）在EF 上任取一点Q ，分别过点Q 作BC ，AB 的垂线，垂足分别是M ，N ，则 CN x +=606030，602-=x CN ，则x BN 2120-=。
2010年中考数学模拟试卷(4)参考答案
2010年中考数学模拟试卷(4)参考答案一、选择题（本大题共10题，每题4分，满分40分）1．D ； 2．C ； 3．D ； 4．B ； 5．A ； 6.D 7.D 8.C 9.D 10.C 二、填空题（本大题共12题，每题4分，满分48分） 11．1x ≠-； 12．12； 13． 略； 14．2000sin α15、4：1 16、（2，4）或（3，4）或（8，4） 三、解答题17、x ＞-4 画数轴略 18、①原式=11-a 4分 ②如a=2时，原式=1，答案不唯一 2分19、（1）解：树状图：略 P=61 3分（2）两个球上数字之和为6时，概率最大，即3162'==p 6分20、 DF=AB 1分 证明：∵四边形ABCD 是矩形∴∠B=Rt ∠ ∴AD ∥BC∴∠DAF=∠BEA （两直线平行，内错角相等） 3分 又∵DF ⊥AE∴∠DFA=∠B=Rt ∠ ∵AD=AE∴△ADF ≌△EAB(AAS) 5分 ∴DF=AB(全等三角形的对应边相等) 6分 21、解：（1）线段O A 对应的函数关系式为：112s t =（012t ≤≤）线段A B 对应的函数关系式为：1(1220)s t =<≤．（2）图中线段A B 的实际意义是：小明出发12分钟后，沿着以他家为圆心，1千米为半径的圆弧形道路上匀速步行了8分钟． （3）如图中折线段C D D B -．22、解：（1）设平均每分钟一道正门可以通过x 名学生，一道侧门为y 名学生。
1分 则⎩⎨⎧=+=+22022602y x y x 解得：⎩⎨⎧==60100y x 5分（2）∵（100+60）×80%×4×2=1024 7分 又∵20×50=1000 ∴1024＞1000 故学生可以安全撤离 8分 23．解：平移后抛物线的解析式为22(2)1y x =-+． (2)∴A 点坐标为（2，1），……………………………………1分 设直线OA 解析式为y kx =，将A （2，1）代入得12k =，直线OA 解析式为12y x =，将3x =代入12y x =得32y =，∴C 点坐标为（3，32）．……1分将3x =代入22(2)1y x =-+得3y =，∴B 点坐标为（3，3）∴A B C 34S = (2)（2）∵PA ∥BC ，∴∠PAB =∠ABC1°当∠PBA =∠BAC 时，PB ∥AC ，∴四边形PACB 是平行四边形，t (分钟)∴32P A B C ==．………………………………………1分∴15(2,)2P ．………………………………………………1分2°当∠APB =∠BAC 时，A P AB A BB C=，∴2ABAP BC=．又∵AB ==∴103A P =………………………………………………1分∴213(2,)3P ……………………………………………1分综上所述满足条件的P 点有5(2,)2，13(2,)3．……………………………1分24．解：（1）方法一：由已知得：C （0，－3），A （－1，0） …………………………1分 将A 、B 、C 三点的坐标代入得⎪⎩⎪⎨⎧-==++=+-30390c c b a c b a 解得：⎪⎩⎪⎨⎧-=-==321c b a ……4分所以这个二次函数的表达式为：322--=x x y ……4分方法二：由已知得：C （0，－3），A （－1，0） ………1分 设该表达式为：)3)(1(-+=x x a y ………2分 将C 点的坐标代入得：1=a ………4分 所以这个二次函数的表达式为：322--=x x y ……4分 （注：表达式的最终结果用三种形式中的任一种都不扣分） （2）方法一：存在，F 点的坐标为（2，－3） ……5分 理由：易得D （1，－4），所以直线CD 的解析式为：3--=x y ∴E 点的坐标为（－3，0） ……………6分 由A 、C 、E 、F 四点的坐标得：AE ＝CF ＝2，AE ∥CF ∴以A 、C 、E 、F 为顶点的四边形为平行四边形 ∴存在点F ，坐标为（2，－3） …………7分 方法二：易得D （1，－4），所以直线CD 的解析式为：3--=x y∴E 点的坐标为（－3，0） ……………5分 ∵以A 、C 、E 、F 为顶点的四边形为平行四边形∴F 点的坐标为（2，－3）或（―2，―3）或（－4，3） 代入抛物线的表达式检验，只有（2，－3）符合 ∴存在点F ，坐标为（2，－3） ……………7分（3）如图，①当直线MN 在x 轴上方时，设圆的半径为R （R>0），则N （R+1，R ）， 代入抛物线的表达式，解得2171+=R …………9分②当直线MN 在x 轴下方时，设圆的半径为r （r>0）， 则N （r+1，－r ）， 代入抛物线的表达式，解得2171+-=r ………11分∴圆的半径为2171+或2171+-． ……………11分。
2010年中考模拟试卷 数学参考答案及评分标准
2010年中考模拟试卷 数学参考答案及评分标准一. 选择题(每小题3分, 共30分)二. 填空题(每小题4分, 共24分)11. 4 。
12. X=5 。
13. x(xy+2)(xy-2) 。
14. x ＜-1或x ＞3 。
15. 232-+或。
16. 517 。
三. 解答题(8小题共66分) 17. (本题6分) 解：（1）15x =，215x =； ··································································································· 2分 （2）21a a+（或1a a +）； ···································································································· 2分（3）二次项系数化为1，得22615x x -=-， 得2222613131555x x ⎛⎫⎛⎫-+-=-+- ⎪ ⎪⎝⎭⎝⎭，213144525x ⎛⎫-=⎪⎝⎭． 开方，得131255x -=±． 解得15x =，215x =． ····································································································· 2分18. (本题6分)（1）作A E ⊥BC 于点E BE=BC-AD=4-1=332tan ==∠BE AE ABC ∴AE=DC=2 ……………（1分） 设),1(1y A -),4(2y B - ∴k y -=1，42ky -=221==-CD y y ∴2)4(=---kk∴38-=k ……………（3分）（2） 38-=k ∴x y 38-=E∴当4-=x 时 32)4(38=-⨯-=y ∴32=BH ……………（5分）∴BH O C ABCD ABH O D S S S 矩形梯形五边形＝+32424121⨯+⨯+⨯）（＝323385＝＝+ … （6分） 19. (本题6分)（1）连接BC 由作图可知：AC=BC=DC 易证：︒=∠90ABD …………… (3分)（2）略 …………… (3分) 20. (本题8分) 解：解：（1）12······················································································································ 1分 （2）13··································································································································· 3分 （3）根据题意，画树状图： ································································································· 6分由树状图可知，共有16种等可能的结果：11，12，13，14，21，22，23，24，31，32，33，34，41，42，43，44．其中恰好是4的倍数的共有4种：12，24，32，44． 所以，P （4的倍数）41164==． ······················································································· 8分或根据题意，画表格： ··········································································································· 6分第一次第二次1 2 3 41 11 12 13 14 2 21 22 23 24 3 31 32 33 34441424344由表格可知，共有16种等可能的结果，其中是4的倍数的有4种，所以，P （4的倍数）41164==． ·································································································· 8分 21. (本题8分)（1）200；……………………………………2分（2）a = 0.45， b = 70 ……………………4分（每空1分） （3）126；……………………………………6分 （4）900. ……………………………………8分 22. (本题10分)1 2 3 4 1 第一次 第二次 1 2 3 4 2 1 2 3 4 3 1 2 3 4 4 开始解：（1）在Rt AEB △中，AC BC =，12CE AB ∴=，CB CE ∴=，CEB CBE ∴∠=∠．90CEF CBF ∠=∠=，BEF EBF ∴∠=∠，EF BF ∴=． 90BEF FED ∠+∠=，90EBD EDB ∠+∠=，FED EDF ∴∠=∠．EF FD =． BF FD ∴=． ················································································································ （3分） （2）由（1）BF FD =，而BC CA =，CF AD ∴∥，即AE CF ∥．若AC EF ∥，则AC EF =，BC BF ∴=．BA BD ∴=，45A ∠=．∴当045A <∠<或4590A <∠<时，四边形ACFE 为梯形． ··························· （6分） （3）作GH BD ⊥，垂足为H ，则GH AB ∥．14DG DA =，14DH DB ∴=． 又F 为BD 中点，H ∴为DF 的中点．GH ∴为DF 的中垂线．GDF GFD ∴∠=∠．点G 在ED h 上，EFD GFD ∴∠∠≥．180EFD FDE DEF ∠+∠+∠=，180GFD FDE DEF ∴∠+∠+∠≤． 3180EDF ∴∠≤．60EDF ∴∠≤．又90A EDF ∠+∠=，3090A ∴∠<≤．∴当3090A ∠<≤时，DE 上存在点G ，满足条件14DG DA =． ···················· （10分） 23. (本题10分)解：（1）购进C 种玩具套数为：50－x －y （或47－54x －1011y ）……2分 （2）由题意得405550()2350x y x y ++-= 整理得230y x =-……5分 （3）①利润＝销售收入－进价－其它费用(5040)(8055)(6550)(50)200p x y x y =-+-+----又∵230y x =-∴整理得15250p x =+……7分②购进C 种电动玩具的套数为：5050(230)803x y x x x --=---=-据题意列不等式组102301080310x x x ≥⎧⎪-≥⎨⎪-≥⎩，解得70203x ≤≤ ∴x 的范围为70203x ≤≤，且x 为整数 x 的最大值是23 ……9分∵在15250p x =+中，15k =＞0 ∴P 随x 的增大而增大∴当x 取最大值23时，P 有最大值，最大值为595元．此时购进A 、B 、C 种玩具分别为23套、16套、11套．……10分AB CD F EM GH24. (本题12分) 解：（1）21(8180)18y x x =--，令0y =得281800x x --=，()()18100x x -+= ∴18x =或10x =-∴(18,0)A ；………………………1分在21410189y x x =--中，令0x =得10y =即(0,10)B -；………………2分 由于B C ∥OA ，故点C 的纵坐标为－10，由2141010189x x -=--得8x =或0x = 即(8,10)C -且易求出顶点坐标为98(4,)9-……………………………………3分于是，(18,0),(0,10),(8,10)A B C --，顶点坐标为98(4,)9-。
2010年中考模拟试卷 数学
2010年中考模拟试卷 数学卷数学参考答案及评分标准一、仔细选一选（每小题3分，共30分）说明：第1和10小题为原创题，其中2；3；5；7；8为课本习题的延伸；4；6；9为借鉴题。
（突出数学的时效性和大众化及生活中的应用） 二. 认真填一填（本题有6个小题，每小题4分，共24分）11、R=52 12.7313、b= -11 147 15、0360)2(⨯-=n S 16、20112010说明：14，16题自编题 ；11，12，13，15属于借鉴。
三. 全面答一答（本题有8个小题，共66分） 17、（本题6分）解：（1）m=2-2---------------------------------2分（2 ︳2-2-1︱+（2-2+6）0=︱1-2︳+1=2-----------------4分 说明：此题想增加数学计算的趣味性而设置了本题。
从一般的计算演变而来。
属于改编。
18、（本题6分）解： 四边形BCFD 为平行四边形-------------1分首先△ADE 绕点E 旋转180︒得到△CFE 可得△AD E ≌△CFE----------1分 ∴DE=EF------------1分又∵D.E 分别为中点∴D E ∥BC 且DE=21BC-------1分 ∴DF=∥BC ----------1分∴四边形BCFD 为平行四边形---------1分说明：旨在考查学生能运用旋转的不变性来证明三角形全等，和应用三角形的中位线的性质来证明一个四边形是平行四边形的性质应用（属于改编）。
19、（本题6分）解： （1）512,51==X X ------------------2分 (2)aa 12+-----------------------------------2分（3）5x 2-26x=-5x 2-526x=-1 x 2-526x+25169=-1+25169(x-513)2=25144(x-513)=±512∴512,51==X X ------------------2分说明：通过观察，归纳，猜想得到第1和第2小题的结论。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2010年中考模拟试卷 数学参考答案及评分标准
一、选择题（每小题3分，共30分）
二、填空题
11. 略 12.
4
1 13．10 x 或1- x
14. 130°或50° 15．21102-+-=x x y 16. 54 ， 54或56或58
三、解答题（6+6+6+8+8+10+10+12=66分） 17．解：分式对3分，化简对3分 18．解：（1）①237+732=969 2分
②362+263=625 625+526=1151
1151+1511=2662 2分 （2）略 2分
19．解：设原行驶速度为 x 千米／时，提速后的速度为（x+10）千米／时
60
2010
240240=+-
x x
3分
解得： x 1=－90 x 2=80 经检验得：x 2=80 2分 因为80+10＜100，所以可以实现提速目标。
1分
20． 解：（1）2分
（2）
(37+30+11)÷200=39﹪ 2分 答，中奖率为39﹪ 1分
购物券
0元
20元 50元
5元 80 60 20 40
（3）1335050200
11200020200
3020005200
372000=⨯⨯
+⨯⨯
+⨯⨯
元 2分
答：商场一天送出的购物券的总金额是13350元。
1分
21．解：（1）4分
（2）4分
22．解：（1）写出两个正确的算式；（略） 2分
（2）规律：任意两个奇数的平方差等于8的倍数。
3分
(3）证明：设m ，n 为整数且m >n ，两个奇数可表示为2m+1和2n+1，则
()()()()()()141212*********
2++-=+-+-++=+-+n m n m n m n m n m 2分
当m 、n 同是奇数或偶数时，m-n 一定为偶数，所以4(m-n)一定是8的倍数 当m 、n 一奇一偶时，则m+n+1一定为偶数，所以4(m+n+1)一定是8的倍数 2分 所以任意两奇数的平方差是8的倍数 1分 23． 解：连接AK ∵M 是AB 边的中点 ∴BMC AMC S s ∆∆=
BMK AMK S S ∆∆= 2分 ∴BMK BMC AMK AMC S S S S ∆∆∆∆-=- 即2==∆∆BKC AKC S S 2分 ∵
3=NC
AN
∴BNC ABN S S ∆∆=3
KNC AKN S S ∆∆=3 2分
图21—3
③ ①
②
④
⑤ ⑥ ①
③
②
④
⑥
⑤
中点
中点
中点
②
中点 中点 ①
③
②
①
③
∴KNC BNC AKN ABN S S S S ∆∆∆∆-=-33 即()633==-=∆∆∆∆BKC
KNC
BNC ABK S S S S 2分
∵BKC ABK AKC ABC S S S S ∆∆∆∆++= ∴10262=++=∆ABC S 2分 24．解：（1）,
m=1 2分
(2) 由（1）可知抛物线的解析式为y=－(x+1）2
+3
即y=－x 2-2x+2
设P （x, －x 2
-2x+2）
因为PQ ∥y 轴，所以设Q(x, 2x)
所以：PQ= （－x 2
-2x+2）－2x =－x 2
－4x+2=－（ x+2）2
+6 2分 当x=－2时，PQ 最大值=6 2分
（3）因为∠PQO 不可能为直角，所以分两种情形讨论：①当∠QPO 为直角时，P 为抛物
线与X 轴的左侧的交点
抛物线： y=－x 2-2x+2， 令y=0 －x 2-2x+2=0，解得：x 1= －1+3 x 2=－1－3 所以P （－1－3，0） 1分
当x=－1－3时，y=2x=2(－1－3)=－2－23 所以Q （－1－3，－2－23 ） 2分
②当∠POQ 为直角时，设PQ 与x 轴交于D 点， 根据题意： △OPD ∽△OQD 得：OD 2=PD ·QD
即x 2=（－x 2
-2x+2）(－2x) 解得x=
441
3±
-，取x ＜0
则x=
441
3-
- 当x=
4
41
3-
-时，y=2x=
2
41
3-
-
所以Q （
4
41
3-
-，
2
41
3-
-） 2分
所以，符合条件的Q 坐标为（－1－3，－2－23 ）或（
4
41
3-
-，
2
41
3-
-）
1分。