最小树问题VS最短路问题
合集下载
最小支撑树与最短路问题（NO25）
(k) ij
iikj((kk11)),,若若LLiij(j(kk))
L (k1) ij
L (k1) ij
第三步：当k=p时终止计算，否则，返回第二步。
14
例题5: 用Warshall-Floyd方法求下图中各顶点间的 最短路，其中弧（边）旁的数字表示弧（边）长。
0 3 4 9
0
4
2
L (0) ij
4
1
0 1 6
3
2
0
1
5 0 3
3 3 0
v6 3 v5
25
0 3 2 4 4 4
0
4
4
1
1
1
0 1 6 9
d2
W
d1
3
2
0
1 * 1
5 0 3 3 3
3 3 0 0 0
0 3 2 4 4 4
L (o) ij
ij
(vi , v j ) A
ij(o)=j (i,j=1,2,…p)
13
第二步：k=r(1rp)时，L(k)中第k行和第k列元素保 持不变，其它元素按下式计算，并填入L(k)=(Lij(k))中：
Lij(k)=min{Lij(k-1),Lik(k-1)+Lkj(k-1)}
相应地，(k)的各元素按下式变化：
8
例题2 用Dijkstra标号法求下图由v1到各顶点的最短路。
4
7 2
6 2
1 3 24
547
4 35
1
2
37
6
5
4
7 2
13 4
23 4
35
6 2
5 7 4 7 10
最小树问题
6.3.1 狄克斯特拉算法 (Dijkstra algorithm, 1959) 计算两节点之间或一个节点到所有节点之间的最短路 令 dij 表示 vi vj 的直接距离(两点之间有边)，若两点之间 没有边，则令 dij = ，若两点之间是有向边，则 dji = ； 令 dii = 0，s 表示始点，t 表示终点 • 对每个节点，用两种标号：T和P，表示从始点到该节点的距 离，P是最短距离(权)，为永久标号，T是目前路径的距离，是 临时标号。 • 通过不断改进T值，当其最小时，将其改为P标号。 • 开始时，令始点有P=0的P标号，其它节点为T=+ .
•（3）Kruskal 算法：将图中所有边 v1 按权值从小到大排列，依次选 1 所剩最小的边加入边集 T，只 v8 要不和前面加入的边构成回路， 5 直到 T 中有 n1 条边，则 T 是最小生成树
v7
4
v2
1
v3
2
4 5
1
3
4
1
v4 5 v5
v0 2 3 v6 2 4
图的矩阵表示
将图的几何形状转化为代数矩阵形式，可大 大方便计算机对图的处理与运算。 1、无权图的矩阵表示：
6.2.3 最小生成树
v5 9 v6 17 10 8 7 11 v4 16 v3 9.5 v2 v1 10
12 7 19.5
10 16 11 10 17 10 9.5 19.5 16 9.5 7 12 7 8 7 11 10 8 9 17 19.5 12 7 9
寻找连通图支撑树的方法有“破圈法”。就是从图中 任取一个圈，去掉一条边。再对剩下的图重复以上步 骤，直到不含圈时为止，这样就得到一个支撑树。 例4 用破圈法求出下图的一个支撑树。 v2 e1 v1 e2 v3 e3 e4 e7 e8 e6 v5
运筹学上机试题5-图论
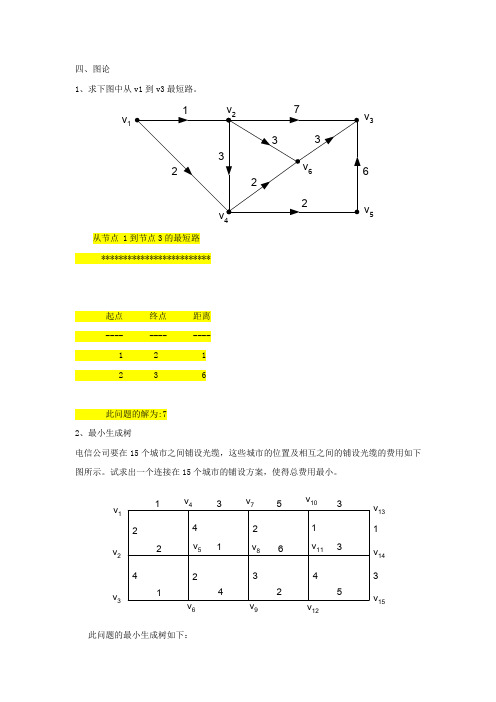
四、图论1、求下图中从v1到v3最短路。
v 1v 3v 546从节点 1到节点3的最短路 *************************起点 终点 距离 ---- ---- ---- 1 2 1 2 3 6此问题的解为:7 2、最小生成树电信公司要在15个城市之间铺设光缆，这些城市的位置及相互之间的铺设光缆的费用如下图所示。
试求出一个连接在15个城市的铺设方案，使得总费用最小。
v 1v 2v 3v 4v 5v 6v 7v 8v 9v 10v 11v 12v 13v 14v 152241131456422323135134此问题的最小生成树如下：*************************起点终点距离---- ---- ----1 4 11 2 22 5 25 8 15 6 26 3 18 7 28 9 39 12 212 11 411 10 110 13 313 14 114 15 3此问题的解为:283、最短路问题例. 求下图中从v1到各点的最短路，并指出有哪些点是不可达到的。
vv7v8v4从节点 1到节点2的最短路*************************起点终点距离---- ---- ---- 1 2 4此问题的解为:41到3没有路1到4没有路从节点 1到节点5的最短路*************************起点终点距离 ---- ---- ---- 1 5 1此问题的解为:1从节点 1到节点6的最短路*************************起点终点距离 ---- ---- ---- 1 5 1 5 6 6此问题的解为:7从节点 1到节点7的最短路*************************起点终点距离 ---- ---- ---- 1 7 3此问题的解为:3从节点 1到节点8的最短路*************************起点终点距离 ---- ---- ---- 1 5 1 5 6 66 8 3此问题的解为:104、最短路问题有6个村庄，各村庄的距离如下图所示。
教学课件：第五章-最小树问题
最小树问题的实际应用
最小树问题在现实生活中具有广泛的应用，如电路设计、网络路由、物流配送等。通过解 决最小树问题，可以优化网络结构、降低成本、提高效率，为实际问题的解决提供重要的 理论支持和实践指导。
最小树问题的未来研究方向
算法优化与改进
尽管已经存在许多有效的算 法用于解决最小树问题，但 随着问题规模的扩大和复杂 度的增加，需要进一步优化 和改进现有算法，以提高求 解速度和精度。
04 最小小生成树问题是在最小生成树问题的基础上，给 每条边赋予一个权重值，目标是寻找一棵权值最小的生成树 。
详细描述
在带权重的最小生成树问题中，每条边都有一个关联的权重 ，表示该边的长度或代价。算法需要选择一组边，这些边能 够连接所有节点并且总权值最小。常见的带权重的最小生成 树算法有普里姆算法和克鲁斯卡尔算法。
理论分析与证明
对于最小树问题的求解算法 ，需要深入的理论分析和证 明，以揭示算法的内在机制 和性能。未来可以进一步研 究算法的理论基础和数学证 明，为算法的设计和分析提 供更严格的依据。
THANKS FOR WATCHING
感谢您的观看
05 总结与展望
最小树问题的研究现状与成果
最小树问题的定义和性质
最小树问题是一类组合优化问题，旨在寻找一棵具有最小权值的树，该树连接给定的顶点 集。最小树问题在计算机科学、运筹学和图论等领域具有广泛的应用。
最小树问题的研究进展
近年来，最小树问题的研究取得了重要的进展。研究者们提出了许多有效的算法和近似算 法，用于解决最小树问题及其变种。这些算法在理论和实践方面都取得了重要的突破，为 解决实际问题提供了有效的工具。
教学课件：第五章-最小树问
目录
• 引言 • 最小树问题的算法 • 最小树问题的实例分析 • 最小树问题的扩展问题 • 总结与展望
最小树问题在现实生活中具有广泛的应用，如电路设计、网络路由、物流配送等。通过解 决最小树问题，可以优化网络结构、降低成本、提高效率，为实际问题的解决提供重要的 理论支持和实践指导。
最小树问题的未来研究方向
算法优化与改进
尽管已经存在许多有效的算 法用于解决最小树问题，但 随着问题规模的扩大和复杂 度的增加，需要进一步优化 和改进现有算法，以提高求 解速度和精度。
04 最小小生成树问题是在最小生成树问题的基础上，给 每条边赋予一个权重值，目标是寻找一棵权值最小的生成树 。
详细描述
在带权重的最小生成树问题中，每条边都有一个关联的权重 ，表示该边的长度或代价。算法需要选择一组边，这些边能 够连接所有节点并且总权值最小。常见的带权重的最小生成 树算法有普里姆算法和克鲁斯卡尔算法。
理论分析与证明
对于最小树问题的求解算法 ，需要深入的理论分析和证 明，以揭示算法的内在机制 和性能。未来可以进一步研 究算法的理论基础和数学证 明，为算法的设计和分析提 供更严格的依据。
THANKS FOR WATCHING
感谢您的观看
05 总结与展望
最小树问题的研究现状与成果
最小树问题的定义和性质
最小树问题是一类组合优化问题，旨在寻找一棵具有最小权值的树，该树连接给定的顶点 集。最小树问题在计算机科学、运筹学和图论等领域具有广泛的应用。
最小树问题的研究进展
近年来，最小树问题的研究取得了重要的进展。研究者们提出了许多有效的算法和近似算 法，用于解决最小树问题及其变种。这些算法在理论和实践方面都取得了重要的突破，为 解决实际问题提供了有效的工具。
教学课件：第五章-最小树问
目录
• 引言 • 最小树问题的算法 • 最小树问题的实例分析 • 最小树问题的扩展问题 • 总结与展望
最小树问题VS最短路问题
2
i 1 j 1 8 8
a67
x12 x13 x24 x34 3; x34 x36 x47 x67 3; x47 x45 x78 x58 3; x x x x x x 5; 12 13 24 47 36 67 st x x x x x x 5; 36 34 45 58 78 67 x12 x13 x36 x67 x78 x58 x45 x24 7; x 7; ij ij xij 8； j=1ٛ 8) 0或1；(i=1ٛ
最小树问题 • 已知有六个城市，它们之间 要 架设电话线，要求任意两个城 市均可以互相通话，并且电话 线的总长度最短
最短路问题（SPP-Shortest Path Problem）
• 一名货柜车司机奉命在最短的时间内将一 车货物从甲地运往乙地. 从甲地到乙地的公 路网纵横交错，因此有多种行车路线，这 名司机应选择哪条线路呢？ • 假设货柜车的运行速度是恒定的，那么这 一问题相当于需要找到一条从甲地到乙地 6 B D 的最短路. 6 5
A 7 C 4至v7点的最短路问题归结为求解整数规划问题。 1
v2
v5 v4 2 3 3 4 v6 4 v7
最短路问题
• 城市中的管道铺设，线路安排，工 厂布局，设备更新，选址问题
min Z aij xij
i 1 j 1 7 7
9
v1
5 v3
2 8
8
1, 最短路径弧(i, j ); 解：设xij 0, 否则
7
x12 x13 1; x12 x 23 x 24 x 25; x13 x 23 x34 x36; x 24 x34 x 45 x 46; st x 25 x 45 x65 x57; x36 x 46 x65 x 67; x57 x67 1; xij 0或1, (i 1…7；j=1
10.3_最短路问题
B）Dijkstra算法和Ford算法都适用于任意边的情况 C）Dijkstra算法仅适用于所有边的权非负的情况，Ford算
法适用于所有边的权为任意实数的情况 D）Dijkstra算法适用于所有边的权为任意实数的情况，
Ford算法适用于所有边的权非负情况
29
OR:SM
试试看——选择题
• 2、以下说法中错误的是（ ）。
4
8
1
v4
vt
1
7
3
6
1
2
v6
7
OR:SM
vs
方式之一：单标号算法
第一步：
T(vs)=∞
v1
2
3
P(vs)=0 vs
9
10
4 7
T(vs)=∞
v2 1
4
3
v3
2
T(vs)=∞
T(vs)=∞
v5
8 1
v4 T(vs)=∞
7
vt T(vs)=∞
6
1
v6
T(vs)=∞
8
OR:SM
方式之一：单标号算法
第二步：
第4年 19 3-4 18
第5年 24 4-5 27
[解]设以vi(i=1,2,3,4,5)表示“第i年初购进一台新设备”这 种状态，以v6表示“第5年末”这种状态；以弧(vi, vj)表示 “第i年初购置的一台设备一直使用到第j年初”这一方案，以
wij表示这一方案所需购置费和维护费之和。于是，该问题就 可归结为从图中找出一条从v1到v6的最短路问题。其网络模型 如下：
本章小结
图论是应用十分广泛的运筹学分支，它已广泛应用在物 理、化学、控制论、信息论、科学管理、电子计算机等 各个领域。
法适用于所有边的权为任意实数的情况 D）Dijkstra算法适用于所有边的权为任意实数的情况，
Ford算法适用于所有边的权非负情况
29
OR:SM
试试看——选择题
• 2、以下说法中错误的是（ ）。
4
8
1
v4
vt
1
7
3
6
1
2
v6
7
OR:SM
vs
方式之一：单标号算法
第一步：
T(vs)=∞
v1
2
3
P(vs)=0 vs
9
10
4 7
T(vs)=∞
v2 1
4
3
v3
2
T(vs)=∞
T(vs)=∞
v5
8 1
v4 T(vs)=∞
7
vt T(vs)=∞
6
1
v6
T(vs)=∞
8
OR:SM
方式之一：单标号算法
第二步：
第4年 19 3-4 18
第5年 24 4-5 27
[解]设以vi(i=1,2,3,4,5)表示“第i年初购进一台新设备”这 种状态，以v6表示“第5年末”这种状态；以弧(vi, vj)表示 “第i年初购置的一台设备一直使用到第j年初”这一方案，以
wij表示这一方案所需购置费和维护费之和。于是，该问题就 可归结为从图中找出一条从v1到v6的最短路问题。其网络模型 如下：
本章小结
图论是应用十分广泛的运筹学分支，它已广泛应用在物 理、化学、控制论、信息论、科学管理、电子计算机等 各个领域。
图与网络分析(GraphTheoryandNetworkAnalysis)
e9
e5 {v1 , v3 } e6 {v3 , v5 }
e7 {v3 , v5 } e8 {v5 , v6 }
e9 {v6 , v6 } e10 {v1 , v6 }
e1
e2
v2
e5 e3 e4 v4
e8
e6
v5 e7 v3
图1
2、如果一个图是由点和边所构成的，则称其为无向图，记作
X={1}, w1=0
p1=0
2
6
1
2
3
1
10
p4=1
5
9
3
4
7
5
6
5
2
3
4
6
7
4
8 8
min {c12,c14,c16}=min {0+2,0+1,0+3}=min {2,1,3}=1 X={1,4}, p4=1
（9） T (v6 ) min[ T (v6 ), P(v5 ) l56 ] min[ , 5 2] 7 （10） P(v6 ) 7
反向追踪得v1到v6的最短路为：v1 v2 v5 v6
求从1到8的最短路径
2
6
1
2
3
1
10
5
9
3
4
7
5
6
5
2
3
4
6
7
4
8 8
v2
v5
v2
v4
v3
v4
v3
一个图G 有生成树的充要条件是G 是连通图。
用破圈法求出下图的一个生成树。
v2
e1 v1
e4 e7 e3 v4 e8
最小树问题
i 2在 , X 2 中e 2 选 ,4 边 E 3 E 2 e 2 4e 1,e 2 2,e 3 2,4 3 X X 2 v 4 v 1 ,v 2 ,v 3 ,v 4 ,X 3 v 5 ,v 6 ,
i 3在 , X 3 中e 4 选 ,5 边 E 4 E 3 e 4 5e 1,e 2 2,e 3 2,e 4 4,5 4 X X 3 v 5 v 1 ,v 2 ,v 3 ,v 4 ,v 5 ,X 4 v 6 ,
i 4在 , X 4 中e 5 选 ,6 边 E 5 E 4 e 5 6e 1,e 2 2,e 3 2,e 4 4,e 5 5,6 5 X X 4 v 6 v 1 ,v 2 ,v 3 ,v 4 ,v 5 ,v 6 V ,
设v1是T的一个悬挂点，考虑图T-｛v1｝，则图T｛v1｝ 的顶点数为K，由归纳假设可得 ：
，因为 m T(v1) nT(v1)1 nT(v1) nT 1 ， nT(v1) nT 1，则 mT(v1) mT1 ，证毕。
定理3：图T是树的充分必要条件是任意两个顶点之间恰 有一条链。
证明：必要性 因T是连通的，故任两个点之 间至少有一条链。但如果某两个点之间有两条链 的话，那么图T中含有圈，这与树的定义矛盾， 从而任两个点之间恰有一条链。
7
4 v6
5
v4
v2 2
v5
4
3
4 v6 v4
v5
4
3
4 v6 v4
v3 5
6
v1 1
7
5
v2 2
v5
v3 5
4
6
3
v1 1
7
4 v6 5
v4
v2 2
v5
4
3
4 v6 v4
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
)
1
将在图中球最小支撑树的问题归结为球整数规划 问题，是列出这个整数规划的数学模型
1 a13 3 a36 6
a12 a34
2 a24 4 a47 a45 Tmin ; 解：设xij 0, 边(i, j ) Tmin min Z aij xij
设x ij＝从点i到点j的流量 max z＝x12＋x13 x12＝x23＋x24＋x25 ; x ＋x ＝x ＋x ; 13 23 34 35 x24＋x34＋x54＝x46 ; x25＋x35＝x54＋x56 ; st x12＋x13＝x46＋x56 ; x12 10，x13 6，x23 4，x24 5，x25 3， x34 5，x35 8，x46 11，x54 3，x56 7; x 0，对所有i，j ij
最小树问题VS最短路问题
• 请注意最短路问题和最小树的异同点：都 要求总赋权数最小是相同点，但最小树要 求经过所有顶点，而最短路不必经历所有 顶点，只要从出发点到终点有一条路线， 使得总赋权数最小即可。
最小树问题
• 公路连接问题:某一地区有若干个主要城市，现准备修建 高速公路把这些城市连接起来， 使得从其中任何一个城 市都可以经高速公路直接或间接到达另一个城市. 假定已 经知道了任意两个城市之间修建高速公路的成本，那么应 如何决定在哪些城市间修建高速公路，使得总成本最小？ 1 3 4 8 1 7 6 3 2 5 5 2 4
最小树问题 • 已知有六个城市，它们之间 要 架设电话线，要求任意两个城 市均可以互相通话，并且电话 线的总长度最短
最短路问题（SPP-Shortest Path Problem）
• 一名货柜车司机奉命在最短的时间内将一 车货物从甲地运往乙地. 从甲地到乙地的公 路网纵横交错，因此有多种行车路线，这 名司机应选择哪条线路呢？ • 假设货柜车的运行速度是恒定的，那么这 一问题相当于需要找到一条从甲地到乙地 6 B D 的最短路. 6 5
2
i 1 j 1 8 8
a67
x12 x13 x24 x34 3; x34 x36 x47 x67 3; x47 x45 x78 x58 3; x x x x x x 5; 12 13 24 47 36 67 st x x x x x x 5; 36 34 45 58 78 67 x12 x13 x36 x67 x78 x58 x45 x24 7; x 7; ij ij xij 8； j=1ٛ 8) 0或1；(i=1ٛ
A 7 C 4 4 F 5 3 E 1
试将图中v1至v7点的最短路问题归结为求解整数规划问题。 1
v2
v5 v4 2 3 3 4 v6 4 v7
最短路问题
• 城市中的管道铺设，线路安排，工 厂布局，设备更新，选址问题
min Z aij xij
i 1 j 1 7 7
9
v1
5 v3
2 8
8
1, 最短路径弧(i, j ); 解：设xij 0, 否则
7
x12 x13 1; x12 x 23 x 24 x 25; x13 x 23 x34 x36; x 24 x34 x 45 x 46; st x 25 x 45 x65 x57; x36 x 46 x65 x 67; x57 x67 1; xij 0或1, (i 1…7；j=1