初三数学专题讲义-存在性问题
中考数学:存在性问题复习说课讲解

中考数学:存在性问题复习初中数学二次函数中的图形构建及存在性问题一、二次函数中有关面积的存在性问题例1(10山东潍坊)如图所示,抛物线与x 轴交于点()()1030A B -,、,两点,与y 轴交于点()03.C -,以AB 为直径作M ⊙,过抛物线上一点P 作M ⊙的切线PD ,切点为D ,并与M ⊙的切线AE 相交于点E ,连结DM 并延长交M ⊙于点N ,连结.AN AD 、 (1)求抛物线所对应的函数关系式及抛物线的顶点坐标; (2)若四边形EAMD 的面积为43,求直线PD 的函数关系式;(3)抛物线上是否存在点P ,使得四边形EAMD 的面积等于DAN △的面积?若存在,求出点P 的坐标;若不存在,说明理由.答案:解:(1)因为抛物线与x 轴交于点()()1030A B -,、,两点,设抛物线的函数关系式为:()()13y a x x =+-, ∵抛物线与y 轴交于点()03C -,, ∴()()30103a -=+-,∴ 1.a =所以,抛物线的函数关系式为:223y x x =--,又()214y x =--,因此,抛物线的顶点坐标为()14-,.(2)连结EM ,∵EA ED 、是M ⊙,的两条切线, ∴EA ED EA AM ED MN =⊥⊥,,,∴EAM EDM △≌△ 又四边形EAMD的面积为∴EAM S =△∴12AM AE =· 又2AM =,∴AE =因此,点E的坐标为(11E -或(21.E --,当E 点在第二象限时,切点D 在第一象限. 在直角三角形EAM中,tan 2EA EMA AM ∠=== ∴60EMA ∠=°,∴60DMB ∠=° 过切点D 作DF AB ⊥,垂足为点F ,∴1MF DF ==,因此,切点D的坐标为(2.设直线PD 的函数关系式为y kx b =+,将((12E D -、的坐标代入得2k b k b=+=-+⎪⎩解之,得k b ⎧=⎪⎪⎨⎪=⎪⎩所以,直线PD的函数关系式为33y x =-+当E 点在第三象限时,切点D 在第四象限.同理可求:切点D 的坐标为()23,-,直线PD 的函数关系式为353.33y x =- 因此,直线PD 的函数关系式为35333y x =-+或353.33y x =-(3)若四边形EAMD 的面积等于DAN △的面积又22EAM DAN AMD EAMD S S S S ==△△△四边形, ∴AMD EAM S S =△△∴E D 、两点到x 轴的距离相等,∵PD 与M ⊙相切,∴点D 与点E 在x 轴同侧, ∴切线PD 与x 轴平行,此时切线PD 的函数关系式为2y =或 2.y =-当2y =时,由223y x x =--得,16x =±; 当2y =-时,由223y x x =--得,12x =±.故满足条件的点P 的位置有4个,分别是()()()123162162122P P P +-+-,、,、,、 ()4122.P --,说明:本参考答案给出了一种解题方法,其它正确方法应参考标准给出相应分数.强化训练★1、(10广东深圳)如图,抛物线y =ax 2+c (a >0)经过梯形ABCD 的四个顶点,梯形的底AD 在x 轴上,其中A (-2,0),B (-1, -3).(2)点M 为y 轴上任意一点,当点M 到A 、B 两点的距离之和为最小时,求此时点M 的坐标;(3)在第(2)问的结论下,抛物线上的点P 使S △PAD =4S △ABM 成立,求点P 的坐标.答案:(1)、因为点A 、B 均在抛物线上,故点A 、B 的坐标适合抛物线方程∴403a c a c +=⎧⎨+=-⎩ 解之得:14a c =⎧⎨=-⎩;故24y x =-为所求(2)如图2,连接BD ,交y 轴于点M ,则点M设BD 的解析式为y kx b =+,则有203k b k b +=⎧⎨-+=-⎩,12k b =⎧⎨=-⎩故BD 的解析式为2y x =-;令0,x =则2y =-,故(0,M -(3)、如图3,连接AM ,BC 交y 轴于点N ,由(2)知,90AMB ∠=︒易知BN=MN=1, 易求AM BM ==122ABMS=⨯=;设2(,4)P x x -, 依题意有:214422AD x -=⨯,即:2144422x ⨯-=⨯解之得:x =±,0x =,故 符合条件的P 点有三个:图2图3123((0,4)P P P --★2、.矩形OBCD 在如图所示的平面直角坐标系中,其中三个顶点分别为O (0,0)、B (0,3)、D (-2,0),直线AB 交x 轴于点A (1,0). (1)求直线AB 的解析式;(2)求过A 、B 、C 三点的抛物线的解析式,并写出其顶点E 的坐标; (3)过点E 作x 轴的平行线EF 交AB 于点F .将直线AB 沿轴向右平移2个单位,与x 轴交于点G ,与EF 交于点H 线上是否存在点P ,使得S △PAG = 34S △PEH 不存在,请说明理由.二、二次函数中构建直角三角形与相似形的存在性问题例2 (甘肃)(12分) 如图,抛物线与x 轴交于A (-1,0)、B (3,0)两点,与y 轴交于点C (0,-3),设抛物线的顶点为D . (1)求该抛物线的解析式与顶点D 的坐标;(2)以B 、C 、D 为顶点的三角形是直角三角形吗?为什么?(3)探究坐标轴上是否存在点P ,使得以P 、A 、C 为顶点的三角形与△BCD 相似?若存在,请指出符合条件的点P 的位置,并直接写出点P 的坐标;若不存在,请说明理由.解:(1)设该抛物线的解析式为c bx ax y ++=2,由抛物线与y 轴交于点C (0,-3),可知3-=c . 即抛物线的解析式为32-+=bx ax y . ………………………1分把A (-1,0)、B (3,0)代入, 得30,9330.a b a b --=⎧⎨+-=⎩解得2,1-==b a .∴ 抛物线的解析式为y = x 2-2x -3. ……………………………………………3分∴ 顶点D 的坐标为()4,1-. ……………………………………………………4分说明:只要学生求对2,1-==b a ,不写“抛物线的解析式为y = x 2-2x -3”不扣分.(2)以B 、C 、D 为顶点的三角形是直角三角形. ……………………………5分理由如下:过点D 分别作x 轴、y 轴的垂线,垂足分别为E 、F.在Rt △BOC 中,OB=3,OC=3,∴182=BC . …………………………6分在Rt △CDF 中,DF=1,CF=OF-OC=4-3=1,∴22=CD . …………………………7分在Rt △BDE 中,DE=4,BE=OB-OE=3-1=2,∴202=BD . …………………………8分∴ 222BD CD BC =+, 故△BCD 为直角三角形. …………………………9分(3)连接AC ,可知Rt △COA ∽ Rt △BCD ,得符合条件的点为O (0,0). ………10分过A 作AP 1⊥AC 交y 轴正半轴于P 1,可知Rt △CAP 1 ∽ Rt △COA ∽ Rt △BCD ,求得符合条件的点为)31,0(1P . …………………………………………11分 过C 作CP 2⊥AC 交x 轴正半轴于P 2,可知Rt △P 2CA ∽ Rt △COA ∽ Rt △BCD ,求得符合条件的点为P 2(9,0). …………………………………………12分∴符合条件的点有三个:O (0,0),)31,0(1P ,P 2(9,0). 三、二次函数中构建等腰三角形的存在性问题例3(10重庆潼南)如图, 已知抛物线c bx x y ++=221与y 轴相交于C ,与x 轴相交于A 、B ,点A 的坐标为(2,0),点C 的坐标为(0,-1). (1)求抛物线的解析式;(2)点E 是线段AC 上一动点,过点E 作DE ⊥x 轴于点D ,连结DC ,当△DCE 的面积最大时,求点D 的坐标;(3)在直线BC 上是否存在一点P ,使△ACP 为等腰三角形,若存在,求点P 的坐标,若不存在,说明理由.答案:解:(1)∵二次函数c x y ++=221的图像经过点A (2,0)C(0,-1) ∴⎩⎨⎧-==++1022c c b 解得: b =-21c =-1 ∴二次函数的解析式为121212--=x x y(2)设点D 的坐标为(m ,0) (0<m <2) ∴ OD =m ∴AD =2-m 由△AD E ∽△AOC 得,OCDEAO AD =∴122DEm =- ∴DE =22m-∴△CDE 的面积=21×22m -×m =242m m +-=41)1(412+--m 当m =1时,△CDE 的面积最大 ∴点D 的坐标为(1,0)(3)存在 由(1)知:二次函数的解析式为121212--=x x y 设y=0则1212102--=x x 解得:x 1=2 x 2=-1 ∴点B 的坐标为(-1,0) C (0,-1)设直线BC 的解析式为:y =kx +b∴ ⎩⎨⎧-==+-10b b k 解得:k =-1 b =-1∴直线BC 的解析式为: y =-x -1 在Rt △AOC 中,∠AOC=900 OA=2 OC=1 由勾股定理得:AC=5ABCED xy o题图26∵点B(-1,0) 点C (0,-1) ∴OB=OC ∠BCO=450①当以点C 为顶点且PC=AC=5时, 设P(k , -k -1) 过点P 作PH ⊥y 轴于H ∴∠HCP=∠BCO=450 CH=PH=∣k ∣ 在Rt △PCH 中k 2+k 2=()25 解得k 1=210, k 2=-210 ∴P 1(210,-1210-) P 2(-210,1210-) ②以A 为顶点,即AC=AP=5设P(k , -k -1),过点P 作PG ⊥x 轴于G AG=∣2-k ∣ GP=∣-k -1∣ 在Rt △APG 中 AG 2+PG 2=AP 2(2-k )2+(-k -1)2=5 解得:k 1=1,k 2=0(舍) ∴P 3(1, -2)③以P 为顶点,PC=AP 设P(k , -k -1) 过点P 作PQ ⊥y 轴于点Q PL ⊥x 轴于点L ,∴L(k ,0)∴△QPC 为等腰直角三角形, PQ=CQ=k 由勾股定理知CP=PA=2k∴AL=∣k -2∣, PL=|-k -1| 在Rt △PLA 中(2k)2=(k -2)2+(k +1)2 解得:k =25∴P 4(25,-27) 综上所述: 存在四个点:P 1(210,-1210-) P 2(-210,1210-) P 3(1, -2) P 4(25,-27) 三、二次函数中构建四边形的存在性问题(一)二次函数中构建梯形的存在性问题例4 (10山东临沂)如图,二次函数y = -x 2+ax +b 的图像与x 轴交于A (-21,0)、 B (2,0)两点,且与y 轴交于点C ;(1) 求该拋物线的解析式,并判断△ABC 的形状;(2) 在x 轴上方的拋物线上有一点D ,且以A 、C 、D 、B 四 点为顶点的四边形是等腰梯形,请直接写出D 点的坐标; (3) 在此拋物线上是否存在点P ,使得以A 、C 、B 、P 四点为顶点的四边形是直角梯形?若存在,求出P 点的坐标;若不存在,说明理由。
初中存在性问题(二)

存在性问题(二)1.y=ax2+bx+4与x轴的一个交点为A(﹣2,0),与y轴的交点为C,对称轴是x=3,对称轴与x轴交于点B. (1)求抛物线的函数表达式;(2)经过B,C的直线l平移后与抛物线交于点M,与x轴交于点N,当以B,C,M,N为顶点的四边形是平行四边形时,求出点M的坐标;(3)若点D在x轴上,在抛物线上是否存在点P,使得△PBD≌△PBC?若存在,直接写出点P的坐标;若不存在,请说明理由.2.l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.(1)y=x2﹣2x﹣3的衍生抛物线的解析式是,衍生直线的解析式是;(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;(3)设(1)中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x 轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.3.y=ax2+bx+c经过A(3,0)、B(0,3)、C(1,0)三点.(1)求抛物线的解析式;(2)若点D的坐标为(-1,0),在直线AB上有一点P,使△ABO与△ADP相似,求出点P的坐标;(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点E,使△ADE的面积等于四边形APCE的面积?如果存在,请求出点E的坐标;如果不存在,请说明理由.4.如图①,点A坐标为(1,-2),点B坐标为(3,-1),二次函数y=-x2图象为l1.(1)平移抛物线l1,使平移后的抛物线经过点A,但不过点B.①满足此条件函数解析式有个.②写出向下平移且经点A解析式.(2)平移抛物线l1,使平移后的抛物线经过A,B两点,所得的抛物线l2,如图②,求抛物线l2的函数解析式及顶点C的坐标,并求△ABC的面积.(3)在y轴上是否存在点P,使S△ABC=S△ABP?若存在,求出点P的坐标;若不存在,请说明理由.5.对称轴为x=2的抛物线经过点A(-1,0),C(0,5)两点,与x轴另一交点为B,已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.(1)求此抛物线的解析式;(2)当a=1时,求四边形MEFP面积的最大值,并求此时点P的坐标;(3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.6.与x 轴交于A 、D 两点,与y 轴交于点B,四边形OBCD 是矩形,点A 的坐标为(1,0),点B 的坐标为(0,4),已知点E (m ,0)是线段DO 上的动点,过点E 作PE ⊥x 轴交抛物线于点P ,交BC 于点G ,交BD 于点H .(1)求该抛物线的解析式;(2)当点P 在直线BC 上方时,请用含m 的代数式表示PG 的长度;(3)在(2)的条件下,是否存在这样的点P ,使得以P 、B 、G 为顶点的三角形与△DEH 相似?若存在,求出此时m 的值;若不存在,请说明理由.24y x bx c 3=-++7.直线y =-x +2与x 轴交于点B,与y 轴交于点C.二次函数图象经过点B ,C 和点A (-1,0).(1)求B ,C 两点坐标;(2)求该二次函数的关系式;(3)若抛物线的对称轴与x 轴的交点为点D ,点E 是线段BC 上的一个动点,过点E 作x 轴的垂线与抛物线相交于点F ,当点E 运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF 的最大面积及此时E 点的坐标;(4)在抛物线的对称轴上是否存在点P ,使△PCD 是等腰三角形?如果存在,直接写出P 点的坐标;如果不存在,请说明问题.8.如图,在平面直角坐标系中,已知点A 的坐标是(4,0),并且OA =OC =4OB ,动点P 在过A ,B ,C 三点的抛物线上.(1)求抛物线的解析式;(2)是否存在点P ,使得△ACP 是以AC 为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)过动点P 作PE 垂直于y 轴于点E ,交直线AC 于点D ,过点D 作x 轴的垂线.垂足为F ,连接EF ,当线段EF 的长度最短时,求出点P 的坐标.129.对称轴为直线x =−的抛物线经过点A(-6,0)和点B (0,4). (1)求抛物线的解析式和顶点坐标;(2)设点E (x ,y )是抛物线上的一个动点,且位于第三象限,四边形OEAF 是以OA 为对角线的平行四边形,求▱OEAF 的面积S 与x 的函数关系式,并写出自变量x 的取值范围;①当▱OEAF 的面积为24时,请判断▱OEAF 是否为菱形?②是否存在点E ,使▱OEAF 为正方形?若存在,求出点E 的坐标;若不存在,请说明理由.72。
第13讲 中考探究之存在性问题

02
考点突破
考点一 特殊三角形存在性问题 【例 1】在平面直角坐标系 xOy 中,已知 A(0,2),动点 P 在 y= 3 x 的图象上运动(不与 O
3 重合),连接 AP.过点 P 作 PQ⊥AP,交 x 轴于点 Q,连接 AQ. (1)求线段 AP 长度的取值范围; (2)试问:点 P 运动的过程中,∠QAP 是否为定值?如果是,求出该值;如果不是,请说 明理由; (3)当△OPQ 为等腰三角形时,求点 Q 的坐标.
BF
AO
BF AO
当 x=2 时,- 1 x2+ 3 x+2=3,∴点 D 的坐标为(2,3), 22
(3)当 BO 为边时,OB∥EF,OB=EF,
设 E(m,- 1 m+2),F(m,- 1 x2+ 3 x+2),
2
22
EF=|(- 1 m+2)-(- 1 x2+ 3 x+2)|=2,解得 m1=2,m2=2-2 2 ,m3=2+2 2 ,
∴tan∠PAQ= PQ = PH = yp = 3 ,则∠QAP=30°; PA AG xp 3
(3)设:OQ=m,则 AQ2=m2+4=4PQ2,
①当 OQ=PQ 时,即 PQ=OQ=m,则 m2+4=4m2,解得:m=± 3 ; 2
②当 PO=OQ 时,同理可得:m=±(4+4 3 );
九年级数学压轴学习讲义 点的存在性问题
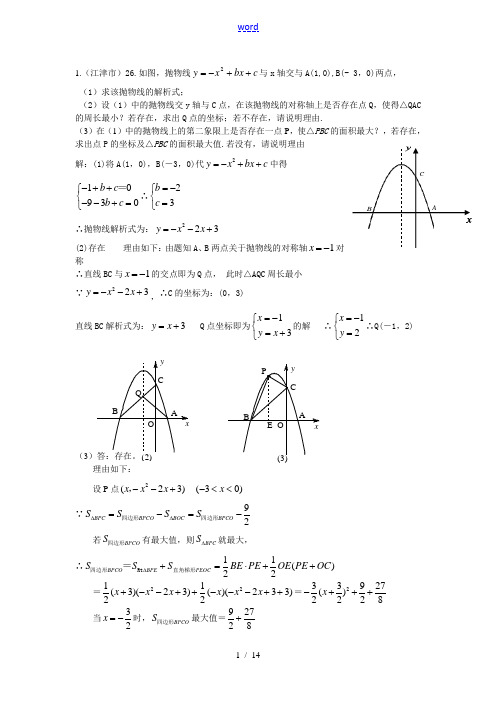
(3)xy ABCPE Ox yAB C Q O(2)1.(江津市)26.如图,抛物线c bx x y ++-=2与x 轴交与A(1,0),B(- 3,0)两点, (1)求该抛物线的解析式;(2)设(1)中的抛物线交y 轴与C 点,在该抛物线的对称轴上是否存在点Q ,使得△QAC 的周长最小?若存在,求出Q 点的坐标;若不存在,请说明理由.(3)在(1)中的抛物线上的第二象限上是否存在一点P ,使△PBC 的面积最大?,若存在,求出点P 的坐标及△PBC 的面积最大值.若没有,请说明理由 解:(1)将A(1,0),B(-3,0)代2y x bx c =-++中得10930b c b c -++⎧⎨--+=⎩=∴23b c =-⎧⎨=⎩ ∴抛物线解析式为:223y x x =--+(2)存在 理由如下:由题知A 、B 两点关于抛物线的对称轴1x =-对称∴直线BC 与1x =-的交点即为Q 点, 此时△AQC 周长最小 ∵223y x x =--+,∴C 的坐标为:(0,3)直线BC 解析式为:3y x =+ Q 点坐标即为13x y x =-⎧⎨=+⎩的解 ∴12x y =-⎧⎨=⎩∴Q(-1,2)(3)答:存在。
理由如下:设P 点2(23) (30)x x x x --+-<<,∵92BPC BOC BPCO BPCO S S S S ∆∆=-=-四边形四边形若BPCO S 四边形有最大值,则BPC S ∆就最大,∴BPE BPCO PEOC S S S ∆+Rt 四边形直角梯形=11()22BE PE OE PE OC =⋅++ =2211(3)(23)()(233)22x x x x x x +--++---++=233927()2228x -+++当32x =-时,BPCO S 四边形最大值=92728+ABC∴BPC S ∆最大=9279272828+-=当32x =-时,215234x x --+=∴点P 坐标为315( )24-,) 2.(某某市)26.(本题满分13分)如图,已知抛物线C 1:()522-+=x a y 的顶点为P ,与x 轴相交于A 、B 两点(点A 在点B 的左边),点B 的横坐标是1.(1)求P 点坐标及a 的值;(4分)(2)如图(1),抛物线C 2与抛物线C 1关于x 轴对称,将抛物线C 2向右平移,平移后的抛物线记为C 3,C 3的顶点为M ,当点P 、M 关于点B 成中心对称时,求C 3的解析式;(4分)(3)如图(2),点Q 是x 轴正半轴上一点,将抛物线C 1绕点Q 旋转180°后得到抛物线C 4.抛物线C 4的顶点为N ,与x 轴相交于E 、F 两点(点E 在点F 的左边),当以点P 、N 、F 为顶点的三角形是直角三角形时,求点Q 的坐标.(5分)解:(1)由抛物线C 1:()522-+=x a y 得顶点P 的为(-2,-5)∵点B (1,0)在抛物线C 1上∴()52102-+=a 解得,a =59(2)连接PM ,作PH ⊥x 轴于H ,作MG ⊥x 轴于G∵点P 、M 关于点B 成中心对称∴PM 过点B ,且PB =MB ∴△PBH ≌△MBG ∴MG =PH =5,BG =BH =3 ∴顶点M 的坐标为(4,5)抛物线C 2由C 1关于x 轴对称得到,抛物线C 3由C 2平移得到 ∴抛物线C 3的表达式为()54952+--=x y (3)∵抛物线C 4由C 1绕点x 轴上的点Q 旋转180°得到∴顶点N 、P 关于点Q 成中心对称 由(2)得点N 的纵坐标为5设点N 坐标为(m ,5) 作PH ⊥x 轴于H ,作NG ⊥x 轴于G 作PK ⊥NG 于K ∵旋转中心Q 在x 轴上∴EF =AB =2BH =6∴FG =3,点F 坐标为(m +3,0)H 坐标为(2,0),K 坐标为(m ,-5),根据勾股定理得 PN 2=NK 2+PK 2=m 2+4m +104PF 2=PH 2+HF 2=m 2+10m +50 NF 2=52+32=34① 当∠PNF =90º时,PN 2+NF 2=PF 2,解得m =443,∴Q 点坐标为(193,0)②当∠PFN =90º时,PF 2+NF 2=PN 2,解得m =103,∴Q 点坐标为(23,0)③∵PN >NK =10>NF ,∴∠NPF ≠90º综上所得,当Q 点坐标为(193,0)或(23,0)时,以点P 、N 、F 为顶点的三角形是直角三角形.3.(某某市)25.(14分)已知,如图1,过点()01E -,作平行于x 轴的直线l ,抛物线214y x =上的两点A B 、的横坐标分别为-1和4,直线AB 交y 轴于点F ,过点A B 、分别作直线l 的垂线,垂足分别为点C 、D ,连接CF DF 、. (1)求点A B F 、、的坐标; (2)求证:CF DF ⊥; (3)点P 是抛物线214y x =对称轴右侧图象上的一动点,过点P 作PQ PO ⊥交x 轴于点Q ,是否存在点P 使得OPQ △与CDF △相似?若存在,请求出所有符合条件的点P 的坐标;若不存在,请说明理由.(1)解:方法一,如图1,当1x =-时,14y =; 当4x =时,4y = ∴1A ⎛⎫- ⎪⎝⎭1,4()44B ,设直线AB 的解析式为y kx b =+(图1)备用图(第25题图)(图1)则1444k b k b ⎧-+=⎪⎨⎪+=⎩ 解得341k b ⎧=⎪⎨⎪=⎩∴直线AB 的解析式为314y x =+当0x =时,1y =()01F ∴,方法二:求A B 、两点坐标同方法一,如图2,作FG BD ⊥,AH BD ⊥,垂足分别为G 、H ,交y 轴于点N ,则四边形FOMG 和四边形NOMH 均为矩形,设FO x =BGF BHA △∽△ BG FG BH AH ∴=441544x -∴=-解得1x =()0F ∴,1(2)证明:方法一:在Rt CEF △中,1,2CE EF ==22222125CF CE EF ∴=+=+=CF ∴=在Rt DEF △中,42DE EF ==,222224220DF DE EF ∴=+=+=DF ∴=由(1)得()()1141C D ---,,,5CD ∴=22525CD ∴==222CF DF CD ∴+=90CFD ∴∠=°∴CF DF ⊥方法二:由 (1)知5544AF AC ===,AF AC ∴=同理:BF BD =ACF AFC ∴∠=∠AC EF ∥ACF CFO ∴∠=∠AFC CFO ∴∠=∠同理:BFD OFD ∠=∠90CFD OFC OFD ∴∠=∠+∠=°即CF DF ⊥(3)存在.解:如图3,作PM x ⊥轴,垂足为点M 又PQ OP ⊥Rt Rt OPM OQP ∴△∽△ PM OM PQ OP ∴=PQ PMOP OM ∴= 设()2104P x x x ⎛⎫> ⎪⎝⎭,,则214PM x OM x ==,(图2)图3①当Rt Rt QPO CFD △∽△时,51225PQ CF OP DF ===21142xPM OMx ∴==解得2x =()121P ∴, ②当Rt Rt OPQ CFD △∽△时,2525PQ DF OP CF ===2142xPM OM x ∴==解得8x =()2816P ∴, 综上,存在点()121P ,、()2816P ,使得OPQ △与CDF △相似. 4.如图①,正方形ABCD 中,点A 、B 的坐标分别为(0,10),(8,4),点C 在第一象限.动点P 在正方形ABCD 的边上,从点A 出发沿A →B →C →D 匀速运动, 同时动点Q 以相同速度在x 轴正半轴上运动,当P 点到达D 点时,两点同时停止运动, 设运动的时间为t 秒.(1)当P 点在边AB 上运动时,点Q 的横坐标x (长度单位)关于运动时间t (秒)的函数图象如图②所示,请写出点Q 开始运动时的坐标及点P 运动速度; (2)求正方形边长及顶点C 的坐标;(3)在(1)中当t 为何值时,△OPQ 的面积最大,并求此时P 点的坐标;(4)如果点P 、Q 保持原速度不变,当点P 沿A →B →C →D 匀速运动时,OP 与PQ 能否相等,若能,写出所有符合条件的t 的值;若不能,请说明理由.解:(1)Q (1,0) ······················································································· 1分 点P 运动速度每秒钟1个单位长度.(2)过点B 作BF ⊥y 轴于点F ,BE ⊥x 轴于点E ,则BF =8,4OF BE ==. ∴1046AF =-=.在Rt △AFB 中,228610AB =+过点C 作CG ⊥x 轴于点G ,与FB 的延长线交于点H . ∵90,ABC AB BC ∠=︒=∴△ABF ≌△BCH . ∴6,8BH AF CH BF ====. ∴8614,8412OG FH CG ==+==+=.A B CDF H M Py∴所求C 点的坐标为(14,12).(3)过点P 作PM ⊥y 轴于点M ,PN ⊥x 轴于点N ,则△APM ∽△ABF . ∴AP AM MP AB AF BF ==.1068t AM MP∴==. ∴3455AM t PM t ==,.∴3410,55PN OM t ON PM t ==-==.设△OPQ 的面积为S (平方单位)∴213473(10)(1)5251010S t t t t =⨯-+=+-(0≤t ≤10)说明:未注明自变量的取值X 围不扣分.∵310a =-<0 ∴当474710362()10t =-=⨯-时,△OPQ 的面积最大. 此时P 的坐标为(9415,5310). (4)当53t =或29513t =时, OP 与PQ 相等.5.(某某市)25.(本小题满分14分)如图13,二次函数)0(2<++=p q px x y 的图象与x 轴交于A 、B 两点,与y 轴交于点C (0,-1),ΔABC 的面积为45。
中考数学复习课件:第2轮第38讲 存在性问题

(1)点 B 的坐标为________;
解:∵四边形 AOCB 是矩形, ∴ BC = OA = 2 , OC = AB = 2 3 , ∠ BCO= ∠BAO=90°, ∴B(2 3,2). 故答案为:(2 3,2);
(2)是否存在这样的点 D,使得△DEC 是等腰三 角形?若存在,请求出 AD 的长度;若不存在,请说 明理由;
经检验,此时四边形 DGCB 为平行四边形,此 时 G 坐标为(-2,5);
综上所述,G 点坐标存在,为(2,-3)或(4,5) 或(-2,5);
∴OE= 3, ∴点 D 横坐标为- 3, ∴点 D 坐标为(- 3, 3+1), 设直线 BD 的函数解析式为 y=kx+b(k≠0),
由题意可得0=3+3k1+=b-, 3k+b, 解得k=- 33,
b= 3, 故直线 BD 的函数解析式为 y=- 33x+ 3;
(3)点 P 在抛物线的对称轴上且在 x 轴下方,点 Q 在射线 BA 上.当△ABD 与△BPQ 相似时,请直 接写出所有满足条件的点 Q 的坐标.
经检验,此时四边形 DCBG 为平行四边形,此 时 G 坐标为(4,5);
③当 DC 为对角线时,则另一对角线是 GB,由 中点坐标公式可知:
线段 DC 的中点坐标为xD+2 xC,yD+2 yC, 即1+2 0,t-2 3,
线段 GB 的中点坐标为xG+2 xB,yG+2 yB, 即m+2 3,m2-2m2-3+0, 此时 DB 的中点与 GC 的中点为同一个点, 则t1-+2230==mm2+2-32,m2-3+0,解得mt==8,-2,
第二轮 专题突破
第38讲 存在性问题
类型 等腰三角形
方法点拨:(1)画出满足条件的所有草图;(2)利 用勾股定理或相似三角形的性质求线段长度;(3)检 查答案的合理性
中考数学专题复习——存在性问题

活动二:挑战自我,超越自我
()如图(),当、 分别移动到边、的延 长线上时,连接与, ()中的结论还成立 吗?(直接回答“是” 或“否”,不需要证 明)
活动二:挑战自我,超越自我
()如图当、分别 在、的延长线上移 动时,连接与,() 中的结论还成立吗? 请你说明理由.
活动二:挑战自我,超越自我
()如图,当、分别 在边、上移动时,连 接和交于点,由于点、 的移动,使得点也随 之运动,请你画出点 的运动路径草图.若, 试求出线段的最小值.
小结
说说看:你有哪些收获?
.动态问题通常要设想整个运动过程,找到并记下 每一个特殊的位置;
.注意考察图形运动经过的某些特殊点,图形变化 而成的特殊形状;
A'
活动一:我自信,我能行
.如图,矩形中,点在边上,将矩形沿 直线翻折,点恰好落在边上的点处. 若,,则的长为.
A
D
E
BF
C
活动一:我自信,我能行
、如图,正方形的边长为,点在边上
且超越自我
正方形中,动点、分别从、两点 同时出发,以相同的速度在直线、 上运动.
.把整个运动过程分解成若干个小过程,逐一考察, 最后再综合考虑。
我们一直在努力, 我们会一直努力!
活动一:我自信,我能行
.如图,将周长为的△沿平移一个单 位得到△,则四边形的周长为( )
.
A
D
B
E
C
F
活动一:我自信,我能行
如图,一块含有角的直角三角形,在水平桌面上 饶点按顺时针方向旋转到’’’的位置.若的长为, 那么丁点从开始到结束经过的路径长为( )
中考数学几何模型22个精选——存在性问题

中考数学几何模型22个精选——存在性问题
1.三角形存在性问题
2.平行四边形存在性问题
目录1
一、直角三角形的存在性
1.几何法平面直角坐标系中已知条线段,构造直角三角形,用的是“两线圆':分别过已知线段的两个端点作已知线段的垂线,再以已知线段为直径作圆。
2.两点间距离公式代数法,代数法解题步:
•(1)表示出A、B、C的坐标
•(2)表示出线段AB、AC、BC的长(两点间距离公式)
•(3)分类列方程
•3)解方程
•(4)检验。
二、等腰三角形的存在
1.“两圆一线”几何法,又叫两圆一中垂。
2.两点间距离公式代数法,代数法解题步骤:
•(1)列出三边长的平方
•(2)分类列方程;
•(3)解方程;
•(4)检验。
注:若△ABC是等腰三角形,那么可以分为①AB=AC;②AB=BC;③AC=BC三种情况
练习
三、平行四边形的存在性
分析:平移法的原理是平行四边形的对应边平行且相等;对点法的原理平行四边形对角线互相平分.
常考类型:1.三定一动2.二定二动。
苏教版初三数学下册《专题讲座:存在性问题(3)》

与二次函数有关的面积的存在性问题一、重点知识和解题策略一般有已知面积或面积的关系求点的坐标,已知面积之间的关系求点的坐标,其中涉及一次函数、二次函数、一元二次方程、相似、三角形函数等知识。
解题策略是设出所求点的坐标直接表示出三角形的面积后,列方程或利用二次函数的的最值进行求解,或将面积关系转化为底或高之间的关系,然后利用相似、三角形函数等知识进行求解。
二、热身运动1、二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点为A(﹣3,0)、B(1,0)两点,与y轴交于点C(0,﹣3m)(其中m>0).(1)求该二次函数的解析式(系数用含m的代数式表示);(2)如图1,当m=2时,点P为第三象限内的抛物线上的一个动点,设△APC的面积为S,试求出S与点P的横坐标x之间的函数关系式及S的最大值.2.如图2,在平面直角坐标系xOy中,抛物线y=ax2-2ax-3a(a<0)与x轴交于A、B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.(1)直接写出点A的坐标,并求直线l的函数表达式(其中k、b用含a的式子表示);(2)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为5 4,求a的值.方法分析这两例都是“在三角形三个顶点‘两定一动’的条件下,探求三角形的相关面积问题”.求解的方法是过三角形的一个不定顶点作x轴的垂线,交过两定点的直线于一点,将原三角形转化为两个同底的两个三角形的和或差.这种题型一般有两种类型,即“垂线”经过三角形的内部以及在三角形的外部,但是结果是一致的,都是等于“不定顶点”与“与过两定点的直线的交点”的纵坐标差的绝对值与“两定点”的横坐标差的绝对值的积的二分之一,在能确定坐标的大小时,可去掉绝对值.上面两例都是可确定对应坐标的大小的.这个方法比较过顶点作坐标轴的平行线构造矩形等方法进行求解要简便.三、例题学习例1、如图,已知二次函数的图象与x轴交于A、B两点,D为顶点,其中点B的坐标为(5,0),点D的坐标为(1,3).(1)求该二次函数的表达式;(2)试问在该二次函数图象上是否存在点G,使得△ADG的面积是△BDG 的面积的?若存在,求出点G的坐标;若不存在,请说明理由.例2.如图,在平面直角坐标系中,直线l 1的解析式为y x =,直线l 2的解析式为132y x =-+,与x 轴、y 轴分别交于点A 、点B ,直线l 1与l 2交于点C .若直线l 2上存在点P (不与B 重合),满足S △COP =S △COB ,请求出点P 的坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三数学讲义 存在性问题教学过程:一、教学衔接(课前环节)1、回收上次课的教案,了解家长的反馈意见;2、检查学生的作业,及时指点3、捕捉学生的思想动态和了解学生的本周学校的学习内容二、知识点解析存在性问题是指判断满足某种条件的事物是否存在的问题,这类问题的知识覆盖面较广,综合性较强,题意构思非常精巧,解题方法灵活,对学生分析问题和解决问题的能力要求较高,是近几年来各地中考的“热点”。
这类题目解法的一般思路是:假设存在→推理论证→得出结论。
若能导出合理的结果,就做出“存在”的判断,导出矛盾,就做出不存在的判断。
由于“存在性”问题的结论有两种可能,所以具有开放的特征,在假设存在性以后进行的推理或计算,对基础知识,基本技能提出了较高要求,并具备较强的探索性,正确、完整地解答这类问题,是对我们知识、能力的一次全面的考验。
一、函数中的存在性问题(相似)1.(2011枣庄10分)如图,在平面直角坐标系xoy 中,把抛物线2y x =向左平移1个单位,再向下平移4个单位,得到抛物线2()y x h k =-+.所得抛物线与x 轴交于A ,B 两点(点A 在点B 的左边),与y 轴交于点C ,顶点为D.(1)写出h k 、的值;(2)判断△ACD 的形状,并说明理由;(3)在线段AC 上是否存在点M ,使△AOM∽△ABC?若存在,求出点M 的坐标;若不存在,说明理由.二、函数中的存在性问题(面积)2. 如图,抛物线()20y ax bx a >=+与双曲线ky x=相交于点A ,B .已知点B 的坐标为(-2,-2),点A 在第一象限内,且tan∠AOX=4.过点A 作直线AC∥x 轴,交抛物线于另一点C . (1)求双曲线和抛物线的解析式; (2)计算△ABC 的面积;(3)在抛物线上是否存在点D ,使△ABD 的面积等于△ABC 的面积.若存在,请你写出点D 的坐标;若不存在,请你说明理由.三、函数中的存在性问题(四边形)3. 如图,二次函数y = -x 2+ax +b 的图像与x 轴交于A (-21,0)、 B (2,0)两点,且与y 轴交于点C ; (1) 求该拋物线的解析式,并判断△ABC 的形状;(2) 在x 轴上方的拋物线上有一点D ,且以A 、C 、D 、B 四点为顶点的四边形是等腰梯形,请直接写出D 点的坐标; (3) 在此拋物线上是否存在点P ,使得以A 、C 、B 、P 四点为顶点的四边形是直角梯形?若存在,求出P巩固练习,及时反馈1.如图,已知抛物线经过A (﹣2,0),B (﹣3,3)及原点O ,顶点为C . (1)求抛物线的解析式;(2)若点D 在抛物线上,点E 在抛物线的对称轴上,且A 、O 、D 、E 为顶点的四边形是平行四边形,求点D 的坐标;(3)P 是抛物线上的第一象限内的动点,过点P 作PMx 轴,垂足为M ,是否存在点P ,使得以P 、M 、A 为顶点的三角形△BOC 相似?若存在,求出点P 的坐标;若不存在,请说明理由.yA BC Ox2.如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=k x+3。
(1) 设点P的纵坐标为p,写出p随k变化的函数关系式。
(2)设⊙C与PA交于点M,与AB交于点N,则不论动点P处于直线l上(除点B以外)的什么位置时,都有△AMN∽△ABP。
请你对于点P处于图中位置时的两三角形相似给予证明;(3)是否存在使△AMN的面积等于3225的k值?若存在,请求出符合的k值;若不存在,请说明理由。
3.已知直角坐标系中有一点A(-4,3),点B在x轴上,△AOB是等腰三角形.(1)求满足条件的所有点B的坐标;(2)求过O、A、B三点且开口向下的抛物线的函数表达式(只需求出满足条件的一条即可);(3)在(2)中求出的抛物线上存在点P,使得以O,A,B,P四点为顶点的四边形是梯形,求满足条件的所有点P的坐标及相应梯形的面积.4、在直角坐标系xoy中,已知点P是反比例函数23=y(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.(1)如图1,⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:①求出点A,B,C的坐标.②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的12.若存在,试求出所有满足条件的M点的坐标,若不存在,试说明理由.5.如图所示,抛物线与x 轴交于点()()1030A B -,、,两点,与y 轴交于点()03.C -,以AB 为直径作M ⊙,过抛物线上一点P 作M ⊙的切线PD ,切点为D ,并与M ⊙的切线AE 相交于点E ,连结DM 并延长交M ⊙于点N ,连结.AN AD 、 (1)求抛物线所对应的函数关系式及抛物线的顶点坐标; (2)若四边形EAMD 的面积为43,求直线PD 的函数关系式;(3)抛物线上是否存在点P ,使得四边形EAMD 的面积等于DAN △的面积?若存在,求出点P 的坐标;若不存在,说明理由.1、【答案】解:(1)∵由平移的性质知,2()y x h k =-+的顶点坐标为D(-1,-4),∴14h k =-=-,。
(2)由(1)得()2=14y x +-.当=0y 时,()2140x +-=. 解之,得1231x x =-=, 。
∴A(30)B 10- ,,(,).又当0x =时,()()22=140143y x +-=+-=-,∴C 点坐标为(0,-3)。
又抛物线顶点坐标D (-1,-4),作抛物线的对称轴1x =-交x 轴于点E ,DF⊥ y 轴于点F 。
易知 在Rt△AED 中,AD 2=22+42=20,在Rt△AOC 中,AC 2=32+32=18,在Rt△CFD 中,CD 2=12+12=2, ∴AC 2+ CD 2=AD 2。
∴△ACD 是直角三角形。
(3)存在.作OM ∥BC 交AC 于M ,M点即为所求点。
由(2)知,△AOC 为等腰直角三角形,∠BAC=450,AC 1832==。
由△AOM∽ △ABC,得AO AMAB AC =。
即39,AM 24432== 。
过M 点作MG⊥AB 于点G ,则AG=MG=29281942164⎛⎫⎪⎝⎭==,OG=AO -AG=3-9344=。
又点M 在第三象限,所以M (-34,-94)。
2、【答案】解:(1)把点B (-2,-2)的坐标代入k y x =得,22k-=-,∴k =4。
∴双曲线的解析式为:4y x=。
设A 点的坐标为(m ,n ).∵A 点在双曲线上,∴mn=4。
又∵tan∠AOX=4,∴m n=4,即m =4n 。
∴n 2=1,∴n=±1。
∵A 点在第一象限,∴n=1,m =4。
∴A 点的坐标为(1,4)。
把A 、B 点的坐标代入2y ax bx =+得,4422a b a b +=⎧⎨-=-⎩,解得,a =1,b =3。
∴抛物线的解析式为:23y x x =+。
(2)∵AC∥x 轴,∴点C 的纵坐标y =4,代入23y x x =+得方程,2340x x +-=,解得x 1=-4,x 2=1(舍去)。
∴C 点的坐标为(-4,4),且AC =5。
又∵△ABC 的高为6,∴△ABC 的面积=12×5×6=15。
(3)存在D 点使△ABD 的面积等于△ABC 的面积。
理由如下:过点C 作CD∥AB 交抛物线于另一点D ,此时△ABD 的面积等于△A BC 的面积(同底:AB ,等高:CD 和AB 的距离)。
∵直线AB 相应的一次函数是:22y x =+,且CD∥AB, ∴可设直线CD 解析式为2y x p =+, 把C 点的坐标(﹣4,4)代入可得,12p =。
∴直线CD 相应的一次函数是:212y x =+。
解方程组23212y x x y x ⎧=+⎨=+⎩,解得,318x y =⎧⎨=⎩。
∴点D 的坐标为(3,18)。
3、答案:[解] (1) 根据题意,将A (-21,0),B (2,0)代入y = -x 2+ax +b 中,得⎪⎩⎪⎨⎧=++-=+--02402141b a b a ,解这个方程,得a =23,b =1,∴该拋物线的解析式为y = -x 2+23x +1,当 x =0时,y =1, ∴点C 的坐标为(0,1)。
∴在△AOC 中,AC =22OC OA +=221)21(+=25。
在△BOC 中,BC =22OC OB +=2212+=5。
AB =OA +OB =21+2=25,∵AC 2+BC 2=45+5=425=AB 2,∴△ABC 是直角三角形。
(2) 点D 的坐标为(23,1)。
(3) 存在。
由(1)知,AC ⊥BC 。
若以BC 为底边,则BC //AP ,如图1所示,可求得直线BC 的解析式为y = -21x +1,直线AP 可以看作是由直线BC 平移得到的,所以设直线AP 的解析式为y = -21x b , y A B COxP把点A (-21,0)代入直线AP 的解析式,求得b = -41,∴直线AP 的解析式为y = -21x -41。
∵点P 既在拋物线上,又在直线AP 上,∴点P 的纵坐标相等,即-x 2+23x +1= -21x -41,解得x 1=25,x 2= -21(舍去)。
当x =25时,y = -23,∴点P (25,-23)若以AC 为底边,则BP //AC ,如图2所示。
可求得直线AC 的解析式为y =2x +1。
直线BP 可以看作是由直线AC 平移得到的,所以设直线BP 的解析式为y =2x +b ,把点B (2,0)代 入直线BP 的解析式,求得b = -4,∴直线BP 的解析式为y =2x -4。
∵点P 既在拋物线 上,又在直线BP 上,∴点P 的纵坐标相等,即-x 2+23x +1=2x -4,解得x 1= -25,x 2=2(舍去)。
当x = -25时,y = -9,∴点P 的坐标为(-25,-9)。
综上所述,满足题目条件的点P 为(25,-23)或(-25,-9)。
练习1、【答案】解:(1)设抛物线的解析式为()20y ax bx c a =++≠,∵抛物线过A (﹣2,0),B (﹣3,3),O (0,0)可得 42=093=3=0a b c a b c c -+⎧⎪-+⎨⎪⎩,解得 =1=2=0a b c ⎧⎪⎨⎪⎩。
∴抛物线的解析式为22y x x =+。
(2)①当AE 为边时,∵A、O 、D 、E 为顶点的四边形是平行四边形,∴DE=AO=2,则D 在x 轴下方不可能,∴D 在x 轴上方且DE=2,则D 1(1,3),D 2(﹣3,3)。
