基于MATLAB平面桁架有限元分析研究_李远瑛
matlab桁架结构有限元计算

matlab桁架结构有限元计算(最新版)目录一、引言二、MATLAB 与桁架结构有限元计算的概述1.MATLAB 简介2.桁架结构有限元计算的基本流程三、MATLAB 在桁架结构有限元计算中的应用实例1.铝制起重机垂直和水平部分的有限元分析2.基于 MATLAB 的三维桁架有限元分析3.五杆桁架有限元分析四、MATLAB 在桁架结构有限元计算中的优势与局限1.优势2.局限五、结论正文一、引言在工程领域中,桁架结构由于其优越的力学性能和简单的结构形式,被广泛应用于桥梁、起重机、输电塔等大型工程项目中。
为了确保桁架结构的安全和稳定,对其进行有限元分析是必不可少的。
而 MATLAB 作为一种强大的数学软件,可以方便地进行有限元计算。
本文将介绍如何利用MATLAB 进行桁架结构有限元计算。
二、MATLAB 与桁架结构有限元计算的概述1.MATLAB 简介MATLAB(Matrix Laboratory)是一款广泛应用于科学计算、数据分析和可视化的软件。
它基于矩阵计算,可以方便地处理大量数据,并提供了丰富的函数库和工具箱。
2.桁架结构有限元计算的基本流程桁架结构有限元计算的基本流程包括以下几个步骤:(1)建立有限元模型:根据实际问题,建立桁架结构的有限元模型,包括节点、单元、约束和载荷等。
(2)组装刚度矩阵:根据有限元模型,组装桁架结构的刚度矩阵。
(3)施加边界条件和载荷:对桁架结构施加边界条件和载荷。
(4)求解:利用求解器求解桁架结构的内力、应力和应变等问题。
(5)后处理:对计算结果进行数据结构化保存,以便进行后期处理和分析。
三、MATLAB 在桁架结构有限元计算中的应用实例1.铝制起重机垂直和水平部分的有限元分析某铝制起重机的垂直和水平部分由铝制成,杨氏模量为 e70,gpa,横截面为 2 cm。
对角桁架构件由钢制成,杨氏模量为 e210,gpa,横截面为3 cm。
结构承受荷载 p6000,n。
假设两个支撑节点固定(即 x 和 y 位移为 0)。
MATLAB在平面桁架计算中的应用

MATLAB在平面桁架计算中的应用作者:王鹏周琪琛姚姗姗来源:《卷宗》2016年第10期摘要:本文基于平面桁架有限元分析的基本原理,利用MATLAB语言编程对有外荷载作用的平面桁架进行有限元分析,结果表明,通过MATLAB软件对平面桁架受力分析的结果与精确解吻合。
本文介绍的方法,在平面桁架有限元中具有普遍的适用性,对复杂的平面桁架结构有限元分析有一定的参考价值。
关键词:平面桁架;MATLAB;有限元分析MATLAB是以矩阵为基本的运算单元,可以灵活地进行矩阵运算、图形绘制、编程开发等,具有编程效率高、可移植性强、计算速度快等特点;有限元分析法是根据变分原理求解数学及物理问题的数值计算方法,它是随着近年来计算机技术的迅速发展而得到的广泛应用。
本文以解决一个实际的平面桁架问题为例,运用有限元分析法,并利用MATLAB软件进行编程计算来演示MATLAB软件在平面桁架中的应用。
接下来,首先介绍解决平面桁架问题的有限元分析方法。
1 平面桁架有限元分析的基本原理在用有限元法对平面桁架受力分析中,平面桁架元是分析的基本单元,它是一种二维有限元,每个平面桁架元有2个节点和3个参数,参数分别为长度L、弹性模量E和横截面积A,当假设桁架元与正方向总体X轴逆时针倾斜θ角时,并令C=Cos(θ),S=Sin(θ),则单元刚度矩阵可表示为:在有限元分析中,通过单元分析,建立单元刚度矩阵k,然后再将单元刚度矩阵通过刚度集成规则集合成结构的整体刚度矩阵K,对于一个有n个节点的结构而言,其整体的刚度矩阵K为2n×2n的矩阵,在实际MATLAB软件操作中,并不需要编写函数程序,而是直接调用相应的函数即可,正是因为这样,在用MATLAB软件进行桁架受力分析时,可以大大提高效率,节省时间。
整体刚度矩阵的函数名称为PlaneTrussAssemble。
一旦得到刚度矩阵K,就可以列出方程:式中,U代表节点的位移矢量,F是结构节点的荷载矢量,这两个边界条件需要手动赋值,然后利用高斯消元法便可求解上述方程组,一旦求解出为止的位移和支反力,就可以利用方程:求解单元的节点力。
基于有限元的桁架结构的动态分析研究

以建 立符合结构真 实力学性质 的有限元模 型_ 。本 文所分析 2 J 作时受到动态反复荷载 的作用 , 它的稳定 性直 接影响架桥 的速 度 化 , 的桁架采用梁单元 、 桁架单元和板单 元的组合结构 形式。所建 立 和质 量 … 。安 全 、 济 、 用 的桁 架 结 构 是 我 们 在 设 计 过 程 中追 经 适 。材料采用钢 材 , 弹性模 量为 2 0G a泊 松 比 0 P , 求 的 目标 , 但是桁架结 构在 动态荷 载 的作用下 往往 出现断 裂 、 损 的结构模型见图 1 为 0 2极 限抗 拉 强度 采 用 30M P。 ., 0 a 伤等 , 对桁架结构 的动态分析研究具 有重要 的意义。桁 架 的动态 性能直接关 系到整 个架桥 机 的运行 , 其强 度 、 刚度 和稳定性 设计 计算 的准确性是 十分重要 的。同时 , 在架桥 过程 中, 整体 系统始
仿真计算 。
2 仿 真结果表 明 , 比例阻 尼隔震结构 与传统 结构相 比 , ) 非 隔 震结构上部的加速度 和层 问位移反应 均 比普通结 构小得多 , 结构 L D J 的高频反应 更小 , 明显有 效地 减轻 了结构 的地震 反应 , 提高 了整
Yo g e g Du Hu , l e F, t . fc f n n p p rin l n fn , i Li Bi i l ec Efe to o — r o t a o o
a 整体模型 b 正视图 ) ) c 俯视图 ) d 节点 大样 图 )
2 有 限元分 析计算
出于控制效果方面的考虑 , 还是 出于技术 、 经济方面 的考虑 , 隔震 结构的隔震层 阻尼 比应尽量控制在合理 的范 围内。
图 1 结 构 的 三 维模 型
matlab桁架结构有限元计算

matlab桁架结构有限元计算摘要:一、引言- 介绍MATLAB在桁架结构有限元计算中的应用- 说明本文的主要内容和结构二、有限元计算原理- 有限元方法的背景和基本原理- 有限元方法在桁架结构分析中的应用三、MATLAB实现桁架结构有限元计算- MATLAB的基本操作和编程基础- 使用MATLAB进行桁架结构有限元计算的步骤和示例四、MATLAB桁架结构有限元计算的应用- 分析不同桁架结构的特点和计算结果- 探讨MATLAB在桁架结构有限元计算中的优势和局限五、结论- 总结MATLAB在桁架结构有限元计算中的应用和优势- 展望MATLAB在桁架结构分析中的未来发展方向正文:一、引言随着计算机技术的不断发展,有限元方法已经成为工程界解决复杂问题的重要手段。
MATLAB作为一款功能强大的数学软件,可以方便地实现桁架结构的有限元计算。
本文将介绍MATLAB在桁架结构有限元计算中的应用,并详细阐述其操作方法和计算原理。
二、有限元计算原理1.有限元方法的背景和基本原理有限元法是一种数值分析方法,通过将连续的求解域离散为离散的单元,将复杂的问题转化为求解单元的线性或非线性方程组。
有限元方法具有适应性强、精度高、计算效率高等优点,广泛应用于固体力学、流体力学、传热等领域。
2.有限元方法在桁架结构分析中的应用桁架结构是一种由杆件组成的结构,其节点只有三个自由度。
有限元方法可以有效地分析桁架结构的强度、刚度和稳定性,为工程设计提供理论依据。
三、MATLAB实现桁架结构有限元计算1.MATLAB的基本操作和编程基础MATLAB是一种功能强大的数学软件,可以进行矩阵运算、绘制图形、编写程序等操作。
在MATLAB中,用户可以通过编写脚本文件或使用图形界面进行各种计算和分析。
2.使用MATLAB进行桁架结构有限元计算的步骤和示例(1) 建立桁架结构模型:根据实际结构绘制桁架的节点和杆件,确定各节点的三自由度。
(2) 离散化:将桁架结构离散为有限个单元,每个单元包含若干个节点。
有限元方法与MATLAB程序设计 第3章 桁架和刚架

Fe keUe
Ue TUe
结构坐标系下的 单元刚度方程
9
结构坐标系下单元刚度矩阵 ke T TkeT
c cos s sin
y
Fe keUe
y
i (xi , yi )
(xj, yj ) x j
x
结构坐标系
cos sin 0
0 1 0 1 0 e cos sin 0
0
ke
EA sin
Fyi
Fxj Fyj
EA l
0
1
0
0 0 0
0 1 0
0
vi
0 0
u v
j j
单元坐标系下的 1 0 1 0
单元刚度矩阵
ke
EA l
0
1
0 0
0 1
0 0
0
0
0
0
7
§3.1.3 整体坐标系下的单元刚度方程
Fxi Fxi cos Fyi sin Fyi Fxi sin Fyi cos Fxj Fxj cos Fyj sin
是结构坐标系x轴正方 向至单元坐标轴x 的角度
y
x
y Fxi i
Fxi Fyi Fyi
x
结构(整体)坐标系
Fyj Fxj sin Fyj cos
Fxi Fyi
Fxj
Fyj
e
cos
sin
0
0
sin cos
0 0
0 0
cos sin
0
e
Fxi
e0Fyi源自sin cosFxj
Fyj
Fe TFe Ue TUe
cos
T sin
0
0
sin cos
运用MATLAB对桁架单元进行有限元分析

np=3; ne=2; nload=1; nb=4; nu=0;% np为节点数,ne为单元数,nload为外力数,nb为约束数,nu 为泊松比np2=np*2; np3=np2-nb;% np2为不受约束时自由度是节点的两倍 ,np3为不受约束的节点自由度个数K=sym(zeros(np2,np2));% 定义受整体刚度空数组F=sym(zeros(np2,1));% 定义节点外力空数组KK=sym(zeros(np3,np3));% 预置自由度刚度空数组FF=sym(zeros(np3,1));% 预置自由度外力空数组syms h A P E L% 定义未知正常数为变量xy=[0,h;sqrt(3)*h,0;0,0];% 节点横纵坐标数组AA=[A;A];% 单元杆件面积load=[2,2,-P];% 荷载数组bound=[1,1,0;1,2,0;3,1,0;3,2,0];% 边界条件数组IJ=[1,2;3,2];% 各杆单元节点编号DW=zeros(1,4);for ie =1:neip=IJ(ie,1);jp=IJ(ie,2);DW(1)=ip*2-1; DW(2)=ip*2; DW(3)=jp*2-1; DW(4)=jp*2; % 给单元节点横纵方向编号x1=xy(ip,1); x2=xy(jp,1); y1=xy(ip,2); y2=xy(jp,2); % 杆单元节点x,y坐标L=sqrt((x2-x1)^2+(y2-y1)^2);% 杆单元长度c=(x2-x1)/L; s=(y2-y1)/L;% c为余弦, s为正弦T=[c,s,0,0;-s,c,0,0;0,0,c,s;0,0,-s,c];% 坐标转换矩阵(将局部坐标转换为整体坐标)A1=AA(ie);ke=[E*A1/L,0,-E*A1/L,0;0,0,0,0;-E*A1/L,0,E*A1/L,0;0,0,0,0];k=T.'*ke*T;% 将局部坐标下单元刚度转换为整体坐标下单元刚度 (转置后面加.可以去掉结果中的虚数)for i =1:4i1=DW(i);for j =1:4j1=DW(j);K(i1,j1)=K(i1,j1)+k(i,j);% 集成整体刚度矩阵endendendfor i =1:nloadi1=(load(i,1)-1)*2+load(i,2);F(i1,1)=F(i1,1)+load(i,3);% 将荷载按节点方向代码累加,计入外力荷载endFuu=sym(zeros(np2,1));% 节点位移NR=zeros(np2,1);for i =1:nbi1=(bound(i,1)-1)*2+bound(i,2);NR(i1)=-i1;% 将有约束的节点的横纵节点编号挑出来变为负数uu(i1)=bound(i,3);% 有约束的四个方向位移为0endj=0;for i =1:np2i1=NR(i);if i1==0j=j+1;NR(i)=j;endend% 此循环目的是为了将没有约束的节点以及方向挑出来for i =1:np2i1=NR(i);if i1>0FF(i1)=F(i);end% 将没有约束的节点方向的外力储存下来for j =1:np2j1=NR(j);if (i1>0 & j1>0)KK(i1,j1)=K(i,j);end% 将没有约束的节点的刚度储存下来endendKKFFfor i =1:np2i1=NR(i);for j =1:np2j1=NR(j);if (i1>0 & j1<0)jj1=abs(j1);FF(i1)=FF(i1)-K(i,jj1)*uu(jj1);end% 由于有约束方向的位移为0,所以无位移的地方FF[i1]不变endendu=sym(zeros(np2,1));u=KK\FF% 求解线性方程for i =1:np2i1=NR(i);if i1>0uu(i)=u(i1);end% 将求解的无约束方向的位移放进总的位移数组相应的位置中去enduudisp('位移')for ip =1:npstr=[ip;uu(ip*2-1);uu(ip*2)];disp(str)% 输出节点位移endfor ie =1:neip=IJ(ie,1);jp=IJ(ie,2);DW(1)=ip*2-1; DW(2)=ip*2; DW(3)=jp*2-1; DW(4)=jp*2; x1=xy(ip,1); x2=xy(jp,1); y1=xy(ip,2); y2=xy(jp,2);L=sqrt((x2-x1)^2+(y2-y1)^2);c=(x2-x1)/L; s=(y2-y1)/L;T=[c,s,0,0;-s,c,0,0;0,0,c,s;0,0,-s,c];A1=AA(ie);ke=[E*A1/L,0,-E*A1/L,0;0,0,0,0;-E*A1/L,0,E*A1/L,0; 0,0,0,0];d=sym(zeros(4,1));for i=1:4d(i)=uu(i);endde=T*d;% 将整体坐标位移转换为局部坐标位移Fe=ke*de;% 杆单元力for j=1:4N=Fe((ie-1)*2+1);% 杆单元轴力sigma=N/A1;enddisp('单元,轴力,应力')str=[ie;N;sigma];disp(str)endF3=K*uu;R=F3-F;disp('支反力');for i =1:nbi1=(bound(i,1)-1)*2+bound(i,2);str=[bound(i,1);bound(i,3);simplify(R(i1))]; disp(str)end。
平面桁架元有限元计算
2
2m
2m
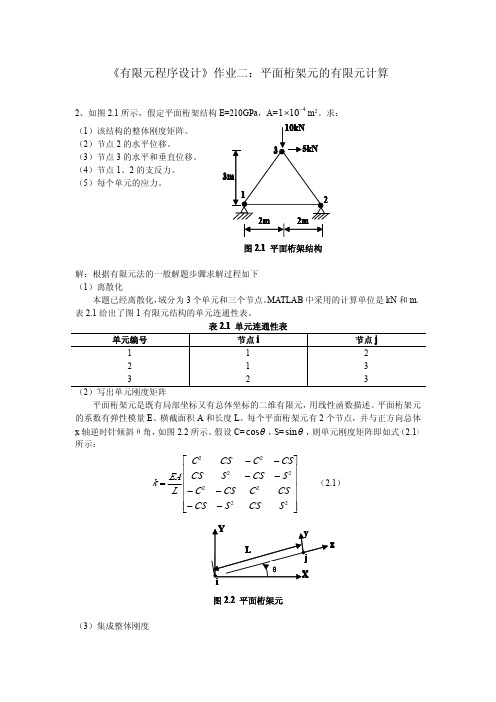
图 2.1 平面桁架结构
解:根据有限元法的一般解题步骤求解过程如下
(1)离散化 本题已经离散化,域分为 3 个单元和三个节点。MATLAB 中采用的计算单位是 kN 和 m。
表 2.1 给出了图 1 有限元结构的单元连通性表。 表 2.1 单元连通性表
单元编号
节点 i
节点 j
1
1
2
《有限元程序设计》作业二:平面桁架元的有限元计算
2、如图 2.1 所示,假定平面桁架结构 E=210GPa,A=1×10−4 m2。求:
(1)该结构的整体刚度矩阵。 (2)节点 2 的水平位移。 (3)节点 3 的水平和垂直位移。 (4)节点 1、2 的支反力。 (5)每个单元的应力。
3m 1
10kN
对一个有 n 个节点的平面结构元而言,其整体刚度矩阵 K 应该是 2n × 2n 矩阵。调用
MATLAB 的 PlaneTrussAssemble 函数可以得到刚度矩阵 K。 (4)引入边界条件
用上一步得到的整体刚度矩阵,就可以列出下列方程组:
[K ]{U}= {F} (2.2)
式中,U 是结构节点的位移矢量,F 是结构节点载荷矢量。其中,边界条件被赋值给矢 量 U 和 F: (5)解方程
K:
[K ]new = [T ][K ]old [T ]T (2.4)
[ ] 式中, T 是 2n × 2n 的变换矩阵,该矩阵通过调用 MATLAB 的 PlaneStrussInclinedSupport
函数得到。假定在节点 i 的支座的倾斜角为α,如图 2.3 所示。
α x
图 2.3 平面桁架的倾斜支座
2
1
3
matlab编程平面梁问题有限元分析

前处理程序clear;clcXY = [1, 0, 02, 2, 03, 2, -2]; %XY为N行3列,N为节点总数ELB = [1, 1, 2, 12, 2, 3, 1]; %ELB为MB行4列,MB为单元总数b = 4.5e-2;h = 2e-1; %截面宽b和高hA1 = b*h;IZ1 = 3e-5; %惯性矩EAIZ = [200e9, A1, IZ1]; %弹性模量与截面积和惯性矩ELPQ = [1, 1, -2e4, 22, 1, -1e4, 2]; %ELPQ第一列为受载荷单元号,第二列为长度C(见下表),三列为载荷大小,四列为载荷类型SU = [1,02, 03,0]; %SU第一列为已知节点位移对应的方程号,第2列为节点位移数值,约束即等于0子程序1function [PO, ii, jj] = dxjd(ELB, XY, ELPQ1)PO = zeros(6,1);k = ELPQ1(1);jj = ELB(k, 3);dxy = [XY(ii, 2), XY(ii, 3)XY(jj, 2), XY(jj, 3)];DY = dxy(2,2) - dxy(1,2);DX = dxy(2,1) - dxy(1,1);L = sqrt(DX^2 + DY^2);C = ELPQ1(2);Q = ELPQ1(3);type = ELPQ1(4);switch typecase 1PO(2) = PO(2) + 0.5*Q*C*(2-2*C^2/L^2 + C^3/L^3);PO(3) = PO(3) + Q*C^2*(6-8*C/L+3*C^2/L^2)/12;PO(5) = PO(5)+Q*C-PO(2);PO(6) = PO(6) - Q*C^3*(4-3*C/L)/12/L;case 2D = L - C;PO(2) = PO(2) + Q*(L+2*C)*D^2/L^3;PO(3) = PO(3) + Q*C*D^2/L^2;PO(5) = PO(5) + Q-PO(2);PO(6) = PO(6) + Q*D*C^2/L^2;case 3D = L - C;PO(1) = PO(1) + Q*D/L;PO(4) = PO(4) + Q*C/L;case 4PO(2) = PO(2) + 7*Q*L/20;PO(3) = PO(3) + Q*L^2/20;PO(5) = PO(5) + 3*Q*L/20;PO(6) = PO(6) + Q*L^2/30;end子程序2function [KE, T] = ketb(dxy, E, A, IZ)DY = dxy(2,2) - dxy(1,2);DX = dxy(2,1) - dxy(1,1);L = sqrt(DX^2 + DY^2);S = DY/L;C = DX/L;a1 = IZ/L;a2 = a1/L;a3 = E/L;KE = a3*[A, 0, 0, -A, 0, 0 0, 12*a2, 6*a1, 0, -12*a2, 6*a10, 6*a1, 4*IZ, 0, -6*a1, 2*IZ-A, 0, 0, A, 0, 00, -12*a2, -6*a1, 0, 12*a2, -6*a10, 6*a1, 2*IZ, 0, -6*a1, 4*IZ]; t = [C, S, 0; -S, C, 0; 0, 0, 1];t1 = zeros(3,3);T = [t, t1; t1, t];end子程序function KZ = kztb(XY, ELB, EAIZ)[N,M] = size(XY);KZ =zeros(9, 9);[MB, m] = size(ELB);for k = 1 :2ii = ELB(k, 2);jj = ELB(k, 3);LTB = ELB(k, 4);dxy = [XY(ii,2), XY(ii,3)XY(jj,2), XY(jj,3)];E = EAIZ(LTB, 1);A = EAIZ(LTB, 2);IZ = EAIZ(LTB, 3);[KE, T] = ketb(dxy, E, A, IZ);CN = [3*ii-2, 3*ii-1, 3*ii, 3*jj-2, 3*jj-1, 3*jj];KE = (T')*KE*T;for i = 1:6for j = 1:6KZ(CN(i), CN(j)) = KZ(CN(i), CN(j)) + KE(i, j);endendend子程序function U = weiyi(KZ, P, SU)[LR, m] = size(SU);for k =1:LRi = SU(k, 1);P(i) = 1e10*SU(k, 2);KZ(i,i) = 1e10*KZ(i, i);endU = KZ\P;end子程序function P = ydx(XY, ELB, EAIZ, ELPQ)[N, m] = size(XY)P = zeros(3*N, 1)[LPQ, m] = size(ELPQ)for j = 1:LPQELPQ1 = ELPQ(j, :)k = ELPQ(j, 1)[PO, ii, jj] = dxjd(ELB, XY, ELPQ1)LTB = ELB(k, 4);dxy = [XY(ii,2), XY(ii,3)XY(jj,2), XY(jj, 3)];E = EAIZ(LTB, 1);A = EAIZ(LTB, 2);IZ = EAIZ(LTB, 3);[KE, T] = ketb(dxy, E, A, IZ );PO = (T')*PO;CN = [3*ii-2, 3*ii-1, 3*ii, 3*jj-2, 3*jj-1, 3*jj]for i = 1:6P(CN(i)) = P(CN(i)) + PO(i);endend后处理程序clc;[N, M] = size(XY);DU = zeros(N,4);for i = 1:NDU(i,1) = i;DU(i,2) = U(3*i-2);DU(i,3) = U(3*i-1);DU(i,4) = U(3*i);end[MB, M] = size(ELB);for i = 1:MBP1(i, 1) = i;end'节点号水平位移竖直位移转角'DU主程序>>GJINPUT;>>KZ = kztb(XY, ELB,EAIZ);>>P = ydx(XY, ELB, EAIZ, ELPQ);>>U = weiyi(KZ, P, SU);>>GJOUTPUT;运行结果:ans ='节点号水平位移竖直位移转角' DU =1.0000 -0.0000 -0.0000 -0.00002.0000 -0.0000 -0.0111 -0.01003.0000 -0.0231 -0.0111 -0.0125。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
桁架结构有限元分析的基本原理
桁架结构在屋架、 桥梁等工程中应用很多. 在
桁架结构中, 各杆件的连接处近似为铰接, 杆件绕 结点可以自由转动, 结构中的各个杆件只受轴力,
收稿日期:2012 - 05 - 26 基金项目: 广 东 省 自 然 科 学 基 金 项 目 ( S2011010001679 ) ; 2011 年梅州市科技计划项目 作者简介: 李远瑛 ( 1973 - ) , 女, 广东平远人, 副教授, 硕士, 主要研究方向: 结构理论研究与计算.
[4 ]
.
32 结点荷载向量 U1 = K1 \ P ;
嘉应学院学报( 自然科学)
2012 年 8 月
U =[ 0 ; 0 ; U1 ( 1 : 9 ) ; 0 ] ; % 生成整体坐标系下结点 位移向量 …… 2 . 4 编制 MATLAB 平面桁架动力特性分析程序 结构动力特性分析方法有矢量迭代法、 子空间 迭代法. MATLAB 提供了计算矩阵特征值的专门函 数, 即 eig 和 eigs, 它们既可以用于求解标准特征值 也可以求解广义特征值问题. 其调用格式为: 问题, E = eig( K , M ) 等. 本文为研究桁架的动力特性, 编制了桁架的动 力特性 计 算 程 序, 得 到 了 结 构 前 9 阶 的 频 率, 见 表 3 . 由于本文篇幅有限, 动力特性计算程序略. 2 . 5 MATLAB 计算结果 表 2 为 MATLAB 编制程序的静力计算结果, 包 括桁架各杆件的轴力和应力. 为直观显示桁架受力 利用 MATLAB 中 line 命令编制了结构 之后的变形, 变形前后的示意图. 图 4 为桁架各结点位移变形示 意图( 变形放大比例为 30 倍) , 实线为变形前, 虚线 为变形后. 表 3 为 MATLAB 编制程序的动力特性计 算结果.
单元 图2 平面桁架计算简图
2 . 1 单元编号, 结点编号 各单元编号, 单元始末端结点编号, 见表 1 所示.
表1 各单元始末端结点编号 单元 ( 6) ( 7) ( 8) ( 9) ( 10 ) 始末端结 点编号 3 →5 4 →5 4 →6 5 →6 2 →5
1. 6 建立结构的刚度方程
( 1)
2 . 5 × 10 - 3 m2 . 在结点 2 和结点 4 施加竖向 200 kn 的集中力. 1. 4 整体坐标下结构总刚度矩阵 K 在结构的整体分析中涉及许多单元及联接它 们的结点, 为避免混淆, 必须对各单元、 结点及结点 位移( 水平位移和竖向位移 ) 进行编号, 由单元刚度 矩 矩阵通过单元定位向量集成结构总刚度矩阵 K, 阵的阶数为结点总数的 2 倍. 单元定位向量由单元 两端的结点位移编号确定. 1. 5 建立结构的结点荷载向量 P
图1
平面桁架杆件单元整体坐标与局部坐标
30 1. 2 坐标转换矩阵
嘉应学院学报( 自然科学)
2012 年 8 月
其中: F e 为局部坐标下单元的轴力; k e 为局部坐标下单元的刚度矩阵; T 为坐标转换矩阵; △ 为整体坐标系下单元的结点位移向量, 由 单元定位向量确定. σ 为局部坐标下单元的应力.
模态 1 2 3 4 5
Freque ncy( hz) MATLAB 35 . 108 76 . 832 95 . 892 184 . 67 226 . 57 ANSYS 35 . 108 76 . 832 95 . 892 184 . 67 226 . 57
模态 6 7 8 9
2 . 6 ANSYS 计算结果 为验证 MATLAB 编制该桁架有限元分析程序 使用 ANSYS 有限元分析软件分别对该结 的正确性, 构进行静力及模态分析计算. 在建立有限元分析模 使用 LINK1 单元, 结果如表 3 及图 5 、 图 6、 图 型中, 7 所示, 二者计算结果完全一致.
31
2 . 2 编制程序流程图 编制 MATLAB 平面桁架静力有限元分析模拟 流程图, 见图 3 所示.
theta8 = 0 ; theta9 = - atan ( 3 / 4 ) * 180 / pi; theta10 = atan( 3 / 4 ) * 180 / pi; % 计算各单元局部坐标与整体 坐标的夹角 k1 = PlaneTrussElementStiffness( E , A, L1 , theta1 ) ; k2 = PlaneTrussElementStiffness( E , A, L2 , theta2 ) ; k3 = PlaneTrussElementStiffness( E , A, L3 , theta3 ) ; k4 = PlaneTrussElementStiffness( E , A, L4 , theta4 ) ; k5 = PlaneTrussElementStiffness( E , A, L5 , theta5 ) ; k6 = PlaneTrussElementStiffness( E , A, L6 , theta6 ) ; k7 = PlaneTrussElementStiffness( E , A, L7 , theta7 ) ; k8 = PlaneTrussElementStiffness( E , A, L8 , theta8 ) ; k9 = PlaneTrussElementStiffness( E , A, L9 , theta9 ) ; k10 = PlaneTrussElementStiffness ( E , A, L10 ,
图 5 桁架各杆件轴力示意图 表2 单元 1 2 3 4 5 静力计算结果 轴力 / 10 5 N -3 1 . 75 2 . 666 7 应力 / 10 N·m - 2
8
图 4 桁架各结点变形示意图 表3 动力特性计算结果 Frequency( hห้องสมุดไป่ตู้) MATLAB 234 . 66 242 . 5 272 . 92 313 . 26 ANSYS 234 . 66 242 . 5 272 . 92 313 . 26
第 30 卷
第8 期
嘉应学院学报( 自然科学) JOURNAL OF JIAYING UNIVERSITY( Natural Science)
Vol. 30
No. 08
2012 年 8 月
Aug. 2012
基于 MATLAB 平面桁架有限元分析研究
李远瑛, 张德生
( 嘉应学院 土木工程学院 , 广东 梅州 514015 ) 摘 要:基于平面桁架有限元分析的基本原理 , 利用 MATLAB 软件对某平面桁架编制了计算程序 , 得到了结构的
内力计算结果、 变形图和结构的动力特性 , 并将计算结果与 ANSYS 有限元分析软件的结果进行比较 . 结果表明, 二者的计算结果一致. 利用 MATLAB 可以编制结构有限元分析程序 , 计算速度快, 数据准确, 并能为复杂结构有 限元分析提供参考. 关键词:MATLAB; 平面桁架; 有限元; ANSYS 中图分类号:TU311. 2 文献标识码: A 文章编号: 1006 - 642X( 2012 ) 08 - 0029 - 05
e e
对于平面桁架单元, 通过坐标系旋转可以完成 从单元局部坐标系到结构整体坐标系的转换. 杆件 转换矩阵为 局部坐标系与整体坐标系的夹角为 α ,
1 . 3 整体坐标系下的杆件单元刚度矩阵 整体坐标系下桁架单元刚度矩阵与局部坐标
2
工程算例
某平面桁架如图 2 所示. 桁架的材料特性为:
e T e 即 系下的单元刚度矩阵关系为 k = T k T, 11 弹性模量 E = 2 . 0 × 10 Pa: 所有单元的横截面积为
始末端结 点编号 1 →2 1 →3 2 →3 2 →4 2 →5
K△ = P △为结构整体坐标下各结点位移向量 . 1. 7 分析各杆件的单元轴力及应力[3] F e = k e T△ e ; σ e = Fe A
( 2) ( 3) ( 4) ( 5)
第 30 卷第 8 期
李远瑛, 张德生
基于 MATLAB 平面桁架有限元分析研究
2 . 3 编制 MATLAB 平面桁架有限元静力分析程序 编制 MATLAB 平面桁架有限元静力分析程序. 程序中 PlaneTrussElementStiffness 为生成单元刚度矩 PlaneTrussAssemble 为集成结构总刚度 阵的子程序, 矩阵的子程序 clear; clc; E = 2 . 0 E11 ; 杆件弹性模量 A = 2 . 5 E - 3 ; % 杆件横截面积 L1 = 4 ; L4 = 4 ; L8 = 4 ; L6 = 4 ; L2 = 5 ; L5 = 5 ; L9 = 5 ; L3 = 3 ; L7 = 3 ; L10 = 5 ; % 计算各单元长度 theta1 = 0 ; theta2 = atan ( 3 / 4 ) * 180 / pi; theta3 = 90 ; theta4 = 0 ; theta5 = - atan( 3 / 4 ) * 180 / pi; theta6 = 0 ; theta7 = 90 ;
展, 有限元分析得到了广泛应用. MATLAB 是效率 可以实现编程计算、 数据 高的工程计算软件工具, 图形化集成. 本文利用 MATLAB 软件, 利用有限元 分析的基本原理对平面桁架进行受力分析, 得到了 结构各杆件的内力、 应力、 结构变形及结构动力特 性, 并将计算结果同 ANSYS 有限元分析软件结果进 行比较. 结果表明, 利用 MATLAB 可以编制结构有 限元分析程序, 计算速度快, 数据准确, 并能为复杂 结构有限元分析提供参考.
轴力 应力 单元 5 8 / 10 N / 10 N·m - 2 2 . 666 7 1 . 066 7 6 7 8 9 10
- 1. 2 0. 7 1 . 066 7
- 3 . 333 3 - 1 . 333 3 1 . 75 2 . 333 3 0. 7 0 . 933 33
