1.1平行线导学案
平行线 第一课时导学案

经过直线外一点,有且只有一条直线与这条直线平行。,
平行公理的推论:
如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
用符号语言表达平行公理推论为:如果b∥a,c∥a,那么()
合作探究
1如图,梯形ABCD中,AB∥CD,连结DB,过C画DB的平行线与AB的延长线交于F,并度量DC与BF的长度,比较DB与CF的大小。
2已知直线a∥b,b∥c,c∥d,则a与d的关系是什么?为什么?
3如图所示,a∥b,a与c相交,那么b与c相交吗?为什么?
课堂小结
本节课我们学习了哪些内容?
达标检测
1在同一平面内,两条直线有种位置关系,它们是;
2.直线m与n在同一平面内不相交,则它们的位置关系是;
3.两条直线相交,交点的个数是________,两条直线平行,交点的个数是_____个.
3.过一点有且只有一条直线平行于已知直线.( )
1、自主检测
2、小组展示
学
(教)后
反思
通过本节课的学习:对自己说,你有哪些收获?
4.平行用符号“”表示,直线AB与CD平行,可以记作“”,
读作:;
两条平行线中一条直线相交,那么这条直线与平行线中的另一边必__________.
7.同一平面内,两条相交直线不可能与第三条直线都平行,这是因为________ .
8.经过直线一点,一条直线与这条直线平行;
第五章
主备人
黄荣华
审核人
审核时间
课型
班级
姓名
流程
导学内容
助教策略
(学习随笔)
目标导学
学习目标:
了解平行线的概念、平面内两条直线的相交和平行的两种位置关系,知道平行公理以及平行公理的推论。
浙教版数学七年级下册 1.1《平行线》导学案1

1.1平行线导学案
【学习目标】
1、认识平行线,了解平行线的位置关系,掌握平行线的符号表示。
2、学会用直尺和三角板画平行线。
3、了解平行线的有关性质。
【导学过程】
一、前置测评
点与直线的位置关系有2种,分别是:点在直线上和点不在直线上。
(动手画出来)
二、自学指导,尝试练习
在同一平面内,两条直线的位置关系有种?
(动手画一画,试一试)
三、探究新知
1、平行线的概念:在同一平面内,不相交的两条直线叫做平行线。
2、你能从现实生活中找出平行线吗?
3、小结:平行线应具备哪几个条件?如何表示?
4、试一试:你能借助三角板和直尺画出平行线并表示出来吗?
5、例题学习:课本第5页
四、合作交流,互动探究
经过直线外一点,你能画出与已知直线平行的直线吗?能画几条?(你有几种画平行线的方法?)
小结:通过画图,你发现了什么?
经过直线外一点,有且只有一条直线与这条直线平行。
五、应用
1、判断:①永不相交的两条直线叫做平行线()
②在同一平面内的两条直线叫做平行线()
③在同一平面内的两条直线不相交,就一定互相平行()
④在同一平面内,不相交的两条线叫做平行线()
2、检验下面每个图形中哪两条线段是平行的并表示出来。
3、能力挑战:
和1号棱平行的有哪些棱?还有哪些棱互相平行?
六、自评归纳
通过今天的学习,你都学会了什么?。
2020初一数学第二节 平行线导学案(1)

第二节 平行线 导学案一、 预习导航上节课我们一起学习了同位角、内错角、同旁内角,它们是我们今后学习平行线的基础. 本节课,我们将系统的学习平行线的概念、表示方法、画法、平行公理及推论.问题1: (1)你能说出生活中一些具有平行线形象的实际例子吗?(2)在同一平面内,任意画出的两条直线,这两条直线有哪几种位置关系?你区分的依据是什么?(3)不相交的两条直线一定是平行线吗?线段的平行是指什么?问题2::阅读数学书本第4页的合作学习你能概括出作已知直线平行线的基本步骤了吗 ?二、自主探究【环节一:认识平行线】平行线:在同一个平面内,__________的两条直线叫做平行线.“平行”用符号“______”表示.若直线AB 和CD 是平行线,记做__________或____________,读作______________【环节二:平行线的画法】1. 已知直线a ,画已知直线a 的平行线.① 说一说:画已知直线a 的平行线你能画出多少条?② 在上述作图过程中,“三线八角”中的什么角始终保持相等的作用?2.已知直线a 和直线外一点P ,过点P 画已知直线a 的平行线.想一想:经过直线外一点P 能画几条直线和已知直线a 平行呢?因此,我们可以得到一个重要事实:平行公理(唯一性):经过直线外一点,______________直线与这条直线平行.a P a议一议: 若直线b//a , c//a , 那么 b//c 吗? 为什么呢? 由此, 我们又可以得到平行线的传递性 (平行公理的推论):如果两条直线都和第三条直线_______,那么这两条直线也________.三、例题讲解如图,点M ,N 代表两个城市,MA ,MB 是已建的两条公路.现规划建造两条经N 市的公路,这两条公路分别与MB ,MA 平行,且在与MB ,MA 的交汇处分别建一座立交桥.问立交桥应建在何处?请画出示意图.练习:如图,过三角形ABC 的顶点分别画对边的平行线,分别交于D 、E 、F 三点.能力提升: 1.已知直线AB 和一点P ,过点P 画直线AB 的平行线,可画( )A .1条B .0条C .1条或0条D .无数条2.下列语句中正确的是( )(A )两条不相交的直线叫做平行线(B )一条直线的平行线只有一条(C )在同一平面内的两条线段,若它们不相交,则一定互相平行(D )过一点可以而且只可以画一条直线与已知直线平行。
浙教版数学七年级下册 1.1《平行线》教案

浙教版七下《1.1 平行线》教学设计一、教材分析平行线是最简单、最基本的几何图形,生活中随处可见,它不仅是研究其他图形的基础,而且在实际中也有着广泛的应用。
因此,探索和掌握好它的有关知识,对学生更好地认识世界、发展空间观念和推理能力都十分重要。
二、学情分析考虑本校地处城乡结合部,大部分学生的基础比较差,缺乏自学能力,动手能力比较弱,本学期应重视学生兴趣和态度的培养,重视学生的自主探索、合作交流及创新意识的培养。
利用七年级学生都有争强好胜的特点,扭转学数学难,数学枯燥的这种局面,形成一种勤动手、勤动脑、勤探索和肯合作交流的良好氛围。
三、教学目标1、进一步认识平行线的概念;2、能用符号表示两条直线互相平行;3、会用三角尺和直尺过直线外一点画这条直线的平行线;4、了解过直线外一点有且仅有一条直线与这条直线平行.四、教学重难点教学重点:平行线的表示法和画法教学难点:平行公理的应用及平行线的画法五、教学方法1、情境导入法——激发学生的学习兴趣,激活学生的思维,迅速进入学习状态;2、小组讨论法——培养学生合作意识的形成;3、探究交流法——营造民主、平等、和谐、宽松的课堂氛围;4、合作质疑法——引导学生积极思考,培养他们良好的思维品质。
六、教具准备白纸、学案、多媒体课件七、教学过程(一)环节一:我来说1、画一画:请学生在白纸上随意地画两条直线2、挑选4幅具有代表性的作品,要求学生根据作品中直线的位置关系对其进行分类;(预设:分四类“有交点”“无交点但延长会相交”“垂直”“无交点且延长也不会相交”.)3、让学生说说生活中具有平行线形象的实例;(课件展示若干幅平行线画面感较强的图片,如田径跑道、整齐的队伍、部分国家的国旗等.)4、继续请学生说说这些具有平行形象的图片带给你的感受(预设:整齐,很工整,很美)5、让学生说说什么是平行线?(预设:请其他学生来评价这位学生的答案,好,好在何处,不好,哪里有欠缺.)【设计意图】让学生由实物的形状想象出平行线的几何图形,使新知识建立在对周围环境直感知的基础上,让学生增强对平行线的生活原型的认识,建立直观、形象的数学模型,进而产生一种美的感受.6、解析平行线的概念:在同一平面内,不相交的两条直线叫做平行线.(板书平行线的概念)强调:(1)为什么要加“在同一平面内”这一前提.?(可从粉笔盒或墙面加以解释)(2)在同一平面内,两条直线有哪几种位置关系?相交与平行(3)思考:在同一平面内的三条直线可能有几个交点?(这一问题可以从最多和最少两个角度来提问,然后启发学生思考可能给有几个交点.)【设计意图】由平面内的两条直线过渡到平面内的三条直线,寻找规律,渗透分类讨论的思想.(二)环节二:我会做1、如图,从长方形ABCD的四条边中选择两条,说说它们的位置关系,并用符号表示出来.(预设:本题请一对同桌合作完成,一个说一个写,写的过程中引出平行的符号表示,自然而然地获取新知)(课本P4做一做)2、一个长方体如图,和AA1平行的棱有几条?和AB平行的棱有几条?请用符号把它们表示出来.AA1//DD1 AA1//BB1 AA1//CC1AB//CD AB//A1 B1 AB// C1 D1(预设:让学生当堂交流结果,用PPT课件动画演示分别与棱AA1和棱AB构成同一对角线平面的棱CC1和棱C1 D1)【设计意图】这组练习,从平面到立体,旨在让学生巩固平行线的概念及平行线的表示,落实基础知识,进一步感知在同一平面这一前提条件.(三)环节三:我会画1、画一条直线与直线a平行,与同桌交流你的画法.2、过点P能画一条直线与直线a平行,这样的直线你能画几条?(预设:尽可能让学生上台演示自己的画法,最后再由教师小结如何借助三角板和直尺来完成推平行线的画法:一贴,二靠,三推,四画.)【设计意图】画平行线是几何画图的基本技能之一,在以后的学习中,常常会遇到画平行线的问题. 本环节是本节课的重点,让学生来演示画法,打破思维局限,最后教师指出画平行线的关键:一贴、二靠、三推、四画,加强直观教学,使学生牢固掌握画平行线这一基本技能.(四)环节四:我发现比较环节三中(1),(2),请学生概括你的发现(1)画直线a的平行线(2)过点P画直线a的平行线结论:经过直线外一点,有且只有一条直线与这条直线平行.【设计意图】通过观察、画图、讨论等探索过程,用类比的方法归纳出平行公理,从而把学生的直观体验上升到理性思维.(五)环节五:我能行1、课本例题:如图,点M,N代表两个城市,MA,MB是已建的两条公路.现规划建造两条经N市的公路,这两条公路分别与MA,MB平行,并在与MB,MA的交汇处分别建一座立交桥.问立交桥应建在何处?请画出示意图.提问:解答中所作的直线NP,NQ是唯一确定的吗?为什么?2、补充练习:课本P5 作业题33、变式训练:如图,A,B,C是三棵树,藏宝地点D与这三棵树恰好是平行四边形的四个顶点,请你画出藏宝地点D.【设计意图】本题由已知条件平行四边形出发,寻找顶点D,练习平行线的画法,进一步渗透分类讨论思想.(六)环节六:我总结1、请学生谈谈本节课的收获2、PPT展示教师的原创小诗(梳理了本节课的知识点)贴靠推画平行线,两线共面不相交;线外一点平行线,有且仅能画一条;平行现象随处见,平行公理要记牢。
初中数学 导学案1:平行线

d图74321cb a DCB1BBA图5图6《平行线》小结与复习【学习目标】:1.对本章知识进行梳理,加深对所学知识的理解,熟练掌握用几何语言说明图形;2.认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行线的性质;理解平移的性质,能利用平移设计图案。
【前置学习】一、我归纳、我画图(画出本章知识结构图)二、我梳理、我思考1.同位角、内错角、同旁内角(1)图3中,∠1与∠2互为 角,∠2与∠3互为 角,∠3与∠4互为 角。
(2)图4的∠1、∠2、∠3中, 是同位角, 是内错角, 是同旁内角。
2.平行线判定与性质(1)怎样判定两条直线平行?平行线有什么性质?(2)比较平行线的性质和判定,它们有何异同?(3)在图5中,当 时,a ∥c,理由是 ;当 时, b ∥c,理由是 ;当a ∥b,b ∥c 时, ____∥___,理由是 。
图821D DCC BB AA EE图9(4)如图6,AB ∥CD,∠A=∠C,试判断AD 与BC 的位置关系?为什么?3.图形平移(1)什么是图形平移?图形平移有那些性质?(2)画平移后图形关键要确定平移的 和平移的 。
如图7,平移长方形ABCD,使点B 移动到点B 1,画出平移后的四边形。
三、疑难摘要(记下你的疑难与困惑,在课堂上交流解决)。
【学习探究】一、合作交流、解决困惑1.小组内互相解答前置学习中存在的困惑。
2.班级展示与教师点拔:(教师结合学生前置学习的完成情况自主生成)二、应用新知、解决问题例1 如图8,AE 平分∠CAD ,∠1=∠B ,试判断∠B 与∠C 有什么关系?为什么?例2 如图9,已知∠AEC=∠A+∠C ,试说明:AB ∥CD.三、巩固新知、变式训练课本P 35-36 复习题5 第1—8题。
(完成于书中) 四、反思小结本节课你学到了哪些知识或方法?还有什么困惑?。
浙教版数学七年级下册 1.1《平行线》导学案2

1.1 平行线导学案一、课前预习1.同一平面内不重合的两条直线的位置关系:________________2.如果两条直线有且只有一个公共点,那么称这两条直线_________,也称它们是__________,这个公共点叫做它们_______3.定义:同一平面内______________的两条直线叫做平行直线.表示方法:若AB与CD平行,记做__________,读做_______________4.平行公理:经过一条直线外一点_________________一条直线与已知直线平行.5.直线的平行关系具有传递性:设a,b,c是三条直线,如果a∥b,b∥c,那么a___c.二、探究(一)摆一摆问:我们每一位同学都有两根筷子,我们把它们近似地看成两条直线,我们在桌面上摆一摆,看它们有哪些位置关系?请把你得到的结论用几何图形画出来.(如图)问:这三种位置关系如果用两条直线的公共点个数来表示,分别是几个公共点?(一个,没有、无数多个)今天我们就研究两条直线没有公共点的情况,这样的两条直线叫做平行线.1.定义:在同一个平面内,不相交的两条直线叫做平行线.(在同一平面内,没有公共点的两条直线叫做平行线.)2.平行线的记法和画法.(1)记法:如图(1),直线AB与直线CD平行,记作AB∥CD,也可记作CD∥AB,因为两条直线平行是相互的.(2)画法:教科书P4(二)实践活动1:(1)已知直线l ,能作几条直线平行于l .(2)P 为直线l 外一点,过P 点能作几条直线平行于l ?基本事实:经过直线外一点,有且只有一条直线与这条直线平行.(平行公理) 实践活动2:如图(5),已知直线EF 和直线外的点A ,D ,分别过A 点和D 点作EF 的平行线.·· 图(5)猜想:若AB ∥EF ,CD ∥EF ,则AB ∥CD .如果两条直线都和第三条直线平行,那么这两条直线也互相平行.三、练习1.判断真假.(1)不相交的两条直线叫做平行线. ( )(2)同一平面内,两条不平行的直线必相交 . ( )(3)有且只有一个公共点的两条直线是相交直线. ( )(4)同一平面内不相交的两条线段必平行. ( )2.选择题.(1)下列推理正确的是( )A 、因为a // d, b // c ,所以c // d ;B 、因为a // c, b // d ,所以c // d ;C 、因为a // b, a // c ,所以b // c ;D 、因为a // b, c // d ,所以a // c .(2)下列说法正确的是( )A 、经过一点有一条直线与已知直线平行 E FCD ABB、经过一点有无数条直线与已知直线平行C、经过一点有且只有一条直线与已知直线平行D、经过直线外一点有且只有一条直线与已知直线平行(3)如图所示,在同一平面内,a∥b, a与c相交,那么b与c相交吗?为什么?cab。
七年级数学下册《平行线的判定》导学案

平行线的导学案一
【学习目标】:
1.掌握直线平行的条件一.二,并会进行简单的应用
2.领悟归纳和转化的数学思想方法
【活动方案】:
活动1:自主探索
阅读课本13—14页的内容,完成下列问题。
1.判定方法1:
简单说成:
结合右图,你能用几何的符号语言描述这个方法Array吗?
∵∠2 =___(已知)
∴___∥
( )
或者∵∠1 =___(已知)
∴___∥
( )
2.判定方法2:
简单说成:
结合上图,你能用几何的符号语言描述这个方法吗?
∵∠3 =___(已知)
∴ ___∥___ ( )
或者∵∠4 =___(已知)
∴ ___∥___ ( )
3.你能用方法1证明方法2吗?请写出证明过程.
【当堂检测】
1.如图2所示,如果∠D=∠EFC,那么( )
F E
D
C
B
A
A.AD∥BC
B.EF∥BC
C.AB∥DC
D.AD∥EF
2.如图,能判断AB∥CE的条件是
( )
A.∠A=∠ACE
B.∠A=∠ECD
C.∠B=∠BCA
D.∠B=∠ACE
3.如图,回答下列问题,并说明理由.
(1)由∠D=∠1,可判定哪两条直线平行?
(2)由∠2=∠3,可判定哪两条直线平行?
F E
A
B
C
D
1 2
E
D
C
B
A。
1.1平行线教案
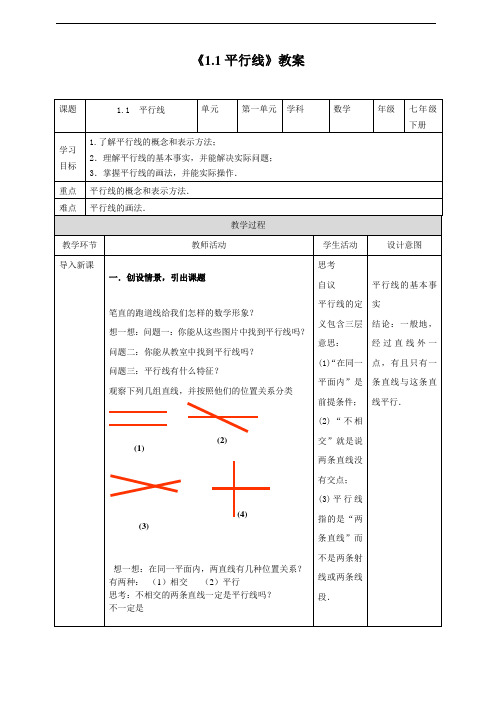
《1.1平行线》教案在同一平面内,不相交的两条直线叫做平行线.平行线特征1.在同一平面2.不相交3.两条直线做一做:一个长方体如图,和AA′平行的棱有多少条?和AB 平行的棱有多少条?请用符号把它们表示出来.和AA′平行的棱有3条:BB′∥AA′,CC′∥AA′,DD′∥AA′.和AB平行的棱有3条:A′B′∥AB,C′D′∥AB,CD∥AB.试一试:给你一条直线AB,及直线外一点P,过点P 如何画出它的平行线?一、帖(线)二、靠(尺)三、移(点)四、画(线)a a aba还有其他画法吗?例1、如图,点M,N代表两个城市,MA,MB是已建的两条公路.现规划建造两条经N市的公路,这两条公路分别与MB,MA平行,且在与MA,MB的交汇处分别建一座立交桥,问立交桥应建在何处?请画出示意图.解:如图,过点N分别作直线NP//MA,交MB是与点P;作直线NQ//MB,交MA是与点Q,所以立交桥应分别建在P,Q处.当堂检测四.巩固训练1.判断正误.(1)不相交的两条直线叫做平行线.( )(2)在同一平面内,两条不平行的直线必相交.( )(3)在同一平面内两条直线的位置只有平行、相交. ( )(4)在同一平面内不相交的两条线段必平行.( )(1)×(2)√(3)√(4)×2.如图所示,将一张长方形纸对折三次,则产生的折痕与折痕间的位置关系是 ( C )A.平行B.垂直C.平行或垂直 D.无法确定3.下列表示方法正确的是 ( D )A.a∥A B.AB∥cdC.A∥B D.a∥b4.如图,在方格纸中,有两条线段AB,BC.利用方格纸完成以下操作:(1)过点A作BC的平行线;(2)过点C作AB的平行线,与(1)中的平行线交于点D;(3)过点B作AB的垂线.解:如图所示.课堂小结1.平行线的概念。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1平行线
班级_________组名____________姓名___________
【学习目标】1、进一步认识平行线的概念
2、用符号表示两条直线互相平行
3、会用三角尺和直尺过直线外一点画这条直线的平行线
4、了解过直线外一点有且只有一条直线与这条直线平行
【学习重点】平行线的表示法和画法
【学习难点】平行线的画法
【自学导航】仔细阅读课本思考
请独立完成:
1、 在生活中,我们把一些大小不同,粗细不等的线、条、管用数学上的直线来表示。
你知道:在同一平面内,两条直线位置关系有__ __或____ ___。
其中:在同一平面内,不相交的两条直线叫做______________. (思考“在同一平面内”能舍去吗? ) 2、平行线的概念、符号、记法和读法
①. 平行用符号_____表示,直线AB 和CD 平行,记作_________,读作____________ ②. 在同一平面内,不相交的两条直线叫平行线,你能找出下面立方体中的与AA’平行的 棱有多少条?和CD 平行的棱有多少条?请用符号把它们表示出来。
探究平行线的画法
3、已知直线AB 和直线外一点P ,过点P 画一条直线和已知直线AB 平行。
a a a
b a
②边画边念 ((练一练过点P 作AB 的平行线))
过P 点你可以画几条:
结论(平行公理):经过直线外一点,
【自学检测】
已知P 是∠AOB 内的一点,按下列要求画图,并回答问题:
(1)过点P 画直线PC ∥OA ,交直线OB 于点C ; P
. A
B B A'
B'D'A D
为什么?能举一例?
(2)过点P画直线PD⊥OB,交直线OA于点D;感谢您的阅读,祝您生活愉快。
