边界层对流换热微分方程组数量级分析法
第四版传热学第五、六,七 八 章习题解答

第五章复习题1、试用简明的语言说明热边界层的概念。
答:在壁面附近的一个薄层内,流体温度在壁面的法线方向上发生剧烈变化,而在此薄层之外,流体的温度梯度几乎为零,固体表面附近流体温度发生剧烈变化的这一薄层称为温度边界层或热边界层。
2、与完全的能量方程相比,边界层能量方程最重要的特点是什么?答:与完全的能量方程相比,它忽略了主流方向温度的次变化率σα22x A ,因此仅适用于边界层内,不适用整个流体。
3、式(5—4)与导热问题的第三类边界条件式(2—17)有什么区别?答:=∂∆∂-=yyt th λ(5—4))()(f w t t h h t-=∂∂-λ (2—11)式(5—4)中的h 是未知量,而式(2—17)中的h 是作为已知的边界条件给出,此外(2—17)中的λ为固体导热系数而此式为流体导热系数,式(5—4)将用来导出一个包括h 的无量纲数,只是局部表面传热系数,而整个换热表面的表面系数应该把牛顿冷却公式应用到整个表面而得出。
4、式(5—4)表面,在边界上垂直壁面的热量传递完全依靠导热,那么在对流换热中,流体的流动起什么作用?答:固体表面所形成的边界层的厚度除了与流体的粘性有关外还与主流区的速度有关,流动速度越大,边界层越薄,因此导热的热阻也就越小,因此起到影响传热大小5、对流换热问题完整的数字描述应包括什么内容?既然对大多数实际对流传热问题尚无法求得其精确解,那么建立对流换热问题的数字描述有什么意义?答:对流换热问题完整的数字描述应包括:对流换热微分方程组及定解条件,定解条件包括,(1)初始条件 (2)边界条件 (速度、压力及温度)建立对流换热问题的数字描述目的在于找出影响对流换热中各物理量之间的相互制约关系,每一种关系都必须满足动量,能量和质量守恒关系,避免在研究遗漏某种物理因素。
基本概念与定性分析5-1 、对于流体外标平板的流动,试用数量级分析的方法,从动量方程引出边界层厚度的如下变化关系式:x xRe 1~δ解:对于流体外标平板的流动,其动量方程为:221xy u v dx d y u v x y u ∂+-=∂∂+∂∂ρρ 根据数量级的关系,主流方的数量级为1,y 方线的数量级为δ则有2211111111δρδδv +⨯-=⨯+⨯ 从上式可以看出等式左侧的数量级为1级,那么,等式右侧也是数量级为1级, 为使等式是数量级为1,则v 必须是2δ量级。
第四章 对流换热_2

体分子和流体微团的动量和
热量扩散的深度.
边界层型对流传热问题的数学描写
热边界层与流动边界层的关系
两种边界层厚度的相对大小取决于流体运动粘度与热扩散率的相对大小; 运动粘度反映流体动量扩散的能力,其值越大流动边界层越厚 。 热扩散率反映物体热量扩散的能力,在其它条件相同的情况下,其值越大 ,热边界层越厚。 称为普朗特数 Pr 令 其物理意义为流体的动量扩散能力与热量扩散能力之比。 a 对于层流边界层,当 Pr
速度边界层
流体流过固体壁面时,由于壁面层流体分子的不滑移特性,在流 体黏性力的作用下,近壁流体流速在垂直于壁面的方向上会从壁 面处的零速度逐步变化到来流速度。
u y
t∞ u
δ 0
t
δ
tw x
垂直于壁面的方向上流体流速发生显著变化的流体薄层定义为 速度边界层(流动边界层)。
边界层型对流传热问题的数学描写
2 13 Nu x 0.332 Re1 Pr x
hx x u x
努塞尔(Nusselt)数
Re x
Pr
a
雷诺(Reynolds)数
普朗特数
注意:特征尺 度为当地坐标x
与 t 之间的关系
u const,
dp 0 dx
动量传递 热量传递 规律相似 =t
边界层型对流传热问题的数学描写
热(温度)边界层 Thermal boundary layer
当流体流过平板而平板的温度tw与来流流体的温度t∞不相等时,在
壁面上方也能形成温度发生显著变化的薄层,常称为热边界层。
当壁面与流体之间的温差达到壁面与来流流体之间的温差的0.99倍时, 即 (t w t ) /(t w t ) 0.99 ,此位置就是边界层的外边缘,而该点到壁面
5.34边界层型对流传热解析

三、边界层换热微分方程组
边界层概念的引入 + 数量级分析 = 简化的换热微分方程组
二维、稳态、强制对流、层流、忽略重力
u v 0 x y
u u p 2u 2u (u v ) ( 2 2 ) x y x x y 2 2 v v p v v (u v ) ( 2 2 ) x y y x y 2 2 t t t t c p u x v y x 2 y 2
u x
雷诺(Reynolds)数
普朗特数
Pr
a
注意:特征 尺度为当地 坐标x
Re:惯性力与粘性力之比的量度。 Nu:壁面上流体的无量纲温度梯度。 Pr:粘性(动量)扩散能力与热扩散能力的量度。
与 t 之间的关系
对于外掠平板的层流流动:
u const ,
2
dp 0 dx
1 1 (1 1
1
)
1 1 ( 2 1
2
2
1
2
ห้องสมุดไป่ตู้
)
2
v v p v v (u v ) ( 2 2 ) x y y x y
1 (1
1
)
(
2
12
) 2
p ~ 0( ) y
p ~ 0(1) x
边界层内的压力梯度仅沿 x 方向变化,而边界层内法向的压力梯度极小
3个方程、3个未知量:
u、v、t,方程封闭
如果配上相应的定解条 件,则可以求解
du dp u dx dx
hx
边界层对流换热微分方程组数量级分析法[专业类别]
![边界层对流换热微分方程组数量级分析法[专业类别]](https://img.taocdn.com/s3/m/efa5115a49649b6648d747af.png)
高级课件
1
主要内容:
6-1 比拟理论、相似原理及量纲分析 6-2 相似原理的应用 6-3 内部流动强制对流换热实验关联式 6-4 外部流动强制对流换热实验关联式 6-5 自然对流换热及其实验关联式
高级课件
2
Quick Review:
5-3 对流换热的边界层微分方程组
(2) 分析无量纲湍流边界层动量和能量方程以及边界条件
(3) 分别得到
U Y
Y 0 c f
Rex 2
Y Y 0 Nux
(4) 通过实验确定cf , 从而获得Nux
(5) 对雷诺比拟进行修正,从而拓展到Pr1的情况
(6) 获得既包含层流又包含湍流的平均Nu 。
高级课件
28
6-1 相似原理及量纲分析
(1)速度边界层的定义、产生、特性和结构
(2)热边界层的定义和特点
(3)量级分析的基本思想
(4)将边界层微分方程组应用于外掠等温平板层流对流换
热过程获得的准则方程:
1
1
(5)和t的关系: hx x 0.332 u x 2 3
a
Nux 高0级.课33件2 Re1x 2 Pr1 3
3
速度边界层特点: ——边界层理论的基本思想
高级课件
26
注意以下几点:
a. Rec 和 Re的区别;
b. xc的计算;
c. 层流和湍流的判断 d. 如果既有层流,也有湍流,则需要采取分段计算热
流密度或上述的平均对流换热系数 e. 如果采用Num时,注意特征长度为换热面全长
高级课件
27
比拟理论求解湍流对流换热方法小结:
(1) 利用边界层的概念,忽略流动方向的扩散作用,得到 边界层内动量(流动)和能量(换热)的微分方程组
5.34边界层型对流传热解析

5.3 边界层型对流传热问题数学描写 5.4流体外掠平板传热层流分析解及比拟理论
对流换热微分方程组:(常物性、无内热源、二维、稳态、不可压 缩牛顿流体,受迫流动忽略重力场)
u v 0 x y
u u p 2u 2u (u v ) ( 2 2 ) x y x x y v v p 2v 2v (u v ) ( 2 2 ) x y y x y
在层流范围内求解上述边界层方程组可得
5.0 x Re x
0.664 cf 1 2 Re x u 2
w
Pr1 3 t
局部表面传热系数的表达式
u hx 0.332 x a
1 x 2 1 3
hx x
u 0.332 a
3个方程、3个未知量:
u、v、t,方程封闭
如果配上相应的定解条 件,则可以求解
du dp u dx dx
hx
t y w, x
t
算例:对于主流场均速 u 、均温 t ,并给定恒定壁温的 情况下的流体纵掠平板换热,即边界条件为
y 0 u 0, v 0, t t w y u u , t t
可视为边界层的又一特性
边界层内任一截面压力与 y 无关而 等于主流压力
p dp x dx
2
u u dp u (u v ) 2 x y dx y
dp du 由上式: u dx dx
du dp 若 0,则 0 dx dx
t t t t u v a( 2 2 ) x y x y
j 称为 j因子,在制冷、低温工业的换热器设计中应用较广
高等热质交换技术 边界层的分析
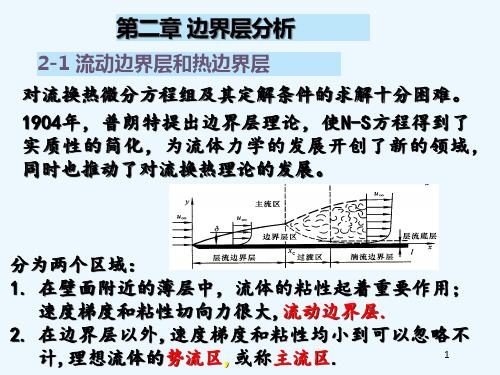
1.速度边界层(流动边界层) 速度发生明显变化 的 流体薄层。
流动边界层厚度 :
u 0.99u
流场的划分: 主流区:y< 理想流体
紊流核 心
u 边界层区: y 速度梯度存在与粘性力的作用区。
边界层的流态: 层流边界层、过渡区、紊流边界层
2
临界距离xc : 边界层从层流开始向紊流过渡的距 离。其大小取决于流体的物性、固体壁面的粗糙度等 几何因素以及来流的稳定度,由实验确定的临界雷诺 数Rc给定。
对流项 导热项
对流项进行比较分析
1.假定Δ/Δ ≥ 1,在这种情形下,导热项的系数就应 该等于 1 1 t P r Re 2 t
由于
1 Re
t
1 Re P r
Pr t
这种情形下成立的条件只能是Pr ≥ 1,意味着这样的流 体,流动边界层厚度大于或等于温度边界层厚度.
温度的无量纲参数采用: T Tw T Tw
变化范围0-1
热边界层厚度δ t度不一定等于流动边界层厚度δ, δ=LΔt , Δt是某个百分数。
无量纲参数:
x X L
y Y L
1 2 2 2 U V 2 2 2 X t Y c p Lu t X Y
导热项是偏微分方程中最高阶项,必须考虑,但 2 2 2 远小于 可以忽略不计。 2 2 X Y
无量纲能量方程
1 1 2 U V 2 X t Y Pr Re 2 Y t
有量纲边界层能量 方程
T T 2T u v x y cp p y 2
u v 0 x y
边界层对流 换热微分方 程组:
边界层对流换热微分方程组数量级分析法共50页文档

边界层对流换热微分方程组数量级分 析法
36、如果我们国家的法律中只有某种 神灵, 而不是 殚精竭 虑将神 灵揉进 宪法, 总体上 来说, 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日,便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持,法律 是丝毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例,它们 迅速累 聚,进 而变成 法律。 ——朱 尼厄斯
40、人类法律,事物有规律,这是不 容忽视 的。— 。 ——德 谟克利 特 67、今天应做的事没有做,明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生,以及整个命运 的,只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
边界层分析求解

5
对于管内的流动运 动,取临界雷诺数 2300
粘性底层:在紊流边界层内,由于紧贴壁面处那一层薄层内
粘滞力甚大,流体仍具有层流的特征。 紊流支层:粘性底层上方称为紊流支层,在该层内粘滞力较 小,流体具有紊流的特点。 边界层厚度=粘性底层+紊流支层
底 =29.4 x w
9
9 1 10
m
t∞ u
流体流过固体壁面的流场就 人为地分成两个不同的区域。
δ 0
t
δ
tw x
其一是边界层流动区,这里流体的黏性力与流体的惯性力共 同作用,引起流体速度发生显著变化;其二是势流区,这里 流体黏性力的作用非常微弱,可视为无黏性的理想流体流动, 也就是势流流动。
2)边界层的厚度
当速度变化达到 u u 0.99 时的空间位置为速度边界层的 外边缘,那么从这一点到壁面的距离就是边界层的厚度 x
0
x
x x 5.0 w x
1
2
5.0 Re
1
2
要使边界层的厚度远小于流动方向上的尺度(即 x x 1 ), 也就是所说的边界层是一个薄层,这就要求雷诺数必须足够 Re 1 的大,即
因此,对于流体流过平板,满足边界层假设的条件就是雷 诺数足够大。由此也就知道,当速度很小、黏性很大时或 在平板的前沿,边界层是难以满足薄层性条件。
3) 临界雷诺数
随着x的增大,δ(x)也逐步增大,同时黏性力对流 场的控制作用也逐步减弱,从而使边界层内的流动变得紊乱。 把边界层从层流过渡到紊流的x值称为临界值,记为xc, 其所对应的雷诺数称为临界雷诺数,即 Re c u xc
流体平行流过平板的 临界雷诺数大约是
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
24
当 Pr 1时,需要进行修正,于是有 契尔顿-柯尔本比拟(修正雷诺比拟):
cf 2
St Pr2 / 3
j
(0.6 Pr 60)
式中, St 称为斯坦顿(Stanton)数,其定义为
St
t y
a
2t y2
边界层对流换热微分方程组:
u v 0
x y
u
u x
v
u y
1
dp dx
2u y 2
t t 2t
3个方程、3个未知量:
u、v、t,方程封闭
如果配上相应的定解条 件,则可以求解
u x v y a y2
实例:
对于主流场均速 u 、均温 t,并给定恒定壁温的情况下的流体 纵掠平板换热,即边界条件为
(2)热边界层的定义和特点
(3)量级分析的基本思想
(4)将边界层微分方程组应用于外掠等温平板层流对流换
热过程获得的准则方程:
1
1
(5)和t的关系:
hx x
0.332
u x
2
3
a
Nux 0.332 Re1x 2 Pr1 3
3
速度边界层特点: ——边界层理论的基本思想
注意:特征 尺度为当地
普朗特数
坐标x
10
平均努塞尔数Nu:
Nul
l
Nu
dx
0.664 Re1 2 Pr1 3
0
x
计算时注意适用条件:
1)Nux,Nul,hx,hl的区别 2)Pr≥1
3)x 和 l 的选取
4)Re5×105
5)定性温度t 取 t t f tw 2
11
六、流动边界层和热边界层比较
13
5-4 流体外掠平板传热的层流分析解及比拟理论
一、流体外掠等温平板传热的层流分析解
假定平板表面温度为常数,边界层动量方程中dp/dx=0,可以求解 得到层流截面上速度场和温度场的分析解。
离开前缘x处的边界层厚度为
局部切应力与
5.0
x
Re x
流动动压头之 比
范宁局部摩擦系数(Fanning friction coefficient)
(1)流场分为主流区和边界层区。只有在边界层区才考虑粘性 的影响,需用粘性流体的微分方程描述。在主流区,流体视为理 想流体,用贝努利程描述; (2)边界层内厚度δ<<壁面尺寸l, δ= δ (x) ; (3)在边界层内,流动状态分为层流、过渡流和紊流;紊流边 界层内紧贴壁面处仍有极薄层保持层流状态,称为层流底层。
(a)
x y
1
1
动量方程:
( u
u x
v
u y
)
p x
(
2u x2
2u y 2
)
(b)
1(1 1 1
1)
1 (2 1
12
1)
2
( u
v x
v
v y
)
p y
(
2v x2
2v y2
)
(c)
1(1
1
)
(3) 分别得到
U Y
Y 0 c f
Rex 2
Y
Y 0
Nux
(4) 通过实验确定cf , 从而获得Nux
11
x xc时,层流,Nux 0.332 Re 2 Pr 3
41
x xc时,湍流,Nux 0.0296Re 5 Pr 3
则平均对流换热系数 hm 为:
hm
0.332
u
1
2
l
xc
1
x2
dx
0.0296
u
4
5
0
l 1 1 x 5 dx Pr 3
c. 层流和湍流的判断 d. 如果既有层流,也有湍流,则需要采取分段计算热
流密度或上述的平均对流换热系数 e. 如果采用Num时,注意特征长度为换热面全长
27
比拟理论求解湍流对流换热方法小结:
(1) 利用边界层的概念,忽略流动方向的扩散作用,得到 边界层内动量(流动)和能量(换热)的微分方程组
(2) 分析无量纲湍流边界层动量和能量方程以及边界条件
Nu
Re Pr
j 称为 j 因子,无量纲表面传热系数,在制冷、低温工业的换热器 设计中应用较广。
此时的准则方程为:
Nux
cf 2
Rex
1
Pr 3
c f 0.0592Rex1 5
41
Nux
0.0296
Re
5 x
Pr 3
25
当平板长度 l 大于临界长度 xc 时,平板上的边界层由层流段和 湍流段组成。其Nu分别为:
——边界层概念的基本思想
五、边界层对流换热微分方程组
根据流动边界层和热边界层的特点,运用数量级分析的方法,将 对流换热微分方程组进行简化,即
边界层概念的引入 + 数量级分析 = 简化的换热微分方程组
数量级分析法:通过比较方程式中各项数量级的相对大小,把量 级大的保留,量级小的舍弃,实现方程式的简化。
第六章 单相对流传热 的实验关联式
主要内容:
6-1 比拟理论、相似原理及量纲分析 6-2 相似原理的应用 6-3 内部流动强制对流换热实验关联式 6-4 外部流动强制对流换热实验关联式 6-5 自然对流换热及其实验关联式
Quick Review:
5-3 对流换热的边界层微分方程组
(1)速度边界层的定义、产生、特性和结构
(2
12
) 2
p dp x dx
p ~ 0( )
y
p ~ 0(1) x
(u
u x
v
u y
)
dp dx
2u y2
能量方程:
u
t x
v
t y
a(
2t x 2
2t y 2
)
(d)
1
1 1
1
(2
1 12
1)
2
u
t x
v
2 4.64 x
0.332
x
Re
x
1 2
Pr
1 3
Nux
hx
1
0.332 Re x 2
1
Pr 3
整个平板表面换热系数:
h 1 l
l
0 hxdx 2hl
1
0.664Re 2
1
Pr 3
1
1
Nu 0.664Re 2 Pr 3
15
计算过程注意事项:
a. Pr 1 ;
b. Nu 与 Nu ,hx 与 h 两对变量的差别;
3
Nu x
0.332
Re
1 x
2
Pr1
3
特征数方程 (准则方程)
9
Nu x
0.332
Re
1 x
2
Pr
1
3
特征数方程 或准则方程
注意上面准则方程的适用条件:
外掠等温平板、层流、无内热源
式中:
Nux
hx x
Re x
u x
Pr
a
努塞尔(Nusselt)数
雷诺(Reynolds)数
解:空气的物性参数按板表面温度和空气温度的平均值 30 ℃确定。30℃时空气的=16×10-6m2/s, Pr=0.701 对长为400mm的平板而言:
Re
ul v
10 0.4 16106
2.5 105
这一Re数位于层流到湍流的过渡范围内。但由图5-9可见,按层流处 理仍是允许的,其流动边界层的厚度按式5-19计算为:
5.0 vx 5.0 16106 m2 / s x
u
10m / s
6.36
103
m
1 2
1
x 0.0636cm 2
x
18
热边界层的厚度可按式5-21计算
t
3 Pr
3
0.701
1.13
及t 计算结果示于图5-11
19
二、比拟理论
基本思想:假设流动的阻力特性与换热特性有一 定的关系,依据这种关系就可以在已知阻力系数 的情况下推算出与之对应的换热系数。
y 0,u 0 ,v 0 ,t 0
y ,u u,v 0 ,t t
21
引入下列7个无量纲量:
U u u
v V
u
Xx l
Yy l
t t
tw tw
Re uL
Pr v a
可以得到边界层内流动和换热的无量纲化微分方程组,即
U U 1 2U
xc
Num 0.664 Re1c 2 0.037(Re4 5 Rec4 5 ) Pr1 3
如果取 Rec 5 105,则上式变为:
Num 0.037 Re4 5 871 Pr1 3
