位数加法器设计报告
加法器电路设计实验报告

加法器电路设计实验报告【加法器电路设计实验报告】一、实验目的本实验的主要目标是通过实际操作,设计并实现一个基础的加法器电路,以深入理解数字逻辑电路的设计原理和工作方式。
通过对半加器、全加器以及多位加法器的设计与搭建,进一步熟悉集成门电路的应用,掌握组合逻辑电路的设计方法,并能对电路的逻辑功能进行有效的验证与分析。
二、实验原理加法器是数字系统中的基本运算单元,其核心工作原理基于二进制数的加法规则。
在最基础的层面上,一个半加器(Half Adder)用于计算两个一位二进制数的和,同时产生一个进位输出;而全加器(Full Adder)在此基础上增加了处理来自低位的进位输入,可以完成三位二进制数的相加。
对于多位二进制数的加法,可以通过级联多个全加器来实现。
1. 半加器:由两个异或门(XOR)实现“和”输出,一个与门(AND)实现“进位”输出,即S=A XOR B,Cout=A AND B。
2. 全加器:除了接收两个数据输入A和B外,还接收一个进位输入Cin,同样由异或门计算“和”,但“进位”输出需要考虑三个输入的与或逻辑关系,即S=A XOR B XOR Cin,Cout=(A AND B) OR (B AND Cin) OR (A AND Cin)。
三、实验步骤1. 半加器设计:首先,利用集成电路库中的逻辑门元件构建半加器,将A 和B作为异或门的输入得到和信号S,将A和B分别连接到与门的两个输入端得到进位信号Cout。
2. 全加器设计:在半加器的基础上,增加一个输入端Cin代表低位的进位,同样运用异或门和与门组合形成全加器的逻辑结构,根据全加器的逻辑表达式连接各门电路。
3. 多位加法器设计:为了实现多位二进制数的加法,将若干个全加器按照从低位到高位的顺序级联起来,每级全加器的进位输出连接到下一级的进位输入。
四、实验结果及分析经过电路设计与仿真测试,成功实现了从半加器到多位加法器的功能转化。
当给定两组多位二进制数后,所设计的加法器电路能够准确无误地计算出它们的和,并正确显示进位信息。
加法器的设计范文

加法器的设计范文加法器是一种用于两个二进制数相加的逻辑电路。
在数字电子系统中,加法器是非常重要的组件之一,常用于CPU中的算术逻辑单元(ALU)。
设计一个加法器可以分为两个主要步骤:设计加法器的结构与功能和选择适合的逻辑门实现电路。
在设计过程中,需要考虑到性能、功耗和面积等因素。
在设计加法器结构与功能时,可以选择全加器、半加器或者其他组合逻辑电路。
全加器能够对两个二进制数和一个进位进行相加,输出相加结果以及下一位的进位。
半加器只能对两个二进制数进行相加,输出相加结果但无法处理进位。
一种常见的设计方法是使用全加器来实现加法器,通过级联多个全加器来实现多位数的相加。
在设计中,可以选择传统的逻辑门(如与门、或门、异或门等)来实现加法器的功能。
另外,也可以选择使用集成电路芯片(如74LS83、74LS283等)来快速实现加法器的功能。
对于n位数的加法器,可以使用n个全加器进行级联。
每个全加器都需要有三个输入端和两个输出端。
三个输入端分别是两个相加的输入端和上一位的进位端。
两个输出端分别是相加结果和下一位的进位端。
这样,可以通过级联多个全加器来实现n位数的加法器。
在选择适合的逻辑门实现电路时,可以考虑一些因素。
例如,与门和或门可以通过级联多个半加器或全加器来实现,但这样会引入更多的延迟和功耗。
上述提到的集成电路芯片可以提供更高的速度和更小的面积,但可能需要一些解码器和编码器来连接输入和输出。
此外,在加法器的设计过程中,还需要考虑到数据宽度、时钟频率和功耗等因素。
根据具体的应用需求,可以选择不同的设计方案来实现功能与性能的平衡。
总之,加法器的设计需要根据具体的应用需求来选择适合的结构与功能,以及适合的逻辑门实现电路。
通过合理的设计和优化,可以实现高性能、低功耗和小面积的加法器。
16位超前进位加法器实验报告
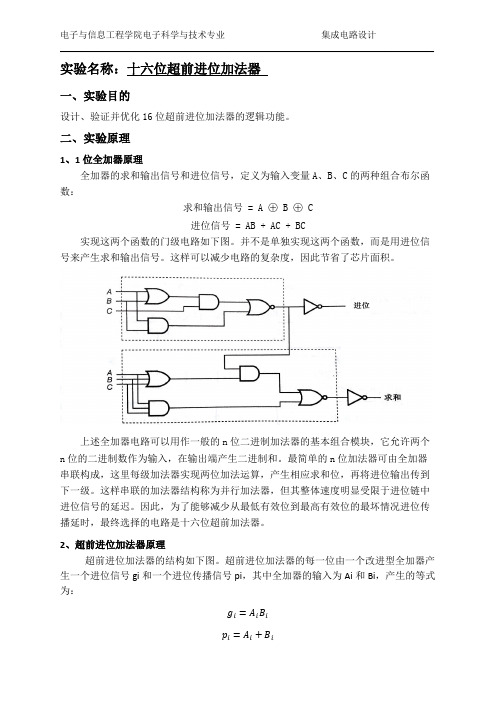
实验名称:十六位超前进位加法器一、实验目的设计、验证并优化16位超前进位加法器的逻辑功能。
二、实验原理1、1位全加器原理全加器的求和输出信号和进位信号,定义为输入变量A、B、C的两种组合布尔函数:求和输出信号 = A ⊕ B ⊕ C进位信号 = AB + AC + BC实现这两个函数的门级电路如下图。
并不是单独实现这两个函数,而是用进位信号来产生求和输出信号。
这样可以减少电路的复杂度,因此节省了芯片面积。
上述全加器电路可以用作一般的n位二进制加法器的基本组合模块,它允许两个n 位的二进制数作为输入,在输出端产生二进制和。
最简单的n位加法器可由全加器串联构成,这里每级加法器实现两位加法运算,产生相应求和位,再将进位输出传到下一级。
这样串联的加法器结构称为并行加法器,但其整体速度明显受限于进位链中进位信号的延迟。
因此,为了能够减少从最低有效位到最高有效位的最坏情况进位传播延时,最终选择的电路是十六位超前加法器。
2、超前进位加法器原理超前进位加法器的结构如下图。
超前进位加法器的每一位由一个改进型全加器产生一个进位信号gi和一个进位传播信号pi,其中全加器的输入为Ai和Bi,产生的等式为:改进的全加器的进位输出可由一个进位信号和一个进位传输信号计算得出,因此进位信号可改写为:式中可以看出,当gi = 1(Ai = Bi = 1)时,产生进位;当pi = 1(Ai =1或Bi = 1)时,传输进位输入,这两种情况都使得进位输出是1。
近似可以得到i+2和i+3级的进位输出如下:下图为一个四位超前进位加法器的结构图。
信号经过pi和gi产生一级时延,经过计算C产生一级时延,则A,B输入一旦产生,首先经过两级时延算出第1轮进位值C’不过这个值是不正确的。
C’再次送入加法器,进行第2轮2级时延的计算,算出第2轮进位值C,这一次是正确的进位值。
这里的4个4位超前进位加法器仍是串行的,所以一次计算经过4级加法器,一级加法器有2级时延,因此1次计算一共经过8级时延,相比串行加法器里的16级时延,速度提高很多。
数字电路加法器实验报告

竭诚为您提供优质文档/双击可除数字电路加法器实验报告篇一:数字电路加法器实验报告中山大学移动信息工程学院本科生实验报告(20XX学年秋季学期)课程名称:数字电路实验任课教师:王军助教:李正一、实验题目Lab9:用3种不同的方法实现4位加法器1.行为级描述的加法器2.行波进位加法器3.超前进位加法器二、实验目的1.更加熟练的运用Ise软件进行实验设计和仿真。
2.加深对verilog语言的理解和运用3.掌握加法器的原理,学会用不同层级实现方法来实现加法器三、实验内容1.实验步骤?编写文本文件并编译?软件仿真?进行硬件配置2.实验原理四、实验结果b9:Ise软件进行4位加法器的设计与实现(行为级描述的加法器)1.1.综合得出的RTL电路图图一:加法器行为级描述RTL图如图一所示,用行为级语言对加法器进行描述即可实现四位加法器。
1.2仿真波形图图二:图一:行为级加法器实现的仿真图如图二所示,当输入a,b二进制的四位数时,输出y 分别是将四位数相加。
cf是最大进位,当a与b相加之后的数大于16,则cf输出为1,其余情况输出为0。
例如,当输入为a=1000,b=0111,时,输出相应的y应为1111,cf为0。
根据加法运算,上述仿真的结果是正确的。
1.3开发板的实际效果图下图的左边前四个开关分别对应a输入从高位到低位的四位二进制数,靠近右边的四个开关别对应输入b从高位到低位的四位二进制数。
输出对应5个LeD灯,从高位到低位分别为靠近左边从左到右的五个灯。
图一:a=1000,b=0101,y=1101,cf=0效果图如上图所示,当输入为a=1000和b=0101,相应的输出为0,1101分别对应相应的第2,3,5盏灯亮图二:a=1000,b=0111,y=1111,cf=0效果图如上图所示,当输入为a=1000和b=0111,相应的输出为0,1111分别对应相应的第2,3,4,5盏灯亮图三:a=1000,b=1000,y=0000,cf=1效果图如上图所示,当输入为a=1000和b=1000,相应的输出为1,0000分别对应相应的第1盏灯亮图四:a=1110,b=1010,y=1000,cf=1效果图如上图所示,当输入为a=1110和b=1010,相应的输出为1,1000分别对应相应的第1,2盏灯亮图五:a=1110,b=1101,y=1011,cf=1效果图如上图所示,当输入为a=1110和b=1101输出为1,1011 分别对应相应的第1,2,4,5盏灯亮2.Ise软件进行4位加法器的设计与实现(行波进位加法器)2.1.综合得出的RTL电路图如上图所示,按照加法器的实验原理,对与相应的进位数c[i],c[i]=a[i]2.2仿真波形图3.Ise软件进行4位加法器的设计与实现(超前进位加法器)3.1RTL图如图所示,根据超前进位的原理,对于相应的位数I,当a[i]=b[i]=1时,由相应进位为=1,即产生进位。
16位累加器设计报告

16位累加器设计报告引言累加器(Accumulator)是一种重要的数字电路,广泛应用于计算机的中央处理器(CPU)中。
累加器的主要功能是将多个数字数据进行相加,并将结果储存到一个寄存器中。
本报告将详细介绍一个基于16位累加器的设计方案。
设计目标本设计的目标是实现一个16位累加器,能够对输入的两个16位数字进行相加,并将结果保存在累加器中。
设计要求如下:1. 输入端包括两个16位的数据A 和B。
2. 输出端为一个16位的累加器结果。
3. 设计采用组合逻辑电路实现。
输入变化时,累加器能够立即给出结果。
设计思路根据设计目标,我们可以分析得出以下设计思路:1. 设计一个16位加法器。
2. 将输入的数据A 和B 输入到加法器中进行相加。
3. 将相加的结果输出到一个16位寄存器中,作为累加器的输出。
16位加法器的设计16位加法器是累加器的核心组件之一。
我们使用全加器来实现16位加法器。
一个全加器能够实现两个输入位和一个进位位的加法,并给出一个输出位和一个进位位。
我们将使用16个全加器来构建16位加法器。
每个全加器的输入为两个加数位和进位位,输出为加法结果和进位结果。
下图是一个全加器的逻辑电路图:plaintext_______AB Full SCi Adder_______Co其中,A 和B 分别是两个输入的加数位,Ci 是输入的进位位,S 是加法结果,Co 是进位结果。
根据全加器的逻辑电路图,我们可以设计一个16位的加法器,将输入的两个16位数字进行相加,并给出16位的输出结果。
累加器的设计基于16位加法器的设计,我们可以构建一个16位累加器。
累加器的设计如下:1. 输入端包括两个16位的数据A 和B。
2. 将输入的两个16位数据A 和B 输入到16位加法器中,进行相加。
3. 将加法器的输出结果输入到一个16位寄存器中,作为累加器的输出。
下图是16位累加器的逻辑电路图:plaintext___________________AB 16-bit Adder___________________Output总结本设计报告介绍了一个基于16位累加器的设计方案。
4位全加器实验报告

四位全加器11微电子黄跃21【实验目的】采用modelsim集成开发环境,利用verilog硬件描述语言中行为描述模式、结构描述模式或数据流描述模式设计四位进位加法器。
【实验内容】加法器是数字系统中的基本逻辑器件。
多位加法器的构成有两种方式:并行进位和串行进位方式。
并行进位加法器设有并行进位产生逻辑,运算速度快;串行进位方式是将全加器级联构成多位加法器。
通常,并行加法器比串行级联加法器占用更多的资源,并且随着位数的增加,相同位数的并行加法器比串行加法器的资源占用差距也会越来越大。
实现多位二进制数相加的电路称为加法器,它能解决二进制中1+1=10的功能(当然还有 0+0、0+1、1+0).【实验原理】表2 全加器逻辑功能真值表图4 全加器方框图图5 全加器原理图多位全加器连接可以是逐位进位,也可以是超前进位。
逐位进位也称串行进位,其逻辑电路简单,但速度也较低。
四位全加器如图9所示,四位全加器是由半加器和一位全加器组建而成:图9 四位全加器原理图【实验步骤】(1)建立新工程项目:打开modelsim软件,进入集成开发环境,点击File→New project建立一个工程项目adder_4bit。
建立文本编辑文件:点击File→New在该项目下新建Verilog源程序文件并且输入源程序。
(2)编译和仿真工程项目:在verilog主页面下,选择Compile— Compile All或点击工具栏上的按钮启动编译,直到project出现status栏全勾,即可进行仿真。
选择simulate - start simulate或点击工具栏上的按钮开始仿真,在跳出来的 start simulate框中选择work-test_adder_4bit测试模块,同时撤销Enable Optimisim前的勾,之后选择ok。
在sim-default框内右击选择test_adder_4bit,选择Add Wave,然后选择simulate-run-runall,观察波形,得出结论,仿真结束。
加法器实验报告
加法器实验报告加法器实验报告概述:本次实验旨在设计和实现一个加法器电路,通过对电路的搭建和测试,验证加法器的正确性和可行性。
加法器是计算机中最基本的算术运算器之一,其在数字逻辑电路中扮演着重要的角色。
1. 实验背景加法器是一种基本的数字逻辑电路,用于实现数字的加法运算。
在计算机中,加法器被广泛应用于算术逻辑单元(ALU)和中央处理器(CPU)等部件中,用于进行各种数值计算和逻辑运算。
因此,了解和掌握加法器的工作原理和设计方法对于理解计算机原理和数字电路设计具有重要意义。
2. 实验目的本次实验的主要目的是通过设计和实现一个4位二进制加法器电路,验证加法器的正确性和可行性。
具体要求如下:- 设计并搭建一个4位二进制加法器电路;- 对电路进行测试,验证其加法运算的正确性;- 分析电路的性能和优化空间。
3. 实验原理加法器是通过逻辑门电路实现的。
在本次实验中,我们将使用全加器电路来实现4位二进制加法器。
全加器是一种能够实现两个二进制位相加并考虑进位的电路。
通过将多个全加器连接起来,可以实现更高位数的二进制加法器。
4. 实验步骤4.1 设计加法器电路的逻辑功能首先,我们需要确定加法器电路的逻辑功能。
在这个实验中,我们需要实现两个4位二进制数的相加运算,并输出结果。
具体的逻辑功能可以通过真值表或逻辑表达式来描述。
4.2 搭建电路根据逻辑功能的要求,我们可以使用逻辑门电路来搭建加法器。
在本次实验中,我们将使用多个全加器电路来实现4位二进制加法器。
通过将多个全加器连接起来,可以实现更高位数的二进制加法器。
4.3 进行电路测试在搭建完电路后,我们需要对电路进行测试,以验证其加法运算的正确性。
可以通过输入一些测试用例,并比较输出结果与预期结果是否一致来进行测试。
5. 实验结果与分析通过对加法器电路的测试,我们可以得到加法器的输出结果。
通过比较输出结果与预期结果,可以验证加法器的正确性。
同时,我们还可以分析电路的性能和优化空间,例如进一步提高加法器的速度和减少功耗等。
加法器实验实训报告
加法器实验实训报告实验目的,通过设计和实现一个加法器电路,加深对数字电路原理和逻辑门的理解,掌握数字电路的设计和实现方法。
实验原理,加法器是一种基本的数字电路,用于将两个二进制数相加得到和。
常见的加法器有半加器、全加器和多位加法器。
在本实验中,我们将使用全加器来设计一个4位二进制加法器。
实验材料和设备:1. 逻辑门集成电路(如74LS08、74LS32等)。
2. 连线材料。
3. 电源。
4. 示波器(可选)。
实验步骤:1. 根据实验要求,确定所需的加法器类型和位数。
在本实验中,我们选择使用4位全加器。
2. 根据全加器的真值表,设计电路连接图。
全加器由两个半加器和一个或门组成,其中半加器用于计算两个输入位的和,或门用于计算进位。
3. 根据电路连接图,使用逻辑门集成电路进行实验电路的搭建。
根据需要,可以使用示波器检测电路的工作情况。
4. 进行电路的调试和测试。
输入不同的二进制数,观察输出结果是否符合预期。
可以使用示波器观察信号波形,以验证电路的正确性。
5. 记录实验数据和观察结果。
包括输入的二进制数、输出的和、进位等信息。
6. 分析实验结果。
比较实验结果与预期结果的差异,找出可能存在的问题并加以解决。
7. 撰写实验报告。
包括实验目的、原理、材料和设备、步骤、数据和结果分析等内容。
实验结果分析:根据实验数据和观察结果,我们可以得出结论,通过设计和实现一个4位二进制加法器电路,我们成功地实现了二进制数的相加操作。
电路的输出结果与预期结果一致,证明电路的设计和实现是正确的。
实验总结:通过本次实验,我们深入学习了数字电路原理和逻辑门的运作方式,掌握了数字电路的设计和实现方法。
同时,我们也了解到了加法器的工作原理和实现过程。
通过实际操作和观察,我们加深了对加法器电路的理解,并提高了实验操作和数据分析的能力。
总的来说,本次实验对我们的学习和实践能力有很大的提升,使我们更加熟悉和了解数字电路的应用。
通过这次实验,我们不仅掌握了加法器的设计和实现方法,还培养了我们的动手能力和问题解决能力。
实验二 加减法运算器的设计实验报告
加减法运算器的设计实验报告实验二加减法运算器的设计一、实验目的1、理解加减法运算器的原理图设计方法2、掌握加减法运算器的VERILOG语言描述方法3、理解超前进位算法的基本原理4、掌握基于模块的多位加减运算器的层次化设计方法5、掌握溢出检测方法和标志线的生成技术6、掌握加减运算器的宏模块设计方法二、实验任务1、用VERILOG设计完成一个4位行波进位的加减法运算器,要求有溢出和进位标志,并封装成模块。
模块的端口描述如下:module lab2_RippleCarry 宽度可定制(默认为4位)的行波进位有符号数的加减法器。
#(parameter WIDTH=4)( input signed [WIDTH-1:0] dataa,input signed [WIDTH-1:0] datab,input add_sub, // if this is 1, add; else subtractinput clk,input cclr,input carry_in, //1 表示有进位或借位output overflow,output carry_out,output reg [WIDTH-1:0] result)2、修改上述运算器的进位算法,设计超前进位无符号加法算法器并封装成模块。
模块的端口描述如下:module lab2_LookaheadCarry // 4位超前进位无符号加法器(input [3:0] a,input [3:0] b,input c0, //carry_ininput clk,input cclr,output reg carry_out,output reg [3:0]sum);3、在上述超前进位加法运算器的基础上,用基于模块的层次化设计方法,完成一个32位的加法运算器,组内超前进位,组间行波进位。
4、用宏模块的方法实现一个32位加减运算器。
三、实验内容1、用VERILOG设计完成一个4位行波进位的加减法运算器,要求有溢出和进位标志,并封装成模块。
加法器实验报告范文
加法器实验报告范文实验目的:本实验通过搭建加法器电路,了解加法器的原理及工作过程,掌握加法器的设计与实现方法。
实验原理:加法器是一种数字电路,用于将两个或多个数字相加。
在数字电路中,加法器常被用于数据的处理和计算。
常见的加法器有半加法器、全加法器和并行加法器。
半加法器是最基本的加法器,只能进行单位数的加法。
它有两个输入A和B以及两个输出S和C,其中S是相加结果,C是进位。
半加法器的真值表如下:A,B,S,C0,0,0,00,1,1,01,0,1,01,1,0,1全加法器是在半加法器的基础上扩展而来的,可以进行多位数的加法。
它有三个输入A、B和Cin(进位输入)以及两个输出S和Cout(进位输出)。
全加法器的真值表如下:A ,B , Cin , S , Cout0,0,0,0,00,0,1,1,00,1,0,1,00,1,1,0,11,0,0,1,01,0,1,0,11,1,0,0,11,1,1,1,1并行加法器是由多个全加法器串联而成的,可以进行多位数的并行计算。
它的输入输出与半加法器和全加法器类似,其中最低位的全加法器没有进位输入,最高位的全加法器没有进位输出。
实验步骤:1.根据真值表,使用逻辑门电路搭建半加法器电路,并使用LED灯等输出结果。
2.根据真值表,使用逻辑门电路搭建全加法器电路,并使用LED灯等输出结果。
3.根据要求确定所需位数(如4位)的并行加法器电路结构。
4.根据电路结构,使用逻辑门电路搭建并行加法器电路,并使用LED 灯等输出结果。
实验结果与分析:1.经过实验,半加法器的电路能够实现两个数字的加法,并正确输出相加结果和进位。
2.经过实验,全加法器的电路能够实现多位数的加法,并正确输出相加结果和进位。
3.经过实验,4位并行加法器的电路能够实现四个4位数的加法,并正确输出相加结果。
结论:通过本次实验,我深入了解了加法器的原理和工作过程,并掌握了加法器的设计与实现方法。
通过搭建半加法器、全加法器和并行加法器电路,我成功实现了数字的相加运算,并正确输出了相加结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4位数加法器设计报告
一、设计任务和要求
1.1、任务描述:
1、系统通过4×4的矩阵键盘输入数字及运算符;
2、可以进行4位十进制数以内的加法运算,如果计算结果超过4位十进制
图2.1 矩阵键盘控制电路
2.2、采用LED数码管显示,数码管图如图2.2.1所示:
下图则是加法器电路的原理图:
AT89C51芯片模型
3.1.1、主要功能特性
(1) 4K字节可编程闪烁存储器。
(2) 32个双向I/O口;128×8位内部RAM 。
(3) 2个16位可编程定时/计数器中断,时钟频率0-24MHz。
(4) 可编程串行通道。
(5) 5个中断源。
(6) 2个读写中断口线。
(7) 低功耗的闲置和掉电模式。
(8) 片内振荡器和时钟电路。
3.1.2、AT89C51的引脚介绍
89C51单片机多采用40只引脚的双列直插封装(DIP)方式,下面分别简单介绍。
(1)电源引脚
电源引脚接入单片机的工作电源。
Vcc(40引脚):+5V电源。
GND(20引脚):接地。
(2)时钟引脚
XTAL1(19引脚):片内振荡器反相放大器和时钟发生器电路的输入端。
XTAL2(20引脚):片内振荡器反相放大器的输出端。
电源接入方式
(3)复位RST(9引脚)
在振荡器运行时,有两个机器周期(24个振荡周期)以上的高电平出现在此引脚时,将使单片机复位,只要这个脚保持高电平,51芯片便循环复位。
(4)EA/Vpp(31引脚)
EA为外部程序存储器访问允许控制端。
当它为高电平时,单片机读片内
口
为该
拉电阻,用来驱动多个数码管。
在访问外部程序和外部数据存储器时,P0口是分时转换的地址(低8位)/数据总线,不需要外接上拉电阻。
(8)Pin1-Pin8为P1.0-P1.7输入输出脚,称为P1口,是一个带内部上拉电阻的8位双向I/0口。
P1口能驱动4个LSTTL负载。
(9)Pin21-Pin28为P2.0-P2.7输入输出脚,称为P2口。
P2口是一个带内部上拉电阻的8位双向I/O口,P2口能驱动4个LSTTL 负载。
端口置1时,内部上拉电阻将端口拉到高电平,作输入用。
对内部Flash 程序存储器编程时,接收高8位地址和控制信息。
在访问外部程序和16位外部数据存储器时,P2口送出高8位地址。
而在访问8位地址的外部数据存储器时其引脚上的内容在此期间不会改变。
(10)Pin10-Pin17为P3.0-P3.7输入输出脚,称为P3口。
图3.3.1 矩阵键盘实际操作图
四、程序设计
本作品实现的功能全部是由C语言程序编写实现。
通过程序的编写使简单的器件实现丰富的功能。
如下所示是主程序流程图
五、系统调试及结果
本设计应用Proteus6及KEIL51软件,首先根据自己设计的电路图用Proteus6软件画出电路模型,关于这个软件的使用通过查一些资料和自己的摸索学习;然后我们用KEIL51软件对所编写的程序进行编译、链接,如果没有错误和警告便可生成程序的hex文件,将此文件加到电路图上使软硬件结合运行。
下图为运行状况图,为首先输入10+990,再加上9999,最后每个数码管上为E,因为为了满足实验要求,当结果超过了9999后显示E.
刚开始为0
输入10
再加上990得到了1000
最后显示E
五、设计个人总结
经过一周的努力终于设计成功,LED数码管的显示结果与理想所保持的一样。
在这一周的设计中,完成这个简易的计算器,虽然精度不高,但是对于一般的计算,是绰绰有余。
起初,电路的设计对我们这些人来说,是一大障碍,通过查找资料,发现一个简易的计算器,似乎没有那么难,只要有心,定能成功。
后来数码管的显示一直困扰着我,但随着慢慢地了解它,在相关资料帮助之下,终于明白如何用C语言写程序去控制数码管的显示。
加之以前学过一些计算机方面的C语言,那并不是针对单片机C语言的,虽有相似之处,但差之甚大,如今已经了逐步地了解,相信若坚持下去,定能学好这一门课程。
通过此次设计课程,使我受益匪浅。
终于更深刻地体会到实践是唯一的真理。
附录 ( 程序 ):
/**********通过用单片机MCU与矩阵及数码管的相互连接构成一个简易的数计算器--------可以进行加减乘除********/
#include <reg51.h>
#define uchar unsigned char
long First,End; //定义全局变量
//此表为 LED 的字模, 共阴数码管 0-9 -
unsigned char code Disp_Tab[] =
{z=y-x;
z=z+100000;} /***最高位用1表示负数***/
return(z);
}
long mul(long x,long y) /***乘法程序***/
{long z;
z=x*y;
return(z);
}
long div(long x,long y) /***除法程序***/
{long z;
z=x/y;
return(z);
}
uchar kbscan(void) /***键盘扫描程序***/ {
uchar sccode;
num[0]=First/100000%10; //十万
num[1]=First/10000%10; //万
num[2]=First/1000%10; //千位
num[3]=First/100%10; //百位
num[4]=First/10%10; //十位
num[5]=First%10; //个位
for(i=5;i>=0;i--)
{P2=dispbit[i]; //位选输出 P1=Disp_Tab[num[i]]; //数据输出 delay(2); //此延时必不可少?
}
}
void main(void) /***主程序***/
{ int k,n;
uchar f,g,key,gn1,i;
n=0;
f=0;
//P1=0; //初始时指示灯灭
while(1) //不断查询是否有按键动作
//P1=1;
delay(280); //有按键时,指示灯的显示时间
//P1=0; //按键指示灭
if(k<10) //为数字键时(0-9)
{
if(f!=0) //为数字键时,如果已经有功能键按下
{
n++; //记录数字键所按次数
gn1=0; //清除标志,再次为功能键时进行运算
g=f; //保存运算标志
if(n==1) //输入为各位数时,直接赋值
First=k;
else if(n>1) //输入为多位数时,将它转化为10进制的多位数
First=First*10+k;
}
else //如果没有功能键按下
case 1: First=add(End,First);break;
case 2: First=sub(End,First);break;
case 3: First=mul(End,First);break;
case 4: First=div(End,First);break;
}
}
End=First; //保存本次结果
}
else if(k==11) //为等于号时(=)
{
n=0;
gn1=1; //接着输入为功能键时可以继续运算
switch(g)
{
case 1: First=add(End,First);break;
case 2: First=sub(End,First);break;
case 3: First=mul(End,First);break;
case 4: First=div(End,First);break;
}。
