42平行线分线段成比例2平行线分线段成比例
平行线分线段成比例定理

平行线分线段成比例定理平行线分线段成比例定理:两条直线被一组平行线所截,截得的对应线段的长度成比例。
推论:平行于三角形一边的直线,截其他两边(或两边延长线)所得的对应线段成比例。
定理定义三条平行线截两条直线,所得对应线段成比例。
这一定理被称为"平行线分线段成比例定理"。
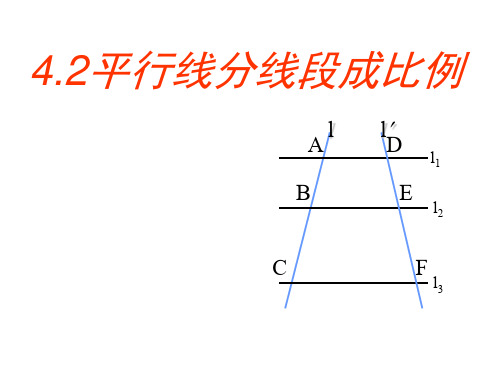
如图,因为AD∥BE∥CF,所以AB:BC=DE:EF;AB:AC=DE:DF;BC:AC=EF:DF。
也可以说AB:DE=BC:EF;AB:DE=AC:DF;BC:EF=AC:DF。
上述图样只是平行线分线段的一种特殊情况。
事实上,直线AC和直线DF可以在平行线之间相交,同样有定理成立。
定理证明设三条平行线与直线1交于A、B、C三点,与直线2交于D、E、F三点。
连结AE、BD、BF、CE根据平行线的性质可得S△ABE=S△DBE,S△BCE=S△BEF∴S△ABE/S△CBE=S△DBE/S△BFE根据不同底等高三角形面积比等于底的比可得:AB/BC=DE/EF由更比性质、等比性质得:AB/DE=BC/EF=(AB+BC)/(DE+EF)=AC/DF定理推论过一点的一线束被平行线截得的对应线段成比例。
平行于三角形一边的直线截其它两边(或两边的延长线)所得对应线段成比例。
平行于三角形一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例。
•平行线分线段成比例定理:三条平行线截两条直线,所得对应线段成比例。
推广:过一点的一线束被平行线截得的对应线段成比例。
定理推论:①平行于三角形一边的直线截其它两边(或两边的延长线)所得对应线段成比例。
②平行于三角形一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例。
•证明思路:该定理是用举例的方法引入的,没有给出证明,严格的证明要用到我们还未学到的知识,通过举例证明,让同学们承认这个定理就可以了,重要的是要求同学们正确地使用它(用相似三角形可以证明它,在这里要用到平移和设三条平行线与直线1交于A、B、C三点,与直线2交于D、E、F三点法1:过A作平行线的垂线交另两条平行线于M、N,过D作平行线的垂线交另两条平行线于P、Q,则四边形AMPD、ANQD均为矩形。
初中数学_ 平行线分线段成比例教学设计学情分析教材分析课后反思

八年级下册——第九章《图形的相似》第二节《平行线分线段成比例》教学设计课标要求:掌握基本事实“两条直线被一组平行线所截,所得的对应线段成比例”.学习目标:1、探索并掌握基本事实“平行线分线段成比例”及其推论.2、经历上述探究过程,体会由特殊到一般的归纳推理的思想与方法.3、通过交流合作,体会到其重要性,感悟几何价值,培养良好的学习习惯.教材分析:本节内容是八年级下册第九章第二节,是2011版新课标新增内容,按照《标准》规定,将“平行线分线段成比例”内容作为基本事实,它是证明相似三角形判定定理的基础.在学习平行线分线段成比例时,教材呈现的顺序是:特殊→一般→特殊.具体来说,教材首先借助方格纸这一工具,引导学生通过观察、计算,由特殊到一般地逐步归纳、猜想,进而明确“平行线分线段成比例”的基本事实;然后把这一基本事实特殊化(应用在三角形中),得到它的一个推论,从而为后面证明相似三角形判定作准备.由于基本事实不需要推理证明,所以本节内容在学生通过一系列的探索活动,直观归纳出结论即可,所以重点就是能找出对应线段,掌握“平行线分线段成比例”及推论,并能简单应用.学情分析:由于学生通过对相交线、平行线、三角形、四边形(主要是平行四边形)等图形的学习,已经积累了一定的数学活动经验,几何直观与推理能力都得到了一定的培养,而通过对前面两课时的学习,对相似图形有了直观的印象,体会到可以用对应线段长度的比来描述两个形状相同的平面图形的大小关系,从而认识了线段的比及成比例线段,通过方格纸的直观性,合作探究,了解了合比性质、等比性质,并通过对其进行证明,发展了学生的逻辑推理的能力,为后面相似的学习奠定了良好的基础,而“平行线分线段成比例”正好是建立在成比例线段基础上来学习的.所以本节课的难点就是如何理解对应线段成比例及其变式应用.评价设计:1.通过学生动手操作,自主思考及课堂展示环节二三,检测目标1的达成。
2.通过环节二、三、四检测目标2的达成。
4.2 平行线分线段成比例

如图3-6中,小方格边长都为1,平行线l1 ∥l2∥ l3.分别 交直线m,n A1,A2 , A3 , B1 , B2 , B3 。
(1)计算 的值,你有什么发现? (2)将l2 向下平移到如图3-7的位置,直线m,n 与 l2 的交点分别为 A2 , B2 你在问题(1)中发现结论还成立吗?如果将 l2平移到其它位置呢?
A B C D E F C D B A E F
3、注意该定理在三角形中的应用
习题巩固
1. 如图,在△ABC中,DE∥BC,AC=4 , AB=3,EC=1.求AD和BD.
解∵AC=4,EC=1, ∴AE=3. ∵ DE∥BC,
∴ ∴AD=2.25,
∴BD=0.75.
拓展延伸 1.如图,△ABC中,DE//BC,DF//AC,AE=4,EC=2, BC=8.求BF和CF的长. 分析:运用平行线分线段成比例定理的推论分 A 别列出比例式求解.
l2
AB C图1DE Fl3 l4
E A
D
B
C
l5
图2(2)
推论 平行于三角形一边的直线与其他两边(或两 边的延长线)相交,截得的对应线段成比例. l l l l A D l E l
1 1
D B
E C
l2
A B
l2
l3
C
l3
平行于三角形一边的直线与其 他两边相交,截得的对应线段 成比例
数学符号语言
DF∥AC, 证明:
OD OF . OA OC
EF∥BC
OF OE , OC OB OD OE . OA OB
课堂小结
1、平行线分线段成比例定理: (1)两直线被一组平行线所截,所得的对应线段成比例 (关键要能熟练地找出对应线段) (2)平行于三角形一边的直线与其他两边(或两边的延 长线)相交,截得的对应线段成比例. 2、要熟悉该定理的几种基本图形
平行线分线段成比例培优

14.2平行线分线段成比例平行线分线段成比例定理及其推论 1. 平行线分线段成比例定理: 三条_________截两条直线, 所得的________线段的比________。
如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=。
2. 平行线分线段成比例定理的推论:平行于三角形一边的直线截其他两边(或两边延长线),所得的_______线段的比_________。
如图,在三角形中,如果DE BC ∥,则AD AE DEAB AC BC==3。
平行的判定定理: 如果一条直线截三角形的两边(或两边的延长线),所得的对应线段成比例,那么这条直线 于三角形的第三边。
如上图,如果有BC DEAC AE AB AD ==,那么DE ∥ BC 。
【例1】 如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长.【例2】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+。
【巩固】如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=.【巩固】如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论。
【例3】 如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作EF CD ∥交AD BC ,于E F ,,求EF 的长。
【巩固】(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
l3l 2l 1F E D C B AA B C DE E D C B AEDCBAFEDCBAFEDCBAFE DCBAOFEDCBAQPF E D CBA2专题二、定理及推论与中点有关的问题(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =, 连接EM 并延长,交BC 的延长线于D ,则BCCD =_______。
4.2平行线分线段成比例定理
BC与EF
两条直线被三条平行线所截,所得的对对A应C线与段DF成比例.
符号语言:l1∥l2∥l3
AB DE BC EF
上上 下下
AB DE AC DF
上上 全全
BC EF AC DF
下下 全全
可以推广到被n条 平行线所截
平行线分线段成比例定理
两条直线被三条平行线所截,所得的对应线段成比例
已知:l1∥l2∥l3 求证:AB DE 连接AE,CE;DB,FB BC EF AB S ABE ,DE S BDE BC S CBE EF S BEF
∵ l1∥l2 S ABE S DBE
∵ l2∥l3 S BCF S BEF
AB DE BC EF
讨论:平行线分线段成比例定理得到的比例式中,所截的 四条线段与两直线的位置有没有关系?!
L5 L4 L1 L2
L3
L5
L4
L1
L2
L3
L5
L4
E
D
L1
A
L2
B
C
L3
几何语言:
DE // BC E D
A
AD AB
=AACE
B
C
L5 L4
L5 L4
A
L1EDL1DEL2AL2
B
C L3 B
C
L3
几何语言: ∵ DE∥BC
∵
AD AB
=
AE AC
几何语言:
∵ DE∥BC
∵
AD AB
C
2、填空题:
ED
如图:DE∥BC,
已知:
—AACE—
=
—2 5
求:
—AADB—
平行线分线段成比例定理

如图,有一块形状为直角梯形的草地,周围均为水泥 如图,有一块形状为直角梯形的草地, 直道,两个拐角A 处均为直角, 直道,两个拐角A、B处均为直角,草地中间另有一条水泥 直道EF垂直于AB 垂足为E.已知AE EF垂直于AB, E.已知AE长 EB长 DF长 直道EF垂直于AB,垂足为E.已知AE长a米,EB长b米,DF长 c米.求CF.
要熟悉该定理的几种基本图形
A B C D B C A E F E D D E F C A B B C C E D B A E F A B E D
F D
C A
16 16 8 CF = DE = , BF = 8= . 3 3 3
B
F
C
例2:三角形内角平分线分对边成两线 三角形内角平分线分对边成两线 这两线段和相邻的两边成比例. 段,这两线段和相邻的两边成比例 这两线段和相邻的两边成比例
A
4 3
E
已知: 是 已知:AD是△ABC中∠A的平 中 的平 分线, 分线, BD AB 求证: 求证:DC
课 堂 小 结
平行线分线段成比例定理与平行线等分线段 定理有何联系? 定理有何联系?
A B D E
AB 当 =1 BC AB 当 ≠1 BC
A B
D E
C
F
C
F
结论:后者是前者的一种特殊情况! 结论:后者是前者的一种特殊情况! 平行线分线段成比例定理: 平行线分线段成比例定理:
三条平行线截两条直线,所得的对应线段成比例. 对应线段成比例 三条平行线截两条直线,所得的对应线段成比例.
l4
l5
问题二 如何不通过测量,运用所学知识,快速将一根绳 如何不通过测量,运用所学知识, 子分成两部分,使这两部分之比是2:3? 子分成两部分,使这两部分之比是2:3?
(完整版)平行线分线段成比例

1.在VABC中,AD是ABC的平分线,35AB=5cm, AC=4cm,BC=7cm,则BD=___9____
2.在VABC中,AD是ABC的平分线, 55 AB-AC=5, BD-CD=3, DC=8,则AB=____3___
3.RtVABC中,B 90, AB 12, BC 5, DE AC于E,
A
D
C
证明: 过C作AD的平行线交AB于点E。 ∴BD︰CD=AB︰AE,∠1=∠AEC ∠CAD=∠ACE ∵∠1=∠CAD ∴∠AEC=∠ACE
∴AE=AC ∴BD︰CD=AB︰AC
直角三角形中的比例(射影定理):
C
A
DB
在直角三角形ABC中,CD为斜边AB边上的高, 则:
CD2 ADgDB; AC2 ADgAB; BC2 BDgAB
1gABgADgsin BAD 2
SVDAC
1 gCDgh 2
1gDAgACgsin DAC 2
SVABD BDgh ABgADgsin BAD SVDAC DCgh ACgADgsin DAC
Q AD为BAC的平分线 BAC DAC
AB BD
B
AC DC
本节内容是关于几何中的一些比例关系,这几 节内容现在在初中课本中已“淡化”,但是这几个 结论在高中的“立体几何”和“平面解析几何”中 有时会用到.因此,在本节中首先把这几个定理内容介 绍给同学们,然后利用这三个定理来解决一些题目.其 中对于“平行线分线段成比例”介绍几条稍有难度 的题目,而“三角形内外角平分线性质定理”和 “直角三角形中的比例”的题目直接围绕定理展开, 难度不大.
平行线分线段成比例定理
三条平行线截两条直线,截得的对应线段成比例
平行线分线段成比例的应用PPT课件

技巧2 等积代换法证比例式
2. 如图,在△ABC中,D是AB上一点,E是△ABC内 一点,DE∥BC,过D作AC的平行线交CE的延长线 于F,CF与AB交于P,连接BF,求证: PE PA . PF PB
证明:∵DE∥BC,∴ PD PE . PB PC
∴PD·PC=PE·PB.
∵DF∥AC,∴ PF PD . PC PA
1. 你真让人感动,老师喜欢你的敢想、敢说、敢问和敢辩,希望你继续保持下去。 2. 这么难的题你能回答得很完整,真是了不起!你是我们班的小爱因斯坦。 3. 你预习的可真全面,自主学习的能力很强,课下把你的学习方法介绍给同学们,好不好? 4. 哎呀. 通过你的发言,老师觉得你不仅认真听,而且积极动脑思考了,加油哇! 四、提醒类
(2)∵△ACE≌△BCD, ∴∠BDC=∠AEC. 又∵∠GCD=180°-∠ACB-∠DCE =60°=∠FCE,CD=CE, ∴△GCD≌△FCE(ASA). ∴CG=CF. ∴△CFG为等边三角形. ∴∠CGF=∠ACB=60°. ∴GF∥CE. ∴ AG AF . GC FE
类型 2 证线段相等
DB ∵CF∥BA, ∴ DE AE AD 1.
EF EC DB ∴DE=EF.
类型 3 证比例和为1
技巧6 同分母的中间比代换法
6. 如图,已知AC∥FE∥BD,求证: AE BE 1. AD BC
证明:∵AC∥EF,
∴ BE BF ①. BC BA
又∵FE∥BD,
∴ AE AF ② . AD AB
①+②,得 BE AE BF AF AB 1. BC AD BA AB AB
即 AE BE 1. AD BC
同学们下课啦
授课老师:xxx
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.2平行线分线段成比例
教学目标
1.理解平行线分线段成比例定理,并能初步应用它进行简单的计算.
2.培养学生类比联想及用运动的思维方式看待问题的能力.
教学重点和难点
平行线分线段成比例定理及应用.
教学过程设计
一、类比联想、发现定理
1.复习平地线等分线段定理的内容及数学表达式,如图5-13.
∵lll,AB=BC,////321∴EF=FG.
2.将上述命题改写成比例的形式.
∵llll,AB:BC=1:1,//////4321ABEF??1∴EF:FG=1:1,则有BCFG3.运用类比方式将比值从1推广到正实数m得出猜想.
教师启发学生思考:
ACAB?1,?1,那么还有类似比例式成立吗? 在图5-13中,llll,AB=BC=CD,//////4231
BDCD12EGABEFAC?,???学生可从图中看出. ,猜想推广应成立
21CDGHFHBD4.举例进一步验证猜想.
教师可再举出图5-14中,AB BC等于其它更一般的实数的两个例子,来进一步验证猜想.
5.(选)用面积法证明猜想.
对于学生程度较好的班级,教师可用三角形面积公式来严格证明猜想成立,具体做法见设计
说明.
二、用运动的观点深刻认识定理的内容
1.让学生归纳以上情况,并用语言准确叙述定理内容,以及画图写出部分数学表达式.
2.教师强调“对应”的含义,并介绍结合图形形象记忆的方法,如:
左上右上左上右上左下右下左上左下左全?,?,?,??
右下右下左全右全左全右全右上右下右全3.用运动的观点识别定理的各种变式图形中的比例线段.(见图5-15,不断平移DF)
强调由平行线分线段成比例定理所得比例式中,四条线段与平行直线和被截
两直线的交点位置无关,尤其是图5-15(a)中的M点,图5-15(c)的N点.
三、应用举例、变式练习
例1 已知:如图5-16,lll. ////312(1)AB=3,DE=2,EF=4,求BC;
(2)AC=8,DE=2,EF=3,求AB.
分析:
(1)根据题目中的已知和所求线段,寻找有关的比例式,注意选择合理简捷的方法.如第
(2)ABDEx216??,解得x=可得,.
问,有以下两种解法:①若选,则设AB=x,BC=8-x
3xDF8?BC52ABABDE16??. ,若选②∵lll,则列出,得AB=////321
32?ACDF85(2)在列比例式求某线段的长时,尽可能将所要求的线段写成比例第一项,从而减少变形引起的错误.
OAOAABBC4111111???,OC. AC,=18cml,例2已知:如图5-17ll,,求////221131
OA31232
分析:设OA1=k,利用OC2=18cm及A1B1B1C1=A2B2B2C2列出关于K的方程,解得k=4cm,A1C1=20cm. ABmDEm?.ll5-18,l求:.(答:) ,已知:如图例3////321BCnDFm?n
练习课本第210页1,2题.
四、师生共同小结
1.平行线分线段成比例定理的内容、条件(平行线组截两条直线)以及结论中“对应”的含义.
2.定理的形象记忆方法.
3.定理的作用:在平行条件下,换比——将一条直线上两条线段的比转移成另一直线上另两
条线段的比.
4.研究问题的方法:从特殊到一般再到特殊,类比联想,运动观点等思维方法的应用.
五、作业
课本第218页第2,3题.
52) 答:.l5-19 lll求x(补充题:如图//////42318
课堂教学设计说明
1.“平行线分线段成比例定理”共4课时.第1课时讲述定理的发现及初步应用;第2课时研究“三角形一边的平行线”以及课本第215页例6的初步应用;第3课时研究“三角形一边
平行线的判定定理”以及性质、判定定理的综合应用;第4课时进行综合练习,重点是比例线段的作图、证明及平行线的证明.
本节教案需一课时完成.
2.本节课定理的发现过程.
采用了课本上的这个定理的引入过程,因为它反映了从特殊(平行线等分线段)到一般(平行线分段成比便定理),再从一般到特殊(它的各种变式图形)研究问题的过程,一符合学生由已知到末知,由直观到抽象,由浅入深的思维认识规律,教师应启发学生运用类比推广、归纳、猜想的思维方法以及运动的观点层层深入地自己动手动脑来探索知识.
3.教师也可采用以下引入程序(见图5-20)
(a)(b)(c)(d)
ADAE2??,DE//BC在图5-20(b)中,ECDB3AEADm?? (m,n为整数),在图5-20(c)中,DE//BC并用面积法证明. ECnDBADEF?在图5-20(d)中,
AF//DE//BC,则. DBECABDE?在图5-20(e)中,lll,则等. ////312
BCEF4.应用面积法证明定理
ABDE? l5-21,ll,求证已知:如图////312BCEF
证明连结AE,BF,BD,CE,则
SSDEAB?AEBDBE??,?.(等高的三角形面BCSEFS?BEF?BEC积比等于底之比)
∵lll,////312∴S=S,S=S.(等底等高的三角形面积相等) BEF△BECAEB△△△DBE SSABDE DBEAEB???,?∴∴
SSBCEF BEF?BEC?。
