五大圆幂定理证明
圆幂定理及其证明

圆幂定理圆幂的定义:一点P 对半径R 的圆O 的幂定义如下:22OP R -所以圆内的点的幂为负数,圆外的点的幂为正数,圆上的点的幂为零。
圆幂定理是相交弦定理、切割线定理及割线定理(切割线定理推论)以及他们推论的统称。
(1) 相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。
如图,AB 、CD 为圆O 的两条任意弦。
相交于点P ,连接AD 、BC ,则∠D=∠B , ∠A=∠C 。
所以△APD ∽△BPC 。
所以 AP PD AP BP PC PD PC BP=⇒⋅=⋅ (2) 切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆焦点的两条线段长的比例中项。
如图,PT 为圆切线,PAB 为割线。
连接TA ,TB ,则∠PTA=∠B (弦切角等于同弧圆周角)所以△PTA ∽△PBT ,所以2PT PA PT PA PB PB PT=⇒=⋅ (3) 割线定理:从圆外一点P 引两条割线与圆分别交于 A.B.C.D 则有PA·PB=PC·PD 。
这个证明就比较简单了。
可以过P 做圆的切线,也可以连接CB 和AD 。
证相似。
存在:PA PB PC PD ⋅=⋅进一步升华(推论):过任意在圆O 外的一点P 引一条直线L1与一条过圆心的直线L2,L1与圆交于A 、B (可重合,即切线),L2与圆交于C 、D 。
则PA·PB=PC·PD 。
若圆半径为r ,则 2222()()||PC PD PO R PO R PO R PO R ⋅=-⋅+=-=-(一定要加绝对值,原因见下)为定值。
这个值称为点P 到圆O 的幂。
(事实上所有的过P 点与圆相交的直线都满足这个值)若点P 在圆内,类似可得定值为2222||R PO PO R -=-故平面上任意一点对于圆的幂为这个点到圆心的距离与圆的半径的平方差的绝 对值。
(这就是“圆幂”的由来)。
圆幂的定理

圆幂的定理
圆幂定理是几何学中的一条定理,它描述了一个点与一个圆之间的关系。
具体来说,圆幂定理说明了如果有一条直线通过一个点P,与一个圆相交于点M和点N,那么这个点P到圆的两个切线段PM和PN的长度的乘积等于点P到圆心O的距离的平方减去圆的半径的平方,即可以表示为PM * PN = PO^2 - r^2。
圆幂定理可以推广到两个圆相交的情况下,即如果有两个圆分别为圆A和圆B,并且它们相交于点M和点N,那么点M和点N到这两个圆心的线段的乘积等于这两个圆心到点M和点N的距离的乘积,即可以表示为MA * MB = NA * NB。
这个式子即为圆A关于圆B的圆幂定理。
圆幂定理有许多应用,其中一个重要的应用是求解圆的切线长度。
通过圆幂定理,可以求解出切线与切点之间的关系,进而解决与圆切线相关的几何问题。
4个圆幂定理及其证明

4个圆幂定理及其证明第一篇:4个圆幂定理及其证明相交弦定理如图,⊙P中,弦AB,CD相交于点P,则AP·BP=CP·PD证明:连结AC,BD,由圆周角定理的推论,得∠A=∠D,∠C=∠B。
∴△PAC∽△PDB,∴PA∶PD=PC∶PB,PA·PB=PC·PD注:其逆定理可作为证明圆的内接三角形的方法.切割线定理如图,ABT是⊙O的一条割线,TC是⊙O的一条切线,切点为则TC²=TA·TB证明:连接AC、BC∵弦切角∠TCB对弧BC,圆周角∠A对弧BC∴由弦切角定理,得∠TCB=∠A又∠ATC=∠BTC∴△ACT∽△CBT∴AT:CT=CT:BT, 也就是CT²=AT·BT弦切角定义:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角C,弦切角定理:弦切角等于它所夹的弧所对的圆周角.定义弦切角定理:弦切角的度数等于它所夹的弧的圆心角的度数的一半.(弦切角就是切线与弦所夹的角)弦切角定理证明证明:设圆心为O,连接OC,OB,OA。
过点A作TP的平行线交BC于D,则∠TCB=∠CDA∵∠TCB=90-∠OCD∵∠BOC=180-2∠OCD∴,∠BOC=2∠TCB切线长定理从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角。
如图中,切线长AC=AB。
∵∠ABO=∠ACO=90°BO=CO=半径AO=AO公共边∴RtΔABO≌RtΔACO(HL)∴AB=AC∠AOB=∠AOC∠OAB=∠OAC割线定理如图,直线ABP和CDT是自点P引的⊙O的两条割线,则PA·PB=PC·PD证明:连接AD、BC∵∠A和∠C都对弧BD∴由圆周角定理,得∠A=∠C又∵∠APD=∠CPB∴△ADP∽△CBP∴AP:CP=DP:BP, 也就是AP·BP=CP·DP圆幂定理圆幂定理是对相交弦定理、切割线定理及割线定理(切割线定理推论)以及它们推论统一归纳的结果。
圆幂定理
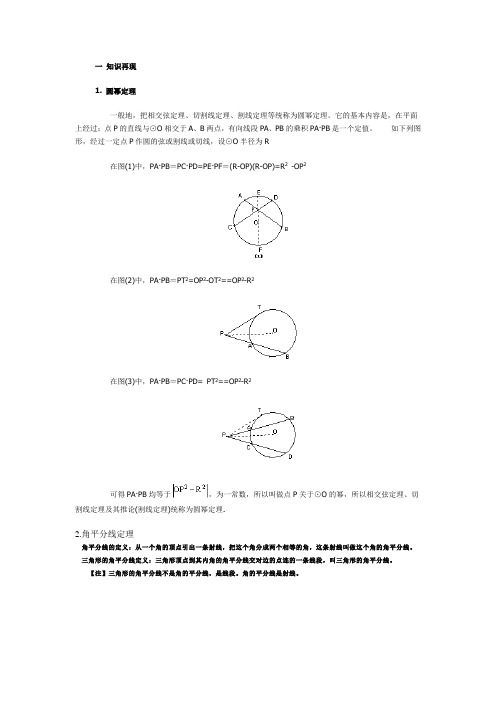
一知识再现1. 圆幂定理一般地,把相交弦定理、切割线定理、割线定理等统称为圆幂定理。
它的基本内容是,在平面上经过;点P的直线与⊙O相交于A、B两点,有向线段PA、PB的乘积PA·PB是一个定值。
如下列图形,经过一定点P作圆的弦或割线或切线,设⊙O半径为R在图(1)中,PA·PB=PC·PD=PE·PF=(R-OP)(R-OP)=R2-OP2在图(2)中,PA·PB=PT2=OP2-OT2==OP2-R2在图(3)中,PA·PB=PC·PD= PT2==OP2-R2可得PA·PB均等于,为一常数,所以叫做点P关于⊙O的幂,所以相交弦定理、切割线定理及其推论(割线定理)统称为圆幂定理.2.角平分线定理角平分线的定义:从一个角的顶点引出一条射线,把这个角分成两个相等的角,这条射线叫做这个角的角平分线。
三角形的角平分线定义:三角形顶点到其内角的角平分线交对边的点连的一条线段,叫三角形的角平分线。
【注】三角形的角平分线不是角的平分线,是线段。
角的平分线是射线。
■拓展:三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等!(即内心)。
■定理1:在角平分线上的任意一点到这个角的两边距离相等。
■逆定理:在一个角的内部(包括顶角),且到这个角的两边距离相等的点在这个角的角平分线上。
■定理2:三角形一个角的平分线分对边所成的两条线段与这个角的两邻边对应成比例,如:在△ABC 中,BD 平分∠ABC ,则AD :DC=AB :BC 3.平行线分线段定理定理 三条平行线截两条直线,所得的对应线段成比例.二 例题讲解例1如图4AB 是⊙O 的弦,P 是AB 上一点,AB = 10cm ,P A : PB = 2 : 3,OP = 5cm ,则⊙O 的半径等于 .解析:设⊙O 的半径为R .∵AB = 10cm ,P A : PB = 2 : 3,∴PA = 4 cm ,PB = 6 cm . 由相交弦定理,得P A ·PB = PC ·PD = R 2-OP 2,即4×6 = R 2-52. 所以,R = 7. 故⊙O 的半径等于7 cm . 例2.如图5,已知P AC 为⊙O 的割线,连接PO 交⊙O 于B ,PB = 2,OP = 7,P A= AC ,则P A 的长为( )A .7B .23C .14D .32解析:延长PO 交⊙O 于D .∵PB = 2,OP = 7,∴OB = 5,即PC = 12. 由切割线定理的推论,得 P A ·AC = PB ·PC . ∵P A = AC ,∴2 P A 2 = 2×12. 所以,P A = 23.故应选B .一、“四心”分类讨论1、外心三解形三条垂直平分线的交点叫做三角形的外心,即外接圆圆心。
圆幂定理,敲重点

圆幂定理,敲重点相交弦定理定理:如图,弦AB与弦CD交于圆O内一点P,则PA·PB=PC·PD.证明:连接AD、BC,根据有圆周角定理可得:∠DAP=∠BCP,∠ADP=∠CBP,∴△APD∽△CPB∴PA:PC=PD:PB∴PA·PB=PC·PD切割线定理定理:如图,P为圆O外一点,PA是圆的切线,PC是圆的割线,求证:PA²=PB·PC.证明:连接AB、AC,根据弦切角定理,可得:∠PAB=∠C,又∠P是公共角,∴△PAB∽△PCA∴PB:PA=PA:PC∴PA²=PB·PC割线定理定理:如图,P是圆O外一点,PB、PD是圆的两条割线,则PA·PB=PC·PD.证明:法一:连接AC、BD,根据圆内接四边形外角等于内对角,可得:∠PAC=∠PDB,∠PCA=∠PBD,∴△PAC∽△PDB∴PA:PD=PC:PB∴PA·PB=PC·PD法二:连接AD、BC,根据圆周角定理,可得:∠B=∠D,又∠P是公共角,∴△PAD∽△PCB∴PA:PC=PD:PB∴PA·PB=PC·PD圆幂定理定义点P到圆O的幂:OP²-r².以上“相交弦定理”、“切割线定理”、“割线定理”统称为“圆幂定理”.(1)相交弦满足:PA·PB=PC·PD=r²-OP²(2)切线满足:PA²=OP²-r²(3)割线满足:PA·PB=PC·PD=OP²-r²【归纳】以上我们考察的量,如PA·PB、PA²等均等于OP²-r²或r²-OP²,故称圆幂定理.。
圆幂定理

圆幂定理圆幂的定义:一点P对半径R的圆O的幂定义如下:所以圆内的点的幂为负数,圆外的点的幂为正数,圆上的点的幂为零.圆幂定理是相交弦定理,切割线定理及割线定理(切割线定理推论)以及他们推论的统称.相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等.如图,AB,CD为圆O的两条任意弦.相交于点P,连接AD,BC,则∠D=∠B,∠A=∠C.所以△APD∽△BPC.所以切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆焦点的两条线段长的比例中项.如图,PT为圆切线,PAB为割线.连接TA,TB,则∠PTA=∠B(弦切角等于同弧圆周角)所以△PTA∽△PBT,所以割线定理:从圆外一点P引两条割线与圆分别交于A.B.C.D 则有PA·PB=PC·PD.这个证明就比较简单了.可以过P做圆的切线,也可以连接CB和AD.证相似.存在:进一步升华(推论):过任意在圆O外的一点P引一条直线L1与一条过圆心的直线L2,L1与圆交于A,B(可重合,即切线),L2与圆交于C,D.则PA·PB=PC·PD.若圆半径为r,则(一定要加绝对值,原因见下)为定值.这个值称为点P到圆O的幂.(事实上所有的过P点与圆相交的直线都满足这个值)若点P在圆内,类似可得定值为故平面上任意一点对于圆的幂为这个点到圆心的距离与圆的半径的平方差的绝对值.(这就是"圆幂"的由来)这些就是圆中非常重要的几个定理,当然在现在的教材中,这几个定理已经被删掉了,教材中唯一余下的就是垂径定理了.可是有很多题,特别是选择填空,用垂径定理做起来是相当的麻烦了.这时候假如你会圆幂定理,那么你的作题速度也就会上去了.另外, 圆幂定理也会给我们提供解大题的思路.当然如果在大题中想要用圆幂定理,那么大家最好还是证明一下.因为你们也看到了, 圆幂定理的证明是非常简单的,就那么几行,一个相似就搞定了.可不能因为麻烦而放弃证明,这样在现在的考试中是很可能会被扣分的哦!借鉴别人的,,请原谅~。
圆幂定理及其证明

圆幂的定义假设平面上有一圆O,其半径为R,有一点P在圆O外,则OP^2-R^2即为P 点到圆O的幂;若P点在圆内,则圆幂为R^2-OP^2;综上所述,圆幂为|OP^2-R^2|。
圆幂恒大于或等于零。
圆幂的由来过任意在圆O外的一点P引一条直线L1与一条过圆心的直线L2,L1与圆交于A、B(可重合,即切线),L2与圆交于C、D。
则PA·PB=PC·PD。
若圆半径为r,则PC·PD=(PO-r)·(PO+r)=PO^2-r^2=|PO^2-r^2| (要加绝对值,原因见下)为定值。
这个值称为点P到圆O的幂。
(事实上所有的过P点与圆相交的直线都满足这个值)若点P在圆内,类似可得定值为r^2-PO^2=|PO^2-r^2|故平面上任意一点对于圆的幂为这个点到圆心的距离与圆的半径的平方差,而过这一点引任意直线交圆于A、B,那么PA·PB等于圆幂的绝对值。
圆幂定理定理内容过任意不在圆上的一点P引两条直线L1、L2,L1与圆交于A、B(可重合,即切线),L2与圆交于C、D(可重合),则有。
[1]圆幂定理的所有情况考虑经过P点与圆心O的直线,设PO交⊙O与M、N,R为圆的半径,则有圆幂定理的证明图Ⅰ:相交弦定理。
如图,AB、CD为圆O的两条任意弦。
相交于点P,连接AB、BD,由于∠B与∠D同为弧AC所对的圆周角,因此由圆周角定理知:∠B=∠D,同理∠A=∠C,所以。
所以有:,即:图Ⅱ:割线定理。
如图,连接AD、BC。
可知∠B=∠D,又因为∠P为公共角,所以有,同上证得图Ⅲ:切割线定理。
如图,连接AC、AD。
∠PAC为切线PA 与弦AC组成的弦切角,因此有∠PAC=∠D,又因为∠P为公共角,所以有易证图Ⅳ:PA、PC均为切线,则∠PAO=∠PCO=直角,在直角三角形中:OC=OA=R,PO为公共边,因此所以PA=PC,所以综上可知,是普遍成立的。
证明完毕。
圆幂定理证明

圆幂定理证明
引言:
圆幂定理又称华罗庚公式,它表明在多项式中,二次项、四次项等次项的系数可以从非二次项的系数中求出来,它最早由科学家英国自然哲学家华罗庚在16世纪完成。
圆幂定理的性质:当z的n次幂展开时(z的n次幂为z的n个相同的因子),各项系数满足公式:a(n)=( -1)^( n-1 ) / ( n - 1 )! * 求和(k= 0到 n-1) [n^k 开始 * a (k)],其中 n 称作次数,k 称作幂数。
证明:
首先,假设z的n次幂有如下公式:z^n = a0 +a1z+...+an-1zn-1 + anzn
我们分类讨论,首先当n为偶数时,如:
z^2 =a0+a1z+a2z^2
因为每一项的系数都是可以由未知系数a0,a1,a2求出来,即:
a0 = ( -1 )^ 1 / 1! * 求和(k= 0到 1) [2^k * a(k)]
当n为奇数时,如:
通过上述两种情况的分析,当n为任意正整数时,它们满足的条件都是一样的,即:a(n)=( -1)^( n-1 ) / ( n - 1 )! * 求和(k= 0到 n-1) [n^k * a(k)],其中n 称作次数,k 称作幂数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五大圆幂定理证明
五大圆幂定理是指:
1. 圆内接正多边形的边数是多边形周长与直径之比的平方。
2. 圆外切正多边形的边数是多边形周长与直径之比的平方。
3. 任意一个正n边形的内切圆半径等于半径与n之和的1/n。
4. 任意一个正n边形的外接圆半径等于半径的n倍。
5. 任意一个正n边形的周长等于n倍的外接圆周长。
下面给出五大圆幂定理的证明:
1. 周长与直径之比的平方
设正n边形的周长为P,直径为d,则n个边的长度之和为2P/n。
因为每个边上的弧长等于周长除以360度,所以每个边的长度为(2P/n)/360度。
因为正n边形的每个内角都相等,所以内角和为(180度/n) * n,即180度。
因此,每个边所对的圆心角为180度除以n,
即36度。
又因为圆周角的大小与圆心角的大小成正比,所以每个圆周所对的圆心角为36度,即每个圆周的长度为2πr,其中r为圆的半径。
因此,每个边的长度等于2πr * (2/360) * n,即πr/3。
因此,直径d等于πr/3,周长P等于3πr,所以正n边形的边数n等于周长P除以直径d的平方,即n=3P/d²。
2. 外切正多边形的边数是周长与直径之比的平方
证明同上,只是将周长P替换为周长与直径之比的平方P/d²。
3. 内切圆半径等于半径与n之和的1/n
设正n边形的边长为a,内接圆的半径为r,则内接圆的周长为2πr,因为内接圆与正n边形相切,所以内接圆的周长等于正n边形的周长除以n,即2πr=P/n。
因此,πr=P/n,即r=P/nπ。
又因为内接圆的半径等于边长a与半径r之差的一半,即r=a-(a/2r)=a*(1-1/n),所以a=2r/n。
因此,内切圆半径等于半径与n之和的1/n,即r=P/2nπ/(n-1)。
4. 外接圆半径等于半径的n倍
设正n边形的边长为a,外接圆的半径为R,则外接圆的周长为2πR,因为外接圆与正n边形相切,所以外接圆的周长等于正n边形的周长
除以n,即2πR=P/n。
因此,πR=P/n,即R=P/nπ。
又因为外接圆的半径等于边长a与外接圆半径R之和,即a+R=2R,所以R=a/2。
因此,外接圆半径等于边长a与半径R之和的1/2,即R=2a/n。
5. 周长等于n倍的外接圆周长
证明同上,只是将周长P替换为周长与直径之比的平方P/d²。
综上所述,五大圆幂定理得证。
