北京工业大学-数学建模4-整数规划与对策论实验201311
北工大工程数学-数学建模实验03
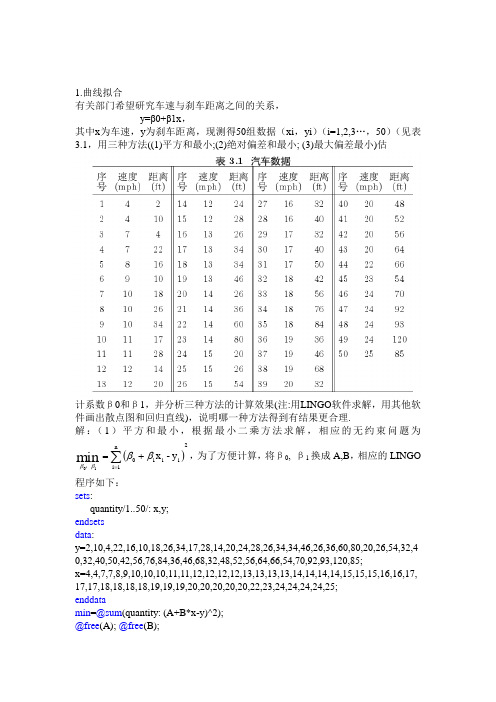
1.曲线拟合有关部门希望研究车速与刹车距离之间的关系, y=β0+β1x ,其中x 为车速,y 为刹车距离,现测得50组数据(xi ,yi )(i=1,2,3…,50)(见表3.1,用三种方法((1)平方和最小;(2)绝对偏差和最小; (3)最大偏差最小)估计系数β0和β1,并分析三种方法的计算效果(注:用LINGO 软件求解,用其他软件画出散点图和回归直线),说明哪一种方法得到有结果更合理. 解:(1)平方和最小,根据最小二乘方法求解,相应的无约束问题为()2n1i i i 10y -x min 10∑=+=ββββ,,为了方便计算,将β0, β1换成A,B ,相应的LINGO程序如下: sets :quantity/1..50/: x,y; endsets data :y=2,10,4,22,16,10,18,26,34,17,28,14,20,24,28,26,34,34,46,26,36,60,80,20,26,54,32,40,32,40,50,42,56,76,84,36,46,68,32,48,52,56,64,66,54,70,92,93,120,85;x=4,4,7,7,8,9,10,10,10,11,11,12,12,12,12,13,13,13,13,14,14,14,14,15,15,15,16,16,17,17,17,18,18,18,18,19,19,19,20,20,20,20,20,22,23,24,24,24,24,25; enddatamin =@sum (quantity: (A+B*x-y)^2); @free (A); @free(B);计算结果如图所示用LINGO解得:A= -17.57909,B=3.932409,所以y= -17.57909+3.932409*x. β0= -17.57909,β1=3.932409(2)绝对偏差和最小,根据最小一乘方法求解,相应的无约束问题为∑=+=ni1ii1y-xmin1ββββ,,为了方便计算,将β0, β1换成A,B,相应的LINGO程序如下:sets:quantity/1..50/: x,y;endsetsdata:y=2,10,4,22,16,10,18,26,34,17,28,14,20,24,28,26,34,34,46,26,36,60,80,20,26,54,32,4 0,32,40,50,42,56,76,84,36,46,68,32,48,52,56,64,66,54,70,92,93,120,85;x=4,4,7,7,8,9,10,10,10,11,11,12,12,12,12,13,13,13,13,14,14,14,14,15,15,15,16,16,17, 17,17,18,18,18,18,19,19,19,20,20,20,20,20,22,23,24,24,24,24,25;enddatamin=@sum(quantity: @abs(A+B*x-y));@free(A); @free(B);计算结果如图所示用LINGO 解得:A= -11.6,B=3.4, 所以y= -11.6+3.4*x. β0= -11.6,β1=3.4(3)最大偏差最小,根据最大偏差的最小的方法求解,相应的无约束问题为i i 101y -x max min 10ββββ+=≤≤ni ,,为了方便计算,将β0, β1换成A,B ,相应的LINGO程序如下: sets :quantity/1..50/: x,y; endsets data :y=2,10,4,22,16,10,18,26,34,17,28,14,20,24,28,26,34,34,46,26,36,60,80,20,26,54,32,40,32,40,50,42,56,76,84,36,46,68,32,48,52,56,64,66,54,70,92,93,120,85;x=4,4,7,7,8,9,10,10,10,11,11,12,12,12,12,13,13,13,13,14,14,14,14,15,15,15,16,16,17,17,17,18,18,18,18,19,19,19,20,20,20,20,20,22,23,24,24,24,24,25; enddatamin =@max (quantity: @abs (A+B*x-y)); @free (A); @free (B); 计算结果如图所示用LINGO解得:A= -12,B=4,所以y= -12+4*x. β0= -12,β1=4X轴为速度,Y轴为距离,蓝色点多已知数据点,y1,y2,y3分别为前三种方法求得的数据点,黑色线为通过蓝色数据点得到的线性回归方程y=1.445x+6.121,比较三种方法得到曲线,可以看到与红色曲线吻合度高于其他两种方法,所以第一种方法得到的结果更为合理。
2011年北京工业大学数学建模复赛试题

2011年北京工业大学“太和顾问杯”数学建模竞赛复赛参赛说明1、北京工业大学数学建模复赛试题共有两道(A、B),请选择你最熟悉的一道题目回答,不必做其他题目。
2、请按规定的时间内上交试卷,过期无效。
试卷要在用A4纸打印完成,手写无效。
3、由于竞赛题目有一定的难度,因此不必做完上一个问题,才能回答下一个问题,而是需要完整地把解题的思想表达出来。
由于有些题目中的问题较多,或难度较大,很可能在一周的业余时间内做不完,你可以对某些问题不作回答,有兴趣的同学可以在竞赛后再作深入研究。
4、由于题目难度不可能完全相同,评审中将向难度较大的题目倾斜,请参赛选手在选题时加以考虑。
5、尽管本次竞赛研究生和本科生均能参加,但在评分上两者的要求是不同的,在阅卷时将对研究生有更高的要求。
6、本次竞赛从开题到5月4日(周三)下午一点半截止,为期一周,5月4号1点30分到2点30分在数理楼2316进行收题工作,请务必准时上交题目纸质版,过时不候。
A题:城市经济数据分析与区域合作改革开放30年来,中国经济取得了巨大的发展,这个发展从整个经济增长水平来看从1978年到2009年我国GDP按照可比价格年均增长在9%以上,其发展水平世界瞩目。
但是我国区域经济发展存在不平衡现象,东部沿海城市与中西部地区差距过大,严重制约了国民经济的进一步发展。
扩大内需、调整经济结构、加快城市化建设进程和促进欠发达地区的经济繁荣是我国国民经济的下一步重要战略决策。
表A.1(见下页)列出了我国99个城市的经济数据,这些数据是根据中国统计信息网公布的2009年度GDP数据及其它网上信息得到的。
表中选择了各省中具有代表性的城市,加上所有直辖市,考察这些城市的经济数据和产业结构。
如果考虑选择其中GDP(生产总值)排在较靠前的城市组成城市集合A,将GDP 排在较靠后的城市组成城市集合B,考虑建立一种经济合作和技术援助的关系,希望通过较发达地区和欠发达地区的人才流动、教育与技术支援、经济合作交流以及国家的一些税收政策等带动和促进欠发达地区的经济繁荣与城市化进程。
北京工业大学-薛毅老师-工程数据建模-实验2-线性规划和整数规划

北京工业大学-薛毅老师-工程数据建模-实验2-线性规划和整数规划北京工业大学-薛毅老师-工程数据建模-实验2-线性规划和整数规划2. 线性规划和整数规划实验2.1 基本实验1. 生产计划安排某工厂生产A,B,C三种产品,其所需劳动力、材料等有关数据见表2.1所示。
表2.1 不同产品的消耗定额产品可用量资源A B C (单位)6 3 5 45 劳动力3 4 5 30 材料产品利润3 14 (元/件)(1)确定获利最大的生产方案;(2)产品A、B、C的利润分别在什么范围内变动时,上述最优方案不变; (3)如果劳动力数量不增,材料不足时可从市场购买,每单位0.4元,问该厂要不要购进原材料扩大生产,以购多少为宜,(4)如果生产一种新产品D,单件劳动力消耗8个单位,材料消耗2个单位,每件可获利3元,问该种产品是否值得生产,解答:(1)LINGO中程序:max = 3*x1 +x2+ 4*x3;6*x1 + 3*x2+5*x3 <= 45;3*x1 + 4*x2+5*x3 <= 30;end程序运行结果如下:Global optimal solution found.Objective value: 27.00000Total solver iterations: 2Variable Value Reduced CostX1 5.000000 0.000000X2 0.000000 2.000000X3 3.000000 0.000000Row Slack or Surplus Dual Price1 27.00000 1.0000002 0.000000 0.20000003 0.000000 0.6000000获利最大的生产方案为:生产A产品5件,B产品0件,C产品3件,获利为27。
(2)产品A利润在2.4-4.8元之间变动,最优生产计划不变。
(3)运行程序LINGO中程序:max=3*x1+x2+4*x3;6*x1+3*x2+5*x3<45;end程序运行结果如下:Global optimal solution found.Objective value: 36.00000Total solver iterations: 0Variable Value Reduced CostX1 0.000000 1.800000X2 0.000000 1.400000X3 9.000000 0.000000Row Slack or Surplus Dual Price1 36.00000 1.0000002 0.000000 0.8000000从程序运行结果可得到:当A、B为0,而C 9件时利润最大,最大利润为36元,应该购入原材料扩大生产,购入15个单位。
实验四:整数规划

实验四:整数规划一、实验目的:整数规划问题建模及软件求解。
二、实验要求:1.掌握一般整数规划、0-1整数规划问题、指派问题的建模;2.了解求解整数规划问题的方法:分支定界法、割平面法、隐枚举法、匈牙利法;3.学会用matlab 、 lingo 软件求解整数规划问题。
三、实验内容:1、求解下列整数规划问题:⎪⎪⎩⎪⎪⎨⎧≥≤+≤++=.,0,30561652..max 2121212121为整数x x x x x x x x t s x x z(1)给出lingo 原始代码;(2)求解结果粘贴。
(1)model :max =x1+x2;2*x1+5*x2<=16;6*x1+5*x2<=30;@gin (x1);@gin (x2);end(2)Global optimal solution found.Objective value: 5.000000Objective bound: 5.000000Infeasibilities: 0.000000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced Cost X1 5.000000 -1.000000 X2 0.000000 -1.000000Row Slack or Surplus Dual Price 1 5.000000 1.000000 2 6.000000 0.000000 3 0.000000 0.0000002、求解下列0-1整数规划问题:⎪⎩⎪⎨⎧==≤+-+-≤--+-+-+-=.5,4,3,2,1,100242645723..4352max 543215432154321i x x x x x x x x x x x t s x x x x x z i或 (1)给出matlab 、lingo 原始代码;(2)求解结果粘贴。
(1)Lingomodel :max =2*x1-x2+5*x3-3*x4+4*x5;3*x1-2*x2+7*x3-5*x4-4*x5<=6;x1-x2+2*x3-4*x4+2*x5<=0;@bin (x1);@bin (x2);@bin (x3);@bin (x4);@bin (x5);!sets: A/1..5/x @(for(A:@bin(x)));end(2)Global optimal solution found.Objective value: 7.000000Objective bound: 7.000000Infeasibilities: 0.000000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced Cost X1 1.000000 -2.000000X2 1.000000 1.000000X3 1.000000 -5.000000X4 1.000000 3.000000X5 1.000000 -4.000000Row Slack or Surplus Dual Price1 7.000000 1.0000002 7.000000 0.0000003 0.000000 0.000000(1)matlabf=[-2 1 -5 3 -4];A=[3 -2 7 -5 -4;1 -2 2 -4 2];b=[6 0];[x,z]=bintprog(f,A,b)z=-z(2)>> exOptimization terminated.x =11111z =-7z =73、(指派问题)现有A,B,C,D,E 5个人,挑选其中4个人去完成4项工作。
数学建模应用中整数线性规划问题的常用解法初探

数学建模应用中整数线性规划问题的常用解法初探作者:***来源:《现代职业教育》2021年第07期[摘要] 在数学建模应用中,整数线性规划问题是一种常见的运筹学问题,其常用的解法有分支定界法、割平面法、蒙特卡罗法等。
试图从数学建模实践的角度,淡化理论证明,仅对这几种典型方法的原理、优缺点、应用范围等作一个简要的分析比较,以供读者在实际的数学建模过程中灵活应用。
[关键词] 整数线性规划;分支定界法;割平面法;蒙特卡罗法[中图分类号] O151.2 [文献标志码] A [文章编号] 2096-0603(2021)07-0178-02一、整数线性规划问题规划问题是运筹学的一个重要分支,从表达形式上看,可以分为线性规划(linear programming,LP)和非線性规划(non-linear programming,NLP);从变量的可行域要求来看,也可以分为整数规划(integer programming,IP)和非整数规划(non-integerprogramming,NIP),若既有表达式上的线性特征,又有变量的取整要求,这样的规划问题我们一般称之为整数线性规划(integer linear programming,ILP)问题[1]。
整数线性规划问题的传统解法是先求解与之对应的松弛问题(即先不考虑变量的整数约束而形成的新的线性规划问题),若刚好得到整数解,则求解过程结束;否则,再通过适当方法(切割平面或分支定界)生成一个或多个新的松弛问题(最初松弛问题加上新的切割或分支条件),重复以上步骤直至求得最优解。
一般而言,整数线性规划问题的求解难度要比普通线性规划问题大,其根本原因在于自变量取值增加了离散特性,但在工程上,离散特性恰好可以被计算机利用。
蒙特卡罗算法是一类随机方法的统称。
这类方法的基本思路是,可以通过随机采样进行计算而得到近似结果,随着采样的增多,得到正确结果的概率将逐渐加大,经过一定的步骤之后,就会尽可能趋近最佳结果。
北京工业大学-薛毅老师-工程数据建模-实验4-图论(组合优化)
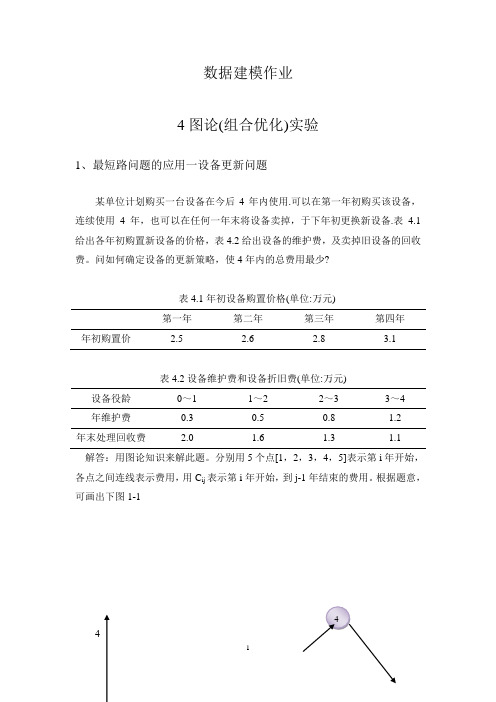
数据建模作业4图论(组合优化)实验1、最短路问题的应用一设备更新问题某单位计划购买一台设备在今后4年内使用.可以在第一年初购买该设备,连续使用4年,也可以在任何一年末将设备卖掉,于下年初更换新设备.表 4.1给出各年初购置新设备的价格,表4.2给出设备的维护费,及卖掉旧设备的回收费。
问如何确定设备的更新策略,使4年内的总费用最少?表4.1年初设备购置价格(单位:万元)第一年第二年第三年第四年年初购置价 2.5 2.6 2.8 3.1表4.2设备维护费和设备折旧费(单位:万元)设备役龄0~1 1~2 2~3 3~4 年维护费0.3 0.5 0.8 1.2年末处理回收费 2.0 1.6 1.3 1.1解答:用图论知识来解此题。
分别用5个点[1,2,3,4,5]表示第i年开始,各点之间连线表示费用,用C ij表示第i年开始,到j-1年结束的费用。
根据题意,可画出下图1-1443 2 1 01 2 3 4 5 6图1-1LINGO 中程序:sets :nodes/1..5/;arcs(nodes,nodes)|&1 #lt# &2:c,x; end sets data :c = 0.8,1.7,2.8,4.2,0.9,1.8,2.9,1.1,2,1.4; enddatan = @size (nodes); min = @sum (arcs:c*x);@for (nodes(i)| i #ne# 1 #and# i #ne# n :@sum (arcs(i,j):x(i,j)) = @sum (arcs(j,i):x(j,i))); @sum (arcs(i,j)| i #eq# 1 : x(i,j)) = 1;程序运行结果如下:Global optimal solution found.Objective value: 3.700000 Total solver iterations: 0Variable Value Reduced Cost N 5.000000 0.000000 C( 1, 2) 0.8000000 0.000000 C( 1, 3) 1.700000 0.000000 C( 1, 4) 2.800000 0.000000 C( 1, 5) 4.200000 0.000000 C( 2, 3) 0.9000000 0.0000001 1 1 12 2 23 3结束C( 2, 4) 1.800000 0.000000C( 2, 5) 2.900000 0.000000C( 3, 4) 1.100000 0.000000C( 3, 5) 2.000000 0.000000C( 4, 5) 1.400000 0.000000X( 1, 2) 1.000000 0.000000X( 1, 3) 0.000000 0.000000X( 1, 4) 0.000000 0.5000000X( 1, 5) 0.000000 0.5000000X( 2, 3) 0.000000 0.000000X( 2, 4) 0.000000 0.3000000X( 2, 5) 1.000000 0.000000X( 3, 4) 0.000000 0.5000000X( 3, 5) 0.000000 0.000000X( 4, 5) 0.000000 0.000000Row Slack or Surplus Dual Price1 0.000000 0.0000002 3.700000 -1.0000003 0.000000 -3.7000004 0.000000 -2.9000005 0.000000 -2.0000006 0.000000 -1.400000结论:从程序运行结果可见,设备应该在第一年年末卖出,在第二年初买入,在第四年末卖出,总费用最小,为3.7万元。
数学建模实验四

X1
X8
X9
Row Slack or Surplus Dual Price
1
2
3
4
5
6
7
8
9
10
11
3
4
5
6
7
8
9
10
11
问题三程序:
model:
max=4*x1+3*x2+3*x3+2*x4+3*x5+2*x6+1*x7+1*x8+2*x9;
Variable Value Reduced Cost
X1
X2
X3
X4
X5
X6
X7
X8
X9
Row Slack or Surplus Dual Price
1
2
3
4
5
6
7
8
9
10
11
问题三求解结果为目标函数值是16,此处6门课程分别是x1=x2=x3=x5=x7=x9=1,其余为零,学分最高为22,答案同问题二。
附录:
问题一程序
model:
min=x1+x2+x3+x4+x5+x6+x7+x8+x9;
x1+x2+x3+x4+x5>2;
x3+x5+x6+x8+x9>3;
x4+x6+x7+x9>2;
Model Class: PILP
Total variables: 9
数学建模作业北工大薛毅实验3.docx

第三次作业1.生产计划安排某公司使用三种操作装配三种玩具一玩具火车、玩具卡车和玩具汽车.对于二种操作可冃时间限制分别是每天430分钟、460分钟和420分钟,玩具火车、玩具代车和玩具汽车的单位收入分別是3美元、2美元和5美元•每辆玩具火车在三种操作的装配时间分別是1分钟、3分钟和1分钟•毎辆玩具K车和每辆玩具汽车相应的时间是(2,0,4)和(1,2,0)分钟(零时间表示不使用该项操作).(1)将间题建立成一个线性规划模型,确定最优的生产方案.(2)对于操作1,假定超过它当前每天43()分钟能力的任何附加时间必须依靠每小时50美元的加班获得•每小时成本包括劳动力和机器运行费两个方面. 对于操作1,使用加班在经济I:冇利吗?如果冇利,最多増加多少时间?(3)假定操作2的操作员已同意每天加班工作2小时,其加班费是45美元•小时.还有,操作自身的成本是•小时10美元.这项活动对于每天收入的实际结果是什么?(4)操作3需要加班时间吗?解:(1)设生产玩具火车、玩具卡车和玩具汽车的数量分别为XI, X2, X3,则H 标函数为:max Z=3X 1+2X2+5X3约朿条件:XI +2X2 +X3V 二4303X1 +2X3<=460XI +4X2 <=420Xl>=0; X2>=0; X3>=0输到ling。
里面的结果为;Global optimal solution found.Objective value:1350.000Infeasibilities: 0.000000Total solver iterations: 2Model Class: LPTotal variables: 3Non linear variables: 0Total constraints: 4Nonlinear constraints:Total non zeros:10Non linear non zeros:VariableValue Reduced CostXI0.000000 4.000000X2100.0000 0.000000X3230.00000.000000RowSlack or SurplusDual Price11350.0001.000000 2 0.000000 1.0000003 0.000000 2.000000420.000000.000000所以玩具火车、玩具卡车和玩具汽车的生产数量分别为:0、100. 230; 最大的收入为1350.(2)表明操作1每工作1分钟的利润是2美元,如果是要加50美元每小时的加工费的话,一定 是赚的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
整数规划和对策论模型实验作业一、基本实验1.工程安排问题三年内有五项工程可以考虑施工。
每项工程的期望收入和年度费用如表4.1.所示。
假定每一项已经选定的工程要在整个三年内完成。
目标是要选出使总收入达到最大的那些工程。
表4.1 每项工程期望收入和年度费用表(单位:千元)解:设0-1变量xi,i=1,2,3,4,5为工程i,i=1,2,3,4,5的投资情况。
Xi=0,说明i项目不投资,xi=1,说明对i项目进行投资。
目标项为:Max z=20*x1+40*x2+20*x3+15*x4+30*x5,约束条件为:5x1+ 4x2+3x3+7x4+ 8x5≤25,X1+ 7x2+9x3+4x4+ 6x5≤25,8x1+10x2+2x3+ x4+10x5≤25,@bin(xi),i=1,2,3,4,5.写成Lingo程序:Max =20*x1+40*x2+20*x3+15*x4+30*x5;5*x1+ 4*x2+3*x3+7*x4+ 8*x5<=25;X1+ 7*x2+9*x3+4*x4+ 6*x5<=25;8*x1+10*x2+2*x3+ x4+10*x5<=25;@bin(x1);@bin(x2);@bin(x3);@bin(x4);@bin(x5);运行结果见solution report-xueyunqiang-chapter4-1:从运行结果可知,对项目1、项目2、项目3、项目4投资,可使总收益最大为95万元。
2.固定费用问题一服装厂生产三种服装,生产不同种类的服装要租用不同的设备,设备租金和其他的经济参数如表4.2所示。
假定市场需求不成问题,服装厂每月可用人工工时为2000小时,该厂如何安排生产可使每月的利润最大?表4.2 服装厂设备租金和其他的经济参数解:设x1,x2,x3分别为生产西服,衬衫和羽绒服的数量。
目标函数(如果生产西服,收益中减去5000,如果生产衬衫,收益中减去2000,如果生产羽绒服,收益中减去3000.如果不生产,就不减去相应租金):Max z= (400-280)*x1+(40-30)*x2+(300-200)*x3-(x1#GT#0)*5000-(x3#GT#0)*2000-(x3#GT#0)*3000,约束条件为:5x1+x2+4x3≤2000,3x1≤300,0.5x2≤300,2x3≤300,X1,x2,x3取正整数。
写成Lingo程序:Max = (400-280)*x1+(40-30)*x2+(300-200)*x3-(x1#GT#0)*5000-(x2#GT#0)*2000-(x3#GT#0)*3000;5*x1+x2+4*x3<=2000;3*x1<=300;0.5*x2<=300;2*x3<=300;@gin(x1);@gin(x2);@gin(x3);程序为xueyunqiang-chapter4-2运行结果见xueyunqiang-chapter4-2:由运行结果可知,生产100件西服,生产600件衬衫,生产150件羽绒服,可使总收益最大,总收益为23000元。
3.串并联系统可靠性问题有一台电器由三个部件组成,这三个部件串联,假如有一个部件发生故障,电器就不能工作。
可以通过在每个部件里安装1到2个备份原件来提高该电器的可靠性(不发生故障的概率)。
表4.3列出了可靠性和成本费用。
假设制造该电器的已有资金共10万元,那么怎样来构造这件电器呢?表4.3 每种原件的可靠性及成本费用(单位:万元)解: 假设xij, i=1,2,3,j=1,2,3为部件i选择并联原件个数为j。
xij为0-1变量,xij=1表明部件i选择并联原件个数j,否则不选择。
则系统的总可靠性为各部件可靠性的乘积(xij=0时,指数值为1,对可靠值不影响):0.6x11*0.8x12*0.9x13*0.7x21*0.8x22*0.9x23*0.5x31*0.7x32*0.9x33目标函数为可靠性最高:Max z=0.6x11*0.8x12*0.9x13*0.7x21*0.8x22*0.9x23*0.5x31*0.7x32*0.9x33,限制条件为:X11+2x12+3x13+3x21+5x22+6x23+2x31+4x32+5x33≤10,X11+x12+x13=1,X21+x22+x23=1,X31+x32+x33=1,Xij=0 or 1.编写Lingo 程序:Max =@pow(0.6,x11)*@pow(0.8,x12)* @pow(0.9,x13)*@pow(0.7,x21)*@pow(0.8,x22)*@pow(0.9,x23)*@pow(0.5,x31)*@pow(0.7,x32)*@pow(0.9,x33);X11+2*x12+3*x13+3*x21+5*x22+6*x23+2*x31+4*x32+5*x33<=10;X11+x12+x13=1;X21+x22+x23=1;X31+x32+x33=1;@bin(x11);@bin(x12);@bin(x13);@bin(x21);@bin(x22);@bin(x23);@bin(x31);@bin(x32);@bin(x33);导入Lingo,见xueyunqiang-chapter4-3:运行结果见xueyunqiang-chapter4-3:由运行结果可知,x22=1,x21=1,x33=1.所以,最优方案为部件1选择2个并联元件;部件2选择1个并联元件;部件3选择3个并联元件;总费用为10万元,系统可靠性为0.504.4.二选一约束条件某汽车公司正在考虑生产3种类型的汽车:微型、中型和大型。
表4.4给出了每种汽车需要的资源及产生的利润。
目前有6000吨钢材和60000小时的劳动时间。
要生产一种在经济效益上可行的汽车,这种汽车必须至少生产1000辆。
试为该公司制定一个使生产利润达到最大的方案。
表4.4 3种汽车的资源和利润解:设x1,x2,x3分别为生产微型汽车、中型汽车和大型汽车的数量。
由于只要xi>0,必须大于1000,因此引入0-1决策变量y1,y2,y3,只要xi<1000,yi=0,反之yi=1.Yi=sign(xi-999), xi<1000,yi=0,不生产;反之yi=1,决策生产.整理规划问题:目标函数为:Max z= y1x1*2000+y2x2*3000+y3x3*4000,约束条件(s.t.):1.5x1y1+ 3x2y2+ 5x3y3≤6000,30x1y1+25x2y2+40x3y3≤60000,X1≥0,x2≥0,x3≥0,Y1=sign(x1-999),Y2=sign(x2-999),Y1=sign(x3-999).写成Lingo程序为:Max = y1*x1*2000+y2*x2*3000+y3*x3*4000;1.5*x1*y1+ 3*x2*y2+ 5*x3*y3<=6000;30*x1*y1+25*x2*y2+40*x3*y3<=60000;y1=@sign(x1-999);y2=@sign(x2-999);y1=@sign(x3-999);运行结果见xueyunqiang-chapter4-4根据分析结果可知,y2=1,y1=0,y3=0,所以生产中型汽车。
X2=2000,生产中型汽车2000辆。
故最优方案为生产2000辆中型汽车,总利润为6000000美元。
5.最小覆盖问题某市管辖6个区(区1-区6)。
这个市必须明确在什么地方修建消防站,在保证至少有一个消防站在每个区的15分钟(行驶时间)路程内的情况下,这个市希望修建的消防站最少。
表4.5给出了该市各个区之间行驶需要的时间(单位为分钟)。
这个市需要多少个消防站,以及他们的所在位置。
表4.5 该市各个区之间行驶需要的时间(单位:分钟)解:设xi,i=1,2,3,4,5,6为在小区i的建设情况,xi=1,表示在小区i建设消防站,xi=0表示小区i不建设。
Tij为小区i到小区j的时间,为了计算方便我们记如果tij<=15,则赋值1,如果tij>15,记为0.用到#LE#逻辑运算:要满足条件,即是使得上述tij*xi>=1,j=1,2,3,4,5,6.(易见至少有一项xi=1,如果xi=0,表明不建设消防站,相应与tij的乘积为0.要想满足要求,需要每一项乘积之和至少为1.)目标函数为建设消防站最少:Min z=x1+x2+x3+x4+x5+x6,约束条件为:6∑( tij#LE#15)*xi≥1,j=1,2,3,4,5,6 1i=Xi=0,1.写成Lingo程序:Min =x1+x2+x3+x4+x5+x6;x1+x2 >=1;x1+x2+x4 >=1;x3+x4 >=1;x3+x4+x5 >=1;x4+x5+x6>=1;x2+x5+x6>=1;@bin(x1);@bin(x2);@bin(x3);@bin(x4);@bin(x5);@bin(x6);运行结果见xueyunqiang-chapter4-5:可见,x2=1,x4=1,只需在小区2和小区4各建立一座消防站即可。
6.对策问题1在一次野餐会上,两个二人组在玩捉迷藏游戏。
共有四个隐藏地点(A,B,C,D),隐藏组的两个成员可以分别藏在四个地点的任何两个,搜寻组人有机会寻找任何两个地点。
如果他们都找到了隐藏组的二个人,搜寻组就可以得到一分奖励,假如没有把两个人都找到,他们就输一分。
其他情况下,结果是平局。
将这个问题表示成一个二人零和对策,求出搜寻最优搜寻策略和它们的赢得值。
解:对于四个隐藏地点(A,B,C,D),设隐藏策略为yi,Y1=(1,1,0,0),Y2=(1,0,1,0),Y3=(1,0,0,1),Y4=(0,1,1,0),Y5=(0,1,0,1),Y6=(0,0,1,1),其中1表示选中所对应的地点,0表示未选择所对应的地点。
搜寻策略为xi, x1=(1,1,0,0), x2=(1,0,1,0), x3=(1,0,0,1), x4=(0,1,1,0), x5=(0,1,0,1), x6=(0,0,1,1),则对于搜寻组的赢得值矩阵为:001100010010100001001100010010100001A -⎧⎫⎪⎪-⎪⎪⎪⎪-⎪⎪=⎨⎬-⎪⎪⎪⎪-⎪⎪-⎪⎪⎩⎭,隐藏组的赢得矩阵为-A 。
利用线性规划法求解:由于赢得矩阵中有0和-1,不能保证ω>0和ν>0.将赢得矩阵的每个元素加上2:221322212232122223221322212232122223A ⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪=⎨⎬⎪⎪⎪⎪⎪⎪⎪⎪⎩⎭求解问题化为两个互为对偶的线性规划问题: (P ’): min x1+x2+x3+x4+x5+x6 s.t. 3x1+2x2+2x3+2x4+2x5+x6≥1, 2x1+3x2+2x3+2x4+x5+2x6≥1, 2x1+2x2+3x3+x4+2x5+2x6≥1, 2x1+2x2+x3+3x4+2x5+2x6≥1,2x1+x2+2x3+2x4+3x5+2x6≥1, x1+2x2+2x3+2x4+2x5+3x6≥1,x1,x2, x3,x4,x5,x6≥0.(D’): may y1+y2+y3+y4+y5+y6s.t. 3y1+2y2+2y3+2y4+2y5+y6≥1,2y1+3y2+2y3+2y4+y5+2y6≥1,2y1+2y2+3y3+y4+2y5+2y6≥1,2y1+2y2+y3+3y4+2y5+2y6≥1,2y1+y2+2y3+2y4+3y5+2y6≥1,y1+2y2+2y3+2y4+2y5+3y6≥1,y1,y2, y3,y4,y5,y6≥0.写成Lingo程序:min =x1+x2+x3+x4+x5+x6;3*x1+2*x2+2*x3+2*x4+2*x5+x6>=1;2*x1+3*x2+2*x3+2*x4+x5+2*x6>=1;2*x1+2*x2+3*x3+x4+2*x5+2*x6>=1;2*x1+2*x2+x3+3*x4+2*x5+2*x6>=1;2*x1+x2+2*x3+2*x4+3*x5+2*x6>=1;x1+2*x2+2*x3+2*x4+2*x5+3*x6>=1;x1+x2+x3+x4+x5+x6=1;x1>=0;x2>=0;x3>=0;x4>=0;x5>=0;x6>=0;max =y1+y2+y3+y4+y5+y6;3*y1+2*y2+2*y3+2*y4+2*y5+y6<=1;2*y1+3*y2+2*y3+2*y4+y5+2*y6<=1;2*y1+2*y2+3*y3+y4+2*y5+2*y6<=1; 2*y1+2*y2+y3+3*y4+2*y5+2*y6<=1; 2*y1+y2+2*y3+2*y4+3*y5+2*y6<=1; y1+2*y2+2*y3+2*y4+2*y5+3*y6<=1; y1>=0;y2>=0;y3>=0;y4>=0;y5>=0;y6>=0;第一个规划求解:第二个规划求解:求解得到:111(,0,0,0,0,),442T x w ==111(,0,0,0,0,),442T y ν==故对策问题的解为:112,'20G G G V V V w ν====-= **1111*2(,0,0,0,0,)(,0,0,0,0,)44221111*2(,0,0,0,0,)(,0,0,0,0,)4422T TG T TG x V x y V y ======即对于隐藏组和搜寻组分别以1/2的概率选择A,B 和C,D(更确切的说是1/2的概率选择A,B,C,D 中任意两个,以1/2的概率选择另外两个),最后的结果是平局。
