数学建模之规划问题
数学建模目标规划方法

30
x1
2x1
12x2 x2
d1 d2
d1 d2
2500 140
x1
d
3
d3
60
a x (,)b
ij j
i
j 1
(i 1,2, , m)
绝对约束
x 0 ( j 1,2, , n) j
d , d 0 (l 1,2, , L) ll
非负约束
K
L
min Z
pk
(kl
d
l
kl
dl
)
k 1
l 1
n
c(l) x d d g ( l 1,2, , L)
三 目标规划方法
通过前面的介绍和讨论,我们知道,目标规划方法 是解决多目标规划问题的重要技术之一。
这一方法是美国学者查恩斯(A.Charnes)和库 伯(W.W.Cooper)于1961年在线性规划的基础上提 出来的。后来,查斯基莱恩(U.Jaashelainen)和李 (Sang.Lee)等人,进一步给出了求解目标规划问题 的一般性方法——单纯形方法。
34
4
所以目标规划模型为:
min Z p d p (7d 12d ) p (d d )
11
2
2
3
34
4
70x 120x d d 50000
1
2
1
1
x 1
d d 200
2
2
x d d 250
生产甲、乙两种产品,
数学建模中规划问题的MATLAB求解

min P ( x, M )
的最优解 x 也是原问题的最优解。
【例 2-10】求非线性规划问题的解
min f ( x) x1 x2 8
2 x1 x2 0 2 s.t. x1 x2 2 0 x , x 0 1 2
2 2
function g=test(x) M=50000; f=x(1)^2+x(2)^2+8; g=f-M*min(x(1),0)-M*min(x(2),0)-M*min(x(1)^2-x(2),0)... +M*abs(-x(1)-x(2)^2+2);
命令窗输入[x,y]=fminunc('test',rand(2,1))
第二章
规划问题的MATLAB求解
2.1 线性规划 2.2 非线性规划
2.3 整数规划
数学规划模型
序:
规划问题是常见的数学建模问题,离散系统的优化问题 一般都可以通过规划模型来求解。因此快速求解规划问题是 数学建模的基本素质。利用MATLAB提供的规划模型求解命 令,可以快速得到想要的结果。
2.1 线性规划
以下介绍外罚函数法,内罚函数法参考PPT“内罚函数 法”。
设规划模型为 min f ( x)
gi ( x ) 0, i 1 ~ r s.t. hi ( x ) 0, i 1 ~ s k ( x ) 0, i 1 ~ t i
取充分大的数 M 0 ,构造函数 P ( x , M ) f ( x ) M max( g i ( x ), 0) M min( hi ( x ), 0)
数学建模测试题-线性规划部分
313数学教育1、2班,510数学教育1、2、3班数学建模上机测试题,需要把运行结果写出来。
模型包括目标函数、约束条件,编写的程序和程序运行结果四部分内容。
写在作业本上。
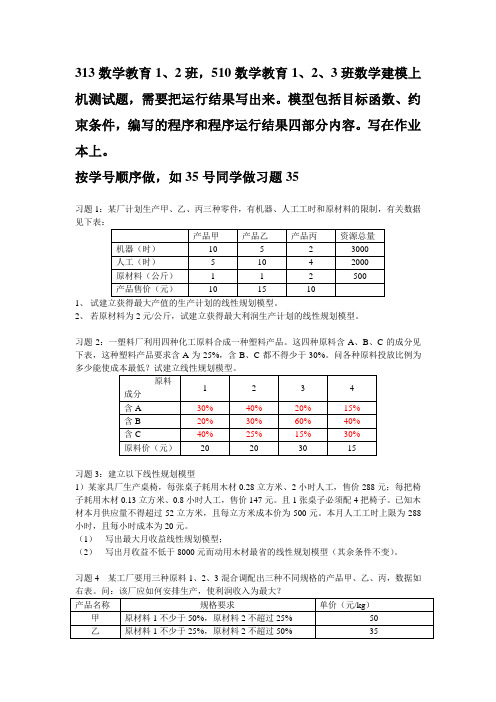
按学号顺序做,如35号同学做习题35习题1:某厂计划生产甲、乙、丙三种零件,有机器、人工工时和原材料的限制,有关数据1、2、若原材料为2元/公斤,试建立获得最大利润生产计划的线性规划模型。
习题2:一塑料厂利用四种化工原料合成一种塑料产品。
这四种原料含A、B、C的成分见下表,这种塑料产品要求含A为25%,含B、C都不得少于30%。
问各种原料投放比例为习题3:建立以下线性规划模型1)某家具厂生产桌椅,每张桌子耗用木材0.28立方米、2小时人工,售价288元;每把椅子耗用木材0.13立方米、0.8小时人工,售价147元。
且1张桌子必须配4把椅子。
已知木材本月供应量不得超过52立方米,且每立方米成本价为500元。
本月人工工时上限为288小时,且每小时成本为20元。
(1)写出最大月收益线性规划模型;(2)写出月收益不低于8000元而动用木材最省的线性规划模型(其余条件不变)。
习题4 某工厂要用三种原料1、2、3混合调配出三种不同规格的产品甲、乙、丙,数据如右表。
问:该厂应如何安排生产,使利润收入为最大?习题5、某部门现有资金200万元,今后五年内考虑给以下的项目投资。
已知:项目A :从第一年到第五年每年年初都可投资,当年末能收回本利110%;项目B :从第一年到第四年每年年初都可投资,次年末能收回本利125%,但规定每年最大投资额不超过30万元;项目C :需在第三年年初投资,第五年末能收回本利140%,但规定最大投资额不能超过80万元;项目D :需在第二年年初投资,第五年末能收回本利155%,但规定最大投资额不能超过100万元;问:a.应如何确定这些项目的每年投资额,使得第五年年末拥有资金的本利金额为最大? b.应如何确定这些项目的每年投资额,使得第五年年末拥有资金的本利在330万元的基础上使得其投资总的风险系数为最小?习题6 某公司计划在三年的计划期内,有四个建设项目可以投资:项目Ⅰ从第一年到第三年年初都可以投资。
数学建模lingo作业-习题讲解

基础题:1.目标规划问题最近,某节能灯具厂接到了订购16000套A 型和B 型节能灯具的订货合同,合同中没有对这两种灯具的各自数量做要求,但合同要求工厂在一周内完成生产任务并交货。
根据该厂的生产能力,一周内可以利用的生产时间为20000min ,可利用的包装时间为36000min 。
生产完成和包装一套A 型节能灯具各需要2min ;生产完成和包装完成一套B 型节能灯具各需要1min 和3min 。
每套A 型节能灯成本为7元,销售价为15元,即利润为8元;每套B 型节能灯成本为14元,销售价为20元,即利润为6元。
厂长首先要求必须按合同完成订货任务,并且即不要有足量,也不要有超量。
其次要求满意销售额达到或者尽量接近275000元。
最后要求在生产总时间和包装总时间上可以有所增加,但过量尽量地小。
同时注意到增加生产时间要比包装时间困难得多。
试为该节能灯具厂制定生产计划。
解:将题中数据列表如下:根据问题的实际情况,首先分析确定问题的目标级优先级。
第一优先级目标:恰好完成生产和包装完成节能灯具16000套,赋予优先因子p1;第二优先级目标:完成或者尽量接近销售额为275000元,赋予优先因子p2; 第三优先级目标:生产和包装时间的增加量尽量地小,赋予优先因子p3; 然后建立相应的目标约束。
在此,假设决策变量12,x x 分别表示A 型,B 型节能灯具的数量。
(1) 关于生产数量的目标约束。
用1d -和1d +分别表示未达到和超额完成订货指标16000套的偏差量,因此目标约束为1111211min ,..16000z d d s t x x d d -+-+=+++-=要求恰好达到目标值,即正、负偏差变量都要尽可能地小(2) 关于销售额的目标约束。
用2d -和2d +分别表示未达到和超额完成满意销售指标275000元的偏差值。
因此目标约束为221222min ,..1520-275000.z d s t x x d d --+=++=要求超过目标值,即超过量不限,但必须是负偏差变量要尽可能地小,(另外:d +要求不超过目标值,即允许达不到目标值,就是正偏差变量要尽可能地小) (3) 关于生产和包装时间的目标约束。
数学建模公交线路规划问题

3. 我校教职员工、学生的出行特点:上班、上课我校师生往返两校区的首要需求,结合我校教职 员工、学生的居住分布特点,因此我校教职员工、学生的出行特点十分明显,表现为时间空间 上的集中,具体特征如下: (1) 时间特点:上下课、上下班时间段(沙河校区—清水河校区:7:20、9:10、13:20、 15:10 、 18:20 ;清水河校区 — 沙河校区: 10:30 、 12:20 、 16:30 、 18:20 、 22 : 20)出行人数骤增,其他时间段出行人数较少,甚至没有。 (2) 路线特点:起点、终点绝大多数为清水河校区、沙河校区两站。 本着 “保障教学科研工作开展, 满足师生往返两校” 的原则, 利用快速公交系统 (Bus Rapid Transit ——BRT)的便利因素、技术特点,结合我校师生出行特点,统筹便利性、社会效益、经济效益, 兼顾公交公司利益,进行方案制定。 2.1 线路选择 本线路以服务科大师生往返新老校区为初衷,所以在选择线路时,要使往返新老校区的时间最 短。由于交管部门数据不足,本文忽略由路况产生的拥塞、限速等情况,即认为路径最短时间最短。 2.2 站点设置 对于选择好的公交线路,在普通时段,与普通公交相同,按既定站点运行。在我校师生集中出 行时段,采用线路组合,即线路组合这种调度方式。首先我们对线路调度进行说明。 2.2.1 线路组合 此调度方式从普通线路按既定站点运行,站站停靠的方式派生出来。线路组合分标准线路、大 站快线、直达线路 ,并根据客流情况选择不同的方式(标准线路、大站快线、直达线路) 。它适用 于客流量大且集中,同时适用于开发分散的市郊区域。 其次对标准线路、大站快线、直达线路三种调度方式进行说明。 (1)标准线路:与普通公交线路相同,每站都停。
摘要
为配合我校和成都市公交规划部门,开设往返新老校区的快速公交线路。以高效便捷地保障广 大师生往返两校的交通需求。 本文解决了该公交线路的路线走向、站点设置、运行时长,发车间隔等设计问题,分析了拟定 的方案对学校的校车运行方案的影响,并作为向公交公司提供的策划论证的技术材料。本设计运用 Dijskra 算法,寻找到最快捷的路线走向。引入站点选择向量,发车间隔两个变量,结合客流量 OD 矩阵和站点距离矩阵,从出行时间成本和线路运营成本两个方面建立目标函数,运用遗传算法,求 解使目标函数最小的站点选择向量和发车间隔。 设计方案为:路线走向,沙河校区,一环路、蜀汉路、蜀西路、土龙路、金辉路、西源大道至 清水河校区。设置站点:电子科技大学沙河校区、苏宁电器建设路店、萤门口立交桥、蜀西路、土 龙路、金辉路、电子科大清水河校区。运行时间:7:30 首发车,21:30 末班车,共 14 小时。发车 间隔:11.43 分钟。
数学建模——规划问题

3.5 习题P 54.2.某工厂用21.A A 两台机床加工B B B 321,,三种不同零件。
已知在一个生产周期内A 1只能工作80机时;A 2只能工作100机时。
一个生产周期内计划加工B 1为70件、B 2为50件、B 3为20件。
两台机床加工每个零件的时间和加工每个零件的成本,分别如下列各表所示:加工每个零件时间表(单位:机时/个)加工每个零件成本表(单位:元/个)问:怎么样安排两台机床一个周期的加工任务,才能使加工成本最低?解:设在A 1机床加工零件B B B 321,,的数量分别为x x x 321,,,在A 2机床加工零件B B B 321,,的数量分别为x x x 654,,,建立如下线性规划模型:x x x x x x Z 654321633532min +++++=s.t.6,5,4,3,2,1,020507010038032635241654321=≥=+=+=+≤++≤++i x x x x x x x x x x x x x i改写成:[]⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=654321633532min x x x x x x Zs.t. 020507010010001001000100110080311000000321654321654321654321≥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡≤⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡x x x x x x x x x x x x x x x x x x结果: 解得7,0,40,0,25,30654321======x x x x x x297760340305253302min =⨯+⨯+⨯+⨯+⨯+⨯=Z 即机床A 1在一个周期加工零件B B B 321,,的数量分别为30件,25件,0件;A 2机床加工零件B B B 321,,的数量分别为40件,0件,7件;加工成本最低为297元。
数学建模作业数学规划模型----供应与选址的问题

再编写主程序liaochang2.m为:
clear
x0=[3 5 4 7 1 0 0 0 0 0 5 11 5 4 7 7];
A=[1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0];
B=[20;20];
Aeq=[1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0
0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0];
使用临时料场的情形:
使用两个临时料场A(5,1),B(2,7).求从料场j向工地 的运送量 .在各工地用量必须满足和各料场运送量不超过日储量的条件下,使总的吨千米数最小,这是线性规划问题。线性规划模型为:
其中 ,i=1,2,…,6,j=1,2,为常数
设X11=X1,X21=X 2,,X31=X 3,X41=X 4,X51=X 5,,X61=X 6
程序截图如下:
程序的运行结果为:
xx =
3.0000
5.0000
0.0000
7.0000
0.0000
1.0000
0.0000
0.0000
4.0000
0.0000
6.0000
10.0000
fval =
136.2275
运行结果截图如下:
即由料场A、B向6个工地运料方案为:
数学建模-整数规划

整数规划
Integer Programming
数信学院 任俊峰
2012-4-15
数学建模之整数规划
整数规划模型(IP)
如果一个数学规划的某些决策变量或全部决策 变量要求必须取整数,则称这样的问题为整数规 划问题,其模型称为整数规划模型。 如果整数规划的目标函数和约束条件都是线性 的,则称此问题为整数线性规划问题.
松弛问题最优解满足整数要求,则该最优解为整数 规划最优解;
数学建模之整数规划
整数线性规划的求解方法
从数学模型上看整数规划似乎是线性规划的 一种特殊形式,求解只需在线性规划的基础上,通 过舍入取整,寻求满足整数要求的解即可。 但实际上两者却有很大的不同,通过舍入得到
的解(整数)也不一定就是最优解,有时甚至不能
1 xj 0
选中第j个项目投资 不 选中第j个项目投资
max Z 160 x 1 210 x 2 60 x 3 80 x 4 180 x 5 210 x 1 300 x 2 150 x 3 130 x 4 260 x 5 600 x x2 x3 1 1 x3 x4 1 x x 1 5 x1 , x 2 , x 3 , x 4 , x 5 0 或 1
1 2
14 x1 9 x 2 51 6 x1 3 x 2 1 x1 , x 2 0
数学建模之整数规划
用图解法求出最优解 x1=3/2, x2 = 10/3 且有 z = 29/6 现求整数解(最优解): 如用“舍入取整法”可得到4 个点即(1,3) (2,3) (1,4) (2,4)。显然,它们都不可能 是整数规划的最优解。
数学建模之整数规划
例5 固定费用问题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、线性规划
1.简介
1.1适用情况
用现有资源来安排生产,以取得最大经济效益的问题。
如: (1)资源的合理利用
(2)投资的风险与利用问题 (3)合理下料问题 (4)合理配料问题 (5)运 输 问 题 (6)作物布局问题
(7)多周期生产平滑模型 (8)公交车调度安排 1.2建立线性规划的条件
(1)要求解问题的目标函数能用数值指标来反映,且为线性函数;
(2)要求达到的目标是在一定条件下实现的,这些约束可用线性等式或不等式描述。
1.3线性规划模型的构成
决策变量、目标函数、约束条件。
2、一般线性规划问题 数学标准形式:
目标函数:
1
max ==
∑ n
j
j
j z c
x
约束条件:1
,1,2,...,,..0,1,2,...,.=⎧==⎪⎨⎪≥=⎩∑n
ij j i j j
a x
b i m s t x j n
matlab 标准形式:
3、可以转化为线性规划的问题 例:求解下列数学规划问题
解:作変量変换1||||,,1,2,3,4,22
+-===i i i i
i x x x x u v i 并把新变量重新排序成一维变量
[]1414,,,,
,⎡⎤
==⎢⎥⎣⎦
T
u y u u v v v ,则可把模型转化为线性规划模型
其中:[]1,2,3,4,1,2,3,4;=T c 12,1,;2⎡⎤=---⎢⎥⎣
⎦T
b 111111131 - - ⎡⎤
⎢⎥= - -⎢⎥⎢⎥ -1 -1 3⎣⎦
A 。
利用matlab 计算得最优解:12342,0,=-===x x x x 最优值z=2。
程序如下: 略
二、整数规划 1.简介
数学规划中的变量(部分或全部)限制为整数时称为整数规划。
目前流行求解整数规划的方法一般适用于整数线性规划。
1.1整数规划特点
1)原线性规划有最优解,当自变量限制为整数后,出现的情况有
①原线性规划最优解全是整数,则整数规划最优解与线性规划最优解一致。
②整数规划无可行解。
③有可行解(存在最优解),但最优解值变差。
2)整数规划最优解不能按照实数最优解简单取整获得。
1.2求解方法分类
(1)分枝定界法—可求纯或混合整数线性规划。
(2)隔平面法—可求纯或混合整数线性规划。
(3)隐枚举法—可求“0-1”整数规划。
(4)匈牙利法—解决指派问题。
(5)蒙特卡洛法—求解各种类型规划. 1.3整数规划的应用模型 (1)固定费用的问题。
(2)指派问题。
(3)合理下料问题。
(4)流动推销员问题。
(5)生产与销售计划问题。
2、一般整数规划模型
目标函数: 约束条件:
例:指派问题的数学模型(0-1型整数规划)
拟分配n 人去做n 项工作,若分配第i 人去做第j 项工作,需花费ij c 单位时间,如何分配工作才能使花费总时间最少? 模型的建立
引入0-1变量1,i j 0第人做第项工作,
,第i 人不做第j 项工作.
⎧=⎨⎩ij x
指派问题的数学模型为
利用匈牙利算法、拍卖算法等求解出最优解。
三、非线性规划 1、简介
目标函数或约束条件中包含非线性函数的规划问题为非线性规划问题。
1.1非线形规划模型的构成
决策变量、目标函数、约束条件。
1.2非线性规划的应用模型
(1)存贮模型
(2)飞行管理问题 (3)森林救火
(4)抽水费用最小问题 (5)钢管下料问题 (6)投资决策问题 (7)供应与选址问题 (8)广告的费用及其效用 2、非线性规划的模型 一般形式: 其中:[]1,
,=T
n x x x 为模型的决策变量。
Matlab 中非线性规划的数学模型
其中:f(x)是标量函数;A,b,Aeq,beq,lb,ub 是相应维数的矩阵和向量;c(x),cex(x)是非线性向量函数。
3、罚函数法
利用罚函数法可将非线性规划问题的求解转化为求解一系列无约束极值问题。
问题
取一个充分大的数M>0,构造函数
(或()()(,)()max min ||()||,00m G x H x p x M f x Msum Msum M k x ⎛⎫⎛⎫
⎛⎫⎛⎫=+-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭这里
[][][]111()(),
,(),()(),
,(),()(),
,(),r s t G x g x g x H x h x h x K x k x k x ===可直接利用matlab
中的max 、min 和sum 函数),则增广目标函数P(x,M)为目标函数的无约束极值问题
minP(x,M)的最优解x 即为原问题的最优解。
注意:
1)如果非线性规划问题要求实时算法,则可用罚函数法,但计算精度较低。
2)如果非线性规划问题不要求实时算法,但要求精度高,可使用Lingo 软件编程求解或使用Matlab 的fmincon 命令求解。
四、目标规划 1、简介
1.1求解目标规划的思路
(1)加权系数法
为每一目标赋一个权系数,把多目标模型转化成单一目标的模型。
但困难是要确定合理的权系数,以反映不同目标之间的重要程度。
(2)优先等级法
将各目标按其重要程度不同的优先等级,转化为单目标模型。
(3)有效解法
寻求能够照顾到各个目标,并使决策者感到满意的解。
由决策者来确定选取哪一个解,即得到一个满意解。
但有效解的数目太多而难以将其一一求出。
1.2建立目标规划的条件
(1)正、负偏差变量。
(2)绝对(刚性)约束和目标约束。
(3)优先因子(优先等级)与权系数。
1.3 目标规划的目标函数
目标规划的目标函数基本三种形式为
(1)第i 个目标要求恰好达到目标值,即正、负偏差变量都要尽可能地小,这时
i i i i min w d w d --++ +.
(2)第i 个目标要求不超过目标值,即允许达不到目标值,就是正偏差变量要尽可能地小,这时
(3)第i 个目标要求超过目标值,即超过量不限,但必须是负偏差变量要尽可能地小,这时
1.4目标规划的模型应用
(1)求多目标下产品利润最优的决策方案。
(2)求多目标下总运费最小的运输调度方案。
2、目标规划的一般数学模型
设(1,2,
,)j x j n =是目标规划的决策变量,共有m 个约束是刚性约束,可能
是等式约束,也可能是不等式约束。
设有l 个柔性目标约束,其目标规划约束的偏差为,(1,2,
,)i i d d i l +-=。
设有q 个优先级别,分别为12,,,q p p p ⋯。
在同一
个优先级k p 中,有不同的权重,分别记为,(1,2,,)ki
ki w w i l +-=。
目标规划模型的
一般数学表达式如下
可用序贯算法求解目标规划。
3、数据包网络分析(DEA ) 3.1适用范围
DEA 特别适用于具有多输入多输出的复杂系统,如技术进步、技术创新、资源配置、金融投资等领域,特别对非单纯利益公共部门,如学校、医院、某些文化设施的评价方面。
3.2特点
1)DEA 以决策单位各输入/输出的权重为变量, 1)数据包络分析的C2R 模型 设有n 个DMU ,每个DMU 都有m 种投入和s 种产出,设1,
,;1,,ij x i m j n ==()表示第
j 个DMU 的第i 种投入量, 1,,1,,rj y r s j n ==(;)表示第 j 个DMU 的第r 种产出量,(1,
,)i v i m =表示第i 种投入的权值,1,
,r u r s =()表示第r 种产出的权值。
向量,(1,
,)j j X Y j n =分别表示决策单元 j 的输入和输出向量,v 和u 分别表示输入输
出权值向量,则12(,,
,)T j j j mj X x x x =,12(,,,),T j j j sj Y x x x =12(,,,)T m u u u u =,
12(,,
,)T S v v v v =。
定义决策单元j 的效率评价指数为
评价决策单元0j 效率的数学模型为
00
max
,
1,1,2,,,..0,0,0,0.
T j T
j T j
T
j
u Y v X u Y j n s t v X u v u v ⎧≤=⎪⎨⎪
≥≥≠≠⎩ (1) 通过Charnes ?Cooper 变换:01
,,()
T j tv tu t v X ωμ===可以将模型(1)转化为等
价的线性规划问题
对于C2R 模型,有如下定义:
(1)若线性规划问题的最优目标01j v =,则称决策单元0j 是弱DEA 有效的。
(2)若线性规划问题存在最优解**0,0,μω>>并且其最优目标值01j V =,则称决策单元0j 是EDA 有效的。
