数学建模(整数规划)
整数规划和动态规划-数学建模

(1.13), (1.14)
max z = ∑ (0.487xi1 + 0.520 xi2 + 0.613 xi3 + 0.720 xi 4 + 0.487 xi 5 + 0.520 xi 6 + 0.640 xi 7 )
i =1
2
于是成为一个有 13 个不等式约束 14 个自然条件的整数线性规划模型,目标是函数 的最大化. (3)问题求解 1) 此模型可用分枝定界法,割平面法求最优解,但用部分枚举法比较便当. 部分枚举法————隐枚举法(Implicit Enumeration) 2) 用 Lingo 软件求解 max=0.487*x11+0.520*x12+0.613*x13+0.720*x14+0.487*x15+0.520*x16+0.640*x17+ 0.487*x21+0.520*x22+0.613*x23+0.720*x24+0.487*x25+0.520*x26+0.640*x27; x11+x21<=8; x12+x22<=7; x13+x23<=9; x14+x24<=6; x15+x25<=6; x16+x26<=4; x17+x27<=8; 2*x11+3*x12+x13+0.5*x14+4*x15+2*x16+x17<=40;
西安理工大学理学院
王秋萍
x13 + x23 ≤ 9 x14 + x24 ≤ 6 x15 + x25 ≤ 6 x16 + x26 ≤ 4 x17 + x27 ≤ 8
数学建模中的整数规划与混合整数规划

数学建模作为一种解决实际问题的方法,旨在从实际问题中抽象出数学模型,并运用数学方法来对模型进行分析和求解。
在数学建模过程中,整数规划与混合整数规划是两种常用的数学工具,适用于解决许多实际问题。
整数规划是指在约束条件下,目标函数为整数变量的线性规划问题。
而混合整数规划是在整数规划的基础上,允许部分变量为实数,部分变量为整数。
这两种规划方法可以广泛应用于许多领域,如物流、生产规划、资源分配等。
整数规划的一个经典问题是背包问题。
假设有一个容量为C的背包,有n个物品,每个物品有自己的重量w和价值v。
目标是在不超过背包容量的情况下,选择装入背包的物品,使得背包中的物品总价值最大化。
这个问题可以用整数规划的方式进行建模和求解,将每个物品视为一个二进制变量,表示是否选择该物品,目标函数为物品价值的总和,约束条件为背包容量不能超过C。
通过对目标函数和约束条件的线性化处理,可以得到整数规划模型,并利用整数规划算法进行求解,得到最优解。
混合整数规划在实际问题中更为常见。
一个典型的实际问题是运输网络设计问题。
假设有一组供应地和一组需求地,需要建立供需之间的运输网络,以满足需求地对各种商品的需求,同时要考虑供给地的产能限制和运输成本。
这个问题可以用混合整数规划的方法进行建模和求解。
将供需地视为节点,建立连通性矩阵表示供需之间的运输路径,将路径的运输量作为决策变量,目标函数可以是运输成本的最小化,约束条件可以包括供给地产能限制和需求地需求量的满足。
通过对目标函数和约束条件的线性化处理,可以得到混合整数规划模型,并利用相应的求解算法进行求解,得到最优的运输网络设计方案。
整数规划与混合整数规划在数学建模中起着重要的作用。
它们既具备一般整数规划问题的优点,可以提高问题的精度和可行性,又具备一般线性规划问题的优点,可以通过线性规划算法来求解。
同时,整数规划与混合整数规划也存在一些挑战,如求解时间长、难以处理大规模问题等。
对于这些问题,研究者们一直在不断提出新的算法和优化方法,以提高整数规划与混合整数规划的求解效率。
数学建模——混合整数规划
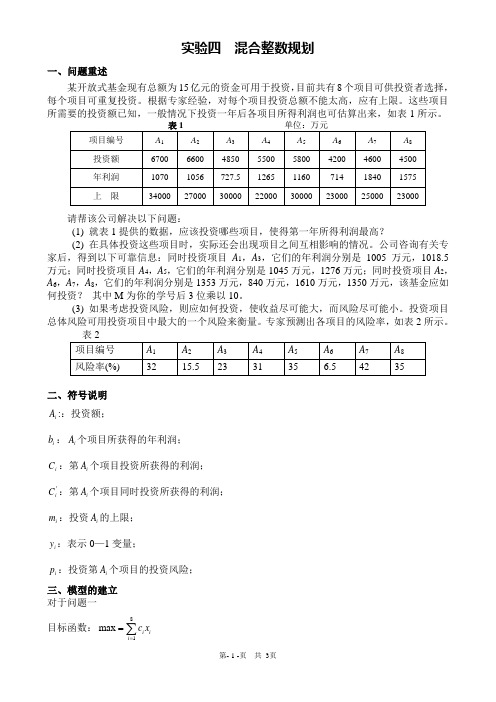
实验四 混合整数规划一、问题重述某开放式基金现有总额为15亿元的资金可用于投资,目前共有8个项目可供投资者选择,每个项目可重复投资。
根据专家经验,对每个项目投资总额不能太高,应有上限。
这些项目所需要的投资额已知,一般情况下投资一年后各项目所得利润也可估算出来,如表1所示。
请帮该公司解决以下问题:(1) 就表1提供的数据,应该投资哪些项目,使得第一年所得利润最高?(2) 在具体投资这些项目时,实际还会出现项目之间互相影响的情况。
公司咨询有关专家后,得到以下可靠信息:同时投资项目A 1,A 3,它们的年利润分别是1005万元,1018.5万元;同时投资项目A 4,A 5,它们的年利润分别是1045万元,1276万元;同时投资项目A 2,A 6,A 7,A 8,它们的年利润分别是1353万元,840万元,1610万元,1350万元,该基金应如何投资? 其中M 为你的学号后3位乘以10。
(3) 如果考虑投资风险,则应如何投资,使收益尽可能大,而风险尽可能小。
投资项目总体风险可用投资项目中最大的一个风险来衡量。
专家预测出各项目的风险率,如表2所示。
二、符号说明i A ::投资额;i b :i A 个项目所获得的年利润;i C :第i A 个项目投资所获得的利润; 'i C :第i A 个项目同时投资所获得的利润;i m :投资i A 的上限; i y :表示0—1变量;i p :投资第i A 个项目的投资风险;三、模型的建立 对于问题一目标函数:81max i i i c x ==∑s.t. 150000i i i i i ib x b x m ⎧≤⎪⎨⎪≤⎩∑对于问题二 设定0—1变量131130...,1...,A A y A A ⎧⎨⎩项目不同时投资项目同时投资 452450...,1...,A A y A A ⎧⎨⎩项目不同时投资项目同时投资 2678326780...,,1...,,A A A A y A A A A ⎧⎨⎩,项目不同时投资,项目同时投资 目标函数:''''11133111332445524455''''322667788322667788max ()(1)()()(1)()()(1)()y x c x c y x c x c y x c x c y x c x c y x c x c x c x c y x c x c x c x c =++-++++-++++++-+++s.t. 11313124545232678267831500001000i i i i i ib x k y x xx x y ky x x x x y k y x x x x x x x x y kb x m ⎧≤⎪⎪=⎪⎪≤⎪⎪≥⎪⎪≤⎨⎪⎪≥⎪⎪≤⎪⎪≥⎪⎪≤⎩∑对于问题三:目标函数:max min max()i iii i i c x b x p =∑s.t. 150000i i i i i ib x b x m ⎧≤⎪⎨⎪≤⎩∑对于问题三模型的简化固定投资风险,优化收益,设a 为固定的最大风险。
数学建模线性规划和整数规划实验

1、线性规划和整数规划实验1、加工奶制品的生产计划(1)一奶制品加工厂用牛奶生产A1, A2两种奶制品,1桶牛奶可以在甲车间用12小时加工成3千克A1产品,或者在乙车间用8小时加工成4千克A2 产品.根据市场需求,生产的A1、A2产品全部能售出,且每千克A1产品获利24元,每千克A2产品获利16元.现在加工厂每天能得到50桶牛奶的供应,每天正式工人总的劳动时间为480小时,并且甲车间的设备每天至多能加工100 千克A1产品,乙车间的设备的加工能力可以认为没有上限限制.试为该厂制订一个生产计划,使每天获利最大,并进一步讨论以下3个附加问题: (i)若用35元可以买到1桶牛奶,是否应作这项投资?若投资,每天最多购买多少桶牛奶?(ii)若可以聘用临时工人以增加劳动时间,付给临时工人的工资最多是每小时几元?(iii)由于市场需求变化,每千克A1产品的获利增加到30元,是否应改变生产计划?(2)进一步,为增加工厂获利,开发奶制品深加工技术.用2小时和3元加工费,可将1千克A1加工成0.8千克高级奶制品B1,也可将1千克A2加工成0.75千克高级奶制品B2,每千克B1可获44元,每千克B2可获32元.试为该厂制订一个生产销售计划,使每天获利最大,并进一步讨论以下问题:(i)若投资30元可增加供应1桶牛奶,投资3元可增加1小时劳动时间,是否应作这项投资?若每天投资150元,或赚回多少?(ii)每千克高级奶制品B1, B2的获利经常有10%的波动,对制订的生产销售计划有无影响?若每千克B1的获利下降10%,计划是否应作调整?解:由已知可得1桶牛奶,在甲车间经过十二小时加工完成可生产3千克的A1,利润为72元;在乙车间经八小时加工完成可生产四千克的A2,利润为64元。
利用lingo软件,编写如下程序:model:max=24*3*x1+16*4*x2;s.t.12*x1+8*x2≤480;x1+x2≤50;3*x1≤100;X1≥0,x2≥0end求解结果及灵敏度分析为:Objective value: 3360.000Total solver iterations: 2Variable Value Reduced CostX1 20.00000 0.000000X2 30.00000 0.000000Row Slack or Surplus Dual Price1 3360.000 1.0000002 0.000000 2.0000003 0.000000 48.000004 40.00000 0.000000Objective Coefficient RangesCurrent Allowable Allowable Variable Coefficient Increase DecreaseX1 72.00000 24.00000 8.000000X2 64.00000 8.000000 16.00000Righthand Side RangesRow Current Allowable AllowableRHS Increase Decrease2 480.0000 53.33333 80.000003 50.00000 10.00000 6.6666674 100.0000 INFINITY 40.00000 分析结果:1)从结果可以看出在供应甲车间20桶、乙车间30桶的条件下,获利可以达到最大3360元。
数学建模线性规划与整数规划

数学建模线性规划与整数规划数学建模是一门将实际问题转化为数学问题,并利用数学方法解决的学科。
线性规划和整数规划是数学建模中常用的两种模型,它们在实际问题中有着广泛的应用。
本文将重点介绍线性规划和整数规划的概念、模型形式以及求解方法。
一、线性规划(Linear Programming)线性规划是一种在约束条件下求解线性目标函数最优解的数学模型,它的基本形式可以表示为:Min(或Max):C₁X₁ + C₂X₂ + ... + CₙXₙSubject to:A₁₁X₁ + A₁₂X₂ + ... + A₁ₙXₙ ≤ b₁A₂₁X₁ + A₂₂X₂ + ... + A₂ₙXₙ ≤ b₂...Aₙ₁X₁ + Aₙ₂X₂ + ... + AₙₙXₙ ≤ bₙX₁, X₂, ... , Xₙ ≥ 0在上述模型中,C₁,C₂,...,Cₙ为目标函数的系数,Aᵢₙ为不等式约束条件的系数,bᵢ为不等式约束条件的右端常数,X₁,X₂,...,Xₙ为决策变量。
线性规划的求解可以通过单纯形法或内点法等算法实现。
通过逐步优化决策变量的取值,可以得到满足约束条件并使目标函数达到最优的解。
二、整数规划(Integer Programming)整数规划是在线性规划基础上增加了决策变量必须取整的要求,其模型形式为:Min(或Max):C₁X₁ + C₂X₂ + ... + CₙXₙSubject to:A₁₁X₁ + A₁₂X₂ + ... + A₁ₙXₙ ≤ b₁A₂₁X₁ + A₂₂X₂ + ... + A₂ₙXₙ ≤ b₂...Aₙ₁X₁ + Aₙ₂X₂ + ... + AₙₙXₙ ≤ bₙX₁, X₂, ... , Xₙ ≥ 0X₁,X₂,...,Xₙ为整数整数规划在实际问题中常用于需要求解离散决策问题的情况,如装配线平衡、旅行商问题等。
然而,由于整数规划问题的整数约束,其求解难度大大增加。
求解整数规划问题的方法主要有分支定界法、割平面法、遗传算法等。
数学建模常用的30个常用算法(python代码)

数学建模常用的30个常用算法(python代码) 数学建模中使用的算法涉及多个领域,包括优化、统计、机器学习等。
以下是一些在数学建模中常用的30个算法的简要说明和Python代码示例。
请注意,这只是一小部分,具体应用场景和需求可能需要使用其他算法。
1.线性规划(Linear Programming):from scipy.optimize import linprog2.整数规划(Integer Programming):from scipy.optimize import linprog3.非线性规划(Nonlinear Programming):from scipy.optimize import minimize4.蒙特卡洛模拟(Monte Carlo Simulation):import numpy as np5.差分方程(Difference Equations):import numpy as np6.梯度下降法(Gradient Descent):import numpy as np7.贪心算法(Greedy Algorithm):def greedy_algorithm(values, weights, capacity):n = len(values)ratio = [(values[i] / weights[i], i) for i in range(n)]ratio.sort(reverse=True)result = [0] * ntotal_value = 0current_weight = 0for _, i in ratio:if weights[i] + current_weight <= capacity: result[i] = 1current_weight += weights[i]total_value += values[i]return result, total_value8.动态规划(Dynamic Programming):def dynamic_programming(weights, values, capacity): n = len(values)dp = [[0] * (capacity + 1) for _ in range(n + 1)]for i in range(1, n + 1):for w in range(capacity + 1):if weights[i - 1] <= w:dp[i][w] = max(dp[i - 1][w], values[i - 1] + dp[i - 1][w - weights[i - 1]])else:dp[i][w] = dp[i - 1][w]return dp[n][capacity]9.遗传算法(Genetic Algorithm):import numpy as np10.模拟退火算法(Simulated Annealing):import numpy as np11.马尔可夫链(Markov Chains):import numpy as np12.蒙特卡洛树搜索(Monte Carlo Tree Search):import numpy as np13.K均值聚类(K-means Clustering):from sklearn.cluster import KMeans14.主成分分析(Principal Component Analysis):from sklearn.decomposition import PCA15.支持向量机(Support Vector Machine):from sklearn.svm import SVC16.朴素贝叶斯分类器(Naive Bayes Classifier):from sklearn.naive_bayes import GaussianNB17.决策树(Decision Tree):from sklearn.tree import DecisionTreeClassifier18.随机森林(Random Forest):from sklearn.ensemble import RandomForestClassifier19.K最近邻算法(K-Nearest Neighbors):from sklearn.neighbors import KNeighborsClassifier20.多层感知器(Multilayer Perceptron):from sklearn.neural_network import MLPClassifier21.梯度提升机(Gradient Boosting):from sklearn.ensemble import GradientBoostingClassifier22.高斯混合模型(Gaussian Mixture Model):from sklearn.mixture import GaussianMixture23.时间序列分析(Time Series Analysis):import statsmodels.api as sm24.马尔科夫链蒙特卡洛(Markov Chain Monte Carlo):import pymc3 as pm25.局部最小二乘回归(Local Polynomial Regression):from statsmodels.nonparametric.kernel_regression import KernelReg26.逻辑回归(Logistic Regression):from sklearn.linear_model import LogisticRegression27.拉格朗日插值法(Lagrange Interpolation):from scipy.interpolate import lagrange28.最小二乘法(Least Squares Method):import numpy as np29.牛顿法(Newton's Method):def newton_method(f, df, x0, tol=1e-6, max_iter=100):x = x0for i in range(max_iter):x = x - f(x) / df(x)if abs(f(x)) < tol:breakreturn x30.梯度下降法(Gradient Descent):def gradient_descent(f, df, x0, learning_rate=0.01, tol=1e-6, max_iter=100):x = x0for i in range(max_iter):x = x - learning_rate * df(x)if abs(df(x)) < tol:breakreturn x以上代码只是简单示例,实际应用中可能需要根据具体问题进行调整和扩展。
integer programming 教材
integer programming 教材整洁美观、通顺流畅的文字,这是每一位写作者都力求追求的目标。
下面是关于integer programming(整数规划)的教材。
整数规划教材第一章:整数规划导论1.1 整数规划的背景和应用领域整数规划作为线性规划的一种扩展形式,在现实生活和工业领域中具有广泛的应用,如物流优化、供应链管理、排产问题等。
1.2 整数规划的基本概念和特点整数规划是在决策变量中引入整数要求的线性规划问题。
与线性规划相比,整数规划的求解更加困难,但也具有更高的实用性和准确性。
第二章:整数规划的数学建模2.1 整数规划模型的建立步骤整数规划的数学建模是解决实际问题的关键步骤。
本节介绍整数规划建模的具体步骤,包括确定决策变量、建立目标函数和约束条件等。
2.2 整数规划的常见模型介绍了整数规划中常见的模型,如整数线性规划、混合整数规划、整数非线性规划等,并以实际案例进行详细说明和分析。
第三章:整数规划的求解方法3.1 精确求解方法介绍了整数规划精确求解方法,如分支定界法、割平面法等,并比较其优缺点和适用范围。
3.2 启发式求解方法介绍了整数规划启发式求解方法,如遗传算法、模拟退火算法等,并以实际案例进行了具体应用和分析。
第四章:整数规划的应用案例4.1 物流优化问题通过实际案例,介绍了整数规划在物流优化中的应用,如配送路径优化、仓库选址等问题。
4.2 生产排产问题以实例为基础,介绍了整数规划在生产排产问题中的应用,如工序调度、资源优化等。
第五章:整数规划的软件工具5.1 整数规划求解软件的选择介绍了目前常用的整数规划求解软件,并对其特点和适用范围进行了分析和比较。
5.2 整数规划求解软件的使用以具体案例为基础,讲解了整数规划求解软件的使用方法,包括数据输入、模型建立和结果分析等。
总结:整数规划作为一种重要的决策分析工具,在实际应用中发挥着广泛的作用。
通过本教材的学习,读者可以熟悉整数规划的基本概念和特点,掌握整数规划的建模方法和求解技巧,实现实际问题的优化和决策。
整数规划(数学建模)
整数规划(数学建模)-16-第⼆章整数规划§1 概论1.1 定义规划中的变量(部分或全部)限制为整数时,称为整数规划。
若在线性规划模型中,变量限制为整数,则称为整数线性规划。
⽬前所流⾏的求解整数规划的⽅法,往往只适⽤于整数线性规划。
⽬前还没有⼀种⽅法能有效地求解⼀切整数规划。
1.2 整数规划的分类如不加特殊说明,⼀般指整数线性规划。
对于整数线性规划模型⼤致可分为两类: 1o变量全限制为整数时,称纯(完全)整数规划。
2o 变量部分限制为整数的,称混合整数规划。
1.2 整数规划特点(i )原线性规划有最优解,当⾃变量限制为整数后,其整数规划解出现下述情况:①原线性规划最优解全是整数,则整数规划最优解与线性规划最优解⼀致。
②整数规划⽆可⾏解。
例1 原线性规划为21min x x z +=0,0,5422121≥≥=+x x x x 其最优实数解为:45min ,45,021===z x x 。
③有可⾏解(当然就存在最优解),但最优解值变差。
例2 原线性规划为21min x x z +=0,0,6422121≥≥=+x x x x 其最优实数解为:23min ,23,021===z x x 。
若限制整数得:2min ,1,121===z x x 。
(ii )整数规划最优解不能按照实数最优解简单取整⽽获得。
1.3 求解⽅法分类:(i )分枝定界法—可求纯或混合整数线性规划。
(ii )割平⾯法—可求纯或混合整数线性规划。
(iii )隐枚举法—求解“0-1”整数规划:①过滤隐枚举法;②分枝隐枚举法。
(iv )匈⽛利法—解决指派问题(“0-1”规划特殊情形)。
(v )蒙特卡洛法—求解各种类型规划。
下⾯将简要介绍常⽤的⼏种求解整数规划的⽅法。
§2 分枝定界法对有约束条件的最优化问题(其可⾏解为有限数)的所有可⾏解空间恰当地进⾏系统搜索,这就是分枝与定界内容。
通常,把全部可⾏解空间反复地分割为越来越⼩的⼦集,称为分枝;并且对每个⼦集内的解集计算⼀个⽬标下界(对于最⼩值问题),这称为定界。
数学建模-数学规划模型
将决策变量、目标函数和约束条件用数学方程表示出来,形成线性规划模型。
线性规划的求解方法
单纯形法
单纯形法是线性规划最常用的求解方法,它通过不断迭代和调整决策 变量的值,逐步逼近最优解。
对偶法
对偶法是利用线性规划的对偶性质,通过求解对偶问题来得到原问题 的最优解。
分解法
分解法是将一个复杂的线性规划问题分解为若干个子问题,分别求解 子问题,最终得到原问题的最优解。
混合法
将优先级法和权重法结合起来,既考虑目标的优先级又考虑目标的 权重,以获得更全面的优化解。
多目标规划的求解方法
约束法
通过引入约束条件,将多目标问题转化为单目标问题求解。常用的约束法包括线性约束 、非线性约束等。
分解法
将多目标问题分解为若干个单目标问题,分别求解各个单目标问题,然后综合各个单目 标问题的解得到多目标问题的最优解。
特点
多目标规划问题通常具有多个冲突的目标, 需要权衡和折衷不同目标之间的矛盾,因此 求解难度较大。多目标规划广泛应用于经济 、管理、工程等领域。
多目标规划的建模方法
优先级法
根据各个目标的重要程度,给定不同的优先级,然后结合优先级 对目标进行优化。
权重法
给定各个目标的权重,将多目标问题转化为加权单目标问题,通过 求解加权单目标问题得到多目标问题的最优解。
数学建模-数学规划 模型
目录
• 数学规划模型概述 • 线性规划模型 • 非线性规划模型 • 整数规划模型 • 多目标规划模型
01
CATALOGUE
数学规划模型概述
定义与分类
定义
数学规划是数学建模的一种方法,通 过建立数学模型描述和解决优化问题 。
分类
数学建模方法详解三种最常用算法
数学建模方法详解三种最常用算法数学建模是指将实际问题转化为数学模型,并通过数学方法进行求解和分析的过程。
在数学建模中,常用的算法有很多种,其中最常用的有三种,分别是线性规划、整数规划和动态规划。
一、线性规划线性规划是一种优化方法,用于在给定的约束条件下,寻找目标函数最大或最小值的一种方法。
它的数学形式是以线性约束条件为基础的最优化问题。
线性规划的基本假设是目标函数和约束条件均为线性的。
线性规划通常分为单目标线性规划和多目标线性规划,其中单目标线性规划是指在一个目标函数下找到最优解,而多目标线性规划则是在多个目标函数下找到一组最优解。
线性规划的求解方法主要有两种:单纯形法和内点法。
单纯形法是最常用的求解线性规划问题的方法,它的核心思想是通过不断迭代改进当前解来达到最优解。
内点法是一种相对较新的求解线性规划问题的方法,它的主要思想是通过从可行域的内部最优解。
二、整数规划整数规划是线性规划的一种扩展形式,它在线性规划的基础上增加了变量必须取整数的限制条件。
整数规划具有很强的实际应用性,它能够用于解决很多实际问题,如资源分配、生产优化等。
整数规划的求解方法通常有两种:分支定界法和割平面法。
分支定界法是一种常用的求解整数规划问题的方法,它的基本思想是通过将问题划分为若干个子问题,并通过求解子问题来逐步缩小解空间,最终找到最优解。
割平面法也是一种常用的求解整数规划问题的方法,它的主要思想是通过不断添加线性割平面来修剪解空间,从而找到最优解。
三、动态规划动态规划是一种用于求解多阶段决策问题的数学方法。
多阶段决策问题是指问题的求解过程可以分为若干个阶段,并且每个阶段的决策都受到之前决策的影响。
动态规划的核心思想是将问题划分为若干个相互关联的子问题,并通过求解子问题的最优解来求解原始问题的最优解。
动态规划通常分为两种形式:无后效性和最优子结构。
无后效性是指一个阶段的决策只与之前的状态有关,与之后的状态无关。
最优子结构是指问题的最优解能够由子问题的最优解推导而来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
整数规划模型实际问题中x x x x f z Max Min Tn "),(),()(1==或的优化模型mi x g t s i ",2,1,0)(..=≤x ~决策变量f (x )~目标函数g i (x )≤0~约束条件多元函数决策变量个数n 和数线性规划条件极值约束条件个数m 较大最优解在可行域学规非线性规划解的边界上取得划整数规划Programming+Integer所有变量都取整数,称为纯整数规划;有一部分取整数,称为混合整数规划;限制取0,1称为0‐1型整数规划。
型整数规划+整数线性规划max(min) nz c x =1j jj n=∑1s.t. (,) 1,2,,ij j i j a x b i m=≤=≥=∑"12 ,,,0 ()n x x x ≥"且为整数或部分为整数+例:假设有m 种不同的物品要装入航天飞机,它们的重量和体积分别为价值为w j 和v j ,价值为c j ,航天飞机的载重量和体积限制分别为W 和V ,如何装载使价值最大化?m1⎧1max j jj c y =∑ 1 0j j y =⎨被装载 s.t. mj j v y V≤∑0j ⎩没被装载1j m=1j j j w y W=≤∑ 0 or 1 1,2,,j y j m=="(Chicago)大学的Linus Schrage教授于1980年美国芝加哥(Chi)Li S h前后开发, 后来成立LINDO系统公司(LINDO Systems Inc.),网址:I)网址htt//li dLINDO: Interactive and Discrete Optimizer (V6.1) Linear(V61) LINGO: Linear Interactive General Optimizer (V8.0) LINDO——解决线性规划LP—Linear Programming,整数规划IP—Integer Programming问题。
LINGO——解决线性规划LP—Linear Programming,非线性规划NLP—Nonlinear Programming,整数规划IP—Integer Programmingg g整划g g g 问题。
1.“>”(或“<”)号与“>=”(或“<=”)功能相同2.甚至回车 但无运算变量与系数间可有空格(甚至车),但算符3.变量名以字母开头,不能超过变量名字母开头,不能超过8个字符4.变量名不区分大小写(包括LINDO 中的关键字)5.目标函数所在行是第一行,第二行起为约束条件6.行号(行名)自动产生或人为定义。
行名以“)”结束7.变量不能出现在一个约束条件的右端变量不能出现在个约束条件的右端8. 表达式中不接受括号“( )”和逗号“,”等任何符号, 例: 400(X1+X2)需写为400X1+400X2 9.表达式应化简,如2X1+3X2‐4X1应写成‐2X1+3X22X13X210.缺省假定所有变量非负;可在模型的“END”语句后用“FREE name”将变量name的非负假定取消11.“END”后对0‐1变量说明:INT n或INT name12.“END”后对整数变量说明:GIN n或GIN12后对整数变量说明name汽车厂生产三种类型的汽车,已知各类型每辆车对钢材、劳动时间的需求,利润及工厂每月的现有量。
材劳动时间的需求利润及工厂每月的现有量。
小型中型大型现有量钢材(吨) 1.5 3 5 600劳动时间(小时)280 250 400 60000利润(万元)2 3 4•制订月生产计划,使工厂的利润最大。
制订月生产计划使工厂的利润最大•如果生产某一类型汽车,则至少要生产80辆,那么最优的生产计划应作何改变?汽车厂生产计划汽车厂产计划模型建立小型中型大型现有量设每月生产小、中、大型模建中钢材1.5 3 5 60060000汽车的数量分别为x 1,x 2,x 3时间280 250 400 利润2 3 4321432x x x zMax ++=线性600535.1..321≤++x x x t s 60000400250280≤++x x x 线规划模型3210,,321≥x x x (LP)模型OBJECTIVE FUNCTION VALUE 求解1)632.2581VARIABLE VALUE REDUCED COST X164.5161290.000000X2167.7419280.000000X30.0000000.946237结果为小数,ROW SLACK OR SURPLUS DUAL PRICES2)0.0000000.7311833)0.0000000.003226怎么办?1)舍去小数:取x 1=64,x 2=167,算出目标函数值z =629,与LP 最优值632.2581相差不大。
2)试探:如取x 1=65,x 2=167;x 1=64,x 2=168等,计算函数值z ,通过比较可能得到更优的解。
•但必须检验它们是否满足约束条件。
3)模型中增加条件:x 1,x 2,x 3均为整数,重新求解。
整数规划(Integer Programming ,简记IP )IP 可用LINDO 直接求解max 321432x x x z Max ++=模型求解2x1+3x2+4x3st600535.1..321≤++x x x t s 60000400250280321≤++x x x 1.5x1+3x2+5x3<600280x1+250x2+400x3<60000end为非负整数321,,x x x “gin 3”表示“前3个变量为gin 3OBJECTIVE FUNCTION VALUE )IP 结果输出整数”,等价于:gin x1i 21)632.0000VARIABLE VALUE REDUCED COST X164.000000‐2.000000gin x2gin x3 的最解6680最值632X2168.000000‐3.000000X3 0.000000 ‐4.000000IP 的最优解x 1=64,x 2=168,x 3=0,最优值z =632汽车厂生产计划汽车厂产计划•若生产某类汽车,则至少生产80辆,求生产计划。
M 80,0,0321≥==x x x 0,80,0321=≥=x x x 321432x x x z Max ++=600535.1..321≤++x x x t s 80,80,0321≥≥=x x x 60000400250280321≤++x x x x x x =0 ≥80×0,0,80321==≥x x x 0,80,80321=≥≥x x x 方法1:分解为8个LP 子模型1,2,3或其中3个子模型应去掉,然后逐一求解比较目标函数值80,0,80321≥=≥x x x 808080≥≥≥x x x ×逐求解,比较目标函数值,再加上整数约束,得最优解:,,3210,,321=x x x ×x 1=80,x 2= 150,x 3=0,最优值z =610•若生产某类汽车,则至少生产80辆,求生产计划。
方法2:引入0‐1变量,化为整数规划产车产产计M 为大的正数,x 1=0 或≥800}1,0{,80,11111∈≥≤y y x My x 可取1000 x 2=0 或≥80x =0 或≥80}1,0{,80,22222∈≥≤y y x My x }1,0{,80,33333∈≥≤y y x My x LINDO 中对0‐1OBJECTIVE FUNCTION VALUE 1)610.00003变量的限定:int y1VARIABLE VALUE REDUCED COST X180.000000‐2.000000‐最优解同前int y2int y3 X2150.000000 3.000000X30.000000‐4.000000Y1 1.0000000.00000010000000000000解同前Y2 1.0000000.000000Y3 0.000000 0.000000售价4800元/吨汽油甲库存500吨(A ≥50%) 原油A汽油乙市场上可买到不超过售价5600元/吨库存1000吨原油B (A ≥60%)1500吨的原油A :•购买量不超过500吨时的单价为10000元/吨;•购买量超过500吨但不超过1000吨时,超过500吨的8000元/吨;该公司应如何安排原油的采购和加部分•购买量超过1000吨时,超过1000吨的部分6000元/吨。
该公司应如何安排原油的采购和加工?问题•利润:销售汽油的收入A 分析利润销售汽油的收购买原油的支出•难点:原油A 的购价与购买量的关系较复杂决策原油A 的购买量,原油A, B 生产汽油甲,乙的数量变量甲(A ≥50%) A购买x →x 11x 12x 214.8千元/吨目标B 乙(A ≥60%) x 22 5.6千元/吨函数c (x ) ~ 购买原油A 的支出利润(千元))()(6.5)(8.422122111x c x x x x z Max −+++=c (x )如何表述?•目标x ≤500吨单价为10千元/吨;•500吨≤x ≤1000吨,超过500吨的8千元/吨;吨超过吨函数⎧•1000吨≤x ≤1500吨,超过1000吨的6千元/吨。
⎪⎨≤≤+≤≤=1000)(500 1000 8500)(0 10)(x x x x x c 约束⎪⎩≤≤+500)1(1000 30006x x 原油供应条件x x x +≤+5001211购买x ↓Ax 11x 500吨10002221≤+x x B 12x 21x 库存库存1000吨1500≤x 22汽油含原油约束A 的比例限制条件x 115.011≥+x x x 2111x x ≥⇔甲(A ≥50%) Ax 12x 21211112x B 乙(A ≥60%)x 22数中是线数是线划6.02212≥+x x 221232x x ≥⇔¾目标函数中c (x )不是线性函数,是非线性规划;¾,一般的非线性规划软对于用分段函数定义的c (x ),般的非线性规划软件也难以输入和求解;想法将型简用成的软件求解¾想办法将模型化简,用现成的软件求解。
x x x ~以价格10, 8, 6(A 模型求解1 ,2 ,3 价格,,(千元/吨)采购的吨数=+x +x c =+8+6目标x x 1x 2x 3, (x ) 10x 18x 26x 3函数)6810()(6.5)(8.432122122111x x x x x x x z Max ++−+++=y 1, y 2 , y 3=1 ~以价格10, 8, 6(千元/吨)采购A 增108加112500500y x y ≤≤223500500y x y ≤≤x 1 , x 2 , x 3 ~以价格10, 8, 6(千元/吨)采购A 的吨数y =0 →x =0约束33500y x ≤y 1,y 2,y 3 =0或1 x >0 →y =1Max 4.8x11+4.8x21+5.6x12+5.6x22‐10x1‐8x2‐6x3stx11+x12‐x<500x21+x22<100005x1105x21>00.5x11‐0.5x21>00.4x12‐0.6x22>0x ‐x1‐x2‐x3=0‐x1500y1<0x2‐500y2<0x3‐500y3<0‐500y2>0x1500y20x2‐500y3>0endint y1yint y2int y30‐1线性规划模型,可用LINDO求解OBJECTIVE FUNCTION VALUE1)5000.000VARIABLE VALUE REDUCED COSTY1 1.0000000.000000Y2 1.0000002200.000000Y3 1.0000001200.000000X110.0000000.80000000000000800000X210.0000000.800000X121500.0000000.000000X221000.0000000.000000X1500.0000000.000000X2500.0000000.000000X30.0000000.400000X 1000.0000000.00000010000000000000000购买1000吨原油A,与库存的500吨原油A和1000吨原油B 一起,生产2500吨汽油乙,利润为5,000千元。
