模式识别实验报告_2
北邮信息工程模式识别实验报告

0.8514 0.4439 0.4272 0.7127 0.4129 0.7840
1.0831 0.4928 0.4353 1.0124 1.0085 0.4158
0.4164 0.5901 0.9869 0.4576 0.7676 1.0315
1.1176 1.0927 0.4841 0.8544 0.8418 0.7533
6、实验要求
1) 请把数据作为样本,根据 Fisher 选择投影方向 W 的原则,使原样本向量在 该方向上的投影能兼顾类间分布尽可能分开, 类内样本投影尽可能密集的要 求,求出评价投影方向 W 的函数,并在图形表示出来。并在实验报告中表 示出来,并求使 J F ( w) 取极大值的 w* 。用 matlab 完成 Fisher 线性分类器 的设计,程序的语句要求有注释。 2) 根据上述的结果并判断 (1, 1.5, 0.6) (1.2, 1.0, 0.55), (2.0, 0.9, 0.68), (1.2,1.5,0.89), (0.23,2.33,1.43) ,属于哪个类别,并画出数据分类 相应的结果图,要求画出其在 W 上的投影。 3) 回答如下问题,分析一下 W 的比例因子对于 Fisher 判别函数没有影响的原 因。
~ m ~ )2 (m 1 2 J F (W ) ~ 2 ~ S1 S 22
1 W * SW (m1 m2 )
上面的公式是使用 Fisher 准则求最佳法线向量的解,该式比较重要。另外,该式这种
2
形式的运算, 我们称为线性变换, 其中 m1 m2 式一个向量,SW 是 SW 的逆矩阵, 如 m1 m2
*
以上讨论了线性判别函数加权向量 W 的确定方法,并讨论了使 Fisher 准则函数极大的 d 维向量 W
孙杨威_12281201_模式识别第7次实验报告(2)

实验报告学生姓名:孙杨威学号:12281201实验地点:九教北401实验室实验时间:2014.11.13一、实验名称:BP神经网络算法二、实验原理:BP网络模型处理信息的基本原理是:输入信号X i通过中间节点(隐层点)作用于输出节点,经过非线形变换,产生输出信号Y k,网络训练的每个样本包括输入向量X和期望输出量t,网络输出值Y与期望输出值t之间的偏差,通过调整输入节点与隐层节点的联接强度取值W ij和隐层节点与输出节点之间的联接强度T jk以及阈值,使误差沿梯度方向下降,经过反复学习训练,确定与最小误差相对应的网络参数(权值和阈值),训练即告停止。
此时经过训练的神经网络即能对类似样本的输入信息,自行处理输出误差最小的经过非线形转换的信息。
三、实验内容:●有一批Iris花,已知这批Iris花可分为3个品种,现需要对其进行分类。
●不同品种的Iris花的花萼长度、花萼宽度、花瓣长度、花瓣宽度会有差异。
●我们现有一批已知品种的Iris花的花萼长度、花萼宽度、花瓣长度、花瓣宽度的数据。
用已有的数据训练一个神经网络用作分类器。
四、实验步骤:1.建立一个新的网络2.使用样本训练这个网络3.使用新的数据集模拟这个网络五、实验代码及分析:bp_test.m%读取测试数据[t1 t2 t3 t4 c] = textread('testData.txt' , '%f%f%f%f%s',75); %测试数据归一化testInput = tramnmx ( [t1,t2,t3,t4]' , minI, maxI ) ;%仿真Y = sim( net , testInput );s=length(c);output1=zeros(s,3);for i = 1 : sif strcmp(c(i),'Isetosa')~=0output1( i , 1 ) = 1;elseif strcmp(c(i),'Iversicolor')~=0output1( i , 2 ) = 1;elseoutput1( i , 3 ) = 1;endend%统计识别正确率[s1 , s2] = size( Y ) ;hitNum = 0 ;for i = 1 : s2[m , Index] = max( Y( : , i ) ) ;if( output1(i,Index) == 1 )hitNum = hitNum + 1 ;endendsprintf('识别率是 %3.3f%%',100 * hitNum / s2 )bp_rain.m%将Iris数据集分为2组,每组各75个样本,每组中每种花各有25个样本。
模式识别专业实践报告(2篇)

第1篇一、实践背景与目的随着信息技术的飞速发展,模式识别技术在各个领域得到了广泛应用。
作为人工智能领域的一个重要分支,模式识别技术对于图像处理、语音识别、生物识别等领域的发展具有重要意义。
为了更好地理解和掌握模式识别技术,提高实际应用能力,我们组织了一次为期一个月的模式识别专业实践。
本次实践旨在通过实际操作,加深对模式识别理论知识的理解,提高解决实际问题的能力。
二、实践内容与过程1. 实践内容本次实践主要包括以下几个方面:(1)图像识别:利用深度学习算法进行图像分类、目标检测等。
(2)语音识别:实现语音信号处理、特征提取和识别。
(3)生物识别:研究指纹识别、人脸识别等生物特征识别技术。
(4)模式分类:运用机器学习算法进行数据分类和聚类。
2. 实践过程(1)理论学习:在实践开始前,我们首先对模式识别的基本理论进行了系统学习,包括图像处理、信号处理、机器学习等相关知识。
(2)项目准备:根据实践内容,我们选取了具有代表性的项目进行实践,如基于深度学习的图像识别、基于HMM的语音识别等。
(3)实验设计与实施:在导师的指导下,我们设计了实验方案,包括数据预处理、模型选择、参数调整等。
随后,我们使用Python、C++等编程语言进行实验编程,并对实验结果进行分析。
(4)问题分析与解决:在实验过程中,我们遇到了许多问题,如数据不足、模型效果不佳等。
通过查阅文献、请教导师和团队成员,我们逐步解决了这些问题。
三、实践成果与分析1. 图像识别我们使用卷积神经网络(CNN)对CIFAR-10数据集进行了图像分类实验。
实验结果表明,经过多次迭代优化,模型在测试集上的准确率达到89.5%,优于传统机器学习方法。
2. 语音识别我们采用HMM(隐马尔可夫模型)对TIMIT语音数据集进行了语音识别实验。
实验结果表明,经过特征提取和模型训练,模型在测试集上的词错误率(WER)为16.3%,达到了较好的识别效果。
3. 生物识别我们研究了指纹识别和人脸识别技术。
模式识别实习报告

一、实习背景随着科技的飞速发展,人工智能、机器学习等技术在各个领域得到了广泛应用。
模式识别作为人工智能的一个重要分支,具有广泛的应用前景。
为了更好地了解模式识别技术,提高自己的实践能力,我在2023年暑假期间参加了某科技有限公司的模式识别实习。
二、实习单位简介某科技有限公司是一家专注于人工智能、大数据、云计算等领域的科技创新型企业。
公司致力于为客户提供智能化的解决方案,业务涵盖智能识别、智能监控、智能分析等多个领域。
此次实习,我将在该公司模式识别部门进行实践学习。
三、实习内容1. 实习前期(1)了解模式识别的基本概念、原理和应用领域;(2)熟悉模式识别的相关算法,如神经网络、支持向量机、决策树等;(3)掌握Python编程语言,学会使用TensorFlow、Keras等深度学习框架。
2. 实习中期(1)参与实际项目,负责模式识别算法的设计与实现;(2)与团队成员协作,完成项目需求分析、算法优化和系统测试;(3)撰写项目报告,总结实习过程中的收获与不足。
3. 实习后期(1)总结实习期间的学习成果,撰写实习报告;(2)针对实习过程中遇到的问题,查找资料、请教同事,提高自己的解决问题的能力;(3)为后续实习工作做好充分准备。
四、实习收获与体会1. 理论与实践相结合通过实习,我深刻体会到理论与实践相结合的重要性。
在实习过程中,我将所学的模式识别理论知识运用到实际项目中,提高了自己的动手能力。
同时,通过解决实际问题,我更加深入地理解了模式识别算法的原理和应用。
2. 团队协作能力实习期间,我学会了与团队成员有效沟通、协作。
在项目中,我们共同面对挑战,分工合作,共同完成项目任务。
这使我认识到团队协作的重要性,为今后的工作打下了基础。
3. 解决问题的能力在实习过程中,我遇到了许多问题。
通过查阅资料、请教同事、独立思考等方式,我逐渐学会了如何分析问题、解决问题。
这种能力对我今后的学习和工作具有重要意义。
4. 深度学习框架的使用实习期间,我学会了使用TensorFlow、Keras等深度学习框架。
模式识别实习报告

实习报告一、实习背景及目的随着科技的飞速发展,模式识别技术在众多领域发挥着越来越重要的作用。
模式识别是指对数据进行分类、识别和解释的过程,其应用范围广泛,包括图像处理、语音识别、机器学习等。
为了更好地了解模式识别技术的原理及其在实际应用中的重要性,我参加了本次模式识别实习。
本次实习的主要目的是:1. 学习模式识别的基本原理和方法;2. 掌握模式识别技术在实际应用中的技巧;3. 提高自己的动手实践能力和团队协作能力。
二、实习内容及过程实习期间,我们团队共完成了四个模式识别项目,分别为:手写数字识别、图像分类、语音识别和机器学习。
下面我将分别介绍这四个项目的具体内容和过程。
1. 手写数字识别:手写数字识别是模式识别领域的一个经典项目。
我们使用了MNIST数据集,这是一个包含大量手写数字图片的数据集。
首先,我们对数据集进行预处理,包括归一化、数据清洗等。
然后,我们采用卷积神经网络(CNN)作为模型进行训练,并使用交叉验证法对模型进行评估。
最终,我们得到了一个识别准确率较高的模型。
2. 图像分类:图像分类是模式识别领域的另一个重要应用。
我们选择了CIFAR-10数据集,这是一个包含大量彩色图像的数据集。
与手写数字识别项目类似,我们先对数据集进行预处理,然后采用CNN进行训练。
在模型训练过程中,我们尝试了不同的优化算法和网络结构,以提高模型的性能。
最终,我们得到了一个识别准确率较高的模型。
3. 语音识别:语音识别是模式识别领域的又一项挑战。
我们使用了TIMIT数据集,这是一个包含大量语音样本的数据集。
首先,我们对语音样本进行预处理,包括特征提取、去噪等。
然后,我们采用循环神经网络(RNN)作为模型进行训练。
在模型训练过程中,我们尝试了不同的优化算法和网络结构。
最后,我们通过对模型进行评估,得到了一个较为可靠的语音识别系统。
4. 机器学习:机器学习是模式识别领域的基础。
我们使用了UCI数据集,这是一个包含多个数据集的数据集。
模式识别关于男女生身高和体重的神经网络算法

模式识别实验报告(二)学院:专业:学号:姓名:XXXX教师:目录1实验目的 (1)2实验内容 (1)3实验平台 (1)4实验过程与结果分析 (1)4.1基于BP神经网络的分类器设计 .. 1 4.2基于SVM的分类器设计 (4)4.3基于决策树的分类器设计 (7)4.4三种分类器对比 (8)5.总结 (8)1)1实验目的通过实际编程操作,实现对课堂上所学习的BP神经网络、SVM支持向量机和决策树这三种方法的应用,加深理解,同时锻炼自己的动手实践能力。
2)2实验内容本次实验提供的样本数据有149个,每个数据提取5个特征,即身高、体重、是否喜欢数学、是否喜欢文学及是否喜欢运动,分别将样本数据用于对BP神经网络分类器、SVM支持向量机和决策树训练,用测试数据测试分类器的效果,采用交叉验证的方式实现对于性能指标的评判。
具体要求如下:BP神经网络--自行编写代码完成后向传播算法,采用交叉验证的方式实现对于性能指标的评判(包含SE,SP,ACC和AUC,AUC的计算可以基于平台的软件包);SVM支持向量机--采用平台提供的软件包进行分类器的设计以及测试,尝试不同的核函数设计分类器,采用交叉验证的方式实现对于性能指标的评判;决策树--采用平台提供的软件包进行分类器的设计以及测试,采用交叉验证的方式实现对于性能指标的评判(包含SE,SP,ACC和AUC,AUC的计算基于平台的软件包)。
3)3实验平台专业研究方向为图像处理,用的较多的编程语言为C++,因此此次程序编写用的平台是VisualStudio及opencv,其中的BP神经网络为自己独立编写, SVM 支持向量机和决策树通过调用Opencv3.0库中相应的库函数并进行相应的配置进行实现。
将Excel中的119个数据作为样本数据,其余30个作为分类器性能的测试数据。
4)4实验过程与结果分析4.1基于BP神经网络的分类器设计BP神经网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。
模式识别实验二_2

1.贝叶斯公式
已知共有 M 类别 i , i 1,2, M ,统计分布为正态分布,已知先验概率 P (i ) 及类条 件概率密度函数 P ( X | i ) ,对于待测样品,贝叶斯公式可以计算出该样品分属各类别的概 率,叫做后验概率;看 X 属于哪个类的可能性最大,就把 X 归于可能性最大的那个类,后 验概率即为识别对象归属的依据。贝叶斯公式为
1
( i )
)
n 1 ln 2 ln S i 2 2
X (i ) 为 i 类的均值向量。
2.最小错误判别准则
1
两类问题 有两种形式,似然比形式:
l( X )
P ( X | 1 ) P ( 2 ) X 1 P ( X | 2 ) P (1 ) 2
h2=-0.5*(x-mean2)'*inv(sigema2)*(x-mean2)-2*log(2*pi)-0.5*log(d et(sigema2))+log(1/3);
h3=-0.5*(x-mean3)'*inv(sigema3)*(x-mean3)-2*log(2*pi)-0.5*log(d et(sigema3))+log(1/3); h(1)=h1; h(2)=h2; h(3)=h3; %比较三个数据的大小,并判断属于哪一类% max=h(1); class=1;
sigema=0; for i=1:2:50 sigema=sigema+(iris{i}-mean1)*(iris{i}-mean1)'; end sigema1=sigema/25;%sigema1为第一类数据的协方差矩阵
4.已经估计出三类数据的统计特征。首先使用最小错误判别准则进行分类,实验中采用对数 形式计算,假设三种类型的先验概率相等,即均为 1/3,在某一 X 下得到的三个后验概率的 函数。比较三个值的大小,哪个最大,就可判断 X 属于哪一类。最后进行了分类器判据结 果的验证。
《模式识别》线性分类器设计实验报告
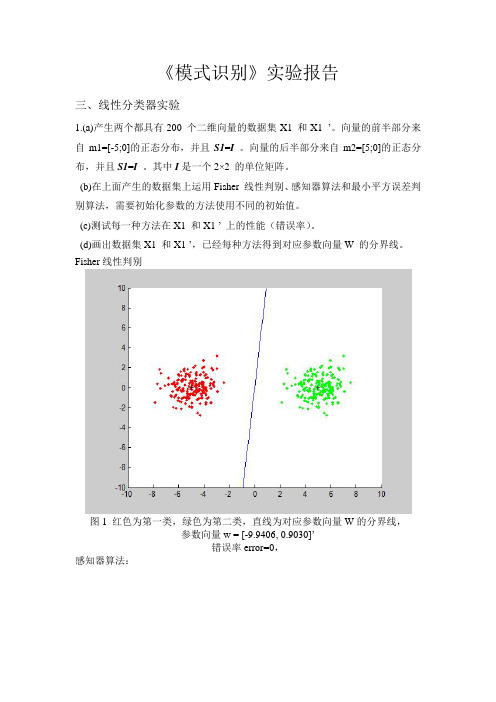
《模式识别》实验报告三、线性分类器实验1.(a)产生两个都具有200 个二维向量的数据集X1 和X1 ’。
向量的前半部分来自m1=[-5;0]的正态分布,并且S1=I 。
向量的后半部分来自m2=[5;0]的正态分布,并且S1=I。
其中I是一个2×2 的单位矩阵。
(b)在上面产生的数据集上运用Fisher 线性判别、感知器算法和最小平方误差判别算法,需要初始化参数的方法使用不同的初始值。
(c)测试每一种方法在X1 和X1 ’ 上的性能(错误率)。
(d)画出数据集X1 和X1 ’,已经每种方法得到对应参数向量W 的分界线。
Fisher线性判别图1 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数向量w = [-9.9406, 0.9030]’错误率error=0,感知器算法:图2 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数的初始值为[0.1;0.1];迭代次数iter=2参数向量w = [-4.8925, 0.0920]’错误率error=0图3 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数的初始值为[1; 1];迭代次数iter=2参数向量w = [-3.9925, 0.9920]’错误率error=0图4 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数的初始值为[10; 10];迭代次数iter=122参数向量w = [-5.6569, 7.8096]’错误率error=0图5 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数的初始值为[50; 50];迭代次数iter=600参数向量w = [-27.0945, 37.4194]’错误率error=0图6 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数的初始值为[50; 100];迭代次数iter=1190参数向量w = [-54.0048, 74.5875]’错误率error=0最小平方误差判别算法:图7 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数的初始值为[0.1; 0.1];参数向量w = [-0.1908, -0.0001]’错误率error=0图8 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数的初始值为[0.5; 0.5];参数向量w = [-0.1924, 0.1492]’错误率error=0图9 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数的初始值为[1; 0.5];参数向量w = [-0.1914, 0.0564]’错误率error=0图10 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数的初始值为[1; 1];参数向量w = [-0.1943, 0.3359]’错误率error= 0.00502.重复1.中的实验内容,数据集为X2 和X2 ’。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模式识别理论与方法课程作业实验报告实验名称:Generating Pattern Classes实验编号:Proj01-01规定提交日期:2012年3月16日实际提交日期:2012年3月13日摘要:在熟悉Matlab中相关产生随机数和随机向量的函数基础上,重点就多元(维)高斯分布情况进行了本次实验研究:以mvnrnd()函数为核心,由浅入深、由简到难地逐步实现了获得N 个d维c类模式集,并将任意指定的两个维数、按类分不同颜色进行二维投影绘图展示。
技术论述:1,用矩阵表征各均值、协方差2,多维正态分布函数:实验结果讨论:从实验的过程和结果来看,进一步熟悉了多维高斯分布函数的性质和使用,基本达到了预期目的。
实验结果:图形部分:图1集合中的任意指定两个维度投影散点图形图2集合中的任意指定两个维度投影散点图形,每类一种颜色数据部分:Fa=9.6483 5.5074 2.4839 5.72087.2769 4.88079.1065 4.1758 1.5420 6.1500 6.2567 4.138710.0206 3.5897 2.6956 6.1500 6.9009 4.024810.1862 5.2959 3.1518 5.22877.1401 3.197410.4976 4.9501 1.4253 5.58257.4102 4.947411.3841 4.5128 2.0714 5.90068.2228 4.48219.6409 5.43540.9810 6.2676 6.9863 4.25308.8512 5.2401 2.7416 6.5095 6.1853 4.87519.8849 5.8766 3.3881 5.7879 6.7070 6.613210.6845 4.8772 3.4440 6.0758 6.6633 3.53818.7478 3.3923 2.4628 6.1352 6.9258 3.39079.5866 6.5308 1.7059 6.6572 6.7514 4.1234 8.2999 3.72600.0852 5.5818 5.5049 4.3525 11.0747 5.0835 1.8681 6.84327.3915 3.704910.2744 4.8616 2.5967 6.45607.1287 3.334511.2732 5.5013 1.7882 6.28637.9292 3.6436 10.9456 4.6985 1.4616 6.56687.0788 5.2986 9.9085 4.6522 2.9579 6.2845 6.7591 3.8167 8.2832 5.3328 1.4134 6.3768 6.6294 4.0419 10.0071 6.6619 1.0918 6.60267.3421 3.72149.6463 3.8060 1.6344 6.1337 6.4823 5.337310.3031 4.3285 2.9541 5.9217 6.0828 3.924711.3827 5.0409 2.74197.05867.6376 4.2837 13.1684 6.2082 1.3748 6.7191 6.8902 3.2330 11.9846 5.91080.9457 6.06727.4720 4.8710 11.1886 4.15430.97477.15167.4619 4.2620 9.2787 5.5863 3.4771 5.5654 6.7469 4.52238.8263 5.6121 2.1450 6.19907.0848 6.27079.0934 4.5884 1.2013 6.2549 6.4784 3.935910.4153 3.7705 2.6803 6.9746 6.7440 5.5763 9.3666 6.5097 2.4297 5.9348 6.5719 4.4739 11.2190 5.5874 1.19057.0840 6.7573 5.61459.3633 5.1353 2.0878 6.28517.2318 4.062410.5450 4.5922 1.68197.6731 6.9293 6.01999.4180 4.5281 2.3995 6.5958 6.8904 3.583210.3244 5.3690 4.0924 6.2067 6.9591 5.2545 10.3441 4.1053 2.6564 6.14147.9662 5.0024 9.5471 5.7258 2.6954 6.30067.1263 4.23438.8897 4.6916 2.0968 6.3380 6.5367 4.83189.1943 6.0874 1.6253 5.95547.5757 5.810110.9947 5.3560 1.3802 6.30677.1168 4.596810.2433 3.67630.71177.27487.0664 5.24619.1907 6.4982 1.9370 6.0473 6.4948 5.033610.8058 4.14500.7211 5.70927.1892 3.80919.0818 4.2633 2.3737 4.9058 6.1640 3.89399.3663 4.8987 2.6602 6.29747.3877 4.840110.3941 4.2046 1.5459 6.29647.4326 3.74408.4875 5.3582 1.7972 6.3595 6.8557 4.13878.9796 3.8901 2.1128 6.0709 6.9327 4.51779.8270 5.7906 2.7458 6.41027.1228 3.8328 Fb=7.2706e-008Fc=8.1479 4.7469 3.0243 5.5812 1.51598.62868.2293 4.2598 2.3764 2.92890.71058.04768.2969 5.0960 2.9152 3.1257-0.17187.62478.5212 4.1134 2.7298 6.0409 1.08127.94178.7216 4.0723 3.5793 3.73440.34488.00307.7519 4.6370 3.4269 4.7549 2.26907.41221.4689 6.52629.59588.6153 1.8746 5.31290.7252 6.55508.8830 6.61990.7224 4.42388.72527.0140 4.64149.25420.6592 5.830010.02947.6141 3.34368.6829-0.1825 5.112611.21917.3080 4.96559.08120.1829 5.99059.55217.1176 3.14549.34660.6371 5.01469.69617.4892 2.98108.64100.2161 5.636110.80409.4255 3.8439 6.9168-0.0959 5.1600 9.84837.1682 2.95819.30720.3703 5.6787 9.60548.1801 3.762010.5036-0.3189 5.5020 9.5593 6.7341 3.84659.31970.0703 4.89489.04297.0763 3.79928.84910.6844 6.032310.11858.5778 3.669610.07350.3946 6.0441 9.46597.3425 3.53459.1105 1.5117 5.7459 9.80647.5425 3.110010.29140.8737 5.4085 11.13327.3167 3.26078.8462 1.1033 4.70938.89358.7706 4.54089.52560.1717 5.16649.1860 6.3056 2.216210.5140-0.4248 5.689610.10168.0046 2.98779.5155-0.1837 5.6127 10.08357.2444 3.798910.6898 1.0766 5.5360 9.92938.2313 3.87557.9165-0.5513 5.6216 11.3417 6.4291 3.37547.61070.5368 6.0762 2.466810.2729 2.3393 1.1392 3.2003 4.6689 -0.11189.2253 1.96660.3000 4.4845 5.0391 1.51468.37010.6157 1.0943 3.7617 4.3484 -0.502210.15810.4752 1.0992 4.2291 4.8148 3.506810.7347-0.67490.8837 3.7837 5.7105 3.08199.9620 3.1265 1.2664 4.1610 5.4902 2.76537.57330.68020.6764 4.3750 3.70771.808310.2191 1.11240.4150 4.0906 5.17192.236711.21250.67620.90493.2792 5.8028 1.15708.0017 1.62660.7252 3.83644.3532 9.61565.4535 3.20308.80037.22538.53077.49167.7935 3.88779.0452 6.05538.60868.3620 5.6559 3.66428.1250 6.44309.3105 6.5492 5.8504 3.16878.94467.16858.95497.0622 6.9555 3.90288.42637.39128.65678.1994 5.4819 3.45698.1752 5.95059.90508.4161 6.8079 3.31187.8120 6.44008.46148.0543 6.6962 3.20678.1270 6.83829.92789.9317 5.2581 3.20569.7804 6.741210.57267.2542 6.7284 3.31647.74407.89419.31857.1946 6.3492 4.18008.32707.752210.17228.7936 5.6577 2.98627.99907.524210.5277附录:(程序清单)%在Matlab版本2009a下运行通过close all;clc;clear;%公共数据N=50;%数据集中的样本个数d=6;%维数c=5;%类数m=10*rand(1,d);%均值向量mS=sprandsym(d,0.5,0.2,1);%协方差矩阵S随机产生(对称正定矩阵)%%aFa=GetNdRandn(N,d,m,S)%%bx=10*rand(1,d);Fb=GetValueRandn(x,m,S)%%cMc=10*rand(c,d);Sc=[];for k=1:c%随机产生每类的协方差矩阵St=sprandsym(d,0.5,0.2,1);St=full(St);%将稀疏矩阵转换成全矩阵Sc=cat(3,Sc,St);endwhile(1)%随机产生每类的个数PiN=randi(2*N/c,1,c-1);if sum(PiN)<Nbreak;endendPiN=cat(2,PiN,N-sum(PiN));Fc=GetNdCCRandn(PiN,Mc,Sc)%%dShowTwoInNdDataSet(randi(d),randi(d),Fa);%%eShowTwoInNdCCDataSet(randi(d),randi(d),PiN,Fc);function F=GetNdRandn(N,d,m,S)%生成N个d维随机向量集合的函数,并适当检查输入参数的有效性%输入参数:向量个数N,向量维数d,高斯分布的均值向量m%和协方差矩阵S为d*d的对称半正定矩阵F=[];[k,n]=size(m);if1~=min(k,n)||d~=max(k,n)fprintf('参数错误:均值向量维数不匹配\n');return;end[k,n]=size(S);if k~=n||k~=dfprintf('参数错误:协方差矩阵维数不匹配\n');return;endtryF=mvnrnd(m,S,N);catch MEfprintf('参数错误,原因如下:\n%s\n%s\n',ME.identifier,ME.message);F=[];Endfunction F=GetValueRandn(x,m,S)%计算d元高斯分布N(m,S)值的函数,并适当检查输入参数的有效性%输入参数:d维向量x,高斯分布的均值向量m%和协方差矩阵S为d*d的对称半正定矩阵F=[];[k,n]=size(x);d=max(k,n);if(min(k,n)>1)||(d<1)fprintf('参数x错误:x应当为一个行向量\n');return;end[k,n]=size(m);if1~=min(k,n)||d~=max(k,n)fprintf('参数m错误:均值向量m维数与x应当保持一致\n');return;end[k,n]=size(S);if k~=n||k~=dfprintf('参数错误:协方差矩阵维数不匹配,\n');return;endtryF=mvncdf(x,m,S);catch MEfprintf('参数错误,原因如下:\n%s\n%s\n',ME.identifier,ME.message);F=[];Endfunction DataSet=GetNdCCRandn(PiN,m,S)%生成N个d维向量的高斯类数据集,分成C类;如果输入参数错误,则输出空数据集%输入参数:每类的个数(先验概率)为PiN1*C,均值向量m C*d%和协方差矩阵S为d*d*C的对称半正定矩阵DataSet=[];[a,C]=size(PiN);if(a>1)||(C<1)fprintf('每类的个数(先验概率)PiN错误:应当为一个行向量\n');return;end[a,dim]=size(m);if a~=Cfprintf('参数m错误:均值向量m的行数与应当与Pi的列数保持一致\n');return;end[a,b,c]=size(S);if(a~=dim)||(b~=dim)||(c~=C)fprintf('参数错误:协方差矩阵S维数不匹配\n');return;endfor k=1:CTemp=GetNdRandn(PiN(k),dim,m(k,:),S(:,:,k));if isempty(Temp)DataSet=[];fprintf('参数错误:协方差矩阵S中数据存在问题(不是对称正定矩阵)\n');return;endDataSet=cat(1,DataSet,Temp);Endfunction ShowTwoInNdDataSet(x,y,S)%在N个d维向量构成的集合中,绘制该集合中的任意指定两个维度投影散点图形%输入参数:维度号x,维度号主,数据集S N*d[N,d]=size(S);if min(x,y)<1||max(x,y)>dfprintf('参数错误:输入的维数x、y超出范围啦\n');return;endfigure;plot(S(:,x),S(:,y),'.')%此处的分号不能有title('集合中的任意指定两个维度投影散点图形');function ShowTwoInNdCCDataSet(x,y,PiN,S)%在N个d维向量构成的集合中,绘制该集合中的任意指定两个维度投影散点图形%输入参数:维度号x,维度号主,每类的个数PiN,数据集S N*d[N,d]=size(S);if min(x,y)<1||max(x,y)>dfprintf('参数错误:输入的维数x、y超出范围啦\n');return;end[k,C]=size(PiN);if(k>1)||(C<1)fprintf('每类的个数(先验概率)PiN错误:应当为一个行向量\n');return;endif N~=sum(PiN)fprintf('参数错误:每类的个数PiN的总和与数据集S的行数不匹配\n');return;endM=max(PiN);%找出最多的一种类的数量Ps=ones(1,C);%算出每一类的起点位置for k=2:CPs(k)=Ps(k-1)+PiN(k-1);endX=zeros(M,C);Y=X;for J=1:Mfor k=1:Cif J<PiN(k)Ps(k)=Ps(k)+1;end%按顺序组装数据,以便每类对应于同一颜色X(J,k)=S(Ps(k),x);Y(J,k)=S(Ps(k),y);endendfigure;plot(X,Y,'x')%此处的分号不能有title('集合中的任意指定两个维度投影散点图形,每类一种颜色');。
