自动控制理论第六讲 方框图
合集下载
自动控制原理方框图
[注意]：
相临的信号相加点位置可以互换；见下例
X1(s)
X2(s)
X3(s)
Y (s)
X1(s)
X3(s)
X 2 (s)
Y (s)
同一信号的分支点位置可以互换：见下例
X1(s)
X (s) G(s) Y (s)
X 2 (s)
X (s) G(s) Y (s)
X 2 (s)
X1(s)
相加点和分支点在一般情况下，不能互换。
§2-３ 控制系统的结构图与信号流图
一、结构图的组成和绘制
１、结构图的组成 由四种基本图形符号组成
（1）函数方块
R(s) r(t) G(s)
C(s) c(t)
(2)信号线
R(s) r(t)
(3)分支点(引出点)
R(s) r(t)
R(s) r(t) R(s) r(t)
（4)综合点(比较点或相加点)
R(s)
R
R1Cs
2I
2
(s)
UI (cs)(s)
R2
R1
Uc (s)
U c (s)
I1 (s)
Uc (s)
几点说明：
（1）在结构图中，每一个方框中的传递函数都应是考虑了负 载效应后的传递函数。
（2）描述一个系统的结构图不是唯一的，选择不同的中间变 量得到不同的结构图；
（3）结构图中的方框与实际系统的元部件并非一定是一一对 应的；
X1(s) G(s) X2(s) N(s)
Y (s)
N(s) ? Y (s) [X1(s) X 2 (s)]G(s), 又 : Y (s) X (s)1G(s) X 2 (s)N(s), N(s) G(s)
把相加点从环节的输出端移到输入端：
自动控制原理方框图的化简课件
化简过程中的误差分析
误差来源分析
分析化简过程中可能产生的误差来源，如近似处理、线性化等。
误差传递与影响
评估误差对系统性能的影响，了解误差传递的方式和程度。
误差补偿与修正
根据误差分析结果，采取适当的补偿和修正措施，减小误差对系 统性能的影响。
化简后系统的性能分析
稳定性分析
通过化简后系统的传递函数或状态方程，分析系统的 稳定性。
方框图的组成元素
总结词
方框图由输入、输出、转换和反馈四个基本元素组成。
详细描述
方框图由输入、输出、转换和反馈四个基本元素组成。输入是系统接收的信号 或信息，输出是系统输出的信号或信息，转换是系统内部对输入进行处理的过 程，反馈则是系统对输出的反应或调整。
方框图的作用
• 总结词：方框图可以清晰地表示系统的结构、功能和动态特性。
04
方框图化简的注意事项
化简方法的适用性
确定化简方法的适用范围
01
不同的化简方法适用于不同类型和规模的方框图，应先判断所
处理的方框图是否适用。
理解化简方法的原理
02
掌握化简方法的原理和步骤，确保正确应用化简方法。
考虑化简后的系统性能
03
在化简方框图时，应考虑化简对系统性能的影响，如稳定性、
动态响应等。
02
通过化简方框图，可以快速识 别故障传递路径和关键环节， 提高故障诊断的效率和准确性 。
03
化简后的方框图可以作为故障 诊断的参考模型，为故障排除 提供指导和支持。
谢谢观看
• 详细描述：方框图具有多种作用。首先，它可以清晰地表示系统的结构，将复杂的系统分解为若干个简单的组成部分， 便于理解和分析。其次，通过方框图可以明确地表示出系统的功能，即各个组成部分的作用及其相互关系。此外，方框 图还可以表示系统的动态特性，例如信号的传递、处理和反馈过程，有助于揭示系统的动态行为和性能。在自动控制原 理中，方框图是分析和设计控制系统的重要工具之一。通过对方框图的分析，可以了解系统的性能、稳定性、可控性和 可观测性等方面的问题，为控制系统的设计和优化提供依据。
自动控制理论传递函数及方块图
因为
G1 (s) X 2 (s) X1 (s)
G 2 (s)
X 3 (s) X 2 (s)
G(s)
X 3 (s) X 2 (s) X 3 (s) G1 (s)G2 (s) X1 (s) X1 (s) X 2 (s)
结论：多个环节串联后总的传递函数等于每个环 节传递函数的乘积。 G(s) = G1(s) G2(s) Gn(s)
R1C2 s
ui ( s )
-
-
1 R1
1 C1s
u (s)
1 R2C2 s 1
uo ( s )
R1C2 s
ui ( s ) -
1 R1
1 C1s
u (s)
1 R2C2 s 1
uo ( s )
16
结构图等效变换例子||例2-11
R1C2 s
ui ( s ) -
1 R1C1 s 1
1 R2C2 s 1
uo ( s )
18
结构图等效变换例子||例2-11
ui ( s ) 1
R1
-
R1 R1C1s 1
C2 s R2C2 s 1
1 C2 s
uo ( s )
ui ( s ) 1
R1
R1C2 s ( R1C1s 1)(R2C2 s 1) R1C2 s
1 C2 s
uo ( s )
uo ( s) 1 G( s) ui ( s) ( R1C1s 1)( R2C2 s 1) R1C2 s
P34 表2-2
1、相加点前移
2、相加点后移
3、引出点前移
4、引出点后移
11
12
13
结构图等效变换例子||例2-11
自动控制理论第六讲 方框图
06
总结与展望
本讲内容总结
方框图基本概念
方框图的绘制方法
介绍了方框图的基本元素，包括方块、箭 头、分支点和交汇点等，以及它们在控制 系统中的含义。
详细讲解了如何根据控制系统的结构和功 能，选择合适的方块和连接方式，绘制出 清晰、准确的方框图。
方框图的分析方法
方框图在控制系统中的应用
介绍了方框图的分析步骤和方法，包括前 向通路、反馈通路、开环传递函数和闭环 传递函数的计算等。
梅森公式介绍
01
梅森公式是一种用于求解复杂控制系统方框图传递函
数的数学方法。
梅森公式应用步骤
02 首先找出所有前向通道、回路和不相交回路的传递函
数；然后按照梅森公式计算系统的总传递函数。
梅森公式在化简复杂方框图中的优势
03
能够简化计算过程，避免繁琐的代数运算，提高求解
效率。
实例分析：典型系统方框图化简过程
05
方框图在控制系统分析中的应用
稳定性分析：通过方框图判断系统稳定性
01
稳定性定义
系统受到扰动后，能够自动恢复到平衡状态的能力。
02 03
稳定性判据
通过方框图中各环节传递函数的极点位置，判断系统是否稳定。若极点 全部位于复平面的左半部分，则系统稳定；若有极点位于复平面的右半 部分，则系统不稳定。
结合实际工程问题进行实践
通过实际工程问题，将所学的方框图知识应用到实践中去，提高分析 和解决问题的能力。
拓展相关领域的知识
学习与自动控制理论相关的其他领域知识，如现代控制理论、智能控 制等，以完善自己的知识体系。
THANKS
感谢观看
方框图的作用
方框图是一种用图形符号表示系统各 环节间相互关系的图解表示法，它简 洁明了地表示了系统的结构和功能。
方框图等效变换和信号流图——《自动控制原理-理论篇》第2
G1 G2
x2
x1
G1 1 G1G2
x2
一个方框的输出信号输入到另一个方框后，得 到的输出再返回到这个方框的输入端，构成输入 信号的一部分。这种连接形式称为反馈连接。
反馈分正反馈和负反馈两种。 当G2(s)=1时，称为单位反馈系统。
（4）分支点（引出点）的移动：
分支点前移：
x1
G1
G2 G3
（6）各分点或合点之间互移
x
x1
x2 x3
x x
x
x x
x4
x1
x3 x2
x4
相邻分点可互换位置、可合并 相邻合点可互换位置、可合并
方框图等效变换基本规律
1、分点前移则函数相乘；分点后移则函数相除； (信息取出点等效变换) 2、而合点前移则函数相除；合点后移则函数相乘； (信息注入点等效变换)
方框图等效变换和信号流图
——《自动控制原理-理论篇》第2.5节
自动化工程学院自动控制原理课程组制
2015年11月
一、方框图的组成和绘制
方框图表示法是一种图解分析方法。 “方框”是对加到方框上的输入信号的一 种运算函数关系，运算结果用输出信号表 示。元件的传递函数，通常写在相应的方 框中，并且 用标明信号流向的箭头将这些 方框链接起来。这样，控制系统的方框图 就清楚地表示了系统中各个元件变量间关 系。
4. 按照系统中信号的传递顺序，依次将各元部件的 结构图连接起来，便可得到系统的结构图。
方框图的特点
能更直观更形象地表示系统中各环节的功能和相 互关系，以及信号的流向和每个环节对系统性能 的影响。更直观、更形象是针对系统的微分方程 而言的。 ② 方框图的流向是单向不可逆的，也没有负载效应。 ③ 方框图不唯一。由于研究角度不一样，传递函数 列写出来就不一样，方框图也就不一样。 ④ 线性叠加性：多个输入同时作用的结果等于各个 输入单独作用得到的结果之和；输入增加多少倍， 输出也相应的增加同样的倍数。
自动控制理论结构图
22
2.4 线性系统的结构图
结构图的等效变换和简化
复杂系统的化简:
串联、并联和反馈连接;层层嵌套
例2.8
R
G1
G2
G3
G4
Y
G1−1G4−1
G1−1G4−1
R
G1G2
G3G4 Y R
G1G2 1+ G1G2
G3G4 Y 1+ G3G4
23
2.4 线性系统的结构图
结构图的等效变换和简化
复杂系统的化简:
G3 Y (s) R(s)
H
G1 +1 G2
G2G3 Y (s) 1+ G2G3H
(a)
(b)
R(s) (G1 + G2 )G3 Y (s)
1+ G2G3H
20
2.4 线性系统的结构图
结构图的等效变换和简化
复杂系统的化简:
串联、并联和反馈连接;层层嵌套
例2.6
方法2: 2后移至3
G1(s)
R(s) 1
+2 -
G2(s)
+3
4 G3(s)
Y(s)
R
H(s)
G1
+
+G2
Y G3 G2H
图2-17 输入补偿型复合控制系统结构图
G(s) = Y (s) = (G1 + G2 )G3
R(s) 1+ G2G3H
21
2.4 线性系统的结构图
结构图的等效变换和简化
例2.7 两输入单输出系统结构图
扰动 D(s)
La J m
d
2ω m (t)
dt 2
+
自动控制原理：方框图的化简..
X o ( s) GB ( s) X i ( s)
注意:我们所指的前向通道的传递函数、反馈回路的 传递函数和开环传递函数都是针对一个闭环系统而 言的。它们都是闭环系统的一部分。系统闭环传递 函数是闭环系统的传递函数。看一个传递函数是什 么具体类型，要从定义出发，而不能只看其符号。
系统闭环传递函数
b.分支点之合并与拆（chai）分
X (s) X (s) X (s) X (s) X (s) X (s) X (s) X (s)
注意：分支点和相加点之间不具有上述等效规则
8.分支点和相加点之间等效规则
X 2 ( s)
X 1 ( s) X 1 ( s) X 2 ( s) X 1 ( s) X 2 ( s)
( Ls R) I a (s) Ed (s) U a (s)
Ed (s) kd (s)
Js( s) M ( s) M L ( s)
M ( s) km I a ( s)
1 I a (s) [U a ( s) Ed ( s)] ( Ls R)
U a ( s)
km
M ( s)
M L ( s)
1 Js
( s )
kd
E (s)
d
1
M L ( s)
-1
1 ( Ls R )
I a (s)
km
M ( s)
M L ( s)
1 Js
( s )
kd
Ed (s)
1 Js
M L ( s)
( s )
Ed (s)
kd km Ls R
M L ( s)
M ( s)
U a ( s)
注意:我们所指的前向通道的传递函数、反馈回路的 传递函数和开环传递函数都是针对一个闭环系统而 言的。它们都是闭环系统的一部分。系统闭环传递 函数是闭环系统的传递函数。看一个传递函数是什 么具体类型，要从定义出发，而不能只看其符号。
系统闭环传递函数
b.分支点之合并与拆（chai）分
X (s) X (s) X (s) X (s) X (s) X (s) X (s) X (s)
注意：分支点和相加点之间不具有上述等效规则
8.分支点和相加点之间等效规则
X 2 ( s)
X 1 ( s) X 1 ( s) X 2 ( s) X 1 ( s) X 2 ( s)
( Ls R) I a (s) Ed (s) U a (s)
Ed (s) kd (s)
Js( s) M ( s) M L ( s)
M ( s) km I a ( s)
1 I a (s) [U a ( s) Ed ( s)] ( Ls R)
U a ( s)
km
M ( s)
M L ( s)
1 Js
( s )
kd
E (s)
d
1
M L ( s)
-1
1 ( Ls R )
I a (s)
km
M ( s)
M L ( s)
1 Js
( s )
kd
Ed (s)
1 Js
M L ( s)
( s )
Ed (s)
kd km Ls R
M L ( s)
M ( s)
U a ( s)
自动控制理论第六讲方框图
【例6】二阶RC电气网 络
1）建立各元件的微分方程
2）将各元件的微分方程进行拉氏变换，并改写 成合适的形式。
3）依次将各元件的方框图按照变量的传递顺序连 接起来，绘出系统的图。、P48 2—9
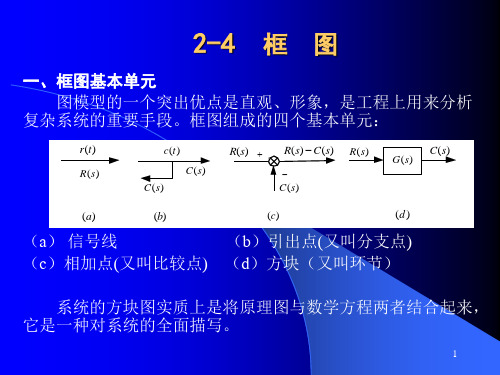
2、信号引出点（线）/测量点 表示信号引出或测量的位置和传递方向。同一信号线上引出的信号， 其性质、大小完全一样。
3、函数方框(环节) 函数方块具有运算功能
4、求和点（比较点、综合点） （1）用符号“”及相应的信号箭头表示 （2）箭头前方的“+”或“-”表示加上此信号或减去此信号
注意符号!!
相邻求和点可以互换、合并、分解。 代数运算的交换律、结合律和分配律。
求和点 引出线 信号线 函数方框 函数方框
三、方框图的运算规则
1、串联运算规则 几个环节串联，总的传递函数等于每个环节的传 递函数的乘积。
例：隔离放大器串联的RC电路
并联运算规则 同向环节并联的传递函数等于所有并联的环节传递 函数之和。
反馈运算规则
四、方框图的等效变换 1、基于方框图的运算规则
【例1】试简化系统结构图，并求系统传递函数。
C ( s ) G ( s ) G ( s ) 1 2 R ( s ) 1 G ( s ) G ( s ) G ( s ) G ( s ) H ( s ) 1 2 1 2 1
【例2】试简化系统结构图，并求系统传递函数。
方法1:
引出点后移
求和点可以有多个输入，但输出是唯一的!!
二、方框图的画法
画出各个模块的方框图。 形象直观地描述系统 中各元件间的相互关 系及其功能以及信号 在系统中的传递、变 换过程。
依据信号的流向 ，将各 元件的方块连接起来组 成整 个系统的方块图。
自动控制理论第六章校正2 41页PPT文档
4. 再作其正反馈根轨迹，求取同伦不动点
D(s) s2 2s
N (s) D (s) N (s) 0
N(s) s2 4s16
sk1 8
Nf(s)s8
5. 以 Gok(s)KgD N (sf)(s)K sg (s(s28)) 为开环传函，作负 反馈根轨迹，同伦不动点为根轨迹的终点，
-1 c 2c
-2
闭环频域指标
b = n
r = 0
Mr = 1
二阶参考模型法校正步骤 • 作原系统的伯德图L0 () • 根据性能指标的要求作二阶参考模型 L () • 两特性的伯德图相减，即得校正装置的伯
德图Lc ()
L c () L () L o () Gc()G()Go()
3=c c 4=cd c
0dB 1
-1 c 2
3 4 -2
1
1 ab
c
2
1 a
c
-3
• 中频段穿越斜率为 -1， 调节2 3 来调节中频段宽度 h ，动态性好。
• 高频段衰减率为 -3，抑制高频噪声，
转折位置由4来调节。
四阶参考模型校正步骤
• 作原系统的伯德图L0 ()
ω1,ω4同时向相反方向调整时，原相位裕度 基本不变
2390 2c 3c 2 2 & & 3 3 const
ω2 ,ω3同时向相同方向调整时，原相位裕度 基本不变
例：已知二阶系统校正前后的开环对数幅频特性
如图所示
-20dB/dec
0dB
12
0.5
-40dB/dec
期望的闭环极点位于根轨迹上。
6.计算根轨迹过希望极点的根轨迹增益
自动控制理论第六章
1
ss 0.5s1 s
解：1）调整K
G0 s
ss
1
0.5s1
s
Kv
lim
s0
G0
s
K
5s 1
2）作未校正系统的Bode图
G1 jω
jω1
5
j0.5ω1
jω
ωc 2.15,γ 20
系统不稳定
2023/12/21
第六章 控制系统的校正
15
自动控制理论
3）选择新的ωc
φ 180 γ ε 180 40 12 128
系数Kv=20s-1，r=50°，20lgKg=10dB
解：
令Gc s
K c
1 Ts
1 Ts
K
1 Ts
1 Ts
1）调整开环增益K，满足Kv的要求
校正前开环传递函数为
G1 s
KG0 s
4K
ss 2
Kv
lim
s0
s4K
ss 2
2K
20 ,
K
10
校正前系统的开环频率特性为
2023/12/21
G1 jω
K v
2s1
2023/12/21
第六章 控制系统的校正
图6-9
4
自动控制理论
2）确定希望的闭环极点
由ωn 4, ξ 0.5,求得sd 2 j2 3，
3）计算超前校正装置在sd处产生的超前角
arg
4
ss
2
ssd
210
超前角: φ 30
4）确定超前校正装置的零、极点
根据θ 60 ,φ 30 ,求得γ 45.按最大α值的设计法,由图解得
基于频率法的滞后-超前校正
自动控制原理第六章
Lc ()
90°
60°
c ()
30°
m
0°
1
m
2
如采用运算放大器进展补偿，那么无源超
前校正网络的传递函数如下
Gc(s)TTss11
假设采用如图6-08所示的有源超前校正
网络，那么其传递函数为
Gc(s)U Uo i((ss))-KcT s s1 1
KcR2R 1R3
RR 22RR 33R4C
T R 4 C T
通常，被控对象是的，而执行器和检测 反响那么根据被控对象的特点、控制要求以 及经济性、可靠性等选定的，这些设备可与 被控对象组合成控制系统的固有局部。
一般情况下，控制系统固有局部的性能 指标是很差的，必须引入附加装置对固有局 部进展改造，才能使控制系统全面满足静态 和动态性能要求。
这些为保证控制系统到达预期的性能指标 要求而有目的引入的附加装置称为控制系统 的校正装置，如图6-05所示。
第二节
常用校正装置及其特性
R(s)
E(s)
B(s)
G1(s)
C(s) G2(s)
H(s)
如果按增益来分，校正装置可分为无源校 正装置和有源校正装置两类，无源校正装置 的放大系数均小于 1 ，而有源校正装置的放 大系数可任意设置。
如果按相角频率特性来分，校正装置可分 为超前校正装置、滞后校正装置和滞后—超 前校正装置三种。
G c(j)j jT T 11
无源超前校正网络的波德图即对数频率特 性如图6-08所示。
00
-10 -20log 0dB/dec
-20
0dB/dec
20dB/dec -10log
Lc ()
90°
60°
c ()
自动控制原理方框图
)
H
(
s) H
(
s)
C(s)
GG55((ss)) CC((ss))
R(s) R(s)
GG1 1((ss)G) G3 1((ss)G) 3
R(sG) 2 (s)G4 (s)
(
s)G3
(
s
)G3 (s)H ( G3 (s) G3 (s)
s) G4 (s) H (s)
H (s)
H
(
s)
C(s) G5 (s)
1
1 U2(s)
R2 I2(s) C2 s
U2(s)
第14页/共32页
引出点移动
G1
H2 G2
G3
G4
G1G2G3G4
H1
1 G2G3H 2 G3G4H3 G1G2G3G4H1
H2
G1
G2
H3
1 G4
G3 a G4 b
H3 H1
第15页/共32页
相加点移动
向同无类用移功动
G3
G2
错！
G1
G2
1 uo (s) C2s
G(s) uo(s)
1
ui (s) (R1C1s 1)(R2C2s 1) R1C2s
第21页/共32页
解法三： ui (s) -
ui (s) -
1 I1(s) - 1 u(s)
R1
I (s) C1s
-
1
R2
1
-
1
R1
C1s
-
1
1 uo (s)
R2 I2(s) C2s
Uc (s)
U c (s)
I1 (s)
第3页/共32页
Uc (s)
自动控制原理_第6章共121页文档
根据负反馈理论所构成的典型控制系统的结构图如下 图所示，其特点是根据偏差e（t）来产生控制作用。偏差 是控制器Gc(s)的输入，而控制器Gc(s)的常常采用比例、 积分、微分等基本控制规律，或者这些规律的组合，其作 用是对偏差信号整形，产生合适的控制信号，实现对被控 对象的有效控制。
2019/11/30
比例—积分调节器主要用于在基本保证闭环系统 稳定性的前提下改善系统的稳态性能。
2019/11/30
EXIT
第6章第23页
2019/11/30
EXIT
第6章第24页
6.2.4比例、积分、微分控制
1.时域方程： m (t)K pe(t)K T ip 0 te(t)d tK pdd de(tt)
具有微分控制作用的控制器称为微分控制器,其传递函数为
Gc(s)=ds
输入偏差与输出控制信号的关系为
m(t)
d
d dt
e(t)
微分规律作用下输出信号与输入偏差的变化率成正比，因此，微分 调节器能够根据偏差的变化趋势去产生相应的控制作用。从频率法的角度 分析可知，由于微分环节具有高通滤波作用，微分调节器只在偏差的变化 过程中才起作用，当偏差恒定或变化缓慢时将失去作用，调节器无输出。 所以单一的微分调节器绝对不能单独使用，必须与其他基本控制规律组合。 微分校正常常是用来提高系统的动态性能,但对稳态精度不起作用。同时， 微分调节器有放大输入端高频干扰信号的缺点。
G2(s) C(s)
(a)
2019/11/30
(b)
EXIT
第6章第12页
6.1.3 频率法校正 (重点)
为图解法，在伯德图上校正居多 增加新环节以改变频率特性曲线形状，使之具有合适的低、 中、高频段，以获得满意的动、静态性能。 ① 分析法：选择一种校正装置，再分析是否满足要求→再 选择→再分析。 ② 期望法（串联校正）： 确定期望频率特性-已有频率特性=校正装置频率特性 只适用于最小相位系统，但有时难以物理实现。
2019/11/30
比例—积分调节器主要用于在基本保证闭环系统 稳定性的前提下改善系统的稳态性能。
2019/11/30
EXIT
第6章第23页
2019/11/30
EXIT
第6章第24页
6.2.4比例、积分、微分控制
1.时域方程： m (t)K pe(t)K T ip 0 te(t)d tK pdd de(tt)
具有微分控制作用的控制器称为微分控制器,其传递函数为
Gc(s)=ds
输入偏差与输出控制信号的关系为
m(t)
d
d dt
e(t)
微分规律作用下输出信号与输入偏差的变化率成正比，因此，微分 调节器能够根据偏差的变化趋势去产生相应的控制作用。从频率法的角度 分析可知，由于微分环节具有高通滤波作用，微分调节器只在偏差的变化 过程中才起作用，当偏差恒定或变化缓慢时将失去作用，调节器无输出。 所以单一的微分调节器绝对不能单独使用，必须与其他基本控制规律组合。 微分校正常常是用来提高系统的动态性能,但对稳态精度不起作用。同时， 微分调节器有放大输入端高频干扰信号的缺点。
G2(s) C(s)
(a)
2019/11/30
(b)
EXIT
第6章第12页
6.1.3 频率法校正 (重点)
为图解法，在伯德图上校正居多 增加新环节以改变频率特性曲线形状，使之具有合适的低、 中、高频段，以获得满意的动、静态性能。 ① 分析法：选择一种校正装置，再分析是否满足要求→再 选择→再分析。 ② 期望法（串联校正）： 确定期望频率特性-已有频率特性=校正装置频率特性 只适用于最小相位系统，但有时难以物理实现。
80自动控制理论第六讲第二章4
自适应性——减小系统参数变化对系统的影响 减小系统参数变化对系统的影响 自适应性 反馈能加快系统的瞬态响应 反馈能减小或消除干扰对系统的影响 反馈使系统的增益变小，稳定性变差。 反馈使系统的增益变小，稳定性变差。
第二章自动控制系统的数学模型 小结
1. 数学模型的基本概念：相似性、简化性和准确性 数学模型的基本概念：相似性、 2. 建立数学模型的方法：解析法和实验测试法 建立数学模型的方法： 3. 非线性数学模型的线性化：小偏差线性化方法 非线性数学模型的线性化： 4. 传递函数的定义、性质和求取方法 传递函数的定义、 5. 系统的动态结构图和等效变换 6. 信号流图的定义、性质、绘制方法和梅逊公式 信号流图的定义、性质、
2.6.2 信号流图的绘制
由系统微分方程绘制信号流图； 现控) 1）由系统微分方程绘制信号流图；(现控) 2）由系统结构图绘制信号流图。 由系统结构图绘制信号流图。
方框图化为信号流图
例：下图为一控制系统方框图，请将其化为信号 下图为一控制系统方框图， 流图并进行简化，求出系统的闭环传递函数。 流图并进行简化，求出系统的闭环传递函数。
上次课内容复习
一、系统动态结构图的定义和组成 二、绘制系统结构图的一般步骤 三、系统结构图的等效变换方法
通过移动引出点或比较点以及交换比较点或 引出点，进行方框运算将串联、并联和反馈连 引出点，进行方框运算将串联、 接的方框合并，减少内回路。 接的方框合并，减少内回路。
四、 系统的开环传递函数和闭环传递函数
L1= –G1 H1 L2= – G3 H3
L3= – G1G2G3H3H1
L5 = – G1G2G3
L1L2= (–G1H1) (–G3H3) = G1G3H1H3
L1L4=(–G1H1)(–G4G3)=G1G3G4H1
第二章自动控制系统的数学模型 小结
1. 数学模型的基本概念：相似性、简化性和准确性 数学模型的基本概念：相似性、 2. 建立数学模型的方法：解析法和实验测试法 建立数学模型的方法： 3. 非线性数学模型的线性化：小偏差线性化方法 非线性数学模型的线性化： 4. 传递函数的定义、性质和求取方法 传递函数的定义、 5. 系统的动态结构图和等效变换 6. 信号流图的定义、性质、绘制方法和梅逊公式 信号流图的定义、性质、
2.6.2 信号流图的绘制
由系统微分方程绘制信号流图； 现控) 1）由系统微分方程绘制信号流图；(现控) 2）由系统结构图绘制信号流图。 由系统结构图绘制信号流图。
方框图化为信号流图
例：下图为一控制系统方框图，请将其化为信号 下图为一控制系统方框图， 流图并进行简化，求出系统的闭环传递函数。 流图并进行简化，求出系统的闭环传递函数。
上次课内容复习
一、系统动态结构图的定义和组成 二、绘制系统结构图的一般步骤 三、系统结构图的等效变换方法
通过移动引出点或比较点以及交换比较点或 引出点，进行方框运算将串联、并联和反馈连 引出点，进行方框运算将串联、 接的方框合并，减少内回路。 接的方框合并，减少内回路。
四、 系统的开环传递函数和闭环传递函数
L1= –G1 H1 L2= – G3 H3
L3= – G1G2G3H3H1
L5 = – G1G2G3
L1L2= (–G1H1) (–G3H3) = G1G3H1H3
L1L4=(–G1H1)(–G4G3)=G1G3G4H1
自动控制理论第六讲__方框图35页PPT
何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间，才能认识自 己。——德国
43、重复别人所说的话，只需要教育； 而要挑战别人所说的话，则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是：在不利与艰 难的遭遇里百折不饶。——贝多芬
自动控制理论第六讲__方框图
11、获得的成功越大，就越令人高兴 。野心 是使人 勤奋的 原因， 节制使 人枯萎 。 12、不问收获，只问耕耘。如同种树 ，先有 根茎， 再有枝 叶，尔 后花实 ，好好 劳动， 不要想 太多， 那样只 会使人 胆孝懒 惰，因 为不实 践，甚 至不接 触社会 ，难道 你是野 人。(名 言网) 13、不怕，不悔(虽然只有四个字，但 常看常 新。 14、我在心里默默地为每一个人祝福 。我爱 自己， 我用清 洁与节 制来珍 惜我的 身体， 我用智 慧和知 识充实 我的头 脑。 15、这世上的一切都借希望而完成。 农夫不 会播下 一粒玉 米，如 果他不 曾希望 它长成 种籽； 单身汉 不会娶 妻，如 果他不 曾希望 有小孩 ；商人 或手艺 人不会 工作， 如果他 不曾希 望因此 而有收 益。-- 马钉路 德。
45、自己的饭量自己知道。——苏联
42、只有在人群中间，才能认识自 己。——德国
43、重复别人所说的话，只需要教育； 而要挑战别人所说的话，则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是：在不利与艰 难的遭遇里百折不饶。——贝多芬
自动控制理论第六讲__方框图
11、获得的成功越大，就越令人高兴 。野心 是使人 勤奋的 原因， 节制使 人枯萎 。 12、不问收获，只问耕耘。如同种树 ，先有 根茎， 再有枝 叶，尔 后花实 ，好好 劳动， 不要想 太多， 那样只 会使人 胆孝懒 惰，因 为不实 践，甚 至不接 触社会 ，难道 你是野 人。(名 言网) 13、不怕，不悔(虽然只有四个字，但 常看常 新。 14、我在心里默默地为每一个人祝福 。我爱 自己， 我用清 洁与节 制来珍 惜我的 身体， 我用智 慧和知 识充实 我的头 脑。 15、这世上的一切都借希望而完成。 农夫不 会播下 一粒玉 米，如 果他不 曾希望 它长成 种籽； 单身汉 不会娶 妻，如 果他不 曾希望 有小孩 ；商人 或手艺 人不会 工作， 如果他 不曾希 望因此 而有收 益。-- 马钉路 德。
45、自己的饭量自己知道。——苏联
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
二、方框图的画法
画出各个模块的方框图。 画出各个模块的方框图。 形象直观地描述系统 形象直观地描述系统 中各元件间的相互关 系及其功能以及信号 在系统中的传递、 在系统中的传递、变 换过程。 换过程。
依据信号的流向 ，将各 元件的方块连接起来组 个系统的方块图。 成整 个系统的方块图。
脱离了物理系统的模型!! 脱离了物理系统的模型!!
CHANG’AN UNIVERSITY
系统数学模型的图解形式!! 系统数学模型的图解形式!!
长安大学电子与控制工程学 院
自动控制理论
方框图
任何系统都可以由信号线、函数方块、 任何系统都可以由信号线、函数方块、信 号引出点及求和点组成的方框图来表示。 号引出点及求和点组成的方框图来表示。
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
注意符号!! 注意符号!!
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
相邻求和点可以互换、合并、分解。 相邻求和点可以互换、合并、分解。 代数运算的交换律、结合律和分配律。 代数运算的交换律、结合律和分配律。
求和点可以有多个输入，但输出是唯一的!! 求和点可以有多个输入，但输出是唯一的!!
自动控制理论
方框图
2、综合点（比较点）的移动 、综合点（比较点）
1）综合点前移 x1 x3 2）综合点后移 G(S) X2 X3 X1 G(S) 1/G(S) X2 X3 x2 x1 x3 x2
G(s)
G(s) G(s)
X1
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
例：隔离放大器串联的RC电路 隔离放大器串联的RC RC电路
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
并联运算规则 同向环节并联的传递函数等于所有并联的环节传递 函数之和。
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
试简化系统结构图，并求系统传递函数。 【例1】试简化系统结构图，并求系统传递函数。
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
长安大学电子与控制工程学 院
自动控制理论
方框图
【例6】二阶RC电气网 二阶RC电气网 RC 络
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
1）建立各元件的微分方程 ）
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
2）将各元件的微分方程进行拉氏变换，并改写 ）将各元件的微分方程进行拉氏变换， 成合适的形式。 成合适的形式。
3）依次将各元件的方框图按照变量的传递顺序连 ） 接起来，绘出系统的图。 接起来，绘出系统的图。
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
作
业
1、P48 2—8 、 2、P48 2—9 、
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
一、方框图的组成要素
1、信号线 带有箭头的直线， 带有箭头的直线，箭头表示信号的 传递方向， 传递方向，直线旁标记信号的时间函 数或象函数。 数或象函数。
2、信号引出点（线）/测量点 信号引出点（ 表示信号引出或测量的位置和传递方向。同一信号线上引出的信号， 表示信号引出或测量的位置和传递方向。同一信号线上引出的信号， 其性质、大小完全一样。 其性质、大小完全一样。
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
【例3】 】
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
【例4】 】
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
5、公式法求系统的传递函数 、 只有一条前向通道的多回路系统的闭环传递函数
自动控制理论
方框图
第六讲 方框图及其等效变换
主要内容 一、方框的组成要素 二、方框图的画法 三、方框的运算规则 四、方框图的等效变换和化简 五、物理系统的方框图绘制方法
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
结构方框图
输入量
输出量
比较
控制器
被控对象
测量电路
求和点 引出线 信号线 函数方框 函数方框
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
三、方框图的运算规则 1、串联运算规则 几个环节串联，总的传递函数等于每个环节的传 递函数的乘积。
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
自动控制理论
方框图
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
试简化系统结构图，并求系统传递函数。 【例2】试简化系统结构图，并求系统传递函数。
方法1: 引出点后移
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
方法2: 引出点前移 方法
方框图
3、引出点的移动 、
1）引出点前移 X1 X1 G(S) X2 X1 G(S) 1/G(S) X1 X2
2）引出点后移 G(S) X2 X2
CHANG’AN UNIVERSITY
X1
X1
G(S) G(S)
X2 X2
长安大学电子与控制工程学 院
自动控制理论
方框图
4、综合点互换
x3 x1 x2 Y x1 x2 x3 Y
自动控制理论
方框图
五、物理系统的方框图绘制方法 1）建立各元件的微分方程 ） 2）将各元件的微分方程进行拉氏变换，并改写 ）将各元件的微分方程进行拉氏变换， 成合适的形式。 成合适的形式。 3）依次将各元件的方框图按照变量的传递顺序连 ） 接起来，绘出系统的图。 接起来，绘出系统的图。
CHANG’AN UNIVERSITY
方框图
反馈运算规则
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
四、方G’AN UNIVERSITY
长安大学电子与控制工程学 院
CHANG’AN UNIVERSITY
-正反馈
+ 负反馈
长安大学电子与控制工程学 院
自动控制理论
方框图
【例5】公式法求取传递函数 】
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
6、代数法求系统传递函数 、
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
相邻综合点之间可以随意调换位置
注意： 注意：相邻引出点和综合 点之间不能互换! 点之间不能互换!
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
4、方框图简化法求系统传递函数的一般步骤 （1）观察系统中是否存在相互交错的局部反馈回路； ）观察系统中是否存在相互交错的局部反馈回路； （2）通过比较点和引出点的移动消除交错回路； ）通过比较点和引出点的移动消除交错回路； （3）先求出并联环节和具有局部反馈环节的传递函 ） 然后求出整个系统的传递函数。 数，然后求出整个系统的传递函数。
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
3、函数方框(环节) 函数方框(环节) 函数方块具有运算功能
4、求和点（比较点、综合点） 求和点（比较点、综合点） 用符号“ （1）用符号“⊕”及相应的信号箭头表示 箭头前方的“+”或 （2）箭头前方的“+”或“-”表示加上此信号或减去此信号
Φ( s) = GA (s) 1 + ∑ (±)GBi ( s)
i =1 n
G A (s) 闭环系统输入量到输出量间的串联环节的总传递函
数即前向通路传递函数的乘积。
GBi (s) 闭环系统中各交错反馈或多环局部反馈的开环传递
函数即每个反馈回路的传递函数的乘积。
n 闭环系统所具有的反馈回路的总数 i 各反馈回路的序号
长安大学电子与控制工程学 院
自动控制理论
方框图
二、方框图的画法
画出各个模块的方框图。 画出各个模块的方框图。 形象直观地描述系统 形象直观地描述系统 中各元件间的相互关 系及其功能以及信号 在系统中的传递、 在系统中的传递、变 换过程。 换过程。
依据信号的流向 ，将各 元件的方块连接起来组 个系统的方块图。 成整 个系统的方块图。
脱离了物理系统的模型!! 脱离了物理系统的模型!!
CHANG’AN UNIVERSITY
系统数学模型的图解形式!! 系统数学模型的图解形式!!
长安大学电子与控制工程学 院
自动控制理论
方框图
任何系统都可以由信号线、函数方块、 任何系统都可以由信号线、函数方块、信 号引出点及求和点组成的方框图来表示。 号引出点及求和点组成的方框图来表示。
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
注意符号!! 注意符号!!
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
相邻求和点可以互换、合并、分解。 相邻求和点可以互换、合并、分解。 代数运算的交换律、结合律和分配律。 代数运算的交换律、结合律和分配律。
求和点可以有多个输入，但输出是唯一的!! 求和点可以有多个输入，但输出是唯一的!!
自动控制理论
方框图
2、综合点（比较点）的移动 、综合点（比较点）
1）综合点前移 x1 x3 2）综合点后移 G(S) X2 X3 X1 G(S) 1/G(S) X2 X3 x2 x1 x3 x2
G(s)
G(s) G(s)
X1
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
例：隔离放大器串联的RC电路 隔离放大器串联的RC RC电路
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
并联运算规则 同向环节并联的传递函数等于所有并联的环节传递 函数之和。
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
试简化系统结构图，并求系统传递函数。 【例1】试简化系统结构图，并求系统传递函数。
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
长安大学电子与控制工程学 院
自动控制理论
方框图
【例6】二阶RC电气网 二阶RC电气网 RC 络
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
1）建立各元件的微分方程 ）
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
2）将各元件的微分方程进行拉氏变换，并改写 ）将各元件的微分方程进行拉氏变换， 成合适的形式。 成合适的形式。
3）依次将各元件的方框图按照变量的传递顺序连 ） 接起来，绘出系统的图。 接起来，绘出系统的图。
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
作
业
1、P48 2—8 、 2、P48 2—9 、
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
一、方框图的组成要素
1、信号线 带有箭头的直线， 带有箭头的直线，箭头表示信号的 传递方向， 传递方向，直线旁标记信号的时间函 数或象函数。 数或象函数。
2、信号引出点（线）/测量点 信号引出点（ 表示信号引出或测量的位置和传递方向。同一信号线上引出的信号， 表示信号引出或测量的位置和传递方向。同一信号线上引出的信号， 其性质、大小完全一样。 其性质、大小完全一样。
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
【例3】 】
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
【例4】 】
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
5、公式法求系统的传递函数 、 只有一条前向通道的多回路系统的闭环传递函数
自动控制理论
方框图
第六讲 方框图及其等效变换
主要内容 一、方框的组成要素 二、方框图的画法 三、方框的运算规则 四、方框图的等效变换和化简 五、物理系统的方框图绘制方法
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
结构方框图
输入量
输出量
比较
控制器
被控对象
测量电路
求和点 引出线 信号线 函数方框 函数方框
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
三、方框图的运算规则 1、串联运算规则 几个环节串联，总的传递函数等于每个环节的传 递函数的乘积。
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
自动控制理论
方框图
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
试简化系统结构图，并求系统传递函数。 【例2】试简化系统结构图，并求系统传递函数。
方法1: 引出点后移
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
方法2: 引出点前移 方法
方框图
3、引出点的移动 、
1）引出点前移 X1 X1 G(S) X2 X1 G(S) 1/G(S) X1 X2
2）引出点后移 G(S) X2 X2
CHANG’AN UNIVERSITY
X1
X1
G(S) G(S)
X2 X2
长安大学电子与控制工程学 院
自动控制理论
方框图
4、综合点互换
x3 x1 x2 Y x1 x2 x3 Y
自动控制理论
方框图
五、物理系统的方框图绘制方法 1）建立各元件的微分方程 ） 2）将各元件的微分方程进行拉氏变换，并改写 ）将各元件的微分方程进行拉氏变换， 成合适的形式。 成合适的形式。 3）依次将各元件的方框图按照变量的传递顺序连 ） 接起来，绘出系统的图。 接起来，绘出系统的图。
CHANG’AN UNIVERSITY
方框图
反馈运算规则
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
四、方G’AN UNIVERSITY
长安大学电子与控制工程学 院
CHANG’AN UNIVERSITY
-正反馈
+ 负反馈
长安大学电子与控制工程学 院
自动控制理论
方框图
【例5】公式法求取传递函数 】
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
6、代数法求系统传递函数 、
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
相邻综合点之间可以随意调换位置
注意： 注意：相邻引出点和综合 点之间不能互换! 点之间不能互换!
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
4、方框图简化法求系统传递函数的一般步骤 （1）观察系统中是否存在相互交错的局部反馈回路； ）观察系统中是否存在相互交错的局部反馈回路； （2）通过比较点和引出点的移动消除交错回路； ）通过比较点和引出点的移动消除交错回路； （3）先求出并联环节和具有局部反馈环节的传递函 ） 然后求出整个系统的传递函数。 数，然后求出整个系统的传递函数。
CHANG’AN UNIVERSITY
长安大学电子与控制工程学 院
自动控制理论
方框图
3、函数方框(环节) 函数方框(环节) 函数方块具有运算功能
4、求和点（比较点、综合点） 求和点（比较点、综合点） 用符号“ （1）用符号“⊕”及相应的信号箭头表示 箭头前方的“+”或 （2）箭头前方的“+”或“-”表示加上此信号或减去此信号
Φ( s) = GA (s) 1 + ∑ (±)GBi ( s)
i =1 n
G A (s) 闭环系统输入量到输出量间的串联环节的总传递函
数即前向通路传递函数的乘积。
GBi (s) 闭环系统中各交错反馈或多环局部反馈的开环传递
函数即每个反馈回路的传递函数的乘积。
n 闭环系统所具有的反馈回路的总数 i 各反馈回路的序号