初中数学浙教版八年级下册第3章 数据分析初步3.2 中位数和众数-章节测试习题(7)
浙教版八年级下《3.2中位数和众数》同步练习含答案
分别为 (
)
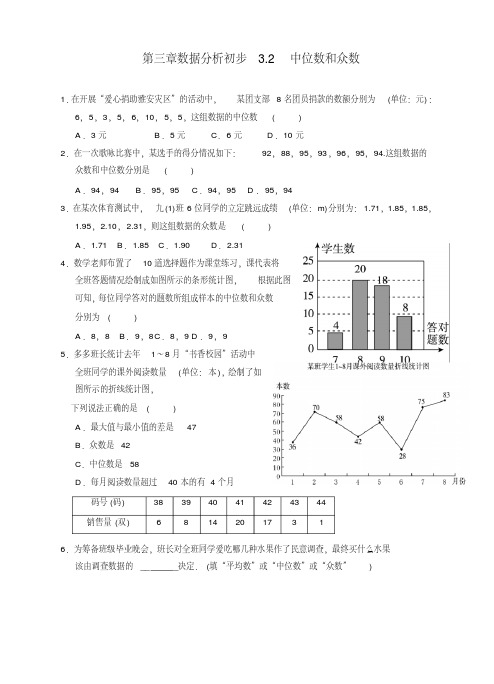
A ．8， 8 B． 9，8 C．8， 9 D ．9， 9 5．多多班长统计去年 1～8 月“书香校园”活动中
全班同学的课外阅读数量 (单位： 本 )，绘制了如 图所示的折线统计图，
下列说法正确的是 (
平”，所以方案 1 不适合作为最后得分的方案． 因为方案 4 中的众数有两个，众数失去了实际意义，所以方案
4 不适合作为
最后得分的方案．
9．如图是某市某景点 6 月份内 1～10 日每天的最高气温 折线统计图， 由图中信息可知该景点这 10 天的最高气Leabharlann 温的中位数是 ____℃ .
10．为了全面了解学生的学习、生活及家庭的基本情况， 加强学校、家庭的联系，梅灿中学积极组织全体教师 开展“课外访万家活动”，王老师对所在班级的全体学生进行实地家访，了解到每名学
第三章数据分析初步 3.2 中位数和众数
1．在开展“爱心捐助雅安灾区”的活动中， 某团支部 8 名团员捐款的数额分别为 (单位：元) ：
6， 5，3， 5， 6， 10， 5，5，这组数据的中位数 (
)
A ．3 元
B．5 元
C． 6 元
D ．10 元
2．在一次歌咏比赛中，某选手的得分情况如下：
92， 88， 95，93，96， 95， 94.这组数据的
(2)64 63 1
15、解： (1) 方案 1 最后得分为 10(3.2 ＋7.0 ＋7.8 ＋ 3× 8＋3×8.4 ＋ 9.8) ＝ 7.7 ；
1 方案 2 最后得分为 8(7.0 ＋ 7.8 ＋3×8＋3×8.4) ＝ 8；
浙教版数学八年级下册 第3章 数据分析初步 3.2 中位数和众数 同步练习题和答案
第3章数据分析初步 3.2 中位数和众数1．七(1)班举行投篮比赛，每人投5球．如图是全班学生投进球数的扇形统计图，则投进球数的众数是( )球A. 3球B. 4球C. 5球D. 2球2. 某地区连续5天的最高气温（单位：℃）分别是30，33，24，29，24.这组数据的中位数是( )A.29B.28C.24D.93.某班七个兴趣小组的人数分别为3,3,4，x,5,5,6，已知这组数据的平均数是4，则这组数据的中位数是( )．A. 2B. 4C. 4.5D. 54.100名学生进行20秒钟跳绳测试，测试成绩统计如下表：A.40＜m≤50B.50＜m≤60C.60＜m≤70D. x＞705. 某6人活动小组为了解本组成员的年龄情况，作了一次调查，统计的年龄如下(单位：岁)：12，13，14，15，15，15，则这组数据中的众数，平均数分别为( )A．12，14 B．12，15 C．15，14 D．15，136. 在一次中学生田径运动会上，参加跳高的15名运动员的成绩如下表：那么这些运动员跳高成绩的众数是( )A．4 B．1.75 C．1.70 D．1.657. 下列说法错误的是( )A．给定一组数据，那么这组数据的平均数一定只有一个B．给定一组数据，那么这组数据的中位数一定只有一个C．给定一组数据，那么这组数据的众数一定只有一个D．如果一组数据存在众数，那么该众数一定是这组数据中的某一个8．若一组数据3，x，4，5，6的众数是6，则这组数据的中位数是( ) A．3 B．4 C．5 D．69. 如表为八(1)班全部43名同学某次数学测验成绩的统计结果，则下列说法正确的是( )A.男生的平均成绩大于女生的平均成绩B．男生的平均成绩小于女生的平均成绩C．男生成绩的中位数大于女生成绩的中位数D．男生成绩的中位数小于女生成绩的中位数10. 甲、乙两组各有12名学生，组长绘制了本组5月份家庭用水量的统计图表，如图：甲组12户家庭用水量统计表比较5月份两组家庭用水量的中位数，下列说法正确的是( )A．甲组比乙组大 B．甲、乙两组相同C．乙组比甲组大 D．无法判断11. 若一组数据 1，1，2，3，x的平均数是3，则这组数据的众数是________．12. 数据2，2，3，4，5的中位数是________．13. 为了了解某班数学成绩情况，抽样调查了13份试卷成绩，结果如下：3个140分，4个135分，2个130分，2个120分，1个100分，1个80分．则这组数据的中位数为____________分．14. 已知一组从小到大排列的数据：2，5，x，y，2x，11的平均数与中位数都是7，则这组数据的众数是_________.15. 一个样本为1，3，2，2，a，b，c，已知这个样本的众数为3，平均数为2，则这组数据的中位数为_________.16. 有19位同学参加歌咏比赛，所得的分数互不相同，取前10位同学进入决赛．某同学知道自己的分数后，要判断自己能否进入决赛，他只需知道这19位同学的_________数.17. 根据PM2.5空气质量标准：24小时PM2.5均值在0～35(微克/立方米)的空气质量等级为优．将环保部门对我市PM2.5一周的检测数据制作成如下统计表，这组PM2.5数据的中位数是_________微克/立方米18. 某市某超市五月份的第一周鸡蛋价格分别为7.2,7.2,6.8,7.2,7.0,7.0,6.6（单位：元/kg）则该超市这一周鸡蛋价格的众数为。
八下第3章数据分析初步3-2中位数和众数习题新版浙教版
为 200 km，所以中位数为 200 km；205 km 出现的次数
最多，所以众数为 205 km；
(2)为了尽可能避免行程中充电耽误时间，又能经济实惠 地用车，请你从相关统计量和符合行程要求的百分比 等进行分析，给出合理的用车型号建议．
【解】A型号汽车的平均里程、中位数和众数均低 于210 km，且只有10%的车辆能达到行程要求，故 不建议选择；B，C型号汽车的平均里程、中位数 和众数都超过210 km，其中B型号汽车有90%符合 行程要求，很大程度上可以避免行程中充电耽误时 间，且B型号汽车比C型号汽车更经济实惠，故建 议选择B型号汽车．
3.
中位数和众数
2
1 [2023·金华]上周双休日，某班8名同学课外阅读的时间
如下(单位：时)：1，4，2，4，3，3，4，5.这组数据
的众数是( D )
A．1时
B．2时 C．3时 D．4时
2 [2023·深圳]下表为五种运动耗氧情况，其中耗氧量的 中位数是( C )
打网球 跳绳 爬楼梯 慢跑 游泳 80 L/h 90 L/h 105 L/h 110 L/数据1，x，5，7有唯一众数，且中 位数是6，则平均数是( ) A．6 B．5 C．4 D．3
【点拨】
∵一组数据 1，x，5，7 有唯一众数， ∴x 的值只能是 1，5，7. ∵中位数是 6，∴x＝7， ∴平均数为14×(1＋5＋7＋7)＝5. 【答案】B
9 有11个正整数，平均数是10，中位数是9，众数只有一 个8，则最大的正整数最大为( ) A．25 B．30 C．35 D．40
【点拨】 ∵11个正整数，平均数是10， ∴和为110. ∵中位数是9，众数只有一个8， ∴当11个正整数为1，1，8，8，8，9，9，10，
初中数学浙教版八年级下册第3章 数据分析初步3.2 中位数和众数-章节测试习题(9)
章节测试题1.【答题】一次数学模考后，李老师统计了20名学生的成绩．记录如下：有6人得了85分，有5人得了80分，有4人得了65分，有5人得了90分．则这组数据的中位数和平均数分别是（）A. 82.5，82.5B. 85，81C. 82.5，81D. 85，82.5【答案】B【分析】根据中位数、平均数的定义分别列出算式，再进行计算即可．【解答】解：∵共有20个数，∴中位数是第10、11个数的平均数，∴中位数是（85+85）÷2=85；平均数是（85×6+80×5+65×4+90×5）=81；选B．2.【答题】一组数据：10、5、15、5、20，则这组数据的平均数和中位数分别是（）A. 10，10B. 10，12.5C. 11，12.5D. 11，10【答案】D【分析】根据中位数和平均数的定义结合选项选出正确答案即可．【解答】解：这组数据按从小到大的顺序排列为：5，5，10，15，20，故平均数为：=11，中位数为：10．选D．3.【答题】一组数据：0，1，2，3，3，5，5，10的中位数是（）A. 2.5B. 3C. 3.5D. 5【答案】B【分析】根据中位数的定义先把这组数据从小到大排列，再求出最中间两个数的平均数即可．【解答】将这组数据从小到大排列为：0，1，2，3，3，5，5，10，最中间两个数的平均数是：（3+3）÷2=3，则中位数是3；选B．4.【答题】在一次体育测试中，小芳所在小组8人的成绩分别是：46，47，48，48，49，49，49，50，则8人体育成绩的中位数是（）A. 47B. 48C. 48.5D. 49【答案】C【分析】将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数，由此计算即可．【解答】解：这组数据的中位数为=48.5．选C．5.【答题】7位同学中考体育测试立定跳远成绩（单位：分）分别是：8，9，7，6，10，8，9，这组数据的中位数是（）A. 6B. 8C. 9D. 10【答案】B【分析】把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数，由此即可确定这组数据中位数．【解答】把这组数据从小到大排序后为6，7，8，8，9，9，10，其中第四个数据为8，∴这组数据的中位数为8．选B．6.【答题】数字1、2、5、3、5、3、3的中位数是（）A. 1B. 2C. 3D. 5【答案】C【分析】将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．【解答】将数据从大到小排列为：1，2，3，3，3，5，5，选C．7.【答题】数据0，1，1，3，3，4的中位数和平均数分别是（）A. 2和2.4B. 2和2C. 1和2D. 3和2【答案】B【分析】根据中位数和平均数的定义求解即可．【解答】解：这组数据的中位数为：（1+3）÷2=2，平均数为：=2．选B．8.【答题】七（1）班的6位同学在一节体育课上进行引体向上训练时，统计数据分别为7，12，10，6，9，6则这组数据的中位数是（）A. 6B. 7C. 8D. 9【答案】C【分析】将该组数据按从小到大依次排列，找到位于中间位置的两个数，求出其平均数即为正确答案．【解答】解：将该组数据按从小到大依次排列为6，6，7，9，10，12，位于中间位置的数为7，9，其平均数为x==8，选C．9.【答题】为了解长城小区“全民健身”活动的开展情况，随机对居住在该小区的40名居民一周的体育锻炼时间进行了统计，结果如下表：这40名居民一周体育锻炼时间的中位数是（）A. 4小时B. 4.5小时C. 5小时D. 5.5小时【答案】C【分析】中位数是将一组数据按大小依次排列，把处在最中间位置的一个数据或者最中间两个数据的平均数叫这组数据的中位数．本组数据中，把数据按照从大到小的顺序排列，最中间的两个数的平均数即为中位数．【解答】由统计表可知：统计表中是按从小到大的顺序排列的，最中间两个人的锻炼时间都是5小时，故中位数是5小时．选C．10.【答题】下列数据3，2，3，4，5，2，2的中位数是（）A. 5B. 4C. 3D. 2【答案】C【分析】求中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数．【解答】题目中数据共有7个，把数据按从小到大的顺序排列为2，2，2，3，3，4，5，故中位数是按从小到大排列后第4个数是3，故这组数据的中位数是3．选C．11.【答题】某射击运动员在一次射击练习中，成绩（单位：环）记录如下：8，9，8，7，10．这组数据的平均数和中位数分别是（）A. 8，8B. 8.4，8C. 8.4，8.4D. 8，8.4【答案】B【分析】根据平均数公式求解即可，即用所有数据的和除以5即可；5个数据的中位数是排序后的第三个数．【解答】解：8，9，8，7，10的平均数为×（8+9+8+7+10）=8.4．8，9，8，7，10排序后为7，8，8，9，10，故中位数为8．选B．12.【答题】一组数据：-1、2、1、0、3，则这组数据的平均数和中位数分别是（）A. 1，0B. 2，1C. 1，2D. 1，1【答案】D【分析】根据中位数的定义和平均数的求法计算即可，中位数是将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．【解答】平均数=（-1+2+1+0+3）÷5=1；把这组数据按从大到小的顺序排列是：-1，0，1，2，3，故这组数据的中位数是：1．选D．13.【答题】爱华中学生物兴趣小组调查了本地区几棵古树的生长年代，记录数据如下（单位：年）：200，240，220，200，210．这组数据的中位数是（）A. 200B. 210C. 220D. 240【答案】B【分析】找中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数．【解答】题目中数据共有5个，按从小到大排列后为：200、200、210、220、240，位于最中间的一个数是210，∴这组数据的中位数是210；选B．14.【答题】一组数据：75、95、85、100、125的中位数是（）A. 85B. 95C. 96D. 100【答案】B【分析】根据中位数的定义计算：将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．【解答】按从小到大的顺序排列为：75，85，95，100，125，根据中位数的定义得；中位数是95．选B．15.【答题】一条葡萄藤上结有五串葡萄，每串葡萄的粒数如图所示（单位：粒）．则这组数据的中位数为（）A. 37B. 35C. 33.8D. 32【答案】B【分析】找中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数．【解答】先对这组数据按从小到大的顺序重新排序：28，32，35，37，37，位于最中间的数是35，∴这组数的中位数是35．选B．16.【答题】十名射箭运动员进行训练，每人射箭一次，成绩如下表：则十名运动员射箭成绩的中位数（环）为（）A. 9B. 8C. 6D. 10或9【答案】A【分析】根据中位数的定义求解即可，将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．【解答】将十名射箭运动员进行训练的成绩按照从小到大的顺序排列为6，6，7，7，9，9，9，10，10，10，∴十名运动员射箭成绩的中位数（环）为（9+9）÷2=9．选A．17.【答题】在“庆祝建党90周年的红歌传唱活动”比寒中，七位评委给某参赛队打的分数为：92、86、88、87、92、94、86，则去掉一个最高分和一个最低分后，所剩五个分数的平均数和中位数是（）A. 89，92B. 87，88C. 89，88D. 88，92【答案】C【分析】要求平均数只要求出数据之和再除以总个数即可；求中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数．【解答】根据去掉一个最高分和一个最低分后，所剩五个分数的平均数为：平均数：（92+86+88+87+92）÷5=89，故平均数是89；将数据按从小到大的顺序排列得：18.【答题】某校开展为“希望小学”捐书活动，以下是八名学生捐书的册数：2，3，2，2，6，7，6，5，则这组数据的中位数为（）A. 4B. 4.5C. 3D. 2【答案】A【分析】把这组数据按照从小到大排列，在中间位置的数就是中位数．【解答】解：2，2，2，3，5，6，6，7在中间位置的是3和5，∴平均数是=4．选A．19.【答题】某地区连续5天的最高气温（单位：℃）分别是：30，33，24，29，24．这组数据的中位数是（）A. 29B. 28C. 24D. 9【答案】A【分析】求中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数．【解答】数据排序为：24、24、29、30、33，∴中位数为29，选A．20.【答题】某校九年级一班体育委员在一次体育课上记录了六位同学托排球的个数分别为37，25，30，35，28，25，这组数据的中位数为（）A. 25B. 28C. 29D. 32.5【答案】C【分析】先把数据按从小到大排列：25，25，28，30，35，37，最中间两个数分别28和30，计算它们的平均数即可．【解答】把数据按从小到大排列：25，25，28，30，35，37，共有6个数，最中间两个数的平均数=（28+30）÷2=29，∴这组数据的中位数为29．选C．。
(新)浙教版八年级数学下册3.2 中位数和众数 习题(含答案)
万元．
20. 为了缓解旱情，某市发射增雨火箭，实施增雨作业. 在一场降雨中，某县测得 10 个面积相等区域的降雨量如下
图表所示：
区域
1 2 3 4 5 6 7 8 9 10
降雨量 (mm) 10 12 13 13 20 15 14 15 14 14
该县这 10 个区域降雨量的众数为 ( ) mm ; 平均降雨量为 ( ) mm .
3.2 中位数和众数
一、选择题
1. 我市某中学举办了一次以“我的中国梦”为主题的演讲比赛，最后确定 7 名同学参加决赛，他们的决赛成绩各
不相同，其中李华已经知道自己的成绩，但能否进前四名，他还必须清楚这七名同学成绩的( )
A. 众数
B. 平均数
C. 中位数
D. 方差
2. 某同学一周中每天完成家庭作业所花时间（单位：分钟）分别为：35，40，45，40，55，40，48．这组数据的众
B. 众数，中位数
C. 平均数，方差
D. 中位数，方差
9. 某校四个绿化小组一天植树的棵数如下：10，x，10，8 . 已知这组数据的众数与平均数相等，则这组数据的中位
数是 ( )
A. 8
B. 9
C. 10
D. 12
10. 某年人校龄数男((子岁 人足)) 球12队2 全15体3 队14员4 的17年5 龄12分6 布如表所示．对于这些数据，下列判断正确的是 (
若抓到糖果数的中位数为 a，众数为 b，则 a + b 的值为
．
14. 在一次体检中，某班学生视力检查结果如下表：
视力 0.5以上 0.7 0.8 0.9 1.0 1.0以上 所占比例 5% 8% 5% 40% 30% 12%
从表中看出全班视力的众数是
初中数学浙教版八年级下册第3章 数据分析初步3.2 中位数和众数-章节测试习题(3)
章节测试题1.【题文】某校在一次数学检测中，八年级甲、乙两班学生的数学成绩统计如下表：请根据表中提供的信息回答下列问题：（1）甲班的众数是多少分，乙班的众数是多少分，从众数看成绩较好的是哪个班?（2）甲班的中位数是多少分，乙班的中位数是多少分，甲班成绩在中位数以上（包括中位数）的学生所占的百分比是多少；乙班成绩在中位数以上（包括中位数）的学生所占的百分比是多少，从中位数看成绩较好的是哪个班?（3）甲班的平均成绩是多少分，乙班的平均成绩是多少分，从平均成绩看成绩较好的班是哪个班?【答案】（1）90 70 甲（2）60％ 54％甲（3）甲班【分析】（1）众数是数据中出现次数最多的数，根据众数的定义回答．（2）从小到大把数据排列，中间的数（或两个数的平均数）是数据的中位数；根据中位数的意义求解．（3）根据平均数公式计算．【解答】解：（1）甲班中分出现的次数最多，故甲班的众数是分；乙班中分出现的次数最多，故乙班的众数是分；从众数看，甲班成绩好.（2）两个班都是人，甲班中的第人的分数是分，故甲班的中位数是分；乙班中的第人的分数是分，故乙班的中位数是分；甲班成绩在中位数以上（包括中位数）的学生所占的百分比为；乙班成绩在中位数以上（包括中位数）的学生所占的百分比为.从中位数看成绩较好的是甲班.（3）甲班的平均成绩为；乙班的平均成绩为.从平均成绩看成绩较好的是乙班．2.【题文】为了全面了解学生的学习、生活及家庭的基本情况，加强学校、家庭的联系，某中学积极组织全体教师开展“课外访万家”活动，王老师对所在班级的全体学生进行实地家访，了解到每名学生家庭的相关信息，现从中随机抽取15名学生家庭的收入情况，统计数据如下表：年收入/2 2.5345 9 13万元(1)求这15名学生家庭年收入的平均数、中位数、众数；(2)你认为用(1)中的哪个数据来代表这15名学生家庭年收入的一般水平较为合适？请简要说明理由．【答案】(1)平均数为4.3万元，中位数为3万元，众数为3万元．(2)中位数或众数，理由见解析【分析】（1）根据平均数、中位数和众数的定义求解即可；（2）根据在平均数，众数两数中，平均数受到极端值的影响较大，所以众数更能反映家庭年收入的一般水平，即可得出答案．【解答】解：(1)这15名学生家庭年收入的平均数是：(2+2.5×3+3×5+4×2+5×2+9+13)÷15=4.3万元；将这15个数据从小到大排列，最中间的数是3，则中位数是3万元；在这一组数据中3出现次数最多的，故众数是3万元；(2)中位数或众数，理由：虽然平均数为4.3万元，但年收入达到4.3万元的家庭只有4个，大部分家庭的年收入未达到这一水平，而中位数或众数3万元是大部分家庭可以达到的水平，因此用中位数或众数较为合适．3.【题文】在一次男子马拉松长跑比赛中，随机抽得12名选手所用的时间(单位：分钟)得到如下样本数据：140146143175125164134155152168 162148(1)计算该样本数据的中位数和平均数；(2)如果一名选手的成绩是147分钟，请你依据样本数据的中位数，推断他的成绩如何？【答案】(1)中位数为150分钟，平均数为151分钟．(2)见解析【分析】（1）根据中位数和平均数的概念求解；（2）根据（1）求得的中位数，与147进行比较，然后推断该选手的成绩．【解答】解：(1)将这组数据按照从小到大的顺序排列为：125，134，140，143，146，148，152，155，162，164，168，175，则中位数为：平均数为：(2)由(1)可得中位数为150分钟，可以估计在这次马拉松比赛中，大约有一半选手的成绩快于150分钟，有一半选手的成绩慢于150分钟，这名选手的成绩为147分钟，快于中位数150分钟，可以推断他的成绩估计比一半以上选手的成绩好．4.【答题】在某校“我的中国梦”演讲比赛中，有9名学生参加决赛，他们决赛的最终成绩各不相同．其中的一名学生想要知道自己能否进入前5名，不仅要了解自己的成绩，还要了解这9名学生成绩的( )A. 众数B. 中位数C. 平均数D. 方差【答案】B【分析】9人成绩的中位数是第5名的成绩．参赛选手要想知道自己是否能进入前5名，只需要了解自己的成绩以及全部成绩的中位数，比较即可．【解答】由于总共有9个人，且他们的分数互不相同，第5的成绩是中位数，要判断是否进入前5名，故应知道中位数的多少．选B.5.【题文】在一次数学考试中，从某班随机抽取的10名学生得分(单位：分)如下：75，85，90，90，95，85，95，95，100，98.(1)求这10名学生得分的众数、中位数和平均数；(2)若该班共有40名学生，估计此次考试的平均成绩约为多少．【答案】（1）众数为95分，中位数为92.5分，平数数为90.8分；（2）90.8分；【分析】（1）先把数据由小到大排列，然后根据众数、中位数和平均数的定义求解；（2）利用样本估计整体，用样本的平均数估计全班的平均数．【解答】解：(1)数据由小到大排列为75，85，85，90，90，95，95，95，98，100，所以这10名学生得分的众数为95分，中位数为＝92.5(分)，平均数为 (75＋85＋85＋90＋90＋95＋95＋95＋98＋100)＝90.8(分)．(2)估计此次考试的平均成绩约为90.8分．6.【答题】一组数据2，4，5，5，6的众数是（）A. 2B. 4C. 5D. 6【答案】C【分析】根据众数的定义解答即可．【解答】在2，4，5，5，6中，5出现了两次，次数最多，故众数为5．选C．7.【答题】某校篮球队12名同学的身高如下表：身高（cm）180 186 188 192 195人数 1 2 5 3 1则该校篮球队12名同学身高的众数是（单位：cm）（）A. 192B. 188C. 186D. 180【答案】B【分析】一组数据中出现次数最多的数据叫做众数，结合表格信息即可得出答案．【解答】身高188的人数最多，故该校篮球队12名同学身高的众数是188cm．选B．8.【答题】在某次体育测试中，九（1）班6位同学的立定跳远成绩（单位：m）分别为：1.71，1.85，1.85，1.95，2.10，2.31，则这组数据的众数是（）A. 1.71B. 1.85C. 1.90D. 2.31【答案】B【分析】根据众数的概念：一组数据中出现次数最多的数据叫做众数求解即可．【解答】数据1.85出现2次，次数最多，∴众数是1.85．选B．9.【答题】在某次体育测试中，九年级（2）班6位同学的立定跳远成绩（单位：米）分别是：1.83，1，85，1.96，2.08，1.85，1.98，则这组数据的众数是（） A. 1.83 B. 1.85 C. 2.08 D. 1.96【答案】B【分析】根据众数的定义：一组数据中出现次数最多的数据求解即可．【解答】这组数据出现次数最多的是：1.85，共两次，故众数为：1.85．选B．10.【答题】某班5位学生参加中考体育测试的成绩（单位：分）分别是35、40、37、38、40．则这组数据的众数是（）A. 37B. 40C. 38D. 35【答案】B【分析】根据众数的定义，找出这组数据中出现次数最多的数，即可求出答案．【解答】在这组数据35、40、37、38、40中，40出现了2次，出现的次数最多，则这组数据的众数是40，选B．11.【答题】为了解七年级学生参与家务劳动的时间，李老师随机调查了七年级8名学生一周内参与家务劳动的时间（单位：小时）分别是1，2，3，3，3，4，5，6，则这组数据的众数是（）A. 2.5B. 3C. 3.375D. 5【答案】B【分析】根据众数的定义找出次数最多的数即可．【解答】∵1，2，3，3，3，4，5，6中，3出现了3次，出现的次数最多；∴这组数据的众数是3；选B．12.【答题】某校七年级有5名同学参加射击比赛，成绩分为为7，8，9，10，8（单位：环）．则这5名同学成绩的众数是（）A. 7B. 8C. 9D. 10【答案】B【分析】根据众数的概念：一组数据中出现次数最多的数据叫做众数求解即可．【解答】数据8出现2次，次数最多，∴众数是8．选B．13.【答题】数据2，4，3，4，5，3，4的众数是（）A. 5B. 4C. 3D. 2【答案】B【分析】根据众数的定义：一组数据中出现次数最多的数据求解即可．【解答】这组数据的众数为：4．选B．14.【答题】学校舞蹈队买了8双舞蹈鞋，鞋的尺码分别为：36，35，36，37，38，35，36，36，这组数据的众数是（）A. 35B. 36C. 37D. 38【答案】B【分析】直接根据众数的定义求解．【解答】数据中36出现了4次，出现次数最多，∴这组数据的众数为36．选B．15.【答题】合作交流是学习数学的重要方式之一，某校九年级每个班合作学习小组的个数分别是：8，7，7，8，9，7，这组数据的众数是（）A. 7B. 7.5C. 8D. 9【答案】A【分析】一组数据中出现次数最多的数据叫做众数，由此可得出答案．【解答】这组数据中7出现的次数最多，故众数为7．选A．16.【答题】某校羽毛球训练队共有8名队员，他们的年龄（单位：岁）分別为：12，13，13，14，12，13，15，13，则他们年龄的众数为（）A. 12B. 13C. 14D. 15【答案】B【分析】由于众数是一组实际中出现次数最多的数据，由此可以确定这组数据的众数．【解答】依题意得13在这组数据中出现四次，次数最多，故他们年龄的众数为13．选B．17.【答题】数据5，7，8，8，9的众数是（）A. 5B. 7C. 8D. 9【答案】C【分析】根据众数是一组数据中出现次数最多的数据解答即可．【解答】数据5、7、8、8、9中8出现了2次，且次数最多，∴众数是8．选C．18.【答题】数据：2，3，3，5，4，3中，众数为（）A. 2B. 3C. 4D. 513【答案】B【分析】一组数据中，出现次数最多的数据就叫这组数据的众数，据此求解即可．【解答】在这组数据中：3出现了3次，次数最多，∴这组数据的众数是3．选B．19.【答题】数据35，38，37，36，37，36，37，35的众数是（）A. 35B. 36C. 37D. 38【答案】C【分析】众数指一组数据中出现次数最多的数据，根据众数的定义就可以求解．【解答】∵37出现的次数最多，∴众数是37；选C．20.【答题】数据8、8、6、5、6、1、6的众数是（）A. 1B. 5C. 6D. 8【答案】C【分析】众数指一组数据中出现次数最多的数据，根据众数的定义即可求解．【解答】6出现的次数最多，故众数是6．选C．。
浙教版数学八年级下册 第3章 数据分析初步 3.2 中位数和众数 同步练习.docx
浙教版数学八年级下册第3章数据分析初步 3．2 中位数和众数同步练习1．数据6，5，7，7，9的众数是____．2．一组数据10，13，9，16，13，10，13的众数与平均数的和是____．3．今年4月10日，在市委宣传部、市教育局等单位联合举办的“走复兴路，圆中国梦”学评委代号 A B C D E F G评分90 92 86 92 90 95 92A．95 B．92 C．90 D．86成绩(m) 1.50 1.60 1.65 1.70 1.75 1.80人数 1 2 4 3 3 2A．4 B．1.75 C．1.70 D．1.655．某次测得一周PM2.5的日均值(单位：μg/m3)如下：50，40，75，50，37，50，40，这组数据的中位数是____．6．小斌所在的课外活动小组在课间活动中练习立定跳远成绩如下(单位：米)：1.96，2.16，2.04，2.20，1.98，2.18，2.12，2.22，2.32，则这组数据的中位数是____米．7．若一组数据3，x，4，5，6的众数是6，则这组数据的中位数是( )A．3 B．4 C．5 D．68．某合作学习小组的6名同学在一次数学测试中，成绩分别为76，88，96，82，78，96，这组数据的中位数是( )A．82 B．85 C．88 D．969．为了丰富学生的课余活动，某校开展歌咏比赛，共有18名同学入围，他们的决赛成绩如成绩(分) 9.40 9.50 9.60 9.70 9.80 9.90人数 2 3 5 4 3 1A．9.70，9.60 B．9.60，9.60 C．9.60，9.70 D．9.65，9.6010．如图，这是交警在一个路口统计的某个时段来往车辆的车速(单位：千米/时)情况．(1)计算这些车的平均速度；(2)车速的众数是多少？(3)车速的中位数是多少？11．有19位同学参加歌咏比赛，所得的分数互不相同，取前10位同学进入决赛．某同学知道自己的分数后，要判断自己能否进入决赛，他只需知道这19位同学的( )A．平均数 B．中位数 C．众数 D．最低分数12．两组数据：3，a，2b，5与a，6，b的平均数都是6，若将这两组数据合并为一组数据，则这组新数据的中位数为____．13．在2016年的体育考试中某校6名学生的体育成绩统计如图所示，则这组数据的众数是____，中位数是____．14．甲、乙、丙三个家电厂家在广告中都声称，他们的某种电子产品在正常情况下的使用寿命都是8年，经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查，统计结果如下(单位：年)：甲厂：4，5，5，5，5，7，9，12，13，15乙厂：6，6，8，8，8，9，10，12，14，15丙厂：4，4，4，6，7，9，13，15，16，16请回答下列问题：(1)分别求出以上三组数据的平均数、众数、中位数；(2)这三个厂家的销售广告分别利用了哪一种表示集中趋势的特征数；(3)如果你是顾客，宜选购哪家工厂的产品？为什么？答案：1. 72. 253. B4. D5. 506. 2.167. C8. B9. B10. 解：(1)这些车的平均速度是：(40×2＋50×3＋60×4＋70×5＋80×1)÷15＝60(千米/时) (2)车速的众数是70千米/时(3)中位数是60千米/时11. B12. 613. 26 2614. 解：(1)甲厂：平均数为8，众数为5，中位数为6；乙厂：平均数为9.6，众数为8，中位数为8.5；丙厂：平均数为9.4，众数为4，中位数为8 (2)甲厂用的是平均数，乙厂用的是众数，丙厂用的是中位数(3)平均数：乙＞丙＞甲；众数：乙＞甲＞丙；中位数：乙＞丙＞甲，顾客在选购产品时，一般以平均数为依据，选平均数大的厂家的产品，因此应选购乙厂的产品初中数学试卷。
初中数学浙教版八年级下册第3章 数据分析初步3.2 中位数和众数-章节测试习题(8)
章节测试题1.【答题】某学习小组7位同学，为玉树地重灾区捐款，捐款金额分别为：5元，10元，6元，6元，7元，8元，9元，则这组数据的中位数与众数分别为（）A. 6，6B. 7，6C. 7，8D. 6，8【答案】B【分析】首先把所给数据按从小到大的顺序重新排序，然后利用中位数和众数的定义就可以求出结果．【解答】把已知数据按从小到大的顺序排序后为5元，6元，6元，7元，8元，9元，10元，∴中位数为7∵6这个数据出现次数最多，∴众数为6．选B．2.【答题】某篮球队员12名队员的年龄情况统计如下表：则这12名队员的众数和中位数分别是（）A. 23岁，21岁B. 23岁，22岁C. 21岁，22岁D. 21岁，23岁【答案】C【分析】众数就是出现次数最多的数，而中位数就是大小处于中间位置的数，根据、定义即可求解．【解答】21出现的次数最多，因而众数是：21岁；12个数，处于中间位置的是21和23，因而中位数是：22岁．选C．3.【答题】某班5位同学参加“改革开放30周年”系列活动的次数依次为：1、2、3、3、3，则这组数据的众数和中位数分别是（）A. 2；2B. 2.4；3C. 3；2D. 3；3【答案】D【分析】众数是一组数据中出现次数最多的数，在这一组数据中3是出现次数最多的，故众数是3；处于这组数据中间位置的那个数是3，那么由中位数的定义可知，这组数据的中位数是3．【解答】在这一组数据中3是出现次数最多的，故众数是3；处于这组数据中间位置的那个数是3，那么由中位数的定义可知，这组数据的中位数是3．选D．4.【答题】某校九年级学生参加体育测试，一组10人的引体向上成绩如下表：这组同学引体向上个数的众数与中位数依次是（）A. 9和10B. 9.5和10C. 10和9D. 10和9.5【答案】D【分析】众数指一组数据中出现次数最多的数据，根据众数的定义就可以求解．【解答】在这一组数据中10是出现次数最多的，故众数是10；处于这组数据中间位置的那个数是9、10，那么由中位数的定义可知，这组数据的中位数是（9+10）÷2=9.5．∴这组同学引体向上个数的众数与中位数依次是10和9.5．选D．5.【答题】已知一组数据：11，15，13，12，15，15，16，15．令这组数据的众数为a，中位数为b，则a______b．A. ＞B. ＜C. =【答案】C【分析】根据中位数和众数的定义分别求出a，b即可．【解答】在这一组数据中15是出现次数最多的，故a=15；而将这组数据从小到大的顺序排列（11，12，13，15，15，15，15，16），处于中间位置的数是15、15，那么由中位数的定义可知，这组数据的中位数是b=（15+15）÷2=15．∴a=b．故选C．6.【答题】某篮球队12名队员的年龄如表：年龄（岁）18 19 20 21人数 5 4 1 2则这12名队员年龄的众数和平均数分别是（）A. 18，19B. 19，19C. 18，19.5D. 19，19.5【答案】A【分析】根据众数及平均数的概念求解．【解答】年龄为18岁的队员人数最多，众数是18；平均数==19．选A．7.【答题】在九年级某次体育测试中，某班参加仰卧起坐测试的一组女生（每组8人）成绩如下（单位：次/分）：45、44、45、42、45、46、48、45，则这组数据的平均数、众数分别为（）A. 44、45B. 45、45C. 44、46D. 45、46【答案】B【分析】根据平均数的定义计算这组数据的平均数，由于数据中45出现了4次，出现次数最多，则可根据众数的定义得到这组数据的众数为45．【解答】解：数据的平均数=（45+44+45+42+45+46+48+45）=45，数据中45出现了4次，出现次数最多，∴这组数据的众数为45．选B．8.【答题】七年级学生完成课题学习“从数据谈节水”后，积极践行“节约用水，从我做起”，下表是从七年级400名学生中选出10名学生统计各自家庭一个月的节水情况：节水量（m3）0.2 0.25 0.3 0.4 0.5家庭数（个） 1 2 2 4 1那么这组数据的众数和平均数分别是（）A. 0.4和0.34B. 0.4和0.3C. 0.25和0.34D. 0.25和0.3 【答案】A【分析】根据众数及平均数的定义，结合表格信息即可得出答案．【解答】解：将数据按从大到小的顺序排列为：0.2，0.25，0.25，0.3，0.3，0.4，0.4，0.4，0.4，0.5，则众数为：0.4；平均数为：（0.2+0.25+0.25+0.3+0.3+0.4+0.4+0.4+0.4+0.5）=0.34．选A．9.【答题】某校初三5名学生中考体育测试成绩如下（单位：分）：12、13、14、15、14，这组数据的众数和平均数分别为（）A. 13，14B. 14，13.5C. 14，13D. 14，13.6【分析】观察这组数据发现14出现的次数最多，进而得到这组数据的众数为14，将五个数据相加求出之和，再除以5即可求出这组数据的平均数．【解答】解：∵这组数据中，12出现了1次，13出现了1次，14出现了2次，15出现了1次，∴这组数据的众数为14，∵这组数据分别为：12、13、14、15、14，∴这组数据的平均数x==13.6．选D．10.【答题】某外贸公司要出口一批食品罐头，标准质量为每听454克，现抽去10听样品进行检测，它们的质量与标准质量的差值（单位：克）如下：-10，+5，0，+5，0，0，-5，0，+5，+10．则这10听罐头质量的平均数及众数为（）A. 454，454B. 455，454C. 454，459D. 455，0【答案】B【分析】首先求得-10，+5，0，+5，0，0，-5，0，+5，+10这10个数的平均数以及众数，然后分别加上454克，即可求解．【解答】解：平均数是：454+（-10+5+0+5+0+0-5+0+5+10）=454+1=455克，-10，+5，0，+5，0，0，-5，0，+5，+10的众数是0，因而这10听罐头的质量的众数是：454+0=454克．11.【答题】某课外学习小组有5人，在一次数学测验中的成绩分别是：120，100，135，100，125，则他们的成绩的平均数和众数分别是（）A. 116和100B. 116和125C. 106和120D. 106和135【答案】A【分析】众数的定义求解；众数是一组数据中出现次数最多的数据，注意众数可以不止一个；再利用平均数的求法得出答案．【解答】在这一组数据中100是出现次数最多的，故众数是100；他们的成绩的平均数为：（120+100+135+100+125）÷5=116．选A．12.【答题】某班主任老师为了对学生乱花钱的现象进行教育指导，对班里每位同学一周大约花钱数额进行了统计，如下表：根据这个统计可知，该班学生一周花钱数额的众数、平均数是（）A. 15，14B. 18，14C. 25，12D. 15，12【答案】A【分析】根据众数、平均数的概念求得结果，判定正确选项．【解答】∵众数是数据中出现次数最多的数，∴该班学生一周花钱数额的众数为15；∵平均数是指在一组数据中所有数据之和再除以数据的个数，∴该班学生一周花钱数额的平均数=（5×7+10×12+15×18+20×10+25×3）÷50=14．选A．13.【答题】某班六名同学在一次知识抢答赛中，他们答对的题数分别是：7，5，6，8，7，9．这组数据的平均数和众数分别是（）A. 7，7B. 6，8C. 6，7D. 7，2【答案】A【分析】根据平均数和众数的概念直接求解，再判定正确选项．【解答】平均数=（7+5+6+8+7+9）÷6=7；数据7出现了2次，次数最多，∴众数是7．选A．14.【答题】王老师为了了解本班学生课业负担情况，在班中随机调查了10名学生，他们每人上周平均每天完成家庭作业所用的时间分别是（单位：小时）：1.5，2，2，2，2.5，2.5，2.5，2.5，3，3.5．则这10个数据的平均数和众数分别是（）A. 2.4，2.5B. 2.4，2C. 2.5，2.5D. 2.5，2【答案】A【分析】根据平均数的定义，以及众数的定义就可以解决．【解答】解：∵这10名学生每人上周平均每天完成家庭作业所用的时间分别是（单位：小时）：1.5，2，2，2，2.5，2.5，2.5，2.5，3，3.5，则根据平均数的计算公式可得：=2.4．这组数据中，2.5出现了4次，是出现次数最多的，即这组数据的众数是2.5．选A．15.【答题】益阳市某年6月上旬的最高气温如下表所示：日期 1 2 3 4 5 6 7 8 9 10最高气温30 28 30 32 34 32 26 30 33 35（℃）那么这10天的最高气温的平均数和众数分别是（）A. 32，30B. 31，30C. 32，32D. 30，30【答案】B【分析】根据众数，平均数的定义就可以解答．【解答】平均数是：（30+28+30+32+34+32+26+30+33+35）÷10=31；30出现3次是最多的数，∴众数为30．选B．16.【答题】为了解初三学生的体育锻炼时间，小华调查了某班45名同学一周参加体育锻炼的情况，并把它绘制成折线统计图（如图所示）．那么关于该班45名同学一周参加体育锻炼时间的说法错误的是（）A. 众数是9B. 中位数是9C. 平均数是9D. 锻炼时间不低于9小时的有14人【答案】D【分析】此题根据众数，中位数，平均数的定义解答．【解答】由图可知，锻炼9小时的有18人，∴9在这组数中出现18次为最多，∴众数是9．把数据从小到大排列，中位数是第23位数，第23位是9，∴中位数是9．平均数是（7×5+8×8+9×18+10×10+11×4）÷45=9，∴平均数是9．由以上可知A、B、C都对，故D错．选D．17.【答题】已知某校女子田径队23人年龄的平均数和中位数都是13岁，但是后来发现其中一位同学的年龄登记错误，将14岁写成15岁，经重新计算后，正确的平均数为a岁，中位数为b岁，则下列结论中正确的是（）A. a＜13，b=13B. a＜13，b＜13C. a＞13，b＜13D. a＞13，b=13 【答案】A【分析】根据平均数的计算公式求出正确的平均数，再与原来的平均数进行比较，得出a的值，根据中位数的定义得出最中间的数还是13岁，从而选出正确答案．【解答】∵原来的平均数是13岁，∴13×23=299（岁），∴正确的平均数a=≈12.97＜13，∵原来的中位数13岁，将14岁写成15岁，最中间的数还是13岁，∴b=13；选A．18.【答题】某班数学兴趣小组10名同学的年龄情况如下表：年龄（岁）12 13 14 15人数 1 4 4 1则这10名同学年龄的平均数和中位数分别是（）A. 13.5，13.5B. 13.5，13C. 13，13.5D. 13，14【答案】A【分析】根据中位数及平均数的定义求解即可．【解答】将各位同学的成绩从小到大排列为：12，13，13，13，13，14，14，14，14，15，中位数是=13.5，平均数是=13.5．选A．19.【答题】在一次信息技术考试中，抽得6名学生的成绩（单位：分）如下：8，8，10，8，7，9，则这6名学生成绩的中位数是（）A. 7B. 8C. 9D. 10【答案】B【分析】根据中位数的定义，把把这组数据从小到大排列，找出最中间的数即可．【解答】把这组数据从小到大排列为：7，8，8，8，9，10，最中间两个数的平均数是（8+8）÷2=8，则中位数是8．选B．20.【答题】为响应“节约用水”的号召，小刚随机调查了班级35名同学中5名同学家庭一年的平均用水量（单位：吨），记录如下：8，9，8，7，10，这组数据的平均数和中位数分别是（）A. 8，8B. 8.4，8C. 8.4，8.4D. 8，8.4【答案】B【分析】根据中位数和平均数的定义求解即可．【解答】解：这组数据按从小到大的顺序排列为：7，8，8，9，10，则中位数为：8，平均数为：=8.4．选B．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
章节测试题1.【答题】下表是我省11个地市5月份某日最高气温（℃）的统计结果：该日最高气温的众数和中位数分别是（）A. 27℃，28℃B. 28℃，28℃C. 27℃，27℃D. 28℃，29℃【答案】B【分析】根据众数和中位数的定义求解即可，中位数是将一组数据从小到大重新排列后，找出最中间的那个数，众数是一组数据中出现次数最多的数．【解答】∵28℃出现了4次，出现的次数最多，∴该日最高气温的众数是28℃，把这11个数从小到大排列为：27，27，27，28，28，28，28，29，30，30，31，∵共有11个数，∴中位数是第6个数是28，选B．2.【答题】下表是我省11个地市5月份某日最高气温（℃）的统计结果：该日最高气温的众数和中位数分别是（）A. 27℃，28℃B. 28℃，28℃C. 27℃，27℃D. 28℃，29℃，【答案】B【分析】根据众数和中位数的定义，结合表格和选项选出正确答案即可．【解答】把这几个数据按从小到大顺序排列为：27，27，27，28，28，28，28，29，30，30，31，故众数为：28，中位数为：28．选B．3.【答题】小华班上比赛投篮，每人投6球，如图是班上所有学生投进球数的饼图．根据图，下列关于班上所有学生投进球数的统计量，哪个是正确的？（）A. 中位数为3B. 中位数为2.5C. 众数为5D. 众数为2【答案】D【分析】根据中位数和众数的定义，结合扇形统计图，选出正确选项即可．【解答】由图可知：班内同学投进2球的人数最多，故众数为2；∵不知道每部分的具体人数，∴无法判断中位数．选D．4.【答题】今年6月某日南平市各区县的最高气温（℃）如下表：区县延平建瓯建阳武夷山浦城松溪政和顺昌邵武光泽气温33 32 32 30 30 29 29 31 30 28（℃）则这10个区县该日最高气温的众数和中位数分别是（）A. 32，32B. 32，30C. 30，30D. 30，32【答案】C【分析】先把10个数按从小到的顺序排列得28，29，29，30，30，30，31，32，32，33，然后根据众数和中位数的定义求解．【解答】解：把10个数按从小到的顺序排列得28，29，29，30，30，30，31，32，32，33，30出现次数最多，∴这10个区县该日最高气温的众数是30；第5个数和第6个数分别为30，30，∴中位数为=30．选C．5.【答题】种植能手李大叔种植了一批新品种黄瓜，为了考察这种黄瓜的生长情况，李大叔抽查了部分黄瓜株上长出的黄瓜根数，得到如图的条形图，则抽查的这部分黄瓜株上所结黄瓜根数的中位数和众数分别是（）A. 13.5，20B. 15，5C. 13.5，14D. 13，14【答案】C【分析】一组数据中出现次数最多的数据叫做众数，结合直方图即可得出众数，中位数．【解答】解：接黄瓜14根的最多，故众数为14；总共50株，中位数落在第25、26株上，分别是13，14，故中位数为=13.5．选C．6.【答题】在一次歌咏比赛中，某选手的得分情况如下：92，88，95，93，96，95，94．这组数据的众数和中位数分别是（）A. 94，94B. 95，95C. 94，95D. 95，94【答案】D【分析】根据众数、中位数的定义求解即可．【解答】这组数据按顺序排列为：88，92，93，94，95，95，96，故众数为：95，中位数为：94．选D．7.【答题】为做好“四帮四促”工作，黔南州某局机关积极倡导“挂帮一日捐”活动．切实帮助贫困村民，在一日捐活动中，全局50名职工积极响应，同时将所捐款情况统计并制成统计图，根据图提供的信息，捐款金额的众数和中位数分别是（）A. 20，20B. 30，20C. 30，30D. 20，30【答案】C【分析】由统计图提供的信息可知，一组数据的众数是这组数中出现次数最多的数，而中位数则是将这组数据从小到大（或从大到小）依次排列时，处在最中间位置的数，据此可知这组数据的众数，中位数．【解答】由统计图可知，捐款30元的有20人，人数最多，故众数是30，中位数=（30+30）÷2=30．选C．8.【答题】每年的4月23日是“世界读书日”．某中学为了了解八年级学生的读数情况，随机调查了50名学生的册数，统计数据如表所示：册数0 1 2 3 4人数3 13 16 17 1则这50名学生读数册数的众数、中位数是（）A. 3，3B. 3，2C. 2，3D. 2，2【答案】B【分析】在这组样本数据中，3出现的次数最多，∴求出了众数，将这组样本数据按从小到大的顺序排列，其中处于中间的两个数都是2，从而求出中位数是2；【解答】解：∵这组样本数据中，3出现了17次，出现的次数最多，∴这组数据的众数是3．∵将这组样本数据按从小到大的顺序排列，其中处于中间的两个数都是2，有=2，∴这组数据的中位数为2；选B．9.【答题】某车间5名工人日加工零件数分别为6，10，4，5，4，则这组数据的中位数和众数分别是（）A. 4，5B. 5，4C. 6，4D. 10，6【答案】B【分析】中位数是将一组数据按照由小到大（或由大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．本题中应是第3个数．众数是指一组数据中出现次数最多的数据．4出现2次．【解答】∵数据由低到高排序为：4，4，5，6，10，∴中位数为5；∵4出现了2次，次数最多，∴众数是4．选B．10.【答题】某排球队12名队员的年龄如下表所示：该队队员年龄的众数与中位数分别是（）A. 19岁，19岁B. 19岁，20岁C. 20岁，20岁D. 20岁，22岁【答案】B【分析】根据中位数和众数的定义求解．【解答】观察图表可知：人数最多的是4人，年龄是19岁，故众数是19．共12人，中位数是第6，7个人平均年龄，因而中位数是20．选B．11.【答题】为参加2012年“河源市初中毕业生升学体育考试”，小峰同学进行了刻苦训练，在投掷实心球时，测得5次投掷的成绩（单位：m）为8，8.5，9，8.5，9.2．这组数据的众数、中位数依次是（）A. 8.64，9B. 8.5，9C. 8.5，8.75D. 8.5，8.5【答案】D【分析】根据众数和中位数的定义求解．找出次数最多的数为众数；把5个数按大小排列，中间位置的数为中位数．【解答】在这一组数据中8.5是出现次数最多的，故众数是8.5；而将这组数据从小到大的顺序排列后，处于中间位置的数8.5，那么由中位数的定义可知，这组数据的中位数是8.5．选D．12.【答题】九（2）班“环保小组”的5位同学在一次活动中捡废弃塑料袋的个数分别为：4，6，8，16，16．这组数据的中位数、众数分别为（）A. 16，16B. 10，16C. 8，8D. 8，16【答案】D【分析】根据众数和中位数的定义求解．找出次数最多的数为众数；把5个数按大小排列，位于中间位置的为中位数．【解答】在这一组数据中16是出现次数最多的，故众数是16；而将这组数据从小到大的顺序排列后，处于中间位置的数是8，那么由中位数的定义可知，这组数据的中位数是8．选D．13.【答题】在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示：这些运动员跳高成绩的中位数和众数分别是（）A. 1.65，1.70B. 1.70，1.70C. 1.70，1.65D. 3，4【答案】C【分析】根据中位数的定义与众数的定义，结合图表信息解答．【解答】15名运动员，按照成绩从低到高排列，第8名运动员的成绩是1.70，∴中位数是1.70，同一成绩运动员最多的是1.65，共有4人，∴，众数是1.65．因此，中位数与众数分别是1.70，1.65．选C．14.【答题】某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量，如表所示：则这20户家庭该月用电量的众数和中位数分别是（）A. 180，160B. 160，180C. 160，160D. 180，180【答案】A【分析】根据众数和中位数的定义就可以解决．【解答】在这一组数据中180是出现次数最多的，故众数是180；将这组数据从小到大的顺序排列后，处于中间位置的两个数是160，160，那么由中位数的定义可知，这组数据的中位数是（160+160）÷2=160．选A．15.【答题】数据8，7，6，5，7，8，8的中位数与众数分别是（）A. 5，7B. 5，8C. 7，7D. 7，8【答案】D【分析】先把这组数据从小到大排列，再找出最中间的数，就是中位数；再找出出现的次数最多的数，就是众数．【解答】把这组数据从小到大排列为5，6，7，7，8，8，8，最中间的数是7，则中位数是7；8出现了3次，出现的次数最多，则众数是8；选D．16.【答题】在某校中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表：这些运动员跳高成绩的中位数和众数分别是（）A. 1.70，1.70B. 1.70，1.65C. 1.65，1.70D. 3，5【答案】C【分析】根据中位数和众数的定义，第8个数就是中位数，出现次数最多的数为众数．【解答】在这一组数据中1.70是出现次数最多的，故众数是1.70；在这15个数中，处于中间位置的第8个数是1.65，∴中位数是1.65．∴中位数是1.65，选C．17.【答题】小明在九年级进行的六次数学测验成绩如下（单位：分）：76、82、91、85、84、85，则这次数学测验成绩的众数和中位数分别为（）A. 91，88B. 85，88C. 85，85D. 85，84.5【答案】D【分析】根据众数的定义：出现次数最多的数，中位数定义：把所有的数从小到大排列，位置处于中间的数，即可得到答案．【解答】众数出现次数最多的数，85出现了2次，次数最多，∴众数是：85，把所有的数从小到大排列：76，82，84，85，85，91，位置处于中间的数是：84，85，因此中位数是：（85+84）÷2=84.5，选D．18.【答题】如表为72人参加某商店举办的单手抓糖果活动的统计结果．若抓到糖果数的中位数为a，众数为b，则a+b之值为何（）A. 20B. 21C. 22D. 23【答案】A【分析】根据中位数与众数的求法，分别求出抓到糖果数的中位数与众数再相加即可解答．【解答】第36与37人抓到的糖果数均为9，故中位数a=9，11出现了13次，次数最多，故众数b=11，∴a+b=9+11=20．选A．19.【答题】安安班上有九位同学，他们的体重资料如下：57，54，47，42，49，48，45，47，50．（单位：公斤）关于此数据的中位数与众数的叙述，下列何者正确？（）A. 中位数为49B. 中位数为47C. 众数为57D. 众数为47【答案】D【分析】根据定义，对选项一一分析，采用排除法选择正确答案．【解答】将9个数值从小到大依序排列如下：42，45，47，47，48，49，50，54，57∵（9+1）÷2=5，∴中位数取第5个数，即中位数=48，∵47公斤的次数最多（2次）∴众数=47，选D．20.【答题】某班同学为西南五省区抗旱救灾捐款，其中七名同学捐款数分别是：20，25，20，30，35，20，30（单位：元），这些数据的众数和中位数分别是（）A. 20，25B. 30，25C. 20，22.5D. 30，22.5【答案】A【分析】先把这组数据从小到大排列，再找出最中间的数，就是中位数；再找出出现的次数最多的数，就是众数．【解答】把这组数据从小到大排列为20，20，20，25，30，30，35，最中间的数是，25，则中位数是25；20出现了3次，出现的次数最多，则众数是20；选A．。