受弯构件的强度.
提高弯曲强度的措施-19
§7-5 提高弯曲强度的措施如前所述，弯曲正应力是影响弯曲强度的主要因素。
根据弯曲正应力的强度条件][max max σσ≤=zW M （a ） 上式可以改写成内力的形式][][max σz W M M =≤ （b ） （b ）式的左侧是构件受到的最大弯矩，（b ）式的右侧是构件所能承受的许用弯矩。
由（a ）和（b ）两式可以看出，提高弯曲强度的措施主要是从三方面考虑：减小最大弯矩、提高抗弯截面系数和提高材料的力学性能。
1．减小最大弯矩1）改变加载的位置或加载方式首先，可以通过改变加载位置或加载方式达到减小最大弯矩的目的。
如当集中力作用在简支梁跨度中间时（6-13a ），其最大弯矩为Pl 41；当载荷的作用点移到梁的一侧，如距左侧l 61处（图6-13b ），则最大弯矩变为Pl 365，是原最大弯矩的倍。
当载荷的位置不能改变时，可以把集中力分散成较小的力，或者改变成分布载荷，从而减小最大弯矩。
例如利用副梁把作用于跨中的集中力分散为两个集中力（图6-13c ）,而使最大弯矩降低为56.0Pl 81。
利用副梁来达到分散载荷，减小最大弯矩是工程中经常采用的方法。
2）改变支座的位置其次，可以通过改变支座的位置来减小最大弯矩。
例如图6-14a 所示受均布载荷的简支梁，22max 125.081ql ql M ==。
若将两端支座各向里移动 （图6-14b ），则最大弯矩减小为l 2.02401ql ,22max 025.0401ql ql M ==只及前者的51。
图6-15a 所示门式起重机的大梁，图6-15b 所示锅炉筒体等，其支承点略向2．提高抗弯截面系数中间移动，都是通过合理布置支座位置，以减小 的工程实例。
1在截面积高。
例如对截maxM ）选用合理的截面形状A 相同的条件下，抗弯截面系数 W 愈大，则梁的承载能力就愈面高度b 的矩形截面梁，梁竖放时h 大于宽度216bh W =；而梁平放时，1226hb W =。
提高构件弯曲强度的措施
提高构件弯曲强度的措施摘要：本文从弯曲正应力的强度条件出发，总结推导出要想提高材料弯曲强度应从两方面考虑：一方面是改善梁的受力情况，另一方面是采用合理的横截面形状。
紧接着结合生活中的工程实例，具体讨论了在满足强度条件下如何设计和选择既经济又合理的构件。
关键词：构件；弯曲强度；正应力；弯矩；抗弯截面系数工程结构或机械的各组成部分，如建筑物的梁和柱、机床的轴等，在规定载荷的作用下当然不应被破坏，例如桥梁不可断裂，储气罐不应爆破等。
若构件横截面尺寸不足或形状不合理，或材料选用不当都不能保证工程结构或机械的安全工作。
相反，也不应不恰当的加大横截面尺寸或选用优质材料，这虽然满足了上述要求却多使用了材料和增加了成本，造成浪费。
弯曲强度是材料力学中一条非常的重要的性质，在工程问题中，常常采取一些措施来提高构件的弯曲强度以提高构件的利用率，节约生产成本。
弯曲正应力是控制梁强度的主要因素，（1）式为弯曲正应力的强度条件。
max σ=WM max ≤[]σ （1） 其中max σ为弯曲正应力，max M 为弯矩，W 为抗弯截面系数。
强度条件是设计梁的主要依据。
从这个条件看出，要提高梁的承载能力，应从两方面考虑：一方面是改善梁（构件）的受力情况，以降低max M 的值；另一方面则是采用合理的横截面形状，以提高W 的值，使材料得到充分利用。
下面分几点讨论。
一、减小最大弯矩⑴改变支座的位置首先，应把梁的支座设置在合适的位置，以尽量降低梁内的最大弯矩，相对地说，也就是提高了梁的强度。
以图1.1（a ）所示均布载荷作用下的简支梁为例，22max 125.08ql ql M == （2）图1.1若将两端支座各向里移动0.2l ，则最大弯矩减小为22max025.040ql ql M == （3） 只及前者的51。
也就是说按图1.1b 布置支座，承载能力即可提高4倍。
图1.2a 所示门式起重机的大梁，图1.2b 所示锅炉筒体等，其支承点略向中间移动，都是通过合理布置支座位置，以减小max M 的工程实例。
第4章结构构件的强度刚度稳定性
2、许用应力
查P12表2-2， 得：
查P45表3-11载荷组合B得：安全系数n=1.34
3、稳定性校核
由于 ，故只需按 计算整体稳定性
查P50表4-2截面属于b类，查P228附表4-2得
所以构件整体稳定性满足要求。
4.2
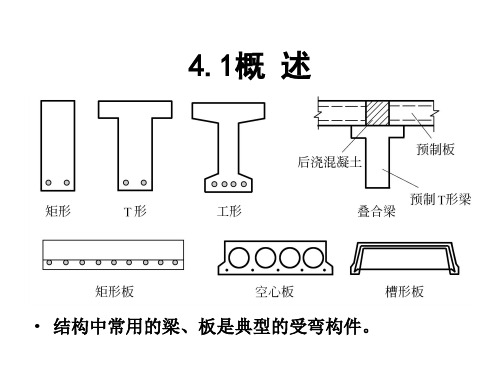
主要承受横向载荷的构件称为受弯构件，实腹式受弯构件简称梁，格构式受弯构件简称桁架。桁架将在后续介绍，本节仅介绍实腹受弯构件的强度、刚度及整体稳定性。
(4-2)
式中： —构件的计算长度,mm；
—许用长细比，《起重机设计规范》GB/T3811-2008规定结构构件容许长细比见表4-1；
—构件截面的最小回转半径,mm。
（4-3）
式中: —构件毛截面面积，mm2；
－构件截面惯性矩，mm４；
表4-1结构构件容许长细比
构件名称
受拉构件
受压构件
主要承载结构件
5
缀条
-缀条所在平面和x-x轴的夹角
注：1、斜腹杆与构件轴线间的倾角应保持在400~700范围内。
2、缀板组合构件的单肢长细比 不应大于40。
例题4-1
已知如图4-6所示工字形截面轴心压杆，翼缘：2-200×10 ，腹板：1-180×6，杆长 ，两端铰支，按载荷组合B求得构件轴心压力 ，钢材为Q235B钢，焊条为E43型，试验算构件强度、刚度及整体稳定性。
(2)
在起重机械结构中，理想构件是不存在的，构件或多或少存在初始缺陷。如：初变形(包括初弯曲和初扭曲)、初偏心(压力作用点与截面型心存在偏离的情况)等等。这些因素，都使轴心压杆在载荷一开始作用时就发生弯曲，不存在由直线平衡到曲线平衡的分歧点。实际轴心压杆的工作情况犹如小偏心受压构件，其临界力要比理想轴心压杆低(图4-4)，当压力不断增加时，压杆的变形也不断增加，直至破坏。载荷和挠度的关系曲线，由稳定平衡的上升和不稳定平衡的下降段组成。在上升段OA，增加载荷才能使挠度加大，内外力处于平衡状态；而在下降阶段AB，由于截面上塑性的发展，挠度不断增加，为了保持内外力的平衡，必须减小载荷。因此，上升阶段是稳定的，下降阶段是不稳定的，上升和下降阶段的分界点A，就是压杆的临界点，所对应的载荷也是压杆稳定的极限承载力 (即压溃力)。
混凝土受弯构件正截面承载力计算
r As f y As a1 fcbx x a1 fc
bh0 bh0 f y bh0 f y h0 f y
令
x
h0
则
r
a1 fc
fy
令b为 = r max时的相对受压区高度，即
rmax
b
a1
f
fc
y
= r max时的破坏形态为受压区边缘混凝土达到极限压
c fc e0 e ecu
n
2
1 60
(
fcu,k
50)
2.0
各系数查表4-3
e0 0.002 0.5( fcu,k 50)105 0.002
ecu 0.0033 0.5( fcu,k 50)105 0.0033
4.钢筋应力—应变关系的假定（本构关系）
Ese e e y fy e ey
4.3钢筋混凝土受弯构件正截面试验研究
一、受弯构件正截面破坏过程
受弯构件正截面破坏分为三个阶段 • 第一阶段：裂缝开裂前 • 第二阶段：从开裂到钢筋屈服 • 第三阶段：从钢筋屈服到梁破坏
（1）第I阶段
当荷载比较小时，混凝土基本处 于弹性阶段，截面上应力分布为三 角形，荷载-挠度曲线或弯矩-曲率 曲线基本接近直线。截面抗弯刚度 较大，挠度和截面曲率很小，钢筋 的应力也很小，且都于弯矩近似成 正比。
My
Mu
Failure”，破坏前
可吸收较大的应变
能。
0
f
2．超筋梁(Over reinforced)破坏
钢筋配置过多，将发生这种破坏。 破坏特征：破坏时钢筋没有达到屈服强度，破坏是由 于压区混凝土被压碎引起，没有明显预兆，为脆性破 坏。
受弯构件
型钢梁
实腹式截面梁
按截面构成方式分
焊接组合截面梁
空腹式截面梁 组合梁
由若干钢板或钢板与型钢连接而成。它 截面布置灵活，可根据工程的各种需要 布置成工字形和箱形截面，多用于荷载 较大、跨度较大的场合。
3
钢结构原理与设计
图4.1 工作平台梁格
1-主梁 2-次梁 3-面板 4-柱 5-支撑
4
钢结构原理与设计
M x Wnx
a
M x f yWnx
a
σ
fy
fy
fy
M xp f yW pnx
M xp f y S1nx S2nx f yWpnx
式中： S1nx、S2nx 分别为中和轴以上、以下截面对中 和轴的面积矩； Wpnx 截面对中和轴的塑性抵抗矩。
(4-2) 5 2) （
16
钢结构原理与设计
2) 梁的抗剪强度 剪应力的计算公式：
VS fv It w
（4.6）
式中：V ——计算截面的剪力； S ——计算剪应力处以上毛截面对中和轴的面积矩； I ——毛截面惯性矩；
17
钢结构原理与设计
3) 梁的局部承压强度
图4.6 梁局部承压应力
18
钢结构原理与设计
式中：F ——集中荷载，动力荷载需考虑动力系数； ψ ——集中荷载增大系数，重级工作制吊车梁ψ＝1.35； Lz ——集中荷载在腹板计算高度上边缘的假定腹板长度，按下式计算： Lz=a+2hy a ——集中荷载沿梁跨度方向的支承长度，吊车梁可取a为50mm； hy ——自吊车梁轨顶或其它梁顶面至腹板计算高度上边缘的距离
t1
ho
t1
b
20
钢结构原理与设计
钢结构5-受弯构件
施工图绘制
完成图纸绘制，准备施工。
优化方法与实例
尺寸优化
调整梁、柱等构件的截面尺寸，以实 现最优承载能力。
形状优化
改变构件的形状，如采用H形、箱形 等，提高稳定性。
优化方法与实例
• 拓扑优化：确定结构中最佳的材料分布，以满足性能要求。
优化方法与实例
大跨度桥梁
05
受弯构件的设计与优化
设计原则与流程
确保结构安全
满足承载力、稳定性和疲劳强度要求。
经济性
优化材料用量，降低成本。
设计原则与流程
• 可持续性：考虑环境影响，选择环保材料和工艺。
设计原则与流程
需求分析
明确结构用途、载荷和约束条件。
初步设计
确定梁、柱等主要构件的尺寸和布局。
设计原则与流程
详细设计
未来发展方向与挑战
高性能材料研发
满足更高强度、韧性和耐久性要求。
跨学科合作
加强结构工程、材料科学、计算机科学等多学科交叉融合。
THANKS
感谢观看
有限元法
利用计算机模拟技术，对钢结构进 行详细的数值分析，可以更准确地 预测其稳定性。
提高稳定性的措施
1 2
加强支撑
增加侧向支撑和加强筋，提高钢梁的侧向刚度和 稳定性。
选择合适的截面形状和尺寸
根据受力要求和稳定性要求，选择合适的截面形 状和尺寸。
3
预应力处理
通过施加预应力来提高钢结构的稳定性，防止失 稳的发生。
钢结构5-受弯构件
目录
• 受弯构件概述 • 受弯构件的受力分析 • 受弯构件的承载能力 • 受弯构件的稳定性分析 • 受弯构件的设计与优化
钢桥受弯构件验算内容-公式
一、受弯构件（一）在主平面内受弯的实腹式构件抗弯强度应符合下列规定1、翼缘板弯曲正应力满足下列要求：双向受弯的实腹式构件：f d ≥γ0(M y W y,eff +M z W z,eff )式中：γ0——结构重要性系数；M y 、M z ——计算截面的弯矩设计值；W y,eff 、W z,eff ——有效截面相对于y 轴和z 轴的截面模量，其中受拉翼缘应考虑剪力滞影响，受压翼缘应同时考虑剪力滞和局部稳定影响。
2、腹板剪应力应满足下列要求。
闭口截面腹板剪应力应按剪力流理论计算。
γ0τ≤f vd式中：γ0——结构重要性系数；τ——剪应力；f vd ——钢材的抗剪强度设计值。
3、平面内受弯实腹式构件腹板在正应力 σx 和剪应力 τ 共同作用时，应满足下列要求。
γ0√(σx f d )2+(τf vd)2≤1 式中：σx ——x 方向正应力；f d ——钢材的抗拉、抗压和抗弯强度设计值。
（二）受弯构件的整体稳定性应符合下列规定1、等截面实腹式受弯构件，应按下列规定验算整体稳定。
γ0(βm,yM y χLT,y M Rd,y +M z M Rd,z )≤1 γ0(M y M Rd,y +βm,z M z χLT,z M Rd,z)≤1 M Rd,y =W y,eff f dM Rd,z =W z,eff f dλLT,y =√W y,eff f y M cr,y ，λLT,z =√W z,eff f y M cr,z式中： M y 、M z ——构件最大弯矩；βm,y、βm,z——等效弯矩系数；χLT,y、χLT,z——M y和M z作用平面内的弯矩单独作用下，构件弯扭失稳模态的整体稳定折减系数；λ̅̅̅LT,y、λLT,z——弯扭相对长细比；W y,eff、W z,eff——有效截面相对于y轴和z轴的截面模量，其中受拉翼缘应考虑剪力滞影响，受压翼缘应同时考虑剪力滞和局部稳定影响。
M cr,y、M cr,z——M y和M z作用平面内的弯矩单独作用下，考虑约束影响的构件弯扭失稳模态的整体弯扭弹性屈曲弯矩，可采用有限元方法计算。
2014年中南大学钢结构作业及答案
《钢结构》学习中心：专业：学号：*名：**作业练习一一、填空题：1、Q 235B ⋅ F 是钢结构中最常用钢种之一，其屈服强度为__、质量等级为___B_____、脱氧方法为__沸腾钢__，与其相匹配的手工电弧焊条是__E43型__。
2、钢材的疲劳破坏属于 脆性 破坏。
3、钢材的主要化学成分是 铁 。
4、结构钢材一次拉伸时的εσ-关系曲线分为以下几个阶段：5、衡量钢材的塑性的指标有钢结构的优点是 ，材质均匀，制造简便，重量轻等。
6、钢材的强度指标是。
7、冷弯性能是判别钢材的综合指标。
8、影响钢材性能的有害化学成分是。
9、钢材的兰脆现象是指温度在时，钢材强度升高，塑性降低的现象。
10、残余应力对轴心受压构件的影响是。
11、钢结构的缺点是12、钢材的塑性指标是。
13、冲击韧性受稳定的影响，设计时根据不同的环境温度提出。
14、可焊性是指15、应力集中。
16、I20a 表示。
二、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把所选项前的字母填在题后的括号内。
1.若结构是失效的，则结构的功能函数应满足（A ） A.0<Z B.0>Z C.0≥Z D.0=Z2.结构钢材的伸长率（ B ） A ．105δδ< B.105δδ> C.105δδ= D.无法确定3.钢材韧性是钢材（ C ）的综合指标。
A.可焊性和腐蚀性B.抗火性和塑性C.强度和塑性D.塑性和耐久性4.钢结构的缺点有 C 。
A 轻质高强B 材质均匀C 易腐蚀D 施工周期短5．钢材的塑性指标为 B 。
A δ2B δ10C δ0D δ16．常温冲击韧性表示 A 冲击韧性值。
A 20 ℃B 0 ℃C -20 ℃D -40 ℃7．钢材的化学成分中脱氧剂为 D 。
A CB OC ND Mn8．建筑钢材主要的钢种有 B 。
A 热扎型钢B 碳素钢C 冷弯薄壁型钢D 不锈钢9．钢构件的主要优点有 C 。
A 易腐蚀B易拆卸 C 塑性和韧性好 D 耐热不耐火10．钢材的强度指标为 B 。
11钢结构基本原理(3-构件强度09)
轴心受拉构件强度计算公式 N f An
An 构件净截面面积 f 抗拉强度设计值
轴心受压构件的强度计算---与受拉构件强度计算完全相同， 仍采用以上公式
注意：轴心受压构件的破坏形式有强度破坏、整体失稳破坏和 局部失稳破坏(设计方法后述)。
——强度计算往往不是起控制作用？
轴心压杆（柱）的设计和计算内容—概述 1． 截面选择
最优截面改变处是离支座1/6跨度处。
b'
≤１：４
M' M1
b
M' M
M
a=l/6 l
1
按强度条件选择梁截面
h
a=l/6
多层翼缘板的梁，可用切断外层板的方法来改变梁的截面。
双层翼缘焊接梁
梁截面一般只改变一次，对于跨度较小的组合梁，不宜改变截面。
四、拉弯、压弯构件的应用和强度计算
压弯（拉弯）构件——同时承受轴向力和弯矩的构件 弯矩的产生
塑性阶 段
弯曲正应力的特点是什么?
受弯构件（梁）的强度
1、正应力—抗弯强度
三种强度准则： 1）按边缘屈服准则
(对需计算疲劳的)
Mx f Wnx
2）按全截面塑性准则
Mx f W pnx
3）按有限塑性准则(规范用公式)
(对一般受弯构件)
Mx f xWnx
梁的抗弯强度计算公式---应用和注意
h he
梁的建筑高度要求决定了梁的最大高度hmax ； 梁的刚度要求决定了最小高度： hmin f l ＝ ； l 1.34 10 6 vT
1
梁的经济条件决定了梁的经济高度：he 7Wx 3 30(cm)
b. 腹板厚度
抗剪要求
受弯构件的强度计算内容
受弯构件的强度计算内容好嘞，今天我们聊聊受弯构件的强度计算。
这个话题听起来有点严肃，不过没关系，我们轻松一点，像喝杯咖啡那样聊聊。
什么是受弯构件呢？简单来说，就是那些在使用过程中受到弯曲的部件，比如梁、板等等。
想象一下，一根长长的木棍，两头压着，中间弯了起来，嘿，这就是受弯构件的典型例子。
说到这里，很多朋友可能会想，哎呀，这受弯的力量到底有多大呢？别急，咱们慢慢来。
受弯构件的强度计算其实是个老生常谈的话题，古今中外，多少工程师为此绞尽脑汁。
可别小看这些计算，搞得不好，后果可不堪设想。
想象一下，一个桥梁，如果设计得不合理，承受不住重量，嘿，危险可就来了！这就像你坐在一个不稳的椅子上，心里想着“我会不会摔个四脚朝天”，那种感觉可真让人心慌。
强度计算离不开材料的性质。
我们常说“木头三分，铁八分”，材料的不同直接影响受弯构件的表现。
比如说，钢铁就比木材要坚固得多，受力的时候不容易变形。
不过，光有好材料还不够，设计也得跟上。
设计得当，才能充分发挥材料的优点。
想象一下，足球场上，好的球员再加上战术配合，那才叫一个精彩。
接下来说说弯矩，听起来挺专业的，其实就是描述弯曲状态的一个量。
就像一根香蕉，越弯越好看，但要是弯得过火了，嘿，香蕉就变成了泥巴。
设计者要计算这个弯矩，确保构件在正常使用中不会出现过大的弯曲，保持稳定。
计算弯矩的时候，很多人会用到弯曲公式。
公式不长，别被它的名字吓到，真正的关键在于理解每个参数的意义。
每个符号都像是那隐藏在草丛里的小虫子，得仔细找出来，才能搞清楚。
然后，咱们再聊聊安全系数。
老话说得好，留得青山在，不怕没柴烧。
这里的安全系数就是留一手，给自己留条后路。
安全系数越大，设计就越安全，然而，太大的安全系数又会造成资源浪费，工程造价上升，真是一把双刃剑。
在这方面，聪明的设计者就像精打细算的主妇，心里得有个平衡，别让钱和资源跑了。
哦，对了，受弯构件还要考虑荷载。
生活中无时无刻不在承受荷载，轻的、重的，真是五花八门。
【干货】受弯构件的计算
235 fy
，应布置横向加劲肋。
3. 当 h0 1 7 0 2 3 5，（受压翼缘扭转受到约束）
tw
fy
或者 h0 1 5 0 2 3 5 （受压翼缘扭转未受到约束）
tw
fy
应布置横向、纵向加劲肋，有轮压时布置短加劲肋。
简 支 梁 不 需 计 算 整 体 稳 定 的 最大l1／b1值
项次
工字形截面l1 / b1 箱形截面l1 / b0
l1
跨中无侧向支撑点的梁
跨中有侧向支撑点的梁
荷载作用在上翼缘 荷载作用在下翼缘 不论荷载作用在何处
13 235 / fy
20 235 / fy
16 235 / fy
h 6,且l1 95 235/ f
位置：梁腹板 与翼缘交界处
局部承压强度验算
式中：
复合应力状态与折算应力验算
复合应力状态
截面上某一点同时出现 2个及以上的应力分量 对工字形梁，腹板边缘处在不利的应力状态
折算应力 zs
x2
2 y
x y
3
x
2 y
fy
判断复合应力是否 屈服的第四强度理论
规范验算公式
zs
2
2 c
c
3
2
1 f
弯曲应力
(1) 有铺板（各种混凝土板、钢板）密铺在梁的受压翼缘上，
• 并与其牢固连接，能阻止梁受压翼缘的侧向位移时。
(2) 工字形截面简支梁：受压翼缘的自由长度l1与其宽度b1之比
• 不超过下表所规定的数值时。
(3) 箱形截面简支梁：截面尺寸满足h／b。≤6，且l1／b1不超
• 过下表所规定的数值时。
• 不符合以上条件的梁，必须经精确计算来判断是否整体稳定
受弯构件
hy
a tw lz=a+2.5hy a 主梁 lz=a+5hy
hy
R
受弯构件局部承压强度
若受弯构件局部承压强度不能满足要求时， 若受弯构件局部承压强度不能满足要求时，通常 设置支承加劲肋，此时局部承压强度可不验算。 设置支承加劲肋，此时局部承压强度可不验算。
受弯构件折算应力 规定： 规定：
在组合梁腹板计算高度处， 在组合梁腹板计算高度处，同时 腹板计算高度处 有较大的正应力σ 较大剪应力τ 有较大的正应力σ1、较大剪应力τ1和 局部压应力σ 局部压应力σc，应对其折算应力进行 验算。其强度验算式为： 验算。其强度验算式为：
受弯构件发生局部失稳后，截面中应力进行重分布， 受弯构件发生局部失稳后，截面中应力进行重分布，故不致引起 受弯构件立刻破坏， 会引起强度、整体稳定和刚度下降， 受弯构件立刻破坏，但会引起强度、整体稳定和刚度下降，故在钢结构 采取构造措施防止局部失稳发生。 中采取构造措施防止局部失稳发生。
受弯构件局部稳定
强度破坏 主要破坏形式 整体失稳 局部失稳 刚度破坏
截面应力分布
整体失稳
局部失稳
受弯构件抗弯强度
受弯构件强度包括：抗弯强度、抗剪强度、 受弯构件强度包括：抗弯强度、抗剪强度、 局部承压强度、折算应力。 局部承压强度、折算应力。
抗弯强度
弯曲应力 三个工作阶段 弹性阶段 弹塑性阶段 塑性阶段
受弯构件抗弯强度
f v——钢材抗剪设计强度 钢材抗剪设计强度
受弯构件局部承压强度
主要用于集中力处（ 主要用于集中力处（如：受支座反力R，集中力 处， 受支座反力 ，集中力F 吊车梁吊车轮压等） 吊车梁吊车轮压等） 无竖向加劲肋时 当翼缘竖向集中力作用处无竖向加劲肋 当翼缘竖向集中力作用处无竖向加劲肋时，腹板边缘 存在沿高度方向的局部压应力。 存在沿高度方向的局部压应力。
受弯构件的强度、整体稳定和局部稳定计算
《钢结构》网上辅导材料受弯构件的强度、整体稳定和局部稳定计算钢梁的设计应进行强度、整体稳定、局部稳定和刚度四个方面的计算。
一、强度和刚度计算1．强度计算强度包括抗弯强度、抗剪强度、局部承压强度和折算应力。
（1）抗弯强度荷载不断增加时正应力的发展过程分为三个阶段，以双轴对称工字形截面为例说明如下：图1 梁正应力的分布1）弹性工作阶段荷载较小时，截面上各点的弯曲应力均小于屈服点f，荷载继续增y加，直至边缘纤维应力达到f（图1b）。
y2）弹塑性工作阶段荷载继续增加，截面上、下各有一个高度为a的区域，其应力σ为屈服应力f。
截面的中间部分区域仍保持弹性（图1c），此时梁处于弹塑性工作阶段。
y3）塑性工作阶段当荷载再继续增加，梁截面的塑性区便不断向内发展，弹性核心不断变小。
当弹性核心完全消失（图1d）时，荷载不再增加，而变形却继续发展，形成“塑性铰”，梁的承载能力达到极限。
计算抗弯强度时，需要计算疲劳的梁，常采用弹性设计。
若按截面形成塑性铰进行设计，可能使梁产生的挠度过大。
因此规范规定有限制地利用塑性。
梁的抗弯强度按下列公式计算：单向弯曲时f W Mnxx x≤=γσ （1）双向弯曲时f W MW Mnyy ynxx x≤+=γγσ （2）式中 M x 、M y —绕x 轴和y 轴的弯矩（对工字形和H 形截面，x 轴为强轴，y 轴为弱轴）；W nx 、W ny —梁对x 轴和y 轴的净截面模量； y x γγ,—截面塑性发展系数，对工字形截面，20.1,05.1==yxγγ；对箱形截面，05.1==yxγγ；f —钢材的抗弯强度设计值。
当梁受压翼缘的外伸宽度b 与其厚度t 之比大于y f /23513 ，但不超过yf /23515时，取0.1=xγ。
需要计算疲劳的梁，宜取0.1==yx γγ。
（2）抗剪强度主平面受弯的实腹梁，以截面上的最大剪应力达到钢材的抗剪屈服点为承载力极限状态。
v wf It VS ≤=τ（3）式中 V —计算截面沿腹板平面作用的剪力设计值；S —中和轴以上毛截面对中和轴的面积矩； I —毛截面惯性矩； t w —腹板厚度；f v —钢材的抗剪强度设计值。
第5章 受弯构件
第5章 受弯构件教学提示：本章着重讲述了受弯构件的可能破坏形式和影响因素；受弯构件的强度和变形；单向和双向受弯构件的整体稳定；受弯及受扭构件的强度和整体稳定；受弯构件的局部稳定。
教学要求： 本章让学生了解受弯构件的种类及应用；掌握梁的拼接和连接主要方法和要求；掌握受弯构件整体稳定和局部稳定的计算原理（难点）；掌握梁的计算方法；5.1受弯构件的可能破坏形式和影响因素只受弯矩作用或受弯矩与剪力共同作用的构件称为受弯构件，俗称梁。
实际工程中，以受弯受剪为主但同时作用着很小的轴力的构件，也常称为受弯构件。
根据使用情况，它可能只在一个主平面内受弯，称为单向受弯构件，也可能在两个主平面内同时受弯，称为双向受弯构件。
钢梁最常用于工作平台梁、楼盖梁、墙梁、擅条和吊车梁等。
受弯构件有两个正交的形心主轴，如图5.1所示的x 轴与y 轴。
其中绕x 轴的惯性矩、截面模量最大，称x 轴为强轴，相对的另一轴（y 轴）则为弱轴。
对于工字形、箱形及T 形截面，其外侧平行于弯曲轴的板称为翼缘、垂直于弯曲轴的板则称为腹板。
x y x y x y x y x y xyx x x xx x y y yy y y图5.1受弯构件的强轴和弱轴按梁的支承情况可将梁分为简支梁、连续梁、悬臂梁等。
按梁在结构中的作用不同可将梁分为主梁与次梁。
按截面是否沿构件轴线方向变化可将梁分为等截面梁与变截面梁。
改变梁的截面会增加一些制作成本，但可达到节省材料的目的。
钢梁按制作方法的不同分为型钢梁和焊接组合梁。
型钢梁又分为热轧型钢梁和冷弯薄壁型钢梁两种。
目前常用的热轧型钢有普通工字钢、槽钢、热轧H型钢等（如图5.2(a)~(c)）。
冷弯薄壁型钢梁截面种类较多，但在我国目前常用的有C形槽钢（图5.2（d））和Z形钢（图5.2 （e））。
冷弯薄壁型钢是通过冷轧加工成形的，板壁都很薄，截面尺寸较小。
在梁跨较小、承受荷载不大的情况下采用比较经济，例如屋面檩条和墙梁。
第八章 圆管构件的强度与稳定计算
推导 当复杂应力状态下变形能等于单轴受力时的变形能时，
钢材即由弹性转入塑性。
Z
z
zx
zy yz
xz
y
xy yx
x
3 2
1 2
X
o单元体受复杂应力Y
状态下的分量
1
3
单元体受
主应力
钢材单元体上的复杂应力状态
在三向应力作用下，钢材由弹性状态转变为塑性状态的条件， 可以用折算应力和钢材在单向应力时的屈服点相比较来判断。
小直径焊管宜采用直缝焊，大直径焊管宜采用螺旋焊
3）圆管构件设计计算方法
由于海上平台的荷载条件和工作环境都比较复杂，设计资料不足， 故目前世界各国的平台规范大多采用容许应力设计法
容许应力法：
s
n
式中： σs ——钢材的屈服强度 n— — 强度安全系数
应考虑结构的重要性、荷载情况、材料不均匀性、制造和安装缺 陷、计算误差等因素来确定强度安全系数n
3）变形和刚度条件
弹性结构在荷载作用下将产生弹性变形或振动，过大的变形或振动会影 响平台的正常工作
受弯构件的刚度用挠度衡量 结构振动用自振周期（或频率）衡量
轴向受力构件的刚度用长细比衡量
2 圆管构件的强度计算
2.1 强度破坏准则 2.2 圆管构件的强度计算
2.1 强度破坏准则
强度计算以钢材的屈服点为极限值，按规范确定容许应力 导管架的构件主要包括腿柱和支撑，它们都由钢管组成
有侧移的刚架压杆有效长度系数共线图
5）局部屈曲和整体屈曲的相互影响
当需要考虑局部屈曲与整体屈曲的相互影响时，有两种确定容许应力的方法： a）分别求出局部屈曲临界应力和整体屈曲临界应力，取两者小值为容许应力， 由此进行稳定性校核。该方法忽略了两种屈曲的相互影响，不安全
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1）当ho/tw<8oJ235/ fy时，对有局部压应力（严o）的梁，应按构造配置横向加劲 肋；但对无局部压应力（c=o）的梁，可不配置加劲肋。
2）当ho/tw>80J235/ fy时，应配置横向加劲肋。其中，当ho/tw>17^/235/fy（受
压翼缘扭转受到约束） 或ho/tw>i5OJ235/ fy（受压翼缘扭转未受到约束时），或按计算需
2.整体稳定系数
式中b—梁的整体稳定系数
式中Mx—绕强轴作用的最大弯矩;
Wx—按受压纤维确定的梁毛截面模量;
b—梁的整体稳定系数。
当梁的整体稳定承载力不足时， 可采用加大梁的截面尺寸或增加侧向支撑的办法予以解 决，前一种办法中以增大受压翼缘的宽度最有效。
三、局部稳定和腹板加劲肋设计
组合梁一般由翼缘和腹板焊接而成，如果采用的板件宽（高）而薄，板中压应力或剪应
用于抗剪计算腹板的通用高厚比为
式中fv—钢材的抗剪切强度设计值。
3)局部压力作用下的临界应力
用于腹板抗局部压力作用时的通用高厚比为
腹板局部稳定的计算
1)配置横向加劲肋的腹板
仅配置横向加劲肋的腹板，其各区格的局部稳定应按下式计算
1/4~1/5高度处，把腹板划分为上、
F两个区格。
①上区格
②下区格
cr1
型钢腹板较厚，一般均能满足上式要求，因此只在剪力最大截面处有较大削弱时，才需 进行剪应力的计算。
(3)局部承压强度
(r
L
—也
图2局部压应力
当梁的翼缘受有沿腹板平面作用的固定集中荷载且该荷载处又未设置支承加劲肋, 有移动的集中荷载时，应验算腹板计算高度边缘的局部承压强度。
假定集中荷载从作用处以1:2.5（在hy高度范围）和1:1（在hR高度范围）
匀分布于腹板计算高度边缘。梁的局部承压强度可按下式计算
式中F—集中荷载，对动力荷载应考虑动力系数;
lz—集中荷载在腹板计算高度边缘的假定分布长度，其计算方法如下
y—计算点至中和轴的距离;
c均以拉应力为正值，压应力为负值;
=0取1=1.1。
2.刚度
刚度验算即为梁的挠度验算。按下式验算梁的刚度
式中v—荷载标准值作用下梁的最大挠度;
的极限状态。对于承受静力荷载和间接承受动力荷载的组合梁,
前屈曲，并利用其屈曲后强度。
图5腹板加劲肋的配置
（1）腹板配置加劲肋的原则
为了提高腹板的稳定性，可增加腹板的厚度，也可设置加劲肋，设置加劲肋更经济。对
于由剪应力和局部压应力引起的受剪屈曲，应设置横向加劲肋，对于由弯曲应力引起的受弯 屈曲，应设置纵向加劲肋，局部压应力很大的梁，必要时尚宜在受压区配置短加劲肋。
[V]—梁的容许挠度值，规范规定的容许挠度值。
、整体稳定
1.整体失稳现象
如图3所示的工字形截面梁，荷载作用在最大刚度平面内，当荷载较小时，仅在弯矩作
用平面内弯曲，当荷载增大到某一数值后，梁在弯矩作用平面内弯曲的同时，将突然发生侧
向弯曲和扭转，并丧失继续承载的能力，这种现象称为梁的弯扭屈曲或整体失稳。
受弯构件的强度、整体稳定和局部稳定计算
钢梁的设计应进行强度、整体稳定、局部稳定和刚度四个方面的计算。
、强度和刚度计算
1.强度计算 强度包括抗弯强度、抗剪强度、局部承压强度和折算应力。
（1）抗弯强度
荷载不断增加时正应力的发展过程分为三个阶段，以双轴对称工字形截面为例说明如
1）弹性工作阶段荷载较小时，截面上各点的弯曲应力均小于屈服点
（2）临界应力的计算
1）弯曲临界应力
用于抗弯计算腹板的通用高厚比
当梁受压翼缘扭转受到约束时
bZhc/twIfy
177
(15a)
当梁受压翼缘扭转未受到约束时
根据通用高厚比b的范围不同，弯曲临界应力的计算公式如下:
式中f—钢材的抗弯强度设计值。
式（16）的三个公式分别属于塑性、弹塑性和弹性范围。
2）剪切临界应力
要时，应在弯曲应力较大区格的受压区增加配置纵向加劲肋。
尚宜在受压区配置短加劲肋。
任何情况下，ho/tw均不应超过250J235/ fy。
此处ho为腹板的计算高度（对单轴对称梁，当确定是否要配置纵向加劲肋时,
为腹板受压区高度he的2倍），tw为腹板的厚度。
3）梁的支座处和上翼缘受有较大固定集中荷载处，宜设置支承加劲肋。
力达到某数值后，腹板或受压翼缘有可能偏离其平面位置，出现波形凸曲，这种现象称为梁 局部失稳。
热轧型钢板件宽厚比较小，能满足局部稳定要求，不需要计算。
1.受压翼缘的局部稳定
般采用限制宽厚比的办法保证梁受压翼缘板的稳定性。
(12)
当按弹性设计，b/t值可放宽为
(13)
(14)
2.腹板的局部稳定
对于直接承受动Βιβλιοθήκη 荷载的或其他不考虑屈曲后强度的组合梁,
加，直至边缘纤维应力达到fy（图1b）。
2）弹塑性工作阶段
荷载继续增加，截面上、下各有一个高度为
a的区域，其应力
6为屈服应力fy。截面的中间部分区域仍保持弹性（图1c）,此时梁处于弹塑性工作阶段。
3）塑性工作阶段当荷载再继续增加，梁截面的塑性区便不断向内发展，弹性核心不
断变小。当弹性核心完全消失（图1d）时，荷载不再增加，而变形却继续发展，形成 铰”，梁的承载能力达到极限。
计算抗弯强度时，需要计算疲劳的梁，常采用弹性设计。若按截面形成塑性铰进行设计, 可能使梁产生的挠度过大。因此规范规定有限制地利用塑性。
梁的抗弯强度按下列公式计算:
单向弯曲时
Mxf
xWnx
Mx
XWnX
Wnx、Wny—梁对X轴和y轴的净截面模量;
y
f—钢材的抗弯强度设计值。
当梁受压翼缘的外伸宽度b与其厚度t之比大于13J235/ fy，但不超过15J235/fy
时,
(2)抗剪强度
主平面受弯的实腹梁，以截面上的最大剪应力达到钢材的抗剪屈服点为承载力极限状 态。
V
式中V—计算截面沿腹板平面作用的剪力设计值;
S—中和轴以上毛截面对中和轴的面积矩;
I—毛截面惯性矩;
tw—腹板厚度;
fv—钢材的抗剪强度设计值。
当抗剪强度不满足设计要求时，常采用加大腹板厚度的办法来增大梁的抗剪强度。
(T
c ,cr1
(—)
cr1
(25)
3.加劲肋的构造和截面尺寸
般采用钢板制成的加劲肋，并在腹板两侧成对布置。 对非吊车梁的中间加劲肋， 为了
省工省料，也可单侧布置。
横向加劲肋的间距a不得小于0.5 ho,也不得大于2ho（对c=0的梁，h0/tw100时,
可米用2.5 ho）。