基金公司的投资策略分析数学建模
数学建模在投资风险管理中的应用

数学建模在投资风险管理中的应用一、引言在现代金融市场中,投资风险是不可避免的。
因此,如何有效地管理风险,达到更好的投资效果,一直是金融工作者们需要解决的核心问题。
数学建模作为一种工具,可以通过对金融数据进行分析、预测和优化,从而帮助投资者更好地管理风险。
二、基础数学知识在投资分析中的应用在投资分析中,基础数学知识如统计学、概率论、线性方程组、微积分等都有着重要的应用。
例如,在股票价格的分析中,投资者可以利用概率分布函数和统计方法来预测股票价格的走势。
同时,利用线性代数和微积分等数学方法,可以对多个股票进行组合投资的裸跑分析。
此外,在金融衍生品的定价分析中,利用微积分和概率论可以推导出定价公式,帮助投资者更好地进行衍生品的买卖和对冲。
三、数据分析在投资管理中的应用随着现代技术的不断发展,大量的投资数据也得到了收集和分析。
在投资管理中,数据分析可以帮助投资者更好地理解市场的趋势和动向,从而做出更为准确的投资决策。
例如,通过对历史股票价格的分析,可以发现股市的波动是有一定规律的,因此投资者可以利用这一规律制定相应的投资策略。
同时,在量化投资中,数据分析技术也被广泛应用,例如通过构建多因子模型来挖掘市场的潜在机会,从而达到更好的投资效果。
四、金融风险管理中的数学模型金融风险是投资过程中需要面对的一个重要挑战,而数学建模可以帮助我们更好地管理这些风险。
例如,在对冲基金风险管理中,利用随机过程和蒙特卡罗模拟等数学方法,可以帮助投资者更好地估计风险值。
同时,利用协方差矩阵和极值理论等数学工具,可以对股票组合进行风险分析和优化配置。
此外,金融市场中还存在着利率风险和信用风险等多种风险,针对不同类型的风险,数学模型也可以提供相应的解决方案。
五、结论综上所述,数学建模在投资风险管理中有着广泛的应用,基础数学知识可以帮助投资者更深入地理解市场的运作机制,数据分析技术可以帮助投资者更好地把握市场的趋势和动向,而金融风险管理中的数学模型则可以帮助投资者更好地管理和控制风险,从而达到更好的投资效果。
基金的投资决策模型与分析工具

基金的投资决策模型与分析工具在金融市场中,基金是一种理财工具,它通过集合投资者的资金,由专业基金经理进行投资管理。
基金的投资决策对于基金的收益和风险非常重要。
为了做出科学的投资决策,基金经理常常使用投资决策模型和分析工具来辅助决策。
本文将介绍几种常用的基金投资决策模型和分析工具。
一、资本资产定价模型(Capital Asset Pricing Model, CAPM)资本资产定价模型是一种用来确定资产预期回报的数学模型。
该模型认为,资产的预期回报与市场风险的关系密切。
投资者可以利用CAPM来估计资产的风险回报特征线,并参考该特征线来评估基金投资的风险与回报。
CAPM的公式如下:E(Ri) = Rf + βi * (E(Rm) - Rf)其中,E(Ri)表示资产i的预期回报,Rf表示无风险利率,βi表示资产i的风险系数,E(Rm)表示市场的预期回报。
利用CAPM模型,基金经理可以合理估计基金的风险与预期回报,从而做出相应的投资决策。
二、技术分析工具技术分析是基于股票价格、成交量等市场数据的研究方法,通过对市场图表和指标的分析,以预测市场未来价格的走势。
在基金投资中,技术分析工具被广泛应用于选股和时机把握。
常见的技术分析工具包括移动平均线、相对强弱指数(RSI)、MACD等。
基金经理可以利用这些工具来判断基金的买入时机和卖出时机,以获得更好的收益。
三、基本面分析工具基本面分析是通过对经济、行业和公司的基本因素进行研究,评估资产的价值。
在基金投资中,基本面分析工具被用来选择具备良好基本面的公司或行业,以及评估它们的长期发展潜力。
常用的基本面分析工具包括财务报表分析、行业研究、竞争对手分析等。
基金经理可以通过基本面分析工具来决策是否投资于某个公司或行业基金。
四、风险管理模型风险管理是基金投资中不可或缺的一环,基金经理需要合理评估并管理投资风险。
常见的风险管理模型包括价值-at-风险(Value-at-Risk, VaR)模型和风险调整收益率(Risk-adjusted Return, RAR)模型。
基金使用计划__数学建模

题目基金使用计划摘要学校基金会有一笔基金,打算将其存入银行或购买国库券,不同的理财方式当然有不同的最终奖金数额,本论文就是通过建模找出是奖金最大化的理财方式,根据题目中的不同利率找出最好的处理方式。
第一个问题在只能存款时使奖金最大,通过对题目中不同年份的存款利率可知,为了使奖金最大化要使奖金不能出现闲置,又因为奖金都是在年末发放,所以活期、半年期都不能选择,依题意可得只有在每年年初可以建立线性方程组,设出奖金,使用lingo软件对其进行编程求解可以计算出奖金的最大额: 万元。
通过解线性方程组还可以求解出每年基金的投资方式以达到Z109.8169最大奖金数额,解出奖金最多的问题。
第二个问题在既可以存款又可以购买国库券时解出奖金的最大数额,通过分析题目中的数据可知国库券的利率要大于存款利率,所以在两种方式都可以的情况下优先考虑购国库券,由题目可知每年都会发放国库券但是发放日期不定。
在这种情况下就要分三种情况讨论,国库券分别每年在年中发放、在年初发放、在其他时期发放。
在国库券分为三种情况发放可以按三种情况分别列出线性方程组。
求解出每种情况下的奖金数额,奖金数额分别为131.7896万元、146.8578万元、127.5222万元,同样可以解出在三种情况下每年年初可以选择的投资方式。
第三个问题是在没有要求采取哪种方式时解出最大奖金额,从题目中给出的条件,在第三年的时候因为学校要举行校庆活动,为了鼓舞师生在这一年中奖金数额要比往年增加20%,解决这个问题可以分为两种情况。
第一种在只能选择存款,这种情况可以利用问题一的模型,只需要把第三年的奖金改为原来的倍。
解出线性方程组,此种情况下的奖金数额是107.5524万元。
第二种在既可以选择国库券又可以存款,在这种情况下又可以分为三种小情况分别是国库券在年中、年初、一年中其他时间。
采用问题二中的模型分别列出线性方程组,求解出每种小情况下的奖金数额129.0966万元、143.7854万元、124.8507万元。
数学建模——混合整数规划
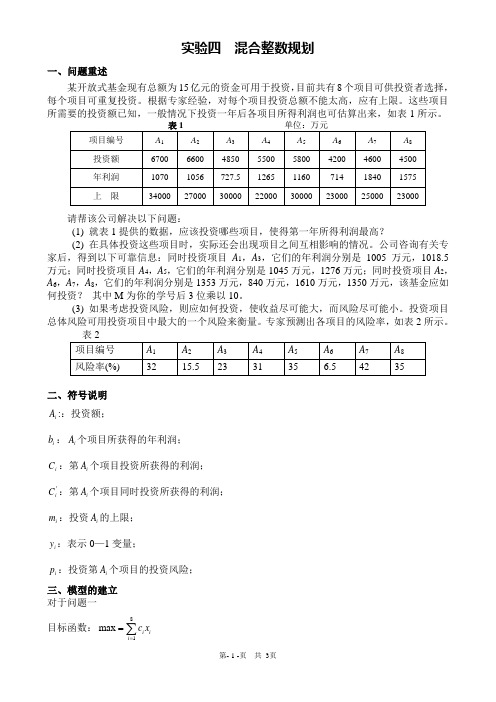
实验四 混合整数规划一、问题重述某开放式基金现有总额为15亿元的资金可用于投资,目前共有8个项目可供投资者选择,每个项目可重复投资。
根据专家经验,对每个项目投资总额不能太高,应有上限。
这些项目所需要的投资额已知,一般情况下投资一年后各项目所得利润也可估算出来,如表1所示。
请帮该公司解决以下问题:(1) 就表1提供的数据,应该投资哪些项目,使得第一年所得利润最高?(2) 在具体投资这些项目时,实际还会出现项目之间互相影响的情况。
公司咨询有关专家后,得到以下可靠信息:同时投资项目A 1,A 3,它们的年利润分别是1005万元,1018.5万元;同时投资项目A 4,A 5,它们的年利润分别是1045万元,1276万元;同时投资项目A 2,A 6,A 7,A 8,它们的年利润分别是1353万元,840万元,1610万元,1350万元,该基金应如何投资? 其中M 为你的学号后3位乘以10。
(3) 如果考虑投资风险,则应如何投资,使收益尽可能大,而风险尽可能小。
投资项目总体风险可用投资项目中最大的一个风险来衡量。
专家预测出各项目的风险率,如表2所示。
二、符号说明i A ::投资额;i b :i A 个项目所获得的年利润;i C :第i A 个项目投资所获得的利润; 'i C :第i A 个项目同时投资所获得的利润;i m :投资i A 的上限; i y :表示0—1变量;i p :投资第i A 个项目的投资风险;三、模型的建立 对于问题一目标函数:81max i i i c x ==∑s.t. 150000i i i i i ib x b x m ⎧≤⎪⎨⎪≤⎩∑对于问题二 设定0—1变量131130...,1...,A A y A A ⎧⎨⎩项目不同时投资项目同时投资 452450...,1...,A A y A A ⎧⎨⎩项目不同时投资项目同时投资 2678326780...,,1...,,A A A A y A A A A ⎧⎨⎩,项目不同时投资,项目同时投资 目标函数:''''11133111332445524455''''322667788322667788max ()(1)()()(1)()()(1)()y x c x c y x c x c y x c x c y x c x c y x c x c x c x c y x c x c x c x c =++-++++-++++++-+++s.t. 11313124545232678267831500001000i i i i i ib x k y x xx x y ky x x x x y k y x x x x x x x x y kb x m ⎧≤⎪⎪=⎪⎪≤⎪⎪≥⎪⎪≤⎨⎪⎪≥⎪⎪≤⎪⎪≥⎪⎪≤⎩∑对于问题三:目标函数:max min max()i iii i i c x b x p =∑s.t. 150000i i i i i ib x b x m ⎧≤⎪⎨⎪≤⎩∑对于问题三模型的简化固定投资风险,优化收益,设a 为固定的最大风险。
数学建模:第六章建模范例三

103.133872
(3)
101.310287
(3,1)
98.472872
(5)
96.731702
(5,1)
94.787533
(5,2)
92.480158
(5,3)
90.844949
(5,3,1)
4108.656375
(5,5)
*
M=5000万元,n=10年基金使用最佳方案(单位:万元)
3
改为
4
利用
5
软件求解(程序略)M=5000万元,
6
n=10年基金使用最佳方案:(单位:万元)
7
*
M=5000万元,n=10年基金使最佳方案(单位:万元)
存1年定期
存2年定期
存3年定期
存5年定期
取款数额(到期本息和)
每年发放奖学金数额
第一年初
105.650679
103.527252
220.429705
2.255
*
由上表可得,任何最佳存款策略中不能存在以下的存款策略(1,1),(2,1),(2,2),(3,2)和(3,3)。
由1,2,3,5四种定期能够组成的策略(5年定期不重复) 只能有(1),(2),(3),(3,1),(5), (5,1), (5,2), (5,3), (5,3,1)九种,
*
根据以上的推理,可得n年的最优存储方案公式二为:
据上公式用
可以求得n=10年,M=5000万元时
基金使用的最优方案:(单位:万元)
每年奖学金:
问题三求解:
方案一:只存款不购买国库券
1
因学校要在基金到位后的第3年举行校庆,所以此年奖金应是其他年度的1.2倍,
数学建模在金融分析中的应用

数学建模在金融分析中的应用随着现代金融市场的不断发展和复杂化,金融分析的需求也越来越高。
如何在市场变化快速、对冲风险明显的现状下,经准确、可靠、快速的方法获取决策并成为了行业内不断追求的目标。
而数学建模作为一种系统的模拟研究方法,其精度和速度受到了各行各业的认可和推崇。
在金融分析领域,数学建模也有显著的应用,包括资产和负债的优化、交易策略的优化、风险管理、定价模型等诸多方面,下面就几个具体的案例来探讨一下。
1、股票市场的涨跌预测数学建模可以通过大量的历史数据来建立金融市场相关的预测模型。
其中常见的是根据预测因素,通过计算机算法进行的数学分析和模型模拟预测。
例如,有一种常见的预测方法叫做基于时间序列的预测方法,通过统计复杂运算,得出了一种预测股票市场涨跌的数学模型,能够很好地与市场的实际表现相对应。
这种方法已经成为许多股票市场的日常工具,在基金管理和股票交易上都有着广泛的应用。
2、债务投资组合的分析债务投资组合是指将资本分散于多种债务证券,以实现资产安全、收益增值和风险控制的投资方式。
对于一个持有债务投资组合的机构而言,难点在于如何找到最优的配置方法,并同时降低风险。
时间序列模型可以应用于预测违约事件,VaR方法(价值风险法)可用于测量风险,线性优化方法可以保持投资组合无风险暴露。
此外,根据资产负债表及债务发行人的信用质量可以建立一定的评价模型和投资策略,从而降低投资风险。
3、工具:匹配估前预测技术在金融资产交易中,不同的资产类别之间有不同的连带关系,这对投资者的交易决策有很大的影响。
为了增加投资决策的准确性,从技术角度来说,需要先发现这些关系,然后再利用数学模型对其进行建模。
匹配估前预测技术是一种常用工具,其能够自动地从大量的金融数据中学习所需知识,通过比对历史数据来找到相关资产的交易关系,并预测下一步的交易风险。
这种技术适用于数据分析,预测和风险控制,能够帮助投资者及时做出决策,并有效降低交易风险。
基金投资的量化分析与模型构建

基金投资的量化分析与模型构建随着金融市场的发展和信息技术的进步,基金投资正逐渐向量化投资的方向发展。
量化投资是利用数学模型和计算机算法进行交易决策的投资方式。
通过对大量历史数据的分析,构建有效的量化模型,可以提高投资效率和风险管理能力。
本文将探讨基金投资的量化分析与模型构建的关键要素和方法。
一、量化分析的关键要素量化分析是基金投资的关键环节,它包括数据收集与清洗、因子选择与策略构建、回测与验证等几个步骤。
1. 数据收集与清洗量化分析的第一步是收集和清洗数据。
投资者可以利用金融数据库和交易所公开的数据,获取股票、债券和其他金融产品的历史价格、财务指标和市场交易数据等信息。
同时,还需要对数据进行清洗,排除错误和异常数据,保证数据的准确性和一致性。
2. 因子选择与策略构建在量化投资中,因子是影响投资收益的关键变量。
通过对历史数据的分析和统计,可以确定哪些因子与收益率存在相关性。
常用的因子包括市盈率、市净率、股息率等。
投资者可以根据自己的投资理念和风险偏好选择适合的因子,并构建相应的投资策略。
3. 回测与验证构建完投资策略后,需要进行回测和验证。
回测是指利用历史数据来模拟策略的表现,验证其对历史市场的适应性和盈利能力。
通过回测,可以评估策略的收益率、风险和稳定性,并进行相应的优化和调整。
二、模型构建的方法模型构建是量化投资的核心,它涉及到数学模型的选择和建立。
以下是几种常用的模型构建方法:1. 统计模型统计模型是量化投资中常用的模型之一。
它基于统计学原理,通过对历史数据的分析和推断,来进行未来走势的预测。
常见的统计模型包括时间序列分析、回归分析和协整分析等。
2. 机器学习模型机器学习模型是近年来在量化投资领域崭露头角的方法。
它通过构建人工智能算法,利用大数据进行模式识别和预测。
常见的机器学习模型包括支持向量机、随机森林和神经网络等。
3. 基于风险模型基于风险模型是量化投资中风险管理的重要手段。
它通过建立投资组合的风险模型,对不同资产的风险进行度量和控制。
基金投资收益预测模型与策略分析

基金投资收益预测模型与策略分析随着金融市场的发展和投资者对于多样化投资的需求增加,基金成为了一种广泛投资的工具。
然而,投资者在选择合适的基金时,往往需要考虑一系列的因素,其中就包括了基金的投资收益。
因此,建立一种有效的基金投资收益预测模型,并制定相应的策略分析,对于投资者做出理性决策具有重要意义。
基金投资收益预测模型是对基金未来收益进行预测的数学模型。
在建立预测模型时,需要考虑多个因素,包括基金的历史业绩、经济指标、市场情绪、基金的投资策略等。
其中,历史业绩是投资者最常用的预测依据,通过分析基金过去的表现,来判断未来的表现。
在选择历史业绩作为预测依据时,需要综合考虑基金的平均收益率、波动性、回撤幅度等指标。
此外,还可以使用经济指标来补充预测模型,例如国内生产总值、通货膨胀率、利率等指标。
市场情绪是指市场参与者的情感状态,通过分析市场情绪指标,可以预测投资者的行为和预期,进而影响基金的收益。
最后,基金的投资策略也是影响收益的重要因素,例如价值投资、成长投资、指数投资等不同的策略会产生不同的收益。
在基金投资收益预测模型建立之后,还需要进行策略分析,即根据预测的收益情况,制定相应的投资策略。
策略分析需要综合考虑投资者的风险偏好、资金规模、投资目标等因素。
对于风险偏好较高的投资者,可以选择具有较高风险但潜在回报较高的基金进行投资,如成长型基金;对于风险偏好较低的投资者,可以选择稳定收益的基金进行投资,如价值型基金。
资金规模对于策略分析也具有一定的影响,较大的资金规模可以考虑选择规模较大的基金进行投资,以保证流动性和分散风险。
而投资目标则决定了投资的期限和需求,例如短期投资可以选择短期债券基金或货币市场基金,长期投资可以选择股票型基金或混合型基金。
然而,需要注意的是,基金投资收益预测模型和策略分析都存在一定的风险。
过于依赖历史业绩进行预测容易忽视市场的变化和风险,过于追求高回报的策略可能会带来更大的风险。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基金公司的投资策略分析摘要对于问题一,我们引入股票变异系数=收益率的标准差/期望收益率来判断各股的价值;由于期望收益率代表着股票的收益,标准差则反映了股票的波动情况,所以变异系数越小,则表示股票相对风险小,收益率高。
我们以20082012年的数据为基础,以期望收益率大于10%为指标进行筛选后,对剩余的股票进行变异系数的计算,选取变异系数为正且最小的厦门钨业作我们认为最有投资价值的股票,并从宏观经济趋势、行业现状及未来发展、企业分析三个方面,在附录一中对其进行价值评估。
对于问题二,我们采用二次指数平滑预测法,计算出问题一中的股票变异系数选出系数最小的10种股票的趋势预测值和涨幅。
以厦门钨业为例,该股在2013年呈现上升趋势,年度最高收盘价趋势预测值为49.94,涨幅为28.12%。
其他各股的涨幅大都在20%40%之间,最低增幅为兖州煤业的4.60%,最高增幅为广汇能源的38.59%。
对于问题三,我们采用层析分析法建立以最优投资组合为目标的层次分析结构,准则层为风险、收益两个指标,方案层为10种股票。
通过Excel软件解得各股在最优投资组合中所占的权重,计算每种股票的投资金额;再根据问题四建立的马克维兹均值—方差模型,求出投资组合的总风险。
对于问题四,我们采用马柯维茨的“期望收益率-方差投资组合模型”,以投资组合的方差最小为目标函数,建立收益期望大于25%的投资组合模型,最后计算出的最小风险为最小风险为13.44%。
对于问题五,我们从经济发展、行业分析、和不同投资组合的风险与收益分析三个方面出发,在附录二中给出了一份完整的投资报告。
关键字:股票变异系数二次指数平滑层次分析法马克维兹均值—方差模型某基金管理公司现有50000万元于2013年1月1日投资附表1中列出的50种股票,于2013年12月31日之前全部卖出所持有的股票。
请你为该基金公司提出投资方案。
公司经理要求回答以下问题:1、以我国经济形势与行业变化的分析为背景,从附表所罗列的50种股票寻中寻找一个最有投资价值的股票做一估值报告。
2、从附表所罗列的50种股票选出10种股票进行投资,预估这10种股票2013年的上涨幅度或者通过其他途径获取这10种股票的上涨幅度。
3、通过建立数学模型确定最优投资组合的决策,即确定在选出的10种股票中分别的投资额和投资组合的总风险。
4、基金公司经理要求至少获得25%预期收益,预计最小风险数值。
5、为基金公司经理撰写一份投资报告。
二、问题分析对于问题一,我们认为最有投资价值的股票即为收益大、风险小且投资方向与我国未来经济形势大致相符的股票。
对于股票的选择,我们先用20112012年股票的年收益率X的期望值E(X)来衡量该股票投资的获利能力,期望值越大,股票的获利能力越强;再以该种股票投资收益率的方差D(X)(收益的不确定性)来衡量该股票的风险,方差越小,投资的风险越小;最后,我们引入一个股票变异系数=收益率的标准差/期望收益率,由于期望收益率为股票的收益,标准差则反映了股票的波动情况,所以变异系数越小,则表示股票相对风险小,收益率高。
对每支股票的变异系数进行排序,变异系数最小的股票即为所选的最有投资价值的股票。
对于股票的估值报告,则从宏观经济趋势、行业现状及未来发展、企业分析三个方面进行价值评估。
对于问题二,可根据问题一中的股票变异系数选出系数最小的10种股票进行投资。
对于预测2013年股票上涨的幅度,我们采用指数二次平滑预测法计算出每只股的趋势预测值,并给出涨幅。
对于问题三,对于10种股票的最优投资组合的决策,相当于确定每种股票在总投资中的权重大小,对此,可采用层次分析法对投资组合问题进行分层后确定合理的权重。
投资组合的总风险则按照问题四中的马克维兹均值—方差模型进行求解。
对于问题四,在要求收益一定的情况下,确定风险值最小的投资组合方案。
对此,可采用马柯维茨的“期望收益率-方差投资组合模型”法,通过量化股票两两选择之间的相互影响,以风险(投资组合的方差)最小为目标函数,以期望收益和权重取值范围为约束条件,得到最小的风险值以及其投资组合方案。
对于问题五,一份完整的投资报告应包含以下内容:(1)国际和我国的经济发展趋势;(2)发展前景可观行业的行业分析;(3)不同投资组合的风险与收益分析。
1、基金公司进行投资期间,社会政策无较大变化经济发展形势较稳定;2、基金公司投资期间所花费的交易费等其他费用不计,只考虑单纯的本金和收益关系;3、不存在无风险资产,每种股票的收益与否相互独立;4、基金公司仅依靠预期的投资风险和收益来做出投资决定;5、基金公司在年初投资股票,年末获得收益,所选股票在决策期间发生的变化不会影响投资决策,即投资期间不会随机撤资或追加投资;6、基金公司用期望收益率来衡量未来实际收益率的总体水平,以收益率的方差(或标准差)来衡量收益率的不确定性(风险)。
7、基金公司都是不知足的和厌恶风险的,遵循占优原则,即:在同一风险水平下,选择收益率较高的股票;在同一收益率水平下,选择风险较低的股票。
四、符号说明符号 解释说明it r 第i 种股票第t 年的年收益率)(i r E 第i 种股票的期望收益率)(i r D 第i 种股票的方差μ 变异系数)(i t S 第t 期第i 次指数平滑值α 指数平滑系数W 权向量i x 第i 种股票在投资组合中的权重p E 投资组合的期望收益ij σ 股票i 和j 之间的协方差2pσ 投资组合的方差五、模型建立及求解5.1问题一:5.1.1模型的建立:为量化最具有投资价值这一指标,可对每种股票的收益情况和风险波动情况进行综合考虑。
收益情况可根据数据中该股票每年的收益率得到期望收益率来反映,风险波动情况可根据该股票总体的方差(标准差)来衡量。
通过变异系数μ得到风险与收益的比值,得到变异系数越小,即风险越小收益越高的股票越好。
年收益率:00100%tn t it t p p r p -=⨯ 其中,P 0表示第i 种股票在第t 年第一次开盘时的价格,表示第i 种股票在第t 年最后一次收盘的价格。
第i 种股票的期望收益率:1()i it tE r r n =∑ 第i 种股票的方差: 21()(())1i it i tD r rE r n =--∑ 得到每种股票收益率的期望()i E r 和方差()i D r 后,引入一个变异系数i μ,以此来评价第i 支股票的投资价值。
计算公式如下:i i μ=第i 种股票的标准差第i 种股票的期望收益率 对于变异系数i μ,若0i μ<,则表示股票收益下降;若0i μ>且趋近于0,则表示股票收益大,风险小。
5.1.2模型的求解:对于题目所给的50种股票数据,为保证时间统一,我们筛选出了重叠年份较多的2008至2012年,将2008年设为第一年,对其数据按照上述模型进行了计算和分析。
为保证能产生一定的收益,我们以期望收益率()10%i E r >为指标进行了一次筛选,再对剩余的股票进行变异系数的计算,得到如下图所示的结果:表1 筛选后剩余股票的数据处理股票 期望收益率 标准差变异系数 600549 厦门钨业 0.553920185 0.845960603 1.527224727 600010 包钢股份 0.186859043 0.3788706912.027574819 600256 广汇能源 0.354929710 0.7926316842.233207480 601318 中国平安 0.223171254 0.4989720262.235825703 600887 伊利股份 0.461606477 1.0540925262.283530621 600058 五矿发展 0.195193458 0.4680932112.398098870 601601 中国太保 0.234766278 0.5829685682.483186989 600111 包钢稀土 0.598592390 1.5255692072.548594391 601699 潞安环能 0.559715907 1.4364268232.566349830 600188 兖州煤业 0.300769226 0.8173559112.717551665 600362 江西铜业 0.481858481 1.3428530552.786820421 600348 阳泉煤业 0.602838228 1.8375826513.048218519 600015 华夏银行 0.101043709 0.3247895573.214347134 600104 上汽集团 0.536105008 1.8253735913.404880691 601088 中国神华 0.132737595 0.4644453643.498973764 601166 兴业银行 0.246563801 0.885074984 3.589638791最后得到最有投资价值的股票为厦门钨业(600549),其期望收益率较大,为55.39%,股票波动即方差较小,为0.7156,即所得变异系数最小,为1.5272。
我们对厦门钨业这一种股票的估值报告见附录一。
5.2问题二:5.2.1模型的建立:按照问题一建立的模型,我们继续以变异系数为标准选取数值最小的10种股票作为所要投资的对象进行预测。
由于一次和二次指数平滑值均存在滞后现象,为提高预测精度,不直接将二次指数作为下一期的预测值,而是考虑建立二次指数平滑预测模型[1]进行预测。
设预测对象第t 期的观测值为t y ,并设原始时间序列为{}n y y y ,,21,令第t 期的一次指数平滑值为)1(t S ,二次平滑指数值为)2(t S ,则一次指数平滑值的递推公式为)1(1)1()1(--+=t t t S y S αα 二次指数平滑值的递推公式为)2(1)1()2()1(--+=t t t S S S ααα两式中:α为指数平滑系数,且0≤α≤1。
则二次平滑预测模型的形式为T b a yn n T n +=+ˆ 式中:)2()1(2nn n S S a -=; ][1)2()1(n n n S S b --=αα; T n y+ˆ为n 期之后第T 期的预测值; n 为原始时间序列的最后一期。
5.2.2模型的求解:(1)为减小误差,我们选取20112012年的数据进行预测,将第t 月最后一天的收盘价作为原始时间序列中的t y 。
由于影响股市的因素复杂多变,数据波动很大,为使预测模型灵敏度高些,能迅速跟上时间序列数据的变化,取平滑系数 6.0=α;令初始值 1)2(0)1(0y S S ==。
由于数据过多,我们选厦门钨业作为代表,列出解答过程,对于剩余的XXX 则直接给出涨幅。
