二元相图计算
武汉理工大学相图第六章第3节
包晶转变是指在一定温度下，由一定成分 的液相与一定成分的固相作用，形成另外一个 一定成分的固相的转变过程。
包析转变是指两个成分一定的固相在恒温 下转变为另外一个新固相的过程。
合晶转变是指由两个液相L1、L2相互作用， 生成一个一定成分的固相的恒温转变。
（2）两个组元在固态完全不溶的二元共晶相图
A、B两个组元在固态完全不溶解，则 它们之间不会形成固溶体，而是以纯组元的形 式存在。两个固相的单相区在相图中压缩成两 条垂线，同时没有固态下的脱溶转变。
（3）固溶体的不平衡凝固 ① 不平衡凝固时，固相的成分不是沿固相
线变化，而是要偏离固相线。 而且，冷却速度越大，偏离固相线
的程度越大。
② 凝固后，固相内部的成分不均匀。这种 现象称为偏析。
而偏析的程度，可以用分布系数K0 来描述。分布系数是指溶质在固相中的
浓度与在液相中的浓度的比值 。
k0
CS CL
相平衡 L1↔S1 L2↔S2 L3↔S3
液相成分 固相成分
L1
S1
L2
S2
L3
S3
T2温度 ：
WL
S2O S2 L2
100 %
WS
OL 2 S2 L2
100 %
固溶体凝固的特点： ① 异分结晶
异分结晶指的是结晶出的固相与母相化学 成分不同的结晶过程，也称为选择结晶。
通常，固相中含有较多的高熔点组元，而 液相中含有较多的低熔点组元。
① 相图分析 特性点 ： a，纯A的熔点 b，纯B的熔点 P，包晶转变液相成分点，也称为转熔点 C，B在A中（或SA(B)固溶体中）的最大溶解度点 D，A在B中（即SB(A)固溶体中）的最大溶解度点
F，室温下B在A中的最大溶解度 G，室温下A在B中的最大溶解度
上海交大-材料科学基础-第六章
例：
（1）固溶体合金的相图所示，试根据相图确定：
a)成分为40%B的合金首 先凝固出来的固体成分； b)若首先凝固出来的固体 成分含60%B，合金的成 分为多少？
2020/4/27
c)成分为70%B的合金最 后凝固的液体成分；
d)合金成分为50%B，凝 固到某温度时液相含有 40%B，固体含有80%B， 此时液体和固体各占多少 分数？
1）由上列数据绘出Ni-Cu的相图，并标明每一区域存 在的相；
2）将50%混合物自1400℃逐渐冷却到1200℃，说明所 发生的变化，并注出开始凝固、凝固终了及1275℃互成 平衡时液相与固相的组成。
2020/4/27
（4）铋（熔点为271.5℃）和锑（熔点为630.7℃）在液 态和固态时均能彼此无限互溶，ωBi=50%的合金在 520℃时开始凝固出成分为ωSb=87%的固相。ωBi=80% 的合金在400℃时开始凝固出成分为ωSb=64%的固相。 根据上述条件，绘出Bi—Sb相图，并标出各线和相区的 名称。
2020/4/27
两组元无限互溶的条件： • 晶体结构相同 • 原子尺寸相近，尺寸差<15% • 相同的原子价 • 相似的电负性（化学亲和力）
2020/4/27
2020/4/27
具有极值的匀晶系相图
2020/4/27
有晶型转变的匀晶系相图
晶型转变曲线
2020/4/27
平衡凝固过程 指凝固过程中的每个阶段都能达到平衡。 在极其缓慢冷却条件下的凝固
2020/4/27
（2）A的熔点为300℃和B的熔点为700℃(650)，A和 B在液态和固态时均能彼此无限互溶，ωA=50%的合 金在500℃时开始凝固出成分为ωB=90%(87)的固相。 ωA=80%的合金在400℃时开始凝固出成分为 ωB=60%(64)的固相。根据上述条件，要求：
二元体系相图wqc
为351.28K，含乙醇95.57 。
最高恒沸混合物
处在最高恒沸点时的混合 物称为最高恒沸混合物（high -boiling azeotrope）。
T
2）A – B二元体系结晶过程
M
a
L
S1 T1 L1
S2
L2
A+L
SE d
ME
E B+L
A+B
A
C
T > T1, 组成为M熔体，处于液相区， f = 2 – 1 + 1 = 2，变量：T, c
T = T1, A饱和而析出，固液两相平衡， f = 2 – 2 + 1 = 1，变量：T 或c
T降低时，液相组成沿aE变化， 固相a量增加。
t/oC
20 40 60 80 100 120 132.8
水相wB% 8.5 7.0 6.4 7.2 9.3 14.0 37 醇相wB% 83.6 81.6 79.0 75.2 70.2 61.5 37
a,b (L’,L”): 共轭溶液 (conjugate solution)
tc: 临界溶解温度 (critical solution temperature) 汇溶温度 (consolute temperature) Akb ----汇溶线 K ---- 分层消失临界点
K
tc
L
a
b
L’ + L”
A wB%
B
二元炉渣相图
CaO-SiO2相图
CaO-SiO2体系中含有四种化合物：
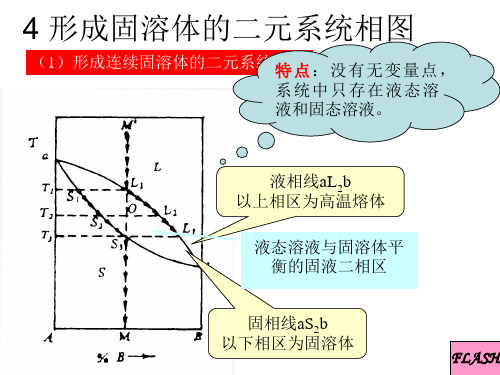
形成固溶体的二元系统相图
界线上任一点的切线与 相应连线的交点实际上 表示了该点液相的瞬时 析晶组成
瞬时析晶组成是指液 相冷却到该点温度， 从该点组成的液相中 所析出的晶相组成
21
（3） 重心规则
判断无变量点的性质
• 如无变量点处于其相应的副三角形的重心位，则该无变 量点为低共熔点；如无变量点处于其相应的副三角形的 交叉位，则为单转熔点；如无变量点处于其相应的副三 角形的共轭位，则为双转熔点。
f=1
E (L C+A+B, f = 0) 固相点 C F M FLASH
16
杠杆规则计算液相量和固相量
液相到达D点时：
固相量 CM 液相量 MD
固相量 CM 固液总量(原始配料量) CD 液相量 MD 固液总量(原始配料量) CD
17பைடு நூலகம்
2 生成一个一致熔融二元化合物
相当于 2 个简 单三元相图 的组合 • 在三元系统 中某二个组分 间生成的化合 物称为二元化 合物 • 二元化合物的 组成点在浓度 三角形的一条 边上 • 一致熔化合物 的组成点在其 初晶区内
2个固溶体
7条线 6个相区 3个无变量点
FLASH
2
析晶路程表示法
液相点
L S B ( A) L M’ L1 E LE S A( B ) S B ( A) , f 0 f=2 f=1
固相点
S1 D H
SB ( A)
SB ( A) S A( B )
着背离C的方向而变化。
9
二、杠杆规则
（1）在三元系统内，由两个相合成一个
新相时，新相的组成点必在原来二相
组成点的连线上；
（2）新相组成点与原来二相组成点的距 离和二相的量成正比。
Sn-Ag,Sn-Au二元系相图的动力学计算
1 研究背景1.1 无铅焊料的研究现状Pb-Sn合金由于熔点低、强度高、导电性能好，而且对多数工程常用的基底材料润湿性比较好，被广泛的应用于电子行业各种金属表面之间的连接[1]。
迄今为止，还未有任何焊料合金能与之匹敌。
但是铅污染环境，危害人体健康也是众所周知的事实。
近年来，无铅焊料的研究和开发被日益受到重视。
1986年美国国会通过立法禁止含铅焊料被用于饮用水管管线。
1990年在更多场合，包括电子工业中限制使用Pb，西欧及欧盟同家也考虑采用法律的手段限制和禁止含铅产品的应用。
从环境保护和人类健康角度出发，在全世界范围内将会禁用含铅焊料。
可以预见，中国对含铅制品的生产使用也会有越来越严格的限制。
许多大城市已经明确规定禁止使用含铅汽油就是一个很好的例子，以先进的材料取代原有的Sn-Pb 焊料势在必行。
国外近年来对二元系无铅焊料进行了较深入广泛的研究，采用的方法都是用另外一种组元取代Sn-Pb共晶合金中的Pb。
研究的体系有[2]：Sn-Bi系、Sn-Ag 系、Sn-In系、Sn-Zn系、Sn-Sb系等。
共晶Sn-Ag焊料对电子工业是很有吸引力的，研究表明在，焊料中该共晶焊料的剪切强度和蠕变抗力都是很优越的，使得接头更为可靠。
但熔点较高(221℃)，在Cu基体上润湿性能也稍差，近年来，在二元Sn-Ag焊料的基础上开发了一系列多元合金焊料，如Sn-Ag-Cu、Sn-Ag-Zn、Sn-Ag-Bi、Sn-Ag-Sb、Sn-Ag-In、Sn-Ag-Cu-Zn等。
1.2 Sn-Ag无铅焊料的研究现状研究开发无铅焊料是我国电子材料行业面临的新课题，而Sn-Ag系是一种有希望替代铅焊料的无铅焊料。
在焊料和基体的作用中，除润湿现象外，还包括形成金属间化合物层的形成，基体金属溶人焊缝。
这些相互作用会影响最终焊接接头的可靠性。
1.2.1金属间化合物的形成在钎料/基体界面上，Sn和共晶Sn-Ag、Sn-Bi都可以形成相同的金属间化合物。
第四章-二元合金相图
G
t/s
70% Sn的过共晶合金的结晶过程分析
概括起来，过共晶合金平衡结晶过程为：
t1温度以上： 液态 L70 L
19
t1~ t2温度： 液相中析出 ， t2温度时发生共晶反应： L61.9 t2温度以下： 初 Ⅱ
97.5
室温组织： 初 + Ⅱ + （+）共晶
一、相律
在恒压下，在纯固态或纯液态情况下，出现的相数 小于等于主元数。在液固共存（恒温）条件下出现 的相数小于等于主元数加一。因而，对二元合金， 固态下出现的相数为1或2，液固共存（恒温）条件 下恒温下出现的相数为2或3。
二、二元匀晶相图的分析
匀晶转变：在一定温度范围内由液相结 晶出单相的固溶体的结晶过程。 二元匀晶相图：指两组元在液态和固态 均无限互溶时的二元合金相图。 具有这类相图的合金系主要有Ni-Cu、 Cu-Au、Au-Ag、Mg-Cd、W-Mo等。
标注在温度— 成分坐标中 无限缓冷下测各 合金的冷却曲线 连接各相变点
确定各合金 的相变温度
确定相
如：0%Cu、20%Cu、40%Cu、60%Cu、80%Cu、100%Cu 六组合金。
Cu20% Cu60%Cu80% Cu Ni Cu40%
1600
1500
1400
1400 1300
L
（L+ ）
T
Ni
WCu(%)
Cu
将铸件加热到低于固相线100~200℃的温 度，进行长时间保温，使偏析元素充分进行扩 散，以达到成分均匀化。
设A、B组元的熔点分别为1450℃和1080℃，它们 在液态和固态都无限互溶，则这两种组元组成的 二元相图叫作二元 相图；先结晶的固溶体 中含 组元多，后结晶的固溶体中含 组元多，这种成分不均匀现象称为 ， 通过 工艺可以减轻或消除这种现 象。
第四章：二元相图
2.杠杆定律： 问题提出： ①当二元合金（成分已知）由两相组成时两相的相对重量是多少？
例：45钢（含C=0.45%）,铁素体（F）和Fe3C两相各占多少？ ②当二元合金两相相对重量已知时，合金成分是多少？
例：金相观察：F:95%; Fe3C：5%；求钢的含碳量？ 杠杆定律可以解决此类问题。
纯金属结晶：在负的温度梯度下---------树枝晶。 在正的温度梯度下------平滑界面（平面长大）
固溶体合金，即使在正的温度梯度下，也会形成树枝晶-------是由于 成分过冷造成的。 （1）成分过冷概念：固溶体合金结晶时，由于液固界面前沿存在溶质 浓度梯度而改变了过冷情况，称为成分过冷。
（2） 产生原因： 以K0<1为例(图示说明) 过冷度：界面前沿液相实际温度<液相平衡结晶温 度 （3） 产生成分过冷的条件： (讨论成分过冷的影响)
④具有共晶转变的二元合金： Pb-Sn Pb-Sb Fe-C(C>2.11%) Al-Si Al-Cu Ag-Cu
第四章：二元相图
4.2.2共晶相图
1.相图分析
以Pb-Sn二元合金相图为例：
三个单相区：L、α、β α：Sn溶入Pb中固溶体 β: Pb溶入Sn中固溶体
AEB-液相线 E点：共晶合金 AMNB-固相线 ME之间：亚共晶 ; EN之间：过共晶合金 MF-Sn在Pb中溶解度曲线，随T↓,溶解度↓ NG- Pb在Sn中溶解度曲线
第四章：二元相图
4.2.2共晶相图
2．典型合金平衡结晶及组织
（2）共晶合金结晶过程(61.9%Sn) 在183℃，由61.9%Sn的液相，同时结 晶出α（19%Sn）和β（97.5%Sn）两 种固溶体。
材料科学基础 -二元合金相图
1、相图分析
（1）相区 单相区：L, a, b 两相区： L+a, L+ b，a+b
（2）相变线
TAP及TBP：L→a, L→b。
TAC及TBD：初生a及b结晶终了线。
CE及DF：
a
→bII，b→
a
。
II
CDP： L＋ a →b。
液相线：TAPTB
固相线：TACDTB
（3）相变点 P：包晶转变点，发生包晶反应的液相成分点。
相区
单相区：L, a, b 两相区： L+a, L+ b，a+b
相变线
TAE及TBE：初生（初晶）a及b析出线 即L→a, L→b
TAM及TBN：初生a及b结晶终了线 MF及NG： a及b溶解度变化线
即a→bII，b→aII MEN： 共晶线，即L→a＋b
相变点
TA及TB：纯组元A、B的熔点 M及N：a及b的最大溶解度点 F及G：a及b室温溶解度点 E：共晶点，发生共晶反应的液相成分点
问题：假定合金分别冷却到1，2，3，4温度开始结晶，获得的组织特点有何不同？
（2）晶内偏析共晶
晶内偏析共晶： 端部固溶体合金非平衡结晶时出现共晶组织
的现象。 由于晶内偏析共晶数量较少，往往以离异
共晶形式存在。 两种情况促使离异共晶形成： ►靠近极限溶解度的端部固溶体的非平衡冷却。 ►靠近极限溶解度的亚共晶合金的平衡冷却。
（3）x2合金
组织组成物：a0＋ b包＋aII ＋bII
Wa II
DF EF
Cx2 CD
100%
相 对 量
Wb II
CE Dx2 EF CD
100%
计 算
Wa0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《二元相图计算》创新课程作业
学生：于永龙班级：焊接2班学号：10850212
一名词解释
1. 体系
体系就是我们研究的对象的总和。
2. 环境
系统以外又与系统密切相关的部分称为环境，环境必须是与系统有相互影响的有限部分。
3. 组元
组成合金的独立的、最基本的单元称为组元，组元可以是组成合金的元素或稳定的化合物。
4. 相
系统中物理性质和化学性质完全相同的均匀部分称为相。
5. 相律
表示平衡物系中的自由度数,相数及独立组分数之间的关系。
数学表达式：ƒ=C-Ф+2
6. 杠杆定律
在结晶过程中，液、固二相的成分分别沿液相线和固相线变化。
7. Gibbus自由能
G=H－TS, G叫做吉布斯自由能。
8. 化学势
等温等压下，在一定浓度的溶液中，加入微量组分B，而引起系统吉布斯函数对组分B物质的量的变化率。
9. 理想溶液
宏观定义：溶液中的任一组分在全部浓度范围内都符合拉乌尔定律的溶液称为理想溶液。
分子模型定义：各组分分子的大小及作用力彼此相似，当一种组分的分子被另一种组分的分子取代时，没有能量的变化或空间结构的变化，即就是当各组分混合成溶液时，没有热效应和体积的变化。
10. 拉乌尔定律
如果溶质是不挥发性的，即它的蒸气压极小，与溶剂相比可以忽略不计，则在一定的温度下，稀溶液的蒸气压等于纯溶剂的蒸气压与其克分子分数的乘积。
二读书报告
关于《相图分析及应用》的读书报告
相图在冶金，化工等工业生产部门及矿物、化学等科学研究领域有着广泛应用和重要指导意义，是解决一些实际问题不可缺少的工具。
在生产及新产品开发过程中，人们经常要遇到相图基础知识和应用相图解决一些实际问题，而《相图
分析及应用》一书可以帮助人们解决一些遇到的问题。
相图是在大量实验结果基础上绘成的，任何相图都不能认为是完美无缺或是最后的，必须进行不断的完善和修正。
体系在发生相变时，结构、物理化学性质和能量等也将发生变化，研究相图的实质，就是利用体系发生相变时引起的性质和能量的变化，准确测出相变温度和相变过程。
通过看书，我了解到研究相平衡的基本方法有动态法和静态法。
其中动态法的实质是通过体系在加热和冷却过程中发生的热效应，画出加热和冷却曲线，以确定相变温度，常用的有两种方法：加热或冷却曲线法和差热分析法。
静态法又称淬冷法，它是将一系列不同组成的混合物，加热到各预定温度下长时间保温，达到平衡状态，然后迅速淬冷，放入水浴、油浴或汞浴中，使其来不及发生各种相变，将高温状态保持到常温，再在常温下对淬火试样进行显微镜或X射线物相分析，就能确定某一组成在某一预定温度下存在的相及数量，把所有组成混合物在各温度下的研究结果，绘成几何图形就得到相图。
就如任何事物都有两面性，每种方法都有其利弊。
动态法测定相图，方法简单，测定相变温度准确，但最大的问题就是它不能确定物质在升温或降温过程中发生相变，产生热效应是何种反应，以及相变物质的种类和数量，必须借助其他研究手段，如配合使用高温X射线衍射、高温电子显微镜等，才能准确完整绘出相图。
静态法测定相变温度准确，方法简单可靠，最大的问题是工作量大、麻烦，因为要想绘制出一个较准确相图，必须确定很多在各个温度下处于相平衡的温度组成点位置，这就必须有大量的实验数据。
相图有二元凝聚体系相图、三元系统相图、四元体系相图，其中三元系统以二元系统为基础，把研究对象扩大为三个独立组分，四元体系含有四个纯组分。
在此主要说一下二元相图。
二元相图为平面图，用二维直角坐标系表示，纵坐标表示温度，横坐标表示组成，一般表示组成的方法有质量百分比和摩尔比百分数。
二元相图分为七类，分别为：（1）组分间无任何作用的简单低共熔型二元相图；（2）具有一个一致熔二元化合物的二元相图；（3）具有一个不一致熔二元化合物的二元相图；（4）具有化合物分解的二元相图；（5）具有晶型转变的二元相图；（6）具有液相分层的二元相图；（7）形成固溶体的二元相图。
相图在材料科学领域具有广泛的应用，它对无机材料，特别是耐火材料的生产、产品开发和应用更具指导意义。
耐火材料等硅酸盐制品，都是将原料按一定比例配制，经高温处理而成，它们多是含有多种晶相和玻璃相（高温下的液相）的多相系统，制品的性能和使用中所表现出来的性状，与其所获得的相组成及其含量有着本质的内在关系，而依据相图就可以阐明和控制制品相的组成、含量及其随温度、组成等改变的变化过程，使我们能够通过一定的工艺处理，生产和研制出具有预期性能和使用效果的制品。
三计算报告：
1. Fe-C相图
计算结果如图1：
图1 计算Fe-C相图
Fe-C相图实验结果，如图2，来自参考文献【http://www.crct.polymtl.ca/fact/pdweb.php】
图2 实验Fe-C相图
2，Fe—Cr相图
计算结果如图3：
图3计算Fe—Cr相图
Fe—Cr相图实验结果，如图4，来自参考文献【http://www.crct.polymtl.ca/fact/pdweb.php】
图4：实验Fe-Cr相图
3，Fe—W相图
计算结果如图5：
图5计算Fe—W相图
Fe—W相图实验结果，如图6，来自参考文献【http://www.crct.polymtl.ca/fact/pdweb.php】
图6：实验Fe-W相图
4，Fe—Cu相图
计算结果如图7：
图7计算Fe—Cu相图
Fe—Cu相图实验结果，如图8，来自参考文献【http://www.crct.polymtl.ca/fact/pdweb.php】
图8：实验Fe-Cu相图
5，Al—Cu相图
计算结果如图9：
图9：计算Al—Cu相图
Al—Cu相图实验结果，如图10，来自参考文献【http://www.crct.polymtl.ca/fact/pdweb.php】
图10：实验 Al—Cu相图:
6，Al--Zn相图
计算结果如图11：
图11：计算Al--Zn相图
Al--Zn相图实验结果，如图12，来自参考文献【http://www.crct.polymtl.ca/fact/pdweb.php】
图12：实验 Al—Zn相图
7，Fe--O相图
计算结果如图13：
图13：计算Fe--O相图
.
Fe--O相图实验结果，如图14，来自参考文献【http://www.crct.polymtl.ca/fact/pdweb.php】
图14：实验Fe--O相图
如有侵权请联系告知删除，感谢你们的配合！
精品。