扩散与固相反应
7 扩散与固相反应(6)

扩散与固相反应
材料科学与工程研究院
1
本章主要内容
7.1 固体中扩散基本特点与宏观动力学方程 7.2 扩散机制和扩散系数
7.3 影响扩散因素 7.4 固相反应
2
7.1 固体中扩散基本特点与 宏观动力学方程
一、固体中扩散的基本特点 二、Fick第一定律与稳定扩散
三、Fick第二定律与不稳定扩散
随时间变化。
7
Fick第一定律: 单位时间内通过垂直于扩散方向的单位面
积上扩散的物质数量和浓度梯度成正比。
数学表达式:
C J=-D x
J 扩散通量,单位时间通过单位截面的质点数(质点数/s/cm2)
D 扩散系数,单位浓度梯度的扩散通量 (m2/s 或 cm2/s)
C 质点数/cm3
“ - ” 表示粒子从高浓度向低浓度扩散,即逆浓度梯度方向扩散
△G
间隙原子扩散势场示意图
5
用途
离子晶体的导电 固溶体的形成 相变过程 硅酸盐 所有过程 固相反应 烧结
金属材料的涂搪瓷
陶瓷材料的封接 耐火材料的侵蚀性
6
二、Fick第一定律与稳定扩散
稳定扩散: 扩散质点浓度不随时间变化
C 0 t
推 动 力: 浓度梯度
特 点: 扩散过程中体系内部各处扩散质点的浓度不
1 C 1 C J= .( 2 ) 2 . 2 x 2 x
由Fick第一定律 x 3 1 2
17
1 2 一 维 D= λ τ 2
三维
1 2 D= 6
1 2 一 维 D= λ τ 2
三维
1 2 D= 6
无规则行走扩散的系数取决于两原子间距 和跃迁频率 !
扩散定律

概述
四、扩散的意义
无机非金属材料制备工艺中很多重要的物理化学过程 都与扩散有关系。例如,固溶体的形成、离子晶体的 导电性、材料的热处理、相变过程、氧化、固相反应 、烧结、金属陶瓷材料的封接、金属材料的涂搪与耐 火材料的侵蚀。因此研究固体中扩散的基本规律的认 识材料的性质、制备和生产具有一定性能的固体材料 均有十分重大的意义。
A
第一节 宏观动力学方程
一、稳定扩散和不稳定扩散
稳定扩散:
扩散物质在扩散层内各处的浓度不 随时间而变化,即dc/dt=0
不 间而变化,即dc/dt0
A
第一节 宏观动力学方程
二、扩散的动力学方程
1、菲克第一定律(Fick’s First Law)
在扩散体系中,参与扩散质点的浓度因位置而异、且可随时间 而变化。
A
第一节 宏观动力学方程
2、 菲克第二定律(Fick’s Second Law)
如图10-2所示,通过横截面积为A,相距为 dx的微小体积元前后的流量分别为J1和J2。 由物质平衡关系可得出:流入Adx体积元的 物质量减去流出该体积的量即为积存在微小 体积元中的物质量。 物质流入速率=J1A
物质流出速率 J2AJ1(JxA )dx 物质积存速率 J1AJ2A J x•A•dx
公式 :
Jx=-Ddc/dx
式中 Jx—— 扩散通量。即单位时间单位 面积上溶质扩散的量。 由于扩散有方向性,故J为矢量, 对于三维有如下公式:
JD(icjckc) x y z
A
第一节 宏观动力学方程
菲克第一定律是质点扩散定量描述的 基本方程。它适于稳定扩散(浓度分 布不随时间变化),同时又是不稳定 扩散(质点浓度分布随时间变化)动 力学方程建立的基础。
固相反应

§7.5 固相反应及其机理
一,固相反应的定义
广义:凡是有固相参与的化学反应,都可称为固 广义:凡是有固相参与的化学反应, 相反应 .
如:固体热分解,氧化及固-固,固-液间的化学反应 固体热分解,氧化及固-
狭义: 狭义:固体与固体间发生化学反应生成新的固体 产物的过程. 产物的过程.
二,固相反应的特点
则,过程为扩散速度控制,称为扩散动力学范围 过程为扩散速度控制,称为扩散动力学范围 (3)当扩散速度远和化学反应速度相当时,即 K ~ D/ δ )当扩散速度远和化学反应速度相当时, 1 1 V= = 1 δ 1 1 + + KC0 DC0 VR max VD max 则,过程速度由上式确定,称为过渡范围 过程速度由上式确定,称为过渡范围 固相反应总速度: 固相反应总速度:
F1 (G) = (1 G) 1 = K1t ′ F2 (G) = ln(1 G) = K1 t
实验验证: 实验验证:
[
2 3
]
(球形模型) 球形模型) (平板模型) 平板模型)
如 NaCO3:SiO2=1:1 ,在740℃下进行固相反应:
Na2CO3 ( s ) + SiO2 ( s ) → Na2 SiO3 + CO2 ( g )
V = VR = VD
则:
KC = D
C0 C
δ
M-MO界面氧浓度: - 界面氧浓度: 界面氧浓度
C0 C= 1 + Kδ D
1 δ + KC0 DC0 1
得:
V = VR = KC =
1 1 1 ∴ = + V KC0 DC0 δ
讨论: 讨论:(1)当扩散速度远大于化学反应速度时,即 K << D/δ 当扩散速度远大于化学反应速度时, 当扩散速度远大于化学反应速度时
材料科学基础 第七章 扩散与固相反应

0
e
2
d
0
第二种情况
C ( x, t )
Q 2 Dt
exp(
x
2
)
4 Dt
第三节
一、扩散推动力
扩散机理和扩散系数
根据热力学,扩散过程的发生与否与系统中化学势有根 本的关系,物质从高化学势流向低化学势是一个普遍规 律,一切影响扩散的外场(电场、磁场、应力场等)都 可以统一于化学势梯度之中。 因此,扩散推动力的本质是化学势梯度,而且只有当化 学势梯度为零时系统扩散方可达到平衡;浓度梯度不是 质点定向扩散推动力的实质。
由热力学理论可知,在多组分的多相系统中任一组分i由α
相迁移到相中,迁移量为dni mol,系统的吉布斯自由能 的变化为: dG dn dn
i i i i
要使上述迁移过程自发进行,必须是 :
dG i dni i dni 0
因式中 dni>0,所以:
不稳定扩散根据边界条件分为两种情况:
一是扩散物质浓度(C0)在晶体表面保持不变; 二是一定量(Q)的物质由表面向晶体内部扩散。
c c0
c
x
x
第一种情况
C ( x, t ) C0 erfc(
erf ( ) 2
x 2 Dt
)
2
e
2
d ,
erfc( ) 1
a、金属离子空位型
造成这种非化学计量空位的原因往往是环境中氧分压升 高迫使部分Fe2+ 、Ni2+ 、Mn2+ 等二价过渡金属离子变成 三价金属离子,如:
2M
M
扩散与固相反应

第七章 扩散与固相反应1、名词解释:非稳定扩散:扩散过程中任一点浓度随时间变化;稳定扩散:扩散质点浓度分布不随时间变化。
无序扩散:无化学位梯度、浓度梯度、无外场推动力,由热起伏引起的扩散。
质点的扩散是无序的、随机的。
本征扩散:主要出现了肖特基和弗兰克尔点缺陷,由此点缺陷引起的扩散为本征扩散(空位来源于晶体结构中本征热缺陷而引起的质点迁移);非本征扩散:空位来源于掺杂而引起的质点迁移。
正扩散和逆扩散:正扩散:当热力学因子时,物质由高浓度处流向低浓度处,扩散结果使溶质趋于均匀化,D i >0。
逆扩散:当热力学因子 时,物质由低浓度处流向高浓度处,扩散结果使溶质偏聚或分相,D i <0。
2、简述固体内粒子的迁移方式有几种?答 易位,环转位,空位扩散,间隙扩散,推填式。
3、说明影响扩散的因素?化学键:共价键方向性限制不利间隙扩散,空位扩散为主。
金属键离子键以空位扩散为主,间隙离子较小时以间隙扩散为主。
缺陷:缺陷部位会成为质点扩散的快速通道,有利扩散。
温度:D=D 0exp (-Q/RT )Q 不变,温度升高扩散系数增大有利扩散。
Q 越大温度变化对扩散系数越敏感。
杂质:杂质与介质形成化合物降低扩散速度;杂质与空位缔合有利扩散;杂质含量大本征扩散和非本征扩散的温度转折点升高。
扩散物质的性质:扩散质点和介质的性质差异大利于扩散;扩散介质的结构:结构紧密不利扩散。
4、在KCl 晶体中掺入10-5mo1%CaCl 2,低温时KCl 中的K +离子扩散以非本征扩散为主,试回答在多高温度以上,K +离子扩散以热缺陷控制的本征扩散为主?(KCl 的肖特基缺陷形成能ΔH s =251kJ/mol ,R=8.314J/mo1·K ) 解:在KCl 晶体中掺入10-5mo1%CaCl 2,缺陷方程为:2'22KCl K K cl CaCl Ca V Cl ∙⨯−−−→++则掺杂引起的空位浓度为'710K V -⎡⎤=⎣⎦欲使扩散以热缺陷为主,则''K K V V ⎡⎤⎡⎤>⎣⎦⎣⎦肖 即7exp()102s H RT-∆-> 即7251000exp()1028.314T -->⨯ 解得T>936.5K5、(1)试述晶体中质点的扩散机构及方式。
6-7扩散与固相反应

1 1 ( )3
4
1 PO2 6
exp(− ∆G / 3 RT )
或DFe 2 + / Fe
FK
3
= KK t
扩散 • 1非稳定扩散:扩散过程中任一点浓度随时间变化。 非稳定扩散: 非稳定扩散 • 稳定扩散 稳定扩散:扩散质点浓度分布不扩散: 热起伏引起的扩散。质点的扩散是无序的、随机的。 • 3互扩散:多元系统往往存在着几种离子同时进行的扩散 , 互扩散: 互扩散 有浓度差的空间扩散称为互扩散。 互扩散推动力: 互扩散推动力:化学位梯度。 • 4 间隙扩散:质点沿间隙位置扩散。 间隙扩散: • 5 本征扩散:主要出现了肖特基和弗兰克尔点缺陷,由此点 本征扩散: 缺陷引起的扩散为本征扩散(空位来源于晶体结构中本征热 缺陷而引起的质点迁移)。 非本征扩散: 非本征扩散:空位来源于掺杂而引起的质点迁移。 • 6.菲克第一定律:J=-Ddc/dx,菲克第一定律应用于稳定扩散 菲克第一定律: 菲克第一定律 菲克第二定律: 菲克第二定律:dc/dt=Dd2c/dx2,菲克第二定律应用于非稳 定扩散。
4、 固相中的扩散 、
D = D0 . exp(−
∆Hm + ∆H f / 2 RT
)
LnD
∆H m + ∆H f / 2 (本征扩散 本征扩散) 本征扩散 − R ∆H m + ∆H 0 / 3 E (非化学计量扩散 非化学计量扩散) 非化学计量扩散 − R ∆H m − (非本征扩散或杂质扩散 非本征扩散或杂质扩散) 非本征扩散或杂质扩散 F R
1/T
5、固相反应的动力学方程 、 化学动力学范围: 化学动力学范围:
扩散动力学范围: 扩散动力学范围:
1 F0 (G) = 1 − (1 − G)3 = K0t 2 - F (G) = (1 − G) 3- =K1t 1 1 1 FJ (G) = [1 − (1 − G)3 ]2 = K J t
华南师范大学材料科学与工程教程第七章 扩散与固态相变(一)

25/11/2018
1
概述
扩散现象:气体和液体中,例如在房间的某处打开一瓶 香水,慢慢在其他地方可以闻到香味,在清水中滴入一滴墨 水,在静止的状态下可以看到他慢慢的扩散。 扩散:由构成物质的微粒 ( 离子、原子、分子 ) 的热运动 而产生的物质迁移现象称为扩散。扩散的宏观表现是物质的 定向输送。
25/11/2018
34268s = 9.52hr
27
例2 一铁棒中碳的原始浓度为0.20%。现在1273K的温度下对 其进行渗碳处理,试确定在距表面0.01cm处碳浓度达到 0.24%所需的时间。已知在渗碳气氛中,铁棒的表面碳浓度 维持在0.40%;碳在铁中的扩散系数与温度的关系为
D (2 105 m 2 / s){exp[(142000 J / mol) / RT ]}
dC J D dx
25/11/2018 18
2) 扩散第二方程
解决问题的关键:搞清问题的起始条件和边界条件,并假定任一时 刻t溶质的浓度是按怎样的规律分布。 对不同的实际问题,可采用不同的浓度分布形式来处理,如正态分 布、误差分布、正弦分布、指数分布等。
解析解通常有高斯解、误差函数解和正弦解等
一维无限长棒中扩 散方程误差函数解:
25/11/2018 30
water
25/11/2018
adding dye
partial mixing
homogenization
time
2
说明
在固体材料中也存在扩散,并且它是固体中物 质传输的唯一方式。因为固体不能象气体或液体那
样通过流动来进行物质传输。即使在纯金属中也同
样发生扩散,用掺入放射性同位素可以证明。 扩散在材料的生产和使用中的物理过程有密切 关系,例如:凝固、偏析、均匀化退火、冷变形后 的回复和再结晶、固态相变、化学热处理、烧结、
实验27__扩散与固相反应实验(张)
实验28 热重分析技术在固相反应研究中的应用一、实验目的固相反应是材料制备中一个重要的高温动力学过程,固体之间能否进行反应、反应完成的程度、反应过程的控制等直接影响材料的显微结构,并最终决定材料的性质,因此,研究固体之间反应的机理及动力学规律,对传统和新型无机非金属材料的生产有重要的意义。
本实验的目的:1.掌握TG法的原理,熟悉采用TG法研究固相反应的方法。
2.通过CaCO3-SiO2系统的反应验证固相反应的动力学规律─杨德方程。
3.通过作图计算出反应的速度常数和反应的表观活化能。
二、实验原理许多固体材料在在高温下加热时,因其中的某些组分分解逸出或固体与周围介质中的某些物质作用使固体物系的重量发生变化,如盐类的分解、含水矿物的脱水、有机质的燃烧等会使物系重量减轻,高温氧化、反应烧结等则会使物系重量增加。
热重分析法(Thermogravimetric Analysis.简称TG) 及微商热重法(derivative thermogravimetry,简称DTG 法)是在程序控制温度下,测量物质质量与温度关系的一种技术。
微商热重法所记录的是TG曲线对温度或时间的一阶导数,所得的曲线称为DTG曲线。
现在的热重分析仪常与微分装置联用,可同时得到TG- DTG曲线。
通过测量物系质量随温度或时间的变化可以间接地揭示固体物系反应的机理和/或反应动力学规律。
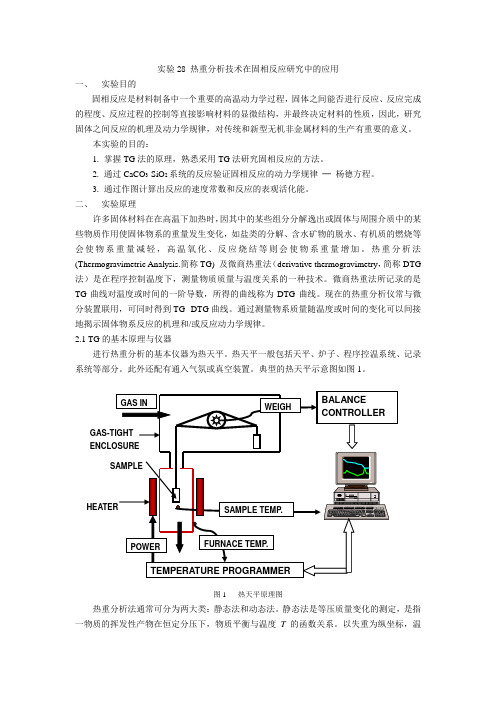
2.1 TG的基本原理与仪器进行热重分析的基本仪器为热天平。
热天平一般包括天平、炉子、程序控温系统、记录系统等部分。
此外还配有通入气氛或真空装置。
典型的热天平示意图如图1。
图1 热天平原理图热重分析法通常可分为两大类:静态法和动态法。
静态法是等压质量变化的测定,是指一物质的挥发性产物在恒定分压下,物质平衡与温度T的函数关系。
以失重为纵坐标,温度T为横坐标作等压质量变化曲线图。
等温质量变化的测定是指一物质在恒温下,物质质量变化与时间t的依赖关系,以质量变化为纵坐标,以时间为横坐标,获得等温质量变化曲线图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空位机制
空位扩散机制中有空位扩散通量, 其大小与原子扩散通量相等,方向 相反。
柯肯达尔效应
将一段纯Cu棒与一段纯Ni棒对焊,焊面 上嵌入W丝作为焊面位置标记。
将Cu-Ni扩散偶加热(但不出现液相), 由于浓度差别,Cu(或Ni)原子会越过标记 面(有W丝)向另一侧扩散。
经长时保温后发现:①标记面向Ni的一 侧移动一定距离;②成分分布如图中曲 线所示。
柯肯达尔效应的分析
惰性的W丝不可能因扩散而移动。 Ni原子直径D=1.32Å(六方)、D=1.24 Å (立方);
Cu原子直径D=1.27 Å 二者原子直径相差不大,向对方等量扩散时,
不会因原子直径差别使界面两侧的体积产生这 样大的差别。 唯一可能的是Ni原子向Cu一侧扩散的多,Cu向 Ni一侧扩散的少,使Cu一侧伸长,Ni一侧缩短。
非化学计量氧化物中的扩散
除掺杂点缺陷引起非本征扩散外,还可 发生在非化学计量氧化物晶体材料中。
扩散系数
② s同样与--有关。
简单立方: s a
D 1 a2 6
面心立方:s 2 a
2
D 1 a2 12
体心立方: s 3 a
2
D 1 a2 8
扩散系数
③ Г与扩散物质本身、扩散机制、温度密切 相关。
只有能量较高的原子的振动,才能克服能 垒,产生跃迁。
设原子总数为N,能垒ΔG,能产生跳动的
菲克第二定律
对于一维扩散问题: 初始条件:在 t 0 时浓度随坐标x的变
化规律 c(x,t 0) f (x) 为已知函数。 边界条件:在边界 x x0 处,浓度随时间
的变化规律 c(x x0,t) g(t) 为已知函数。 求得c(x,t) ,即:体系任何时间t,任
何位置x处,扩散质点的浓度c。
按浓度均匀程度 按扩散方向分 按原子的扩散方向分
(4)原子的扩散激活能
7.2 扩散动力学方程
固体中许多反应都受扩散的控制,对扩散 的研究主要有2方面: 对定向扩散流建立数学方程式,总结宏观规
律。
① 已知边界条件和扩散系数,计算浓度分布情况; ② 通过实验,利用公式,求扩散系数。
搞清微观本质,探讨微观运动与扩散系数的 关系,分析影响扩散的因素。
kT
kT
扩散系数
为方便起见,习惯上将各种晶体结构中空位 或间隙扩散系数统一于如下表达式:
扩散系数
对扩散激活能Q而言: 间隙扩散:只与--有关(迁移能) 置换扩散:等于--。
实际晶体的1nD~1/T图,得到--而 不是直线。因为实际晶体中的空位有两 部分:--缺陷、--缺陷。
本征扩散与非本征扩散
7. 扩散与固相反应
扩散概念。 扩散是由于大量原子的--引起的物质
宏观迁移。 物质的迁移可通过--两种方式进行。 扩散是固体中物质传输的--方式。
7.1 扩散现象及分类
(1)扩散现象:
(2)晶体中扩散的基本特征: 明显的质点扩散开始温度--。 晶体结构限制质点每一步迁移的----
(3)从不同角度对扩散进行分类
(1)菲克第一定律
内容 稳定扩散:
菲克第一定律
扩散通量 J : 量纲: 单位:
菲克第一定律
若扩散沿x轴单向进行,则菲克第一定律的数学 表达式为:
扩散过程中溶质原子的分布
菲克第一定律
注意: ① 关系式不涉及系统内部原子运动的微观
过程; ② 扩散系数反映系统特征,不仅仅取决于
某一组元的特征;
原子数为n,原子振动频率为ν,则Γ与ν的
关系为:
exp( G )
kT
扩散系数
除原子跳动的能量条件之外,还需满足 --条件。
① 间隙扩散:空的间隙位置数近似等于-
-。
Z exp( G )
kT
② 置换扩散:某一原子周围的空位数取决
于平衡--。
Z A exp( G ) exp( QA )
柯肯达尔效应的解释
Ni原子比Cu原子扩散的快,有一个净Ni原子流 越过W丝流向Cu一侧,同时有一个空位流越过 W丝流向Ni。
Cu一侧空位浓度↘(低于平衡浓度),则Ni一 侧空位浓度↗(高于平衡浓度)。
当两侧空位浓度恢复到平衡浓度时,Cu一侧将 因空位↗而伸长,Ni一侧将因空位↘而缩短,这 相当于W丝向Ni一侧移动一段距离。
菲克第一定律
③ 适用于系统的任何位置,而且适用于扩 散过程的任一时刻。
④ D>0,扩散由--向--进行,扩散 的结果是浓度在不同空间位置的差别- -,即--扩散; D <0,
溶质原子流动方向与浓度降低方向一致
(2)菲克第二定律
非稳态扩散: 若扩散沿x轴单向进行,菲克第二定律的
数学表达式为:
本征扩散: 非本征扩散:
本征扩散与非本征扩散
体系中的空位浓度(Nν)包含--两部分。 即:
1nD~1/T图出现有弯曲或转折现象,是 由于两种扩散的--差异所致。
7.5 扩散驱动力
--称为扩散驱动力。 热力学研究表明,扩散的驱动力是-- 无论下坡扩散、上坡扩散,都要满足热
力学原理,要求不同空间位置的化学位 差越来越--。
两种机制比较:
原子扩散时的“中转站”: 间隙位置本身是不能移动的,而空位是
可以移动的。
扩散系数
D s2 Pห้องสมุดไป่ตู้
扩散系数D与跃迁距离s的平方、跃迁 方向几率P、跃迁的频率Г成正比。
① P是与--有关的参数。
以立方结构为例:
间隙扩散: P 1
6
即
D 1 s2 6
空位扩散:还需引入一个相关因子 。
晶体中原子(离子)扩散的微观机制主 要有两种:--。
(1)间隙机制
间隙扩散: 间隙原子在跳动时必须克服一个--。 在--固溶体中,溶质原子的扩散是间
隙扩散
(2)空位机制
空位扩散: 实现空位扩散的条件是:
① 扩散原子邻近有-- ② 原子具有-- 在--固溶体中,溶质原子和溶剂原子 的迁移就是通过空位机制实现的。
菲克第二定律
若在空间三个方向均有浓度梯度,且三个 方向的扩散系数相同,则三维扩散的第二 定律为:---
菲克第二定律
第二定律的数学解:
c(x,t) c0 erfc(x / 2 Dt )
若实验测得 c(x,t) ,即可求得扩散深度与 扩散时间的近似关系:--
7.3 扩散的微观机制
原子的扩散可沿晶体表面进行,也可沿 晶体中--进行,在晶体内通过晶体点 阵进行。
