山西省运城市2014-2015学年高一上学期期中数学试卷 Word版含解析

合集下载

2014-2015学年山西大学附属中学高一上学期期中考试数学试卷(带解析)

2014-2015学年山西大学附属中学高一上学期期中考试数学试卷（带解析）一、选择题1.设全集，集合，则（）A． B． C． D．【答案】A【解析】试题分析：根据所给全集，注意表示正整数集，再由集合求出，根据补集定义求出.考点：1.集合的交集、并集、补集运算； 2.运算工具（韦恩图、数轴、平面直角坐标系）.2.函数的定义域为（）A． B． C． D．【答案】C【解析】试题分析：首先考虑使函数解析式有意义的要求考点:1.函数的定义域； 2.对数的定义；3.已知且，下列四组函数中表示相等函数的是（）A．与B．与C．与D．与【答案】B【解析】试题分析：两个函数解析式表示同一个函数要求定义域相同且对应法则相同。

中的函数定义域要求，函数定义域要求，由于定义域不同，所以不是同一函数；中的函数定义域要求，而函数定义域为，由于定义域不同，所以不是同一函数；中函数的定义域要求，而函数的定义域要求，由于定义域不同，所以不是同一函数；只有中两个函数定义域均为，且满足要求。

考点：1.函数的定义域； 2.对数的定义； 3.对数运算公式4.下列函数中值域为的是（）A．B．C．D．【答案】C【解析】中的函数，由于，所以函数值域为，中函数值域为，中函数，由于，；故选择.试题分析：考点：1.函数的值域； 2.指数函数图象与性质； 3.对勾函数图象；5.已知幂函数的图像过点,则的值为（）A． B． C． D．【答案】A【解析】试题分析：由于幂函数的图象经过点，则，则，则考点：1.幂函数的定义； 2.指数、对数运算； 3.换底公式；6.在下列区间中，函数的零点所在的区间为（）A． B． C． D．【答案】C【解析】试题分析：可采用图象法解题，先画出的图象，再画出的图象，图象交点的横坐标在内，下面进行细致验证：当时，；当时，，，；则;考点：1.指数函数图象与性质； 2.零点的概念及零点范围的求法； 3.数形结合思想解题；7.三个数的大小关系为（）A．B．C．D．【答案】D【解析】试题分析：借助指数函数的图象，由于函数在上为减函数，，可知考查，在由对数函数和的图象考查，得；考点：指数函数图象和性质； 2.对数函数图象和性质；8.当，不等式恒成立，则实数的取值范围是（）A． B． C． D．【答案】B【解析】试题分析：利用数形结合思想解题，先画出在的图象（抛物线的一部分），由于不等式恒成立，所以只能，而且时，，则，所以.考点：1.对数函数图象与性质； 2.二次函数图象； 2.零点的概念及零点范围的求法9.若函数为定义在上的奇函数，且在为增函数，又，则不等式的解集为（）A．B．C．D．【答案】D【解析】试题分析：因为不等式可化为去解。

山西省山大附中2014-2015学年高一上学期期中考试数学Word版含答案

山西大学附中2014~2015学年高一第一学期期中考试（总第二次）数学试题考试时间：90分钟满分：100分一、选择题（本大题共10小题，每小题4分，共40分）1．设全集{}*|6U x N x =∈<，集合{}{}1,3,3,5A B ==，则()U C A B =( )A ．{}2,4B ．{}1,5C ．{}1,4D ．{}2,52．函数()lg(2)f x x =+的定义域为( ) A ．(2,1)-B ．[2,1)-C ．(2,1]-D ．[]1,2-3．已知0a >且1a ≠，下列四组函数中表示相等函数的是( )A ．log a y x = 与1(log )x y a -=B ．2y x =与2log x a y a =C ．log a xy a=与y x = D ．2log a y x =与2log a y x =4．已知函数21()21x x f x -=+,若()f a b =，则()f a -=( )A ．bB ．b -C ．1bD ．1b-5．下列函数中值域为()0,+∞的是( )A ．xy -=215 B ．()10y x x x =+> C ．xy -⎪⎭⎫⎝⎛=131D ．()11y x x x=-≥6．已知幂函数()y f x =的图像过点(,则4log (2)f 的值为( )A ．14 B ．14- C ．2 D ．2- 7．在下列区间中，函数()43xf x e x =+-的零点所在的区间为( )A ．1,04⎛⎫- ⎪⎝⎭B ．10,4⎛⎫ ⎪⎝⎭C ．11,42⎛⎫ ⎪⎝⎭D ．13,24⎛⎫ ⎪⎝⎭8．三个数 3.3320.99,log ,log 0.8π的大小关系为( )A ． 3.332log 0.99log 0.8π<<B ． 3.323log 0.8log 0.99π<<C ． 3.3230.99log 0.8l og π<<D ． 3.323log 0.80.99log π<< 9．当(1,2)x ∈，不等式2(1)log a x x -<恒成立，则实数a 的取值范围是（）A ．(1,2)B ．(1,2]C ．[)2,+∞ D ．(2,)+∞10．若函数()f x 为定义在R 上的奇函数，且在()0,+∞为增函数，又(2)f 0=，则不等式[]1ln ()0x f x e ⎛⎫⋅⋅< ⎪⎝⎭的解集为( ) A ．()()2,02,-+∞ B ．()(),20,2-∞-C ．()()2,00,2-D ．()(),22,-∞-+∞二、填空题：（本大题共5小题，每小题4分，共20分）11．函数()log 12a y x =++(01)a a >≠且恒过定点，其坐标为．12．设1232,2()log (1),2x e x f x x x -⎧<⎪=⎨-≥⎪⎩，则((2))f f 的值为．13．已知函数()xf x e x =+，若关于x 的方程()f x k =有两个不同的实根，则实数k 的取值范围是．14．已知函数)(x f 满足：)()()(q f p f q p f ⋅=+，2)1(=f ，则：)2013()2014()7()8()5()6()3()4()1()2(f f f f f f f f f f +++++ = ． 15．给出下列四个命题：①函数2212-+-=x x y 为奇函数；②奇函数的图像一定通过直角坐标系的原点； ③函数xy 12=的值域是()0,+∞；④若函数)2(x f 的定义域为[1,2]，则函数)2(xf 的定义域为[1,2]； ⑤函数()x x y 2lg 2+-=的单调递增区间是(]0,1．其中正确命题的序号是．（填上所有正确命题的序号）三、解答题（本大题共5小题，共40分．解答应写出必要的文字说明，证明过程或演算步骤）16．（本小题满分8分）计算：（Ⅰ）()20.532025270.1100964π--⎛⎫⎛⎫++-⋅⎪ ⎪⎝⎭⎝⎭；（Ⅱ）82715lg lg lg12.5log 9log 828-+-⋅+2ln 2e ．17．（本小题满分8分）已知集合{}22|280A x x ax a =--≤．（Ⅰ）当1a =时，求集合R C A ；（Ⅱ）若0a >，且(1,1)A -⊆，求实数a 的取值范围．18．（本小题满分8分）已知二次函数a ax x x f -+-=2)(2在区间[]0,1上有最大值2，求实数a 的值．19．()1,1-上的函数．（Ⅰ）用定义法证明函数()x f 在()1,1-上是增函数；（Ⅱ）解不等式()()01<+-x f x f ．20．（本小题满分8分）已知函数4()log (41)()x f x kx k R =++∈是偶函数．（Ⅰ）求k 的值；（Ⅱ）设44()log (2)3x g x a a =⋅-,若函数()f x 与()g x 的图象有且只有一个公共点，求实数a 的取值范围．山西大学附中2014~2015学年高一第一学期期中考试（总第二次）数学答案二、填空题：（本大题共5小题，每小题4分，共20分）11． ()0,2 12． 2． 13．()1,+∞ 14．2014 15．①④⑤三、解答题（本大题共5小题，共40分．解答应写出必要的文字说明，证明过程或演算步骤）16．（本小题满分8分）计算：（Ⅰ）()20.532025270.1100964π--⎛⎫⎛⎫++-⋅⎪ ⎪⎝⎭⎝⎭；（Ⅱ）82715lg lg lg12.5log 9log 828-+-⋅+2ln 2e ．解：（Ⅰ）319；……………………4分（Ⅱ）133……………………8分17．（本小题满分8分）已知集合{}22|280A x x ax a =--≤．（Ⅰ）当1a =时，求集合R C A ；（Ⅱ）若0a >，且(1,1)A -⊆，求实数a 的取值范围．解：（Ⅰ）当1=a 时，解不等式0822≤--x x ，得42≤≤-x …………………2分 ∴{}|42R C A x x x =><-或 ………………………………………3分（Ⅱ）∵22280x ax a --≤，∴0)2)(4(≤+-a x a x又∵0a > ∴24a x a -≤≤ ∴[]2,4A a a =- ……………………5分又∵()1,1A -⊆ ∴1214aa-≥-⎧⎨≤⎩ …………………………………………7分解得21≥a ，故实数a 的取值范围是1[,)2+∞ …………………………………8分 18．（本小题满分8分）已知二次函数a ax x x f -+-=2)(2在区间[]0,1上有最大值2，求实数a 的值解析：由a a a x x f -+--=22)()(，得函数)(x f 的对称轴为：x a =，……1分 ①当0<a 时，()f x 在]1,0[上递减， 2)0(=∴f ，即2,2-=∴=-a a ； ……………………3分 ②当1>a 时，()f x 在]1,0[上递增， 2)1(=∴f ，即3=a ； ……………………5分③当01a ≤≤时，()f x 在],0[a 递增，在[,1]a 上递减，2)(=∴a f ，即22=-a a ，解得：12-=或a 与01a ≤≤矛盾；……………7分综上：2a =-或3a = ……………………8分19．（本小题满分8()1,1-上的函数．（Ⅰ）用定义法证明函数()x f 在上是增函数；（Ⅱ）解不等式()()01<+-x f x f ．解：（Ⅰ）证明：对于任意的()1,1,21-∈x x ，且21x x <，则()()()()()()()()()()()()()()22212121222112212122212122212222112111111111111x x x x x x x x x x x x x x x x x x x x x x x x x f x f ++--=++-+-=+++-+=+-+=- 1121<<<-x x ， ()()011,0222121>++<-∴x x x x ，01,12121>-∴<∴x x x x ． ()()021<-∴x f x f ，即()()21x f x f <．∴函数()21xf x x =+在()1,1-上是增函数．…………………… 4分（Ⅱ）由已知及（Ⅰ）知，()f x 是奇函数且在()1,1-上递增，()()()()()()2102111201111111101<<⇔⎪⎪⎩⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧<<<-<<⇔-<-<<-<-<-⇔-<-⇔-<-⇔<+-x x x x x x x x x f x f x f x f x f x f ∴不等式的解集为10,2⎛⎫⎪⎝⎭．…… 8分．20．（本小题满分8分）已知函数4()log (41)()x f x kx k R =++∈是偶函数．（Ⅰ）求k 的值；（Ⅱ）设44()log (2)3x g x a a =⋅-,若函数()f x 与()g x 的图象有且只有一个公共点，求实数a 的取值范围．解：（Ⅰ）由函数()f x 是偶函数，可知()().f x f x =-kx kx x x -+=++∴-)14(log )14(log 44,kx x x 21414log 4-=++-即, ,24log 4kx x -= 2x kx ∴=-对一切 x R ∈恒成立21-=∴k ……………3分（Ⅱ）函数()f x 与()g x 的图象有且只有一个公共点,即方程4414log (41)log (2)23x x x a a +-=⋅-有且只有一个实根,化简得: 方程142223x x x a a +=⋅-有且只有一个实根 ……………………4分令20x t =>,则方程24(1)103a t at ---=有且只有一个正根,①314a t =⇒=-,不合题意; ……………………5分②若304a ∆=⇒=或3-；若3,24a t ==-则,不合题意；若132a t =-⇒= ,符合题意③若方程一个正根与一个负根,即1011a a -<⇒>- ……………………7分综上:实数a 的取值范围是{}3(1,)-⋃+∞ ……………………8分。

山西省运城市2014～2015学年第一学期期末高三调研测试理科数学试题

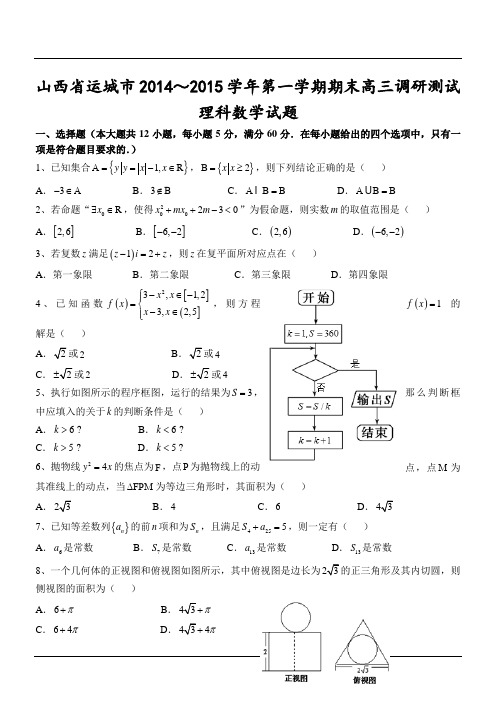
山西省运城市2014～2015学年第一学期期末高三调研测试理科数学试题一、选择题（本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1、已知集合{}1,R y y x x A ==-∈，{}2x x B =≥，则下列结论正确的是（） A ．3-∈A B ．3∉B C ．A B =B D ．A B =B2、若命题“0R x ∃∈，使得200230x mx m ++-<”为假命题，则实数m 的取值范围是（）A ．[]2,6B ．[]6,2--C ．()2,6D ．()6,2-- 3、若复数z 满足()12z i z -=+，则z 在复平面所对应点在（） A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限4、已知函数()[](]23,1,23,2,5x x f x x x ⎧-∈-⎪=⎨-∈⎪⎩，则方程()1f x =的解是（）A2 B或4 C．或2 D．或4 5、执行如图所示的程序框图，运行的结果为3S =，那么判断框中应填入的关于k 的判断条件是（） A ．6k >? B ．6k <? C ．5k >? D ．5k <?6、抛物线24y x =的焦点为F ，点P 为抛物线上的动点，点M 为其准线上的动点，当F ∆PM 为等边三角形时，其面积为（）A． B ．4 C ．6 D． 7、已知等差数列{}n a 的前n 项和为n S ，且满足4255S a +=，则一定有（） A ．6a 是常数 B ．7S 是常数 C ．13a 是常数 D ．13S 是常数8、一个几何体的正视图和俯视图如图所示，其中俯视图是边长为的正三角形及其内切圆，则侧视图的面积为（）A ．6π+ B．π C ．64π+ D．4π 9、已知三棱锥C S -AB 的四个顶点都在一个半径为r 的球面上，球心O 在AB 上，S O ⊥底面C AB，C A =，则球的体积与三棱锥体积之比是（）A ．πB ．2πC ．3πD ．4π10、已知不等式组3410043x y x y +-≥⎧⎪≤⎨⎪≤⎩表示区域D ，过区域D 中任意一点P 作圆221x y +=的两条切线且切点分别为A 、B ，当∠APB 最大时，cos ∠APB =（） A．B ．12 C． D ．12- 11、已知函数()sin cos f x a x b x =+（R x ∈），若0x x =是函数()f x 的一条对称轴，且0tan 2x =，则点(),a b 所在的直线为（）A ．20x y -=B ．20x y +=C ．20x y -=D ．20x y += 12、设函数()sin x f x e x =+，()2g x x =-，设()()11,x f x P ，()()22Q ,x g x （10x ≥，20x >），若直线Q//P x 轴，则P ，Q 两点间最短距离为（）A ．2B ．3C ．4D ．5 二、填空题（本大题共4小题，每小题5分，共20分．） 13、已知1a =，2b =，3a b +=，则a 与b 的夹角为． 14、如图所示，在矩形C OAB 内任取一点P ，则点P 恰落在图中阴影部分中的概率为．15、若正数a ，b 满足1a b +=，则11a ba b +++的最大值为． 16、已知双曲线22221x y a b-=（0a >，0b >）上一点C ，过双曲线中心的直线交双曲线于A ，B 两点，记直线C A ，C B 的斜率分别为1k ，2k ，当12122ln ln k k k k ++最小时，双曲线离心率为．三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．） 17、（本小题满分10分）设C ∆AB 的内角A ，B ，C 所对边的长分别为a ，b ，c ，且cos C sin a b =+B ． ()1求B ；()2若1c =，3a =，C A 的中点为D ，求D B 的长．18、（本小题满分12分）如图，已知四棱锥CD P -AB ，底面CD AB 为菱形，PA ⊥平面CD AB ，C 60∠AB =，E ，F 分别是C B ，C P 的中点．()1证明：D AE ⊥P ；()2若2AB =，2PA =，求二面角F C E -A -的余弦值．19、（本小题满分12分）2014年11月10日C APE 会议在北京召开，某服务部需从大学生中招收志愿者，被招收的志愿者需参加笔试和面试两部分，把参加笔试的40名大学生的成绩分组：第组[)75,80，第2组[)80,85，第3组[)85,90，第4组[)90,95，第5组[)95,100，得到的频率分布直方图如图所示：()1分别求出成绩在第3，4，5组的人数；()2现决定在笔试成绩较高的第3、4、5组中用分层抽样抽取6人进行面试．①已知甲和乙的成绩均在第3组，求甲或乙进入面试的概率；②若从这6名学生中随机抽取2名学生接受考官D 的面试，设第4组中有X 名学生被考官D 面试，求X 的分布列和数学期望．20、（本小题满分12分）设数列{}n a 的前n 项和为n S ，且首项13a ≠，13n n n a S +=+（n *∈N ）．()1求证：{}3n n S -是等比数列；()2若{}n a 为递增数列，求1a 的取值范围．21、（本小题满分12分）已知椭圆:E 22221x y a b+=（0a b >>）过点()2,1M ，焦距为．()1求椭圆E 的方程；()2若直线平行于OM ，且与椭圆E 交于A 、B 两个不同的点（与M 不重合），连接MA 、MB ，MA 、MB 所在直线分别与x 轴交于P 、Q 两点，设P 、Q 两点的横坐标分别为s ，，探求s t +是否为定值？若是，求出该定值；若不是，请说明理由．22、（本小题满分12分）设函数()2ln f x x bx a x =+-．()1若2x =是函数()f x 的极值点，和0x 是函数()f x 的两个不同零点，且()0,1x n n ∈+，n ∈N ，求n ；()2若对任意[]2,1b ∈--，都存在()1,x e ∈（e 为自然对数的底数），使得()0f x <成立，求实数a 的取值范围．运城市2014～2015学年第一学期期末高三调研测试试题理科数学参考答案。

山西省运城市数学高一上学期理数期中考试试卷

山西省运城市数学高一上学期理数期中考试试卷姓名:________班级:________成绩:________一、选择题 (共 8 题；共 16 分)1. （2 分）已知集合，或，则的充要条件是（）A. B. C. D.2. （2 分） (2015 高一上·雅安期末) 定义在 R 上的偶函数 f（x）满足 f（x+1）= ﹣2]上是减函数，若 α，β 是锐角三角形的两个内角，则（）A . f（sinα）＞f（sinβ） B . f（cosα）＞f（cosβ） C . f（sinα）＞f（cosβ） D . f（sinα）＜f（cosβ），且 f（x）在[﹣3，3. （2 分）等边三角形 ABC 的边长为 1， A.3 B . -3,那么等于（）C.D.4. （2 分）已知数列{an}满足：，则 a2009=（）A.第 1 页共 10 页B.5C.D.5. （2 分）将函数 y=sin（2x+ ）的图象向右平移个单位，再纵坐标不变，横坐标变为原来的 2 倍，所得新图象的函数解析式是（）A . y=sin4x B . y=sinxC . y=sin（4x﹣ ）D . y=sin（x﹣ ） 6. （2 分） (2020 高二下·南宁期末) 以下四个命题：①若为假命题，则 p，q 均为假命题；②对于命题则 Øp 为：；③是函数在区间上为增函数的充分不必要条件；④为偶函数的充要条件是其中真命题的个数是（）A.1B.2C.3D.47. （2 分）设函数 f (x)＝x3－4x＋a，0＜a＜2．若 f (x)的三个零点为 x1 ， x2 ， x3 ，且 x1＜x2＜x3 ，则（）A . x1＞－1第 2 页共 10 页B . x2＜0 C . x2＞0 D . x3＞2 8. （2 分）已知集合 M={（x，y）|y=f（x）}，若对于任意（x1 ， y1）∈M，存在（x2 ， y2）∈M，使得 x1x2+y1y2=0 成立，则称集合 M 是“理想集合”．给出下列 4 个集合：①M={（x，y）|y= }；②M={（x，y）|y=sinx}；③M={（x，y）|y=ex﹣2}； ④M={（x，y）|y=lgx}．其中所有“理想集合”的序号是（） A . ①③ B . ②③ C . ②④ D . ③④二、填空题 (共 6 题；共 6 分)9. （1 分） (2018 高二上·寻乌期末)________．10. （1 分） (2016 高一上·嘉兴期中) 已知函数 f（x）=．则 f（f（﹣1））=________．11. （1 分）命题“若 a＞1 且 b＞1，则 a+b＞2”的否命题是________ 命题（填“真”或“假”）12. （1 分） (2018·孝义模拟) 已知向量与的夹角是角是________．，且，则向量与的夹13. （1 分） (2019 高三上·铁岭月考) 已知函数数根，则的最大值是________．若方程恰有两个不同的实14. （1 分） (2019 高一上·伊春期中) 函数 f(x)为奇函数，且 x>0 时，f(x)＝第 3 页共 10 页＋1，则当 x<0 时，f(x)＝________.三、解答题 (共 6 题；共 50 分)15. （10 分）已知函数 f（x）= sin cos ﹣ sin2 ．（1）求 f（x）的最小正周期；（2）设△ABC 的内角 A、B、C 的对边分别为 a、b、c，且 c= ，f（C）=0，若向量 =（1，sinA）与向量 =（，sinB）共线，求 a，b．16. （10 分） (2017 高三上·珠海期末) 已知{an}为等比数列，a1=1，a4=27； Sn 为等差数列{bn} 的前 n 项和，b1=3，S5=35．（1）求{an}和{bn} 的通项公式；（2）设数列{cn} 满足 cn=anbn（n∈N*），求数列{cn} 的前 n 项和 Tn ．17. （10 分） (2018·吕梁模拟) 已知抛物线：交于两点，，与轴交于点.，过轴上一点（不同于原点）的直线与（1）若，，求的值；（2）若此定直线.，过，分别作的切线，两切线交于点，证明：点在定直线方程上，求出18. （10 分） (2020·江西模拟) 在中，角所对的边分别为，若，.（1）求；（2）当时，求的面积.19. （5 分）已知函数．（Ⅰ）求曲线 y=f（x）在点（0，5）处的切线方程；第 4 页共 10 页（Ⅱ）求函数 f（x）的极值． 20. （5 分） (2018·浙江) 已知等比数列{an}的公比 q>1，且 a3+a4+a5=28，a4+2 是 a3 ， a5 的等差中项．数列{bn}满足 b1=1，数列{（bn+1−bn）an}的前 n 项和为 2n2+n ．（Ⅰ）求 q 的值；（Ⅱ）求数列{bn}的通项公式．第 5 页共 10 页一、选择题 (共 8 题；共 16 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、二、填空题 (共 6 题；共 6 分)9-1、 10-1、 11-1、 12-1、 13-1、 14-1、三、解答题 (共 6 题；共 50 分)参考答案第 6 页共 10 页15-1、 15-2、 16-1、 16-2、第 7 页共 10 页17-1、 17-2、 18-1、第 8 页共 10 页18-2、19-1、20-1、第 9 页共 10 页第 10 页共 10 页。

山西省运城市高一上学期期中考试数学试卷

2016-2017学年山西省运城市高一（上）期中数学试卷一、选择题：本大题共10个小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．满足{1，3}∪A={1，3，5}的所有集合A的个数（）A．1个B．2个C．3个D．4个2．设全集U={1，3，5，7，9}，集合A={1，|a﹣5|，9}，∁U A={5，7}，则实数a的值是（）A．2 B．8 C．﹣2或8 D．2或83．已知函数y=f（x），则函数f（x）的图象与直线x=a的交点（）A．有1个B．有2个C．有无数个 D．至多有一个4．函数y=x2+x （﹣1≤x≤3 ）的值域是（）A．[0，12]B．[﹣，12]C．[﹣，12]D．[，12]5．设f（x）=，则f（5）的值为（）A．10 B．11 C．12 D．136．若函数f（x）满足f（3x+2）=9x+8，则f（x）是（）A．f（x）=9x+8 B．f（x）=3x+2C．f（x）=﹣3﹣4 D．f（x）=3x+2或f（x）=﹣3x﹣47．设，则（）A．y3＞y1＞y2B．y2＞y1＞y3C．y1＞y3＞y2D．y1＞y2＞y38．已知lga，lgb是方程2x2﹣4x+1=0的两个根，则的值是（）A．4 B．3 C．2 D．19．若函数y=f（x）是定义在R上的偶函数，在（﹣∞，0]上是减函数，且f（2）=0，则使函数值y ＜0的x取值范围为（）A．（﹣2，2）B．（2，+∞）C．（﹣∞，2）D．（﹣∞，2]10．对于函数f（x）的定义域中任意的x1、x2（x1≠x2），有如下结论：①f（x1+x2）=f（x1）•f（x2）；②f（x1•x2）=f（x1）+f（x2）；③＞0；④f（）＜．当f（x）=2x时，上述结论中正确的有（）个．A．3 B．2 C．1 D．0二、填空题（每题4分，满分24分，将答案填在答题纸上）11．若函数f（x）=为奇函数，则m=．12．幂函数的图象过点（2，），则它的解析式是．13．函数f（x）=log（x2﹣4x﹣5）的单调递减区间为．14．若，则a，b，c大小关系是（请用”＜”号连接）15．方程2x=x2有个根．16．函数f（x）的反函数为y=3x（x∈R），则f（x）=．三、解答题（本大题共4小题，共36分.解答应写出文字说明、证明过程或演算步骤.）17．（9分）已知A={x|﹣1＜x≤3}，B={x|m≤x＜1+3m}（1）当m=1时，求A∪B；（2）若B⊆∁R A，求实数m的取值范围．18．（9分）化简或求值：（1）（2）计算．19．（9分）已知函数f（x）=log a（x+1）﹣log a（1﹣x），a＞0且a≠1．（1）求f（x）的定义域；（2）判断f（x）的奇偶性并予以证明．20．（9分）李庄村电费收取有以下两种方案供农户选择：方案一：每户每月收管理费2元，月用电不超过30度每度0.5元，超过30度时，超过部分按每度0.6元．方案二：不收管理费，每度0.58元．（1）求方案一收费L（x）元与用电量x（度）间的函数关系；（2）李刚家九月份按方案一交费35元，问李刚家该月用电多少度？（3）李刚家月用电量在什么范围时，选择方案一比选择方案二更好？2016-2017学年山西省运城市高一（上）期中数学试卷参考答案与试题解析一、选择题：本大题共10个小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（2016•南充三模）满足{1，3}∪A={1，3，5}的所有集合A的个数（）A．1个B．2个C．3个D．4个【考点】并集及其运算．【专题】计算题．【分析】由题意得1，3和5可能是集合B的元素，把集合B所有的情况写出来．【解答】解：∵{1，3}∪A={1，3，5}，∴1和2和3可能是集合B的元素，则集合B可能是：{5}，{1，5}，{3，5}，{1，5，3}共4个．故选D．【点评】本题的考点是并集及运算的应用，即根据并集的运算确定元素和集合的关系，再把它们写出来．2．（2007•石景山区一模）设全集U={1，3，5，7，9}，集合A={1，|a﹣5|，9}，∁U A={5，7}，则实数a的值是（）A．2 B．8 C．﹣2或8 D．2或8【考点】补集及其运算．【专题】计算题．【分析】根据补集的定义和性质可得3∈A，|a﹣5|=3，解出实数a的值．【解答】解：由题意可得3∈A，|a﹣5|=3，∴a=2，或a=8，故选D．【点评】本题考查集合的表示方法、集合的补集的定义和性质，判断|a﹣5|=3 是解题的关键．3．（2016秋•运城期中）已知函数y=f（x），则函数f（x）的图象与直线x=a的交点（）A．有1个B．有2个C．有无数个 D．至多有一个【考点】函数的概念及其构成要素．【专题】综合法．【分析】根据函数的定义，当自变量在定义域内任取一值时，y有且只有一个值与之对应，由此即可判断．【解答】解：由函数的定义，当a在定义域内时，y有且只有一个值与之对应，即直线x=a与函数图象只有一个交点；当a不在定义域内时，此时y没有值与之对应，即此时直线与图象无交点．综上可知，直线与函数图象至多一个交点．故选：D．【点评】本题考查函数的概念．属于基础题．4．（2008秋•广州期末）函数y=x2+x （﹣1≤x≤3 ）的值域是（）A．[0，12]B．[﹣，12]C．[﹣，12]D．[，12]【考点】二次函数在闭区间上的最值．【专题】计算题．【分析】先将二次函数配方，确定函数在指定区间上的单调性，从而可求函数的值域．【解答】解：由y=x2+x得，∴函数的对称轴为直线∵﹣1≤x≤3，∴函数在上为减函数，在上为增函数∴x=时，函数的最小值为x=3时，函数的最大值为12∴≤y≤12．故值域是[，12]故选B．【点评】本题重点考查二次函数在指定区间上的值域，解题的关键是配方，确定函数的单调性，属于基础题．5．（2010•云南模拟）设f（x）=，则f（5）的值为（）A．10 B．11 C．12 D．13【考点】分段函数的解析式求法及其图象的作法；函数的值．【分析】欲求f（5）的值，根据题中给出的分段函数，只要将问题转化为求x≥10内的函数值即可求出其值．【解答】解析：∵f（x）=，∴f（5）=f[f（11）]=f（9）=f[f（15）]=f（13）=11．故选B．【点评】本题主要考查了分段函数、求函数的值．属于基础题．6．（2015秋•淮北期末）若函数f（x）满足f（3x+2）=9x+8，则f（x）是（）A．f（x）=9x+8 B．f（x）=3x+2C．f（x）=﹣3﹣4 D．f（x）=3x+2或f（x）=﹣3x﹣4【考点】函数解析式的求解及常用方法．【专题】函数的性质及应用．【分析】利用换元法，令t=3x+2，则x=代入f（x）中，即可求得f（t），然后将t换为x即可得f（x）的解析式．【解答】解：令t=3x+2，则x=，所以f（t）=9×+8=3t+2．所以f（x）=3x+2．故选B．【点评】本题主要考查复合函数解析式的求法，采取的方法一般是利用配凑法或者换元法来解决．属于基础题．7．（2012秋•潮阳区期末）设，则（）A．y3＞y1＞y2B．y2＞y1＞y3C．y1＞y3＞y2D．y1＞y2＞y3【考点】指数函数的单调性与特殊点．【专题】函数的性质及应用．【分析】化简这三个数为2x的形式，再利用函数y=2x在R上是增函数，从而判断这三个数的大小关系．【解答】解：∵=21.8，=（23）0.48=21.44，=21.5，函数y=2x在R上是增函数，1.8＞1.5＞1.44，∴21.8＞21.5＞21.44，故y1＞y3＞y2，故选C．【点评】本题主要考查指数函数的单调性和特殊点，体现了转化的数学思想，属于基础题．8．（2016秋•运城期中）已知lga，lgb是方程2x2﹣4x+1=0的两个根，则的值是（）A．4 B．3 C．2 D．1【考点】根的存在性及根的个数判断．【专题】方程思想；转化法；函数的性质及应用．【分析】运用二次方程的韦达定理和对数的运算性质，结合配方法，计算即可得到所求值．【解答】解：lga，lgb是方程2x2﹣4x+1=0的两个根，可得lga+lgb=2，lgalgb=，则=（lga﹣lgb）2=（lga+lgb）2﹣4lgalgb=22﹣4×=4﹣2=2．故选：C．【点评】本题考查对数的运算性质，以及二次方程根的韦达定理的运用，考查配方法，属于基础题．9．（2016秋•运城期中）若函数y=f（x）是定义在R上的偶函数，在（﹣∞，0]上是减函数，且f （2）=0，则使函数值y＜0的x取值范围为（）A．（﹣2，2）B．（2，+∞）C．（﹣∞，2）D．（﹣∞，2]【考点】奇偶性与单调性的综合．【专题】转化思想；转化法；函数的性质及应用；不等式的解法及应用．【分析】由题意可得f（x）在[0，+∞）上为增函数，则y＜0即f（x）＜0，即有f（|x|）＜f（2），即|x|＜2，解不等式即可得到所求范围．【解答】解：函数y=f（x）是定义在R上的偶函数，在（﹣∞，0]上是减函数，且f（2）=0，可得f（x）在[0，+∞）上为增函数，则y＜0即f（x）＜0，即有f（|x|）＜f（2），即|x|＜2，解得﹣2＜x＜2．则使函数值y＜0的x取值范围为（﹣2，2）．故选：A．【点评】本题考查函数的性质和运用，主要考查函数的奇偶性和单调性的运用：解不等式，注意运用偶函数的性质：f（x）=f（|x|）是解题的关键，属于中档题．10．（2016秋•运城期中）对于函数f（x）的定义域中任意的x1、x2（x1≠x2），有如下结论：①f（x1+x2）=f（x1）•f（x2）；②f（x1•x2）=f（x1）+f（x2）；③＞0；④f（）＜．当f（x）=2x时，上述结论中正确的有（）个．A．3 B．2 C．1 D．0【考点】命题的真假判断与应用．【专题】简易逻辑．【分析】利用函数的性质验证命题的真假即可．【解答】解：当f（x）=2x时，①f（x1+x2）===f（x1）•f（x2）；①正确；由①可知②f（x1•x2）=f（x1）+f（x2）；不正确；③＞0；说明函数是增函数，而f（x）=2x是增函数，所以③正确；④f（）＜．说明函数是凹函数，而f（x）=2x是凹函数，所以④正确；故选：A．【点评】本题考查函数的基本性质的应用，考查命题的真假的判断，是基础题．二、填空题（每题4分，满分24分，将答案填在答题纸上）11．（2016秋•运城期中）若函数f（x）=为奇函数，则m=﹣3．【考点】函数奇偶性的性质．【专题】计算题；函数思想；综合法；函数的性质及应用．【分析】根据f（x）为奇函数便可得出，化简即可得到x2﹣（m+3）x+3m=x2+（3+m）x+3m，从而求出m的值．【解答】解：f（x）为奇函数，则f（﹣x）=﹣f（x）；∴；∴（﹣x+3）（﹣x+m）=（x+3）（x+m）；∴x2﹣（m+3）x+3m=x2+（3+m）x+3m；∴﹣（m+3）=m+3；∴m=﹣3．故答案为：﹣3．【点评】考查奇函数的定义，以及多项式相等的充要条件．12．（2016秋•运城期中）幂函数的图象过点（2，），则它的解析式是y=x﹣2．【考点】幂函数的概念、解析式、定义域、值域．【分析】已知函数为幂函数，求其解析式，假设解析式为y=x m，幂函数图象过点（2，），只需把点代入解析式中，求出m的值即可．【解答】解：设幂函数的解析式为y=x m，已知幂函数的图象过点（2，），所以2m=，即m=﹣2，所以它的解析式为y=x﹣2．故答案为y=x﹣2【点评】首先明白什么是幂函数，再利用待定系数法求幂函数的解析式，是函数的基本知识．13．（2016秋•运城期中）函数f（x）=log（x2﹣4x﹣5）的单调递减区间为（5，+∞）．【考点】复合函数的单调性．【专题】转化思想；换元法；函数的性质及应用．【分析】先求出函数的定义域，利用复合函数的单调性之间的关系进行求解即可．【解答】解：要使函数有意义，则x2﹣4x﹣5＞0，即x＞5或x＜﹣1．设t=x2﹣4x﹣5，则当x＞5时，函数t=x2﹣4x﹣5单调递增，当x＜﹣1时，函数t=x2﹣4x﹣5单调递减．∵函数y=log t，在定义域上为单调递减函数，∴根据复合函数的单调性之间的关系可知，当x＞5时，函数f（x）单调递减，即函数f（x）的递减区间为（5，+∞）．故答案为：（5，+∞）【点评】本题主要考查复合函数单调性的判断，利用复合函数同增异减的原则进行判断即可，注意要先求出函数的定义域．14．（2016秋•运城期中）若，则a，b，c大小关系是b＜a＜c （请用”＜”号连接）【考点】指数函数的单调性与特殊点．【专题】函数的性质及应用．【分析】先比较a，b的大小，根据幂函数的单调性可判定，然后比较a，c的大小，利用指数函数的单调性进行判定，从而得到所求．【解答】解：∵，，∴考察幂函数y=的单调性，函数y=在（0，+∞）上单调递增，∵＞，∴a＞b，∵，，∴考察指数函数y=的单调性，函数y=在（0，+∞）上单调递减，∵，∴a＜c，综上所述：b＜a＜c．故答案为：b＜a＜c．【点评】本题主要考查利用指数函数的单调性，幂函数的单调性，进行比较大小，同时考查了分析问题的能力，属于基础题．15．（2016秋•运城期中）方程2x=x2有3个根．【考点】根的存在性及根的个数判断．【专题】数形结合；函数的性质及应用．【分析】在同一坐标系中作出函数y=2x和y=x2的图象，由图象易知答案．【解答】解：在同一坐标系中作出函数y=2x和y=x2的图象，如图：故答案为：3．【点评】本题考查方程得根的存在性问题．利用数形结合的方法是解题捷径．属于基础题．16．（2016秋•运城期中）函数f（x）的反函数为y=3x（x∈R），则f（x）=log3x（x＞0）．【考点】反函数．【专题】方程思想；转化思想；函数的性质及应用．【分析】由y=3x（x∈R），解得x=log3y，把x与y互换即可得出．【解答】解：由y=3x（x∈R），解得x=log3y，把x与y互换可得：y=log3x（x＞0）．∴f（x）=log3x（x＞0）故答案为：y=log3x（x＞0）．【点评】本题考查了反函数的求法、指数与对数式的互化，考查了推理能力与计算能力，属于基础题．三、解答题（本大题共4小题，共36分.解答应写出文字说明、证明过程或演算步骤.）17．（9分）（2015秋•河南校级期末）已知A={x|﹣1＜x≤3}，B={x|m≤x＜1+3m}（1）当m=1时，求A∪B；（2）若B⊆∁R A，求实数m的取值范围．【考点】并集及其运算；集合的包含关系判断及应用．【专题】计算题．【分析】（1）将m的值代入集合B中确定出B，找出既属于A又属于B的部分，即可确定出两集合的并集；（2）由全集R求出A的补集，由B为A补集的子集，列出关于m的不等式，求出不等式的解集，即可得到m的范围．【解答】解：（1）当m=1时，A={x|﹣1＜x≤3}，B={x|1≤x＜4}，则A∪B={x|﹣1＜x＜4}；（2）∵全集为R，A={x|﹣1＜x≤3}，∴C R A={x|x≤﹣1或x＞3}，∵B⊆C R A，当B=∅时，m≥1+3m，即m≤﹣；当B≠∅时，m＜1+3m，即m＞﹣，此时1+3m≤﹣1或m＞3，解得：m＞3，综上，m的范围为m≤﹣或m＞3．【点评】此题考查了并集及其运算，以及集合的包含关系判断及应用，熟练掌握并集的定义是解本题的关键．18．（9分）（2016秋•运城期中）化简或求值：（1）（2）计算．【考点】对数的运算性质；有理数指数幂的化简求值．【专题】计算题．【分析】（1）利用指数幂的运算法则即可得出；（2）利用对数的运算法则即可得出．【解答】解：（1）原式==．（2）分子=lg5（3+3lg2）+3（lg2）2=3lg5+3lg2（lg5+lg2）=3；分母=（lg6+2）﹣lg6+1=3；∴原式=1．【点评】本题考查了指数幂的运算法则、对数的运算法则，属于基础题．19．（9分）（2016春•东城区期末）已知函数f（x）=log a（x+1）﹣log a（1﹣x），a＞0且a≠1．（1）求f（x）的定义域；（2）判断f（x）的奇偶性并予以证明．【考点】函数奇偶性的判断；函数的定义域及其求法．【专题】函数的性质及应用．【分析】（1）使函数各部分都有意义的自变量的范围，即列出不等式组，解此不等式组求出x范围就是函数的定义域；（2）根据函数奇偶性的定义进行证明即可．【解答】解：（1）由题得，使解析式有意义的x范围是使不等式组成立的x范围，解得﹣1＜x＜1，所以函数f（x）的定义域为{x|﹣1＜x＜1}．（2）函数f（x）为奇函数，证明：由（1）知函数f（x）的定义域关于原点对称，且f（﹣x）=log a（﹣x+1）﹣log a（1+x）=﹣log a（1+x）+log a（1﹣x）=﹣[log a（1+x）﹣log a（1﹣x）]=﹣f（x）所以函数f（x）为奇函数．【点评】本题主要考查函数定义域的求法，以及函数奇偶性的判断，利用函数奇偶性的定义是解决本题的关键20．（9分）（2015秋•黄冈期末）李庄村电费收取有以下两种方案供农户选择：方案一：每户每月收管理费2元，月用电不超过30度每度0.5元，超过30度时，超过部分按每度0.6元．方案二：不收管理费，每度0.58元．（1）求方案一收费L（x）元与用电量x（度）间的函数关系；（2）李刚家九月份按方案一交费35元，问李刚家该月用电多少度？（3）李刚家月用电量在什么范围时，选择方案一比选择方案二更好？【考点】函数模型的选择与应用．【专题】应用题；函数思想；分析法；函数的性质及应用．【分析】（1）分0≤x≤30、x＞30两种情况讨论即可；（2）通过分别令0≤x≤30、x＞30时L（x）=35计算即得结论；（3）通过分别令0≤x≤30、x＞30时L（x）＜0.58x计算即得结论．【解答】解：（1）当0≤x≤30时，L（x）=2+0.5x；当x＞30时，L（x）=2+30×0.5+（x﹣30）×0.6=0.6x﹣1，∴（注：x 也可不取0）；（2）当0≤x≤30时，由L（x）=2+0.5x=35得x=66，舍去；当x＞30时，由L（x）=0.6x﹣1=35得x=60，∴李刚家该月用电60度；（3）设按第二方案收费为F（x）元，则F（x）=0.58x，当0≤x≤30时，由L（x）＜F（x），得：2+0.5x＜0.58x，解得：x＞25，∴25＜x≤30；当x＞30时，由L（x）＜F（x），得：0.6x﹣1＜0.58x，解得：x＜50，∴30＜x＜50；综上，25＜x＜50．故李刚家月用电量在25度到50度范围内（不含25度、50度）时，选择方案一比方案二更好．【点评】本题考查函数模型的选择与应用，考查运算求解能力，注意解题方法的积累，属于中档题．。

2014-2015学年高一上学期第三次月考(期中)数学试题Word版含答案

2014-2015学年第一学期高一年级期中考试数学试卷一、选择题(本大题共12小题，每小题5分，共60分,在每小题给出的四个选项中，只有一项符合题目要求)1．全集{}1,2,3,4,0U =----，{}{}1,2,0,3,4,0A B =--=--，则()U C A B ⋂=（） A. {}0 B. {}3,4-- C. {}1,2-- D. ∅ 2. 下列四组函数，表示同一函数的是（） A. ()f x =()g x x = B. ()f x x =,()2x g x x= C. ()f x =()g x = D. ()1f x x =+, ()1,11,1x x g x x x +≥-⎧=⎨--<-⎩3．设1232,2,()log (1),2,x e x f x x x -⎧ <⎪=⎨-≥⎪⎩，则[(2)]f f 的值为（） A ．0 B ．1 C ．2 D ．3 4. 已知点(tan ,sin )P αα在第三象限，则角α在（） A ．第一象限B ．第二象限C ．第三象限D ．第四象限5. 函数()y f x =的定义域为[1,5]，则函数y f x =-()21的定义域是（） A ．[1,5] B ．[2,10] C ．[1,9] D ．[1,3]6. 若0.52a =，log 3b π=，1ln3c =，则（） A ．b c a >> B ．b a c >> C ．a b c >> D ．c a b >>7. 已知tan 2θ=，则22sin sin cos 2cos θθθθ+-=（）A. 43-B.54 C. 34- D. 458．在下列区间中，函数()43xf x e x =+-的零点所在的区间为（）A. 1,04⎛⎫- ⎪⎝⎭B. 10,4⎛⎫ ⎪⎝⎭C. 11, 42⎛⎫ ⎪⎝⎭D. 13,24⎛⎫ ⎪⎝⎭9. 设2()2f x ax bx =++是定义在[]1,2a +上的偶函数，则)(x f 的值域是（）A ．[10,2]-B ．[12,0]-C ．[12,2]-D ．与,a b 有关，不能确定10. 已知函(2)1,1,()log ,1a a x x f x x x ⎧--≤⎪=⎨⎪>⎩若()f x 在(,)-∞+∞上单调递增，则实数a 的取值范围为（）A ．(1,2) B ． (2,3) C ．(2,3]D ． (2,)+∞ 11. 函数sin 2x y x =，(,0)(0,)22x ππ∈-⋃的图象可能是下列图象中的（）12. 设()f x 为R R ++→的函数，对任意正实数x ，()()x f x f 55=，当[1,5]x ∈时()32--=x x f ，则使得()()665f x f =的最小实数x 为（）A ．45 B. 65 C. 85 D. 165二、填空题（本大题共4小题，每小题5分，共20分，请将答案填在答题卡相应位置）13. 已知角α终边上一点(4,3)P -，则cos()sin()2119cos()sin()22παπαππαα+---+的值为_________. 14. 设(2)+f x 是奇函数，且(0,2)x ∈时，()2f x x =，则(3.5)f =_________.15. 已知函数()()23log 5f x x ax a =+++，()f x 在区间(),1-∞上是递减函数，则实数a 的取值范围为_________.16. 设定义域为R 的函数121(1)()(1)x x f x ax --⎧+≠⎪=⎨⎪=⎩，若关于x 的方程22()(23)()30f x a f x a -++=有五个不同的实数解，则a 的取值范围是_________.三、解答题（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤） 17. (本题满分10分)已知函数()f x =的定义域为集合A ，函数()()0121≤≤-⎪⎭⎫⎝⎛=x x g x的值域为集合B ,U R =.(1) 求 ()U C A B ⋂；(2)若{}|21C x a x a =≤≤-且B C ⊆,求实数a 的取值范围,18. (本题满分12分)已知函数()m x x f ++⎪⎭⎫ ⎝⎛+=2162sin π的图像过点⎪⎭⎫⎝⎛0,125π (1)求实数m 的值及()x f 的周期及单调递增区间； (2)若⎥⎦⎤⎢⎣⎡∈2,0πx ，求()x f 的值域.19. (本题满分12分) 某企业常年生产一种出口产品，根据预测可知，进入2l 世纪以来，该产品的产量平稳增长．记2008年为第1年，且前4年中，第x 年与年产量()f x (万件)之若()f x 近似符合以下三种函数模型之一：12(),()2,()log x f x ax b f x a f x x a =+=+=+．（1）找出你认为最适合的函数模型，并说明理由，然后选取08年和10年的数据求出相应的解析式；（2）因遭受某国对该产品进行反倾销的影响，2014年的年产量比预计减少30％，试根据所建立的函数模型，确定2014年的年产量．20．(本题满分12分)已知函数()lg(33)xf x =-， (1)求函数)(x f 的定义域和值域；(2)设函数()()()lg 33x h x f x =-+，若不等式()h x t >无解，求实数t 的取值范围．21. (本题满分12分)定义在R 上的函数()f x 是最小正周期为2的奇函数, 且当(0,1)x ∈时,2()41xxf x =+ . (1)求()f x 在(1,1)-上的解析式；(2)用单调性定义证明()f x 在(1,0)-上时减函数； (3)当λ取何值时, 不等式()f x λ>在R 上有解.22．（本题满分12分）设函数*()(,,),()log (0,1)k k a f x x bx c k N b c R g x x a a =++∈∈=>≠.(1)若1b c +=，且1(1)()4k f g =，求a 的值； (2)若2k =，记函数()k f x 在[1,1]-上的最大值为M ，最小值为m ，求4M m -≤时的b的取值范围；(3)判断是否存在大于１的实数a ，使得对任意1[,2]x a a ∈，都有22[,]x a a ∈满足等式：12()()g x g x p +=，且满足该等式的常数p 的取值唯一？若存在，求出所有符合条件的a 的值；若不存在，请说明理由.高一期中考试数学试卷答案1-12 BDCDD CDCAC DB 13. 34-14.1- 15. [3,2]-- 16. （1，32）∪（32，2） 17.答案：（1）{}1……………………………………………………..5分（2）⎥⎦⎤ ⎝⎛∞-23,……………………………………………………..10分18.解：（1）由题意可知，02161252sin =++⎪⎭⎫ ⎝⎛+⨯m ππ，所以21-=m ……….2分所以()⎪⎭⎫⎝⎛+=62sin πx x f ，T=π……………………3分递增区间为：πππππk x k 226222+≤+≤+- )(Z k ∈……………………………5分解得：ππππk x k +≤≤+-63所以()x f 的单调递增区间为⎥⎦⎤⎢⎣⎡++-ππππk k 6,3)(Z k ∈……………………………7分（2）因为20π≤≤x 所以π≤≤x 20所以67626πππ≤+≤x ………………………………….9分所以162sin 21≤⎪⎭⎫ ⎝⎛+≤-πx 所以()x f 的值域为⎥⎦⎤⎢⎣⎡-1,21……………….12分 19.解：（1）符合条件的是()f x ax b =+， -----------------------------1分若模型为()2xf x a =+，则由1(1)24f a =+=，得2a =，即()22xf x =+，此时(2)6f =,(3)10f =,(4)18f =，与已知相差太大，不符合. -----------3分若模型为12()log f x x a =+，则()f x 是减函数，与已知不符合. -----------4分由已知得437a b a b +=⎧⎨+=⎩，解得3252a b ⎧=⎪⎪⎨⎪=⎪⎩所以35()22f x x =+，x ∈N .-------------------8分（2）2014年预计年产量为35(7)71322f =⨯+=,，---------------9分 2014年实际年产量为13(130%)9.1⨯-=，-----------------11分.答：最适合的模型解析式为35()22f x x =+，x ∈N .2014年的实际产量为9.1万件。

2014-2015学年上学期高一期中测试数学试题(含答案)

2014-2015学年上学期高一期中测试数学试题（含答案）第I 卷（选择题共60分）一、选择题（本大题共12小题，每小题5分，共60分，在每个小题给出的四个选项中，只有一项是符合要求的）1．下列函数中，既是偶函数又在+∞（0，）单调递增的函数是（）A ．3y x =B ． 1y x =+C ．21y x =-+D ． 2x y -=2．在同一坐标系中，表示函数log a y x =与y x a =+的图象正确的是（）A B C D3．若1log 12a<，则a 的取值范围是( ) A ．1(0,)(1,)2+∞ B ．1(,1)2 C ．(1,)+∞ D ．1(,1)(1,)2+∞4．已知函数f(x)为定义在R 上的奇函数，当x≥0时， ()22xf x x m =++ (m 为常数)，则(1)f -的值为( )A ．－3B ．－1C ．1D ．35．设全集U =R ，{}|0P x f x x ==∈R （），，{}|0Q x g x x ==∈R （），，{}|0S x x x ϕ==∈R （），，则方程22f x x x ϕ=（）+g （）（）的解集为（）A ． P Q SB ．P QC ．P Q S （）D ． P Q S u （C ）5．设9.0log 5.0=a ，9.0log 1.1=b ，9.01.1=c ，则c b a , ,的大小关系为（）A ．c b a <<B ．c a b <<C ．a c b <<D ．b c a <<6．设}3 2, ,21 ,31 ,1{-∈α，若函数αx y =是定义域为R 的奇函数，则α的值为（）A ．3 ,31B ．3 ,31 ,1- C ．3 ,1- D ．31,1- 7．已知函数)(x f 是奇函数，当0>x 时，)1 ,0( )(≠>=a a a x f x，且3)4(log 5.0-=f ，则a的值为（）A ．3B ．3C ．9D ．238．已知函数⎪⎩⎪⎨⎧>-≤=-)1( )23(log )1( 2)(2x x x x f x ，若4)(=a f ，则实数=a （） A ．2-或6 B ．2-或310 C ．2-或2 D ．2或3109．方程21231=⎪⎭⎫ ⎝⎛--x x 的解所在的区间为（）A ．) 1 ,0 (B ．) 2 ,1 (C ．) 3 ,2 (D ．) 4 ,3 (10．已知函数bx ax y +=2和xb a y =|)| || ,0(b a ab ≠≠在同一直角坐标系中的图象不可能是（）11．已知函数)3(log 221a ax x y +-=在区间) ,2[∞+上是减函数，则a 的取值范围是（）A ．)4 ,(-∞B ．]4 ,4[-C ．]4 ,4(-D ．]4 ,(-∞12．若在直角坐标平面内B A ,两点满足条件：①点B A ,都在函数)(x f y =的图象上；②点B A ,关于原点对称，则称B A ,为函数)(x f y =的一个“黄金点对”．那么函数=)(x f ⎪⎩⎪⎨⎧>≤-+)0( 1)0( 222x x x x x 的“黄金点对”的个数是（）A ．0个B ．1个C ．2个D ．3个第Ⅱ卷（非选择题，共90分）二、填空题：本题共4小题，共20分.13．已知集合}06|{2=--=x x x M ，}01|{=+=ax x N ，且M N ⊆，则由a 的取值组成的集合是．14．若x x f =)(log 5，则=-)9log 2(log 255f ．15．已知定义在R 上的偶函数)(x f 满足0)1(=-f ，并且)(x f 在)0 ,(-∞上为增函数．若0)( <a f a ，则实数a 的取值范围是．16．已知函数()x f 的定义域是}0|{≠∈=x R x D ，对任意D x x ∈21 ,都有：=⋅)(21x x f)()(21x f x f +，且当1>x 时，()0>x f ．给出结论：①()x f 是偶函数；②()x f 在()∞+ ,0上是减函数．则正确结论的序号是．三、解答题：本大题共6小题，共70分，解答应写出必要的文字说明、证明过程及演算步骤。

XXX2014-2015学年高一上学期期中考试数学试题 Word版含解析

XXX2014-2015学年高一上学期期中考试数学试题 Word版含解析没有明显有问题的段落需要删除，只需修改格式错误和语言表达不清的地方。

XXX2014-2015学年第一学期期中考试高一数学试题第Ⅰ卷选择题（共30分）一、选择题（本题共10小题，每小题3分，共30分。

在每小题给出的四个选项中，只有一项符合题目要求。

）1、已知集合$S=\{x|x+1\geq2\}$，$T=\{-2,-1,0,1,2\}$，则$S\cap T=$（）A。

$\{2\}$。

B。

$\{1,2\}$。

C。

$\{0,1,2\}$。

D。

$\{-1,0,1,2\}$解题思路】：题目给出了集合$S$和$T$，需要先求出它们的具体表达内容，再求它们的交集。

$S$是一次函数不等式的解，$S=\{x|x\geq1\}$；$S\cap T=\{1,2\}$，故选B。

2、用阴影部分表示集合$C\cup A\cup B$，正确的是（）解题思路】：题目给出了四个图形，需要判断哪个图形表示$C\cup A\cup B$。

利用XXX求解，A中阴影部分表示$C\cup(A\cup B)$，B中阴影部分表示$(C\cup A)\cap B$，C中阴影部分表示$A\cap B$，D中阴影部分表示$C\cup A\cup B$，故选D。

3、函数$y=\log_{\frac{1}{2}}(x-1)$的定义域是（）A。

$(1,+\infty)$。

B。

$[1,+\infty)$。

C。

$(0,+\infty)$。

D。

$[0,+\infty)$解题思路】：题目给出了函数$y=\log_{\frac{1}{2}}(x-1)$，需要求出它的定义域。

由$\log_{\frac{1}{2}}(x-1)>0$得$x-1>0$，即$x>1$，故选A。

4、下列函数中，在其定义域内既是奇函数又是减函数的是（）A。

$y=-|x|$。

B。

$y=x$。

C。

$y=|x|$。

[精品]2014-2015年山西省运城市高一(上)数学期中试卷与答案

山西省康杰中学2013-2014学年高一上学期期中数学试题Word版含答案

康杰中学2013—2014学年度第一学期期中考试高一数学试题2013.11一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．集合A ＝{1,3}，B ＝{2,3,4}则A∩B ＝( )A ．{1}B ．{2}C ．{3}D ．{1,2,3,4}2．下列集合中结果是空集的是( )A ．{x ∈R|x 2－4＝0}B ．{x|x>9或x<3}C ．{(x ，y)|x 2＋y 2＝0}D ．{x|x>9且x<3}3．下列函数中，定义域为(0，＋∞)的是( )A ．y ＝1xB ．y ＝xC ．y ＝1x 2D ．y ＝12x4．函数f(x)＝125x x -+-的零点所在区间为( )A ．(0,1)B ．(1,2)C ．(2,3)D ．(3,4)5．函数f(x)＝|lgx|，则f(14)、f(13)、f(2)的大小关系是( )A ．f(2)>f(13)>f(14)B ．f(14)>f(13)>f(2)C ．f(2)>f(14)>f(13)D ．f(13)>f(14)>f(2)6．若函数y ＝f(x)的定义域是[2,4]，则y ＝f(12log x )的定义域是( )A ．[12，1]B ．[116，14]C ．[4,16]D ．[2,4]7．函数y ＝－1x －1＋1的图象是下列图象中的( )8．已知f(x)＝ax 7－bx 5＋cx 3＋2，且f(－5)＝m ，则f(5)＋f(－5)的值为( )A ．0B ．4C ．2mD ．－m ＋49．函数y ＝log 0.6(6＋x －x 2)的单调增区间是( )A ．(－∞，12]B ．[12，＋∞)C ．(－2，12]D ．[12，3)10．函数32++=bx ax y 在(]1,-∞-上是增函数，在[)+∞-,1上是减函数，则（） A ．00<>a b 且B ．02<=a bC ．02>=a bD ．的符号不确定b a ,11．下面四个结论：①偶函数的图象一定与y 轴相交；②奇函数的图象一定通过原点； ③偶函数的图象关于y 轴对称；④既是奇函数又是偶函数的函数一定是()f x ＝0（x ∈R ），其中正确命题的个数是（） A ．4 B. 3C ． 2 D. 112．函数()log |1|a f x x =+，当(1,0)x ∈-时，恒有()0f x >，有（）A ．()f x 在(,1)-∞-上是增函数B ．()f x 在(,0)-∞上是减函数C ．()f x 在(0,)+∞上是增函数D ．()f x 在(,)-∞+∞上是减函数二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 13．设集合A ＝{－1,0,3}，B ＝{a ＋3,2a ＋1}，A∩B ＝{3}，则实数a 的值为________． 14. 函数11x y a-=+(a>0,且a≠1)的图象恒过定点 .15．已知函数{2log 0()20xx x f x x >=≤,则满足1()2f a <的a 的取值范围是________. 16. 若幂函数y=(m 2-2m-2)x -4m-2在x ∈(0,+∞)上为减函数,则实数m 的值是 . 三、解答题(本大题共6个小题，共70分，解答应写出文字说明) 17．(本小题满分10分)已知集合A ＝{x|x≤a ＋3}，B ＝{x|x<－1或x>5}．(1)若a ＝－2，求A∩∁R B ； (2)若A ⊆B ，求a 的取值范围．18．(本小题满分12分) (1)计算：3333212log 2log 3log 92--； (2)已知27,64x y ==.化简并计算：19．(本小题满分12分)已知函数f(x)＝x 2＋2ax ＋2，x ∈[－5,5]． (1)当a ＝－1时，求函数的最大值和最小值；(2)求实数a 的取值范围，使y ＝f(x)在区间[－5,5]上是单调函数．20．(本小题满分12分)已知函数f(x)＝log a (1＋x)，g(x)＝log a (1－x)，(a ＞0，a≠1)．(1)设a ＝2，函数f(x)的定义域为[3,63]，求f(x)的最值； (2)求使f(x)－g(x)＞0的x 的取值范围．21．(本小题满分12分)函数f (x )＝ax ＋b x 2＋1是定义在(－∞，＋∞)上的函数，且f (12)＝25，f (1)=1.(1)求实数a 、b ，并确定函数f (x )的解析式；(2)判断f (x )在(－1,1)上的单调性，并用定义证明你的结论．22．(本小题满分12分)已知定义域为R 的单调函数()f x 是奇函数，当0x >时，()23x f x x=-. （I ）求()1f -的值；（II ）求()f x 的解析式；（III ）若对任意的t R ∈，不等式22(2)(2)0f t t f t k -+-<恒成立，求实数k 的取值范围.高一数学参考答案一、选择题1-5 CDACB 6-10 BABDB 11-12 DA 二、填空题13． a ＝0或1 14. (1,2) 15． (－∞，－1)∪(0，2) 16. m=3 三、解答题17．[解析] (1)当a ＝－2时，集合A ＝{x|x ≤1}，∁R B ＝{x|－1≤x ≤5}；∴A ∩∁R B ＝{x|－1≤x ≤1}．(2)∵A ＝{x|x ≤a ＋3}，B ＝{x|x<－1或x>5}， A ⊆B ，∴a ＋3<－1， ∴a<－4.18．[解析] (1) 原式＝log 34－log 3329－1233log= log 34－log 3329＋log 38＝log 3(4×932×8)＝log 39＝2∴原式＝24×(26)16＝48.19．[解析] (1)a ＝－1，f(x)＝x 2－2x ＋2.对称轴x ＝1，f(x)min ＝f(1)＝1，f(x)max ＝f(－5)＝37， ∴f(x)max ＝37，f(x)min ＝1.(2)对称轴x ＝－a ，当－a ≥5时，f(x)在[－5,5]上单调减函数， ∴a ≤－5. 当－a ≦－5时f(x)在[－5,5]上单调减函数， ∴a ≥5.综上a ≤－5或a ≥5。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2014-2015学年山西省运城市高一（上）期中数学试卷一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（4分）已知全集U=R，A={x|x＞0}，B={x|x＞1}，则A∩∁U B（）A．{x|0＜x＜1} B．{x|0＜x≤1} C．{x|0≤x＜1} D．{x|0≤x≤1}2．（4分）下列函数中，在区间（0，+∞）上为增函数的是（）A．y=ln（x+2）B．y=﹣C．y=（）x D．y=|x﹣1|3．（4分）下列函数中，不是奇函数的为（）A．y=ln B．y=﹣x3C．y=e x+e﹣x D．y=x|x|4．（4分）函数f（x）=2x+x2﹣2在区间（0，1）内的零点个数是（）A．0B．1C．2D．35．（4分）设a=ln2，b=（ln2）2，c=ln，则（）A．a＞b＞c B．a＞c＞b C．c＞a＞b D．c＞b＞a6．（4分）已知函数f（x）=（）x﹣log2x，若实数x0是方程f（x）=0的解，且0＜x1＜x0，则f（x1）（）A．恒为负值B．等于0 C．恒为正值D．不大于07．（4分）对于函数f（x）=2x，总有（）A．f（）=B．f（）≠C．f（）≤D．f（）≥8．（4分）函数y=a x﹣（a＞0，a≠1）的图象可能是（）A．B．C．D．9．（4分）设函数则不等式f（x）＞f（1）的解集是（）A．（﹣3，1）∪（3，+∞）B．（﹣3，1）∪（2，+∞）C．（﹣1，1）∪（3，+∞）D．（﹣∞，﹣3）∪（1，3）10．（4分）在R上定义的函数f（x）是偶函数，且f（x）=f（2﹣x）．若f（x）在区间[1，2]上是减函数，则f（x）（）A．在区间[﹣2，﹣1]上是增函数，在区间[3，4]上是增函数B．在区间[﹣2，﹣1]上是增函数，在区间[3，4]上是减函数C．在区间[﹣2，﹣1]上是减函数，在区间[3，4]上是增函数D．在区间[﹣2，﹣1]上是减函数，在区间[3，4]上是减函数二、填空题（共6小题，每小题4分，共24分）11．（4分）（）0﹣（1﹣0.5﹣2）÷=．12．（4分）若2a=5b=10，则=．13．（4分）函数f（x）=log2（2x+1）的单调递增区间是．14．（4分）函数f（x）=的定义域为．15．（4分）已知y=f（x）+x2是奇函数，且f（1）=1，若g（x）=f（x）+2，则g（﹣1）=．16．（4分）若关于x的不等式x2﹣log c x≤0在x∈（0，]上恒成立，则实数c的取值范围是．三、解答题（本大题共4小题，满分36分，解答应写出文字说明，证明过程或验算步骤）17．（8分）已知集合A={x|a﹣1＜x＜a+1，x∈R}，集合B={x|2x≤2，或2x≥8}．（1）若A∩B=∅，A∪B=R，求实数a；（2）若A⊆∁R B，求实数a．18．（8分）已知函数f（x）=1﹣（a＞0，且a≠1）是定义在（﹣∞，+∞）上的奇函数．（1）求实数a；（2）求函数f（x）的值域．19．（10分）已知函数f（x）=4x+m•2x+1有且只有一个零点．（1）求m的取值范围；（2）求该零点．20．（10分）已知函数f（x）对任意的实数x均有f（x）=﹣2f（x+2），且f（x）在区间[0，2]上有表达式f（x）=x（x﹣2）．（1）求f（﹣1），f（2.5）的值；（2）写出f（x）在区间[﹣3，3]上的表达式；（3）指出f（x）在区间[﹣3，3]上的单调区间（不需证明）．2014-2015学年山西省运城市高一（上）期中数学试卷参考答案与试题解析一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（4分）已知全集U=R，A={x|x＞0}，B={x|x＞1}，则A∩∁U B（）A．{x|0＜x＜1} B．{x|0＜x≤1} C．{x|0≤x＜1} D．{x|0≤x≤1}考点：交、并、补集的混合运算．专题：集合．分析：先求出B的补集，再求出其补集与A的交集即可．解答：解：∵C U B={x|x≤1}，∴A∩C U B={x|0＜x≤1}，故选：B．点评：本题考查了集合的运算，是一道基础题．2．（4分）下列函数中，在区间（0，+∞）上为增函数的是（）A．y=ln（x+2）B．y=﹣C．y=（）x D．y=|x﹣1|考点：函数单调性的判断与证明．专题：函数的性质及应用．分析：本题可以对选项中的函数单调进行研究，找出符合条件的选项，得到本题结论．解答：解：选项A，y=ln（x+2），∵x+2＞0，∴x＞﹣2．∴y=ln（x+2）在（﹣2，+∞）上单调递增，∴y=ln（x+2）在（0，+∞）上为递函数．适合题意．选项B，，∵x+1≥0，∴x≥﹣1，∴在[﹣1，+∞）上单调递减，∴在（0，+∞）上单调递减，不合题意．选项C，y=在（﹣∞，+∞）上单调递减，不合题意．选项D，y=|x﹣1|，，当0＜x＜1时，y=1﹣x单调递减，即y=|x﹣1|在区间（0，1）上单调递减，不合题意．故选A．点评：本题考查的是函数的单调性，还考查了分类讨论的数学思想，本题难度不大，属于基础题．3．（4分）下列函数中，不是奇函数的为（）A．y=ln B．y=﹣x3C．y=e x+e﹣x D．y=x|x|考点：函数奇偶性的判断．专题：计算题；函数的性质及应用．分析：根据喊话说的奇偶性的定义，对选项加以判断，即可得到不是奇函数的函数．解答：解：对于A．定义域为（﹣1，1），关于原点对称，f（﹣x）+f（x）=ln+ln=ln1=0，则为奇函数，故A不满足；对于B．定义域R，f（﹣x）=﹣f（x），则为奇函数，故B不满足；对于C．定义域R，有f（﹣x）=f（x），则为偶函数，故C满足；对于D．定义域R，且有f（﹣x）=﹣f（x），则为奇函数，故D不满足．故选C．点评：本题考查函数的奇偶性的判断，考查定义法的运用，属于基础题．4．（4分）函数f（x）=2x+x2﹣2在区间（0，1）内的零点个数是（）A．0B．1C．2D．3考点：根的存在性及根的个数判断．专题：计算题；函数的性质及应用．分析：根据函数f（x）=2x+x2﹣2在区间（0，1）内单调递增，f（0）f（1）＜0，可得函数在区间（0，1）内有唯一的零点．解答：解：由于函数f（x）=2x+x2﹣2在区间（0，1）内单调递增，又f（0）=﹣1＜0，f（1）=1＞0，所以f（0）f（1）＜0，故函数f（x）=2x+x2﹣2在区间（0，1）内有唯一的零点，故选B．点评：本题考查函数零点的定义以及函数零点判定定理的应用，属于中档题．5．（4分）设a=ln2，b=（ln2）2，c=ln，则（）A．a＞b＞c B．a＞c＞b C．c＞a＞b D．c＞b＞a考点：对数值大小的比较．专题：函数的性质及应用．分析：利用对数的运算性质、作差法即可得出．解答：解：∵0＜a=ln2＜1，∴b=（ln2）2，＜ln2，b﹣c=（ln2）2﹣ln=ln2（ln2﹣）=ln2（ln﹣）＞0，∴a＞b＞c．故选：A．点评：本题考查了对数的运算性质、作差法、不等式的性质，属于基础题．6．（4分）已知函数f（x）=（）x﹣log2x，若实数x0是方程f（x）=0的解，且0＜x1＜x0，则f（x1）（）A．恒为负值B．等于0 C．恒为正值D．不大于0考点：函数单调性的性质．专题：计算题；函数的性质及应用．分析：由于y=（）x在x＞0上递减，log2x在x＞0上递增，则f（x）在x＞0上递减，再由条件即可得到答案．解答：解：由于实数x0是方程f（x）=0的解，则f（x0）=0，由于y=（）x在x＞0上递减，log2x在x＞0上递增，则f（x）在x＞0上递减，由于0＜x1＜x0，则f（x1）＞f（x0），即有f（x1）＞0，故选C．点评：本题考查函数的单调性及运用，考查运算能力，属于基础题．7．（4分）对于函数f（x）=2x，总有（）A．f（）=B．f（）≠C．f（）≤D．f（）≥考点：指数函数的图像与性质．专题：函数的性质及应用．分析：根据函数的凹凸性质即可得到答案．解答：解：因为函数f（x）=2x为凹函数，故有f（）≤，故选：C点评：本题主要考查了函数凹凸性，属于基础题．8．（4分）函数y=a x﹣（a＞0，a≠1）的图象可能是（）A．B．C．D．考点：函数的图象．专题：函数的性质及应用．分析：讨论a与1的大小，根据函数的单调性，以及函数恒过的定点进行判定即可．解答：解：函数y=a x﹣（a＞0，a≠1）的图象可以看成把函数y=a x的图象向下平移个单位得到的．当a＞1时，函数y=a x﹣在R上是增函数，且图象过点（﹣1，0），故排除A，B．当1＞a＞0时，函数y=a x﹣在R上是减函数，且图象过点（﹣1，0），故排除C，故选D．点评：本题主要考查了指数函数的图象变换，指数函数的单调性和特殊点，体现了分类讨论的数学思想，属于基础题．9．（4分）设函数则不等式f（x）＞f（1）的解集是（）A．（﹣3，1）∪（3，+∞）B．（﹣3，1）∪（2，+∞）C．（﹣1，1）∪（3，+∞）D．（﹣∞，﹣3）∪（1，3）考点：一元二次不等式的解法．专题：不等式的解法及应用．分析：先求f（1），依据x的范围分类讨论，求出不等式的解集．解答：解：f（1）=3，当不等式f（x）＞f（1）即：f（x）＞3如果x＜0 则x+6＞3可得x＞﹣3，可得﹣3＜x＜0．如果x≥0 有x2﹣4x+6＞3可得x＞3或0≤x＜1综上不等式的解集：（﹣3，1）∪（3，+∞）故选A．点评：本题考查一元二次不等式的解法，考查分类讨论的思想，是中档题．10．（4分）在R上定义的函数f（x）是偶函数，且f（x）=f（2﹣x）．若f（x）在区间[1，2]上是减函数，则f（x）（）A．在区间[﹣2，﹣1]上是增函数，在区间[3，4]上是增函数B．在区间[﹣2，﹣1]上是增函数，在区间[3，4]上是减函数C．在区间[﹣2，﹣1]上是减函数，在区间[3，4]上是增函数D．在区间[﹣2，﹣1]上是减函数，在区间[3，4]上是减函数考点：偶函数．分析：根据函数的性质，作出函数的草图，观察图象即可得答案．解答：解：由f（x）=f（2﹣x）可知f（x）图象关于x=1对称，又∵f（x）为偶函数，∴f（x）=f（x﹣2）∴f（x）为周期函数且周期为2，结合f（x）在区间[1，2]上是减函数，可得f（x）草图．故选B．点评：本题属于函数性质的综合应用，解决此类题型要注意：（1）明确周期性、对称性、奇偶性的关系．（2）培养数形结合的思想方法．二、填空题（共6小题，每小题4分，共24分）11．（4分）（）0﹣（1﹣0.5﹣2）÷=3．考点：有理数指数幂的化简求值．专题：计算题；函数的性质及应用．分析：由题意，（）0=1，0.5﹣2=4，3=，即可算出值．解答：解：（）0﹣（1﹣0.5﹣2）÷=1﹣（1﹣4）÷=1﹣（﹣2）=3．故答案为：3．点评：本题考查了指数幂的运算与化简，属于基础题．12．（4分）若2a=5b=10，则=1．考点：对数的运算性质．专题：计算题．分析：首先分析题目已知2a=5b=10，求的值，故考虑到把a和b用对数的形式表达出来代入，再根据对数的性质以及同底对数和的求法解得，即可得到答案．解答：解：因为2a=5b=10，故a=log210，b=log510=1故答案为1．点评：此题主要考查对数的运算性质的问题，对数函数属于三级考点的内容，一般在高考中以选择填空的形式出现，属于基础性试题同学们需要掌握．13．（4分）函数f（x）=log2（2x+1）的单调递增区间是（﹣，+∞）．考点：对数函数的单调区间．专题：函数的性质及应用．分析：利用复合函数的单调性即可求出．解答：解：令t=2x+1＞0，求得x＞，可得函数的定义域为（﹣，+∞），且f（x）=log2t，故本题即求函数t在定义域内的增区间．再利用一次函数的性质可得函数t在定义域内的增区间为（﹣，+∞），故答案为：（﹣，+∞）．点评：本题主要考查复合函数的单调性，一次函数的性质，体现了转化的数学思想，属于基础题．14．（4分）函数f（x）=的定义域为（0，]．考点：对数函数的定义域．专题：函数的性质及应用．分析：根据开偶次方被开方数要大于等于0，真数要大于0，得到不等式组，根据对数的单调性解出不等式的解集，得到结果．解答：解：函数f（x）=要满足1﹣2≥0，且x＞0∴，x＞0∴，x＞0，∴，x＞0，∴0，故答案为：（0，]点评：本题考查对数的定义域和一般函数的定义域问题，在解题时一般遇到，开偶次方时，被开方数要不小于0，；真数要大于0；分母不等于0；0次方的底数不等于0，这种题目的运算量不大，是基础题．15．（4分）已知y=f（x）+x2是奇函数，且f（1）=1，若g（x）=f（x）+2，则g（﹣1）=﹣1．考点：函数奇偶性的性质；函数的值．专题：计算题．分析：由题意，可先由函数是奇函数求出f（﹣1）=﹣3，再将其代入g（﹣1）求值即可得到答案解答：解：由题意，y=f（x）+x2是奇函数，且f（1）=1，所以f（1）+1+f（﹣1）+（﹣1）2=0解得f（﹣1）=﹣3所以g（﹣1）=f（﹣1）+2=﹣3+2=﹣1故答案为：﹣1．点评：本题考查函数奇偶性的性质，利用函数奇偶性求值，解题的关键是根据函数的奇偶性建立所要求函数值的方程，基本题型．16．（4分）若关于x的不等式x2﹣log c x≤0在x∈（0，]上恒成立，则实数c的取值范围是[，1）．考点：函数恒成立问题．专题：计算题；函数的性质及应用．分析：由关于x的不等式x2﹣log c x≤0在x∈（0，]上恒成立，可得，由此，即可求出实数c的取值范围解答：解：∵关于x的不等式x2﹣log c x≤0在x∈（0，]上恒成立，∴，∴≤c＜1即实数c的取值范围是c∈[，1）故答案为：[，1）．点评：本题考查函数恒成立问题，考查学生分析解决问题的能力，确定是关键．三、解答题（本大题共4小题，满分36分，解答应写出文字说明，证明过程或验算步骤）17．（8分）已知集合A={x|a﹣1＜x＜a+1，x∈R}，集合B={x|2x≤2，或2x≥8}．（1）若A∩B=∅，A∪B=R，求实数a；（2）若A⊆∁R B，求实数a．考点：交、并、补集的混合运算．专题：函数的性质及应用．分析：（1）由题意得方程组，解出a的值即可；（2）由题意得得不等式组，解出即可．解答：解：（1）∵B={x|x≤1或x≥3}，由题意得A=C R B=（1，3），故，∴a=2；（2）∵A⊆C R B，∴，∴2≤a≤2，故a=2．点评：本题考查了集合的运算，是一道基础题．18．（8分）已知函数f（x）=1﹣（a＞0，且a≠1）是定义在（﹣∞，+∞）上的奇函数．（1）求实数a；（2）求函数f（x）的值域．考点：函数奇偶性的判断；函数的值域．专题：计算题；函数的性质及应用．分析：（1）由于f（x）是定义在（﹣∞，+∞）上的奇函数，则f（0）=0，即可求出a，注意检验；（2）f（x）=1﹣，运用指数函数的值域，即有2x+1＞1，再由不等式的性质，即可得到值域．解答：解：（1）由于f（x）是定义在（﹣∞，+∞）上的奇函数，则f（0）=0，即1﹣=0，解得，a=2．即有f（x）=1﹣=，f（﹣x）===﹣f（x），则有f（x）为奇函数．故a=2；（2）f（x）=1﹣，由于2x+1＞1，则﹣2＜＜0，则f（x）∈（﹣1，1），故值域为：（﹣1，1）．点评：本题考查函数的奇偶性及运用，考查函数的值域的求法，考查运算能力，属于中档题．19．（10分）已知函数f（x）=4x+m•2x+1有且只有一个零点．（1）求m的取值范围；（2）求该零点．考点：函数的零点．专题：计算题；函数的性质及应用．分析：（1）由题意，利用换元法化简y=t2+mt+1（t＞0），从而求解；（2）由题意，4x﹣2•2x+1=0，从而解出方程的解即可．解答：解：（1）由题意，令t=2x，则y=t2+mt+1（t＞0），则，解得，m=﹣2；（2）由（1）知，f（x）=4x﹣2•2x+1=0，解得2x=1，则x=0．即函数f（x）=4x+m•2x+1的零点是0．点评：本题考查了函数的零点与方程的根的关系，属于基础题．20．（10分）已知函数f（x）对任意的实数x均有f（x）=﹣2f（x+2），且f（x）在区间[0，2]上有表达式f（x）=x（x﹣2）．（1）求f（﹣1），f（2.5）的值；（2）写出f（x）在区间[﹣3，3]上的表达式；（3）指出f（x）在区间[﹣3，3]上的单调区间（不需证明）．考点：函数单调性的判断与证明；函数解析式的求解及常用方法；函数的值．专题：函数的性质及应用．分析：（1）通过已知条件即可得到f（﹣1）=﹣2f（﹣1+2）=﹣2f（1）=2，f（2.5）=f（0.5+2）=﹣=，所用的方法就是将自变量的值变到区间[0，2]上；（2）要求f（x）在区间[﹣3，3]上的表达式，需要上f（x）在[0，2]上的表达式，所以可将区间[﹣3，3]分成几个区间，并且能将每个区间变到区间[0，2]上：x∈[﹣3，﹣2]，（x+4）∈[1，2]；x∈（﹣2，0），（x+2）∈（0，2）；x∈[0，2]；x∈（2，3]，（x﹣2）∈（0，1]，这样即可求出每个区间上的f（x）表达式，从而写出f（x）在[﹣3，3]上的表达式；（3）根据（2）求出的f（x）的解析式，根据二次函数的单调性，判断每段函数在对应区间上的单调性，从而求出f（x）在[﹣3，3]上的单调区间．解答：解：（1）由已知条件得f（﹣1）=﹣2f（1）=﹣2×1×（1﹣2）=2，f（2.5）=f（0.5+2）=﹣==；（2）x∈[﹣3，﹣2]时，（x+2+2）∈[1，2]；∴f（x）=﹣2f（x+2）=4f（x+4）=4（x+4）（x+2）=4x2+24x+32；x∈（﹣2，0）时，（x+2）∈（0，2）；∴f（x）=﹣2f（x+2）=﹣2（x+2）x=﹣2x2﹣4x；x∈[0，2]时，f（x）=x（x﹣2）=x2﹣2x；x∈（2，3]时，x﹣2∈（0，1]；∴==；∴f（x）=；（3）4x2+24x+32的对称轴为x=﹣3，∴该函数在[﹣3，﹣2]单调递增；﹣2x2﹣4x的对称轴为x=﹣1，∴该函数在（﹣2，﹣1]上单调递增，在（﹣1，0）上单调递减；x2﹣2x的对称轴为x=1，∴该函数在[0，1]上单调递减，在（1，2]上单调递增；y=的对称轴为x=3，∴该函数在（2，3]上单调递增；∴综上得f（x）的递增区间是[﹣3，﹣1]，（1，3]；f（x）的递减区间是（﹣1，1]．点评：考查运用题中所给条件的能力，将所给区间分成几个区间，从而通过条件将每个区间变到已知表达式的区间上，从而求出该区间表达式的方法，以及二次函数的单调性及单调区间．。