基本初等函数测试题及答案
(2)基本初等函数 Word版含答案

(2)基本初等函数1、下列函数中,与函数y=有相同定义域的是( )A.()f xB.1()f x x =C.()f x ()||f x x =D.()f x =2、在映射:f A B →中,{(,)|,}A B x y x y R ==∈,且:(,)(,)f x y x y x y →-+,则与A 中的元素(1,2)-对应的B 中的元素为( )A.(3,1)-B.(1,3)C.(1,3)--D.(3,1)3、下列函数中,在定义域内既是奇函数又是减函数的是( )A. ()R y x x =∈B. ()R y x x =∈C. ()21R 0y x x x =∈≠且D.()3R y x x =∈4、函数()223f x x x =++的单调递减区间是( )A. (),1-∞B. ()1,+∞C. (),2-∞D. ()2,+∞5、实数,a b 满足2510a b ==,则下列关系正确的是( ) A. 111a b+= B. 212a b += C. 122a b += D. 1212a b += 6、函数221()()3x x f x +=的值域是( ) A .(,3)-∞ B .(0,)+∞ C .(0,3] D .[3,)+∞7、据统计,第x 年到鄱阳湖国家湿地公园越冬的白鹤数量:y (只)近似满足:()3log 2y a x =+,观测发现第1年有越冬白鹤3 000只,估计第7年有越冬白鹤( )A.4 000 只B.5 000 只C.6 000 只D.7 000 只8、(多选)函数2log (5)a y a -=-中,实数a 的取值可能是( ) A.52B.3C.4D.5 9、函数212log (56)y x x =-+的单调增区间为( ) A.52⎛⎫+∞ ⎪⎝⎭, B.(3)+∞, C.52⎛⎫-∞ ⎪⎝⎭, D.(2)-∞,10、35y x =在[]1,1-上是( )A.增函数且是奇函数B.增函数且是偶函数C.减函数且是奇函数D.减函数且是偶函数11、函数3()3(15)x f x x -=<≤的值域是____________.12、函数()213log 54y x x =--的单调递减区间为__________. 13、函数()221f x ax x =-+,若()y f x =在区间11,22⎡⎤-⎢⎥⎣⎦上有零点,则实数a 的取值范围为 .14、为了预防流感,某学校对教室采用药熏消毒法进行消毒,已知药物释放过程中,室内每立方米空气中的含药量 ()y mg 与时间 ()t h 成正比;药物释放完毕后, y 与t 的函数关系式为116t a y -⎛⎫= ⎪⎝⎭ (a 为常数),如图所示,根据图中提供的信息,回答相关问题。
高一数学基本初等函数精选测试题

基本初等函数练习卷一、选择题(本大题共12小题,每小题5分,共60分) 1、函数1213log (1)(1)y x x -=++-的定义域是()A .(-1,0)B .(-1,1)C .(0,1)D .(0,1]2、下列函数在(0,+∞)上是增函数并且是定义域上的偶函数的是( )A .23y x = B .12xy ⎛⎫= ⎪⎝⎭C .y =ln xD .y =x 2+2x +33、已知x x f 26log )(=,则=)8(f ( )A.34 B. 8 C. 18 D.21 4、已知函数e 1,1,()ln ,1,x x f x x x ⎧-≤=⎨>⎩那么f (ln 2)的值是( )A .0B .1C .ln(ln 2)D .25、函数x y a =与log (0,1)a y x a a =->≠且在同一坐标系中的图象可能是( )A B C D6、设a =log 0.50.6,b =log 1.10.6,c =1.10.6,则a ,b ,c 的大小关系是( )A .a <b <cB .b <c <aC .b <a <cD .c <a <b 7、函数(为自然对数的底数)对任意实数、,都有( )A. B. C. D. 8、已知幂函数()f x 的图象经过点(4,2), 则下列命题正确的是( )A. ()f x 是偶函数B. ()f x 是单调递增函数C. ()fx 的值域为R D. ()f x 在定义域内有最大值9、若y=log a (2-ax)在[0,1]上是减函数,则a 的取值范围为( ) (A)(0,1) ( B)(1,2) (C)(0,2) (D)(1,+∞)10、已知函数2()1,()43x f x e g x x x =-=-+-,若有()()f a g b =,则b 取值范围( )()()()f x y f x f y =+()()()f x y f xf y =()()()fx y fx fy +=+()()()f x y f x f y +=y x e ()xf x e=yxyxyxy xA. 22,22⎡⎤-+⎣⎦B. (22,22)-+C. []1,3D. ()1,311、函数y =e|-ln x |-|x -1|的图象大致是( )12、给出幂函数①f(x)=x ;②f(x)=x 2;③f(x)=x 3;④f(x)=x ;⑤f(x)=1x. 其中满足条件f 12()2x x +>12()()2f x f x + (x 1>x 2>0)的函数的个数是 ( ) A .1个 B .2个 C .3个 D .4个 二、填空题(本大题共4小题,每小题4分,共16分)13、当a >0且a ≠1时,函数f (x)=a x -2-3必过定点 . 14、函数652-+-=x x y 的单调增区间是15、已知函数2()f x x bx c =++,对任意x R ∈都有(1)()f x f x +=-,则(2)f -、 (0)f 、(2)f 的大小顺序是 .16.下列说法中:① 若2()(2)2f x ax a b x =+++(其中[21,4]x a a ∈-+)是偶函数,则实数2b =; ② 20132013)(22-+-=x x x f 既是奇函数又是偶函数;③ 函数()()43ln 2--=x x x f 的减区间是⎪⎭⎫ ⎝⎛+∞,23;④ 已知()f x 是定义在R 上的不恒为零的函数,且对任意的,x y R ∈都满足()()()f x y x f y y f x ⋅=⋅+⋅,则()f x 是奇函数。
初等函数习题附答案

函数、基本初等函数练习(一)一、选择题1. 已知函数2y ax bx c =++,如果a b c >>且0a b c ++=,则它的图象可能是( ) D2.已知函数()213axy -=是定义域上的减函数,则字母a 的取值范围是( )A.01a <<B.1a <<C.11a -<<D.10a -<<C3.已知函数()()2log 03(0]xx x f x x ⎧∈+∞⎪=⎨∈-∞⎪⎩,,,,,,则14f f ⎡⎤⎛⎫ ⎪⎢⎥⎝⎭⎣⎦等于( )A.9 B.19C.9- D.19-B4.已知2312a ⎛⎫= ⎪⎝⎭,322b -=,1312c ⎛⎫= ⎪⎝⎭,则下列关系中正确的是( )A.b a c <<B.c a b << C.a c b << D.a b c <<A5.若()f x 是定义在区间[66]-,上的偶函数,且(3)(1)f f >-,则下列各式中一定成立的是( ) A.(1)(3)f f <- B.(0)(6)f f <C.(3)(2)f f >D.(2)(0)f f >A6.已知A B ,两地相距150千米,某人开汽车以60千米/小时的速度从A 地到达B 地,在B 地停留1小时后再以50千米/小时的速度返回A 地,把汽车离开A 地的距离x 表示为时间t (小时)的函数表达式是( ) A.60x t =B.6050x t t =+C.60(0 2.5)1505( 3.5)t t x t x ⎧=⎨->⎩, ,≤≤D.600 2.5150(2.5 3.5)15050( 3.5)(3.5 6.5)t t x t t t ()⎧⎪=<⎨⎪--<⎩, , ,≤≤≤≤D二、填空题7.已知函数()12g x x =-,[]221()x f g x x-=,则12f ⎛⎫=⎪⎝⎭.15 8.函数e 1e 1xxy -=+的值域为 .(11)-,9.327log 2log 64= .1210.若1()2ax f x x +=+在区间(2)-+∞,上是增函数,则a 的取值范围是 .12a >11.设函数2()4(1)5f x x a x =-++在[1)-+∞,上是增函数,在(1]-∞-,上是减函数,则(1)f -= .112.函数1log (54)xx y +=-的定义域为.4(10)(0log 5)- ,,三、解答题13.已知01a <<,x y ,满足2log (log )3log 3a a a y x x =-+,如果y有最大值4,求此时a 和x 的值.14a =,18x =14.根据信息产业部、国家计委、财政部《关于电信资费结构性调整的通知》和江苏省邮电管理局、江苏省物价局相关文件通知,盐城市因特网业务资费(以下简称上网资费)自2006年1月21日起执行新标准.用户有两种上网方式可供选用:①使用163拨号上网,每月上网资费用1y (元)表示;②使用宽带接入方式上网,每月上网资费用2y (元)表示,根据新标准,得到上网资费和使用时间x (小时)之间的函数关系图(如下图,每月以30天,即720小时计算).(1)写出12y y ,的函数表达式;(2)现在已知某用户平均每天上网2小时,该用户用哪种方式上网,每月的上网资费更少? (3)该用户每月上网总时间满足什么条件时,选用第一种上网方式更划算? (1)1 2.450(0720)y x x =+≤≤,299(0720)y x =≤≤;(2)该用户使用宽带接入方式上网,每月的上网资费更少; (3)每月上网点时间不多于52012小时时,选用第一种上网方式更划算.15.设函数22()21(01)f x x ax a x =-+++≤≤. (1)求()f x 的最大值()M a ;(2)求[11]a ∈-,时,求函数()M a 的值域. (1)2210()10121a a M a a a a a a ⎧+<⎪=+⎨⎪+>⎩2,2,;≤≤(2)[13],.函数、基本初等函数练习(二)一、选择题1.下列各式正确的是( )A.35a-=32x =C.111111248824a a a a ⎛⎫⨯⨯--⎪⎝⎭= D.112333142212xx x x --⎛⎫-=- ⎪⎝⎭D2.设函数2()(0)f x x x a a =++>,若存在实数m ,使()0f m <,则必有( ) A.(1)0f m -<且(1)0f m +< B.(1)0f m ->且(1)0f m +> C.(1)0f m ->且(1)0f m +<D.(1)0f m -<且(1)0f m +>B3.设0x >,且1x x a b <<,0a b >,,则a b ,的大小关系是( ) A.1b a <<B.1a b <<C.1b a <<D.1a b <<B4.下列函数中,值域为(0)+∞,的函数是( )A.12x y =B.112xy -⎛⎫= ⎪⎝⎭C.y =D.y =B5.设a b c ,,都是正数,且346a b c==,则以下正确的是( ) A.221cab=+B.111cab=+C.122cab=+D.212cab=+A6.某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为21 5.060.15L x x =-和22L x =,其中x 为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得的最大利润为( ) A.45.606万元 B.45.56万元 C.45.6万元 D.45.51万元C二、填空题 7.函数y =的单调递减区间是 .[13],8.奇函数()f x 在区间[15],上递减,且在[15],上的最大值是10,在区间[51]--,上的最大值是1,则(5)2(1)f f --=.199.若函数()f x 是定义在R 上的偶函数,在(0]-∞,上是减函数,且(2)0f =,则使得()0f x <的x 的取值范围是 .(22)-,10.二次函数2y ax bx c =++中,若0a c < ,则函数的零点个数是 个.两11.5255log log (2)log log log (4)x x x x y x x =++ ,且2284y x= ,则y =.2112.王老师给出一个函数()y f x =,四个学生甲、乙、丙、丁各指出这个函数的一个性质: 甲:对于x ∈R ,都有(1)(1)f x f x +=-; 乙:在(0]-∞,上是减函数; 丙:在(0)+∞,上是增函数; 丁:(0)f 不是函数的最小值.现已知其中恰有三个说得正确,则这个函数可能是 (只须写出一个这样的函数即可).2(1)y x =-三、解答题13.设()f x 在[]a b ,上的图象是连续不断的一条曲线,且()a f x b ≤≤,求证:在[]a b ,中至少有一个常数,使()f c c =. 证明略.14.已知11()212xf x x ⎛⎫=+⎪-⎝⎭. (1)指出()f x 的奇偶性,并予以证明; (2)证明()0f x >.(1)偶函数,证明略; (2)证明略. 15.设函数2221()log log (1)log ()1x f x x p x x +=+-+--(其中1p >). (1)求()f x 的定义域;(2)()f x 是否存在最大值或最小值?如果存在,请把它求出来;若不存在,请说明理由. (1)(1,)p ;(2)13p <≤时,()f x 即无最大值又无最小值;当3p >时,()f x 有最大值22(1)log 4p +,但没有最小值,理由略.DBBBAC [13], 19 (22)-, 2 21 2(1)y x =-。
(完整版)基本初等函数测试题及答案

基本初等函数测试题一、选择题 (本大题共 12 个小题,每题 5 分,共 60 分.在每题给出的四个选项中,只有一项为哪一项切合题目要求的)1.有以下各式:① na n = a ; ②若 a ∈ R ,则 (a 2- a + 1)0= 1;③ 3 x 44y ; ④6- 2 2= 3- 2.y3x3此中正确的个数是 ()A . 0B . 1C .2D .3|x|的图象是 ()2.函数 y = a (a>1)3.以下函数在 (0,+∞ )上是增函数的是 ()-xB . y =- 2x1A . y = 3C . y = logxD . y = x24.三个数 log 21, 20.1,2-1 的大小关系是 ()51-1--11 -A . log 25<2<2 1 B . log 25<2 1<20.1 C . 2<2 1<log 25 D . 2<log 25<215.已知会合 A = { y|y = 2x , x<0} , B = { y|y =log 2x} ,则 A ∩ B = ()A . { y|y>0}B . { y|y>1}C . { y|0<y<1}D .6.设 P 和 Q 是两个会合,定义会合 P -Q = { x|x ∈ P 且 x?Q} ,假如 P ={ x|log x < 1} ,Q2= { x|1<x<3} ,那么 P -Q 等于 ( )A . { x|0< x < 1}B . { x|0< x ≤ 1}C . { x|1≤ x <2}D . { x|2≤ x < 3}17.已知 0<a<1, x = log a 2+ log a 3, y =2log a 5,z =log a 21- log a 3,则 ( )A . x>y>zB . x>y>xC . y>x>zD . z>x>y8.函数 y = 2x - x 2 的图象大概是 ()9.已知四个函数① y = f 1(x);② y = f 2 (x);③ y =f 3(x);④ y = f 4( x)的图象以以下图:- 1 -则以下不等式中可能建立的是 ()A . f (x + x )= f (x )+ f (x )B . f (x + x )=f (x )+ f(x )112111 22122122C . f 3(x 1+ x 2) =f 3(x 1)+ f 3(x 2 )D . f 4(x 1+ x 2)=f 4(x 1)+ f 4(x 2)f ( x)12-1, f 3 2,则 f 1 2 310.设函数x 2(x)= x(2010))) 等于 ()1, f (x)= x ( f (fB . 2010211A . 2010 C.2010 D. 201211.函数 f(x)=3x 2 + lg(3 x + 1)的定义域是 ( )1-xA. -∞,- 1B. - 1, 133 3C. -1, 1D. - 1,+∞332e x -1, x<2,12. (2010 石·家庄期末测试)设 f(x)=则 f[ f(2)] 的值为 ()log 3 x 2- 1 , x ≥ 2.A . 0B . 1C . 2D . 3二、填空题 (本大题共 4 小题,每题 5 分,共 20 分.把答案填在题中横线上 )13. 给出以下四个命题:(1)奇函数的图象必定经过原点;(2)偶函数的图象必定经过原点;1(3)函数 y = lne x 是奇函数; (4)函数 yx 3 的图象对于原点成中心对称.此中正确命题序号为 ________. (将你以为正确的都填上 )14. 函数 y log 1 (x 4) 的定义域是.215.已知函数 y = log a (x +b)的图象以以下图所示,则 a = ________, b = ________.16.(2008 上·海高考 )设函数 f(x)是定义在 R 上的奇函数, 若当 x ∈ (0,+∞ )时,f(x)= lgx ,则知足 f(x)>0 的 x 的取值范围是 ________.- 2 -三、解答题 (本大题共 6 小题,共 70 分.解答应写出必需的文字说明、证明过程或演算步骤 )17. (本小题满分 10 分 )已知函数 f( x)= log 2(ax + b),若 f(2)= 1, f(3)= 2,求 f(5).118. (本小题满分 12 分 )已知函数 f (x)2 x 2 .(1)求 f(x) 的定义域; (2) 证明 f(x)在定义域内是减函数.2x - 1 19. (本小题满分 12 分 )已知函数f( x)=2x + 1.(1)判断函数的奇偶性; (2) 证明: f( x)在(-∞,+∞ )上是增函数.220. (本小题满分 12 分 )已知函数 f x(m 2 m 1)x mm 3是幂函数 , 且 x ∈ (0,+∞ )时, f(x)是增函数,求 f(x)的分析式.21. (本小题满分 12 分 )已知函数 f( x)= lg(a x -b x ), (a>1>b>0) .(1)求 f(x)的定义域;(2)若 f(x)在 (1,+∞ )上递加且恒取正当,求a ,b 知足的关系式.1122. (本小题满分 12 分 )已知 f(x)= 2x -1+2 ·x.(1)求函数的定义域;(2)判断函数 f(x)的奇偶性;(3)求证: f(x)>0.- 3 -参照答案答案速查: 1-5 BCDBC6-10 BCACC11-12 CC1.分析: 仅有②正确. 答案: Ba x , x ≥0 ,2.分析: y = a |x|=-且 a>1 ,应选 C.答案: Ca x, x<0 ,3.答案: D4.答案: B5.分析:A = { y|y = 2x ,x<0} = { y|0<y<1} ,B = { y|y = log 2x} = { y|y ∈ R} ,∴ A ∩ B ={ y|0<y<1} .答案: C6.分析: P ={ x|log 2x<1} = { x|0<x<2} , Q ={ x|1<x<3} ,∴ P - Q = { x|0<x ≤1} ,应选 B.答案: B17.分析: x = log a 2+ log a 3= log a 6= 2log a 6, z = loga21- loga 3= loga 7= 2log 7.1a∵ 0<a<1 ,∴ 111log a 7.2 log a 5> log a 6> 22 即 y>x>z.答案: C8.分析: 作出函数 y =2x 与 y = x 2 的图象知,它们有3 个交点,因此 y =2x - x 2 的图象与x 轴有 3 个交点,清除B 、C ,又当 x<- 1 时, y<0,图象在 x 轴下方,清除 D.应选 A.答案: A9.分析: 联合图象知, A 、 B 、 D 不建立, C 建立. 答案: C10.分析: 依题意可得 f 3(2010) = 20102, f 2(f 3(2010))22 -1-2 = f 2(2010 ) =(2010 ) = 2010 ,∴ f 1(f 2(f 3(2010))) = f 1(2010 - 2-2 1-11 .)= (2010) =2010=20102答案: C1-x>0x<1-111.分析: 由 ?1? <x<1. 答案: C3x +1>0x>- 3312.分析: f(2) = log 3(22- 1)= log 33= 1,∴ f[f(2)] = f(1) = 2e 0= 2.答案: C13.分析: (1) 、 (2)不正确,可举出反例,如1, y = x -2,它们的图象都可是原点. (3)y = x中函数 y = lne x=x ,明显是奇函数.对于(4) , y =x 13是奇函数,而奇函数的图象对于原点对称,因此 (4)正确.答案: (3)(4)- 4 -14.答案: (4,5]15.分析: 由图象过点 (- 2,0), (0,2)知, log a (- 2+ b)= 0, log a b = 2,∴- 2+ b =1,∴ b= 3, a 2= 3,由 a>0 知 a = 3.∴ a = 3, b = 3.答案: 3 316.分析: 依据题意画出 f(x)的草图,由图象可知,f(x)>0 的 x 的取值范围是-1<x<0 或x>1.答案: (- 1,0)∪ (1,+∞ )17.解:由 f(2) log 2 2a + b =12a + b =2 ? a = 2, = 1,f(3)= 2,得 3a + b = 2? ∴ f(x)= log 2(2xlog 2 3a + b =4 b =- 2. - 2),∴ f(5)= log 28 =3.18.∵ x 2>x 1≥ 0,∴ x 2- x 1>0, x 2+ x 1>0,∴ f(x 1) - f(x 2)>0 ,∴ f(x 2)<f( x 1).于是 f(x)在定义域内是减函数.19.解: (1) 函数定义域为 R.2-x - 11- 2x2x - 1f(- x)=- x+ 1 =x =-x=- f(x),21+ 22 + 1因此函数为奇函数.1 2< +∞ ,(2)证明:不如设- ∞<x <x∴ 2x 2>2x 1.又由于 f(x 2)- f(x 1)= 2x 2- 1 - 2x 1- 1 = 2 2x 2- 2x 12 1 1 2x 2>0,2x + 1 2x + 1 2x + 1 +1∴ f(x 2)> f(x 1).因此 f(x)在 (- ∞ ,+ ∞ )上是增函数.20.解: ∵ f(x)是幂函数,∴ m 2- m - 1= 1, ∴ m =- 1 或 m = 2,∴ f(x)= x -3 或 f(x)= x 3,而易知 f(x)= x -3 在 (0,+ ∞ )上为减函数,f(x)=x 3 在 (0,+ ∞ )上为增函数. ∴ f(x)= x 3.21.解: (1) 由 a x- b x>0,得 a x>1.ba∵ a>1>b>0,∴ b >1, ∴ x>0.即 f(x)的定义域为 (0,+ ∞ ).(2)∵ f( x)在 (1,+ ∞ )上递加且恒为正当,∴ f(x)>f(1) ,只需 f(1)≥ 0,即 lg(a - b)≥ 0,∴ a - b ≥1.∴ a ≥ b + 1 为所求22.解: (1) 由 2x - 1≠ 0 得 x ≠0,∴函数的定义域为 { x|x ≠0, x ∈ R} . (2)在定义域内任取 x ,则- x 必定在定义域内. 1 1 f(- x)= 2-x - 1+ 2 (- x)=2xx +1 ( -x) =- 1+2x ·x = 2x +1 ·x.1-2 22 1- 2x 2 2x - 111 2x + 1而f(x)=2x - 1+2 x = 2 2x -1 ·x , ∴ f(- x)= f(x).∴ f(x)为偶函数.(3)证明:当 x>0 时, 2x >1,11∴2x - 1+2 ·x>0.又 f(x)为偶函数,∴当 x<0 时, f(x)>0.故当 x ∈ R 且 x ≠ 0 时, f(x)>0.。
高一数学基本初等函数Ⅰ试题答案及解析

高一数学基本初等函数Ⅰ试题答案及解析1.方程的根的情况是()A.仅有一根B.有两个正根C.有一正根和一个负根D.有两个负根【答案】C【解析】主要考查指数函数、对数函数的图象和性质。
解:采用数形结合的办法,在同一坐标系中,画出的图象可知。
2.已知 .【答案】8【解析】主要考查指数函数、二次函数的性质。
利用换元法。
解:可化为,令,又因为所以,,,故。
3.若下列命题正确的个数为()A.0B.1C.2D.3【答案】B【解析】主要考查对数运算法则。
解:根据对数的运算性质易知只有④是正确的。
4.已知_____________【答案】【解析】主要考查对数运算。
解:5.已知镭经过100年,剩留原来质量的95.76%,设质量为1的镭经过x年的剩留量为y,则y 与x的函数关系是A.y=(0.9576)B.y=(0.9576)100xC.y=()x D.y=1-(0.0424)【答案】A【解析】设每年减少q%,因为镭经过100年,剩留原来质量的95.76%,所以=95.76%, q%=1-(0.9576),所以=(0.9576)。
故选A。
【考点】主要考查函数的概念、解析式,考查应用数学知识解决实际问题的能力。
点评:审清题意,构建函数解析式。
6.一个体户有一种货,如果月初售出可获利100元,再将本利都存入银行,已知银行月息为2.4%,如果月末售出可获利120元,但要付保管费5元,问这种货是月初售出好,还是月末售出好?【答案】当成本大于525元时,月末售出好;成本小于525元时,月初售出好.【解析】解:设这种货的成本费为a元,则若月初售出,到月末共获利润为:y1=100+(a+100)×2.4%若月末售出,可获利y2=120-5=115(元)y 2-y1=0.024a-12.6=0.024(a-525)故当成本大于525元时,月末售出好;成本小于525元时,月初售出好.【考点】主要考查函数模型的广泛应用,考查应用数学知识解决实际问题的能力。
基本初等函数经典复习题+答案
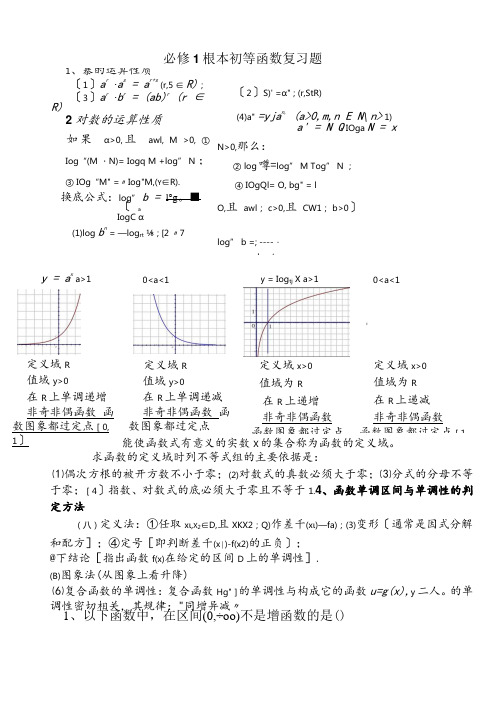
必修1根本初等函数复习题求函数的定义域时列不等式组的主要依据是:⑴偶次方根的被开方数不小于零;(2)对数式的真数必须大于零;⑶分式的分母不等于零;[4〕指数、对数式的底必须大于零且不等于1.4、函数单调区间与单调性的判定方法(八)定义法:①任取xι,X 2∈D,且XKX2;Q)作差千(xι)—fa);(3)变形〔通常是因式分解和配方];④定号[即判断差千(x∣)-f(x2)的正负〕;@下结论[指出函数f(x)在给定的区间D 上的单调性].(B)图象法(从图象上看升降)⑹复合函数的单调性:复合函数Hg"]的单调性与构成它的函数u=g(x),y 二人。
的单调性密切相关,其规律:"同增异减〃 1、以下函数中,在区间(0,÷oo)不是增函数的是()1、暴的运算性质 〔1〕a r ∙a s = a r+s (r,5 ∈ R); 〔3〕a r ∙b r = (ab)r (r ∈ R) 2对数的运算性质 如果 α>0,且 awl, M >0, ① Iog“(M ・N)= Iogq M +log” N ; ③ IOg“M" =〃Iog"M,(Y ∈R). 换底公式:log” b = l°g 。
■ 〔 a IogC α(1)log b n= —log rt ⅛ ; [2 〃7 〔2〕S)' =α" ; (r,StR)(4)a" =yja n, (a>0,m,n E N ∖n> 1) a' = N Q IOga N = x N>0,那么:② log 噂=log” M Tog” N ;④ IOgQl= O, bg" = lO,且 awl ; c>0,且 CW1; b>0〕 log” b =; ---- ∙log/y = a x a>1 0<a<1 y = Iog tj X a>1 II0<a<1定义域R 值域y>0 在R 上单调递增 非奇非偶函数 函数图象都过定点[0, 1〕 3、定义域: 定义域R 值域y>0 在R 上单调递减 非奇非偶函数 函数图象都过定点〔〕 定义域x>0 值域为R在R 上递增 非奇非偶函数 函数图象都过定点定义域x>0值域为R 在R 上递减 非奇非偶函数 函数图象都过定点[1, 能使函数式有意义的实数X 的集合称为函数的定义域。
基本初等函数(选择题第一部分)

基本初等函数(选择题第一部分)1. 已知函数)(x f 是定义R 上的奇函数且)2()(+-=x f x f ,当10≤≤x 时,2)(x x f =,那么使21)(-=x f 成立的x 的集合为 A.},2|{Z n n x x ∈= B.},12|{Z n n x x ∈-= C.},14|{Z n n x x ∈-= D.},14|{Z n n x x ∈+=2. 设奇函数f (x )在[-1,1]上是增函数,且f (-1)= -1,若函数f (x )≤t 2-2at+1对所有的x ∈[-1,1]都成立,则当a ∈[-1,1]时,t 的取值范围是A.t ≥2或t ≤-2或t=0B.-2≤t ≤2C.21t 21≤≤-D.0t 21t 21t =-≤≥或或 3. 已知两个函数)(x f 和)(x g 的定义域和值域都是集合{1,2,3},其定义如下表.填写下列)]([x f g 的表格,其三个数依次为A.,1,2B.2,1,3C. 1,2,3D. 3,2,14. 在实数的原有运算法则中,我们补充定义新运算“⊕”如下:当a b ≥时,a b a ⊕=; 当a b <时,a b b ⊕=2。
则函数[]()f x x x x x ()()()=⊕-⊕∈-1222·,的最大值等于(“·”和“-”仍为通常的乘法和减法)A.-1B.1C.6D.125. 若0<a <b <1,则在a b ,b a ,log a b,log b a 这四个数中,最大的一个是A.a bB.b aC.log a bD.log b a6. 函数f (x)=|ax 2+bx +c |(a ≠0)的定义域分成四个单调区间的充要条件是 02ab -D. 04C.b 02a b -B. 040.22<>->>->ac ac b a A 且 7. 某集镇近20年来的常住人口y(千人)与时间x(年)的函数如右图,考虑下列说法: ①前16年的常住人口是逐年增加的;②第16年后常住人口实现零增长; ③前8年的人口增长率大于1;④第8年到第16年的人口增长率小于1. 在上述说法中,只有一种说法是错误的,这个错误的说法是A.①B.②C.③ D ④8. 设集合A 和B 都是自然数集合N,映射f:B A →把集合A 中的元素n,映射到集合B 中的元n n +2,则在映射 f 下,象20的原象是A .4B .3C .2D . 5X(年)9. 已知g (x 2+1)=x 4+x 2-6,那么g (x 2+1)的最小值是D.g(1) 41C.g(1) 41-B.g(1) )0(.+g A 10. 函数y =|x -3|-|x +1|的值域是A.[0,4]B.[-4,0]C.[-4,4]D.(0,+∞)11. ,0)0(),22(2)()(,)(≠-•+=+f b a b a f b f a f b a x f 且都有对任意实数已知函数则f(x)是 A 奇函数 B 偶函数 C .既是奇函数也是偶函数 D . 既非奇函数又非偶函数12. 的单调递增区间是那么已知)(),1()(,28)(2x g x f x g x x x f -=-+=A.(-∞,1〕B. (-∞,0〕C.[-3,0]D.[0,3]13. 之间的那么上单调递增在区间已知偶函数)41(log ),2(),(,],0[ )(2f f f x f πππ--大小关系是)41(log )2()(. )2()41(log )(.22f f f B f f f A >->-->>-ππππ )()2()41(log )()41(log )2(.22ππππ->->->>-f f Df f f f C 14. 函数y=f(x)在区间(0,2)上是增函数,函数y=f(x +2)是偶函数,则下列结论正确的是)1()25()27(. )27()25()1(.f f f B f f f A <<<< )27()1()25(. )25()1()27(.f f f D f f f C <<<< 15. 已知y=f(x)有反函数,那么方程f(x)=a (a 为常数)A .无实数根B .只有一个实数根C .无实数根或只有一个实数根D .至少有二个实数根16. 已知奇函数f(x)有反函数f -1(x ),那么下结论中正确的是A. f -1(x )也是奇函数B . f(x)在定义域上是单调函数C . f -1(x )与f(x)图象关于直线y=x 成轴对称D .设f(x)的定义域是M ,值域是G ,若f(x)在M 上是单调增函数,那么f -1(x )在G 上也是单调函数17. 下列四个命题:①函数y=f -1(x )的反函数是y=f (x );②若点M(a,b )在y=f (x )的图象上,则点M'(b,a )一定在其反函数y=f -1(x )的图象上;③关于直线y=x 成轴对称的两个图形一定是互为反函数的一对函数图象;④因为函数y=f (x )与其反函数y=f -1(x )的图象关于直线y=x 对称,所以y=f (x )与y=f -1(x )的图象不能相交.其中错误的命题的个数为A.1B.2C.3D.418. 设f (x )是定义在R 上的奇函数,且f (x )= -f (x +2),当时 10≤≤x 时f (x )=x ,则 f (7.5)=A .7.5B .-1.5C .0.5D .-0.519. 设f(x)是定义在R 上的任意一个增函数,F(x)=f(x)-f(-x),那么F -1(x )必是A .增函数且奇函数B .增函数且偶函数C .减函数且奇函数D .减函数且偶函数20. 已知c>b>a >0,那么下列不等式成立的是a cbc c b c a c a c b b c a c B A )1()1()1()1.( .ππππππππ<<<<<< c a c b b c a c a c b c c b c a C ππππππππ1111log log log D.log log log log log .<<<>>> 21. 设函数y=f (x )的定义域是R,则函数y=f (x -1)与y=f (1-x )的图象关于A .直线x =1对称B .直线x =0对称C .直线y =1对称D .直线y =0对称22. 函数f (x )的图象无论经过平移或沿直线翻折后仍不可能与y=log 2 x -1的图象重合,则f (x )是A .y =2 -xB .y =2log 4 xC .y =log 2(x +1)D .y =2 2x +123. 函数y =|2 x -2|A.在(-∞,+∞)上单调递增B.在(-∞,1]上是减函数,在[1,+∞)上是增函数C.在(-∞,1]上是增函数,在[1,+∞)上是减函数D.在(-∞,0]上是减函数,在[0,+∞)上是减函数24. 已知函数f 1(x )的图象(不过原点的曲线)与f 2(x )的图象关于y 轴对称,f 3(x )与f 4(x )的图象关于x 轴对称,那么f 1(x )与f 4(x )的图象关于A.原点对称 B.x 轴对称 C.直线y = -x 对称 D.y 轴对称25. 已知定义域为R的偶函数y=f (x )的一个单调递增区间是(2,6),则函数y=f (2-x )图象A.对称轴为x = -2,且一个单调减区间是(4,8)B.对称轴为x = -2,且一个单调减区间是(0,4)C.对称轴为x = 2,且一个单调增区间是(4,8)D.对称轴为x = 2,且一个单调增区间是(0,4)26. 的值是则已知函数 )]41f[f( 0)(x 30)(x log )(x 2⎩⎨⎧≤>=x x f 91-D. 9-C. 91B. 9.A27. 函数y=f (x )和函数y=g(x)的图象如下图所示,则y=f(x)·g(x)的图象可能是28. 已知y=f(x)是(0,+∞)上的增函数,且方程f(x)+x=p 与f -1(x )+x=p (p >0)的解分别是x 1,x 2,则x 1+x 2等于A.0.5pB.2pC.pD.无法确定29. 函数f(x)是定义在[a ,b ](a<b )上的单调减函数,则它的反函数是A.在[f (a ) , f (b )]上的增函数B.在[f (a ) , f (b )]上的减函数C.在[f (b ) , f (a )]上的增函数D.在[f (b ) , f (a )]上的减函数30. 在100个学生中,有篮球爱好者60人,足球爱好者65人,则既爱好篮球又爱好足球人数的最小值,最大值分别是A.0、60B.25、60C.35、65D.25、6531. 设函数y=f (x )为奇函数,把y=f (x )的图象沿x 轴正向平移2个单位得到图象c,又设图象c 1与c 关于原点对称,则c 1所对应的函数是A.y = -f (x -2)B.y=f (x -2)C.y = -f (x +2)D.y =f (x +2)32. 方程f (x,y )=0的曲线如图,那么方程f (2-x,y )=0的曲线是33. 经过变换得到曲线将曲线1 =x y A.向左平移2个单位,向上平移3个单位; B.向左平移2个单位,向下平移3个单位;C.向右平移2个单位,向上平移3个单位;D.向右平移2个单位,向下平移3个单位.34. 如果函数:f (x )=x 2-ax +3≥x 对一切实数x 恒成立, 则132)32(1-D. 3232-C. 32-1B. )321(.A -≤≤+≤≤+>+-<a a a a35. 已知f (x )=(x-a )(x-b )-2,并且m,n 是方程f (x )=0的两根,实数a,b,m,n 的大小可能是A .n<a<b<mB .a<n<m<bC .a<n<b<mD .n<a<m<b36. 已知函数f(x)是R 上的增函数,A(0,-1)、B(3,1)是其图象上的两点,那么|f (x +1)|<1的解集是A.(1,4)B.(-1,2)C.(-∞,1)∪[4,+∞)D.(-∞,-1]∪[2,+∞)37. 的值是则且如果)2001()2002()5()6()3()4()1()2(,2)1(),()()(f f f f f f f f f y f x f y x f ++++==+ A.1999 B.2000 C.2001 D.200238. 已知不恒为零的函数f (x )对任意实数x,y 都满足f (x+y )+f (x-y )=2[f (x )+f (y )],则f (x )是A.偶函数B.奇函数C.既是奇函数又是偶函数D.非奇非偶函数39. 的大小关系是则的图象如图所示设函数 ,,,)(2c b a cx b ax x f ++= A.a >b >c B.a >c >bC.b >a >cD.c >a >b40. 对某种产品市场销量情况如图所示,其中:l 1表示产品各年年产量的变化规律;l 2表示产品各年的销售情况,下列叙述:(1)产品产量、销售量均以直线上升,仍可按原生产计划进行下去;(2)产品已经出现了供大于求的情况,价格将趋跌; (3)产品的库存积压将越来越严重,应压缩产量或扩大销量,你认为较合理的叙述的是A.(1)(2)(3)B.(1)(3)C.(2)D.(2)(3)41. 设函数,2)2(),0()4()0(2)0( )(2-=-=-⎩⎨⎧>≤++=f f f x x c bx x x f 若则关于x 的方程x x f =)(解的个数为A.1B.2C.3D.442. 函数()()log 11a y x a =+>的大致图像是. A 2yx 2y x -2y x -2y x B C Dl 2l 1O y(万吨)x(年份)43. 已知函数f(x)满足f(x+2)=21)2(),()(1)(1=∈-+f R x x f x f ,则f (2004)等于. A.21 B.1 C.2 D.3 44. 对于函数a ax y +-=1的图象C ,有下列命题:① C 关于l :x -y =0对称;② C 关于l :x +y =2a 对称;③C 关于A (a ,a )对称;④ C 关于B (-a ,-a )对称 其中假命题是A.①B.②C.③D.④45. 已知)(x f y =是定义在R 上的单调函数,实数21x x ≠,,1,121λλλ++=-≠x x a λλβ++=112x x ,若|)()(||)()(|21βαf f x f x f -<-,则 A.0<λ B.0=λ C.10<<λ D.1≥λ 46. 是那么是有理数是无理数已知函数)( )(x 1)(x 0)(x f x f ⎩⎨⎧=A.奇函数且为周期函数B.偶函数且为周期函数C.非奇非偶函数且非周期函数D.偶函数且非周期函数 47. 的图象分别是函数 1)(,1,1)(,1)(4321x x f x f x x f x x f +=+=-=-=点集C 1,C 2,C 3,C 4,这些图象关于直线x =0的对称曲线分别是点集D 1,D 2,D 3,D 4,现给出下列四个命题:①D 1⊆D 2;②D 1∪D 3=D 2∪D 4;③D 4⊆D 3;④D 1∩D 3=D 2∩D 4.其中,正确命题的序号是A.①③B.①②C.③④D.②④48. 已知f(x)的定义域为R,对任意x 都有f (1-x )=f (1+x ),且当x ∈(-3,-1)时f(x)=3x -2;则当x ∈(3,5)时f(x)的解析式为A.3x-8B.3x-1C.1-3xD.4-3x49. 如果函数使得存在常数对任意实数,,)(M x x f 不等式个函下面有为有界泛涵那么就称函数恒成立4,)(,)(x f x M x f ≤数:①1)(=x f ; ②2)(x x f =;③x x x x f )cos (sin )(+=; ④1)(2++=x x xx f .其中有两个属于有界泛涵,它们是.A.①,②B.③,④C.①,③D.②,④50. 如右图,在直角坐标系的第一象限内,△AOB 是边长2的等边三角形,设直线l :x=t (0≤t ≤2),截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f (t ),则函数s =f (t )的图象只可能是O x y O x y -1 O 1 xy-1 O 1 x y AB51.的表达式为则已知)(,)11(x f x x x f =+-1x 2x D. 1x -1C. 1-x 1x B. 11.+++-+x x x A 52. f (x )是定义在区间[-c,c ]上的奇函数,其图象如图所示。
基本初等函数含答案,附上学生版

基本初等函数1.若函数y =f (x )的定义域是[0, 2 018],则函数g (x )=f (x +1)x -1的定义域是________. 解析:要使函数f (x +1)有意义,则0≤x +1≤2 018,解得-1≤x ≤2 017,故函数f (x +1)的定义域为[-1,2 017],所以函数g (x )有意义的条件是⎩⎪⎨⎪⎧-1≤x ≤2 017x -1≠0,解得-1≤x <1或1<x ≤2 017.故函数g (x )的定义域为[-1,1)∪(1,2 017]. 2解析:∵ƒ(x )=log 2(x 2+a )且ƒ(3)=1,∴1=log 2(9+a ),∴9+a =2,∴a =-7. 答案:-73.若幂函数y =(m 2-3m +3)·x (m-2)(m +1)的图象不经过原点,则实数m 的值为________.解析:由⎩⎪⎨⎪⎧m 2-3m +3=1,(m -2)(m +1)≤0,解得m =1或2,经检验m =1或2都适合.答案:1或24.下列函数在其定义域上既是增函数又是奇函数的是________. A .f (x )=sin xB .f (x )=x 3+1C .f (x )=log 2(x 2+1+x )D .f (x )=1-2x1+2x解析:依题意,对于选项A ,注意到f (0)=f (π),因此函数f (x )=sin x 在其定义域上不是增函数;对于选项B ,注意到f (x )的定义域为R ,但f (0)=1≠0,因此函数f (x )=x 3+1不是奇函数;对于选项C ,注意到f (x )的定义域是R ,且f (-x )=log 2(x 2+1-x )=log 21x 2+1+x=-log 2(x 2+1+x )=-f (x ),因此f (x )是奇函数,且f (x )在R 上是增函数;对于选项D ,注意到f (x )=1-2x 1+2x =-1+21+2x 在R 上是减函数.故选C. 5.函数f (x )=|log 2 x |+x -2的零点个数为_______.解析:函数f (x )=|log 2 x |+x -2的零点个数,就是方程|log 2 x |+x -2=0的根的个数.令h (x )=|log 2 x |,g (x )=2-x ,画出两函数的图象,如图.由图象得h (x )与g (x )有2个交点,∴方程|log 2 x |+x -2=0的解的个数为2.6.已知a =log 372,b =⎝⎛⎭⎫1413,c =log 1315,则a ,b ,c 的大小关系为 .A .a >b >cB .b >a >cC .c >b >aD .c >a >b解析:∵ c =log 1315=log 35,a =log 372,又y =log3x 在(0,+∞)上是增函数, ∴ log35>log372>log33=1,∴ c >a >1.∵ y =14x 在(-∞,+∞)上是减函数,∴ 1413<140=1,即b <1.∴ c >a >b . 故选D.7.已知定义在R 上的偶函数f (x )满足对任意的0<x 1<x 2,f (x 2)-f (x 1)x 2-x 1>0均成立,若a =f (334),b=f (943-),c =f (-543),则a ,b ,c 的大小关系为( )A .b <a <cB .a <b <cC .c <b <aD .b <c <a解析:因为偶函数f (x )满足对任意的0<x 1<x 2,f (x 2)-f (x 1)x 2-x 1>0均成立,所以f (x )在(0,+∞)上是增函数.因为幂函数y =x 43在(0,+∞)上是增函数,指数函数y =3x 在(0,+∞)上是增函数,所以343<543,943-=383-<334<343,故c =f (-543)=f (543)>a =f (334)>b =f (943-),故b <a <c ,故选A.8.已知f (x )是R 上的奇函数,且f (x )=则f = .[解析] f=-f =-f =-f =-log 2=-log 22-1=1.9.若函数y =⎝⎛⎭⎫12|1-x |+m 的图象与x 轴有公共点,则实数m 的取值范围是________. 解析:∵|1-x |≥0,∴0<⎝⎛⎭⎫12|1-x |≤1,由题意得0<-m ≤1,即-1≤m <0. 答案:[-1,0)10.已知函数f (x )在定义域(0,+∞)上是单调函数,若对于任意x ∈(0,+∞),都有f =2,则f的值是 . 因为函数f (x )在定义域(0,+∞)上是单调函数,且f=2恒成立,所以f (x )-为一个大于0的常数,令这个常数为n (n>0),则有f (x )-=n ,且f (n )=2,所以f (n )=+n=2,解得n=1,所以f (x )=1+,11.设m ∈N ,若函数f (x )=2x -m 10-x +10存在整数零点,则符合条件的m 的个数为 .解析:由f (x )=0得m =2x +1010-x .又m ∈N ,因此有⎩⎪⎨⎪⎧10-x >0,2x +10≥0,解得-5≤x <10,x ∈Z ,∴x=-5,-4,-3,…,1,2,3,…,8,9,将它们分别代入m =2x +1010-x,一一验证得,符合条件的m 的取值为0,4,11,28,共4个.12.已知函数f (x )=⎩⎪⎨⎪⎧|x +2|,-3≤x <0,log a x ,x >0,其中a >0且a ≠1,若函数f (x )的图象上有且仅有一对点关于y 轴对称,则实数a 的取值范围是 . 解析:∵函数f (x )的图象上有且仅有一对点关于y 轴对称,∴f (x )=|x +2|(-3≤x <0)的图象关于y 轴对称的图象与f (x )=log a x (x >0)的图象有且只有一个交点.记f (x )=|x +2|(-3≤x <0)的图象关于y 轴对称的图象对应的函数为g (x ),则g (x )=|x -2|(0<x ≤3),作出函数f (x )与g (x )的大致图象.当0<a <1时,如图(1),显然g (x )的图象与f (x )(x >0)的图象有且只有一个交点,符合题意;当a >1时,如图(2),要使g (x )的图象与f (x )(x >0)的图象有且只有一个交点,则需log a 3>1,∴ 1<a <3.综上a ∈(0,1)∪(1,3).13.已知函数f (x )=⎩⎪⎨⎪⎧|log 3x |,0<x <3,13x 2-103x +8,x ≥3,若存在实数a 、b 、c 、d ,满足f (a )=f (b )=f (c )=f (d ),其中d >c >b >a >0,则abcd 的取值范围是 .解析:画出f (x )的图象,如图.由图象知0<a <1,1<b <3,则f (a )=|log 3a |=-log 3a ,f (b )=|log 3b |=log 3b ,∵f (a )=f (b ),∴-log 3a =log 3b ,∴ab =1.又由图象知,3<c <4,d >6,点(c ,f (c ))和点(d ,f (d ))均在二次函数y =13x 2-103x +8的图象上,故有c +d 2=5,∴d =10-c ,∴abcd =c (10-c )=-c 2+10c =-(c -5)2+25,∵3<c <4,∴21<-(c -5)2+25<24,即21<abcd <24.14.已知f (x )=2|x |+x 2+a 有唯一的零点,则实数a 的值为________.解析:设函数g (x )=2|x |+x 2,因为g (-x )=g (x ),所以函数g (x )为偶函数,当x ≥0时,g (x )=2x +x 2,为增函数;当x <0时,g (x )=⎝⎛⎭⎫12x +x 2,为减函数,所以g (x )≥g (0)=1.因为f (x )=2|x |+x 2+a 有唯一的零点,所以y =g (x )与y =-a 有唯一的交点,即a =-1. 答案:-115.已知函数f (x )=|log 3x |,实数m ,n 满足0<m <n ,且f (m )=f (n ),若f (x )在[m 2,n ]上的最大值为2,则nm=________.解析:∵f (x )=|log 3x |,正实数m ,n 满足m <n ,且f (m )=f (n ),∴-log 3m =log 3n ,∴mn =1.∵f (x )在区间[m 2,n ]上的最大值为2,函数f (x )在[m 2,1)上是减函数,在(1,n ]上是增函数,∴-log 3m 2=2或log 3n =2.若-log 3m 2=2,得m =13,则n =3,此时log 3n =1,满足题意.那么n m =3÷13=9.同理:若log 3n =2,得n =9,则m =19,此时-log 3m 2=4,不满足题意.综上,可得nm=9.答案:916.函数f (x )的定义域为D ,若满足f (x )在D 内是单调函数,且存在[a ,b ]⊆D ,使得f (x )在[a ,b ]上的值域为,则称函数f (x )为“成功函数”.若函数f (x )=log m (m x +2t )(其中m>0且m ≠1)是“成功函数”,则实数t 的取值范围为 .[解析] 无论m>1还是0<m<1,f(x)=log m(m x+2t)都是R上的增函数,故应有则问题可转化为已知f(x)=,即log m(m x+2t)=,即m x+2t=在R上有两个不相等的实数根,求实数t的取值范围.令λ=(λ>0),则m x+2t=可化为2t=λ-λ2=-+,结合图像(图略)可得t∈.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本初等函数测试题一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.有下列各式:①na n=a ; ②若a ∈R ,则(a 2-a +1)0=1;43x y =+; ④6?-2?2=3-2.其中正确的个数是( )A .0B .1C .2D .32.函数y =a |x |(a >1)的图象是( )3.下列函数在(0,+∞)上是增函数的是( ) A .y =3-x B .y =-2x C .y =log 0.1x D .y =x 124.三个数log 215,20.1,2-1的大小关系是( )A .log 215<20.1<2-1B .log 215<2-1<20.1C .20.1<2-1<log 215 D .20.1<log 215<2-15.已知集合A ={y |y =2x ,x <0},B ={y |y =log 2x },则A ∩B =( ) A .{y |y >0} B .{y |y >1} C .{y |0<y <1} D .∅6.设P 和Q 是两个集合,定义集合P -Q ={x |x ∈P 且x ?Q },如果P ={x |log 2x <1},Q ={x |1<x <3},那么P -Q 等于( )A .{x |0<x <1}B .{x |0<x ≤1}C .{x |1≤x <2}D .{x |2≤x <3}7.已知0<a <1,x =log a 2+log a 3,y =12log a 5,z =log a 21-log a 3,则( )A .x >y >zB .x >y >xC .y >x >zD .z >x >y 8.函数y =2x -x 2的图象大致是( )9.已知四个函数①y =f 1(x );②y =f 2(x );③y =f 3(x );④y =f 4(x )的图象如下图: 则下列不等式中可能成立的是( )A .f 1(x 1+x 2)=f 1(x 1)+f 1(x 2)B .f 2(x 1+x 2)=f 2(x 1)+f 2(x 2)C .f 3(x 1+x 2)=f 3(x 1)+f 3(x 2)D .f 4(x 1+x 2)=f 4(x 1)+f 4(x 2)10.设函数121()f x x =,f 2(x )=x -1,f 3(x )=x 2,则f 1(f 2(f 3(2010)))等于( ) A .2010 B .20102 C.12010 D.1201211.函数f (x )=3x 21-x+lg(3x +1)的定义域是( )A.⎝⎛⎭⎫-∞,-13 B.⎝⎛⎭⎫-13,13 C.⎝⎛⎭⎫-13,1 D.⎝⎛⎭⎫-13,+∞ 12.(2010·石家庄期末测试)设f (x )=⎩⎪⎨⎪⎧2e x -1, x <2,log 3?x 2-1?, x ≥2. 则f [f (2)]的值为( )A .0B .1C .2D .3二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上) 13.给出下列四个命题:(1)奇函数的图象一定经过原点;(2)偶函数的图象一定经过原点; (3)函数y =lne x是奇函数;(4)函数13y x =的图象关于原点成中心对称. 其中正确命题序号为________.(将你认为正确的都填上)14. 函数y =的定义域是 .15.已知函数y =log a (x +b )的图象如下图所示,则a =________,b =________. 16.(2008·上海高考)设函数f (x )是定义在R 上的奇函数,若当x ∈(0,+∞)时,f (x )=lg x ,则满足f (x )>0的x 的取值范围是________.三、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)已知函数f (x )=log 2(ax +b ),若f (2)=1,f (3)=2,求f (5). 18.(本小题满分12分)已知函数12()2f x x =-.(1)求f (x )的定义域;(2)证明f (x )在定义域内是减函数. 19.(本小题满分12分)已知函数f (x )=2x -12x +1.(1)判断函数的奇偶性;(2)证明:f (x )在(-∞,+∞)上是增函数. 20.(本小题满分12分)已知函数()223(1)mm f x m m x +-=--是幂函数, 且x ∈(0,+∞)时,f (x )是增函数,求f (x )的解析式.21.(本小题满分12分)已知函数f (x )=lg(a x -b x ),(a >1>b >0). (1)求f (x )的定义域;(2)若f (x )在(1,+∞)上递增且恒取正值,求a ,b 满足的关系式. 22.(本小题满分12分)已知f (x )=⎝⎛⎭⎫12x -1+12·x .(1)求函数的定义域; (2)判断函数f (x )的奇偶性; (3)求证:f (x )>0.参考答案答案速查:1-5 BCDBC 6-10 BCACC 11-12 CC 1.解析:仅有②正确.答案:B2.解析:y =a |x |=⎩⎪⎨⎪⎧a x ,?x ≥0?,a -x ,?x <0?,且a >1,应选C.答案:C3.答案:D4.答案:B5.解析:A ={y |y =2x ,x <0}={y |0<y <1},B ={y |y =log 2x }={y |y ∈R },∴A ∩B ={y |0<y <1}. 答案:C6.解析:P ={x |log 2x <1}={x |0<x <2},Q ={x |1<x <3},∴P -Q ={x |0<x ≤1},故选B.答案:B7.解析:x =log a 2+log a 3=log a 6=12log a 6,z =log a 21-log a 3=log a 7=12log a 7.∵0<a <1,∴12log a 5>12log a 6>12log a 7.即y >x >z . 答案:C8.解析:作出函数y =2x 与y =x 2的图象知,它们有3个交点,所以y =2x -x 2的图象与x 轴有3个交点,排除B 、C ,又当x <-1时,y <0,图象在x 轴下方,排除D.故选A.答案:A9.解析:结合图象知,A 、B 、D 不成立,C 成立.答案:C 10.解析:依题意可得f 3(2010)=20102,f 2(f 3(2010)) =f 2(20102)=(20102)-1=2010-2,∴f 1(f 2(f 3(2010)))=f 1(2010-2)=(2010-2)12=2010-1=12010.答案:C11.解析:由⎩⎪⎨⎪⎧1-x >03x +1>0?⎩⎪⎨⎪⎧x <1x >-13?-13<x <1. 答案: C 12.解析:f (2)=log 3(22-1)=log 33=1,∴f [f (2)]=f (1)=2e 0=2. 答案:C13.解析:(1)、(2)不正确,可举出反例,如y =1x ,y =x -2,它们的图象都不过原点.(3)中函数y =lne x =x ,显然是奇函数.对于(4),y =x 13是奇函数,而奇函数的图象关于原点对称,所以(4)正确.答案:(3)(4)14. 答案:(4,5]15.解析:由图象过点(-2,0),(0,2)知,log a (-2+b )=0,log a b =2,∴-2+b =1,∴b =3,a 2=3,由a >0知a = 3.∴a =3,b =3.答案:3 316.解析:根据题意画出f (x )的草图,由图象可知,f (x )>0的x 的取值范围是-1<x <0或x >1.答案:(-1,0)∪(1,+∞)17.解:由f (2)=1,f (3)=2,得⎩⎪⎨⎪⎧ log 2?2a +b ?=1log 2?3a +b ?=2?⎩⎪⎨⎪⎧ 2a +b =23a +b =4?⎩⎪⎨⎪⎧a =2,b =-2.∴f (x )=log 2(2x -2),∴f (5)=log 28=3. 18.∵x 2>x 1≥0,∴x 2-x 1>0,x 2+x 1>0, ∴f (x 1)-f (x 2)>0,∴f (x 2)<f (x 1). 于是f (x )在定义域内是减函数. 19.解:(1)函数定义域为R .f (-x )=2-x -12-x +1=1-2x 1+2x =-2x -12x +1=-f (x ),所以函数为奇函数.(2)证明:不妨设-∞<x 1<x 2<+∞, ∴2x 2>2x 1.又因为f (x 2)-f (x 1)=2x 2-12x 2+1-2x 1-12x 1+1=2?2x 2-2x 1??2x 1+1??2x 2+1?>0, ∴f (x 2)>f (x 1).所以f (x )在(-∞,+∞)上是增函数. 20.解:∵f (x )是幂函数, ∴m 2-m -1=1, ∴m =-1或m =2, ∴f (x )=x-3或f (x )=x 3,而易知f (x )=x -3在(0,+∞)上为减函数,f (x )=x 3在(0,+∞)上为增函数. ∴f (x )=x 3.21.解:(1)由a x -b x >0,得⎝⎛⎭⎫a b x>1.∵a >1>b >0,∴ab >1,∴x >0.即f (x )的定义域为(0,+∞).(2)∵f (x )在(1,+∞)上递增且恒为正值, ∴f (x )>f (1),只要f (1)≥0, 即lg(a -b )≥0,∴a -b ≥1.∴a ≥b +1为所求22.解:(1)由2x -1≠0得x ≠0,∴函数的定义域为{x |x ≠0,x ∈R }.(2)在定义域内任取x ,则-x 一定在定义域内. f (-x )=⎝⎛⎭⎫12-x -1+12(-x )=⎝⎛⎭⎫2x 1-2x +12(-x )=-1+2x 2?1-2x ?·x =2x+12?2x -1?·x . 而f (x )=⎝⎛⎭⎫12x -1+12x =2x+12?2x -1?·x ,∴f (-x )=f (x ). ∴f (x )为偶函数.(3)证明:当x >0时,2x >1, ∴⎝⎛⎭⎫12x -1+12·x >0. 又f (x )为偶函数, ∴当x <0时,f (x )>0.故当x ∈R 且x ≠0时,f (x )>0.。
