规范化无损分解及保持函数依赖
[总结]关系数据库设计基础（函数依赖、无损连接性、保持函数依赖、范式、……）
![[总结]关系数据库设计基础（函数依赖、无损连接性、保持函数依赖、范式、……）](https://img.taocdn.com/s3/m/af34390811a6f524ccbff121dd36a32d7375c7be.png)
[总结]关系数据库设计基础（函数依赖、⽆损连接性、保持函数依赖、范式、……）≏≎≟≗≖≍≭∼∽≁≃≂≅≊≈≉≇≳⪞⪆⋧⪊≵≲⪝⪅⋦⪉≴⊂ subset ⋐⊄⊊ ⊈⊃⊇ ⋑⊅⊋ ⊉≺⪯≼⋞≾⪷⋨⪵⪹⊀≻⪰≽⋟≿⪸⋩⪶⪺⊁ in ∋∉∌∝≬⊸函数依赖（Function Dependency）定义设关系模式R（U），属性集合U= {A1，A2，…，An}，X，Y为属性集合U的⼦集，如果对于关系模式R(U)的任⼀可能的关系r，r中的任意两个元组u、v，若有 u[X]=v[X]，就有u[Y]=v[Y]，则称X函数决定Y，或称Y函数依赖于X。
⽤符号X→Y表⽰。
其中X为决定因素，Y为被决定因素。
若对于R（U）的任意⼀个可能的关系r，r中不可能存在两个元组在X上的属性值性等，⽽在Y上的属性值不等。
(1) 函数依赖是语义范畴的概念，只能根据语义来确定⼀个函数依赖关系。
(2) 函数依赖X→Y的定义要求关系模式R的任何可能的关系r中的元组都满⾜函数依赖条件。
术语 (1)若X→Y，则X称作决定因素（Determinant） (2)若X→Y，Y→X，称作X<->Y。
(3)若Y不函数依赖于X，称作X -/-> Y。
(4)X→Y，若Y不包含X,即X ⊄ Y，则称X→Y为⾮平凡的函数依赖。
正常讨论的都是⾮平凡的函数依赖。
(5)X→Y，若Y包含X，即X ⊂ Y，则称X→Y为平凡的函数依赖。
(6)完全函数依赖(full functional dependency)：在R(U)中，设X、Y是关系模式R（U）中不同的属性⼦集(即X ⊂ U,Y ⊂ U), 若存在 X→Y，且不存在 X的任何真⼦集X'(即 X' ⊊ X)，使得 X'→Y，则称Y完全函数依赖 ( full functional dependency ) 于X。
记作 X-F->Y。
(7)部分函数依赖：在关系模式R（U）中，X、Y是关系模式R（U）中不同的属性⼦集(即X ⊂ U,Y ⊂ U), 若X→Y成⽴，如果X中存在任何真⼦集X'(即 X' ⊊ X)，⽽且有X'→Y也成⽴，则称Y对X是部分函数依赖，记作：X-P->Y。
关系模式分解的无损连接和保持函数依赖
关系模式分解的无损连接和保持函数依赖一、引言关系模式是关系数据库中的核心元素之一，它描述了数据的结构和关系。
在设计关系数据库时，我们常常需要对关系模式进行分解，以满足数据库的需求。
本文将讨论关系模式分解的无损连接和保持函数依赖的相关概念和方法。
二、关系模式分解关系模式分解是将一个关系模式拆分成多个较小的关系模式的过程。
在分解关系模式时，我们需要考虑两个重要的性质：无损连接和保持函数依赖。
2.1 无损连接无损连接是指在关系模式分解后，通过对分解后的关系进行连接操作能够恢复原始关系模式。
换句话说，无损连接要求分解后的关系能够完整地保留原始关系中的所有信息。
2.2 保持函数依赖保持函数依赖是指在关系模式分解后，分解后的关系中依然能够保持原始关系中的函数依赖关系。
函数依赖是指一个属性或者属性集合的值决定了另一个属性或者属性集合的值。
三、关系模式分解的方法关系模式分解有多种方法，下面介绍三种常用的方法：自然连接、垂直分解和水平分解。
3.1 自然连接自然连接是指通过公共属性将两个或多个关系模式进行连接，得到一个具有完整信息的新关系模式。
自然连接的特点是能够保持原始关系中的所有信息和函数依赖。
3.2 垂直分解垂直分解是指根据属性集合的划分，将一个关系模式分解成多个关系模式。
垂直分解的优点是能够消除冗余数据，提高查询效率。
但是需要注意的是，垂直分解可能会造成关系丢失或信息损失。
3.3 水平分解水平分解是指将一个关系模式的元组进行水平划分，得到多个关系模式。
水平分解的特点是能够提高并发性能和容错性。
但是需要注意的是，水平分解可能会造成查询的复杂性增加和数据的分布不均衡。
四、关系模式分解的应用关系模式分解在实际的数据库设计中有着广泛的应用。
下面介绍两个例子以说明关系模式分解的应用。
4.1 学生课程关系考虑一个学生选课系统，其中包含学生和课程两个关系模式。
学生关系模式包括学生ID、姓名和年龄等属性，课程关系模式包括课程ID、课程名称和教师名称等属性。
关系模式无损及保持函数依赖的判定
关系模式无损及保持函数依赖的判定在数据库的世界里，有一门课非常重要，听起来复杂，其实一旦了解了，就像喝水一样简单。
这门课就是关于关系模式无损及保持函数依赖的判定。
说实话，乍一听这名字，很多人都会觉得有点绕。
但是，咱们可以轻松搞定这事儿。
想象一下你家里的冰箱。
里面各种各样的食材，鱼、肉、蔬菜，真是五花八门。
每次打开冰箱门，看到那些东东，你就知道要做什么了。
可是，如果这些食材全乱七八糟地放在一起，那可就糟了，找个东西就得翻半天。
关系模式就有点像这个冰箱，食材（数据）得好好分门别类。
无损性在这里就相当于我们把冰箱整理得井井有条，随取随用，不会出错。
比如，牛肉和鸡肉放在一起，那你一不小心把牛肉用错了，哎呀，可就麻烦了。
再说说保持函数依赖，这就像家里的规矩。
比如，家里规定：晚饭前不可以玩手机。
这样一来，大家都得遵守这个规矩，才能和谐相处。
在数据库中，函数依赖就是指某些数据项之间的关系。
如果有一个函数依赖存在，就意味着一个数据项的值决定了另一个数据项的值。
比如，学生的学号决定了他的姓名，学号就是那个“规矩”，保证大家都能遵循。
咱们可不能随便乱来，要保持这些依赖关系，才能让数据的完整性得到保障。
再回到关系模式无损的事情上。
无损分解就像咱们把冰箱里的食材分类，保证每种食材都能用得上。
比如，先把鱼和肉分开，再把鸡蛋和蔬菜放在一边，这样无论你想做什么，都能很方便地找到需要的食材。
如果分解得不好，可能一分开，整个菜都做不好了。
要是你把肉和蔬菜分开，但在某个地方漏掉了牛肉，那你就可能做不出你想要的红烧肉了。
无损性就像是保证了这个分解过程的有效性，确保你分开了，但是每样东西还在，没丢。
这里再给大家讲一个小故事。
前几天我去朋友家做客，看到他家冰箱简直乱得像个战场，啧啧，根本找不到东西。
后来他跟我说，最近工作太忙，没时间整理。
于是，我就给他提议，不如一起分类一下，把常用的东西放在最上面，少用的放在下面。
你猜怎么着？他真的开始整理了，整理完之后，连我都觉得轻松多了。
数据库保持函数依赖的分解
2NG
a1
a2
a3
思考：不保持函数依赖的 分解会导致什么问题？
例: 分, G ) 职工工号 工资级别 工资数目 R上的FD集为： F= { N→S, /* 每个职工只有一个工资级别 */ S →G /* 一个工资级别只有一个工资数目*/ } 将R分解为:ρ ={ NS, SG }， ρ保持依赖？无损分解？ 解：PNS(F)={N→S}， PSG(F)={S→G}。 因为PNS(F)∪PSG(F)= F, 所以ρ保持函数依赖； 也是无损分解：
1A 1AB 2AC a1 a1 2B a2 b22 3C b13 a3
例: 分解是否保持FD集,是否无损分解
设有关系模式：R(ABC), R上的FD集为： F= { C→B, B→A } 将R分解为:ρ ={ AB, AC }， ρ保持依赖？无损分解？ 解：PAB(F)={B→A}， PAC(F)={C→A}。 ρ不保持依赖(丢失C→B) ； 也是损失分解：
问题：如何在保证无损和保持依赖的前提下，使分解所 得的关系模式集符合尽可能高的范式？ 目前有三个算法： 1. 保持依赖且无损地分解成3NF关系模式集 2. 无损地分解成BCNF关系模式集 3. 无损地分解成4NF关系模式集(超出课程范围, 不讲)
则称分解ρ保持函数依赖集F。
两个函数依赖集F和G是等价的，当且仅当：
1) 凡是能够由F推出的FD都能够由G推出； 2) 凡是不能由F推出的FD也不能由G推出。
例: 分解是否保持FD集,是否无损分解
设有关系模式：R( N, S, G ) 职工工号 工资级别 工资数目 R上的FD集为： F= { N→S, /* 每个职工只有一个工资级别 */ S →G /* 一个工资级别只有一个工资数目*/ } 将R分解为:ρ ={ NS, NG }， ρ保持依赖？无损分解？ 解：PNS(F)={N→S}， PNG(F)={N→G}。 因为根据N→S和N→G推不出S →G, 所以ρ不保持 函数依赖； 但是是无损分解：
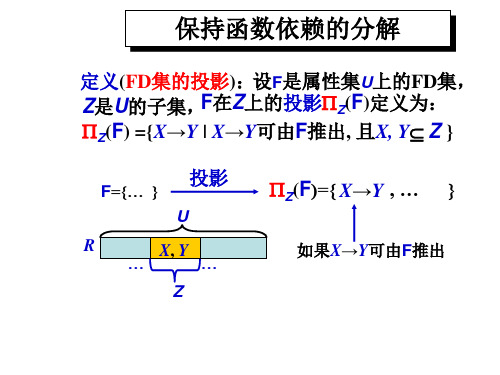
规范化无损分解及保持函数依赖
AB BC CD
a1
a2
b13 a3 a3
b14 b24 a4
b 21 a 2 b31 b32
无损分解的测试方法
（2)把表格看成模式R的一个关系，反复检查F中每个FD在表格中是否成立， 若不成立，则修改表格中的值。修改方法如下： 对于F中一个FD X Y ，如果表格中有两行在X值上相等，在Y值上不相等， ai 那么把这两行在Y值上也改成相等的值。如果Y值中有一个是 ，那么另一 aj aj bij 个也改成 ；如果没有 ，那么用其中一个 替换另一个值（尽量把下标 ij改成较小的数）。一直到表格不能修改为止。 （3)若修改的最后一张表格中有一行全 是a，即 a1a 2 a n ，那么称ρ 相对于F 是无损分解，否则称有损分解。 A B C D
分解成3NF模式集既无损 又保持函数依赖的方法
① 对于关系模式R和R上成立的FD集F，先求出F的最小依赖集，然后再把最小依 赖集中那些左部相同的FD用合并性合并起来。 ② 对最小依赖集中每个FD X→Y去构成一个模式XY。 ③ 在构成的模式集中，如果每个模式都不包含R的候选键，那么把候选键作为一 个模式放入模式集中。
保持函数依赖的模式分解
设关系模式R<U,F>被分解为若干个关系模式 R1<U1,F1>，R2<U2,F2>，…，Rn<Un,Fn> （其中U=U1∪U2∪…∪Un，且不存在Ui Uj，Fi为F 在Ui上的投影），若F所逻辑蕴含的函数依赖一定
也由分解得到的某个关系模式中的函数依赖Fi所逻
辑蕴含，则称关系模式R的这个分解是保持函数依
, Rk 是R
例：设关系模式R（ABCD），R分解成 {AB, BC, CD} 。如果R上成立的函数依赖 集 F1 {B A, C D}，那么ρ 相对于F 是否无损分解？如果R上成立的函数依赖集 1 F2 {A B, C D} 呢？ （1)构建一张k行n列的表格，每 列对应一个属性 A j 1 j n ，每行 对应一个模式 R i 1 i K 。如 果 A j在 R i 中，那么在表格的第i行 第j列处填上符号 a j ，否则填上 bij。 A B C D
无损连接和保持函数依赖的关系
无损连接和保持函数依赖的关系引言在数据库管理系统中，数据的一致性和完整性对于数据的正确性非常重要。
在设计和组织数据库时，无损连接和保持函数依赖是两个关键概念。
它们用于确保数据库中的数据能够正确地存储和检索。
在本文中，我们将深入探讨无损连接和保持函数依赖的关系，以及它们在数据库设计中的重要性。
无损连接什么是无损连接无损连接是指数据库中的数据能够在连接操作中保持完整性和一致性。
也就是说，当我们将数据拆分成多个表时，并通过连接操作将它们关联起来，数据之间的关系应该能够正确地重建。
无损连接确保了数据在表之间的关联上是完整的。
无损连接的实现方法无损连接的实现方法有两种：函数依赖和多值依赖。
函数依赖函数依赖是指一个数据集中的一组属性的取值能够决定另外一组属性的取值。
在数据库中，函数依赖用于建立关系数据库表之间的连接。
通过定义表之间的函数依赖关系，我们可以在数据插入、更新或删除时保持数据的一致性。
多值依赖多值依赖是指一个数据集中的一组属性的取值能够决定另外一组属性的取值，但不能由单个属性的取值决定。
与函数依赖不同，多值依赖处理的是属性之间的多对多关系。
保持函数依赖什么是保持函数依赖保持函数依赖是指在数据库设计中，通过分解关系数据库表来满足函数依赖的要求。
当一个关系数据库表中存在多个函数依赖时，我们可能需要对其进行拆分，以满足函数依赖的要求。
保持函数依赖的方法保持函数依赖的方法主要有：分解、合成和冗余消除。
分解分解是将一个关系数据库表拆分成两个或多个表的过程。
在分解时，我们需要确保新的表能够保持函数依赖关系。
通过分解，我们可以消除冗余和提高数据的一致性和完整性。
合成合成与分解相反，是将多个表合并成一个表的过程。
合成主要用于优化查询和降低数据访问的开销。
然而，在合成时，我们需要确保合并后的表能够保持函数依赖关系和数据的一致性。
冗余消除冗余消除是指通过合并表或优化表结构来消除冗余数据。
冗余数据可能会导致数据的不一致性和完整性问题。
无损分解与函数依赖的判断
一：大部分是对一个关系模式分解成两个模式的考察，分解为三个以上模式时无损分解和保持依赖的判断比较复杂，考的可能性不大，因此我们只对“一个关系模式分解成两个模式”这种类型的题的相关判断做一个总结。
以下的论述都基于这样一个前提：R是具有函数依赖集F的关系模式，（R1 ，R2）是R的一个分解。
首先我们给出一个看似无关却非常重要的概念：属性集的闭包。
令α为一属性集。
我们称在函数依赖集F下由α函数确定的所有属性的集合为F下α的闭包，记为α+ 。
下面给出一个计算α+的算法，该算法的输入是函数依赖集F和属性集α，输出存储在变量result中。
算法一：result:=α;while(result发生变化)dofor each 函数依赖β→γ in F dobeginif β∈result then result:=result∪γ;end属性集闭包的计算有以下两个常用用途：·判断α是否为超码，通过计算α+（α在F下的闭包），看α+ 是否包含了R中的所有属性。
若是，则α为R的超码。
·通过检验是否β∈α+，来验证函数依赖是否成立。
也就是说，用属性闭包计算α+，看它是否包含β。
（请原谅我用∈符号来表示两个集合之间的包含关系，那个表示包含的符号我找不到，大家知道是什么意思就行了。
）看一个例子吧，2005年11月系分上午37题：● 给定关系R(A1，A2，A3，A4)上的函数依赖集F={A1→A2，A3→A2，A2→A3，A2→A4}，R的候选关键字为________。
（37）A. A1 B. A1A3 C. A1A3A4 D. A1A2A3首先我们按照上面的算法计算A1+ 。
result=A1，由于A1→A2，A1∈result，所以resul t=result∪A2=A1A2由于A2→A3，A2∈result，所以result=result∪A3=A1A2A3由于A2→A4，A2∈result，所以result=result∪A3=A1A2A3A4由于A3→A2，A3∈result，所以result=result∪A2=A1A2A3A4通过计算我们看到，A1+ =result={A1A2A3A4}，所以A1是R的超码，理所当然是R的候选关键字。
保持函数依赖的分解
定义(保持函数依赖的分解)： 设ρ={R1,…,Rk}是关 系模式R的一个分解，F是R上的FD集，如果: PR1(F)∪…∪ PRk(F)与F等价，
则称分解ρ保持函数依赖集F。
两个函数依赖集F和G是等价的，当且仅当：
1) 凡是能够由F推出的FD都能够由G推出； 2) 凡是不能由F推出的FD也不能由G推出。
1A 1AB 2AC a1 a1 2B a2 b22 3C b13 a3
1A 1AB 2AC a1 a1
2B a2 a2
3C b13 a3
例: 分解是否保持FD集,是否无损分解
设有关系模式：R(ABC), R上的FD集为： F= { A→B, B→C } 将R分解为:ρ ={ AB, AC }， ρ保持依赖？无损分解？ 解：PAB(F)={A→B}， PAC(F)={A→C}。 ρ不保持依赖(丢失B→C)；但是是无损分解：
1A 1AB 2AC a1 a1 2B a2 b22 3C b13 a3
总结
根据是否保持依赖、是否无损分解将分解分成四类： 无损分解 保持依赖 YES YES NO NO YES NO YES NO 说明 最好 (不丢失数据和依赖) 可接受 (丢失依赖, 会导致异常) 不能接受(丢失数据) 不能接受(丢失数据)
1N 1NS a1 2S a2 3G b13
2NG
a1
b22
a3
例: 分解是否保持FD集,是否无损分解
设有关系模式：R( N, S, G ) 职工工号 工资级别 工资数目 R上的FD集为： F= { N→S, /* 每个职工只有一个工资级别 */ S →G /* 一个工资级别只有一个工资数目*/ } 将R分解为:ρ ={ NS, NG }， ρ保持依赖？无损分解？ 解：PNS(F)={N→S}， PNG(F)={N→G}。 因为根据N→S和N→G推不出S →G, 所以ρ不保持 函数依赖； 但是是无损分解：
简述关系规范化的过程
关系规范化的过程
1、对给定的关系模式和最小函数集，画出函数依赖或图，找出所有候选码
2、根据范式定义，判断该关系属于第几范式
3、逐步分解为更高一级的范式
4、保持依赖和无损分解。
规范化理论把关系应满足的规范要求分为几级，满足最低要求的一级叫做第一范式(1NF)，在第一范式的基础上提出了第二范式(2NF)，在第二范式的基础上又提出了第三范式(3NF)，以后又提出了BCNF范式，4NF，5NF。
范式的等级越高，应满足的约束集条件也越严格。
对于存在数据冗余、插入异常、删除异常问题的关系模式，应采取将一个关系模式分解为多个关系模式的方法进行处理。
一个低一级范式的关系模式，通过模式分解可以转换为若干个高一级范式的关系模式，这就是所谓的规范化过程。
关系模式分解的无损连接和保持函数依赖
关系模式分解的无损连接和保持函数依赖一、关系模式分解的概念关系模式分解是指将一个复杂的关系模式分解为若干个简单的关系模式的过程。
在实际应用中，由于某些原因（如性能、数据冗余等），需要将一个大型的关系模式分解成多个小型的关系模式，从而提高数据库系统的效率和可维护性。
二、无损连接和保持函数依赖在进行关系模式分解时，有两种重要的约束条件：无损连接和保持函数依赖。
无损连接是指在进行关系模式分解后，仍然能够通过连接操作得到原始数据集合。
保持函数依赖是指在进行关系模式分解后，仍然能够维护原始数据集合中所有函数依赖。
三、无损连接和保持函数依赖的定义1. 无损连接假设R是一个关系模式，R1和R2是R的两个投影。
如果存在一个连接操作J(R1,R2)，使得J(R1,R2)中包含了所有R中元组，则称R1和R2对于R具有无损连接。
2. 保持函数依赖假设R是一个关系模式，F是R上的一组函数依赖集合。
如果对于F中任何一个函数依赖X→Y，都存在一个关系模式R1和R2，使得R=R1⋈R2，且X和Y分别属于R1和R2的属性集合，则称关系模式分解后，仍然能够维护原始数据集合中所有函数依赖。
四、无损连接和保持函数依赖的算法在进行关系模式分解时，需要考虑如何保证无损连接和保持函数依赖。
以下是两种常用的算法。
1. 剖析算法剖析算法是一种自顶向下的分解方法。
该方法首先将原始关系模式拆分成两个投影，并检查它们是否具有无损连接。
如果没有，则再次拆分，并重复该过程直到满足无损连接为止。
剖析算法的优点是简单易懂，容易实现。
但是缺点也很明显，即可能会产生大量冗余数据。
2. 合成算法合成算法是一种自底向上的分解方法。
该方法首先将原始关系模式拆分为多个小型关系模式，并检查它们是否能够维护原始数据集合中所有函数依赖。
如果不能，则将两个小型关系模式合并，并重复该过程直到满足保持函数依赖为止。
合成算法的优点是能够保证数据的最小化，减少数据冗余。
但是缺点也很明显，即实现难度较大。
数据库保持函数依赖的分解
解：PAB(F)={A→B}， PAC(F)={ }。 ρ保持依赖； 也是无损分解：
1A 2B 3C 1AB a1 a2 b13 2AC a1 b22 a3
1A 2B 3C 1AB a1 a2 b13 2AC a1 a2 a3
例: 分解是否保持FD集,是否无损分解
设有关系模式：R(ABC), R上的FD集为： F= { A→B, B→C }
将R分解为:ρ ={ AB, AC }， ρ保持依赖？无损分解？
解：PAB(F)={A→B}， PAC(F)={A→C}。 ρ不保持依赖(丢失B→C)； 但是是无损分解：
1A 2B 3C 1AB a1 a2 b13 2AC a1 b22 a3
1A 2B 3C 1AB a1 a2 b13 2AC a1 b22 a3
总结
根据是否保持依赖、是否无损分解将分解分成四类：
无损分解 保持依赖
说明
YES
YES
最好 (不丢失数据和依赖)
YES
NO 可接受 (丢失依赖, 会导致异常)
NO
YES
不能接受(丢失数据)
NO
NO
不能接受(丢失数据)
问题：如何在保证无损和保持依赖的前提下，使分解所 得的关系模式集符合尽可能高的范式？
例: 分解是否保持FD集,是否无损分解
设有关系模式：R( N,
S,
G)
职工工号 工资级别 工资数目
R上的FD集为：
F= {
N→S, /* 每个职工只有一个工资级别 */
S →G /* 一个工资级别只有一个工资数目*/
}
将R分解为:ρ ={ NS, NG }， ρ保持依赖？无损分解？
练习-无损连接性和保持函数依赖
习题
（判定无损连接性和保持函数依赖）
1、设有关系模式R<U，F>，U={X，Y，Z，S，W}，F={X→S，W→S，S→Y，YZ→S，SZ→XY}，设R 分解成P={R1(WS)，R2(YZS)，R3(XZS)}，判断该分解是否保持函数依赖，并判断此分解是否具有无损连接性。
解：求出F的最小函数依赖集F’={X→S，W→S，S→Y，YZ→S，ZS→X}
若R分解为={R1(WS)，R2(YZS)，R3(XZS)}，
)+，则R<U,F>的分解р={R1，R2，R3}保持函数依赖。
因为： F’+ =( F
i
所以，该分解能保持函数依赖关系。
（5分）
所以，可以得到没有一行全为a,所以该分解为有损分解。
2．设有关系模式R(ABCDEG)，其函数依赖集为：
F={E→D，C→B，CE→G，B→A}
判断R的一个分解ρ={R1(AB),R2(BC),R3(ED),R4(EAG)}是否无损连接和保持函数依赖。
证：
（1）判断无损连接
A1A2A3A4A5A6，该分解有损
（2）判断是否保持函数依赖（5分）
从F={E→D，C→B，CE→G，B→A}得到：
R1(AB)，其F1={ B→A }
R2(BC)，其F2={C→B}
R3(ED)，其F3={E→D}
R4(EAG)，其F4={EAG→EAG }
G=F1∪F2∪F3∪F4={ B→A ，C→B ，E→D ，EAG→EAG }
由于CEG+={CEBA}，即CE→G不能由G根据Armstrong公理推导出来故F+!=(F1∪F2∪F3∪F4)+，故不保持函数依赖。
3NF既具有无损连接性又保持函数依赖的分解算法
3NF既具有无损连接性又保持函数依赖的分解算法3NF (Third Normal Form) 是关系数据库设计的一个最常用的范式。
它是在满足2NF (Second Normal Form) 的基础上进一步消除了非关键字对主键的传递依赖。
在进行3NF分解算法时，我们需要遵循以下步骤：1.对关系模式进行分析，找出主键和所有函数依赖。
2.检查关系模式是否满足2NF。
如果关系模式满足2NF，转到步骤43.找出所有非关键字的传递依赖，并进行分解。
4.对所有非主属性进行冗余消除分解。
下面将详细描述3NF分解算法的具体步骤：1.对关系模式进行分析：对于给定的关系模式R，我们需要找出其主键和所有函数依赖。
主键是可以唯一标识关系中的每条记录的那个属性或属性组合。
函数依赖是属性间的关系，其中一个或一组属性的值确定另一个或一组属性的值。
2.检查关系模式是否满足2NF：2NF要求关系模式R的所有非主属性都完全函数依赖于主键，即不能存在部分依赖。
如果关系模式已经满足2NF的要求，则可以跳过步骤3，直接进行步骤43.分解传递依赖：针对存在传递依赖的关系模式，我们需要进行分解。
传递依赖是指当一个非关键字属性依赖于另一个非关键字属性时，在关系模式中存在传递依赖。
首先，我们需要找出所有的传递依赖关系。
通常，我们可以通过观察属性之间的函数依赖来找出传递依赖。
如果存在函数依赖X→Y和Y→Z，那么我们可以推断出X→Z为传递依赖。
其次，对于每个传递依赖关系X→Z，我们需要创建一个新的关系模式XZ，并将X和Z以及它们的函数依赖复制到新的模式中。
然后，我们需要从原来的关系模式R中删除属性Z，创建一个新的关系模式YZ，并将Y和Z的函数依赖复制到新的模式中。
最后，我们需检查新的关系模式是否满足2NF，并重复这个过程，直到所有的传递依赖都被消除。
4.冗余消除分解：在消除传递依赖之后，我们需要对所有非主属性进行冗余消除分解。
对于每个非主属性A，我们创建一个新的关系模式A，并将A以及它所决定的所有属性复制到新的模式中。
关系模式的分解-无损连接与保持函数依赖
例如：设关系模式S(SNO,CLASSNO,DEPTNO)在某一时刻的关系r如下表5-14
在将一个关系模式分解为三个或者更多个关系模式的情况下，要判别分解是否具有无损连接性需要比较复杂的算法。然而若将一个关系模式分解为两个关系模式，则很容易判别分解是否具有无损连接性。
关系模式R(U,F)分解为关系模式R1(U1,F1),R2(U2,F2)是具有无损连接性的分解的充分必要条件是（U1∩U2→U1-U2）∈F+，或者（U2∩U1→U2-U1）∈F+。
S1
D1
S2
D2
S3
D2
S4
D1
表5-16
CLASSNO
DEPTNO
C1
D1
C2
D2
C3
D1
对分解后的两个关系作自然连接r11*r12，得到r'如表5-17如下：
表5-17
SNO
CLASSNO
DEPTNO
S1
C1
D1
S1
C3
D1
S2
C2
D2
S3
C2
D2
S4
C1
D1
S4
C3
D1
r'中的元组S1C3D1和S4C1D1都不是原来r中的元组。就是说，我们无法知道原来r中到底有哪些元组，这是我们不希望的。
定义1：设关系模式R(U,F)分解为关系模式R1(U1,F1)，R2(U2,F2)，…，Rn(Un,Fn)，若对于R的任何一个可能的关系r，都有r=r1*r2…*rn，即r在R1,R2,…,Rn上的投影的自然连接等于r，则称关系模式R的这个分解是具有无损连接性的。
保持函数依赖的分解
保持函数依赖的分解
保持函数依赖的分解是指在关系型数据库的规范化过程中，将一个关系（或表）分解为多个较小的关系，同时保持这些关系满足函数依赖。
这样做可以消除数据冗余，减少数据插入、更新和删除操作时的异常问题，提高数据的一致性和完整性。
保持函数依赖的分解通常遵循以下几个步骤：
1. 识别函数依赖：首先需要确定关系中的所有函数依赖。
函数依赖是指一个或多个属性的值可以决定另一个属性的值。
例如，在“学生”表中，如果“学号”和“课程号”可以决定“成绩”，那么“学号”和“课程号”就决定了“成绩”。
2. 确定范式：在确定了所有的函数依赖后，需要确定当前的范式级别。
范式是数据库设计的规范，用于消除数据冗余和提高数据一致性。
常见的范式有第一范式（1NF）、第二范式（2NF）、第三范式（3NF）等。
3. 规范化：如果当前关系不满足某个范式的要求，就需要将其分解为多个较小的关系，直到满足该范式的要求。
这个过程就是规范化。
例如，如果一个关系不满足第二范式的要求，就需要将其分解为两个关系，其中一个关系满足第二范式的要求，另一个关系满足第一范式的要求。
4. 检查函数依赖：在分解后，需要检查新的关系是否仍然满足所有
的函数依赖。
如果某个函数依赖在新的关系中不再成立，就需要重新设计该关系。
5. 实施分解：如果所有的函数依赖都得到满足，就可以将原来的关系替换为新的关系。
通过以上步骤，可以保持函数依赖的分解，并实现数据库的规范化设计。
这种设计有助于提高数据的一致性和完整性，减少数据冗余和异常问题。
3NF的无损连接和保持函数依赖的分解、BCNF的无损连接的分解
3NF的⽆损连接和保持函数依赖的分解、BCNF的⽆损连接的分解⾸先，需要了解3NF、BCNF范式的要求。
3NF：不存在⾮主属性对码的传递函数依赖或部分函数依赖。
如AB->C,A->C 码为（A,B），A,B是主属性，C是⾮主属性，C部分函数依赖于码，即不满⾜3NFBCNF：每个决定因素都包含码（相⽐于3NF，优点是加上了对主属性的限制）另⼀种说法：①主属性完全函数依赖于不含它的码②没有任何属性完全函数依赖于⾮码的任何⼀组属性③所有⾮主属性对每⼀个码都是完全函数依赖在分解前应掌握求函数依赖集最⼩覆盖的⽅法。
（见例⼀）下⾯看例⼦例⼀：设关系模式R(A,B,C,D,E)上的函数依赖集F是{A->BC,ABD->CE,E->D}1：计算F的最⼩覆盖。
⾸先将右部不唯⼀的依赖分解。
得到{A->B,A->C,ABD->C,ABD->E,E->D}然后对每⼀个依赖判断：对A->B，令G=F-{A->B},查看B是否属于A关于G的闭包。
即A是否能从G推导出B。
经推，不能。
所以，保留A->B。
同理 A->C 保留；ABD->C 删除（因为A->C）；ABD->E 保留；E->D 保留第⼆步，对左部不唯⼀的依赖进⾏判断：对ABD->E，依次去掉A/B/D，查看(ABD-A/B/D)关于F的闭包是否包含E，是则⽤其取代原依赖。
经推，发现AD->E满⾜条件。
所以，综上所述。
F的最⼩覆盖为{A->B,A->C,AD->E,E->D}2：直接写出R的所有关键字。
易知，码为(A,D) (A,E)3：直接将R分解到3NF，且满⾜⽆损连接性和依赖保持性。
对F的最⼩覆盖进⾏处理：⾸先，按左部相同原则分组 A->B,A->C为R1({ABC},{A->B,A->C}) AD->E为R2({A,D},{AD->E}) E->D为R3({E,D},{E->D})然后，将具有包含关系的元组进⾏合并 R2包含R3，所以将R2,R3合并为新的R2({A,D,E},{AD->E,E->D})最后，判断分解后的关系模式中是否含有码，若含有则为⽆损连接且保持依赖的3NF否则，则是保持依赖但不是⽆损连接的3NF，此时需要新建⼀个关系模式，将码放⼊其中（若此题不含，则加R3({A,D},{∅})）。
简述关系模式分解的两大准则
简述关系模式分解的两大准则
关系模式分解是数据库设计中的重要步骤之一，它通过将一个大型关系模式分解成多个较小的、相关的关系模式，来提高数据库的性能和可维护性。
关系模式分解需要遵循以下两大准则：
第一，无损连接（Lossless Join）准则。
即分解后所得到的关系模式能够保持对原始关系模式中所有可能连接的支持，即能够无损地连接起来。
这意味着分解后的关系模式能够通过连接操作得到与原始关系模式相同的结果，不会因为分解而引入额外的元组或导致遗失某些元组。
无损连接准则确保了数据的完整性和一致性。
第二，函数依赖（Functional Dependency）准则。
即分解后的关系模式要能够保持原始关系模式中的所有函数依赖。
对于给定的关系模式R，如果存在函数依赖A → B，那么在分解后的关系模式中，A和B仍然在同一个关系模式中，并且该函数依赖仍然有效。
这意味着分解后的关系模式要能够保持数据的一致性和完整性。
通过遵循无损连接和函数依赖准则，关系模式分解能够确保分解结果的数据完整性和一致性，提高数据库的性能和可维护性。
数据库保持依赖且无损地分解成3NF算法
数据库保持依赖且无损地分解成3NF算法数据库的设计是数据管理的重要步骤，一个良好设计的数据库可以提高数据的存储和检索的效率。
在数据库设计中，一个常见的目标是将关系数据库保持依赖且无损地分解至第三范式（Third Normal Form, 3NF），本文将介绍一种用于实现这一目标的算法。
在介绍算法之前，我们先了解一下数据库范式的概念。
关系数据库的范式是一套用于规范化数据库设计的规则。
3NF是最常用的范式之一，它要求一个关系模式中的所有非主属性都只能依赖于候选键，而不能依赖于其他非主属性。
现在，我们来介绍一种算法实现将数据库分解至3NF。
以下是算法的步骤：步骤一：识别候选键首先，我们需要识别出关系模式的候选键（Candidate Key）。
候选键是可以唯一标识关系模式中的每个元组的属性或属性集合。
在关系模式中，可能会存在多个候选键。
步骤二：识别函数依赖接下来，我们需要分析关系模式中的属性之间的函数依赖关系。
函数依赖是指一个或多个属性的值（非主属性）决定其他属性的值（主属性）。
通过识别函数依赖，我们可以确定模式中的非主属性和主属性。
步骤三：分解关系模式在识别出候选键和函数依赖之后，我们可以开始将关系模式分解成多个子模式。
分解的目的是消除冗余和数据重复，并满足3NF的要求。
首先，我们将函数依赖中的非主属性提取出来，作为子模式的主属性。
例如，如果一个函数依赖是A->B，其中A和B都是关系模式的属性，那么我们可以将B作为一个新的子模式的主属性。
其次，我们需要考虑不同子模式之间的关系。
如果多个子模式有相同的候选键，那么它们之间应该通过外键来建立关联。
外键将一个子模式的候选键作为另一个子模式的主属性，建立起它们之间的关系。
最后，我们需要检查子模式是否满足3NF的要求。
如果出现了非平凡的传递依赖（Transitive Dependency），则需要继续分解子模式，直到达到3NF。
步骤四：验证并进行优化在算法执行结束后，我们需要验证所得到的子模式是否满足3NF要求。
无损连接和保持函数依赖的关系
无损连接和保持函数依赖的关系无损连接和保持函数依赖的关系在数据库中，无损连接和保持函数依赖是两个非常重要的概念。
它们之间存在着密切的关系，本文将会对这种关系进行详细的介绍。
1. 什么是无损连接？无损连接是指在关系型数据库中，通过将数据分解成多个关系的形式，达到减少数据冗余和提高数据的一致性的目的。
具体而言，在进行关系分解时，如果原始关系R可以分解为多个关系R1，R2，...，Rn，并且分解后的每个关系都可以通过某种方式连接起来，使其等效于原来的关系R，那么就称这种分解为无损连接。
无损连接的一个重要作用是避免数据冗余。
通过将数据分成多个关系，我们可以避免将相同的数据多次存储，从而节约存储空间。
此外，通过将数据分解为多个关系，我们还可以提高数据一致性，即当数据更新时，只需要在某个关系中进行更新，而不需要在多个关系中更新。
2. 什么是函数依赖？函数依赖是指在一个关系中，一个或多个属性的值可以唯一确定其他属性值的一种关系。
具体而言，如果在一个关系R中X和Y是两个属性集，且对于关系R的任何一个可能的实例t，当X相同时，Y的值也必须相同，那么我们称Y对于X具有函数依赖。
函数依赖的一个重要应用是在数据库设计中进行规范化。
通过对关系中的属性进行分析，我们可以确定哪些属性对于其他属性具有依赖关系，从而将一个不符合规范化要求的关系分解为多个规范化的关系。
3. 无损连接和保持函数依赖的关系无损连接和保持函数依赖是两个重要的关系。
在进行关系分解时，我们需要保证分解后的每个关系都能够保持原始关系中的所有函数依赖。
此外，通过无损连接，我们可以保证分解后的多个关系之间的数据一致性，并避免数据冗余。
具体而言，如果我们对一个关系R进行分解，得到多个关系R1，R2，...，Rn。
如果分解后的每个关系都可以通过某种方式连接起来，使其等效于原始关系R，并且分解后每个关系都能够保持原始关系中的所有函数依赖，那么我们就称这种关系分解为无损连接和保持函数依赖的关系分解。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
AB BC 所以相对与 F1 ，R分解成ρ 是无损分解。 CD
a1 a1
a2 a2
b13 a3 a3
b14 a4 a4
b31 b32
无损分解的测试方法
相对于F 2 ，Chase过程如下：
A
B
C
D
A
B
C
D
AB BC CD
a1
a2
b13 a3 a3
b14 b24 a4
b 21 a 2 b31 b32
(a)
AB BC CD
a1
a2
b13 a3 a3
b14 b24 a4
b 21 a 2 b31 b32
无损分解的测试方法
（2)把表格看成模式R的一个关系，反复检查F中每个FD在表格中是否成立， 若不成立，则修改表格中的值。修改方法如下： 对于F中一个FD X Y ，如果表格中有两行在X值上相等，在Y值上不相等， ai 那么把这两行在Y值上也改成相等的值。如果Y值中有一个是 ，那么另一 aj aj bij 个也改成 ；如果没有 ，那么用其中一个 替换另一个值（尽量把下标 ij改成较小的数）。一直到表格不能修改为止。 （3)若修改的最后一张表格中有一行全 是a，即 a1a 2 a n ，那么称ρ 相对于F 是无损分解，否则称有损分解。 A B C D
, Rk 是R的一个分解，F是R上的FD集，如果有 定义：设 R1，
那么称分解ρ 为保持函数依赖集பைடு நூலகம்。
k i=1
k i=1
π R1 F |=F ，
π R1 F |=F
k
保持函数依赖情况有：
F|=
i=1
π R1 F
k + π F R1 =F i=1
无损分解
设R是一个关系模式，F是R上的一个FD集。R分解成数 , Rk 。如果对R中满足F的每一个关系r， 据库模式 R1， 都有
R=∏R1(r) ∏R2(r) …… ∏Rk(r)
那么称ρ相对于F是“无损分解”，否则称“损失分解”。
无损分解的测试方法
An ，F是R上成立的函数依赖集， R1, 关系模式 R A 1 的一个分解。判断ρ 相对于F是否具有无损分解特征。
设关系模式R(ABCDE)，R的最小依赖集为{A→B,C→D}.从依赖集可知R的候选键ACE。
ρ={AB,CD,ACE}
+
具有无损连接性的模式分解
关系模式R<U,F>的一个分解 ρ={ R1<U1,F1>， R2<U2,F2>， …，Rn<Un,Fn>} 若R与R1、R2、…、Rn自然连接的结果相等，则称关 系模式R的这个分解ρ具有无损连接性（Lossless join）
具有无损连接性的分解保证不丢失信息 无损连接性不一定能解决插入异常、删除异常、修改复 杂、数据冗余等问题
赖的（Preserve dependency）
模式分解与模式等价问题
模 式 设 计
数据等价
无损分解
依赖等价
依赖闭包相等
例：关系模式R(ABC),ρ=AB,AC是R的一个分解。试分析分别在 F 1 ={A B},F 2 ={A C,B C},F 3 ={B A},F 4 ={C B,B A} 情况下，ρ 是否具有 无损分解和保持FD的分解特性。
保持函数依赖的模式分解
设关系模式R<U,F>被分解为若干个关系模式 R1<U1,F1>，R2<U2,F2>，…，Rn<Un,Fn> （其中U=U1∪U2∪…∪Un，且不存在Ui Uj，Fi为F 在Ui上的投影），若F所逻辑蕴含的函数依赖一定
也由分解得到的某个关系模式中的函数依赖Fi所逻
辑蕴含，则称关系模式R的这个分解是保持函数依
AB BC CD
a1
a2
b13 a3 a3
b14 a4 a4
b 21 a 2 b31 b32
(b)
此时表格(b)中没有一行是全a行，因此相对于 F2 ，R分解成ρ 是损失分解。
保持函数依赖的分解
定义：设F是属性集U上的FD集，Z是U的子集，F在Z上的投影用 z F 表示， 定义为：
z F {X Y|X Y F+ , 且XY Z}
, Rk 是R
例：设关系模式R（ABCD），R分解成 {AB, BC, CD} 。如果R上成立的函数依赖 集 F1 {B A, C D}，那么ρ 相对于F 是否无损分解？如果R上成立的函数依赖集 1 F2 {A B, C D} 呢？ （1)构建一张k行n列的表格，每 列对应一个属性 A j 1 j n ，每行 对应一个模式 R i 1 i K 。如 果 A j在 R i 中，那么在表格的第i行 第j列处填上符号 a j ，否则填上 bij。 A B C D
分解成3NF模式集既无损 又保持函数依赖的方法
① 对于关系模式R和R上成立的FD集F，先求出F的最小依赖集，然后再把最小依 赖集中那些左部相同的FD用合并性合并起来。 ② 对最小依赖集中每个FD X→Y去构成一个模式XY。 ③ 在构成的模式集中，如果每个模式都不包含R的候选键，那么把候选键作为一 个模式放入模式集中。