工程数学 圆柱坐标系与球坐标系
球形和圆柱形坐标系介绍

常用坐标系
1.球坐标系
定义:假设P 点在三维空间的位置的三个坐标是。
那么,0 ≤r是从原点到P 点的距离,0 ≤θ≤π是从原点到P 点的连线与正z-轴的夹角,0 ≤φ< 2π是从原点到P 点的连线在xy-平面的投影线,与正x-轴的夹角。
解释
假设P(x,y,z)为空间内一点,则点P也可用这样三个有次序的数(r,θ,φ)来确定,
其中:r为原点O与点P间的距离;
θ为有向线段OP与z轴正向的夹角,通常把它称之为仰角;
φ,为从正z轴来看,自x轴按逆时针方向转到OM所转过的角,这里M 为点P在xOy面上的投影,通常把它称之为方位角;
这样的三个数r,θ,φ叫做点P的球面坐标,显然,这里r,θ,φ的变化范围为r∈[0,+∞),φ∈[0, 2π],θ∈[0, π] ,
与直角坐标系间的转换
1).球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系:
X=rsinθcosφ
y=rsinθsinφ
z=rcosθ
2).反之,直角坐标系(x,y,z)与球坐标系(r,θ,φ)的转换关系为:
r=sqrt(x*2 + y*2 + z*2);
θ= arccos(z/r);
φ=arctan(y/x);
.圆柱坐标系
如图右,P 点的圆柱坐标是(ρ,φ,z)。
ρ是 P 点与 z-轴的垂直距离(相当于二维极坐标中的半径r),φ是线 OP 在xy-面的投影线与正 x-轴之间的夹角(相当于二维极坐标中的θ),z与直角坐标的z等值,即P点距x-y平面的距离。
与直角坐标系间的转换
x=ρcosφ
y=ρsinφ
z=z。
圆柱坐标系和球坐标系
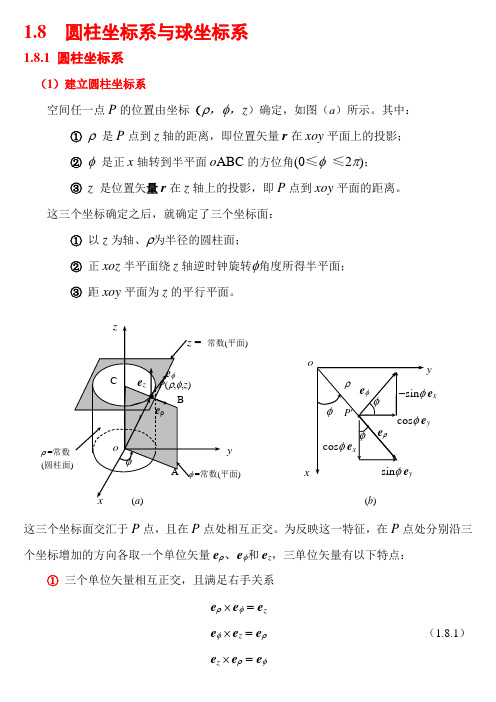
1.8 圆柱坐标系与球坐标系1.8.1 圆柱坐标系(1)建立圆柱坐标系空间任一点P 的位置由坐标(ρ,φ,z )确定,如图(a )所示。
其中:① ρ 是P 点到z 轴的距离,即位置矢量r 在xoy 平面上的投影; ② φ 是正x 轴转到半平面o ABC 的方位角(0≤φ ≤2π); ③ z 是位置矢量r 在z 轴上的投影,即P 点到xoy 平面的距离。
这三个坐标确定之后,就确定了三个坐标面:① 以z 为轴、ρ为半径的圆柱面;② 正xoz 半平面绕z 轴逆时钟旋转φ角度所得半平面; ③ 距xoy 平面为z 的平行平面。
这三个坐标面交汇于P 点,且在P 点处相互正交。
为反映这一特征,在P 点处分别沿三个坐标增加的方向各取一个单位矢量e ρ、e φ和e z ,三单位矢量有以下特点: ① 三个单位矢量相互正交,且满足右手关系e ρ ⨯ e φ = e ze φ ⨯ e z = e ρ (1.8.1) e z ⨯ e ρ = e φ(b )yxye x (平面))ρ =常数(圆柱面y② 除e z 是常矢外,e ρ和e φ 的方向都有可能随P 点的不同而变化,它们是坐标函数:yx y x e e e e e e φφφφφρcos sin sin cos +-=+=e ρ、e φ、e z 对坐标ρ、φ、z 求偏导⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫=∂∂=∂∂=∂∂=∂∂-=∂∂=∂∂=∂∂=∂∂=∂∂0000000z z z zzze ,e ,e e ,e e ,e e ,e e ,e φρφρφρφρφφρφρρ矢量F (ρ、φ、z )在圆柱坐标系下的表示式z z A A A e e e A ++=φφρρ (1.8.2)(2)线元矢量、面元和体积元当点的位置发生微小变化导致了微分位移,用线元矢量d l 表示z z e e e l d d d d ++=φρφρρ (1.8.3)三个坐标微分增量d ρ、d φ、d z 所形成的体积元d Vz V d d d d φρρ= (1.8.4)两坐标变量的微小变化将形成三个典型面元,它们的正方向分别沿坐标ρ、φ、z 的正方向(a )(b )d zd ρρd φPQ d ld zd ρρd φd zρd φd ρd s zd s ρd s φ⎪⎭⎪⎬⎫===φρρρφρφρd d d d d d d d d z S z S z S (1.8.5)(3)圆柱坐标系中的三度表达式对于连续、可微的标量场f (ρ、φ、z ),按多元函数的全微分链式法则表示微增量z zf f f f d d d d ∂∂+∂∂+∂∂=φφρρ作改写()z z z z f f f z zff f f e e e e e e d d d 1d d d d ++⋅⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂=∂∂+∂∂+∂∂=φρφρφρρφρρφφρρ对照梯度定义式 l d d ⋅∇=f f ,得圆柱坐标系下梯度和del 算符的表达式z zff f f e e e ∂∂+∂∂+∂∂=∇φρφρρ1 )0(≠ρ (1.8.6) zz ∂∂+∂∂+∂∂=∇e e e φρρφρ1 )0(≠ρ (1.8.7) 按∇与z),,(φρF 的运算还可以得出散度和旋度的表达式:0)(1)(1z),,(≠∂∂+∂∂+∂∂=⋅∇ρφρρρρφρφρzF F F zF (1.8.8)),,(z φρF ⨯∇⎥⎦⎤⎢⎣⎡∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=φρρρρφρρφρφφρF F F z F z F F z z z )(11e e ezzF F F z φρφρρφρρρ∂∂∂∂∂∂=e e e 11(1.8.9)进而可得标量场的拉普拉斯表达式0)(11z),,(z),,(222222≠∂∂+∂∂+⎪⎪⎭⎫ ⎝⎛∂∂∂∂=∇⋅∇=∇ρφρρρρρφρφρzff f f f (1.8.10)例1-6 已知z z z e e F -=φρρ),(,试就z =1平面上半径为2的圆形回路及其所围区域,验证斯托克斯定理。
圆柱,圆球坐标系
1 ∂ 1 ∂Fφ ∂Fz ∇ ⋅ F (ρ ,φ ,z) = (ρ Fρ ) + + ρ ∂ρ ρ ∂φ ∂z
1
ρ
eρ
eφ ∂ ∂φ ρ Fφ
1
ρ
ez
∇ × F (ρ ,φ ,z )
=
∂ ∂ρ Fρ
∂ ∂z Fz
1.8 圆柱坐标系与球坐标系
CQU
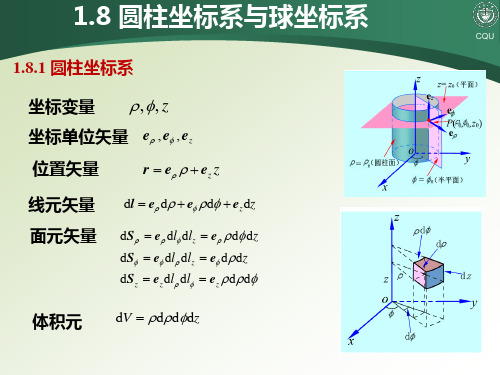
1.8.2 球面坐标系 坐标变量
r ,θ , φ
坐标单位矢量 er , eθ , eφ 位置矢量 线元矢量 面元矢量
= 0, ∂ρ ∂e z = 0, ∂ρ
= −eρ , ∂φ ∂e z = 0, ∂φ
1.8 圆柱坐标系与球坐标系
CQU
圆柱坐标系中的三度表达式
∇ = eρ
∇f =
∂ 1 ∂ ∂ + eφ + ez ∂ρ ρ ∂φ ∂z
∂f 1 ∂f ∂f eρ + eφ + ez ∂ρ ρ ∂φ ∂z
(ρ ≠ 0)
e ρ = cos φ e x + sin φ e y eφ = −sin φ e x + cosφ e y
∂e ρ ∂ρ ∂eφ = 0, ∂e ρ ∂φ ∂eϕ = eφ , =0 ∂z ∂eφ = 0 ∂z ∂e z =0 ∂z ∂e ρ
eρ、eφ、ez对坐标ρ、φ、z求偏导 求偏导
1.8 圆柱坐标系与球坐标系
1.8.1 圆柱坐标系 坐标变量
1
CQU
ρ ,φ , z
r = eρ ρ + ez z
dl = eρ dρ + eφ ρ dφ + e z dz
坐标单位矢量 eρ , eφ , e z 位置矢量 线元矢量 面元矢量
数学课件:1.5 柱坐标系和球坐标系

������ = ������.
题型一 题型二 题型三 题型四 题型五
正解∵r= ������2 + ������2 + ������2 = 12 + 12 + ( 2)2 = 2,
z=rcos φ= 2, ∴ cos ������ = 22.
(2)(π,π,π).
解:设点的直角坐标为(x,y,z).
(1)∵(ρ,θ,z)=(2,0,-2), ������ = 2cos0 = 2,
12
2.球坐标系 (1)定义:设空间中一点 M 的直角坐标为(x,y,z),点 M 在 xOy 坐标
面上的投影点为 M0,连接 OM 和 OM0.如图所示,设 z 轴的正向与向量
������������的夹角为������, ������轴的正向与������������0的夹角为������, ������点到原点������的距离 为������, 则由三个数������, ������, ������构成的有序数组 ������, ������, ������ 称为空间中点������的球
A.
2
2,
π 6
,
3π 4
C.
2
2,
π 3
,
π 4
B.
2
2,
π 6
,
π 4
D.
2
2,
π 3
,
3π 4
解析:设 M 的球坐标为(r,θ,φ),
3 = ������sin������cos������, 则 1 = ������sin������sin������,
圆柱坐标系与球坐标系的使用

圆柱坐标系与球坐标系的使用1. 引言在数学和物理学中,我们经常会遇到需要描述三维空间中点的位置的问题。
为了更方便地描述这些点,人们引入了不同的坐标系。
在这篇文档中,我们将会介绍圆柱坐标系和球坐标系,并探讨它们的使用方法和特性。
2. 圆柱坐标系2.1 定义圆柱坐标系是一种二维坐标系,它由一个平面和一个直线上的点组成。
圆柱坐标系使用以下三个坐标来描述一个点的位置: - r:点到坐标系原点的距离(半径)。
- θ:点在平面上的极角,用弧度表示,通常取值范围为[0, 2π)。
- z:点到平面的垂直距离。
2.2 二维平面转换圆柱坐标系可以通过以下公式与直角坐标系(笛卡尔坐标系)相互转换:x = r * cos(θ)y = r * sin(θ)z = z其中,θ是弧度制的极角。
这些公式使得我们可以在不同坐标系间进行转换。
2.3 三维空间转换要在三维空间中描述一个点的位置,我们可以将圆柱坐标系的极坐标(r,θ)和直角坐标系的z坐标组合起来:x = r * cos(θ)y = r * sin(θ)z = z这种转换使得我们可以在三维空间中更方便地描述点的位置。
3. 球坐标系3.1 定义球坐标系是一种三维坐标系,用于描述点在三维空间中的位置。
球坐标系使用以下三个坐标来描述一个点的位置: - r:点到坐标系原点的距离(径向距离)。
-θ:点在平面上的极角,用弧度表示,通常取值范围为[0, π]。
- φ:点与正z轴的夹角,用弧度表示,通常取值范围为[0, 2π)。
3.2 三维空间转换球坐标系可以通过以下公式与直角坐标系相互转换:x = r * sin(θ) * cos(φ)y = r * sin(θ) * sin(φ)z = r * cos(θ)这些公式使得我们可以在不同坐标系间进行转换,并在三维空间中描述点的位置。
4. 应用场景圆柱坐标系和球坐标系在物理学、工程学和计算机图形学中有很多应用。
其中一些应用包括: - 物理学中的电荷分布和电场计算; - 机械工程中的摆动运动和旋转机构的描述; - 三维计算机图形学中的场景渲染和动画效果。
球面坐标系和柱面坐标系的定义及其应用

球面坐标系和柱面坐标系的定义及其应用球面坐标系和柱面坐标系是数学中关键的方法,经常用来描述和解决一些几何和物理问题,它们与直角坐标系、极坐标系一样,是一种坐标系的表示方式。
一、球面坐标系球面坐标系是以球面为基础的坐标系,它是由半径、极角和方位角确定的。
坐标轴上的点对应着球面上的一个点,可以用三个参数(r、θ、φ)来描述它的位置。
其中,r是从坐标原点到球面上某一点的距离,是一个实数;θ是竖直方向的极角,它的范围在0到π之间;φ是水平方向的方位角,它的范围在0到2π之间。
坐标系的原点是球心,竖直方向的坐标轴是与地球赤道垂直的轴线,水平方向的坐标轴则是经过原点和北极点的轴线。
球面坐标系在物理学和天文学等领域应用广泛,例如测量地球上某一点的纬度和经度、描述电磁场的分布等。
二、柱面坐标系柱面坐标系是一种由高度、半径和角度确定的坐标系,它通常用来描述长方形坐标系缺陷的问题。
柱面坐标系可以是圆柱面坐标系或斜柱面坐标系,但都表示同样的信息。
在圆柱坐标系中,一点的坐标为(r,θ,z),其中r表示离坐标轴的距离,θ表示与x轴的夹角,z表示高度。
而在斜柱面坐标系中,一点的坐标为(r,θ,z'),其中r和θ用同样的方式表示,z'是某个平面内的高度。
只有当某一平面中的z'为零时,斜柱面坐标系才与圆柱坐标系相同。
类似于球面坐标系的应用,圆柱坐标系和斜柱坐标系在物理学、工程学和计算机图形学等领域中有广泛的应用。
例如在计算机图形学中,柱面坐标系被用来描述某些对象的形状和运动,在计算机辅助设计(CAD)中,也被用来表示机械元件的三维空间位置。
总的来说,球面坐标系和柱面坐标系是一组非常实用的工具,它们有助于我们更好地理解和描述现实世界中的各种问题。
了解和掌握这些坐标系的基础和应用,有助于我们更好地应用它们来解决实际问题。
柱坐标系与球坐标系PPT教学课件

#思想核心: 大一统(“新”所在)
天人感应
“天子受命于天,天下受命于天子”;“古之造文者,三画 连其中,谓之王,三画者,天地人,而连其中,通其道也, 谓之王。”
董仲舒认为道源于天。“天不变,道亦不变。” “天道”就是“三纲五常三”纲:君为臣纲,父为子纲,夫为妻纲
五常:仁、义、礼、智、信
崇
“有为”而治。
独 尊 儒 术
罢黜百家 独尊儒术
董仲舒: 中国古代著名的思想家。 (前179——前104年)广
川人(今河北景县人)向 汉武帝提出“罢黜百家 独尊儒术”的主张,创立 新儒学。
2、董仲舒的新儒学的思想内涵
#思想来源: 以《公羊春秋》为骨干, 融合阴阳家,黄老之学 以及法家思想而形成的 新的思想体系。
坐标系. 有序数组(ρ,θ,Z)叫点P的柱
坐标,记作(ρ,θ,Z). 其中
ρ≥0, 0≤θ< 2π, -∞<Z<+∞
柱坐标系又称半极坐标系,它是由 平面极坐标系及空间直角坐标系中的 一部分建立起来的.
空间点P的直角坐标(x, y, z)与柱坐
标 (ρ,θ,Z) 之间的变换公式为
x cos
y
• 兴办学校,有利于教 育的发展。
• 确立了儒学在中国的 统治地位。
总结
原 西汉初年,
因
经济残败 百业待兴。
无为不适应集权
原 新儒学的大一统 因 统治者的有为愿望
黄
老 内 治身、治国 之 容 无为而无不为 学
独
尊
内 容
天人感应 实行仁政
儒
术
作 经济恢复 用 国力增强
作 巩固国家统一
用
限制君主权利 儒学独尊地位
柱坐标系和球坐标系 课件

z=5,
∴(1,1,5)为所求.
点(r,θ,z)是三维空间坐标系中的点的坐标,在平面 xOy
内实际为极坐标系,且 r≥0,0≤θ<2π,在竖直方向上,z 为
任意实数.化点的柱坐标(r,θ,z)为直角坐标(x,y,z),需
要运用公式yx==rrscions θθ z=z
转化为三角函数的求值与运算即得.
∴(-1,-1,- 2)为所求.
首先要明确点的球坐标(r,φ,θ)中角 φ,θ 的边与数轴 Oz,Ox 的关系,注意各自的限定范围,即 0≤φ≤π,0≤θ <2π.
化点的球坐标(r,φ,θ)为直角坐标(x,y,z),需要运用
公式yx==rrssiinn
φcos φsin
θ, θ,
z=rcos φ
转化为三角函数的求值与1,建立空间直角坐标系 O-xyz.设 M(x,y, z)为空间一点,并设点 M 在 xOy 平面上的投影点 P 的极坐标 为(r,θ),则这样的三个数 r,θ,z 构成的有序数组(r,θ,z) 就叫作点 M 的 柱坐标 ,这里规定 r,θ,z 的变化范围为 0≤r <+∞,0≤θ<2π,-∞<z<+∞.
图 1-3-1
特别地, r=常数,表示的是以 z 轴为轴的圆柱面; θ=常数,表示的是过 z 轴的半平面; z=常数,表示的是与 xOy 平面平行的平面.
2.球坐标系 设 M(x,y,z)为空间一点,点 M 可用这样三个有次序的 数 r,φ,θ 来确定,其中 r 为原点 O 到点 M 间的距离,φ 为
2.在空间的柱坐标系中,方程 r=r0(r0 为不等于 0 的常 数),θ=θ0,z=z0 分别表示什么图形?
【提示】 在空间的柱坐标系 中,方程 r=r0 表示中心轴为 z 轴,底 半径为 r0 的圆柱面,它是上述圆周沿 z 轴方向平行移动而成的.方程 θ=θ0 表示与 zOx 坐标面成 θ0 角的半平 面.方程 z=z0 表示平行于 xOy 坐标面 的平面,如图所示.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.8.1 圆柱坐标系 坐标变量
1
CQU
ρ ,φ , z
r = eρ ρ + ez z
dl = eρ dρ + eφ ρ dφ + e z dz
坐标单位矢量 eρ , eφ , e z 位置矢量 线元矢量 面元矢量
dS ρ = eρ dlφ dlz = eρ ρ dφ dz dSφ = eφ dlρ dlz = eφ dρ dz dS z = e z dlρ dlφ = e z ρ dρ dφ
1.8 圆柱坐标系与球坐标系
CQU
三单位矢量e 有以下特点: 三单位矢量 ρ、eφ和ez有以下特点
三个单位矢量相互正交,且满足右手关系, 三个单位矢量相互正交,且满足右手关系,即 er× eθ= eφ; eθ× eφ = er ; eφ × er = er ∂ 1 ∂ 1 ∂ + eθ + eφ ∂r r ∂θ rsinθ ∂φ
= 0, ∂ρ ∂e z = 0, ∂ρ
= −eρ , ∂φ ∂e z = 0, ∂φ
1.8 圆柱坐标系与球坐标系
CQU
圆柱坐标系中的三度表达式
∇ = eρ
∇f =
∂ 1 ∂ ∂ + eφ + ez ∂ρ ρ ∂φ ∂z
∂f 1 ∂f ∂f eρ + eφ + ez ∂ρ ρ ∂φ ∂z
(ρ ≠ 0)
r = er r
dl = er dr + eθ rdθ + eφ rsinθ dφ
dSr = er dlθ dlφ = er r 2 sinθ dθ dφ
dSθ = eθ dlr dlφ = e z rsinθ drdφ dSφ = eφ dlr dlθ = eφ rdrdθ
体积元
dV = r 2 sinθ drdθ dφ
本章小结 本章小结
CQU
1、场的概念 标量场和矢量场的概念, 标量场和矢量场的概念,矢量场的分类以及每类矢量场的基本 特征。 特征。 2、场的三度计算 标量场的梯度 ∇f 、矢量场的散度 ∇ ⋅ F 和旋度 ∇ × F ; 要求牢记▽算符的矢量特性和微分特性; 要求牢记▽算符的矢量特性和微分特性; 牢固掌握在直角坐标系下的三度计算式,实施正确计算; 牢固掌握在直角坐标系下的三度计算式,实施正确计算; 在其它坐标系下,给定三度的计算式后, 计算场 在其它坐标系下,给定三度的计算式后,会计算场。 三度的计算式后 3、要会进行场的高阶计算 要做到此项,必须牢记矢量的点积、叉积,重要的矢量恒等式。 要做到此项,必须牢记矢量的点积、叉积,重要的矢量恒等式。 4、正确理解高斯散度定理和斯托克斯定理、正确认识赫姆 正确理解高斯散度定理和斯托克斯定理、 霍兹定理。 霍兹定理。
∇⋅F =
1 ∂ 2 1 ∂ 1 ∂Fφ (r Fr ) + (sinθ Fθ ) + r 2 ∂r rsinθ ∂θ r sinθ ∂φ
1 er 1 eθ rsinθ ∂ ∂θ rFθ 1 eφ r ∂ ∂φ rsinθ Fφ (r ≠ 0)
(r ≠ 0)
r 2sinθ ∂ ∇× F = ∂r Fr
1 ∂ 1 ∂Fφ ∂Fz ∇ ⋅ F (ρ ,φ ,z) = (ρ Fρ ) + + ρ ∂ρ ρ ∂φ ∂z
1
ρ
eρ
eφ ∂ ∂φ ρ Fφ
1
ρ
ez
∇ × F (ρ ,φ ,z )
=
∂ ∂ρ Fρ
∂ ∂z Fz
1.8 圆柱坐标系与球坐标系
CQU
1.8.2 球面坐标系 坐标变量
r ,θ , φ
坐标单位矢量 er , eθ , eφ 位置矢量 线元矢量 面元矢量
e ρ = cos φ e x + sin φ e y eφ = −sin φ e x + cosφ e y
∂e ρ ∂ρ ∂eφ = 0, ∂e ρ ∂φ ∂eϕ = eφ , =0 ∂z ∂eφ = 0 ∂z ∂e z =0 ∂z ∂e ρ
eρ、eφ、ez对坐标ρ、φ、z求偏导 求偏导
体积元
dV = ρ dρ dφ dz
1.8 圆柱坐标系与球坐标系
CQU
三单位矢量e 有以下特点: 三单位矢量 ρ、eφ和ez有以下特点
三个单位矢量相互正交, ① 三个单位矢量相互正交,且满足右手关系 eρ × e φ = e z e φ × ez = eρ e z × eρ = e φ ② 除ez是常矢外,eρ和eφ 的方向都有可能随 点的不同 是常矢外, 的方向都有可能随P点的不同 而变化,它们是坐标函数: 而变化,它们是坐标函数
