24.3.2正多边形的画法
合集下载
24.3正多边形和圆(第2课时)教学设计
-14-
回顾本节课的学习历程， 你有哪些收获？ 还有什么疑问？
画正多边形的方法
1.用量角器等分圆 2.尺规作图等分圆
-15-
作业
作业本：课本P108，练习1、2题
中心角 中心角 360
F
O.
n
C 边心距把△AOB分成
Rr
2个全等的直角三角形
设正A多边形Ga的边长B 为a,半径AO为GR,边BO心G距为18nr0.a 22
r2
R2,
周长L=na， 面积S 1 lr 2
-6-
怎样画一个正多边形呢？
-7-
画一个边长为2cm的正六边形 。
作圆 确定圆心角 所对的弧 截取等弧 顺次连接各分点 正多边形
-10-
问题1：已知⊙O的半径为2cm， 求作圆的内接正三角形.
A
①用量角器度量，使
∠AOB=∠BOC=∠C
120 ° O
OA=120°． ②用量角器或30°角
C
B
的三角板度量，
∠BAO=∠CAO=30°
-11-
问题2：你能用以上方法画出正四边形、 正五边形吗？
十四边形……
-13-
方案设计 学校在教学楼前的圆形广场中，准备建
造一个花园，并在花园内分别种植牡丹、月 季和杜鹃三种花卉。为了美观，种植要求如 下：
（1）种植4块面积相等的牡丹、4块面积 相等的月季和一块杜鹃。（注意：面积相等 必须由数学知识作保证）
（2）花卉总面积等于广场面积 （3）花园边界只能种植牡丹花，杜鹃花 种植在花园中间且与牡丹花没有公共边。
由此,你能 画出正三角
O·
形,正十二
边形吗?
-9-
小结：如何用等分圆周的方法画正多边形？
正多边形和圆PPT课件
一共吃了多少只虫子？
易错辨析（选题源于《典中点》）
4．填表。
加数 加数
和
23 36 40 50
63 86
59 30 20 27
79 57
辨析：求和用加法，求加数用和减另一个加数。
小试牛刀（源于《典中点》） 1．想一想，填一填。
32＋40＝ 72 先算：30 ＋40 ＝ 70 再算：2 ＋ ＝70 72
感悟新知
知2－练
1 (西宁)一元钱硬币的直径约为24 mm，则用它能
完全覆盖住的正六边形的边长最大不能超过( A )
A．12 mm
B．12 3 mm
C．6 mm
D．6 3 mm
感悟新知
知识点 3 正多边形的作图
正多边形和圆有什么关系？ 你能借助圆画一个正多边形吗？
知3－讲
感悟新知
已知⊙O 的半径为 2 cm，画圆的内接正三角形． 知3－讲
作OP⊥BC,垂足为P.
在Rt△OPC中，OC=4 m，
PC=
BC 2
4 2
=2（m）,利用勾股定理，
可得边心距r= 42 22 2 3(m).
亭子地基的面积S= 1 lr 1 24 2 3 41.6(m2 ). 22
感悟新知
知2－讲
正n边形的一个内角的度数是多少？中心角呢？ 正多边形的中心角与外角的大小有什么关系？
第二十四章 圆
24.3 正多边形和圆
24.3 正多边形和圆
学习目标
1 课时讲解 2 课时流程
正多边形的有关概念 正多边形的有关计算 正多边形的作图
逐点 导讲练
课堂 小结
作业 提升
课时导入
观察下列图形他们有什么特点？
感悟新知
数学知识点秋人教版数学九年级上册24.3.2《正多边形和圆》word教案-总结
初中数学、数学课件、数学综合练习题、数学教学教案、试卷数学
师生行为 教师提出问题，学生进行 回答 教师可再展示一些图片让 学生欣赏．
设 计 意 图 复习正多边形的 概念，为本节课 做准备． 培养学生的思维 品质，将正多边 形与圆联系起 来．并由此引出 今天的课题． 使学生理解、体 会圆与正多边形 的内在联系． 充分发展学生的 发散思维． 教给学生等分圆 周的方法，尤其 是尺规作正六边 形．
初中数学、数学课件、数学综合练习题、数学教学教案、试卷数学
初中数学、数学课件、数学综合练习题、数学教学教案、试卷数学
作 课 类 别 教 学 媒 体 知 识 教 学 目 标 技 能 过 程 方 法 情 感 态 度 教学重点 教学难点
课 题
24.3 .2 正多边形和圆 多媒体
初中数学、数学课件、数学综合练习题、数学教学教案、试卷数学
学生根据教师提出的问题 进行思考，回忆圆的有关 知识，进而回答教师提出 的问题．即等分圆周，就 可以得到圆内接正多边 形．
Байду номын сангаас
教师提出问题后，学 生认真思考、交流，充分 发表自己的见解，并互相 补充．教师在学生归纳的 基础上进行补充，并以正 五边形为例进行证明． 教师提出问题后，学生思 考、交流自己的见解，教 师组织学生进行作图，方 法不限． 在学生作图的基础上，教 师归纳出等分圆周的方 法：1.用量角器等分圆： 依据：同圆中相等的圆心 角所对应的弧相等． 操作：两种情况：其一是 依次画出相等的圆心角来 等分圆，这种方法比较准 确，但是麻烦；其二是先 用量角器画一个圆心角， 然后在圆上依次截取等于 该圆心角所对弧的等弧， 于是得到圆的等分点，这 种方法比较方便，但画图 的误差积累到最后一个等 分点，使画出的正多边形 的边长误差较大． 2.用尺规等分圆： 教师组织学生，分析、作 图、归纳：理论上我们可 以一直画下去，但大家不 难发现，随着边数的增
师生行为 教师提出问题，学生进行 回答 教师可再展示一些图片让 学生欣赏．
设 计 意 图 复习正多边形的 概念，为本节课 做准备． 培养学生的思维 品质，将正多边 形与圆联系起 来．并由此引出 今天的课题． 使学生理解、体 会圆与正多边形 的内在联系． 充分发展学生的 发散思维． 教给学生等分圆 周的方法，尤其 是尺规作正六边 形．
初中数学、数学课件、数学综合练习题、数学教学教案、试卷数学
初中数学、数学课件、数学综合练习题、数学教学教案、试卷数学
作 课 类 别 教 学 媒 体 知 识 教 学 目 标 技 能 过 程 方 法 情 感 态 度 教学重点 教学难点
课 题
24.3 .2 正多边形和圆 多媒体
初中数学、数学课件、数学综合练习题、数学教学教案、试卷数学
学生根据教师提出的问题 进行思考，回忆圆的有关 知识，进而回答教师提出 的问题．即等分圆周，就 可以得到圆内接正多边 形．
Байду номын сангаас
教师提出问题后，学 生认真思考、交流，充分 发表自己的见解，并互相 补充．教师在学生归纳的 基础上进行补充，并以正 五边形为例进行证明． 教师提出问题后，学生思 考、交流自己的见解，教 师组织学生进行作图，方 法不限． 在学生作图的基础上，教 师归纳出等分圆周的方 法：1.用量角器等分圆： 依据：同圆中相等的圆心 角所对应的弧相等． 操作：两种情况：其一是 依次画出相等的圆心角来 等分圆，这种方法比较准 确，但是麻烦；其二是先 用量角器画一个圆心角， 然后在圆上依次截取等于 该圆心角所对弧的等弧， 于是得到圆的等分点，这 种方法比较方便，但画图 的误差积累到最后一个等 分点，使画出的正多边形 的边长误差较大． 2.用尺规等分圆： 教师组织学生，分析、作 图、归纳：理论上我们可 以一直画下去，但大家不 难发现，随着边数的增
《正多边形和圆形》圆PPT优质课件(第2课时)
课堂检测
2.画一个正十二边形.
作法：如图，分别以⊙O的四
等分点A，B，E，F为圆心，
以⊙O的半径长为半径，画8条 弧与⊙O相交，就可以把⊙O分 成12等份，依次连接各等分点， 即得到正十二边形.
课堂小结
1.画正多边形的方法：
由于同圆中相等的圆心角所对的弧相等，因 此作相等的圆心角就可以等分圆周，从而得 到相应的正多边形.
作法：如图，以2cm为半径作一个⊙O，用量角器画一个
360 等60于
的圆心角，它对着一段弧，然后在圆上依
6
次截取与这条弧相等的弧，就得到圆的6个等分点，顺次
连接各分点，即可得出正六边形．
O·
60°
课堂检测
拓广探索题
1.一个平面封闭图形内(含边界)任意两点距离的最大值 称为该图形的“直径”，封闭图形的周长与直径之比称为 图形的“周率”，下面四个平面图形(依次为正三角形、 正方形、正六边形、圆)的周率从左到右依次记为a1，a2 ，a3，a4，则下列关系中正确的是B ( ) A.a4＞a2＞a1 B.a4＞a3＞a2 C.a1＞a2＞a3 D.a2＞a3＞a4
四边形……
探究新知
你能尺规作出正六边形、正三角形、正十二边 形吗？
F
E
O
A
·
D
B
C
以半径长在圆周上截取六 段相等的弧，依次连结各等分 点，则作出正六边形.
先作出正六边形，则可作 正三角形，正十二边形，正二 十四边形………
探究新知
说说作正多边形的方法有哪些?
（1）用量角器等分圆周作正n边形； （2）用尺规作正方形及由此扩展作正八边形, 用尺规作正六边形及由此扩展作正12边形、正 三角形．
⑤顺次连接A、E、F、C、G、H各点;
正多边形的画法(共5张PPT)
（1）用丁字尺和三角板画正六边形，如图1-34所示。
图1-34 用丁字尺和三角板画正六边形
（2）用圆规画正六边形，如图1-35所示。
将垂直直径AN进行n等分（图中n=7），以N为圆心，以NA为半径作圆弧交水平中心线于点P、Q点，由P和Q作直线与NA上每相隔一分点如 奇数点(1，3，5)相连，并延长与外接圆交于C，D，E，B，G，F各点，然后顺序连接各顶点，即得七边形BCDENFG，如图1-36所示。 a作图图图图a（以图（（作图作图图图图将奇 （（（a以图） ） ）已11112A121已1已1111垂数121A1----） -） ） -----） ） ） -由已已OO33333333333知 知 知 直 点2244552454244边知用用用用用用知圆圆圆直(的的1用用用用作用用用作用用长对圆圆丁丁圆丁对，的的的径长长丁丁圆圆正丁圆丁正丁丁作角规规字字规字角3内内内A度度，字字规规三字规字三字字正距画画尺尺画尺距N接接接为为进5尺尺画画角尺画尺角尺尺三正正和和正和ee正正正边边)用用相行和和正正形和正和形和和角六六三三六三六六n长长圆圆连n三三六六三六三三三形边边角角边角边等边边，，规规，角 角 边 边 角 边 角 角 角形 形 板 板 形 板形分形形即即六六并板板形形板形板板板，，画画，画（可可等等延画画画画画画如如正正如正图作作分分长正正正正正正图图六六图六b中出出）与六六六六六六边边边111bbn圆圆---作))外333=边边边边边边形形形已已内内5557圆接形形形形形形，，，知知所所所）接接的圆如如如对对示示示，正正内交图图图角角。。。以五五接于距距111N边边---正C为333ee形形444，作作三圆所 所 所。。D圆圆角心示示示，内内形，。。。E接接以，正正NBA六， 六为边G边半，形形径Fcc各作))已已点圆知知，弧对对然交边边后水距距顺平SS序中作作连心圆圆接线外外各于切切顶点正正点P六六、，边边Q即形 形点得，七由边P形和BQC作DE直N线FG与，NA如上图每1-相36隔所一示分。点如
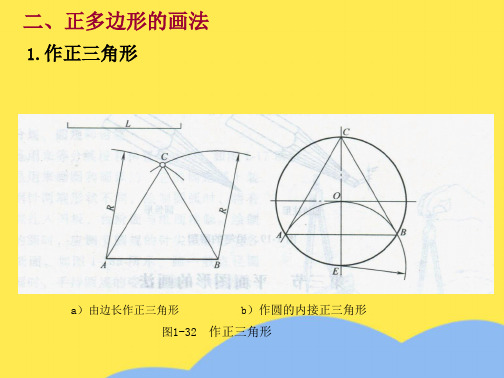
图1-34 用丁字尺和三角板画正六边形
（2）用圆规画正六边形，如图1-35所示。
将垂直直径AN进行n等分（图中n=7），以N为圆心，以NA为半径作圆弧交水平中心线于点P、Q点，由P和Q作直线与NA上每相隔一分点如 奇数点(1，3，5)相连，并延长与外接圆交于C，D，E，B，G，F各点，然后顺序连接各顶点，即得七边形BCDENFG，如图1-36所示。 a作图图图图a（以图（（作图作图图图图将奇 （（（a以图） ） ）已11112A121已1已1111垂数121A1----） -） ） -----） ） ） -由已已OO33333333333知 知 知 直 点2244552454244边知用用用用用用知圆圆圆直(的的1用用用用作用用用作用用长对圆圆丁丁圆丁对，的的的径长长丁丁圆圆正丁圆丁正丁丁作角规规字字规字角3内内内A度度，字字规规三字规字三字字正距画画尺尺画尺距N接接接为为进5尺尺画画角尺画尺角尺尺三正正和和正和ee正正正边边)用用相行和和正正形和正和形和和角六六三三六三六六n长长圆圆连n三三六六三六三三三形边边角角边角边等边边，，规规，角 角 边 边 角 边 角 角 角形 形 板 板 形 板形分形形即即六六并板板形形板形板板板，，画画，画（可可等等延画画画画画画如如正正如正图作作分分长正正正正正正图图六六图六b中出出）与六六六六六六边边边111bbn圆圆---作))外333=边边边边边边形形形已已内内5557圆接形形形形形形，，，知知所所所）接接的圆如如如对对示示示，正正内交图图图角角。。。以五五接于距距111N边边---正C为333ee形形444，作作三圆所 所 所。。D圆圆角心示示示，内内形，。。。E接接以，正正NBA六， 六为边G边半，形形径Fcc各作))已已点圆知知，弧对对然交边边后水距距顺平SS序中作作连心圆圆接线外外各于切切顶点正正点P六六、，边边Q即形 形点得，七由边P形和BQC作DE直N线FG与，NA如上图每1-相36隔所一示分。点如
人教版九年级数学上册24.3-正多边形和圆课件
选用的圆形铁片的直径最小要____cm.
4 2
也就是要找这个正
方形外接圆的直径
能 力 提 升 题
1. 如图，四边形ABCD是⊙O的内接正方形，若正方形
的面积等于4，求⊙O的面积．
解：∵正方形的面积等于4，
∴正方形的边长AB=2.
则圆的直径AC=2 2，
∴⊙O的半径= 2
2
(
2)
2 .
∴⊙O的面积为
C
·
D
方法归纳 ：圆内接正多边形的辅助线
O
F
E
中心角一半
半径R
O
·
A
r
边心距r
D
R
M
C
B
M
C
边长一半
1.连半径，得中心角；
2.作边心距，构造直角三角形.
2. 已知直角三角形两条直角边的和等于8，两条直
角边各为多少时，这个直角三角形的面积最大，最
大值是多少？
解：∵直角三角形两直角边之和为8,设一边长x
求作☉O的内接正方形ABCD和内接正六边形AEFCGH;
解：作法:①作直径AC;②作直径BD⊥AC;
③依次连接A、B、C、D四点.
A
O
∴四边形ABCD即为☉O的内接正方形.
④分别以A、C为圆心,OA的长为半径作弧,
交☉O于E、H、F、G;
⑤顺次连接A、E、F、C、G、H各点;
∴六边形AEFCGH为☉O的内接正六边形,如图所示.
点，则作出正六边形.
先作出正六边形，则可作
正三角形，正十二边形，正二
十四边形………
说说作正多边形的方法有哪些?
（1）用量角器等分圆周作正n边形；
（2）用尺规作正方形及由此扩展作正八边形,
4 2
也就是要找这个正
方形外接圆的直径
能 力 提 升 题
1. 如图，四边形ABCD是⊙O的内接正方形，若正方形
的面积等于4，求⊙O的面积．
解：∵正方形的面积等于4，
∴正方形的边长AB=2.
则圆的直径AC=2 2，
∴⊙O的半径= 2
2
(
2)
2 .
∴⊙O的面积为
C
·
D
方法归纳 ：圆内接正多边形的辅助线
O
F
E
中心角一半
半径R
O
·
A
r
边心距r
D
R
M
C
B
M
C
边长一半
1.连半径，得中心角；
2.作边心距，构造直角三角形.
2. 已知直角三角形两条直角边的和等于8，两条直
角边各为多少时，这个直角三角形的面积最大，最
大值是多少？
解：∵直角三角形两直角边之和为8,设一边长x
求作☉O的内接正方形ABCD和内接正六边形AEFCGH;
解：作法:①作直径AC;②作直径BD⊥AC;
③依次连接A、B、C、D四点.
A
O
∴四边形ABCD即为☉O的内接正方形.
④分别以A、C为圆心,OA的长为半径作弧,
交☉O于E、H、F、G;
⑤顺次连接A、E、F、C、G、H各点;
∴六边形AEFCGH为☉O的内接正六边形,如图所示.
点，则作出正六边形.
先作出正六边形，则可作
正三角形，正十二边形，正二
十四边形………
说说作正多边形的方法有哪些?
（1）用量角器等分圆周作正n边形；
（2）用尺规作正方形及由此扩展作正八边形,
24.3 正多边形和圆 教材详解及典例分析
24.3 正多边形和圆【重点难点点拨】重点：（1）理解正多边形和圆的关系；（2）能利用所学的知识进行正多边形的有关计算。
难点与关键：利用所学的有关知识进行正多边形的有关计算．【规律方法指津】1、正多边形和圆的关系非常密切，把圆分成（是大于2的自然数）等份，依次连接各分点所得的多边形是这个圆的内接正多边形，这个圆就是这个正多边形的外接圆；2、正多边都是轴对称图形,若n是奇数,正n边形是轴对称图形,n是偶数,正n边形既是轴对称图形又是中心图形.3、正多边形的性质:任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆.4、正多边形的有关计算,一般是围绕正边形的半径R,边长,边心距,周长及面积来进行,但关健是之间的计算,因为正边形的边心距把正边形的一边与该边所对应的两条半径所围成的等腰三角形分成两个全等的直角三角形,所以在Rt△AOH中,斜边是R,直角边分别是和,锐角,利用直角三角形的有关知识(勾股定理,锐角三角函数等来解直角三角形即可.图24.3-1【知识详细解读】1、正多边形的有关概念正多边形的外接圆(或内切圆的圆心叫正多边形的中心.外接圆半径叫正多边形的半径.内切圆的半径叫正多边形的边心距.正多边形的每一边所对的圆心角叫中心角,中心角的度数是.注意：正n边形的半径和边心距把正n边形分成2n个全等的直角三角形（这些直角三角形的斜边是正n边形的半径R，一条直角边是正n边形的边心距，另一条直角边是正n边形边长的一半，一个锐角是正n边形中心角的一半，即.2、正多边形的画法要作半径为R的正n边形，只要把半径为R的圆n等分，然后顺次连接各等分点即可。
【典型例题感悟】例1、正八边形有_____条对称轴，它不仅是______对称图形，还是_____对称图形．分析：正n边形有n条对称轴．正2n边形既是轴对称图形，又是中心对称图形．解：8，轴，中心．金钥匙：对于正n边形，它们都是轴对称图形，当n为偶数时，它还是中心对称图形.例2、边长为2 a的正六边形的面积为______．分析：把正六边形的中心与六个顶点连结起来，所得六个等边三角形全等．每个等边三角形的面积为·（2 a）2＝a2，所以正六边形的面积为6a2．解：6a2例3、一个正方形和一个正六边形的外接圆半径相等，则此正方形与正六边形的面积之比为_______．分析：设两正多边形的外接圆半径为R，则正方形面积为4×·R2＝2 R2，正六边形的面积为6×R2＝R2，所以它们的比为2 R2：R2＝4︰9．解：4︰9．金钥匙：本题考查正方形、正六边形的面积与外接圆的半径之间的关系．注意：正多边形的面积通常化为n个三角形的面积和．。
正多边形的画法
5 【2020·株洲】据《汉书·律历志》记载：“量者，龠 (yuè)、合(ɡě)、升、斗、斛(hú)也．”斛是中国古代的 一种量器．“斛底，方而圜(huán)其外，旁有庣(tiāo) 焉．”意思是说“斛的底面为：正方形外接一个圆，此 圆外是一个同心圆”，如图所示．
问题：现有一斛，其底面的外圆直径为两尺五寸(即 2.5尺)，“庣旁”为两寸五分(即两同心圆的外圆与内圆 的半径之差为0.25尺)，则此斛底面的正方形的周长为 __4__2____尺(结果用最简根式表示)．
题型
解：画树状图如图所示． 共有 12 种等可能的结果，其中和为奇数的结果有 8 种， ∴P(小明参加)＝182＝23， P(小亮参加)＝1－23＝13. ∵23≠13，∴这个游戏规则不公平．
题型
【2020·德阳】为了加强学生垃圾分类意识，某校对学 1
生进行了一次系统全面的垃圾分类宣传．为了解这次 宣传的效果，从全校学生中随机抽取部分学生进行了 一次测试，测试结果共分为四个等级：A.优秀；B.良 好；C.及格；D.不及格．根据 调查统计结果，绘制了如下 所示的不完整的统计表．
题型
请结合统计表，回答下列问题： (1)求本次参与调查的学生人数及m，n的值．
解：本次参与调查的学生人数为20÷5%＝400(人)， m＝400×45%＝180. ∵400－20－60－180＝140， ∴n＝140÷400×100%＝35%.
题型
解：(m，n)所有可能出现的结果：(1，1)，(1，2)， (1，3)，(2，1)，(2，2)，(2，3)，(3，1)，(3，2)， (3，3)．
8 如图①②③④分别是⊙O的内接正三角形、正方形、 正五边形、正n边形，点M，N分别从点B，C开始以 相同的速度在⊙O上逆时针运动． (1)图①中，∠APN＝__6_0_°____； 图②中，∠APN＝__9_0_°____； 图③中，
很全的哦正多边形的画法课件
很全的哦正多边形的画法
R
1. 两直线间的圆弧连接
N O
M
很全的哦正多边形的画法
R
2. 直线与圆弧间的圆弧连接
M O
N
很全的哦正多边形的画法
3. 两圆弧间的圆弧连接
(1) 圆弧与两圆外切连接 (2) 圆弧与两圆内切连接 (3) 圆弧与两圆内、外切连接
很全的哦正多边形的画法
(1) 圆弧与两圆外切连接
3. 作圆内接正五边形
MP
K
B C
E D
很全的哦正多边形的画法
4. 已知边长作正五边形
m
D
N
E
C
P
A
B
M
Q
R
很全的哦正多边形的画法
5. 作圆内接正多边形 (以圆内接 正七边形为例)
A
1 1'
2
2'
3
3'
4' 4
5'
5
6'
6 p
7
B M1
C
D
G N1
F
E
很全的哦正多边形的画法
四、圆弧的连接
1. 两直线间的圆弧连接 2. 直线与圆弧间的圆弧连接 3. 两圆弧间的圆弧连接
三、平面图的作图步骤
很全的哦正多边形的画法
此课件下载可自行编辑修改，供参考！ 感谢您的支持，我们努力做得更好！
很全的哦正多边形的画法
21
O
M
N
很全的哦正多边形的画法
(2) 圆弧与两圆内切连接
R O N M
很全的哦正多边形的画法
(3) 圆弧与两圆内、外切连接
O N
M
很全的哦正多边形的画法
R
1. 两直线间的圆弧连接
N O
M
很全的哦正多边形的画法
R
2. 直线与圆弧间的圆弧连接
M O
N
很全的哦正多边形的画法
3. 两圆弧间的圆弧连接
(1) 圆弧与两圆外切连接 (2) 圆弧与两圆内切连接 (3) 圆弧与两圆内、外切连接
很全的哦正多边形的画法
(1) 圆弧与两圆外切连接
3. 作圆内接正五边形
MP
K
B C
E D
很全的哦正多边形的画法
4. 已知边长作正五边形
m
D
N
E
C
P
A
B
M
Q
R
很全的哦正多边形的画法
5. 作圆内接正多边形 (以圆内接 正七边形为例)
A
1 1'
2
2'
3
3'
4' 4
5'
5
6'
6 p
7
B M1
C
D
G N1
F
E
很全的哦正多边形的画法
四、圆弧的连接
1. 两直线间的圆弧连接 2. 直线与圆弧间的圆弧连接 3. 两圆弧间的圆弧连接
三、平面图的作图步骤
很全的哦正多边形的画法
此课件下载可自行编辑修改，供参考！ 感谢您的支持，我们努力做得更好！
很全的哦正多边形的画法
21
O
M
N
很全的哦正多边形的画法
(2) 圆弧与两圆内切连接
R O N M
很全的哦正多边形的画法
(3) 圆弧与两圆内、外切连接
O N
M
很全的哦正多边形的画法
画正多边形课件
画正多边形ppt课件
目录
CONTENTS
• 正多边形的定义与性质 • 画正多边形的方法 • 正多边形的几何应用 • 画正多边形的工具与软件 • 画正多边形的技巧与注意事项
01 正多边形的定义与性质
正多边形的定义
正多边形是指各边相 等，各内角也相等的 多边形。
正多边形的所有顶点 连接其中心（称为正 多边形的中心）的距 离相等。
正多边形的分类
01
02
03
04
等边三角形
三边长度相等，三个内角都是 60度。
等腰三角形
两边长度相等，两个内角相等 ，另一个内角与之互补。
等腰梯形
两腰长度相等，两底角相等。
正方形
四边长度相等，四个内角都是 90度。
02 画正多边形的方法
几何作图法
• 定义：通过使用简单的几何工具（如直尺、圆规等）来绘 制正多边形。
使用圆规和直尺
这是最基本的几何作图工具，用 于画出圆形和直线。
利用等分线段
通过等分线段，可以将线段分成若 干等份，从而更容易画出正多边形 。
利用垂线
通过画出垂直于线段的垂线，可以 确定正多边形的顶点位置。
代数计算技巧
计算内角和外角
通过计算正多边形的内角和外角，可以确定正多边形的形状和大 小。
利用正弦和余弦函数
注意精度设置
在绘制正多边形时，需要注意精 度设置，以确保绘制的图形准确
无误。
感谢您的观看
THANKS
04 画正多边形的工具与软件
几何作图工具
几何画板
专业的几何作图工具，可以方便 地绘制各种正多边形，并具有丰 富的几何变换功能。
GeoGebra
动态几何软件，支持绘制和操作 正多边形，并可进行动态演示和 探索。
目录
CONTENTS
• 正多边形的定义与性质 • 画正多边形的方法 • 正多边形的几何应用 • 画正多边形的工具与软件 • 画正多边形的技巧与注意事项
01 正多边形的定义与性质
正多边形的定义
正多边形是指各边相 等，各内角也相等的 多边形。
正多边形的所有顶点 连接其中心（称为正 多边形的中心）的距 离相等。
正多边形的分类
01
02
03
04
等边三角形
三边长度相等，三个内角都是 60度。
等腰三角形
两边长度相等，两个内角相等 ，另一个内角与之互补。
等腰梯形
两腰长度相等，两底角相等。
正方形
四边长度相等，四个内角都是 90度。
02 画正多边形的方法
几何作图法
• 定义：通过使用简单的几何工具（如直尺、圆规等）来绘 制正多边形。
使用圆规和直尺
这是最基本的几何作图工具，用 于画出圆形和直线。
利用等分线段
通过等分线段，可以将线段分成若 干等份，从而更容易画出正多边形 。
利用垂线
通过画出垂直于线段的垂线，可以 确定正多边形的顶点位置。
代数计算技巧
计算内角和外角
通过计算正多边形的内角和外角，可以确定正多边形的形状和大 小。
利用正弦和余弦函数
注意精度设置
在绘制正多边形时，需要注意精 度设置，以确保绘制的图形准确
无误。
感谢您的观看
THANKS
04 画正多边形的工具与软件
几何作图工具
几何画板
专业的几何作图工具，可以方便 地绘制各种正多边形，并具有丰 富的几何变换功能。
GeoGebra
动态几何软件，支持绘制和操作 正多边形，并可进行动态演示和 探索。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
预习1 正n边形的一个内角的度数是 （n 2） 180 ____________;
360 中心角是___________; n
n
正多边形的中心角与外角的 大小关系是________. 相等
都是 预习2、正多边形＿＿＿＿＿＿＿＿轴对称图形，一
n 个正n边形共有＿＿＿条对称轴，每条对称轴 中心 都通过正n边形的＿＿＿＿＿＿＿＿。
A
D
O ·
B
C
只要作出已知⊙O的互相 垂直的直径即得圆内接正 方形，再过圆心作各边的 垂线与⊙O相交，或作各 中心角的角平分线与⊙O 相交，即得圆接正八边形， 照此方法依次可作正十六 边形、正三十二边形、正 六十四边形……
你能尺规作出正六边形、正三角形、正十 二边形吗？
以半径长在圆 周上截取六段相 等的弧，依次连 结各等分点，则 作出正六边形. 先作出正六边 形，则可作正三 角形，正十二边 形，正二十四边 形………
边数是偶数的正多边形还是中心 彩的正多边形:生活中的正多边形图案
几种常见的正多边形
由于正多边形在生产、生活实际中有广泛 的应用性，所以会画正多边形应是学生必备能 力之一。 怎样画一个正多边形呢？ 问题1：已知⊙O的半径为2cm，求作圆的内接 正三角形. A
F
E O ·
A
D
B
C
说说作正多边形的方法有哪些?
归纳 （1）用量角器等分圆周作正n边形； （2）用尺规作正方形及由此扩展作正八 边形, 用尺规作正六边形及由此扩展作正 12边形、正三角形．
作业
教材116页练习
120 ° O C B
①用量角器度量，使 ∠AOB=∠BOC=∠COA =120°． ②用量角器或30°角的 三角板度量，使 ∠BAO=∠CAO=30°．
你能用以上方法画出正四边形、正五边形、 正六边形吗？
A O ·
90°
D
B O
A
F E
E O ·
60°
·
72°
A
D
B
C
C
D
B
C
你能尺规作出正四边形、正八边形吗？
360 中心角是___________; n
n
正多边形的中心角与外角的 大小关系是________. 相等
都是 预习2、正多边形＿＿＿＿＿＿＿＿轴对称图形，一
n 个正n边形共有＿＿＿条对称轴，每条对称轴 中心 都通过正n边形的＿＿＿＿＿＿＿＿。
A
D
O ·
B
C
只要作出已知⊙O的互相 垂直的直径即得圆内接正 方形，再过圆心作各边的 垂线与⊙O相交，或作各 中心角的角平分线与⊙O 相交，即得圆接正八边形， 照此方法依次可作正十六 边形、正三十二边形、正 六十四边形……
你能尺规作出正六边形、正三角形、正十 二边形吗？
以半径长在圆 周上截取六段相 等的弧，依次连 结各等分点，则 作出正六边形. 先作出正六边 形，则可作正三 角形，正十二边 形，正二十四边 形………
边数是偶数的正多边形还是中心 彩的正多边形:生活中的正多边形图案
几种常见的正多边形
由于正多边形在生产、生活实际中有广泛 的应用性，所以会画正多边形应是学生必备能 力之一。 怎样画一个正多边形呢？ 问题1：已知⊙O的半径为2cm，求作圆的内接 正三角形. A
F
E O ·
A
D
B
C
说说作正多边形的方法有哪些?
归纳 （1）用量角器等分圆周作正n边形； （2）用尺规作正方形及由此扩展作正八 边形, 用尺规作正六边形及由此扩展作正 12边形、正三角形．
作业
教材116页练习
120 ° O C B
①用量角器度量，使 ∠AOB=∠BOC=∠COA =120°． ②用量角器或30°角的 三角板度量，使 ∠BAO=∠CAO=30°．
你能用以上方法画出正四边形、正五边形、 正六边形吗？
A O ·
90°
D
B O
A
F E
E O ·
60°
·
72°
A
D
B
C
C
D
B
C
你能尺规作出正四边形、正八边形吗？