多孔介质
多孔介质分类

多孔介质分类嘿,朋友们!今天咱来聊聊多孔介质分类这个有意思的事儿。
你说这多孔介质啊,就像是一个神秘的大宝藏,里面藏着各种各样的奇妙世界。
多孔介质其实就在我们身边呢,就好比那海绵,那就是典型的多孔介质呀!它能吸水,能容纳好多东西,这就是多孔介质的一个特点。
咱先说说颗粒型多孔介质吧。
这就好像是一群小颗粒聚在一起,形成了好多小洞穴小空隙。
想象一下,那是不是有点像一群小朋友手拉手围在一起,中间就有了空间呀?这种多孔介质在很多地方都能见到呢,像沙子呀,石子呀。
再来说说纤维型多孔介质。
这就好像是一堆细细的线交织在一起,也留出了好多缝隙。
哎呀,这让我想起了妈妈织的毛衣,那毛线交织的地方不就是一个个小小的孔嘛!这种多孔介质在一些过滤材料里比较常见哦。
还有那泡沫型多孔介质呢!哇,这就像是一个个小泡泡聚在一起组成了一个大集体。
你看那洗碗用的海绵擦,不就是这样嘛,好多好多的小泡泡组成了它。
多孔介质分类可真是丰富多彩啊!不同类型的多孔介质都有着自己独特的用处和特点。
就拿颗粒型的来说,它可以用来过滤污水呀,让脏东西留在小颗粒之间。
纤维型的呢,能很好地过滤空气中的杂质。
泡沫型的就更有趣啦,能让我们的生活变得更加方便,比如刚才说的海绵擦。
咱生活中到处都有这些多孔介质的身影呢,它们就像是一个个默默工作的小助手,为我们的生活带来便利。
你难道不觉得神奇吗?它们虽然看起来普普通通,可实际上却有着大用处。
所以啊,大家可别小瞧了这多孔介质分类,这里面的学问可大着呢!它们就像是生活中的小惊喜,等待着我们去发现和利用。
让我们一起好好珍惜这些奇妙的多孔介质吧,说不定哪天它们就能给我们带来意想不到的收获呢!这就是多孔介质分类,有趣又实用!。
多孔介质力学特性与应用研究

多孔介质力学特性与应用研究多孔介质是指由固体颗粒或纤维构成的具有孔隙结构的材料。
多孔介质广泛存在于自然界和工程应用中,如土壤、岩石、海绵、过滤器等。
研究多孔介质的力学特性和应用具有重要的理论和实际意义。
一、多孔介质的力学特性1. 孔隙率与渗透性孔隙率是描述多孔介质中孔隙占据空间比例的参数。
多孔介质的孔隙率决定了其渗透性,即流体在多孔介质中的渗流能力。
孔隙率越大,渗透性越好。
渗透性的研究对于地下水资源开发、油气勘探以及土壤水分运动等领域具有重要意义。
2. 孔隙结构与力学性能多孔介质的孔隙结构对其力学性能具有重要影响。
孔隙结构包括孔隙的尺寸、形状、连通性等参数。
孔隙尺寸越小,多孔介质的强度和刚度越高。
孔隙连通性对于多孔介质的渗透性和传质性能起着关键作用。
通过研究孔隙结构,可以深入了解多孔介质的力学行为和应力传递机制。
3. 多相流与多孔介质多孔介质中的流体运动涉及多相流动,如气体与液体的相互作用、多组分混合等。
多相流动的研究对于石油开采、地下水污染治理等领域具有重要意义。
通过建立多相流动模型,可以预测多孔介质中的流体行为,并优化工程设计。
二、多孔介质力学特性的应用研究1. 岩土工程中的应用岩土工程中的土体是一种典型的多孔介质。
研究土体的力学特性对于岩土工程设计和施工具有重要意义。
通过实验和数值模拟,可以预测土体的变形、强度和稳定性,并指导工程实践。
例如,通过研究土体的渗透性和孔隙结构,可以优化地基处理方案,提高土体的承载能力。
2. 水资源与环境工程中的应用多孔介质在水资源与环境工程中有广泛的应用。
例如,研究土壤的渗透性和水分运动规律,可以指导农田灌溉和水资源管理。
研究地下水的流动与污染传输,可以预测地下水的质量和污染扩散范围,为地下水资源保护和污染治理提供科学依据。
3. 石油与天然气工程中的应用多孔介质力学在石油与天然气工程中具有重要应用。
研究油气藏中的多相流动和渗流规律,可以预测油气的产量和开采效果。
多孔介质流动及其应用研究

多孔介质流动及其应用研究多孔介质是指由固体颗粒、纤维或膜等所构成的具有连续空隙结构的物质。
在自然界和工程应用中,多孔介质流动现象普遍存在,如土壤水分运移、石油开采中的岩石渗流、过滤器中的颗粒分离等。
对多孔介质流动进行研究,不仅可以深入理解流体在多孔介质中的行为,更可以为工程应用提供指导和优化方案。
本文将介绍多孔介质流动的基本原理和应用研究进展。
一、多孔介质流动的基本原理多孔介质流动的基本原理可以通过达西定律和达西定律的延伸模型进行描述。
达西定律是描述单相流体在均质多孔介质中的流动规律,它表示了单位时间内通过单位面积的流体体积与流动梯度之间的关系。
而达西定律的延伸模型则可以描述多相流体在非均质多孔介质中的流动行为,如饱和流动、非饱和流动和两相流动等。
二、多孔介质流动的应用研究进展1. 土壤水分运移土壤是地球上最常见的多孔介质,对于农田灌溉和地下水资源管理具有重要意义。
多孔介质流动理论可以应用于土壤水分运移模型的建立和水资源管理的优化。
通过对土壤孔隙结构、土壤含水量等因素的研究,可以改进灌溉方案,提高农田水分利用效率。
2. 岩石渗流石油开采过程中,岩石渗流是一个重要的研究内容。
利用多孔介质流动理论,可以模拟岩石中油、水和气体等多相流体的运移,并预测石油开采的产能和渗流规律。
这对于石油工程的设计和优化具有重要的意义。
3. 过滤器中的颗粒分离过滤器是一种常见的多孔介质设备,广泛应用于水处理、空气净化等领域。
多孔介质流动理论可以应用于过滤器中颗粒的分离和截留机制的研究。
通过对多孔介质结构和颗粒特性的分析,可以提高过滤器的效率和寿命。
4. 化学反应和传质过程多孔介质不仅可以进行流体的传输,还可以进行物质的化学反应和传质过程。
多孔介质流动理论可以应用于模拟多相反应和传质过程,并优化反应器的设计和操作。
此外,多孔介质还可以用于催化剂的载体,提高催化反应的效率。
5. 生物医学领域应用多孔介质在生物医学领域也有广泛的应用。
多孔介质的物理性质研究

多孔介质的物理性质研究多孔介质是指一些由气体,液体或其它物质所占据的不规则,颗粒状物体。
由于多孔介质具有一些独特的物理特性,因此在很多领域都是非常重要的。
例如在土力学、漏洞学、岩石物理学,环境工程学、化学工业,石油工业,甚至是医学等方面都有着广泛的应用。
多孔介质中的孔隙结构是主要的研究对象,和孔径、表面积等物理特征有着密切的联系。
为此,人们通过各种技术和方法来研究多孔介质的物理性质。
本文将从以下几个方面入手,对多孔介质的物理性质研究展开论述。
一、孔隙率和孔径分布孔隙率是指多孔介质内孔隙的体积比,也就是孔隙体积除以总体积。
孔径是指孔隙的直径大小。
这两个参数是研究多孔介质的基础。
利用X射线衍射仪、低温氮吸附分析仪等先进的实验测量方法,可以测得不同孔径范围内孔隙的孔径分布和孔隙率。
通过分析孔径分布,可以了解孔径大小对某些物理性质的影响程度,如渗透性和多孔介质的强度等等。
二、渗透性多孔介质的渗透性是指在一定条件下,液体、气体在多孔介质中的渗透速度。
渗透系数是衡量不同多孔介质渗透性大小的重要参数。
利用渗透率,可以判断多孔介质在特定条件下的渗透效果,并进一步了解多孔介质内流体行为的规律。
研究多孔介质的渗透性不仅有助于我们了解多孔介质内的水、气体的传输规律,也是对地下储层中石油、天然气等资源勘探和开采方面的重要研究。
三、表面积和介电常数多孔介质的表面积是指孔隙介质固-液、固-气相间的表面积,是描述多孔介质化学和物理反应的重要参数,同时也是液体或气体在多孔介质中传输的重要因素。
多孔介质的表面性质跟介质的物理性质、化学性质、生物性质等有关。
研究介质表面性质可以了解界面反应、分子吸附和离子交换等反应规律。
同时,多孔介质的介电性质是介质物理特性中的重要参数之一,它受介质的几何形态、介质材料的性质、湿度等因素的影响。
研究多孔介质的介电性质在信号传输、通讯、电力传输等领域具有应用前景。
四、多孔介质的力学性质多孔介质在线性和非线性力学方面有着广泛的应用。
多孔介质模型的参数设置

多孔介质模型的参数设置1. 引言多孔介质是指由一些具有孔隙结构的实体组成的材料,孔隙可以是连通的或者不连通的。
多孔介质模型是描述多孔介质中流体运动的数学模型。
在进行多孔介质模拟时,合理设置参数是非常重要的,本文将对多孔介质模型的参数设置进行全面、详细、完整且深入地探讨。
2. 多孔介质模型的基本理论2.1 多孔介质的物理特性多孔介质通常具有以下几个重要的物理特性:•孔隙度:衡量多孔介质中孔隙的占据空间的百分比。
•渗透性:衡量多孔介质允许流体通过的能力。
•孔隙结构:包括孔隙大小分布、形状以及连通性等。
2.2 多孔介质流动模型多孔介质流动模型可以分为宏观尺度模型和微观尺度模型。
宏观尺度模型假设多孔介质具有连续均匀的介质性质,通过Darcy定律描述多孔介质中的流动。
微观尺度模型考虑具体的孔隙结构,通过Navier-Stokes方程描述多孔介质中的流动。
3. 多孔介质模型的参数设置方法3.1 多孔介质几何参数的设置方法多孔介质的几何参数包括孔隙度、孔隙结构等。
合理设置多孔介质的几何参数是建立模型的基础,常用的方法有:1.实验测量方法:通过实验手段测量多孔介质样本的孔隙度、孔隙结构等参数。
2.数值模拟方法:使用计算流体力学方法对多孔介质样本进行数值模拟,得到几何参数。
3.2 多孔介质流动参数的设置方法多孔介质中的流动参数包括渗透性、渗透率等。
合理设置流动参数可以准确描述多孔介质中的流动行为,常用的方法有:1.实验测量方法:通过渗透实验等手段测量多孔介质的渗透性、渗透率等参数。
2.数值模拟方法:使用计算流体力学方法对多孔介质中的流动进行数值模拟,得到流动参数。
3.经验公式方法:根据多孔介质样本的物理特性,利用经验公式估计流动参数。
4. 多孔介质模型参数的影响因素4.1 孔隙度对模型参数的影响孔隙度是多孔介质模型中一个重要的参数,它对模型的流动行为有着重要的影响。
较大的孔隙度会降低多孔介质的渗透性和渗透率,而较小的孔隙度则会增加多孔介质的渗透性和渗透率。
多孔介质比表面积

多孔介质比表面积一、引言多孔介质是指具有孔隙结构的物质,其表面积与体积比非常高,因此具有很高的比表面积。
在吸附、催化等领域中得到广泛应用。
本文将从多个角度探讨多孔介质的比表面积。
二、什么是比表面积1.定义比表面积是指单位质量或单位体积物质所具有的表面积。
2.计算方法(1)单位质量物质的比表面积计算公式:SBET=m/ρS,其中m为样品的质量,ρ为样品的密度,S为样品的总表面积。
(2)单位体积物质的比表面积计算公式:SBET=V/SV,其中V为样品体积,SV为样品孔隙体积。
三、多孔介质的特点1.孔径分布广泛多孔介质中存在不同孔径大小和形状的微小通道,这些通道可以提供更大的内部表面积和更好的吸附性能。
2.内部结构复杂多孔介质内部结构复杂,存在不同形态和大小的空隙和通道,在吸附、催化等反应过程中可以提供更多的反应位点。
3.比表面积高由于多孔介质内部结构的复杂性,其表面积与体积比非常高,因此具有很高的比表面积。
四、多孔介质比表面积的影响因素1.孔径大小和分布不同孔径大小和分布会影响多孔介质的比表面积,一般来说,孔径越小、分布越均匀,则比表面积越大。
2.形态和结构多孔介质的形态和结构也会影响其比表面积,一般来说,形态越复杂、结构越分散,则比表面积越高。
3.制备方法不同制备方法会对多孔介质的内部结构和形态产生不同影响,从而影响其比表面积。
五、多孔介质在吸附领域中的应用1.气体吸附由于多孔介质具有较高的比表面积和内部结构复杂性,因此可以用于气体吸附。
例如,活性炭就是一种常见的气体吸附材料。
2.水处理多孔介质还可以用于水处理领域。
例如,膜过滤器、活性炭等都可以用于去除水中的污染物,提高水的质量。
3.催化剂载体多孔介质还可以作为催化剂的载体。
在催化反应中,多孔介质可以提供更多的反应位点和更好的分散性,从而提高催化效率。
六、结论多孔介质具有很高的比表面积,这是由于其内部结构的复杂性所导致的。
比表面积受到多个因素影响,包括孔径大小和分布、形态和结构以及制备方法等。
多孔介质名词解释

多孔介质名词解释
多孔介质是指具有多个连续、通过的孔隙,或称为小孔、空隙的介质,随着其
纳米结构的大小和形状的不同,可演化出不同的物理性能,被广泛应用于化学工程学及材料科学的领域中。
多孔介质的性能取决于其结构特征,可以根据其内部表面积和孔隙率来进行定
量衡量。
多孔介质具有大量可渗透空气、水和其他液体的优势,结合精细控制孔隙大小、形状和弹性力学及化学特性等方面的优势,可以实现高效的对液M介的分离、过滤和催化反应。
多孔介质的应用领域极其广泛,比如,可以应用于气体吸附剂、电子芯片、膜分离工艺、催化剂和生物纳米能源等。
多孔介质的应用也使得传统的能源和化学工艺受到持续的改善,比如:它可以
有效改善能源密度,在可再生能源开发和储存方面发挥重要作用,这也就是要提高能源效率和减少能源损耗;另一方面,多孔介质可以有效增加有机分散体系的活性,在医药和农业中都有广泛应用。
因此,多孔介质对于减少能源消耗和推动部分传统行业向高效、环保、可持续
发展提供了可行解决方案,同时多孔介质的研究仍有很大的潜力,今后会发挥更大的价值,以促进社会经济的可持续发展。
多孔介质——精选推荐
多孔介质及其描述多孔介质是含有大量空隙的固体,可以从以下几个方面来定义和描述多孔介质:(1)多孔介质是多相介质占据的空间,其中的固相部分称为固体骨架,被非固相部分所占据的空间称为孔隙。
非固相部分可以是气体或液体,也可以是多相混合的流体。
(2)固相骨架和孔隙均应遍布在整个介质中。
如果在介质中任意取一个适当大小的体积元,则在该体积元内必定含有一定比例的固体颗粒和孔隙。
(3)由孔隙所占据空间的部分或大部分必须是相互连通的。
换句话说,流体应能在部分或大部分孔隙之间流动。
相互连通的孔隙空间称为有效孔隙空间,不相互连通的空间称为无效孔隙空间。
如果孔隙只在一个确定的局部空间内相互连通而与该空间之外的孔隙不连通,则对于整个空间来讲该局部空间相当于一个无效孔隙空间。
无论是天然的还是人造的多孔介质,其结构都是非常复杂和无规律的,因而不可能对多孔介质的内部结构进行精确的数学描述。
为了克服这一困难,一般是选取一个在宏观上足够小(宏观无限小)的体积来考察多孔介质的性质。
因此,对于多孔介质的描述只能通过一定意义下的平均值来进行。
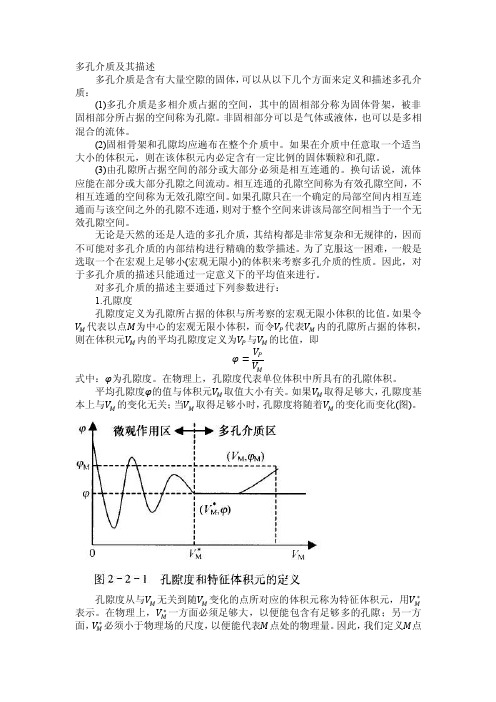
对多孔介质的描述主要通过下列参数进行:1.孔隙度孔隙度定义为孔隙所占据的体积与所考察的宏观无限小体积的比值。
如果令V M代表以点M为中心的宏观无限小体积,而令V P代表V M内的孔隙所占据的体积,则在体积元V M内的平均孔隙度定义为V P与V M的比值,即φ=V P V M式中:φ为孔隙度。
在物理上,孔隙度代表单位体积中所具有的孔隙体积。
平均孔隙度φ的值与体积元V M取值大小有关。
如果V M取得足够大,孔隙度基本上与V M的变化无关;当V M取得足够小时,孔隙度将随着V M的变化而变化(图)。
孔隙度从与V M无关到随V M变化的点所对应的体积元称为特征体积元,用V M∗表示。
在物理上,V M∗一方面必须足够大,以便能包含有足够多的孔隙;另一方面,V M∗必须小于物理场的尺度,以便能代表M点处的物理量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.4.3 可压缩流动的求解策略可压缩流动求解中速度、密度、压力和能量的高度耦合以及可能存在的激波导致求解过程不稳定。
有助于改善可压缩流动计算过程稳定性的方法有:● (仅适用于基于压力求解器)以接近于滞止条件的流动参数进行初始化(即,压力很小但不为零,压力和温度分别等于进口总压和总温)。
在迭代过程的最初几十步不求解能量方程。
设置能量方程的亚松驰因子等于1,压力的亚松驰因子0.4,动量的亚松驰因子0.3。
求解过程稳定后再加入能量方程的求解,并将压力的亚松驰因子提高到0.7。
● 设置合理的温度和压力限制值以避免求解过程发散。
● 必要时,先以较低的进、出口边界压力比进行求解,然后再逐步升高压力比直到预定工况。
对于低Mach 数流动,也可以先求解不可压缩流动,然后以所得到的解作为可压缩流动的迭代初值。
某些情况下,也可以先求解无粘性流动作为迭代初值。
2.5 无粘性流动在高Re 数流动中,惯性力相对于粘性力而言起支配作用,可忽略粘性的影响。
例如高速飞行器在空气动力学方案分析阶段可以采用无粘性流动计算初步确定外形,然后进行粘性计算,将流体粘性和湍流粘性对升力和阻力的影响计入。
无粘性流动计算的另一个用途是给复杂的流动提供好的迭代初值。
对于特别复杂的问题,有时这是唯一能使求解过程进行下去的方法。
无粘性流动的计算求解Euler 方程。
其中,质量方程与粘性流动的相同: ()m v S tρρ∂+∇⋅=∂ (2.34) 其动量方程与粘性流动的相比,没有粘性应力项τ∇⋅: ()()v vv p g F tρρρ∂+∇⋅=-∇++∂ (2.35) 能量方程与粘性流动相比,没有导热项()eff k T ∇⋅∇和粘性耗散项()eff v τ∇⋅⋅ : ()()()j j h j E v E p h J S t ρρ∂⎛⎫+∇⋅+=-∇⋅+ ⎪∂⎝⎭∑ (2.36) 式(2.34) ~ 式(2.36)中符号的意义与粘性流动控制方程的相同(见2.1.1 ~ 2.1.3节)。
2.6 多孔介质模型多孔介质(Porous Media )模型可用于模拟许多问题,包括流过填充床、滤纸、多孔板、布流器、管排等的流动。
多孔介质模型在流体区上定义(见17.2.1节)。
此外,一个被称为多孔阶跃面(porous jump )的多孔介质模型的一维简化可用于模拟已知速度−压降特性的薄膜。
多孔阶跃面在界面区上定义。
多孔阶跃面比多孔介质模型更健壮,收敛性更好,应首选采用(见 节)。
2.6.1 基于表观速度的多孔介质动量方程对于单相介质和多相介质,多孔介质模型可以使用表观速度或物理速度形式的公式。
基于表观速度的多孔介质模型根据多孔介质区中的体积流量率计算表观相速度或混合物速度。
基于表观速度的多孔介质模型能够较好模拟多孔介质区内部的压力损失。
但是,在多孔介质区与非多孔介质区的交界面处的表观速度与的速度是相同的,不能反映实际速度变化所引起的动量变化,对计算精度不利。
多孔介质模型通过在动量方程中增加源项来模拟计算域中多孔性材料对流体的流动阻力。
该源项由两部分组成,即Darcy 粘性阻力项和惯性损失项: ()33111 ,,2i ij j ij j j j S D v C v v i x y z μρ==⎛⎫=-+= ⎪⎝⎭∑∑ (2.37) 其中,D 和C 分别为粘性阻力和惯性损失系数矩阵。
这个负的动量源项导致多孔介质单元中的压力降。
同时,在全部变量的输运方程和连续性方程中,瞬态项变为()tγρφ∂∂,其中γ为孔隙率。
对于简单的均匀多孔介质,分别在系数矩阵D 和C 中对角线项代入1/α和C 2,而其它项为零,则有 ()()21 ,,2i i iS v C v v i x y z μρα=-+= (2.38) 其中,α为渗透率;C 2为惯性阻力系数。
也可以用速度大小的幂函数来模拟阻力: ()11100 ,,C C i i S C v C v v i x y z -=-=-= (2.39) 式中,C 0和C 1为经验系数,且C 0的单位为SI 制。
采用幂函数时,压力降为各向同性的。
2.6.2 Darcy 粘性阻力项多孔介质中流动为层流时,典型情况下压力降与速度成正比,即多孔介质模型简化为Darcy 定律:p v μα∇=- (2.40) 于是,在三个坐标方向上的压力降为 ()31 ,,i j i ij j p v n i x y z μα=∆=∆=∑ (2.41) 式中,1/α ij 为系数矩阵D 的项;Δn i 为多孔介质在三个坐标方向上的厚度。
2.6.3 惯性损失项当速度比较高,或模拟多孔板和管排时,有时可忽略渗透项,只保留惯性损失项,则多孔介质方程简化为 ()()3211 ,,2ij i j p C v v i x y z ρ=∇=-=∑ (2.42) 或写成三个坐标方向上的压力降: ()3211 ,,2i ij i j j p C n v v i x y z ρ=∆≈∆=∑ (2.43) 式中,C 2,ij 为系数矩阵C 中的项;Δn i 为多孔介质在三个坐标方向上的厚度。
2.6.4 多孔介质中能量方程的处理对多孔介质修正了扩散项和瞬态项的能量方程为 ()()()()()1h f f s s f f eff j j eff f jE E v E p k T h J v S t γργρρτ∂⎛⎫+-+∇⋅+=∇⋅∇-+⋅+ ⎪∂⎝⎭∑ (2.44) 其中,E f 为流体总能;E s 为多孔介质基体固体总能;γ为孔隙率;h f S 为流体焓的源项;k eff 为多孔介质的有效导热系数,采用流体导热系数(包括湍流有效导热系数)k f 与多孔介质中固体材料的导热系数k s 的体积加权平均:()1eff f s k k k γγ=+- (2.45) 采用UDF 可以定义各向异性的有效导热系数。
孔隙率γ定义为多孔介质区中流体的体积分数,也就是介质中空的部分所占的比例。
孔隙率影响传热计算、输运方程中的非稳态项、以及介质中的化学反应和体积力。
如果希望模拟介质为全空(即没有固体介质)的情况,应给定孔隙率等于1。
2.6.5 多孔介质中湍流的处理在多孔介质中,当介质的渗透性很大且介质的几何尺度与湍流涡的尺度不发生相互作用时,可以认为固体基体对湍流的生成和耗散率没有影响。
但其它情况下应降低多孔介质中湍流的影响。
当采用湍流模型时(LES 除外),可通过将多孔介质指定为层流区(Laminar Zone )而使湍流粘性μt 为零来抑制多孔介质区中湍流效应。
此时,进口湍流量被输运穿过多孔介质区,而其对流体混合及动量的影响被忽略,同时介质中湍流生成被置为零。
2.6.6 粘性阻力系数和惯性阻力系数阻力系数一般是基于流体在多孔介质中的表观速度定义的。
阻力源项的计算可以采用相对速度或绝对速度。
选择Relative V elocity Resistance Formulation (相对速度阻力公式)选项可以更精确计算有动网格和运动参考坐标系时的源项。
对于高度各向异性的多孔介质,当使用基于压力求解器时,选择Alternative Formulation (非常规公式)选项可以使求解过程更稳定。
采用非常规公式时,通过多孔介质的压力损失取决于速度矢量第i 个方向分量的大小: 12i i i i S C v v ρ= (2.46) 计算粘性阻力系数和惯性阻力系数的方法如下:(1) 已知压力降,计算基于表观速度的阻力系数使用多孔介质模型时,FLUENT 假定单元中没有多孔介质的固体基体,即单元是100%开孔的(100%open ),且所给定的阻力系数值是基于这一假设的。
在已知流体流过实际设备中多孔介质的压力降Δp 与速度的关系时,可计算C 2。
流体流过开孔率为open %的多孔板时,基于实际流动速度的压力损失系数K L 定义为:2%12L open p K v ρ∆= (2.47) 式中,%open v 为流过多孔板的实际流速。
对于100%开孔时的压力损失系数值LK ',有 2100%12L p K v ρ'∆= (2.48) 式中,100%v 为流过开孔率100%多孔板时的流速。
而在相同流量下,速度与开孔率成反比,将K L 折算为100%开孔时的压力损失系数值LK ': ()()22%100%100%%open L L L v K K K v open '=⨯=⨯ (2.49) 阻力系数C 2为单位厚度多孔板的压力损失系数:2L K C n'=∆ (2.50) 式中,Δn 为多孔板厚度。
(2) 使用Ergun 公式计算通过层床的阻力系数在湍流时,层床用渗透率和惯性损失系数模拟。
对于多种类型的层床,在较宽的Re 数范围内阻力系数可以采用半经验的Ergun 公式计算: ()()22233150 1.7511p p p v v L D D μρεεεε∆--=+¥¥ (2.51) 当层床中为层流时,忽略式(2.51)中的第二项,可得Blake - Kozeny 方程: ()2231501pp v L D μεε∆-=¥ (2.52) 式中,μ为粘性系数;D p 为平均颗粒直径;L 为床厚度;ε为孔隙率,其定义为孔隙体积与层床总体积之比。
比较式(2.40)、式(2.42)和式(2.51),可得各方向粘性阻力系数和惯性损失系数()22311150p D εαε-= (2.53) ()2313.5p C D εε-= (2.54)(3) 使用经验公式计算流过多孔板湍流的阻力系数流过锐边孔多孔板的压力损失系数可以采用V an Winkle 等的公式计算(适用于孔呈等边三角形布置的情况):f m CA = (2.55) 式中,m为通过板的流量;A f 为孔的总面积;A p 为板的总面积;C 为适用于不同Re 数范围和不同孔径厚度比D /t 情况下的系数,t /D > 1.6且Re > 4000时(Re 数的特征尺寸为孔径,特征速度为孔内的速度),C ≈ 0.98。
利用式(2.55)和p mvA ρ= ,可得 ()2221112f p A A p v x C tρ-∆=∆ (2.56) 式中,v 为表观速度而非孔内的流速。
与式(2.42)比较可得在垂直于板方向的阻力系数C 2: ()22211f p A A C C t-= (2.57) (4) 用实验数据计算流过纤维状材料层流的阻力系数在已知任意排列的纤维材料的无量纲渗透率B 与纤维体积分数之间关系的情况下,粘性阻力系数1/α可由无量纲渗透率的定义B = α/a 2(a 为纤维直径)确定。
(5) 用压力降与速度关系实验数据计算阻力系数可以用通过多孔介质的压力降Δp 与速度v 关系的实验数据确定阻力系数。
