普通物理学第六版第八章到第十二章部分题目
大学物理参考答案(白少民)第12章 相对论基础

' l⊥ = l ' sin θ '
由尺缩效应公式得
' ' ' ' lx = lx 1 − υ 2 / c 2 = l ' cos θ ' 1 − υ 2 / c 2 , l ⊥ = l ⊥ = l sin θ
由此得
2 l = l x2 + l y = l ' 1−
(3)从地球上看电子相对于飞船的速度 (4)从地球上看电子相对于光子的速率 (5)从地球上看光子相对于飞船的速率
u电子 −υ = 0.89c − 0.5c = 0.39c u电子 − u 光子 = 0.89c − ( −1.0c ) = 1.89c
υ − u 光子 = 0.5c − ( −1.0c ) =1.5c
2 2
由此解得
υ = 1 − tan 2 30 0 c = 1 − c =
1 3
2 c 3
12.14 求火箭以 0.15c 和 0.85c 的速率运动时,其运动质量与静止质量之比. 解:当 υ = 0.15c ,
m 1 1 = = = 1.01 2 2 m0 1 −υ / c 1 − 0.15 2
当 υ = 0.85c 时
= 4.7 ×10 −14 J = 2.95 ×10 5 eV
−27 12.17 一 个 质 子 的 静 质 量 为 m p = 1.67265 ×10 kg , 一 个 中 子 的 静 质 量 为
m n = 1.67495 ×10 −27 kg , 一 个 质 子 和 一 个 中 子 结 合 成 的 氘 核 的 静 质 量 为
大学物理第章习题分析与解答(精品).doc

第八章恒定磁场8-1均匀磁场的磁感强度〃垂直于半径为/•的圆面.今以该圆周为边线,作一半球面S,则通Hs]hi的磁通量的大小为[]。
(A) 2 K r 2 B (B) nr2B(C) 0 (D)无法确定分析与解根据高斯定理,磁感线是闭合曲线,穿过圆平面的磁通量与穿过半球面的磁通量相等。
正确答案为(B)。
8-2下列说法正确的是[]。
(A)闭合回路上各点磁感强度都为零时,冋路内一定没有电流穿过(B)闭合冋路上各点磁感强度都为零时,冋路内穿过电流的代数和必定为零(C)磁感强度沿闭合冋路的积分为零时,冋路上各点的磁感强度必定为零(D)磁感强度沿闭合冋路的积分不为零时,冋路上任意点的磁感强度必定为零分析与解由磁场屮的安培环路定理,磁感强度沿闭合冋路的积分为零时,冋路上备点的磁感强度不一定为零;闭合冋路上备点磁感强度为零时,穿过冋路的电流代数和一定为零。
正确答案为(B)。
8-3磁场屮的安培环路定理#严.d/ = 人说明稳恒电流的磁场是[i = 1(A)无源场(B)有旋场(C)无旋场(D)有源场分析与解磁场的高斯定理与安培环路定理是磁场性质的重要表述,在恒定磁场屮B的环流一般不为零,所以磁场是涡旋场;而在恒定磁场屮,通过任意闭合曲面的磁通量必为零, 所以磁场是无源场;静电场屮E的环流等于零,故静电场为保守场;而静电场屮,通过任意闭合面的电通量可以不为零,故静电场为有源场。
正确答案为(B)。
8-4 —半圆形闭合平面线圈,半径为R,通有电流/,放在磁感强度为3的均匀磁场屮,磁场方向与线圈平面平行,则线圈所受磁力矩大小为[]。
(A) InR2B(B) (C) (D) 0分析与解对一匝通电平面线圈,在磁场屮所受的磁力矩可表示为M = ISjxB ,而且对任意形状的平面线圈部是适用的。
正确答案为(B)。
8-5 —长直螺线管是由直径d=0.2mm的漆包线密绕而成。
当它通以/=0. 5A的电流时,其内部的磁感强度3= ______________ o (忽略绝缘层厚度,u o=4 n X 10'7N/A2)分析与解根据磁场屮的安培环路定理可求得长育螺线管内部的磁感强度大小为B = |i o nZ ,方向由右螺旋关系确定。
大学普通物理--习题答案(程守洙-江之勇主编--第六版)省公开课获奖课件市赛课比赛一等奖课件

2hw 2sec 2wt
tg
wt
结束 目录
1-14滑雪运动员离开水平滑雪道飞入空 中时旳速率v =110km/h,着陆旳斜坡与水
平面成 q = 450角,如图所示。
(1)计算滑雪运动员着陆时沿斜坡旳位 移(忽视起飞点到斜面旳距离);
(2)在实际旳跳跃中,运动员所到达旳 距离L=165m, 此成果为何
(3)式中 t 以s为单位,x、y以m为单位,
求:质点在t = 4 时旳速度旳大小和方向。
结束 目录
x =3t +5
y=
1 2
t 2+3t
4
解: (1)
r
=
(
3t
+5)
i+
(
1 2
t
2+ 3 t
4) j
(2)
y
=
1 2
(
x
5 3
)2+
3
(
x
5 3
)
4
(3) v =3 i + (t +3) j =3 i + 7 j
v/(m.s-1)
-10
o
t/s 10 20 30 40 50 60
-10
-10
结束 目录
解:由v~t 图旳总面积可得到旅程为:
S
=
1 2
(30+10)×5
+
1 2
(20×10)
=200(m)
总位移为:
Δx
=
1 2
(30+10)×5
所以平均速度也为零
1 2
(20×10)
=0
结束 目录
1-4.直线 1与圆弧 2分别表达两质点A、B
(NEW)马文蔚《物理学》(第6版)(上册)配套题库【名校考研真题+课后习题+章节题库+模拟试题】

目 录第一部分 名校考研真题第1章 质点运动学第2章 牛顿定律第3章 动量守恒定律和能量守恒定律第4章 刚体的转动第5章 静电场第6章 静电场中的导体与电介质第7章 恒定磁场第8章 电磁感应 电磁场第二部分 课后习题第1章 质点运动学第2章 牛顿定律第3章 动量守恒定律和能量守恒定律第4章 刚体的转动第5章 静电场第6章 静电场中的导体与电介质第7章 恒定磁场第8章 电磁感应 电磁场第三部分 章节题库第1章 质点运动学第2章 牛顿定律第3章 动量守恒定律和能量守恒定律第4章 刚体的转动第5章 静电场第6章 静电场中的导体与电介质第7章 恒定磁场第8章 电磁感应 电磁场第四部分 模拟试题马文蔚等《物理学》(第6版)配套模拟试题及详解第一部分 名校考研真题第1章 质点运动学一、选择题1.某物体的运动规律为,式中的k为大于零的常数,当t =0时,初速度为,则速度v与时间t的函数关系是( ).[郑州大学2007研]A.B.C.D.【答案】C2.一质点沿半径为R的圆周作为匀速率运动,每t秒转一圈,则在2t时间间隔中,其平均速度的大小与平均速率的大小分别为( ).[电子科技大学2006研]A.B.C.D.【答案】B二、填空题1.半径为R=2m飞轮作转速转动时,轮边缘上一点的运动学方程为(国际单位制).则当此点的速率v=30m/s时,其切向加速度为______,法向加速度为______.[南京航空航天大学2008研]【答案】6m/s2;450m/s22.一质点作平面运动,运动方程,则t时刻质点的速度为______,加速度为______.[南京理工大学2005研]【答案】3.一质点在平面上运动,已知质点位置矢量的表达式为:(a、b为常量),则该质点作______运动.[北京工业大学2004研]【答案】匀加速直线运动三、计算题1.已知某质点的运动方程为(SI),则在t=1s时该质点的切向加速度和法向加速度大小各为多少?[浙江大学2007研]解:,则:,则2.如图1-1所示,导弹A与靶机B在同一高度作水平飞行,某时刻导弹正处于原点O,而靶机则位于导弹正东1000米处,靶机以500米/秒的速度向东偏北30°的方向匀速飞行,导弹以1000米/秒的匀速率飞行,且飞行方向时正对靶机,求此刻导弹的加速度矢量和它的飞行轨道在O 点的曲率半径.[山东大学1997研]图1-1解:加速度,所以:m·s-2(垂直于速度方向向上)因为,所以曲率半径为 3.一正在行驶的汽船,发动机关闭后,得到一个与船速方向相反,大小与船速平方成正比的加速度.设关闭发动机时船的速度为,经过时间后减小为/2.求:(1)发动机关闭后,t时刻船的速度的大小;(2)发动机关闭后,经过时间t船行驶的距离x.[厦门大学2006研]解:设发动机关闭时船的位置为坐标原点.(1)由题意可知:两边积分,得:解得:代入条件t=10s,得:或。
普通物理学第六版答案

普通物理学第六版答案一、选择题(本题共16小题,1-14为单项题、15-16题多选题、每题均2分,共32分)1.下列说法符合日常生活的是( )A.中学生高度约2mB.人的正常体温是390CC.人步行速度约10m/sD.物理课本的宽度接近19cm2.下列有关误差的说法中,正确的是( )A.多次测量取平均值可以减小误差B.误差就是测量中产生的错误C.只要认真测量,就可以避免误差D.选用精密的测量仪器可以消除误差3.下列运动不属于机械运动的是( )A.火车减速进站B.房屋着火C.划破夜空的流星D.骑自行车上学4.关于速度,以下各种说法正确的是( )A.运动路程越长,速度越大B.运动时间越短,速度越大C.相同时间内,通过路程越长,速度越大D.通过相同的路程,所用时间越长,速度越大5.三个同学同时登一座山,他们登山的平均速度为:甲是3.5km/h,乙是1m/s,丙是每分钟走63m,则谁最先登上山( )A.甲B.乙C.丙D.同时到达6.在公共场所轻声说话是文明的表现,而在旷野中要大声喊叫才能让较远处的人听见。
这里的轻声和大声是指声音的( )A. 音调B. 响度C. 音色D. 频率7.以下各组中全属于声音可以传递信息的是( )A.用超声波清除眼镜片上的垢迹B.声波清洗精细的机械C.医生用超声波为病人除去体内的结石D.B超探病8. 关于雨、露、霜、雾跟物态变化的关系,下面说法中正确是( )A雨水是水的升华形成的 B.露水是水的汽化形成的C.霜是水蒸气凝华形成的D.雾是水蒸气凝华形成的9.下列实例中,属于光的折射现象的是( )A.斜插在水中的筷子变弯了B.湖边垂柳在湖面形成美丽的倒影C.人在路灯下行走,地面上会出现人的影子D.阳光穿过茂密的树叶间隙,在地面形成圆斑1 0.用图象可以表示物体的运动规律,图中用来表示物体做匀速直线运动的是( )A.甲和丁B.甲和丙C.甲和乙D.乙和丁11、有一种望远镜由两组凸透镜组成。
物理第六版习题册参考答案

练习答案第一章怎样描述物体的运动§1.1 走近运动一.填空题1.地面太阳2.4 33.5 时刻时间4.1800米2200米二、选择1.D 2.C 3.A 4.D 5.D三、计算题:1.路程220米,位移100米2.2R A到B πR 0§1.2 怎样描述运动的快慢一、填空题:1.快慢位移位移2.运动位移速率速率3.5m/s4.瞬时瞬时二、选择题:1.B2.C3.B4.D5.C6..A三、计算题:1.(1)汽车在前2秒内通过的路程s1=2m+4m=6m,前3秒内通过的路程s2=2m+4m+6m=12m,则汽车在前2秒内的平均速度v1=s/t=6/2=3m/s,(2)前3秒内的平均速度v2=1=s/t=12/3=4m/s,2.(1)由v=st得:在反应过程所用的时间t1=s1/t1=14/20=0.7s;(2)制动过程中的平均速度v=s/t=162.3m/s≈6.96m/s;(3)紧急停车全程所用时间t=t1+t2=0.7s+2.3s=3s全程的平均速度v=s/t=303m/s=10m/s。
§1.3 怎样描述速度变化的快慢一、填空题:1.加速度 变化2.快慢 变化 大小 方向 矢量3.相同 定正 相反 负4.大5.匀速 减速 匀速二、选择题:1.C2.C3.B4.D5.A三、计算题1.由题意得v 0=0m/s ,末速度v =700m/s ,时间t =0.002s ;根据加速度的定义式有:a ==700/0.002m/s 2=3.5×105 m/s 22.由题意得v 0=30m/s ,末速度v =0m/s ,时间t =5s ;根据加速度的定义式有:a ==-30/5m/s 2=-6m/s 23. (1)由表中可知第2 s 末的瞬时速度为s m /2 (2)220/1/112s m s m t v v a t =−=−=(3)v =x t =6.5-5.51 m/s =1 m/s.第二章伽利略与落体运动§2.1伽利略对落体运动的探索一、填空题1.古希腊亚里士多德 20002.意大利阻力相同3.假设推理实验二、问答题:1.静止匀加速直线运动2.阻力不同3.同时落地§2.2 自由落体运动一、填空题:1.重力静止重力加速度 9.8 竖直向下2. √2ℎg3.√2gℎ4.45 小二、选择题1.D2.C3.B4.B5.B三、计算题gt2 =44.1m1.V=gt,t=3s, h=122.下落时间t=2s,一半时间下落高度h=1gt2 =5m2gt2 =80m3.(1)v=gt=40m/s (2)h=12§2.3 匀变速直线运动一、填定题at21.v=v0+at ,x=v0t+122.8.75 63.匀加速直线 1 匀速直线 4 0 匀减速 -4 0二、选择题1.B2.C3.D4.D5.C三、计算题1.v=v0+at t=10s v2-v02=2ax x=110m2.汽车3s内停止运动,当t=2s时X=24m;6秒内位移就是3秒内位移为27m。
大学物理8-13电磁题解
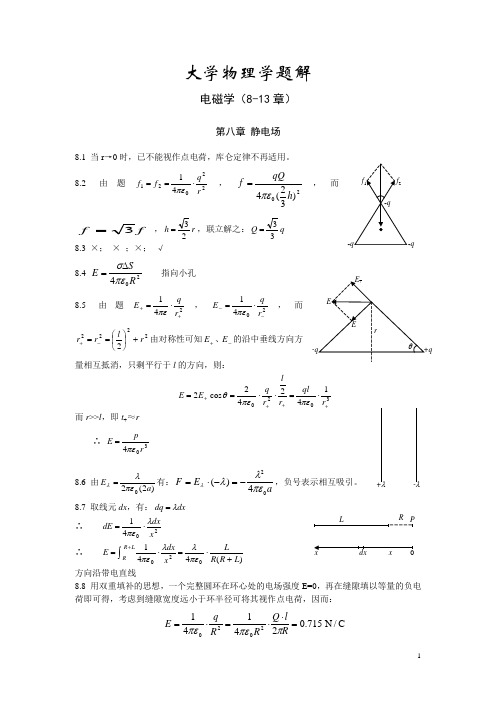
k ( 2r 2 − b 2 ) 4ε 0
(3) 由 E=0 有: r =
2 b 2
8.26 用双重填补的思想,一个完整的无限大平板形成的场强大小 E1 =
σ0 ,方向垂直于板 2ε 0 指 向板 外, 在此 之上 在有 小孔 的区 域叠 加相 同面 密度 的相 反电 荷, 即叠 加电 场大小
E2 =
E=
1 4πε 0
⋅
q Q ⋅l 1 = ⋅ = 0.715 N / C 2 2 R 4πε 0 R 2πR
1
方向沿径向指向缺口。 8.9 取线元 dl,有: dl = R ⋅ dθ d d λRdθ 1 1 ∴ dE = λ θ θ ⋅ = ⋅ d ⋅ − R sin ( 0 0) 4πε 0 4πε 0 R R2 ∴
⋅ 10 − 4 = Ee 0 ⋅ 10 − 4 = 6.64 × 10 5 。 e
4πR ⋅ (−e)
8.17 (1) 0,无;(2)
q 4πε 0 r
2
,沿径向外;(3)
q 4πε 0 r 2
,沿径向向内
d → 8.18 作半径 r 的同心球面, ∫ E ⋅ ds = E ⋅ 4πr 2 ,由高斯定理:
E x = −∫
2π 0
2π 0
λ0 sin θ cos θdθ = 0 4πε 0 R
E y = −∫
λ0 λ sin 2 θdθ = − 0 4πε 0 R 4ε 0 R
8.10 由 对 称 可 知 两 半 无 限 长 直 线 在 0 处 的 场 强 叠 加 为 平 行 干 直 线 方 向 向 左 , 且 λ λ λ , 而半圆环在圆心处的场强为 E 2 = , 方向沿水平向右, 而 R=a。 = E1 = 2 ⋅ 4πε 0 a 2πε 0 a 2πε 0 R ∴E=0 8.11 取宽度为 dx 的无限长,其在 P 点的场强为:
普通物理学第六版下册答案

普通物理学第六版下册答案【篇一:普通物理学第二版课后习题答案(全)】>1.1国际单位制中的基本单位是那些?解答,基本量:长度、质量、时间、电流、温度、物质的量、光强度。
基本单位:米(m)、千克(kg)、时间(s)、安培(a)、温度(k)、摩尔(mol)、坎德拉(cd)。
力学中的基本量:长度、质量、时间。
力学中的基本单位:米(m)、千克(kg)、时间(s)。
1.2中学所学习的匀变速直线运动公式为12s?v0t?at,2 各量单位为时间:s(秒),长度:m(米),若改为以h(小时)和km(公里)作为时间和长度的单位,上述公式如何?若仅时间单位改为h,如何?若仅v0单位改为km/h,又如何?解答,(1)由量纲dim v?3?lt?1,dim a?lt?2,改为以h(小时)和km(公里)作为时间和长度的单位时,1?3m/s?10km/h?10?3600km/h3600?3.6km/h12?3m/s?10km/(h)2?10?3?36002km/h23600?3.6?3600km/h212s?3.6v0t??3.6?3600at,2(速度、加速度仍为单位下的量值)验证一下:2siv0?2.0m/s, a?4.0m/s, t?3600s?1.0h12s?v0t?at,2利用计算得:12s?2?3600??4?36002?7200?25920000?25927200(m)12s?3.6v0t??3.6?3600at,2利用计算得 12s?3.6?2?1??3.6?3600?4?12?7.2?25920?25927.2(km)(2). 仅时间单位改为h?1由量纲,dim adim v?lt?lt?2得若仅时间单位改为h,得:1m/s?m/h?3600m/h3600?3600m/h12m/s?m/(h)2?36002m/h2360022?3600m/h验证一下:122s?3600v0t??3600at,22v0?2.0m/s, a?4.0m/s, t?3600s?1.0h 12 s?v0t?at,2利用计算得:12s?2?3600??4?36002?7200?25920000?25927200(m)122s?3600v0t??3600at,2利用计算得: 122s?3600?2?1??3600?4?12?7200?25920000?25927200(m) (3). 若仅v0单位改为km/h由量纲dim v?lt?3?1,得1m/s?10km/(h)?3.6km/h,36001km/h?m/s3.6仅v0单位改为km/h,因长度和时间的单位不变,将km/h换成m/s得验证一下:112s?v0t?at,3.62v0?2.0m/s, a?4.0m/s2, t?3600s?1.0h12s?v0t?at,2利用计算得:12s?2?3600??4?36002?7200?25920000?25927200(m)112s?v0t?at,3.62利用计算得: 12?10?312s???3600??4?36003.61/36002?7200?25920000?25927200(m)1.3设汽车行驶时所受阻力f与汽车的横截面积s成正比,且与速率 2vv之平方成正比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8-5【磁通量的计算】在地球北半球的某区域,磁感应强度的大小为T 5104-⨯,方向与铅直线成ο60角.求(1)穿过面积为12m 的水平平面的磁通量;(2)穿过面积为12m 的竖直平面的磁通量的最大值和最小值.解:(1)取水平面1S 的法线方向向上为正,则该面积的法线方向与磁感应强度的夹角为ο60.穿过的磁通量为W b BS S B 51110260cos -⨯==⋅=Φο(2)取竖直平面2S 的法线方向向南为正时,该面积的法线方向与磁感应的夹角为ο30.穿过的磁通量最大,为b 1046.330cos 522max W BS S B -⨯==⋅=Φο取竖直平面3S 的法线方向向北为正时,该面积的法线方向与磁感应强度的夹角为ο30.穿过的磁通量最小,为b 1046.3150cos 533min W BS S B -⨯-==⋅=Φο8-19 【毕奥-萨代尔定律的应用】一个塑料圆盘,半径为R ,电荷q 均匀分布于表面,圆盘绕通过圆心垂直于盘面的轴动,角速度为ω.求圆盘中心处的磁感应强度.解:如解图8-19所示,在圆盘上取半径为r 宽为dr 的圆环,环上的电量为rdr R q rdr R q rdr dq 22222===πππσ根据电流的定义,dtdq dI =dq 就是在圆盘绕轴转动的一个周期T 内,垂直通过盘的径向宽为dr 线段的电荷量.所以,有dr R q dq T dq dI 22πωπω===圆电流dl 在盘心的磁感应强度大小为dr R q rdIdB 20022πωμμ==匀角速率转动的带电圆盘在盘心的磁感应强度大小为⎰⎰===R R q dr R q dB B 002022πωηπωηB 的方向沿轴线,与ω成右手螺旋关系.8-24 【安培环路定理】如图所示的空心柱形导体半径分别为21R R 和,导体内载有电流Ι,设电流Ι均匀分布在导体的横截面上.求证导体内部各点(21R r R <<)的磁感应强度B 由下式给出:rR r R R IB 21221220)(2--=πη 试以1R =0的极限情形来检验这个公式.2R r =时又怎样?证明:设导体横截面上的电流密度为δ,有)(2122R R I-=πδ 在导体如截图8-24所示的截面上,以圆柱轴线到考察点P 的距离r为半径作同轴的闭合回路L ,令L 的绕行方向与电流成右手螺旋关系.根据电流分布的轴对称可知,磁感应线具有同样的轴对称分布,在回路L 上,各处dl 的方向与B 的方向一致.运用安培环路定理,有⎰'=⋅=⋅LI r B dl B 02ηπ式中'I 是环绕L 所围电流, 2122212212)(R R R r I R r I --=-='δπ所以,离轴r 处的磁感应强度B 的大小为)()(2121222120)(2-R r R R R r R r I B <<-=πμ命题得证.在上式中,令1R =0,有2202R IrB πη=这是实心的柱形载流导线内离轴r 处磁感应强度B 的大小. 在导线表面,r=R 2,磁感应强度B 的大小为202R I B πη=8-30 【洛伦磁力的概念与应用】一质子以1.0×107m/s 的速度射入磁感应强度为B=1.5T 的均匀磁场中,其速度方向与磁场方向成300角.计算:(1)质子做螺旋运动的半径;(2)螺距;(3)旋转频率.解:(1)质子作匀速率圆周运动的向心力R v mB ev F 2⊥⊥==圆周运动的半径为 m eBmv eB mv R 21048.3sin -⊥⨯===θ(2)螺距为m eBmv v R v T v h 38.0cos 22cos //====⊥θππθ(3)旋转频率为 171028.221-⨯===s meBT v π 8-39 【安培定律】如图所示,在长直导线旁有一矩形线圈,导线中通有电流I 1=20A ,线圈中通有电流I 2=10A.已知d=1cm,b=9cm,l=20cm,求矩形线圈上收到的合力是多少?解:线圈左段导线受力的大小为dl I I l B I F πη221012==左方向向左.右段导线受力的大小)(221012b d l I I l B I F +='=πη右方向向右.线圈所受合力的大小为N b d d l I I F F F 4210102.7])(11[2-⨯=+-=-=πη右左合力F 的方向向右.9-2 【法拉第电磁感应定律和楞次定律的应用】在两平行导线内,有一矩形线圈,如图所示,如导线中电流Ι随时间变化,试计算线圈中的感生电动势.解:取坐标轴Ox ,如解图9-2所示.两电流x 处的磁感应强度大小为xId d x IB πμπμ2)(20120-+-=B 的方向垂直纸面向里.取顺时针为回路的绕行方向,通过面元dx 1l d =S 的磁通量为dx l x I d d x I dS B dS B d 102102)(2⎥⎦⎤⎢⎣⎡-+-=⋅=⋅=Φπμπμ通过矩形线圈的磁通量为)(22)(22221211010120222d l d In d l d In Il dx l x I d d x I l d d +-+=⎥⎦⎤⎢⎣⎡-+-=Φ⎰+πμπμπμ 矩形线圈中的感生电动势为dtdI d l d In d l d In l dt d i )(222212110+-+-=Φ-=πμε 当dtdI>0时,有i ε<0,表明回路中感生电动势的方向与绕行方向相反,为逆时针.若dtdI<0,则有i ε>0,回路中感生电动势的方向与绕行方向一致.9-4 【动生电动势的计算】PM 和MN 两段导线,其长均为10cm,在M 处相接成300角,若使导线在磁场中以速度v=15m/s 运动,方向如图,磁场方向垂直纸面向内,磁感应强度为B=25×10-2T ,问P 、N 两端之间的电势差为多少?哪一端电势高?解:设运动导线上的动生电动势P →M →N,即MN PM PN εεε+=式中PM ε是导线PM 上的动生电动势PM PM PM vBl vBl l B v -==⋅⨯=πεcos )(MN ε是导线MN 上的动生电动势00cos30150cos MN MN MN vBl vBl l B v -==⋅⨯=)(ε两式中MN PM l l =,所以有V Bl PN MN PM PN 3107)30cos 1(v -⨯-=︒+-=+=εεε式中“-”号表明导线上的动生电动势方向与所设正方向相同,由N 指向P ,即沿N →M →P.P 、N 两端的电势差为V V V U PN N p PN 3100.7-⨯=-=-=ε即运动导线上P 端的电势高.9-11 【感生电动势和感生电场的计算】有一螺旋管,每米有800匝.在管内中心放置一绕有30圈的半径为1cm 的圆形回路,在0.01s 时间内,螺线管中产生5A 的电流.问小回路中产生的感生电动势为多少?解:螺线管内的均匀磁感应强度的大小为nI B 0μ=通过小回路的磁通链数为 20r NnI NRS N πμ==Φ=ψ 小回路中的电动势为V dtdIr n N dt d i 3201047.4-⨯==ψ=πμε 式中 s A sAdt dI m r n N /50001.05,01.080030=====,, 9-18 【自感和互感的计算】一截面为长方形的螺绕管,其尺寸如图所示,共有N 匝,求此螺线管的自感.解:设螺绕环中通有电流I ,根据安培环路定理,可有NI r H dl H L=⋅=⋅⎰π2可得到管内距轴线r 处的磁场强度和磁感应强度的大小为rNI H B r NIH πμμπ2,20===通过螺绕管的磁通链数为1220202221R R In Ih N r dr Ih N BdS N N S R R πμπμ⎰⎰===Φ=ψ 螺绕环的自感系数为12202R R In h N I L πμ=ψ=10-1 【谐振动的运动学问题】一个小球与轻弹簧组成的系统,按)38cos(05.0ππ+⨯=t x的规律振动,式中t 以s 为单位,x 以m 为单位.试求:(1)振动的角频率、周期、振幅、初相、速度及加速度的最大值; (2)T=1s 、2s 、10s 等时刻的相位各为多少? (3)分别画出位移、速度、加速度与时间的关系曲线.解:(1)将小球的运动学方程与谐振动的一般形式)cos(0ϕω+=t A x 作比较,可得3,25.02,/12.258,05.00πϕωππω======s T s rad m A小球振动速度为)/()38sin(4.0)38sin(805.0)sin(0s m t t t A dt dx v ππππππϕωω+-=+⨯-=+-==小球振动速度最大值的绝对值为速度振幅m v ,m/s 26.14.0===πωA v m小球振动的加速度为)/)(38cos(2.3)38cos()8(05.0)cos(22202s m t t t A dt dv a ππππππϕωω+-=+⨯-=+-==小球振动加速度最大值的绝对值为加速度振幅m a ,222/6.312.3s m A a m ===πω(2)t=1s 时的相位为32538|)(|11πππϕωϕ=+=+===t t t t=2s 时的相位为349316|)(|22πππϕωϕ=+=+===t t t t=10s 时的相位为3241380|)(|1010πππϕωϕ=+=+===t t t(3)x (t )、v (t )、a (t )曲线如解图10-1所示.10-2 【谐振动的运动学问题】有一个轻弹簧相连的小球,沿x 轴作振幅为A 的振动,周期为T.运动学方程用余弦函数表示.若t=0时,球的运动状态为: (1)A x -=0;(2)过平衡位置向x 正方向运动; (3)过2Ax =处向x 负方向运动; (4)过2Ax =处向x 正方向运动.试用矢量图示法确定相应的初相位的值,并写出振动表达式. 解:由题设条件可知,对同一个简谐运动系统,由于所处的初始状态不同,小球作频率相同处相不同的谐振动.各谐振动对应的旋转矢量图见解图10-2.(1).;0,00πϕ±==-=v A x振动表达式为 ))(cos(SI t A x πω+=(2).;0,0max 00πϕ-=>==v v x振动表达式为 ))(2cos(SI t A x πω-=(3).3;0,200πϕ=<=v A x振动表达式为 ))(3cos(SI t A x πω+=(4).4;0,200πϕ-=>=v A x振动表达式为 ))(4cos(SI t A x πω-=10-9 【谐振动的动力学问题】一弹簧振子作谐振动,振幅A=0.20m ,如弹簧的劲度系数k=2.0N/m ,所系物体的质量m=0.50kg ,试求:(1)当动能和势能相等时,物体的位移是多少?(2)设t=0时,物体正在最大位移处,达到动能和势能相等处所需的时间的是多少?(在一个周期内.)解:(1)振子作谐振动时,有 )cos(0ϕω+=t A x 动能和势能分别为)(sin 212102222ϕωω+==t mA mv E k )(cos 212102222ϕωω+==t mA kx E p动能和势能相等时,有 1)(tan 02=+ϕωt 即 ,...)2,1,0(2)21()t (0=+=+j j πϕω动能和势能相等时的位移为m A x 14.022±=±= 或者,由动能和势能相等时,有),21(2121,2122kA kx E E P ==即 得 A x 22±= (2)据题意可有.0,0,000===ϕ得v A x 所以,谐振动表达式为 t A x ωcos = 式中 s rad s rad m k /2/5.00.2===ω 当A x 22±=时,动能和势能相等,即有 ,...)2,1,0(4)12(2=+==j j t t πω所以,在开始计时后的一个周期内,动能和势能相等的时刻为st st st st 7.2870.2852.18339.084321========ππππ10-22 【简谐运动的合成】一个质点同时参与两个在同一直线上的谐振动:)652cos(03.0)62cos(04.021ππ-=+=t x t x 试求其合振动的运动学方程(式中x 以m 计,t 以s 计).解:这两个谐振动的相位在任何时刻都反相,由旋转矢量图可知,合矢量A 在A 1方位如解图10-22所示.所以,合振幅为m m m A A A 01.003.004.021=-=-=初相位为 6100πϕϕ==合振动的运动学方程为 ))(62cos(01.021m t x x x π+=+=11-2 【波动的特征量各量之间的关系】一横波沿绳子传播时的波动表达式为)410cos(05.0x t y ππ-=x,y 的单位是m ,t 的单位是s.(1)求此波的振幅、波速、频率和波长;(2)求绳子上各质点振动的最大速度和最大加速度;(3)求x=0.2m 处的质点在t=1s 时的相位,它是原点处质点在哪一时刻的相位?(4)分别画出t=1s 、1.25s 、1.50s 各时刻的波形. 解:(1)将绳中横波的表达式)410cos(05.0x t y ππ-=与标准波动表达式⎥⎦⎤⎢⎣⎡+-=022cos ϕλππx vt A y比较可得 m Hz v m A 5.0,5,05.0===λ并有 0,/5.20===ϕλs m v u(2)各质点振动的最大速度为 s m A v m /57.15.0===πω 各质点振动的最大加速度为 222/3.495s m A a m ===πω(3)x=0.2m 处质点在t=1s 时的相位为πππϕ2.9)2.04110(1,2.0=⨯-⨯=)(s m这是t 时刻前,坐标原点x=0处质点的振动相位为πππϕ2.9)0410(1,0=⨯-=t s m )(得 t=0.92s(4)t=1s 时的波动方程为)(4cos 05.0)410cos(05.0m x x y πππ=-=t=1.25s 时的波动方程为)(4sin 05.0)45.12cos(05.0m x x y πππ=-=t=1.50s 时的波动方程为)(4cos 05.0)415cos(05.0m x x y πππ-=-=11-7 【根据已知物理量或波形建立波动表达式】一平面简谐波在t=0s 时的波形曲线如图所示,波速u=0.08m/s. (1)写出该波的波动表达式; (2)画出8Tt =时的波形曲线.解:(1)由波形曲线可知.4.0,04.0m m A ==λ由v u λ=,得s rad v Hz v /4.02,2.0ππω===t=0时,x=0处质点的运动状态为y 0=0,v 0<0,根据旋转矢量图可知,20πϕ=所以,O 点处质点的振动表达式为))(24.0cos(04.0)cos()(0m t t A t y o ππϕω+=+=波动表达式为))(254.0cos(04.02)08.0(4.0cos 04.0)(cos ),(0m x t x t u x t A t x y πππππϕω+-=⎥⎦⎤⎢⎣⎡+-=⎥⎦⎤⎢⎣⎡+-=(2)8T 时波形如下图波形中实线所示,将波向右移动8λ即可.11-11【波的能量】一平面简谐声波的频率为500Hz ,在空气中以速度u=340m/s 的速度传播.到达人耳时,振幅A=10-4cm,试求人耳接受到声波的平均能量密度和声强(空气的密度ρ=1.29kg/m 3). 解:人耳接收到声波的平均能量密度为3622/1037.621m J A -⨯==ωρω 人耳接收到声波的声强为23/1016.2m W u I -⨯==ω11-29 【波的干涉和驻波】若弦线上的驻波表达式为)(20cos 2sin 2.0SI tx y ππ=求形成该驻波的两行波的表达式.解:设弦线上两同振幅的相干波相向而行,在x=0处的振动相位分别为21ϕϕ和,波动表达式分别为)2cos()2cos(2211ϕλπωϕλπω++=+-=x t A y x t A y在弦线上形成的合成波即驻波为)2cos()22cos(2121221ϕϕωϕϕλπ++-+=+=t x A y y y将上式与弦线上的驻波表达式相比较,应有mA t t xx 2.0220cos )2cos(2sin )22cos(1212==++=-+πϕϕωπϕϕλπ可解得 2221πϕπϕ-==,所以,两行波表达式分别为))(2220cos(1.0))(2220cos(1.021m x t y m x t y ππππππ-+=+-=12-10 【双缝干涉条纹的计算】在双缝干涉实验中,两缝的间距为1mm ,屏离缝的距离为1m ,若所用光源含有波长600nm 和540nm 两种光波.试求:(1)两光波分别形成的条纹间距;(2)两组条纹之间的距离与级数之间的关系; (3)这两组条纹有可能重合吗?解:已知.600,540,1,121nm nm m D mm d ====λλ (1)两光波分别形成的条纹间距21x x ∆∆和为nmm m d D x m mm m d D x 60.0100.610600101154.0104.51054010114932249311=⨯=⨯⨯⨯==∆=⨯=⨯⨯⨯==∆------λλ(2)在两光波各自的干涉条纹中,第k 级铭文中心位置分别为2211,λλdD kx dD kx k k == 它们的间隔为mm k m k dDk d D kx k 2512106106)(--⨯=⨯⨯=∆=-=∆λλλ 不同波长、相同级数的条纹的间隔k x ∆随着干涉条纹的增大而增大.(3)在两组干涉条纹中,当2λ的k 级和1λ的(k+1)级条纹重合时,有211λλdD k d D k =+)(得 9540600540121=-=-=λλλk从2λ=600nm 的k=9开始,都将有)1(2)2(1++<k k x x ,即两组条纹重合. 12-15 【薄膜干涉条纹的计算】白光垂直照射在空气中厚度为0.4mμ的玻璃片上.玻璃的折射率为1.50.试问在可见光范范围内(nm 700~400=λ),哪些波长的光在反射中增强?哪些波长的光在透射中增强?解:设波长为λ的光波在玻璃片的上、下表面反射加强,有...)3,2,1(22==+k k en λλ得 124-=k neλ 在可见光范围内,反射加强的波长对应k=3(其他值均在可见光范围外).所以,nm nm 4801321040.050.143=-⨯⨯⨯⨯=λ在玻璃片上、下表面反射减弱(即透射加强)的光波满足条件...)3,2,1()12(22=+=+k k en λλ即 kne2=λ 在可见光范围内,托摄加强的光波波长为K=2时, nm ne600221==λ K=3时, nm ne400321==λ 12-30 【单缝衍射和光栅衍射】用波长nm nm 70040021==λλ和的混合光垂直照射单缝.在衍射图样中1λ的第k 1级明纹中心恰与2λ的第k 2级暗纹中心位置重合.求k 1和k 2.试问1λ的暗纹中心位置能否与2λ的暗纹中心位置重合?解:当1λ的第k 1级明纹恰与2λ的第k 2级暗纹位置重合时,这两个条文在θ方向上的光程差相等,即有22112)12(sin λλθk k a =+=得 472121221==+λλk k 使上式成立,可取k 1=3,k 2=2.当取k 1=6,k 2=10,...值时,上式虽也成立,但单缝衍射的光强已很弱.若1λ的第k 1级暗纹恰与2λ的第k 2级暗纹位置重合,有2211sin λλθk k a ==得 221221λλλk k k == 使上式成立,可取k 1=7,k 2=4.12-33 【单缝衍射和光栅衍射】已知一个每厘米刻有4000条缝的光栅,利用这个光栅可以产生多少个完整的可见光谱(nm 700~400=λ)? 解:根据题意可得光栅常数为m m N L b a 62105.24000101--⨯=⨯==+设λ为可见光中红光的波长(最大波长),在光栅方程λθk b a =+sin )(中,令1sin =θ,可得红光主极大的最高级次29.310760105.296=⨯⨯=+=--λba k 取整数,k=3.所以,中央主极大一侧,可以有三个从紫色到红色的可见光谱.12-47 【光的偏振】如果起偏振器和检偏器的偏振化方向之间的夹角为300.(1)假定偏振是理想的,则非偏振光通过起偏器和检偏器后,其出射光强与原来的光强之比是多少?(2)如果起偏振器和检偏振器分别吸收了10%的可通过光线,则出射光强与原来光强之比是多少?解:设非偏振光的两个互相垂直光振动的光强分别为P S I I 和(P S I I ≠),有P S I I I +=0设起偏器P 1的偏振化方向与S I 光振动方向之间的夹角为θ,则与P I 振动方向之间的夹角为θπ-2,如解图12-47所示.(1)通过理想起偏振器P 1的光强为θθ221sin cos P S I I I +=通过理想检偏器P 2后的透射强度为PS P S P S I I I I I I I I I I +︒+=︒+=︒=30cos )sin cos (30cos )sin cos (30cos 22202222212θθθθ当非偏振光为自然光时,有2I I I P S ==, 375.0432130cos 21202=⨯=︒=I I(2)P 1吸收10%的光能时,)sin cos (1.011.012211θθP S I I I I +-=-=')()(P 2也吸收10%的光能时,︒+-=︒'-='30cos )sin cos (1.0130cos 1.012222212θθP S I I I I )()(当非偏振光为自然光时,有304.030cos )1.01(2130cos )1.01(2122022202=︒-='︒-='I I I I 12-52 【光的偏振】二氧化碳激光器谐振腔的布儒斯特窗一般用诸来制成,使能对10.6m μ附近的红外激光有较大的透射率.如果诸的折射率为4.5,如图所示,试计算用诸制成的布儒斯特窗与放电管轴线所成之角α.解:设诸板的折射率为n ,0i 为沿传播方向的光在诸板表面入射的布儒斯特角,有n i =0tan827747.775.4arctan arctan 0'︒=︒===n i所以 2312900'︒=-︒=i α。
