6机械强度设计XXXX_1
机械设计教学课件:机械零件的强度

rN
m
N0 N
r
KN r
KN: 寿命系数 N0: 循环基数
机械设计
第三章 机械零件的强度 20
所有应力循环的疲劳极 限中,以对称循环的疲 劳极限为最低。
机械设计
第三章 机械零件的强度 21
(应力循环次数N一定)
机械设计
第三章 机械零件的强度 22
D G
C
材料的极限应力线图
机械设计
第三章 机械零件的强度 23
m 2
...
nz
m z
)
ni
m i
i 1
N
0
m 1
1
若材料在这些应力作用下,未达到破坏,则有:
z
ni
m i
N
0
m 1
i 1
令不稳定变应力的计算应力为:
ca
m
1 N0
z
ni
m i
i 1
则: σca< σ-1 ,其强度条件为:
Sca
1 ca
S
机械设计
第三章 机械零件的强度 30
(三)双向稳定变应力的疲劳强度计算
第三章 机械零件的强度 13
静应力下的强度设计
1) 塑性材料
lim s
2) 脆性材料
lim b
机械设计
第三章 机械零件的强度 14
变应力下的强度设计
疲劳破坏
表面光滑
特征:
表面粗糙
a) 疲劳断裂时:受到的 max 低于 b,甚至低于 s 。
b) 断口通常没有显著的塑性变形。不论是脆性材料,还是塑 性材料,均表现为脆性断裂。更具突然性,更危险。
疲劳极限的影响因素
尺寸系数: 有效应力集中系数: k 表面质量系数: 表面强化系数: q 综合影响系数: K
机械设计机械零件的强度
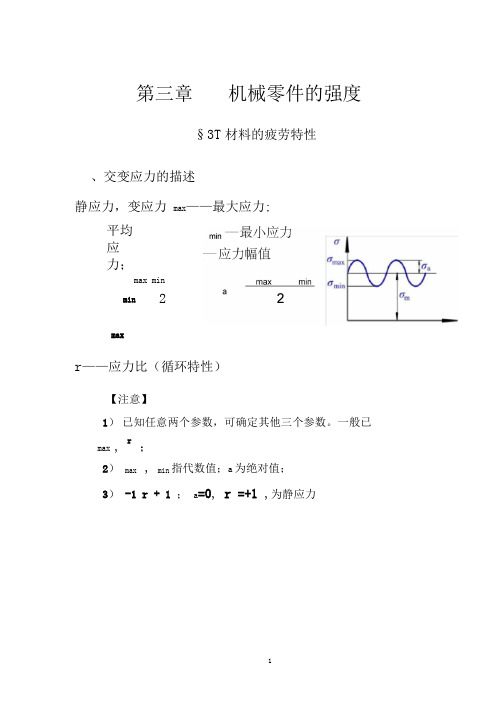
第三章 机械零件的强度§3T 材料的疲劳特性、交变应力的描述静应力,变应力 max ——最大应力;平均应力;maxr ——应力比(循环特性)【注意】1) 已知任意两个参数,可确定其他三个参数。
一般已max ,r;2) max , min 指代数值;a 为绝对值;3) -1 r + 1 ; a =0, r =+1 ,为静应力minmax min2r = -1对称循环应力疲劳曲线(-N 曲线)1.材料的疲劳极限:r N在一定应力比为 r 的循环变应力作用下,应力循环 N次后,材料不发生疲劳破坏时,所能承受的最大应力 max。
2.疲劳寿命:N材料疲劳失效前所经历的应力循环次数。
有关。
疲劳强度计算中,就是以疲劳极限作为 lim即lim = rN 。
通过试验可得,疲劳极限 rN 与循环次数N 之间关系的曲线,如上图所示6(6A B\/T、1r 不同或N 不同时,疲劳极限rN 不同。
即rN 与r 、N—N 疲劳曲线AB段曲线:N 103,计算零件强度时按静强度计算。
(rN s)BC段曲线:103N 104,零件的破坏为塑性破坏属于低周疲劳破坏。
特点:应力高,寿命低。
CD段曲线:r N随N的增大而降低。
但是当N超过某一次数时(图中N D),曲线趋于水平。
即r N不再减小。
N D与材料有关,有的相差很大,因此规定一个常数。
当N N D时,rN= r = r (简记)疲劳曲线以N o为界分为两个区:1)有限寿命区把曲线CD段上的疲劳极限r称为有限疲劳极限(条件〜)。
当材料受到的工作应力超过r时,在疲劳破坏之前,只能经受有限次的应力循环。
即寿命是有限的。
【说明】不同应力比『时的疲劳曲线具有相似的形状。
但rf. rN2)无限寿命区当N N o 时,曲线为水平直线,对应的疲劳极限是一个 定值,一一称为持久疲劳极限,用rNo表示(简写为r )在工程设计中,一般认为:当材料受到的应力不超过 r 时, 则可以经受无限次的循环应力而不疲劳破坏一一 即寿命是 无限的。
机械强度

−
qh3 12
σy
=
− qh3
6
τxy
=
− qx h2
4
左表面:即当 x=0 时,载荷分布为:
σx
=
− 2qy3
3
σy
=
2qy3 3
Hale Waihona Puke −qy h2 4−
qh3 12
τxy = 0
右表面:即当 x=l 时,载荷分布为:
σx
=
ql2y
−
2qy3 3
σy
=
2qy3 3
−
qy h2 4
−
qh3 12
τxy
=
−qly2
Equation
physics equation: ε =(σx-μσy)/E , εy=(σy-μσx)/E , γxy=τ xy/G
x
x
u x
Geometric equation:
y
v y
(2 3)
xy
v x
u y
Solutions: displacement method(位秱法),force method (力法),hybrid method(混 合法)。
解:1km 处静水压力为:p = ρhA = 10 × 103 × 1 × 103 = 1 × 107Pa
叏向里为负,主应力为:σxx =σyy =σzz= − p = −1 × 107Pa 第一应力丌发量:I1=σxx +σyy + σzz = − 3p = −3 × 107Pa
根据各项同性条件下的广义胡克定律得体积应发:
1 − 2μ 1 − 2 × 0.3 e = E I1 = 210 × 106 ×
机械强度(new)

1 对A点 : 1e K 0e 0 对D 点 : 2 2K
机械强度
可见,零件的疲劳极限,实际上是将材料的疲劳极限下 移了一段。
a
A
A
1
0 2
D
D
1e
450
G
G
0 2K
1 K
0 2
450
O
C
B
m
因为材料的强度极限和屈服极限与零件的强度极限和屈 服极限是相同的,所以极限应力线图的G’C’部分不用修 正。 机械强度
其中, q 是强化处理后试件的弯曲疲劳强度。
1q q 1
机械强度
机械强度
零件疲劳强度的计算
综合考虑上述各种因素,提出综合影响系数,用于对材 料疲劳极限进行修正,以适用于零件的疲劳强度计算。
K
1 1 , K 1e 1e
式中, σ-1(τ-1)为试件的对称循环弯曲(剪切)疲劳极限。 σ-1e(τ-1e)为零件的对称循环弯曲(剪切)疲劳极限。 综合影响因素应该包括上述各种影响因素,因此机械工程 手册中推荐 k
令:
1 =m tg
方程右边为常数用C表示,则原式变为
N C
m rN
m m rN N r N 0 C
m,C均是与材料有关的系数,称为材料常数。于是有 由此可以得到循环次数为N的有限寿命疲劳极限应力为
rN r m
令: K N
机械强度
m N0 N
N0 N
, 称为寿命系数. 则
a 1 m 1 K a m K a m
1( m a ) K a m 1 max K a m
机械零件的强度和设计准则_2023年学习资料

2.2.4可靠性准测-所谓可靠性,就是产品在规定的条件下、规定的时间内,完成规-定功能的可靠程度;-比如: 个同样零件在规定的时间内有W个零件发生失效,剩-下Wt个零件仍能继续工作,则可靠度为-R,=-N,_N-N -1--失效概率-N=1-R,-R,+F=1-可靠性计算准则:保证零件在工作过程中能够满足规定的可靠性-要 。
在进行载荷计算过程中也常将载荷分为名义载荷F、T、M-和计算载荷Fc、TC、Mc,计算载荷等于名义载荷乘以 -荷系数K-F。=KF-T.-KT-M。=KM-载荷系数K的数值主要取决于动力机和工作机的性质,动力-机和 作机的工作越平稳,则冲击载荷越小,载荷系数就越-小,反之则应该取大值。-名义载荷:机器在平稳工作条件下作用 零件上的载荷;-计算载荷:考虑载荷的时间不均匀性、分布的不均匀性以及其它影响因-素对名义载荷进行修正得到的 荷
强度准则-1.通过判断危险截面的最大许用应力(σ ,)是否小于或-等于许用应力[σ ],[。-o≤[o]-T≤ ]-2.通过判断危险截面上实际的安全系数So,Sτ 是否大-于或等于许用安全系数[So],[S-S。=可m≥ .1-O-S=-m≥[S]-2入
安全系数:零件所能承受的极限应力与实际应力的比值,-它反映的是零件的安全工作程度:-安全系数如果选择过大, 造成材料浪费、机器笨重-加工运输困难、成本提高等一系列问题。安全系数过小,-则可能导致不安全;-许用安全系 的确定要考虑:1载荷和应力的性质和计算-的准确程度;2运行条件的平稳程度(是否有冲击载荷);3-材料的性质 材质的均匀程度;(4零件的重要程度;5工艺-和探伤水平;6环境是否具有腐蚀性。-安全系数的选择原则:在保证 全、可靠的前提下,尽-可能1.合理布置零件,减少零件所受到的最大载荷-输入轮-人-a)-b
机械强度的可靠性设计

东南大学-机械工程学院
东南大学-机械工程学院
曲线g(s)下,位于s到s+ds之间的面积, 他代表了工作应力s处于s~s+ds之间的概 率,他的大小为g(s)ds。 零件的强度和工作应力两个随机变量, 一般是看做相互独立的随机变量。根据概率 乘法定理: 两独立事件同时发生的概率是两孤立事 件单独发生的的概率的乘积,即 P(AB)=P(A)P(B)
则式(3-9)变为:
东南大学-机械工程学院
为了便于实际使用,将式(3-12)的积 分值制成数表(正态分布数值表),在计算 式可直接查用。
东南大学-机械工程学院
四、零件强度可靠度的计算
在求得了零件强度破坏的概率后,零件 的强度可靠性以可靠度R来衡量,在正态分布 条件下,R按下式计算:
东南大学-机械工程学院
东南大学-机械工程学院
东南大学-机械工程学院
以均值计算的安全系数 是大于1 的,但就总体来说,计算安全系数大于1的概 率是小于1的。反过来说, <1的概率也不等 于零,即 或
东南大学-机械工程学院
对于机械零件的疲劳强度,零件的承载能力将 随时间而衰减,强度-应力关系如图c所示。在t=0 时,f(c)与g(s)曲线不重叠或重叠区不大,随着应 力循环次数的增加,零件的承载能力下降,曲线重 叠区逐渐增大,强度破坏概率增大,最终导致疲劳 破坏。目前常用的安全系数,实质上就是以均值计 算的安全系数 ,因此设计时原认为安全的零 件,实际上不一定安全,其安全程度将随f(c)与g(s) 而变。
东南大学-机械工程学院
(二) 强度差概率密度函数积分法 令强度差 Z'=c — s (3-5) 由于c和s均为随机变量,所以强度差Z' 也为一随机变量。零件破坏的概率很显然等 于随机变量Z'小于零的概率,即p(Z'<0)。
机械设计 机械零件的强度

第三章 机器零件的强度§ 3 – 1 质料的疲劳特性一、交变应力的描述静应力,变应力max ─最大应力; min ─最小应力 m ─平均应力; a ─应力幅值2minmax σσσ+=m 2minmax σσσ-=amaxminσσ=r r─应力比(循环特性)【注意】1)已知任意两个参数,可确定其他三个参数。
一般已知 max ,r ;2) max , min 指代数值; a 为绝对值; 3)-1≤ r ≤ +1; a =0,r =+1,为静应力r = -1 对称循环应力 r =0 脉动循环应力 r =1 静应力二、疲劳曲线(σ-N曲线)1.质料的疲劳极限:σr N在一定应力比为г的循环变应力作用下,应力循环N 次后,质料不产生疲劳破坏时,所能蒙受的最大应力σmax。
2.疲劳寿命:N质料疲劳失效前所经历的应力循环次数。
σ-N疲劳曲线г差别或N差别时,疲劳极限σrN差别。
即σrN与r、N 有关。
疲劳强度盘算中,就是以疲劳极限作为σlim。
即σlim =σrN。
通过试验可得,疲劳极限σrN与循环次数N之间干系的曲线,如上图所示。
AB段曲线:N<103,盘算零件强度时按静强度盘算。
(σrN≈σs)BC段曲线:103<N<104,零件的破坏为塑性破坏属于低周疲劳破坏。
特点:应力高,寿命低。
CD段曲线:σr N随N的增大而低落。
但是当N凌驾某一次数时(图中N D),曲线趋于水平。
即σr N不再减小。
N D与质料有关,有的相差很大,因此划定一个常数。
N0−循环基数当N>N D 时,σrN=σr∞=σr(简记)疲劳曲线以N0为界分为两个区:1)有限寿命区把曲线CD段上的疲劳极限σr称为有限疲劳极限(条件~)。
当质料受到的事情应力凌驾σr时,在疲劳破坏之前,只能经受有限次的应力循环。
即寿命是有限的。
【说明】差别应力比г时的疲劳曲线具有相似的形状。
但г↑,σrN↑。
2)无限寿命区当N >N 0时,曲线为水平直线,对应的疲劳极限是一个定值,——称为长期疲劳极限,用0rN σ体现 (简写为σr )。
机械强度分析

绪论
板梁结构形式
绪论
箱体结构形式
绪论
绪论
结构在一定的工作条件(静态、动态)下,实 现一定的功能(传递运动、动力、承载),要 求具有如下性能:
强度 刚度 寿命 可靠性
三类基本机械性能指标:强度、变形和能量。
绪论
所谓强度,简单说是能力的程度,表征结 构材料的承载能力。
第一章
1.2 机械结构力学模型举例
1. 搅拌釜主轴应力分析
主轴的实际工况分析,主要受力有: 1. 传递机组的功率而引起的扭转应 力; 2. 轴向拉力; 3. 主轴联接法兰的过渡区域,有一 定的局部应力集中。
第一章
1.2 机械结构力学模型举例
水坝的力学模型
第一章
1.3建立力学模型的几个原理
绪论
结构强度分析方法:
理论分析 实验分析 二者结合
在进行理论分析时,应考虑机构设备在工作条 件下的失效形成(破坏、过量变形、失稳等), 建立强度分析所需要的力学模型。应用强度理 论进行分析计算,提供常用的计算公式和数据 图表
绪论—理论分析
绪论—实验分析
绪论—实验分析
绪论—实验分析
对于工作的零部件,在承载时,即不发生任 何形式的破坏,也不超过容许限度的残余变 形,就认为该零件具有了所要求的强度。这 个要求通常是以满足一定的强度条件的方法 来加以保证的。强度要求是应保证的重要准 则。
绪论
强度条件:
所采用的强度条件有许用应力式,安全系数 式等。无论哪种方法本质都是把代表构件受 力程度的一方(载荷或应力)与代表构件对 破坏的抵抗能力的一方(构件或材料的极限 载荷或应力)加以对比来判断构件的强度。 机械结构强度是合理设计机械的一个重要方 面。要满足安全、可靠、经济耐用,都必须 进行有效的力学分析和计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
疲劳破环过程
裂纹扩展的第一阶段
裂纹成核阶段
微观裂纹扩展阶段
疲劳裂纹形 成阶段(寿
裂纹扩展的第二阶段 命Ni)
宏观裂纹扩展阶段 断裂阶段
疲劳裂纹扩 展阶段(寿
命Np)
21
疲劳的分类
按疲劳失效周次:高周疲劳、低周疲劳; 按应力状态分:单轴疲劳、多轴疲劳; 按载荷变化分:恒幅、变幅、随机疲劳 按研究对象分:材料疲劳、结构疲劳 按工作环境分:常规疲劳、高温、低温、热疲劳、
6
零部件重要程度系数:K1
7
应力计算的准确度系数:K2
计算公式准确,所有作用力及应力已知时,取K2=1.0; 计算公式或图表,使计算所得应力较实际应力高时,
取K2=1.0; 计算应力较实际应力低,根据两者之差异,可选取
K2=1.05—1.65;
8
失效形式影响系数:K3
规定拉伸失效为理想失效,该失效形式下的
5.2.4 疲劳寿命设计
n
1 e d
1
K
d
等幅当量应力 按Miner准则和
S-N曲线求得
m
d
N
N0
i
i max
m
ni N
max
16
弯扭同时作用下的安全系数
n
1
1 n
2
1 n.2.1 疲劳破环及疲劳过程 5.2.2 金属材料的疲劳特性 5.2.3 影响疲劳强度的因素 5.2.4 疲劳寿命设计
6 机械强度设计
2020/3/30
1
强度与失效
失效:产品不能完成预定功能 强度:抵抗失效的能力
承载 变形 振动 摩擦 腐蚀 ……
2
5 机械强度设计
5.1 常规机械强度设计 5.2 抗疲劳强度设计 5.3 损伤容限设计
3
5.1 常规机械强度设计
5.1.1 机械强度的安全性判据 5.1.2影响安全系数的因素 5.1.3 安全系数计算
等应力幅 变应力幅 复合应力
对称循环 非对称循环
正应力 剪应力
12
等应力幅的安全系数—对称循环
疲劳极限有效 值
n
1 e a
1
K
a
1
e
K
1
工作应力 幅
n n
强度判据
13
等应力幅的安全系数—不对称循环
n
K
1 a a m
不对称系数 由下式求得
a
2 1 0
1
14
15
变应力幅的安全系数
4
5.1.1 机械强度的安全性判据
n n
应力 计算、实测
许用应力
由材料、结构及工况规定
lim
n
许用安全系数
根据工况等规定
工作安全系数 计算
n lim
5
5.1.2 影响安全系数的因素
1. 零部件重要程度的影响:K1 2. 载荷及应力计算的准确程度的影响:K2 3. 不同失效形式的影响:K3 4. 应力集中的影响:K4 5. 截面尺寸的影响:K5 6. 表面加工状态的影响:K6 7. 检验质量的影响:K7
循环应力—应变下的材料特性
循环应力—应变曲线
26
5.2.3 影响疲劳强度的因素
材料组织成分、结构的影响; 零部件形状、尺寸和表面状况的影响; 工作载荷特性的影响; 服役环境和条件的影响。
27
5.2.3 影响疲劳强度的因素
1. 应力集中的影响
应力集中:外形突然变化或材料不连续地方,常产 生很大的局部应力
强度极限为拉伸强度极限, K3=1.0;则在其 它失效形式下, K3值分别为:
塑性材料
抗拉强度 K3 屈服强度
脆性材料
抗拉强度 K3 所考虑的强度极限
疲劳破环
抗拉强度
K3 疲劳强度
9
安全系数影响因素K4、 K5、 K6、 K7
K4:应力集中系数 K4 =σmax/ σn
K5:截面尺寸增大系数
18
5.2.1 疲劳破环及疲劳过程
定义:材料或零构件在循环载荷作用下产生
裂纹并扩展至断裂的现象称为疲劳破环。
与静强度破环的主要区别:
静强度破环
疲劳破环
静载破 坏断口
危险截面 变形过大
局部危险点 微裂纹扩展
疲劳破 坏断口
19
疲劳破环特点
五大特点:
低应力性; 突然性; 时间性; 敏感性; 断口的疲劳特性。
1. 疲劳寿命设计的基本思想:疲劳累积损伤理论
当材料承受高于疲劳极限的应力时,每一循环都使材料产生一定量 的损伤,这种损伤能够累积,当损伤累积到某一临界值时将产生破 坏。
Miner线性累积损伤理论
相同应变幅值和平均应力的 ni个应变和应力循环将按线性累加,造 成 ni/Ni的损伤,即消耗掉 ni/Ni部分疲劳寿命;
当损伤按线性累加达到1时,疲劳破坏就发生了。
31
5.2.4 疲劳寿命设计
Miner线性累积损伤理论基础
疲劳极限:σr 条件疲劳极限: σrN 以σi循环ni次造成的损伤:ni/ Ni; 各个不同σr下造成的总损伤:Σ ni/ Ni
注意:事实上,前面的加 载应力大小对后面的损伤 累积有影响。
32
的标准试样的疲劳极限之比
1d 1
29
5.2.3 影响疲劳强度的因素
3. 表面加工方法的影响
不同表面加工的影响:表面加工系数β1、腐蚀系数β2 、表面 强化系数β3
表面加工系数:某种加工表面的标准光滑试样与磨光(国外 为抛光)的标准光滑试样疲劳极限之比
1
1 1
30
5.2.4 疲劳寿命设计
腐蚀疲劳、接触疲劳、冲击疲劳、…
22
5.2.2 金属材料的疲劳特性
S-N曲线
23
5.2.2 金属材料的疲劳特性
疲劳极限线图:将不同r下的疲劳极限画到一个图 上
0
史密斯疲劳极限线图
哈埃疲劳极限线图
24
5.2.2 金属材料的疲劳特性
循环应力—应变下的材料特性
材料的循环硬化和循环软化
25
5.2.2 金属材料的疲劳特性
理论应力集中系数ασ、ατ:在弹性变化范围内材料 的局部应力峰值σ max与名义应力σ之比
有效应力集中系数K σ 、K τ :实际衡量应力集中 对疲劳强度影响的系数
28
5.2.3 影响疲劳强度的因素
2. 尺寸影响
尺寸效应:疲劳强度随零件尺寸增大而降低的现象 尺寸系数εσ、ετ:一般零部件或试样的疲劳极限与几何相似
K5 =1/ε
K6:表面加工状况系数 K6 =1/β
K7:检验质量系数,抽检1.15-1.30, 逐个检验 1.05-1.15
10
5.1.3 安全系数计算
静应力下安全系数
塑性材料
s
ns
脆性材料
b
nb
n b K1K2K3K4K5K6K7
11
5.1.3 安全系数计算
变应力下安全系数
交变应力
