大学物理05_5麦克斯韦速率分布律
05-2.麦克斯韦分布
2.方均根速率
v v f (v)dv
2
___ 2
m0 4 e 0 2kT 3kT 3RT M m
0
3/ 2
m0 v 2 2 kT
v dv
3RT v M RT 然速率----在T为定值的气体中,气体分子最可能具有的 df ( v ) 速率值 v p 。
以N 表示某平衡态下气体分子总数,f(v)表示速率分布函 数,分子在v1到v2速率间隔内所有气体分子数的总和
v2
v1
Nf (v)dv
图示两气体分子f(v)-v 曲线,分别表示 H2 和 O2 在同一温 度下的麦克斯韦分布曲线,则由图形分析可知 O2 分子的 最概然速率为 A.2000m/s B.500m/s C.50m/s D.200m/s
v v v (m / s)
100以下 100---200 200---300 300---400 400---500 500---600
N / N
N
是 对 应 区 间 的 分 子 数
1.4% 8.1%
17.0% 21.4% 20.4% 15.1%
600---700
700---800
9.2%
f (v )
T1
令
dv
0
___ 2
3RT v M
___ 2
v
v
2 RT RT 1.41 M M
vpv
vp 2kT m0
RT 1.73 M
8RT RT v 1.60 M M
1930-1934年我国物理学家葛正权(1895-1988)测 了铋(Bi)蒸汽分子的速率分布 实验装置如图
5麦克斯韦速率分布

2.平均速率
v
气体分子在各种速率的都有,那么 平均速率是多大呢? 假设:速度为v1的分子有 N1 个, 速度为v2的分子有N 2 个, 平均速率为: v N1v1 N 2v2 N nvn N n
i 1
N i v i
N
§6. 麦克斯韦速率分布律/三.麦克斯韦速率分布律应用
N 解得:a 8v 0
a ( v 5 v 0 )dv N v0 NF ( v )
M
• 2)速率分布在2v03v0 间隔内的分子数N
N N FM ( v )dv
2 v0 3 v0 3 v0 2 v0
a
3 3adv 3av0 N 8
v0
v
§6. 麦克斯韦速率分布律/五.例题
§6. 麦克斯韦速率分布律/四.麦克斯韦速率分布律验证
例4:假想的气体分子,其速率分布如图 所示。当v>5v0时分子数为零。试求 1)根据N和v0,表示常数a的值; 2)速率在2v0到3v0间隔内的分子数; 3)分子的平均速率。
解:根据速率分布 曲线,速率分布可 表示为
NFM ( v )
3a 2a
§6. 麦克斯韦速率分布律/ 二、麦克斯韦速率分布规律
1865年春辞去教职回到家乡系统地总结他 的关于电磁学的研究成果,完成了电磁场理论的 经典巨著《论电和磁》,并于1873年出版。 1871年受聘为剑桥大学新设立的卡文迪什实验 物理学教授,负责筹建著名的卡文迪什实验室, 1874年建成后担任这个实验室的第一任主任, 直到1879年11月5日在剑桥逝世。
2kT vp m
T1 T2
T2 T1
曲线的峰值右移, 由于曲线下面积 为1不变,所以峰 值降低。 o
麦克斯韦气体速率分布律

麦克斯韦气体速率分布律Maxwell Velocity Distribution大家知道,由气体的温度公式可以得出气体分子的方均根速率。
例如在时,氦气。
氧气。
但我们要注意的是,方均根速率仅是运动速率的一种统计平均值,并非气体分子都以方均根速率运动。
事实上,处于平衡状态下的任何一种气体,各个分子均以不同的速率、沿各个方向运动着。
有的速率大于方均根速率,有的速率小于方均根速率,它们的速率可以取零到无穷大之间的任意值。
而且由于气体分子间的相互碰撞,每个分子的速度也在不断地改变,所以在某一时刻,对某个分子来说,其速度的大小和方向完全是偶然的。
然而就大量分子整体而言,在平衡状态下,分子的速率分布遵守一个完全确定的统计性分布规律又是必然的。
下面我们介绍麦克斯韦应用统计理论和方法导出的分子速率分布规律。
气体分子按速率分布的统计规律,最早是由麦克斯韦于1859年在概率论的基础上导出的,1877年玻耳兹曼由经典统计力学中也导出该规律。
由于技术条件的限制,测定气体分子速率分布的实验,直到本世纪二十年代才实现。
1920年斯特恩(O.Stern首先测出银蒸汽分子的速率分布;1934年我国物理学家葛正权测出铋蒸汽分子的速率分布;1955年密勒(Mlier和库士(Kusch测出钍蒸汽分子的速率分布。
斯特恩实验是历史上最早验证麦克斯韦速率分布律的实验。
限于数学上的原因和本课程的要求,我们不推导这个定律,只介绍它的一些基本内容。
*麦克斯韦(J. C. Maxwell,1831—1879)英国物理学家,经典电磁理论的奠基人,气体动理论的创始人之一。
他提出了有旋电场和位移电流概念,建立了经典电磁理论,这个理论包括电磁现象的所有基本定律,并预言了以光速传播的电磁波的存在。
1873年,他的《电磁学通论》问世,这本书凝聚着杜费、富烂克林、库仑、奥斯特、安培、法拉第……的心血,这是一本划时代巨著,它与牛顿时代的《自然哲学的数学原理》并驾齐驱,它是人类探索电磁规律的一个里程碑。
(完整版)麦克斯韦速率分布律的推导与验证

麦克斯韦速度分布律的推导与实验验证摘要:本文对麦克斯韦速度分布律的内容及其历史来历做了简略概述,重点是用初等方法 推导了麦克斯韦速度分布律,同时简单地描述了一下它的实验验证。
关键词:速度分布函数,实验验证。
一. 内容1麦克斯韦速度分布律的内容当气体处于平衡态时,气体分子的速度在 v~v dv 间隔内,及分子速度分量在V x ~ V x dV x , V y ~ V y dV y , J dV z 间隔内的分子数dN(v)占总分子数 N的比率为:其中m 为分子的质量,T 为气体温度,k 为波尔兹曼常数,-m(v 2 v : v ;) - mv 22 2为气体分子平动能。
dN °)表示速度矢量的端点在速度体元d 内的分子数占总 N 分子数的比率,换言之,一个分子取得 v~v dv 间隔内速度的几率。
2、分子速度分布函数3m 2 m& V: v Z)/ 2kT ( )2e y2 kTf (v )的物理意义是:分子速度在 v 附近,单位时间间隔内的分子数占总分 子数的比率。
3、速度分量分布函数3、麦克斯韦速率分布律dN ( v)m(v X v y v Z )/ 2kTdv x dV y dv Z ,dN(v) NdydV y dV z=( Nd*2 kTdN(V y )NdV y(2 kTdN(V z ) ,m ,(1m 7mv X /2kT )2e xf (VX ) f( V y )fz1 x 2mv Z /2kT)e詁mv y /2kT)e热学研究(论文)将以V x ,V y ,V z 为轴的笛氏坐标进行坐标变换,变为球坐标V,,2v sin d d dv4、分子速率分布函数3i m ,2 ( )2e 2 kT物理意义:分子速率在v 附近,单位速率间隔内的几率。
二. 历史1859年4月,麦克斯韦偶然的读到克劳修斯关于平均自由路程的那篇论文, 很受鼓舞,重燃了他原来在土星卫环问题上运用概率理论的信念,认为可以 用所掌握的概率理论对动理论进行更全面的论证。
大学物理麦克斯韦分子速率分布定律资料

11
例: 设有N个气体分子,其速率分布函数为
f
(
)
A
(0 0
)
0 0 0
求: (1)常数A;(2)最概然速率,平均速率和方均根;
(3)速率介于0~0/3之间的分子数;(4)速率介于0~ 0/3
之间的气体分子的平均速率。
f()
解: (1)气体分子的分布曲线如图
2 1300
N
dN
0
3 Nf ( )d
0
0 3
0
N
6
3 0
(0
)d
7N 27
13
(4)速率介于0~0/3之间的气体分子平均速率为
0~0 3
0
3 dN
0 0
0 3
0
N
6 v03
2
(
0
)d
30
7N 27
14
3 dN 0
注意:速率介于 1~ 2之间的气体分子的平均速率
的计算是
2f ( )d
1~2
1
2 f ( )d
1
而非
1 ~2
2f ( )d
1
14
作业题
设. 有N个粒子,其速率分布函数 f v 为
f
v
Av 30 v
0
v 30 v 30
求: (1)归一化常数A的值;(2)最概然速率
(3)N个粒子的平均速率 v
15
§3.4 麦克斯韦分子速率分布定律
任何一个分子,速度大小和方向都是偶然的, 不可预知。但在平衡态下,大量气体分子的速度分布 将具有稳定的规律 — 麦克斯韦速度分布律。
只考虑速度大小的分布—麦克斯韦速率分布律。
第四、五讲 麦克斯韦分布律 能均分定理

N 0 dvx dvy dvznvx f (vx , vy , vz )dt dA
n
0
vx
f
(vx
)dvxdAdt
kT
2 m
1/
2
dAdt
1 nv dAdt
4
单位时间内与单位面积相碰的分子数 为
N 1 nv dtdA 4
v 为平均速率
§4.7 能量按自由度均分定理
§4.5 麦克斯韦分布律
大量分子整体在一定的条件下,它们的速度的分布却遵 从一定的统计规律,这个规律叫麦克斯韦速度分布律。若不考 虑分子速度的方向,则叫麦克斯韦速率分布律。
一、麦克斯韦按速度分布律
设气体总分子数为N,处于温度为T的平衡态时,
速度介于 vx vx dvx , vy vy dvy , vz vz dvz
质量为M的理想气体的内能为
M1
U
(t r 2s)RT
M 2
温度改变,内能改变量为
U M 1 (t r 2s)RT M 2
对于理想气体,等体过程 đQ dU
摩尔等体热容量为
CV ,
(
đQ dT
)V
dU dT
1 (t r 2
2s)R
例如:对于双原子分子气体, t r 2s 7
7 CV , 2 R
在v1—v2区间
dN f (v)dv N
N v2 f (v)dv
N
v1
f (v)
在0—区间有
dS
dN N
=面积
N 面积 N
f (v)dv 1
v 0 ——归一化条件 O v v dv v1 v2
三种统计速率
(1)最概然速率 vp 与f(v)极大值对应的速率。
推导麦克斯韦速度分布律、速率分布律的简单方法

推导麦克斯韦速度分布律、速率分布律的简单方法麦克斯韦速度分布律是量子力学中重要的一部分。
1860年,麦克斯韦发现在粒子系统中,粒子运动的速度都遵循一定的分布关系,即概率密度函数与速度成反比,这就是麦克斯韦速度分布律。
那么,如何推导出麦克斯韦速度分布律和速率分布律?
首先,考虑一个温度为T的系统,采用能量有限的情况下可以把粒子的运动视为马尔可夫链的形式。
由于能量有限,可以认为处在同一状态的粒子的总体数量就构成了该状态的热平衡状态。
由此可推出粒子的速度分布概率:
P(v) = e^(-mv^2/2kT)
其中,m为粒子的质量,T为温度,k为Boltzmann常数。
将此式作为粒子的速度分布函数,即可推出其速率分布函数。
即:
f(v) = e^(-mv^2/2kT) * Usqrt(m/2πkT)
此式也叫麦克斯韦分布,概率密度与粒子速率成反比,即概率密度随着粒子速率的增加而减少。
通过此式,可以推导出麦克斯韦速度分布律和速率分布律。
以上便是推导麦克斯韦速度分布律以及速率分布律的简单方法。
虽然在实际应用中,还有许多根据环境情况改变相关参数的变体,但基础思想是一致的:概率密度随着粒子运动速度的增加而减少。
大学物理第8章第5节-麦克斯韦-玻尔兹曼分布律

f (v)dv
f (v)dv
a
2v 0
v0 v0
f (v)dv
f (v)dv 1
2v 0
0
v0
2v0
v
0
(a v0 )vdv
2v0
v0
[2a (a v0 )v]dv 0dv 1
2v0
a 1 v0
(3) 由图可知, 分布曲线在 v 0 处取极大
0
a v v dv 2 0
7 v0 0.778v0 9
说明: (4)、(5)、(6)中有误.
麦克斯韦速度分布律
2 2 2 m(vx v y vz ) dN m dvx dv y dvz exp N 2 k T 2 k T B B 在 vx ~ vx dvx , vy ~ vy dvy , vz ~ vz dvz 区 32
值
2a
f (v)
a
0
v0
2v0
v
v p v0
(4) N 个粒子的平均速率
v vf (v)dv
0
v0
(a v0 )v 2 dv v[2a (a v0 )v]dv v 0dv v0
0 v0 2v 0
2v 0
(5) 0~ v0 2 内的粒子数
v0 2
N
0
v0 2
dN
0
v0 2
Nf (v)dv
0
N a N vdv v0 8
(6) v0 2 ~ v0 内分子的平均速率
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
气体分子速率可以取从0到∞之间
的一切数值。速率很大和速率很
小的分子数所占的比率都很小,
f(0)=f(∞)=0 , 而 具 有 中 等 速 率 的
分子数所占的比率却很大。
上页 下页 返回 退出
例题5-5 从速率分布函数推算分子的三个统计速率
(1)算术平均速率
v
vf (v)dv
v4π(
m
)
3
2
O
v exp
mv2 2kT
共同作用的结果。
上页 下页 返回 退出
麦克斯韦(James Clerk Maxwell 1831—1879)
•他提出了有旋电场和位移电流概念,建 立了经典电磁理论(麦克斯韦方程组), 预言了以光速传播的电磁波的存在。
•1873年,他的《电磁学通论》问世,这 是一本划时代巨著,它与牛顿的《自然哲 学的数学原理》并驾齐驱,它是人类探索 19世纪伟大的英国 电磁规律的一个里程碑。 物理学家、数学家。 经典电磁理论的奠 •在气体动理论方面,他还提出气体分子 基人,气体动理论 按速率(速度)分布的统计规律。 的创始人之一。
当 v 0时,v dv ;N dN; 2. 速率分布函数 f(v) 的定义 f(v)
f (v) lim N dN v0 vN Ndv
注意:
在平衡态下,f(v)仅是v的函数。 O
v v+Δv
v
上页 下页 返回 退出
3. 速率分布函数 f(v) 的意义:概率密度函数
※分布在速率 v 附近单位速率间隔内的分子数占总 分子数的百分比(比率);
m不变,T vp
2kT m
曲线的峰值右移,由于曲线下 面积为1不变,所以峰值降低。O
T2 T1
T2 T1
vp1 vp2
v
同一气体,不同温度
不同气体,相同温度: f (v)
T不变,m vp
2kT m
曲线的峰值左移,由于曲线下 面积为1不变,所以峰值升高。O
m2 m1
m1 m2
vp2 vp1
上页 下页 返回 退出
四、麦克斯韦速率分布函数 f(v) 的性质
(1) f (v)dv 速率在v-v+dv内的分子数占总分子数的百分比
(2) Nf (v)dv 速率在v-v+dv内的分子数
(3) v2 f (v)dv 速率在v1→v2内的分子数占总分子数的百分比 v1
(4) v2 Nf (v)dv 速率在v1→v2内的分子数 v1
vp 100
vp 50
把这些量值代入前式即得
N N
4 π
99 100
2
e
99 100
2
1 50
1.6601%
说明:若以W=1代入更为方便。
N 4 12 e12 1 1.6604%
Nπ
50
可见误差极其微小!
上页 下页 返回 退出
选择进入下一节 §5-0 教学基本要求 §5-1 热运动描述 理想气体模型和状态方程 §5-2 分子热运动和统计规律 §5-3 理想气体的压强和温度公式 §5-4 能量均分定理 理想气体内能 §5-5 麦克斯韦速率分布律 §5-6 麦克斯韦-玻尔兹曼能量分布律 重力场中粒
e
mv2 2 kT
v
2
dv
0
0
2πkT
8kT 8RT 1.60 RT
πm
πM mol
M mol
(2)方均根速率
v2
v2 f (v)dv
v2 4π(
m
)
3
2
e
mv2 2 kT
v
2
dv
0
0
2πkT
v2 3kT 3RT 1.73 RT
m
M mol
M mol
上页 下页 返回 退出
(3)最概然速率(the most probable speed):vp
上页 下页 返回 退出
分子速率分布实验曲线(柱状图)如下所示:
相 对 分 子 数
O
v
分子速率分布实验曲线
上页 下页 返回 退出
二、速率分布函数
1.研究气体分子的速率分布 •把速率分成若干相等区间 •求气体在平衡态下分布在各区间内的分子数 •各区间的分子数占气体分子总数的百分比 速率分布:把速率可能出现的值分成若干相等区间, 全部分子如何分配到这些区间中去的问题。
2RT M
RT 2 103
1000
m/s
(vp )H2
RT 103
f (v)
1.41103 m/s
He
( v 2 )H2
3RT M H2
H2
1.73103m/s O 1000
v (m/s)
上页 下页 返回 退出
例题5-6 试计算气体分子热运动速率的大小介于
vp-vp/100 和 vp+vp/100 之间的分子数占总分子数的 百分比。
O dv
v v1 v2
上页 下页 返回 退出
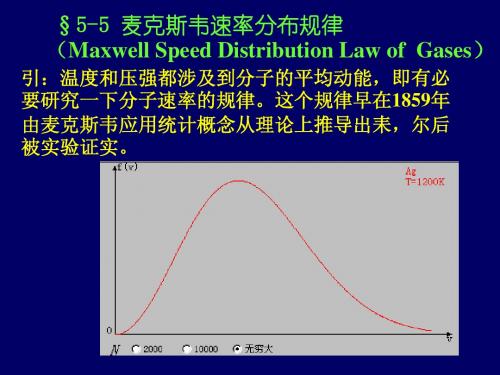
三、麦克斯韦速率分布律
早在1859年,麦克斯韦应用统计概念和力学原理 导出在平衡态下气体分子速率分布函数的具体形式
f (v) 4π(
m
) e v 3 2
mv2 2 kT
2
2πkT
麦克斯韦速 率分布函数
f (v)
麦克斯韦速率分布曲线
它是二次函数 v2 与指数函数
(10) N (1 mv2 ) f (v)dv 速率比 v 大的所有分子平动动能之和 v2
v2 vf v dv
(11)
v1
f v2
速率在v1→v2区间所有分子速率的平均值
v dv
v1
(12) v2 vf v dv 无实际物理意义! v1
上页 下页 返回 退出
同一气体,不同温度: f (v)
解:按题意
v
vp
vp 100
99 100
vp
v
vp
vp 100
vp
vp 100
vp 50
在此利用vp,引入W=v/vp,把麦克斯韦速率 分布律改写成如下简单形式:
N 4 W 2eW 2 W Nπ
请作为公式记住此 麦克斯韦速率分布 律的简化式!
上页 下页 返回 退出
现在 W v 99 , W v 1
※对单个分子来说,它表示分子速率落在该单位速 率间隔内的概率。
4. 速率分布曲线
在v-v+dv区间的分子数占总分子数的百分比(概率)为
dN
N 在v1-v2区间
f (v)dv N
v2
dN N
f (v)dv
面积
f (v)
N
v1
N 面积 N
在0-区间有 f (v)dv 1 0 ——归一化条件
最概然速率是指在任一温度T 时,气体中分子最可能
具有的速率值。即在v =vp时,分布函数取极大值。
df dv
4π(
m
)
3
2
[2ve
m 2kT
v2
2πkT
v2
m kT
m v2
ve 2kT ]vvp
0
vp
2kT m
2RT 1.41 RT
M mol
M mol
f (v)
(4)三种速率的关系
vp v v2
上页 下页 返回 退出
当铝钢圆柱体以给定角
速度 转动时,只有满足下
列关系式的原子才能顺利通
过细槽出口:
长为 L=20.40 cm、刻有螺旋形 细槽的铝钢圆柱体。
tL v
vL
这里的斜槽是一速率选择器。
而其它速率的原子则将沉积在槽壁上而不能通
过。改变角速度,检测器D则测出通过细槽的不
同速率的原子射线强度,于是可得原子蒸气的速率 分布,见下图。
分布表 分布曲线 分布函数 将速率分成若干相等的区间,如
0 ~ 10 m/s; 10 m/s ~ 20 m/s; 20 m/s ~ 30 m/s; L
上页 下页 返回 退出
设任一速率区间为: v ~ v v
设总的气体分子数为N,在该区间内的分子数为ΔN
N ——分布在速率 v附近单位速率间隔内的分子数 v N ——分布在速率 v 附近单位速率间隔内的分子数 vN 占总分子数的比率。
vp : v : v2 1.41:1.60 :1.73
O
vpv v2
v
上页 下页 返回 退出
它们的数量级一般在几百米 每秒至几千米每秒。
三种统计速率有不同的应用:
在讨论速率分布时,要用到最概然速率;在计 算分子碰撞频率时,要用到平均速率;在计算分子 的平均平动动能时,则要用到方均根速率。
(5)
Nf (v)dv
速率比 v 大的分子数
v
(6)
v
Nf (v)dv
速率比 v 小的分子数
0
上页 下页 返回 退出
(7)
1 (
mv2 )
f
(v)dv
所有分子平动动能的平均值
02
(8) (v) f (v)dv (v) 0
(9) v2 Nvf (v)dv 速率在v1→v2内所有分子速率的总和 v1
v 1.60 RT 1.60 8.31 300 447 m / s
M
0.032
可见在相同温度下: v2 > v > vp
上页 下页 返回 退出
练习二、氦气的速率分布曲线如图所示, 求:(1) 试在图上画出同温度下氢气分子速率分布曲线的大致图;
(2) 氢气在该温度时的最概然速率和方均根速率。
解:(2) (vp )He
§5-5 麦克斯韦速率分布律
平衡态下,理想气体分子速度分布是有规律的, 这个规律叫麦克斯韦速度分布律。若不考虑分子速度 的方向,则叫麦克斯韦速率分布律。
