有限自动机理论06章图灵机-简化
有限自动机理论05章下推自动机(简化)

接收语言L={(ab)n|n≥0}
< q1,a,Z0,q2,AZ0> < q2,b,A,q1,ε> < q1,ε,Z0,q1,ε > 规则是不确定的。
n 接收语言L={(ab) |n>0}
< q0,a,Z0,q0,AZ0> < q0,b,A,q1,ε> < q1,a,Z0,q2,AZ0> < q2,b,A,q1,ε> < q1,ε,Z0,q1,ε> 规则是不确定的。
NFA:δ(q,x)= {q1,q2,… qn} 单态的PDA: <x,q, q1 > <x,q, q2 > … <x,q, qn >
NFA:
若 q ∈δ*(q0,w) 单态的PDA: 有 (*,w,q0)=>*(*,ε,q)
NFA:
若q∈F 则 单态的PDA: <ε,q,ε>
q0∈Q是开始状态 Z0∈Г是栈底符号 FQ是接收状态集合
δ:Q×(∑∪{ε})×Г→Q×Г* 对于确定的PDA,有 δ(q,x,D)=( q′,V) 对于不确定的PDA,有 ( q′,V) ∈δ(q,x,D)
一般
使用 <q,x,D,q′,V> 表示δ函数
定义5-2 PDA格局(或瞬间描述ID) 格局代表某个时刻PDA的情况 PDA的格局是一个三元式 (q,w,ζ)
不确定 PDA 对于某一格局可 能会有不同的下一格局。
+ 用=> 代表格局的多次变换
* 用=> 代表格局的任意次变换
5.1.3 PDA接收语言的两种方式
定义 5-3 PAD 以空栈方式接收的语 言为L(M),且 L(M)={w|(q0,w,Z0) =>*(q , ε , ε) q∈Q}
理论计算机科学中的图灵机

理论计算机科学中的图灵机图灵机是理论计算机科学中的一个重要概念。
它被认为是能够计算任何可计算问题的最基本的计算机模型。
理解图灵机对于对计算机科学的学习和研究都至关重要。
一、图灵机的定义和原理图灵机是由英国数学家图灵提出的一种计算模型。
它包括一个有限控制器和一条无限长的纸带。
纸带被划分为一系列的单元格,每个单元格上可以写上一个字符。
控制器通过读取纸带上的字符和控制器内部的状态来进行计算。
它可以进行有限的计算,而且可以处理无限长的输入。
在图灵机模型中,所有的操作都是基于读取和写入单元格上的字符来进行。
图灵机具有非常简单的结构,但它却能够计算出任何可计算问题。
二、图灵机的应用图灵机能够计算出任何可计算问题,因此它在理论计算机科学中有着非常重要的应用。
它被用于证明计算机科学中的许多重要问题,例如停机问题和可计算性问题。
通过证明一个问题是不可计算的,我们可以得出它是无法用计算机解决的。
这对于计算机的设计和实现都有着重要的指导意义。
此外,图灵机还被广泛应用于计算机语言和自动机理论的研究中。
我们可以使用图灵机来描述计算机语言的语法和语义,并且使用它来定义自动机模型。
这在编程语言的编译、解释和分析中都有着广泛的应用。
三、图灵机的限制尽管图灵机是一种非常强大的计算模型,它仍然存在着一些限制。
其中最明显的一点是图灵机的速度。
尽管图灵机能够计算出任何可计算问题,但某些问题可能需要非常长的时间才能得到结果。
例如,计算出一个长文本的哈希值可能需要几分钟,而对于一个复合的问题,甚至需要几个世纪才能计算得出。
此外,图灵机还无法解决某些问题,例如非计算问题和不规则问题。
这些问题之所以无法用图灵机解决,是因为它们没有确定的方法来解决它们。
这些问题是无法用算法来解决的,并且需要人类直接进行解决。
四、结语图灵机是理论计算机科学中最重要的概念之一。
它被认为是能够计算出任何可计算问题的最基本计算机模型。
通过图灵机的研究,我们可以深入理解计算机科学的基本原理,理解计算机能力和限制。
图灵机计算机的理论模型

图灵机——计算机的理论模型
机器的程序是五元组{Si , X , Y , L(R或N) , Sj}形式的指 令集,定义了机器在一个特定状态下读入一个特定字符时所 采取的动作。 五个元素的含义如下:
①Si 表示机器当前的状态;
②X 表示机器从方格中读入的内容,也即当前内容; ③Y 表示机器用来代替X 写入方格中的内容; ④L、R、N 分别表示左移一格、右移一格和不移动; ⑤Sj 表示机器下一步的状态。
图灵机——计算机的理论模型
图灵机的计算开始于初始状态,设为S0,终止于停止(HALT)状态,设为SH。 例: 设计能够实现“a+1”运算的图灵机,计算完成后要求读写头回到原位。
图灵机进行“a+1”运算的控制规则表
输入
当前状态 (Si) S0 S1 S1 S1 S2 S2 S2 S3 S3 S3 S4 当前内容 (X ) b 0 1 b 0 1 b 0 1 b 任意 重写的新内容 (Y) b 1 0 b 1 0 1 0 1 b b
英国科学家阿兰.图灵 (1912-1954)
图灵证明,只有图灵机能解决的 计算问题,实际计算机才能解决。
“图灵奖”是美国计算机协会于1966年设立的。
什么是图灵机? 图灵机由一条无限长的纸带、读/写头及控制
器构成。
图灵机模型
控制器内包括控制规则表,它能够通过读/写头对纸带上 的符号进行读或写,读写头可以在纸带上左右移动。 纸带分成了一个个的小方格,每个方格中可以记录机器 字母表里的符号,如0或1等。
பைடு நூலகம்输出
读写头移动方向 (L,R或N) L R L R R L L R R N R 进入的新状态 (Sj) S1 S3 S2 SH S3 S2 S4 S3 S3 SH S3
turingmachine图灵机

图灵机的意义
图灵机模型理论是计算科学最核心的理论之一 图灵机模型为计算机设计指明了方向 图灵机模型是算法分析和程序语言设计的基础
理论
图灵机概述
所谓的图灵机就是指一个抽象的机器,它有 一条无限长的纸带,纸带分成了一个一个的 小方格,每个方格有不同的颜色。有一个机 器头在纸带上移来移去。机器头有一组内部 状态,还有一些固定的程序。在每个时刻, 机器头都要从当前纸带上读入一个方格信息, 然后结合自己的内部状态查找程序表,根据 程序输出信息到纸带方格上,并转换自己的 内部状态,然后进行移动。
读写头
状态控制器
图灵机的组成
一个确定型单带图灵机由以下四个部分组成 (见上页图): ·无限长的带子 TAPE,带子划成小格, 格子标记 … , -3,-2,-1,0,1,2, 3,… ·读写头HEAD ·控制规则表TABLE ·状态存储器
图灵机的组成-TAPE
纸带被划分为一个接一个的小格子,每个格 子上包含一个来自有限字母表的符号,字母 表中有一个特殊的符号 表示空白。纸带上 的格子从左到右依此被编号为 0, 1, 2, ... , 纸带的右端可以无限伸展。
图灵机的基本思想
用机器来模拟人们用纸笔进行数学运算的过 程,该过程可分为如下两个简单动作:
➢在纸上写上或擦除某个符号 ➢把注意力从纸的一个位置移动到另一个位置
而在每个阶段,人要决定下一步的动作,依 赖于:
➢此人当前所关注的纸上某个位置的符号 ➢此人当前思维的状态。
… -2 -1 0 1 2 3 …
图灵机计算思想
计算机系统应该有: 存储器(相当于存储带)
中央处理器(控制器及其状态)
为了能够将数据保存到存储器并将计算结 果从存储器送出来展示给用户,计算机系 统还应该有输入设备和输出设备如键盘、 鼠标、显示器和打印机等。
高级语言及其语法描述-有限自动机理论

文法G2对句子aaabb的推导: S => A B S A B => a A B A a A => a a A B A a A => a a a B A a => a a a b B B b B => a a a b b B b
27
e.g. 文法产生的语言
S a S b | ab
文法G3对句子aaaabbbb的推导: S => a S b S a S b => a a S b b S a S b => a a a S b b b S a S b => a a a a b b b b S a b
E (E) (E+E) (i+E) (i+i)
17
+ ,从 出发,经一步或若干步,可 1 n 1 推导出n, ≥1 ,从 出发,经0步或若干步,可推 1 n 1 导出n , ≥0 + 故1n,相当于=或
18
三种推导的比较
• 直接推导()的长度为1 • 直接推导序列( +)的长度n≥1 • 广义推导( *)的长度≥0
7
得到语法分析树: <句子> <主语> <代词> <谓语> <间接宾语> <动词> <直接宾语> <名词>
<代词> <冠词>
He
gave
me
a
book
8
• 上下文无关文法的定义: 一个上下文无关文法G是一个四元式 G=(VT,VN,S,P),其中
–VT:终结符集合(非空) –VN:非终结符集合(非空),且VT VN=
形式化的方法
图灵和图灵机模型PPT课件

15
第十五页,共24页。
图灵简介
• 随后,应邀于美国普林斯顿大学与美国著名 数学家和逻辑学家邱奇合作,并于1938年取 得博士学位。在这里,还研究了布尔1854年 创建的逻辑代数,自己动手用继电器搭建逻 辑门,组成了乘法器。在美国,还遇到了普 林斯顿大学教师天才科学家冯·诺伊曼。
– 1946年5月以前由于找不到称心的助手,一直“单枪匹马”,直到威尔 金森(1970年图灵奖获得者)成了图灵得力助手,此时ACE已到第5版, 前4版由于图灵不善于也不重视保管文档资料而不知去向。
– ACE是一种存储程序式计算机,但其存储程序思想并非受冯·诺伊曼论文的影响,而 是他自己的构思。冯·诺伊曼本人也从来没有说过存储程序的概念是他的发明,却不 止一次地说过图灵是现代计算机设计思想的创始人。
– 图灵机
– 几何定理的机器证明
• 对计算本质的真正认识取决于形式化研究的进程
2
第二页,共24页。
形式化研究进程
• 1275年,思维机器“旋转玩具” 是一种形式化的产物,标志着形式 化思想革命的开始
• 形式化方法和理论的研究学的重要基础 – 希尔伯特纲领:将每一门数学的分支构成形式系统或形式理论,并在以此
– 反映了计算学科的抽象、理论和设计3个过程
• 抽象和理论两个过程关心的是解决具有能行性和有效性 的模型问题
• 设计过程关心的是模型的具体实现问题
10
第十页,共24页。
从计算角度认知思维、视觉和生命过程
• 符号主义者认为:认知是一种符号处理过程, 因此思维就是计算(认知就是计算)
形式语言与自动机理论--第六章(蒋宗礼)

• 右句型(right sentencial form)
–最右派生得到的句型可叫做右句型。
• 最左归约(leftmost reduction)
–与最左派生对相的归约叫做最右归约。
6.1.1 上下文无关文法的派生树
• 规范派生(normal derivation)
–最右派生。
• 规范句型(normal sentencial form)
• 必要性
–设Anα ,现施归纳于派生步数n,证明存在结果为α 的A-子树。 设n≤k(k≥1)时结论成立,往证当n=k+1时结论也成立:令 Ak+1α,则有: AX1X2…Xm *α1X2…Xm *α1α2…Xm … * α 1 α 2 … α m
6.1.1 上下文无关文法的派生树
6.1.1 上下文无关文法的派生树
• CSL
– CSG、LBA。
教材及主要参考书目
1.蒋宗礼,姜守旭. 形式语言与自动机理论. 北京: 清华大学出版社,2003年 2. John E Hopcroft, Rajeev Motwani, Jeffrey D Ullman. Introduction to Automata Theory, Languages, and Computation (2nd Edition). Addison-Wesley Publishing Company, 2001 3. John E Hopcroft, Jeffrey D Ullman. Introduction to Automata Theory, Languages, and Computation. Addison-Wesley Publishing Company, 1979
6.1.1 上下文无关文法的派生树
【计算理论】图灵机(图灵机示例)
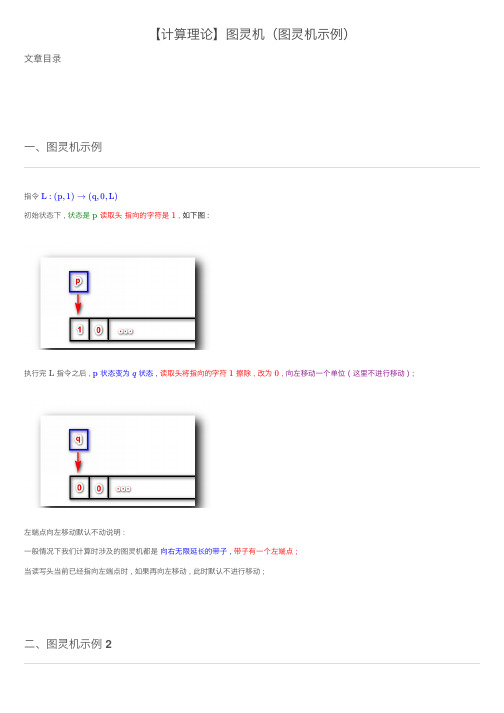
【计算理论】图灵机(图灵机⽰例)⽂章⽬录⼀、图灵机⽰例指令 初始状态下 , 状态是 读取头 指向的字符是 ,如下图 :执⾏完 指令之后 , 状态变为 状态 , 读取头将指向的字符 擦除 , 改为 ,向左移动⼀个单位 ( 这⾥不进⾏移动 ) ;左端点向左移动默认不动说明 :⼀般情况下我们计算时涉及的图灵机都是 向右⽆限延长的带⼦ , 带⼦有⼀个左端点 ;当读写头当前已经指向左端点时 , 如果再向左移动 , 此时默认不进⾏移动 ;⼆、图灵机⽰例 2L :(p,1)→(q,0,L)p 1L p q 10任务 : 设计⼀个图灵机 , 给定输⼊之后 , 图灵机会 在输⼊中寻找 字符 ;算法 :如果 找到了 字符 , 就会将该字符转变成 字符 , 然后将当前状态改为接受状态 , 然后停下来 ;如果带⼦上的字符都读取完毕后 , 没有找到 , 只找到了空⽩字符 , 将该空⽩字符改为 , 然后向左移动⼀格 , 然后停下来 ;( ⾃动机停下的前提是处于可接受状态 )根据上述算法 , 构造图灵机 ;图灵机设计 :① 状态集 , 其中 是开始状态 , 是接受状态 ;② 输⼊字符集 ;③ 带⼦字符集 , 其中 是空⽩字符 ;④ 指令 ⑤ 指令 ⑥ 指令 上述图灵机设计中 , 最关键的部分是三条指令 ;图灵机处于开始状态 , 读头指向 字符 , 左端的 是输⼊字符 , 查看图灵机是否接受 字符串 ;下⾯图灵机后续都是空⽩字符 ;根据指令 指令 , 当前状态 , 当前指向字符 , 输出内容是 ,即 状态变为 , 读头指向的字符变为 , 向右移动⼀个字符 ;如下图 :110f 11Q ={q,f}q f Σ={0,1}Γ={0,1,B}B δ(q,0)=(q,0,R)δ(q,1)=(f,0,R)δ(q,B)=(q,1,L)q 00000B δ(q,0)=(q,0,R)q 0q,0,R q 0此时继续 根据指令 指令 , 当前状态 , 当前指向字符 , 输出内容是 ,即 状态变为 , 读头指向的字符变为 , 向右移动⼀个字符 ;如下图 :此时继续 根据指令 指令 , 当前状态 , 当前指向字符 , 输出内容是 ,即 状态变为 , 读头指向的字符变为 , 向左移动⼀个字符 ;如下图 :δ(q,0)=(q,0,R)q 0q,0,R q 0δ(q,B)=(q,1,L)q B q,1,L q 1此时继续 根据指令 指令 , 当前状态 , 当前指向字符 , 输出内容是 ,即 状态变为 , 读头指向的字符变为 , 向右移动⼀个字符 ;如下图 :此时继续 根据指令 指令 , 当前状态 , 当前指向字符 , 输出内容是 ,即 状态变为 , 读头指向的字符变为 , 向右移动⼀个字符 ;此时的状态 是接受状态 , ⾃动机停⽌运⾏ ;如下图 :δ(q,0)=(q,0,R)q 0q,0,R q 0δ(q,1)=(f,0,R)q 1f,0,R f 0f图灵机 与 ⾃动机 接受的条件是不同的 ;图灵机计算过程中 , ⼀旦到达接受状态 , ⽴刻停机 , 不再继续进⾏计算 ; 并且称该图灵机是可接受的 ;⾃动机即使到达接受状态 , 也要把⾃动机读取的字符读取完毕 , 才停⽌计算 ; 然后在查看最终的状态是否是接受状态 ;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
使用=>+代表格局的多次变换 使用=>*代表格局的任意次变换
定义6-4
图灵机 M= ( Q , ∑,
q 0 , qα , δ ) 在字母表 ∑ 上接收的语言为 L(M) , 则 L(M)={w|存在w1,w2∈(∑′)* 有 q0w =>* w1qαw2 }
定义6-5 完全的图灵机
如果图灵机对于一切输入串都能够停 机----完全的图灵机。 完全的图灵机接收的语言 L 称为递归 语言(图灵可判定语言)
③在 seek_a 状态时,没有再发现 a ,需 检查是否所有的b都已经被扫描过。 <seek_a,$,check,$,R> <check,$,check,$,R> <check,B,accept,B,N>
某些不需要定义的规则 <start,b,? > //无a
<start,B,? > //无a 无b <del_b,B,? > //b少 <seek_a,B,? > //无b <seek_a,b,? > //不可能 <check,b,? > //b多
6.1 图灵机的基本模型
6.1.1 图灵机的定义
图灵机的物理模型
a1 a2 a3 … aj … an an+1 …
FSC
一个有限状态控制器(FSC) 一个外部的存储设备 可以向右扩展的无限长度带 带上具有左端点,使用“┣”表示 图灵机直接扫描输入带上左端点右边 的第一个符号。
带分解为单元,每个单元可以为 空或存放字母表上的字母符号 带的空白单元标记为B 有限状态控制器通过一个读/写头 与带进行耦合。
②处于状态 del_b ,扫描到 b ,用 # 代替 它,向左寻找a,(从①重复循环) <del_b,b,seek_a,#,L> <seek_a,#,seek_a,#,L> <seek_a,a,del_b,#,R> //最右的a
③seek_a状态时,没有再发现 a(都已被 # 所代替 ) ,还需要检查是否所有的 b 都已经被扫描过。 <seek_a,├,check, ├ ,R> <check,#,check,#,R> <check,B,accept,B,N>
②处于状态 del_b ,扫描到 b ,用 $ 代替 它,向左寻找a,(从①重复循环) <del_b,b,seek_a,$,L> <seek_a, $,seek_a, $ ,L> <seek_a, # ,seek_a, # ,L> <seek_a,a,del_b,#,R>
③在 seek_a 状态时,没有再发现 a (都 已经被#所代替) 需检查是否所有的b都已经被扫描过 还必须注意#与$的顺序。
指令
<start,a,s_a,a,R> <s_a,a,s_a,a,R> (扫描a) <s_a,b,s_b,b,R> <s_b,b,s_b,b,R> (扫描b) <s_b,B,first,B,L> <first,b,first,b,L> <first,a,first,a,L>
已经保证顺序 <first,┣,new_start,┣,R> (开始检查a和b的个数是否相等) <new_start,a,del_b,#,R> <del_b,a,del_b,a,R> <del_b,#,del_b,#,R> <del_b,b,seek_a,#,L>
<seek_a,#,seek_a,#,L> <seek_a,a,del_b,#,R> <seek_a,┣,check,┣ R> (检查是否有多余的b) <check,#,check,#,R> <check,B,accept,B,N>
例6-8接收语言{
TM=(Q,∑,
n n n a b c |n>0}
五元式描述动作
<q,x,q′,W,{L,R,N}> 其中:x,W∈∑ ′( ∑的增广集合) 图灵机处于状态q,扫描到符号x, 则 状态变换为q′,印刷上新的符号W, 读/写头向左、或向右 或不移动。
例6-1 用TM接收 语言{a2n |n≥0}
图灵机带上符号串为: ┣aaa…aaaB 图灵机初始处于状态even,将要扫描 第一个a,则
<check2 ,!,check3,! ,R> 识别第一个! <check3 ,! , check3, ! , R> 跳过剩余! <check3 , B , accept , B , N>
<seek_a,┣,check1,┣,R> <check1,#,check1,#,R> <check1,$,check2,$,R> <check2,$,check2 ,$,R> <check2,B,accept,B,N>
例6-6 {
n n a b |n>0}的第二种算法
当图灵机遇到a时,将a改写为# 向右寻找b,找到b,将b改写为$
思路1:
当图灵机遇到a时,将a改写为#
向右寻找b,找到b,将b改写为# 再向左找a … 直到所有a都找完。 (向左找的a是整个a串最左边的a)
指令为 ①读到一个a,用#代替它,向右找b <start,a,del_b,#,R> <del_b,a,del_b,a,R> <del_b,#,del_b,#,R>
再向左找a (此时的a是整个a串最左边的a) …,直到所有a都找完。
指令
①读到一个a,用#代替它,向右寻找b <start,a,del_b,#,R> <del_b,a,del_b,a,R> <del_b,$,del_b,$,R>
②处于状态 del_b ,扫描到 b ,用 $ 代替, 向左寻找a,(从①重复循环) <del_b,b,seek_#,$,L> <seek_#,$,seek_#,$,L> <seek_#,a,seek_#,a,L>//跳过a串 <seek_#,#,seek_a,#,R> //最右# <seek_a,a,del_b,#,R> //最左a
6.1.2 图灵机的构造
例6-3接收仅有一个1的0、1串 TM=({q0,q1,q2},{0,1}, q0,q2,δ)
∑′={0,1,B}
<q0,0,q0,0,R> <q0,1,q1,1,R> <q1,0,q1,0,R> <q1,B,q2,B,N>
例6-4 构造图灵机
接收语言{ anbn|n>0}
②处于状态 del_b时,扫描到b,用 $代替 它,向右寻找c: <del_b , b , del_c , $ , R> <del_c , b , del_c , b , R> <del_c , $ , del_c , $ , R> <del_c ,! , del_c ,! , R>
③处于状态del_c时,扫描到c,用!代替 它,向左找a,(从①开始又重复循环) <del_c , c , seek_a ,! ,L> <seek_a ,! , seek_a,!,L> <seek_a ,b ,seek_a , b , L> <seek_a ,$ ,seek_a , $ , L> <seek_a ,# ,seek_a , # , L> <seek_a ,a ,del_b , # , R>
问题
该图灵机能接收anbn的所有串
但该图灵机也能接收aababb 等 原因:使用#代表已扫描的a和b 没有保证a和b的顺序。
为了区别原来的字母a和b
使用#和$分别代替字母a和b 当a和b都识别后,带上的串为 ├###…##$$$…$$B
例6-5 修改上例: ①读到一个a,用#代替它,向右寻找b <start,a,del_b,#,R> <del_b,a,del_b,a,R> <del_b,#,del_b,#,R> <del_b,$,del_b,$,R>
在某个时刻,有限状态控制器处 于某个状态,读/写头将扫描带上的 一个单元 依照状态和扫描到的带上符号, 图灵机将有一个动作如下:
有限状态控制器的状态进行改变; 把刚刚扫描过的单元上符号擦除掉, 并印刷上一个新的符号(有可能印刷上 与原来符号相同的符号); 读/写头向左或者向右移动一个单元; 或者读/写头不移动。
start, accept,δ) Q={start , del_b , del_c , seek_a , check1,check2,check3,accept} ∑={a,b,c} ∑′={a,b,c,B,#,$,!}
指令
①读到一个a,用#代替它,向右寻找b <start, a , del_b , # , R> <del_b , a , del_b , a, R> <del_b ,# ,del_b, #, R> <del_b ,$, del_b ,$, R>
定义6-2 图灵机的格局ID
w1qw2∈ w1是读/写头左边带上的符号串 q是图灵机当前所处的状态 w2是读/写头右边的带上的符号串
(∑′)*Q(∑′)*
δ(q,x)
图灵机在格局w1qw2时停机
若w1qw2=w1qxw对于 ? 无定义。
定义6-3 格局的转换
若 M 在 w1qw2 上不停机,则如下定义
