有限元作业1
有限元 1-2-杆单元
第2章杆系单元和杆系结构整体分析2.1杆系单元2.2杆系结构整体分析第2章杆系单元和杆系结构整体分析2.1杆系单元2.2杆系结构整体分析对象、任务对象任务对象：研究有限大小的个体(element)对象研究有限大小的个体任务：1. 建立应变与结点位移分量之间的关系;2. 建立应力与结点位移分量之间的关系;33. 建立结点力与结点位移分量之间的关系;4. 把作用在单元内的外载转化成结点荷载，即单元等效节点力。
一、分离单元1 结构离散取杆件与杆件交点、集中力作用点、杆件与支承的交点为节点。
相邻两节点间的杆件段是单元。
节点编号时力求单元两端点号差最小。
YX2 坐标系有限元中的标系有体标系和局部标系有限元中的坐标系有整体坐标系和局部坐标系。
对于一个结构，整体坐标系一般只有一个；而局部坐标系有很多个，一个单元就有一个局部坐标。
并标系有很多个个单元就有个局部标并且局部坐标系每一个单元的规定都是相同的，这样，同类型单元刚度矩阵相同。
YX杆系结构单元主要有铰接杆单元和梁单元两种类型。
它们都只有2个节点i 、j 。
¾约定：单元坐标系的原点置于节点i ；节点i 到j 的杆轴（形心轴）方向为单元坐标系中x 轴的正向。
y 轴、z 轴都与x 轴垂直，并符合右手螺旋法则。
¾对于梁单元，y 轴和z 轴分别为横截面上的两个惯性主轴惯性主轴。
·x yj·z i土木工程学院有限单元法二、杆单元单元分析维杆单元下图示出了一维铰接杆单元，横截面积为A ，长1、一维杆单元度为l ，弹性模量为E ，轴向分布载荷为p x 。
单元有2，单元坐标为一维坐标轴个结点i ，j ，单元坐标为维坐标轴x 。
··i j x p x u ju i l LINK土木工程学院有限单元法P-8··i x p x j l u ju i LINK⎫⎧=i e u ⎧单元结点位移向量{}⎭⎬⎩⎨j u δ单元结点力向量：⎬⎫⎨=j i e F F F }{⎭⎩（1）位移模式和形函数①位移模式因为只有2个结点，每个结点位移只有1个自由度，因此单元的位移模式可设为：12u a a x =+（3）式中a 1、a 2为待定常数，可由结点位移条件时x =x i 时，u =u ix =x j 时，u =u j确定。
(完整版)有限元考试试题——第一组
有限元考试试题一、简答题（5道，共计25分）。
1.有限单元位移法求解弹性力学问题的基本步骤有哪些？（5分）2. 在划分网格数相同的情况下，为什么八节点四边形等参数单元精度大于四边形矩形单元？（5分）3.轴对称单元与平面单元有哪些区别？（5分）4.有限元空间问题有哪些特征？（5分）5.简述四节点四边形等参数单元的平面问题分析过程。
（5）分）二、论述题（3道,共计30分）。
1. 简述四节点四边形等参数单元的平面问题分析过程。
（10分）2.轴对称问题的简单三角形单元是否是常应力，常应变？为什么？（10分）3.在薄板弯曲理论中做了哪些假设？薄板单元和厚板单元的基本假设有什么不同？（10分）三、计算题（3道，共计45分）。
ν=；1.如图所示等腰直角三角形单元，其厚度为t，弹性模量为E，泊松比0单元的边长及结点编号见图中所示。
求(1)形函数矩阵N(2)应变矩阵B和应力矩阵S(3)单元刚度矩阵e K（12分）2.如图所示的四结点矩形单元，求出节点3的位移。
设厚度t＝1m，μ＝0，E 为常量。
（13分）注：对于四节点矩形单元有：()()()()()()()()()⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫+-=++=-+=--=ηξηξηξηξ1141114111411141.14321N N N N →)4,3,2,1()1)(1(41=++=i N i i i ηηξξ()[][][][]eT Aek k k k k k k k k k k k k k k k y x t B D B k ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==⎰⎰44434241343332312423222114131211d d .2，[][][][][][][]()()()()())4,3,2,1,( 3111311a 212123111311218d d d d 21111=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+-+-+⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+-===⎰⎰⎰⎰--j i b a b b a a b Et B D B abt y x t B D B k j i j i j i j i j i j i j i j i j i j i j i j i jTijTAiijηηξξμξξηηηξμξμηηξμξμηξξηημηηξξμηξ3.有一如图3(a)所示的剪力墙，墙顶作用竖向荷载P 。
弹性力学：平板弯曲问题的有限元分析(1)
平板弯曲问题的有限元分析(1) Kirchhoff弹性薄板理论
参考文献： “弹性力学(下册)”第13章。徐芝纶
x
2w
2 (z2
2
2
)dz 4
E 3 12(1 2 )
x
2w
(c)
同样，在y为常量的截面上，每单位宽度内的 y , yx , yz
也分别合成如下的弯矩，扭矩，和横向剪力：
M y
2 2
z
y dz
E
12(1
3
2
)
(
2w y2
2w x2
)
(d)
M yx
2
2
z yxdz
E 3 12(1 2 )
(9-6)
( z )z q
(f)
2
将(9-6)式代入薄板上板面的边界条件：
得：
E
12(1
3
2
)
4
w
q
(9-7)
或 D4w q， (9-8)
其中
D
E
12(1
3
2
)
(9-9)
薄板的弹性曲面微分方程
为薄板的弯曲刚度
§9-３ 薄板横截面上的内力
► 薄板横截面上的内力，称为薄板内力，是指薄板横截面的单 位宽度上，由应力合成的主矢量和主矩。
对z积分，得到： z
2(1 2 )
2
( 4
z
z2 )4w 3
F3 (x,
有限元分析报告（1）
有限元分析报告（1）有限元仿真分析实验⼀、实验⽬的通过刚性球与薄板的碰撞仿真实验，学习有限元⽅法的基本思想与建模仿真的实现过程，并以此实践相关有限元软件的使⽤⽅法。
本实验使⽤HyperMesh 软件进⾏建模、⽹格划分和建⽴约束及载荷条件，然后使⽤LS-DYNA软件进⾏求解计算和结果后处理，计算出钢球与⾦属板相撞时的运动和受⼒情况，并对结果进⾏可视化。
⼆、实验软件HyperMesh、LS-DYNA三、实验基本原理本实验模拟刚性球撞击薄板的运动和受⼒情况。
仿真分析主要可分为数据前处理、求解计算和结果后处理三个过程。
前处理阶段任务包括：建⽴分析结构的⼏何模型，划分⽹格、建⽴计算模型，确定并施加边界条件。
四、实验步骤1、按照点－线－⾯的顺序创建球和板的⼏何模型（1）建⽴球的模型：在坐标(0,0,0)建⽴临时节点，以临时节点为圆⼼，画半径为5mm的球体。
（2）建⽴板的模型：在tool-translate⾯板下node选择临时节点，选择Y-axis,magnitude输⼊，然后点击translate+，return;再在2D－planes-square ⾯板上选择Y-axis,B选择上⼀步移下来的那个节点，surface only ,size=30。
2、画⽹格（1）画球的⽹格：以球模型为当前part，在2D－atuomesh⾯板下，surfs 选择前⾯建好的球⾯，element size设为，mesh type选择quads，选择elems to current comp,first order，interactive。
（2）画板的⽹格：做法和设置同上。
3、对球和板赋材料和截⾯属性（1）给球赋材料属性：在materials⾯板内选择20号刚体，设置Rho为,E为200000,NU为。
（2）给球赋截⾯属性：属性选择SectShll,thickness设置为，QR设为0。
（3）给板赋材料属性：材料选择MATL1，其他参数：Rho为,E为100000,Nu 为，选择Do Not Export。
第2章_弹性力学基础及有限元法的基本原理1
W U
当外力的形式是多样的时，外力的虚功等于：
W f Pc f Pv dV f Ps dS
T T T v s
• 1.4 平面问题定义
严格地讲，任何结构都是空间的。对于某些特殊情 况，空间问题可以转化为平面问题。
（1）平面应力问题 满足条件： 1）几何条件 厚度尺寸远远小于截面尺寸； 2）载荷条件 载荷平行于板平面且沿厚度方向均匀 分布，而板平面不受任何外力作用。
1）位移函数 分片插值→ 假设一种函数来表示单元位移分布 一般选取多项式（简单而且易求导）
可用于离散的单元： • 三角形单元； • 矩形单元； • 不规则四边形单元。 DOF 节点的自由度：节点所具有的位移分量的数量。 一个单元所有节点的自由度总和称为单元自由度。 （1）单元参数只能通过节点传递到相邻单元 （2）单元和节点必须统一编号
2.2 单元分析（位移、应力、应变） 任务：形成单元刚度矩阵，建立单元特性方程 因此必须建立坐标系，如下图：
1D问题的弹性模量
E杨氏弹性模量
泊松比是指材料在单向受拉或受压时，横向正应变与轴向 正应变的绝对值的比值，也叫横向变形系数，它是反映材 料横向变形的弹性常数。 若在弹性范围内加载，横向应变εx与纵向应变εy之间存 在下列关系： εx=- νεy 式中ν为材料的一个弹性常数，称为泊松比。泊松比是 量纲为一的量。 可以这样记忆：空气的泊松比为0，45#钢0.3，水的泊松 比为0.5，中间的可以推出。
• 未知数 应力 6个+应变 6个+位移 3个=15个 • 方程个数 平衡方程 3个+几何方程6个+物理方程6个=15个 原则上可以根据15个方程求出15个未知物理量 但实际求解时先求出一部分再通过方程求解剩下的。 目前有限元法主要采用的是位移法，以三个位移 分量为基本未知量。位移-应变-应力，应力和外力平衡
国科大有限元作业1
作业1
1.叙述弹性力学中三维空间问题的平衡方程、几何方程、物理方程、力边界条
件和位移边界条件，并写出矩阵形式的表示式。
2.分别写出平面应力问题和平面应变问题的平衡方程、几何方程、物理方程、
力边界条件和变形协调方程，请以矩阵形式表示。
3.叙述最小势能原理，并写出其数学表示式。
4.试用流程图的形式概括有限单元法的分析过程。
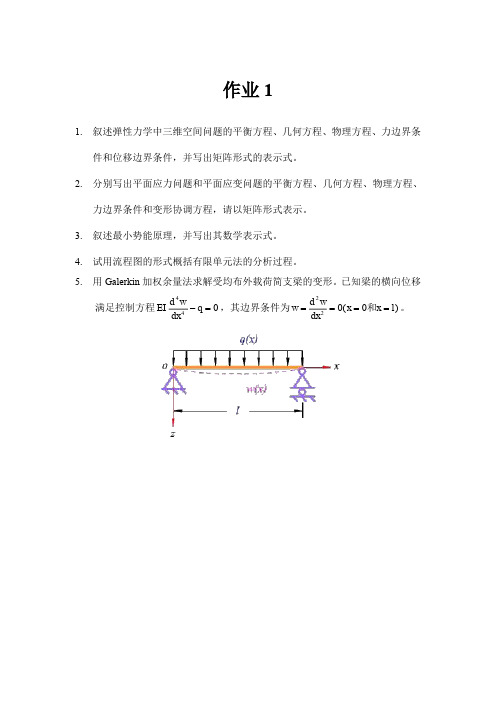
5.用Galerkin加权余量法求解受均布外载荷简支梁的变形。
已知梁的横向位移
满足控制方程
4
4
w
d
EI q
dx
-=，其边界条件为
2
2
0(0)
d w
w x x l
dx
====
和。
第五章 有限元法-1-泛函与变分
设待求变分问题（5-4）的解答（极值函数）为 y=y(x) （5-7）
因y是x的函数，但讨论的是y的变化
设想函数y从极值解（5-7）稍稍变动到y+dy，并把变分dy改记为：eh(x)，
e是一个任意给定的微量实参数（实变量）；
h(x)是定义于区间[x1，x2]，且满足齐次边界条件的任意选定的可微函数，即有： h(x1)=h(x2)=0。
15
与多元函数的极值问题相对应，在几何、力学上的求解泛 函极值的问题。 最速降线问题。
研究当质点从定点A自由下滑到定点B时，为使滑行时间最短，试 求质点应沿着怎样形状的光滑轨道y=y(x)下滑。 取A点为坐标原点，y轴竖直向下（图5-1）。
则沿曲线y=y(x)滑行线段ds所需的时间为
16
18
在最速下降问题，在端点x1和x2给定的无数个函数之中， y ( x) 仅有一个函数 能使式（ 5-2a）中的定积分达到极小 y ( x) 值函数，这一函数 被称为极值函数。 所谓变分问题就在于寻求使泛函达到极值的该极值函数， 即分析研究泛函的极值问题。 物理学各分支都存在有相应的变分问题（变分原理），例 如
因此
式中
26
故可得
简写为
将上式与式（5-6）相比较，只相差一个数值因子e。
27
故（5-8）等价于变分方程
也即
（线性主部）
利用分部积分，根据变分与微分顺序可以互换的原理，即 dy’=(dy)’，得
28
在变分问题中，变分dy在端点保持为零
于是，必要条件（5-12）成为
有限元分析第4章 平面问题有限单元法1
6
P
3
4 5
4
2
位移协调条件：各单元共享节点的位移相等 节点平衡条件：各节点单元内力与节点外力构成平衡力系
最终数学模型： K Q
基本概念
单元（element） 节点 (node)
回顾
单元节点位移 (node displacement)
单元节点内力 (node force)
单元刚度矩阵 (element stiffness matrix)
e
bx u by v
d
S
e p
px u py v dS
代入
u v
N
e
{} [B]{ }e
{ } [S]{ }e
得
内力虚功＝
e x x y y xy xy d
T d
cj
y)v j
(am
bmx
cm y)vm ]
二、平面问题三角形单元分析
三角形单元形函数
形函数
u x,
y
1 2A
[(ai
bi x
ci
y)ui
(a j
bj x
cj
y)u j
(am
bm x
cm
y)um ]
v x,
y
1 2A
[(ai
bi x
ci
y)vi
(a j
插值系数的确定：待定系数法
ui a1 a2 xi a3 yi u j a1 a2 x j a3 y j um a1 a2 xm a3 ym