第四章 三铰拱
合集下载
结构力学5三铰拱课件

拱架搭设
根据设计要求,选用合适的材料搭设拱架;
施工流程与工艺要求
02
01
03
拱体安装
按照从两端向跨中的顺序,对称安装拱体构件;
拱顶合拢
在拱顶设置临时支撑,确保拱体稳定;
施工监测
对施工过程进行实时监测,确保施工安全和质量。
施工流程与工艺要求
工艺要求 拱架搭设应符合设计要求,确保稳定性和承载力;
拱体安装应保证构件对接准确,避免出现错位和扭曲;
施工流程与工艺要求
01
临时支撑设置应合理,确保拱体 在合拢过程中保持稳定;
02
施工监测应实时进行,及时发现 和解决施工中的问题。
安装方法与注意事项
安装方法 采用分段吊装法,将拱体分成若干段,分别吊装到位;
对接安装时,应保证对接位置准确,避免出现错位和扭曲;
安装方法与注意事项
• 合拢时,应设置临时支撑,确保拱体稳定。
结构力学5三铰拱课件
目
CONTENCT
录
• 三铰拱概述 • 三铰拱的力学分析 • 三铰拱的设计与计算 • 三铰拱的施工与安装 • 三铰拱的维护与加固
01
三铰拱概述
定义与特点
定义
三铰拱是一种静定结构,由两个 固定端和三个铰链支承构成。
特点
拱顶在竖向荷载作用下主要承受 压力,并通过铰链传递水平推力 ,保持拱的平衡。
保持三铰拱的清洁,避免 积尘、腐蚀等影响其使用 寿命的因素。
紧固与润滑
对三铰拱的连接部位进行 紧固,对活动部位进行润 滑,确保其正常运转。
常见问题与处理方法
1 2
结构损伤
如发现三铰拱出现裂纹、变形等损伤,应立即采 取措施进行修复或更换。
连接松动
根据设计要求,选用合适的材料搭设拱架;
施工流程与工艺要求
02
01
03
拱体安装
按照从两端向跨中的顺序,对称安装拱体构件;
拱顶合拢
在拱顶设置临时支撑,确保拱体稳定;
施工监测
对施工过程进行实时监测,确保施工安全和质量。
施工流程与工艺要求
工艺要求 拱架搭设应符合设计要求,确保稳定性和承载力;
拱体安装应保证构件对接准确,避免出现错位和扭曲;
施工流程与工艺要求
01
临时支撑设置应合理,确保拱体 在合拢过程中保持稳定;
02
施工监测应实时进行,及时发现 和解决施工中的问题。
安装方法与注意事项
安装方法 采用分段吊装法,将拱体分成若干段,分别吊装到位;
对接安装时,应保证对接位置准确,避免出现错位和扭曲;
安装方法与注意事项
• 合拢时,应设置临时支撑,确保拱体稳定。
结构力学5三铰拱课件
目
CONTENCT
录
• 三铰拱概述 • 三铰拱的力学分析 • 三铰拱的设计与计算 • 三铰拱的施工与安装 • 三铰拱的维护与加固
01
三铰拱概述
定义与特点
定义
三铰拱是一种静定结构,由两个 固定端和三个铰链支承构成。
特点
拱顶在竖向荷载作用下主要承受 压力,并通过铰链传递水平推力 ,保持拱的平衡。
保持三铰拱的清洁,避免 积尘、腐蚀等影响其使用 寿命的因素。
紧固与润滑
对三铰拱的连接部位进行 紧固,对活动部位进行润 滑,确保其正常运转。
常见问题与处理方法
1 2
结构损伤
如发现三铰拱出现裂纹、变形等损伤,应立即采 取措施进行修复或更换。
连接松动
拱合理拱轴线

由于规定y 向上为正, x 向右为正,q 向下为 正,故上式右边为正号。
中南大学
退出
返回
08:29
§4-3 三铰拱的合理拱轴线
或
结构力学
d dy dx dx dy 1 dx
1
2
p( x) FH
p ( x) dy sh dx. FH dx 如p(x)=常数=p ,则
中南大学
退出
返回
08:29
§4-2 三铰拱的数值解
(3) 求内力 由水平推力 FH 82.5 kN 得 0
结构力学
(2) 求支座反力,结果为: FVA 105 kN , FVB 115 kN
FSD 105 kN 100 kN 5 kN
FSD FS0D cos D FH sin D
中南大学
退出
返回
08:29
§4-3 三铰拱的合理拱轴线
结构力学
例4-2 设三铰拱上作用沿水平向均布的竖向荷载q q 试求拱的合理轴线。
M0 解:由式(4-5) y FH
C Y f A B X
在均布荷载q作用下, 代梁的弯矩方程为
ql qx 2 q M x x(l x) 2 2 2
0
l 2
l 2
q
A B
拱的水平推力为
0 MC ql 2 FH f 8f
ql 2
x
ql 2
4f 代入公式(4-4)得 y 2 x(l x) l
退出 返回
中南大学
08:29
§4-3 三铰拱的合理拱轴线
结构力学
三铰拱在水平的均布荷载作用下,其合理 拱轴线为二次抛物线。
第4章-三铰拱和悬索结构的受力分析

得
l2
y x x2
FVA=70kN 4m
4m 4m l=16m
4m FVB=50kN
q=10kN/m A
FP=40kN B
2) 求φ
16
tany 1x
DCE 16m
8
代入各x值,即可查得相应的φ值。
F
0 VA
F
0 VB
为绘内力图将拱沿跨度分为8个等分,计有9个控制截面
,求出各截面的y、 φ等值,列于表中。
(3) 在竖向荷载作用下,梁的截面内没有轴力,而拱的 截面内轴力较大,且一般为压力(拱轴力仍以拉力为 正、压力为负)。
小结
(4) 内力与拱轴线形式(y,j)有关。
(5) 关于φ值的正负号:左半跨φ取正号;右半跨φ取负 号,即式(4-2)中,cos(- φ) = cos φ ,sin(- φ) = -sin φ 。
用同样的方法和步骤,可求得其它控制截面的内力。列表进行计算,如 表4-1所示。
(4)作内力图
C D
15
A
20
15
5
E
20
5
B
M图(kN·m)
78
67
60.6
60
60.6
76 58.1
91.9
D
C
E
78 77.8
A
B
FN图(kN)
C 4.9 17.9
4 7.1
A
E
D 4.9
10 17.9
4
B
7
FQ图(kN)
二、三铰拱的合理拱轴线
1 、合理拱轴线
在固定荷载作用下,使拱处于无弯矩状态的轴线,称为 合理拱轴线。 2 、合理拱轴的数解法
三铰拱

M
O
0 FN ( FN d FN ) 0
可得 d FN 0 合理拱轴线方程为
FN q
FN =常数
d 2 qd 0
沿s-s 写出投影方程为
2 FN sin sin d 2
圆弧线
因 d 极小
d 2
返 章
M
0
FH
合理拱轴线方程
例4-2 试求图a所示对称三铰拱在图示荷载作用下的合理拱轴 线。
解:相应简支梁(图b)的弯矩方程为
M
0
1 2
qx ( l x )
0
三铰拱的推力为
FH
0
MC f
4f l
2
ql
2
8f
合理拱轴线方程为
y
M
FH
x (l x )
北京建筑工程学院
三铰拱合理拱轴线形状的确定
三铰拱
14kN m
A
50kN
B
C
75.5kN 58.5kN
175.5 201
M图(kNm)
与三铰拱相应弯矩相比,要大 很多。
北京建筑工程学院
结构力学教研室
三铰拱
计算图(a)斜拱的支反力 时为避免解联立方程,可将反力
分解如图(b)。
由平衡条件可得 (a
F AV F
0 AV
, F BV F
0
FS F AV F1
0 0
轴力以压力为正
北京建筑工程学院
结构力学教研室
三铰拱
三铰拱的内力不但与荷载及三个铰的位置有关,而 且与拱轴线的形状有关。 由于水平推力的存在,拱的弯矩比相应简支梁的弯矩要 小。 三铰拱在竖向荷载作用下轴向受压。
结构力学第四章三铰拱

l/2
l/2
三铰拱在沿水平均 匀分布的竖向荷载 作用下,其合理拱 轴线为一抛物线。
q ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
ql/2 l ql/2 13
西华大学土木工程学院 王周胜讲授
例4-3 求在填土重量下三铰拱的合理拱轴线。q=q0+γy
d 2 y M 0dx)M 0 1 (2 y ( x2) (q0 2 g y) q(x) HH dx dx
8
Q YA P ,
西华大学土木工程学院 王周胜讲授
解: (1)求反力
1kN/m ↓↓↓↓↓↓↓↓↓
4kN
4m B
4 4 812 V A (2)作相应简支梁的N V A0 7k 16 A 6kN M°图和12 8 4 4 Q°图 0 8m VB VB 5k N 16 7kN 1kN/m (3)截面几何参数 0 ↓↓↓↓↓↓↓↓↓ M C 58 4 4 H 6k N 4f x(16 x) 4 y ( x) f 2 x(l x) l 16 7 + dy 4 f 8 x tg 2 (l 2 x) dx l 8 Q°图(kN)1
在填土重量作用下,三铰拱 的合理拱轴线是一悬链线。
14
西华大学土木工程学院 王周胜讲授
求均匀水压力作用下的三铰拱的合理拱轴线。 n q
t
d / 2
N+dN
r ∵拱处于无弯矩状态,∴各截面上只有轴力。
d
N
由 t 0, N cos
d d N dN cos 0, 得 dN 0 2 2 由于d很小, 即拱截面上的轴力N为常数。 d d d d 由 n 0, N sin N dN sin qds 0, 取 sin , 2 2 2 2 得 Nd qds 0 并略去高阶微量,
04三铰拱

解:相应简支梁(图b)的弯矩方程为 相应简支梁( )
M0 =
三铰拱的推力为
1 qx(l − x) 2
0 M C ql 2 FH = = f 8f
合理拱轴线方程为
M0 4f y= = 2 x(l − x) FH l
求均匀水压力作用下的三铰拱的合理拱轴线。
q
r
在均匀水压力作用下,三铰拱的合理拱轴线是圆弧线。
2、内力的计算 、
相应简支梁K截面的弯矩为 相应简支梁 截面的弯矩为M 0 截面的弯矩为 相应简支梁K截面的剪力为 相应简支梁 截面的剪力为FS0 截面的剪力为
M = M0 − FH y
FS = F cosϕ − FH sin ϕ
0 S
FN = FS0 sin ϕ + FH cosϕ
x y
压力为正
Hale Waihona Puke ∑Fx= 0 FAH = FBH = FH
取左半拱为隔离体
可 得 相应简支梁
FAV l1 − F1 (l1 − a1 ) ∑ M C = 0 FH = f 三铰拱的反力只与 0 荷载及三个铰的位 FAV = FAV 置有关, 置有关,与拱轴线 0 FBV = FBV 形状无关;推力FH 形状无关;推力 0 成反比。 与拱高 f 成反比。 MC FH = f
拱顶 拱轴线 拱趾 拱高
f
起拱线
拱趾
跨度
l
f / l → 高跨比(或矢跨比)
平拱: 平拱: 两拱趾在同一水平线上 斜拱: 斜拱: 两拱趾不在同一水平线上
§4-2 三铰拱的计算
1、支座反力的计算 、
由拱的整体平衡
∑ M B = 0 FAV ∑M
A
∑ Fb =
M0 =
三铰拱的推力为
1 qx(l − x) 2
0 M C ql 2 FH = = f 8f
合理拱轴线方程为
M0 4f y= = 2 x(l − x) FH l
求均匀水压力作用下的三铰拱的合理拱轴线。
q
r
在均匀水压力作用下,三铰拱的合理拱轴线是圆弧线。
2、内力的计算 、
相应简支梁K截面的弯矩为 相应简支梁 截面的弯矩为M 0 截面的弯矩为 相应简支梁K截面的剪力为 相应简支梁 截面的剪力为FS0 截面的剪力为
M = M0 − FH y
FS = F cosϕ − FH sin ϕ
0 S
FN = FS0 sin ϕ + FH cosϕ
x y
压力为正
Hale Waihona Puke ∑Fx= 0 FAH = FBH = FH
取左半拱为隔离体
可 得 相应简支梁
FAV l1 − F1 (l1 − a1 ) ∑ M C = 0 FH = f 三铰拱的反力只与 0 荷载及三个铰的位 FAV = FAV 置有关, 置有关,与拱轴线 0 FBV = FBV 形状无关;推力FH 形状无关;推力 0 成反比。 与拱高 f 成反比。 MC FH = f
拱顶 拱轴线 拱趾 拱高
f
起拱线
拱趾
跨度
l
f / l → 高跨比(或矢跨比)
平拱: 平拱: 两拱趾在同一水平线上 斜拱: 斜拱: 两拱趾不在同一水平线上
§4-2 三铰拱的计算
1、支座反力的计算 、
由拱的整体平衡
∑ M B = 0 FAV ∑M
A
∑ Fb =
第4章_三角拱

因此,若拱轴为合理拱轴线,根据定义,则任一截面有
M M0 Hy 0
M 0 ( x) 即 y H
(4-4)
这就是合理拱轴线应满足的方程。 下面举例说明如何确定合理拱轴线。
例2 对称三铰拱受载如图示,求其合理拱轴线。 解 建立如图所示坐标系 相应简支梁任一截面的弯 矩方程为
y q C f l
y
FN+dFN FQ+dFQ
d
FQ cos
M FN
FQ
d FN FN dFN sin 0 2
∵d很小 d d ∴ sin , cos d 1 2 2 2 因此(a)式整理可得
dFQ ds
FN
q
(b)
由
Y 0
得
d d d FN cos FN dFN cos FQ FQ dFQ sin 0 (c) 2 2 2 上式整理可得 FQ dFN (d) ds 由 Mo F 0 得
∴
FNK F sin K H cos K 0 FQK FQK cos K H sin K
0 QK
y
Fp1
MK
K
FNK
H
K FQK yK x
(4-3)
VA
xK
Fp1
F0QK
VA0
(3)三铰拱的内力图
图(c)
有了上述任意截面的内力方程,不难画出其内力图。与梁刚
解
由于荷载 q 也与拱轴的形状有关, 故此时无法直接应用(4-4)式。
q C f l
qd
x
B
对(4-4)式两边微分得
∵
A
y
∴
1 d 2 M 0 ( x) y H dx 2
结构力学 三铰拱
9 / 13
À
第四章 静定拱
试求图示对称三铰拱在均布荷载作用下的合理拱轴线
q y A x q f C B
FH=ql2/8f M0=qlx/2-qx2 /2 =qx(l-x)/2 y=M0/FH=4fx(l-x)/l2
l
x
抛物线À
10 / 13
第四章 静定拱
荷载布置改变,合理拱轴亦 改变 荷载确定、拱脚位置确定, 则顶铰位置决定水平反力, 因此,有无限多个相似图形 可作合理拱轴 三铰位置确定,合理拱轴唯 一确定 设计时只能根据主要荷载选 择近似合理拱轴
第四章 静定拱 §4-1 概述
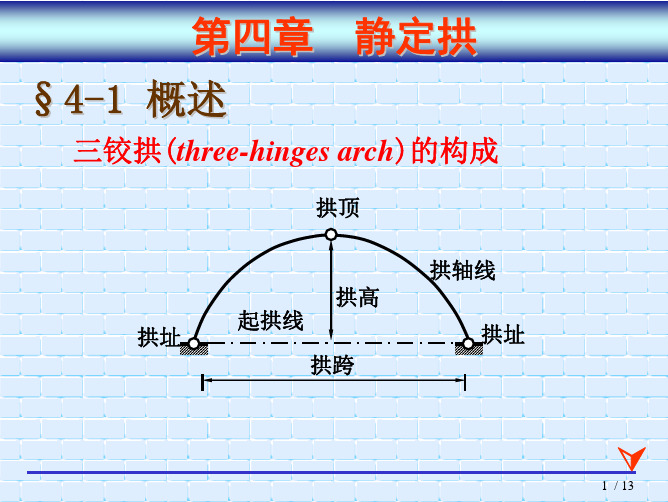
三铰拱(three-hinges arch)的构成
拱顶 拱轴线 拱高 拱址 起拱线 拱跨 拱址
1 / 13
ÀБайду номын сангаас
第四章 静定拱
1)拱的分类
三铰拱 拉杆拱1
两铰拱
无铰拱
拉杆拱2
斜拱
2 / 13
À
第四章 静定拱
2)拱的受力特点
FP
曲梁
FP • 在竖向荷载作用下 会产生水平推力。
6 / 13
À
第四章 静定拱
拱的内力图
− y ⎤⎧M ⎫ ⎧M ⎫ ⎡1 0 ⎪ 0⎪ ⎪ ⎪ ⎢ ⎥ ⎨FS ⎬ = ⎢0 cosϕ − sinϕ⎥⎨ FS ⎬ ⎪F ⎪ ⎢0 sinϕ cosϕ ⎥⎪ F ⎪ ⎦⎩ H ⎭ ⎩ N⎭ ⎣
0
由于拱轴线是弯曲的,所以内力图都是曲线形 的,内力图要通过逐点描图的方法绘制。
拱
• 由于水平推力的存 在,使得拱内弯矩大 大减小。
3 / 13
À
第四章 静定拱 §4-2 三铰拱的计算
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 三铰拱
三、三铰拱的内力图
1.画三铰拱内力图的方法 描点法。
2.画三铰拱内力图的步骤 1)计算支座反力; 2)计算拱圈截面的内力(可以每隔一定水平距离取 一截面,也可以沿拱轴每隔一定长度取一截面); 3)按各截面内力的大小和正负绘制内力图。
注:
1)仍有V=dM/ds 即剪力等零处弯矩达极值; 2)M、V、N 图均不再为直线; 3)集中力作用处V 图将发生突变; 4)集中力偶作用处M 图将发生突变。
第四章 三铰拱
§4-1 概述 一、实例——拱桥
拱桥是承受轴向压力为主的拱圈或拱肋作为主要承重构 件的桥梁,拱结构由拱圈(拱肋)及其支座组成。
赵州桥,建于隋大业(公元605-618)年间
第四章 三铰拱
世界上最古老的铸铁拱桥(1781年,英国科尔布鲁克 代尔桥)
第四章 三铰拱
万县长江大桥:主跨420米,桥面宽24米,世界上跨 度最大的混凝土拱桥
第四章 三铰拱
二、梁与拱
P
P
HA=0 A
B HA=0A
B
P
拱:杆轴线为曲线,且 在竖向荷载作用下会产 HA≠0 A 生水平推力的结构。
B
第四章 三铰拱
曲梁
杆轴线为曲线 在竖向荷载作 用下不产生水 平反力。
FP
拱--杆轴线为曲 线,在竖向荷载 作用下会产生水 平推力的结构。
三铰拱
第四章 三铰拱
三、拱常用的形式
第四章 三铰拱
二、三铰拱的内力
截面内弯矩要和竖向力及 水平力对K点构成的力矩
H
A
相平衡,设使下侧的纤维
受拉为正
MK 0
M (x) H y (VA x M KAP ) 0
括号内之值等于代梁上相 应K截面的弯矩,所以
M (x) VA x M KAP Hy
M 0 (x) Hy
H
三铰拱
两铰拱
பைடு நூலகம்无铰拱
静定拱 超静定拱
第四章 三铰拱
四、拱的有关概念
顶铰
拱轴线
平拱
拱趾铰
跨度
拱轴线 拱趾铰
拱(矢)高
斜拱
拉杆拱
第四章 三铰拱
§4-2 三铰拱的支座反力和内力
一、支反力
1、竖向反力
M A 0, VBl M ABP 0 H A
A
VB
Piai M ABP
l
l
VA
同跨度同荷载简支梁(代
q PC
A
VA
l1
f B
HB
l l1 VB
P
q
y
VA0 PV)(x
M(x
) N(x)
k
VB0
Ky
Ax
x
VA
第四章 三铰拱
二、三铰拱的内力
A面KK脱切离线体上上投所影有,的可力得在:截H A
q PC
f
A
B
HB
V (x) VA cosK P cosK H sinK VA l1
l l1 VB
(VA P) cosK H sinK
梁)的支座反力:
q PC
f B
HB
l1
l l1 VB
P
q
VB0
M ABP l
VA0
VB0
故得: VB VB0 带‘0’上标的量均为代梁对应的值
同理:
M B 0,
VA
M BAP l
且:VA VA0
第四章 三铰拱
2、水平反力
X 0, HA HB H
取AC段为脱离体,由: H A A
MC 0, Hf VAl1 MCAP 0 VA
P
q
V 0 cosK H sinK
AK脱离体上所有的力沿截
面K的法线方向投影,可得 N:(x) (VA P) sinK H cosK
y
VA0 PV)(x
M(x
) N(x)
k
Ky
VB0
V 0 sinK H cosK
H Ax
x
VA
第四章 三铰拱
VA VA0
M (x) M 0 (x) Hy
第四章 三铰拱
第四章 三铰拱
教学内容: 三铰拱的支座反力和内力,合理拱轴。
教学要求: 1、了解静定拱的合理拱轴线的概念; 2、理解静定拱的基本概念及基本特点; 3、掌握静定拱的反力及内力计算。
重点:静定拱反力、内力的计算。 难点:静定拱的内力计算。
第四章 三铰拱
第四章 三铰拱
§4-1 概述 §4-2 三铰拱的支座反力和内力 §4-3 压力线与合理拱轴
得:H
1 f
(VA
l1
M CAP )
M
0 C
f
P
q PC
f B
HB
l1
l l1 VB
P
q
在12))竖支竖H向A座向荷反支载A力座作与反用拱力下轴与,线拱三C形高铰V状无拱C 无关H的关。C支,座而反与力三有V个A0如铰下的特位点置:有关。
VB0
3)当荷载和V跨A 度固定时,拱的水平反力H与拱高 f 成反比,即拱高 f 越大,水平反力H越小,反之,拱高 f 越小,水平反力H越大。
cos
1 1 ( y ')2 ,
sin y 'cos
(4 7)
其中,cos为 正值, si的n正负取决于 的符y号' 。
第四章 三铰拱
三铰拱受力特点:
(1)在竖向荷载作用下有水平反力H; (2)由拱截面弯矩计算式可见,比相应简支梁小得多; (3)拱内有较大的轴向压力N。
拱比梁能更有效的发挥材料作用,适用于较大跨度和较 重的荷载。由于主要受压,便于利用抗压性能好而抗拉性 能差的材料(砖、石、混凝土等)。但基础承受推力,所以 三铰拱的基础比梁的基础要大(桥梁),或需使用拉杆拱 (屋顶)。
支反力:VB VB0
H
M
0 C
f
K截面内力:V V 0 cosK H sin K N V 0 sin K H cosK
公式(4-1)—(4-6)中:
VA0
,VB0 ,
M
0 C
,
M
0 ,V
0
分别表示相应简支代梁的支反力和对 应截面的内力。在计算时,应代入相
应的正、负号。
M 0 (x) 以下侧受拉为正;V 0以使脱离体顺时针转为正。
第四章 三铰拱
[例4-1]三铰拱及其所受荷载如图所示,拱的轴线为抛物线: y=4fx(l-x)/l2,求支座反力,并绘制内力图。
4m
1kN/m
解: (1) 反力计算
y ↓↓↓↓↓↓↓↓↓
4kN
VA
VA0
44
1 8 12 16
7kN
HA
A
C
y(x)
4f l2
D x(l x)
x
B
HB
VB
VB0
18 4 16
4 12
VA
8m
1kN/m ↓↓↓↓↓↓↓↓↓
4m
4m VB
4kN
5kN
H
M
0 C
58 4 4
VA0 6kN ()
VB0
f
4
第四章 三铰拱
[例4-1]三铰拱及其所受荷载如图所示,拱的轴线为抛物线: y=4fx(l-x)/l2,求支座反力,并绘制内力图。
4m
(2) 内力计算 D截面几何参数
xD 12m 4f
yD l2 x(l x)
y
6kN 7kN
1kN/m
↓↓↓↓↓↓↓↓↓
4kN
C
A
y(x)
4f l2
D x(l x)
