34三铰拱
合集下载
3_4三铰拱
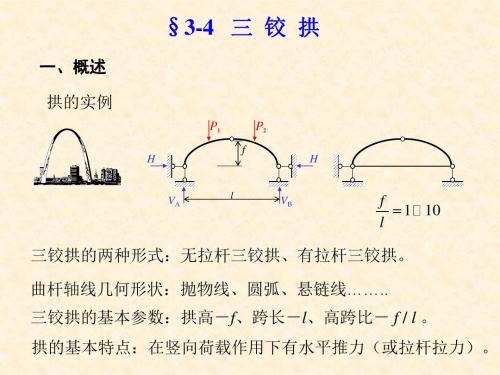
二、三铰拱的计算 (在竖向荷载作用下的平拱) 1、支座反力 与同跨度同荷载对应简支梁比较
a1
d P1 a 2
D HA C
b1 b2
P2
MA 0
VB
1 Pa 1 1P 2 a2 l
VB VB
A
VA
y
f
l2
x
l1 l
B
HB
MB 0
VA
1 Pb 1 1P 2b2 l
y x
M
x
H
q ql 2 4 f 2 x l x x l x l 2 8f
Mo
A
V
A
N Q sin H cos
D
H
3、受力特点 (1)在竖向荷载作用下,拱有水平推力 H ; (2)由于推力 H 的存在,拱截面弯矩比相应简支梁小; (3)在竖向荷载作用下,拱内有轴力 N,且一般为压力。
q=2kN∙m y
1 0 3 4 5
P=8kN
例 1、三铰拱及所受荷载如图
0.667
2 33 41,sin 2 0555 . ,cos 2 0832 .
(注意截面6处 Q 有突变)
o
N 2 Q2 sin 2 H cos 2 11 2 3 0.555 7.5 0.832 9.015kN
绘制内力图
q y C q B l/2 x A B x
A
l/2
f
M x [解] 由式 y x H
ql 2
ql 2
先列出简支梁的弯矩方程
q M x x l x 2
拱的推力为:
注意
结构力学-三铰拱

曲梁
拱
拱 (arch)
一、概述
2.拱的受力特点 拱的受力特点 拱
曲梁
P
拱比梁中的弯矩小
拱 (arch)
一、概述
3.拱的分类 拱的分类
超静定拱
静定拱
两铰拱
三铰拱 拉杆 拉杆拱
高差h 高差
超静定拱
无铰拱 斜拱
拱 (arch)
一、概述
4.拱的有关名称 拱的有关名称 顶铰 拱肋 拱趾铰 跨度 拱肋 拱趾铰 矢高
1 l l a1 b1 不再顶部,或 铰C不再顶部 或 不再顶部 FH = [Y A × − P1 ( − a1 )] f 2 2 0 b a2右边的结2 YB0 YA不是平拱 不是平拱,右边的结 l l
M c0 = [Y A0 × − P1 ( − a1 )]
YB=YB YA=YA0 XA=XB =FH
二、三铰拱的数解法 ----支反力计算 支反力计算 P1 三铰拱的竖向反 P2 C 力与其等代梁的 XB 反力相等 水平反 f FH 反力相等;水平反 A B 力与拱轴线形状0 XA Mc YA l/2 l/2 无关.荷载与跨度 无关 荷载与跨度 YB YA l 一定时, 一定时,水平推 YA0 等代梁 P1 P2 A C 力与矢高成反比. 力与矢高成反比 B 请问:有水平荷载 有水平荷载,或 请问 有水平荷载 或
32kN.m C C 32kN.m
8m B 4m 4m 2kN 2kN A 4m 4m
8m B 2kN
A 2kN
32kN.m
16kN.m
16kN.m
16kN.m
水平反力的作用:使相应水平代梁弯矩 水平反力的作用:使相应水平代梁弯矩MC0 降至为零。 降至为零。
三铰拱PPT课件

F B
FS
FN FQ0sin FS cos
I
l/2
FVB
.
【例2】求图示三铰拱式屋架在竖向荷载作用下的支反力和内力。
解: (1) 计算支座反力
F H 0 , F V A F V 0 A , F V B F V 0 B
(2)计算拉杆内力:F S
M
0 C
f
(3)计算拱身内力
q
y FH
A FVA
受轴向压力FN作用。
仅在左半跨作用均布 荷载时的M图
仅在左半跨作用均布 荷载时的FQ图
仅在右半跨作用均布 荷载时的M图
仅在右半跨作用均布 荷载时的FQ图
(3) 这种在给定荷载作用下,拱处于无弯矩状态的拱轴线,是三
铰拱最合理的拱轴线( reasonable axis of arch) 。
.
• 三铰拱的合理拱轴线计算公式:
.
三铰拱压力线的求解步骤
设三铰拱所承受荷载如图4-8a所 示,现作其压力线。 第一步,作合力多边形
• 第二步,确定各截面合力的作 用线。
• 第三步,确定压力线 多边形AHIJB是由拱各段的 合力作用线构成的,称为三 铰拱在所给荷载作用下的压 力多边形,简称压力线 。 压力线应通过A、B、C三个 铰的铰心。
第五章 三铰拱( three-hinged arch )
.
内容: 三铰拱的支座反力和内力,合理拱轴。
要求: 1、了解静定拱的合理拱轴线的概念; 2、理解静定拱的基本概念及基本特点; 3、掌握静定拱的反力及内力计算。
重点:静定拱反力、内力的计算。 难点:静定拱的内力计算。
.
§5-1 概述 一、实例——拱桥(Arch Bridge)
.
结构力学 三铰拱

4 4 yk 2 4(16 4) 3m 求MK 16 MK 0 MK 12.5 4 10 3 20kN.m(下拉)
求MJ
yJ 3m
M
J
0
M J 7.5 4 10 3 30 30 0
3. 求FQ、FN的计算公式
拱轴任意截面D切线与水平线夹角为φ。 相应代梁中, F 设为正方向。
FP1=15kN K FHA A yk 4m
l/2
C f=4m
MC 0
FVA
4m
l l FVA FHA f FP1 0 2 4 0 MC 1 l l FHA ( FVA FP1 ) () f 2 4 f
0 上式中,M C 为代梁C截面弯矩。
M FHB () f
0 ND右 QD右 sin D H cosD 12 0.555 10.5 0.832 15.4kN
重复上述步骤,可求出各等分截面的内力,作出内力图。
三、三较拱的合理轴线
在给定荷载作用下,三铰拱任一截面弯 矩为零的轴线就线为合理拱轴。 三铰拱任一截面弯矩为 M M FH y
超静定拱
拉杆拱 静定拱
拱顶
C
拱轴线 拱高 f
B
拱趾
A
起拱线 跨度 l
f l
f
高跨比
l 通常 f l 在1-1/10之间变化,f 的值对内力有 很大影响。
工程实例
拱桥 (无铰拱)
超静定拱
世界上最古老的铸铁拱桥(英国科尔布鲁克代尔桥)
万县长江大桥:世界上跨度最大的混凝土拱桥
二、三铰拱的计算
A 12.5kN K左 Fº =12.5kN QK左 A 12.5kN
三铰拱

M
O
0 FN ( FN d FN ) 0
可得 d FN 0 合理拱轴线方程为
FN q
FN =常数
d 2 qd 0
沿s-s 写出投影方程为
2 FN sin sin d 2
圆弧线
因 d 极小
d 2
返 章
M
0
FH
合理拱轴线方程
例4-2 试求图a所示对称三铰拱在图示荷载作用下的合理拱轴 线。
解:相应简支梁(图b)的弯矩方程为
M
0
1 2
qx ( l x )
0
三铰拱的推力为
FH
0
MC f
4f l
2
ql
2
8f
合理拱轴线方程为
y
M
FH
x (l x )
北京建筑工程学院
三铰拱合理拱轴线形状的确定
三铰拱
14kN m
A
50kN
B
C
75.5kN 58.5kN
175.5 201
M图(kNm)
与三铰拱相应弯矩相比,要大 很多。
北京建筑工程学院
结构力学教研室
三铰拱
计算图(a)斜拱的支反力 时为避免解联立方程,可将反力
分解如图(b)。
由平衡条件可得 (a
F AV F
0 AV
, F BV F
0
FS F AV F1
0 0
轴力以压力为正
北京建筑工程学院
结构力学教研室
三铰拱
三铰拱的内力不但与荷载及三个铰的位置有关,而 且与拱轴线的形状有关。 由于水平推力的存在,拱的弯矩比相应简支梁的弯矩要 小。 三铰拱在竖向荷载作用下轴向受压。
3.3 三铰拱
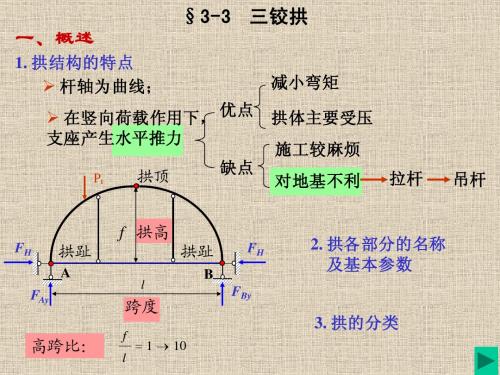
0 FAy = FAy
FAH A
y
∑ Fx = 0
P1
FAH = FBH = FH
x
l1
FBy
FAy
d
c
FAH
∑ MC = 0
FAy ⋅ l1 − P ⋅ d − FH ⋅ f = 0 1
o MC M − FH ⋅ f = 0 ∴ FH = f o C
0 MC
P1
P2
f l1
c
F
0 Ay
x
0 FBy
q y A l/2 C f l/2 B x
M 0 (x ) [解] 由式 y ( x ) = 解 FH
先列出简支梁的弯矩方程: 先列出简支梁的弯矩方程
M 0 (x ) =
拱的推力为: 拱的推力为: B
q x(l − x ) 2
q A
ql 2
x
c
ql 2
0 M C ql 2 FH = = f 8f
所以拱的合理轴线方程为: 所以拱的合理轴线方程为:
0.600 0.354 0.000 1.125
6m
1.500 1.125 0.000
6m
0.375 4.500 0.375 0.000 0.600 11.700
M图 kN.m
0.003
0.472
1.000
3.331
1.060
9.015
7.749
7.500
7.433
6.796 11.235
13.300
7.5kN x2=3m FAy =11kN 3m 6m 6m
(2)内力计算 )
以截面2为例 以截面2
(1)计算支座反力 ) 2× 6× 9 + 8× 3 0 FH = 7.5kN FAy = FAy = = 11kN 12 FBy = 9kN 2× 6× 3 + 8× 9 0 FBy = FBy = = 9kN 12 0 M C 11× 6 − 2 × 6 × 3 FH = = = 7.5kN f 4
三铰拱

[拱结构]
杆轴为曲线且在竖向荷载作用下能产生水平推力的结构。
拱与梁的区别——水平推力的存在。
曲梁拱[常见的三铰拱]
(1)无拉杆的三铰拱
(2)有拉杆的三铰拱
[三铰拱]
拱的两端支座处称拱趾,两拱趾间的水平距离称拱的跨度。
拱轴最高处称拱顶,拱顶至两支座联线的竖直距离称为矢高。
矢高与跨度之比称为拱的矢跨比。
[三铰拱的支座反力计算]
三铰拱的支座竖向反力等于相应简支梁两支座的竖向反力,水平推力等于相应简支梁与拱中间铰对应的截面的弯矩除以矢高。
可见,水平推力只与荷载及三个铰的位置有关,而与拱轴形状无关。
矢高愈大
愈小,反之愈小则愈大。
若则,此时三个铰位于同一直线上,为瞬变体系。
[三铰拱的内力计算]
内力符号规定:弯矩使内侧受拉为正,剪力绕顺时针转为正,轴力以拉力为正。
求指定截面的内力:
、为相应简支梁截面的弯矩与剪力。
的符号在左半拱取正,右半拱取负。
由于水平推力的存在,拱的弯矩比相应梁结构的弯矩小得多。
[三铰拱的压力线]
三铰拱的截面的内力为弯矩、剪力与轴力,三者可合成为一合力,合力在截面上存在一个作用点,所有各个截面的这些作用点联接起来便成为一条折线或曲线,称之为拱的压力线。
[三铰拱的合理拱轴]
在已知荷载作用下,如所选择的三铰拱轴线能使所有截面上的弯矩均等于零,这样的拱轴称为合理拱轴。
第三章静定结构受力分析三铰拱

(1)求反力:Fy (2)列弯矩方程
(3)令M (x) 0 y
qL A FV B 2
M (x) Fy Ax
1 FH
(Fy Ax
1 2
12qFxHq2x)2q8q8LFfL2fH2
y
(1 2
qLx
1 2
qx2
)
4f L2
(L x)x
结论:均布荷载作用下,合理拱轴线方程为抛物线。
§3-3 三铰拱
a2
b2
F =F YA
YA0
F =F XA
XB
=FH
FYB0
M
0 c
[FYA0
l 2
l P1( 2
a1)]
FH= MC0 / f
§3-3 三铰拱
结论: ①简支梁不存在水平推力,三铰结构水平推力不为零;
②对于平拱、竖向反力与拱高无关; 平拱
③反力与拱轴线形式无关,只与三个铰的位置有关;
④水平推力与拱高成反比。
例2:求集中荷载作用下的合理拱轴线
(1)求反力:Fy A FyB 1.5P
(2)求合理拱轴线
FH
1 (1.5P 2a P a) a
2P
AD段 : M (x)
DC段 : M (x)
1.5Px FH y
1.5Px P(x a)
0
FH
y
y0
3x 4
y
(直线)
1 (0.5Px 2P
Pa)
§3-3 三铰拱
MK
M
0 K
FH y
FQK
FQ
0 K
cos FH
sin
FNK
F Q
0 K
sin FH
cos
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
可求两个竖向支座反力:
P1
A
HA VA
l1
C
f
l2 l
P2
B HB
VB
VA
Pibi l
由 X 0
VB
Pi ai l
得: H A HB H
等代梁
A
P1
a1 (推力) VA0
C
b1 a2
P2
B
b2VB0
另考虑中间铰C处弯矩为零:MC 0
以左部分为例
则: MC VAl1 P1(l1 a1) Hf 0
0.000 1.125 1.500 1.125 0.000 0.375 4.500 0.375 0.000
q=2kN .m
P=8kN
y
1 0
A
34
2
2
y2
x
5 6
6m
6m
绘制内力图
7
8
B
M2 M2 Hy2 11 3 2 31.5 7.5 3
1.5kN m
Q2 Q2 cos 2 H sin 2 11 2 3 0.832
当 f 等于零,H趋于无穷大;此时三铰共线。 几何瞬变体系。
5) 三铰拱受向内的推力,因此需给基础施加向外的推力。 所以三铰拱的基础要比简支梁的基础大,或加拉杆, 以减小对墙的推力。
静定拱
2. 内力的计算公式 <1> 弯矩计算公式
MK VAxK P1(xK a1) HyK
VA VA0
静定拱
§3.4.1 三铰拱的组成和类型
拱--杆轴线为曲线,在竖向荷载 作用下会产生水平推力的结构。
FP
三铰拱
静定拱
拱的拱趾铰
拱趾铰
跨度
斜拱
拉杆拱
静定拱
静定拱
三铰拱
超静定拱
超静定拱
两铰拱
无铰拱
静定拱
§3.4.2三铰拱的支座反力及截面内力计算
P1
C
P2
VB=VB0
A
HA
P=8kN
y
34
5
2 1
2
y2
0
6 7 8
例 1、三铰拱及其所受荷载如 f=4m 图所示拱的轴线为抛物线方程
7.5kN
x
A
x2=3m 6m
6m
3m
B
H 7.5kNy
4f l2
xl x
VB 9kN 制内力图。
计算反力并绘
VA 11kN
(2)内力计算 以截面2为例
y2
4f l2
xl
x
44 122
分析:
MK
M
0 K
HyK
显然,由于推力
H
存在, M K
M
0 K
静定拱
<2> 剪力计算公式 QK VA cosK P1 cosK H sinK
VA P1 cosK H sinK
QK0 cosK H sinK
QK0 为相应简支梁K截面处的剪力。
注:K 在左半拱为正,右半拱为负。
静定拱
a1
l2 l
VB
P2
CB
b1
上式中的分子 VAl1 P1(l1 a1)
VA0
a2
b2VB0
恰恰与简支梁截面C处的弯矩
M
0 C
相同。
H
M
0 C
f
即,推力H等于相应简支梁截面C处的弯矩
M
0 C
除以拱高
f。
静定拱
特点:
1) 由于推力的存在,三铰拱截面弯矩比简支梁弯矩小。
MC VAl1 P1(l1 a1) Hf 0
7.5 0.555 0.0025kN 0.003kN
M图
kN.m N2 Q2 sin2 H cos2 11 230.555
7.50.832 9.015kN
0.600 0.354 0.003 0.472 1.000 3.331 1.060 0.600
Q图 kN
13.300 10.958 9.015 7.749 7.500 7.433 1.421 6.796 3.325 11.235 11.665 11.700
312
3
3m
tg 2
dy dx
x3
4f l
1 2lx
x3
44 12
1
2123
0.667
(1)计算支座反力
VA
VA
2
6
9 12
8
3
11kN
VB
VB
2
6
38 12
9
9kN
H
M
C
11 6 2 6 3 7.5kN
f
4
2 3341,sin 2 0.555,cos 2 0.832
静定拱
所以推力:
H VAl1 P1(l1 a1) f
静定拱
分析两个竖向支座反力
P1 C
P2
VA
Pibi l
VB
Pi ai l
A
f
B HB
与简支梁的支座反力:
VA0
Pibi l
VB0
Pi ai l
HA VA VA0 VA
l1
VB VB0
等代梁
A
P1
分析 推力H 式:
H
VAl1 P1(l1 a1) f
(1)不管拱轴区段上是否有分布荷载,拱的各内力图在区段
上均为曲线形状; (2)在竖向集中力FP作用点两侧截面,拱的轴力和剪力有突 变,突变值分别为FP sinΨK 和FP cosΨK,弯矩图在该点转折; 在集中力偶M作用点两侧截面,弯矩有突变,突变值为M,轴 力和剪力不受影响。
<3> 轴力计算公式
NK VA P1 sinK H cosK
QK0 sinK H cosK
拱的任一截面上一般有三个内力(M, Q, N),内力计算的 基本方法仍是截面法。与直杆件不同的是拱轴为曲线时, 截面切线角度不断改变,截面上内力(Q, N)的方向也相 应改变。
静定拱
q=2kN .m
3、带拉杆的三铰拱,其支座反力可由整体的平衡条件完全求 得;水平推力由拉杆承受。可将顶铰和拉杆切开,取任一部分 求出拉杆中的轴力。
静定拱
三、 拱的内力图特征 1、拱的内力图特征
Mk Mk H y
Qk Qk cosk H sink
Nk Qk sink H cosk
由上式分析可知,当拱轴为曲线时。有:
l1
VA
等代梁 P1
A
f l2
l
C
a1
VA0
b1 a2
B HB
VA=VA0 H= MC0 / f
VB
P2
B
三铰拱的反力只 与荷载及三个铰 的位置有关,与 拱轴线形状无关 荷载与跨度一定 时,水平推力与 矢高成反比
b2 VB0
静定拱
支座反力共四个分量 需列出四个方程:
由整体平衡方程:
MA 0 和 MB 0
三铰拱C处弯矩
M
0 C
VAl1
P1 (l1
a1)
简支梁C处弯矩
2) 梁无轴力(在竖向载荷作用下) 拱的截面轴力较大,且一般为压力。
3) 推力只与三个铰和载荷位置有关,与拱轴形状无关;
即只与 f/l 有关。
静定拱
4) 当载荷和拱的跨度不变时,推力与拱高 f 成反比。 f 越大,H越小;反之, f 越小,H越大;
N图 kN
静定拱
Mk Mk H y
Qk Qk cosk H sink
Nk Qk sink H cosk
上式可作为拱内力的计算公式用,特别是在作拱的内力图时。 但须注意以下几点: 1、上式要在以拱的左底铰为原点的平面直角坐标中应用,并 仅考虑了竖向荷载的作用。
2果在、取右式是半中与拱水时k为平所方为k计向负算的。K锐截角面考处虑拱,轴则切K线截与面水在平左x半坐拱标时的夹k为角正。,如
P1
A
HA VA
l1
C
f
l2 l
P2
B HB
VB
VA
Pibi l
由 X 0
VB
Pi ai l
得: H A HB H
等代梁
A
P1
a1 (推力) VA0
C
b1 a2
P2
B
b2VB0
另考虑中间铰C处弯矩为零:MC 0
以左部分为例
则: MC VAl1 P1(l1 a1) Hf 0
0.000 1.125 1.500 1.125 0.000 0.375 4.500 0.375 0.000
q=2kN .m
P=8kN
y
1 0
A
34
2
2
y2
x
5 6
6m
6m
绘制内力图
7
8
B
M2 M2 Hy2 11 3 2 31.5 7.5 3
1.5kN m
Q2 Q2 cos 2 H sin 2 11 2 3 0.832
当 f 等于零,H趋于无穷大;此时三铰共线。 几何瞬变体系。
5) 三铰拱受向内的推力,因此需给基础施加向外的推力。 所以三铰拱的基础要比简支梁的基础大,或加拉杆, 以减小对墙的推力。
静定拱
2. 内力的计算公式 <1> 弯矩计算公式
MK VAxK P1(xK a1) HyK
VA VA0
静定拱
§3.4.1 三铰拱的组成和类型
拱--杆轴线为曲线,在竖向荷载 作用下会产生水平推力的结构。
FP
三铰拱
静定拱
拱的拱趾铰
拱趾铰
跨度
斜拱
拉杆拱
静定拱
静定拱
三铰拱
超静定拱
超静定拱
两铰拱
无铰拱
静定拱
§3.4.2三铰拱的支座反力及截面内力计算
P1
C
P2
VB=VB0
A
HA
P=8kN
y
34
5
2 1
2
y2
0
6 7 8
例 1、三铰拱及其所受荷载如 f=4m 图所示拱的轴线为抛物线方程
7.5kN
x
A
x2=3m 6m
6m
3m
B
H 7.5kNy
4f l2
xl x
VB 9kN 制内力图。
计算反力并绘
VA 11kN
(2)内力计算 以截面2为例
y2
4f l2
xl
x
44 122
分析:
MK
M
0 K
HyK
显然,由于推力
H
存在, M K
M
0 K
静定拱
<2> 剪力计算公式 QK VA cosK P1 cosK H sinK
VA P1 cosK H sinK
QK0 cosK H sinK
QK0 为相应简支梁K截面处的剪力。
注:K 在左半拱为正,右半拱为负。
静定拱
a1
l2 l
VB
P2
CB
b1
上式中的分子 VAl1 P1(l1 a1)
VA0
a2
b2VB0
恰恰与简支梁截面C处的弯矩
M
0 C
相同。
H
M
0 C
f
即,推力H等于相应简支梁截面C处的弯矩
M
0 C
除以拱高
f。
静定拱
特点:
1) 由于推力的存在,三铰拱截面弯矩比简支梁弯矩小。
MC VAl1 P1(l1 a1) Hf 0
7.5 0.555 0.0025kN 0.003kN
M图
kN.m N2 Q2 sin2 H cos2 11 230.555
7.50.832 9.015kN
0.600 0.354 0.003 0.472 1.000 3.331 1.060 0.600
Q图 kN
13.300 10.958 9.015 7.749 7.500 7.433 1.421 6.796 3.325 11.235 11.665 11.700
312
3
3m
tg 2
dy dx
x3
4f l
1 2lx
x3
44 12
1
2123
0.667
(1)计算支座反力
VA
VA
2
6
9 12
8
3
11kN
VB
VB
2
6
38 12
9
9kN
H
M
C
11 6 2 6 3 7.5kN
f
4
2 3341,sin 2 0.555,cos 2 0.832
静定拱
所以推力:
H VAl1 P1(l1 a1) f
静定拱
分析两个竖向支座反力
P1 C
P2
VA
Pibi l
VB
Pi ai l
A
f
B HB
与简支梁的支座反力:
VA0
Pibi l
VB0
Pi ai l
HA VA VA0 VA
l1
VB VB0
等代梁
A
P1
分析 推力H 式:
H
VAl1 P1(l1 a1) f
(1)不管拱轴区段上是否有分布荷载,拱的各内力图在区段
上均为曲线形状; (2)在竖向集中力FP作用点两侧截面,拱的轴力和剪力有突 变,突变值分别为FP sinΨK 和FP cosΨK,弯矩图在该点转折; 在集中力偶M作用点两侧截面,弯矩有突变,突变值为M,轴 力和剪力不受影响。
<3> 轴力计算公式
NK VA P1 sinK H cosK
QK0 sinK H cosK
拱的任一截面上一般有三个内力(M, Q, N),内力计算的 基本方法仍是截面法。与直杆件不同的是拱轴为曲线时, 截面切线角度不断改变,截面上内力(Q, N)的方向也相 应改变。
静定拱
q=2kN .m
3、带拉杆的三铰拱,其支座反力可由整体的平衡条件完全求 得;水平推力由拉杆承受。可将顶铰和拉杆切开,取任一部分 求出拉杆中的轴力。
静定拱
三、 拱的内力图特征 1、拱的内力图特征
Mk Mk H y
Qk Qk cosk H sink
Nk Qk sink H cosk
由上式分析可知,当拱轴为曲线时。有:
l1
VA
等代梁 P1
A
f l2
l
C
a1
VA0
b1 a2
B HB
VA=VA0 H= MC0 / f
VB
P2
B
三铰拱的反力只 与荷载及三个铰 的位置有关,与 拱轴线形状无关 荷载与跨度一定 时,水平推力与 矢高成反比
b2 VB0
静定拱
支座反力共四个分量 需列出四个方程:
由整体平衡方程:
MA 0 和 MB 0
三铰拱C处弯矩
M
0 C
VAl1
P1 (l1
a1)
简支梁C处弯矩
2) 梁无轴力(在竖向载荷作用下) 拱的截面轴力较大,且一般为压力。
3) 推力只与三个铰和载荷位置有关,与拱轴形状无关;
即只与 f/l 有关。
静定拱
4) 当载荷和拱的跨度不变时,推力与拱高 f 成反比。 f 越大,H越小;反之, f 越小,H越大;
N图 kN
静定拱
Mk Mk H y
Qk Qk cosk H sink
Nk Qk sink H cosk
上式可作为拱内力的计算公式用,特别是在作拱的内力图时。 但须注意以下几点: 1、上式要在以拱的左底铰为原点的平面直角坐标中应用,并 仅考虑了竖向荷载的作用。
2果在、取右式是半中与拱水时k为平所方为k计向负算的。K锐截角面考处虑拱,轴则切K线截与面水在平左x半坐拱标时的夹k为角正。,如
