工程电磁场第三章剖析
工程电磁场课后答案1(完整)

0.29K
7401
VOH 74LS00
2.9.1 驱动: 负载: 拉电流: 灌电流: 扇出:
2.9.2 VOH > VIH VOL < VIL IOH > IIH IOL > IIL
第三章 组合逻辑电路分析与设计
3.1.2证明(C)A ABC ACD C D E
A ACD (C D )E
(b) _______ ________ _______ ________
A B C D C D A D
( A B)(C D) (C D)( A D)
(C D)( A B D)
AC AD BC BD CD D
AC BC D
3.2.1展开最小项(a) L A(B C) A BC A(B B)(C C) ( A A)BC
mi
3.2.2 (a)
______________________
___________________
AC ABC BC ABC AC BC BC ABC
灌电流多余: (8-4.8)/0.4=8
N=min(8,17)=8
2.4.5
__________________ ____ ____
L AB BC D E
AB BC D E
2.4.6 RP计算 (1)拉电流时
VCC R IP IH 74LS 00 VOH 7401
D=0 选中低位片1;D=1 选中高位片2
01234
56789
1
0
1
A B C D
0
2
0
4.2.9 7位数字译码显示电路
电磁场 恒定磁场

工程电磁场导论:恒定磁场
2)无外场时,各分子环流无规取向,总体磁矩为零,此时无宏观 磁场。有外场时,这些微磁矩受到力矩
的作用,趋于沿外场方向排列(
)。此时,出现
的有
序分布,总磁场不再为零,宏观上呈现磁性。这个过程,称为物 质(媒质)的磁化。 3)磁化的后果,就是媒质产生附加的磁场,叠加于外磁场之上, 空间的磁场,由二者共同决定。
(沿 R 方向)那么前者对后者的磁场作用力可表示为
eR方向由施力者指向
受力者
其中 ,称为真空磁导率。
工程电磁场导论:恒定磁场
• 这个规律没有官方的名称,但常常称为 Ampere 定律,
其在磁场中的地位与 Coulomb 定律在电场中的地位相
当。因此,对于真空中的两个载流回路 的作用力 和 , 对
工程电磁场导论:恒定磁场
•
也可以定义磁力线( B 线),其微分方程:
工程电磁场导论:恒定磁场
【例3-1】有限长直线电流的磁场问题。
•
考虑对称性,选取柱坐标,导线中点为坐标原点,导线与 z 轴重 合。显然,磁场与 维度无关。
取元电流
在 z′处,其在 P
点产生的元磁场
其中
工程电磁场导论:恒定磁场 因此
故
工程电磁场导论:恒定磁场
工程电磁场导论:恒定磁场
• 各向同性线性磁介质,有本构方程
称为磁化率,是一个无量纲的纯数。此时有
其中
为相对磁导率,
为磁导率。
工程电磁场导论:恒定磁场 一些磁介质的性能
工程电磁场导论:恒定磁场
• 对于铁磁介质,情况十分复杂。
等式 仍然成立,但是
不成立。 M~H 间没有线性关系。
工程电磁场导论:恒定磁场
工程电磁场--第3章--恒定电场的基本原理

fe Ee lim qt 0 q t
q t 为试验电荷的电荷量。
19
提供局外力的装置就是电源。 在电源中,其他形式的能量转换为电能。 在整个闭合回路中,电能又转换为别的 形式的能量。
20
2.电动势
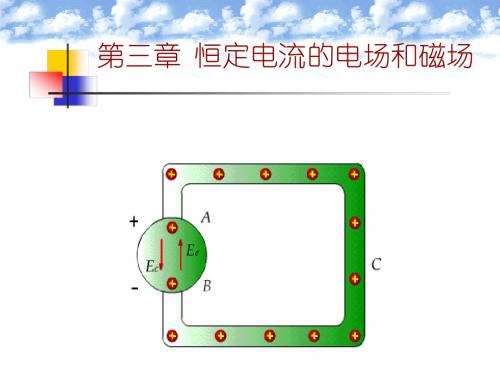
下图是一个典型的导电回路, 蓝色部分为导 电媒质,黄色部分为电源。 电源中除库仑电场 外,还存在局外电场。 电源之外的导电媒 质中只有库伦电场。
0 1 E ex , D ex 1 x 1 x
自由电荷体密度
0 0 D ( )=2 x 1 x (1 x)
32
D E E E
E
E
E E E 2 E J 上式说明积累自由电荷的体密度与 的空间 变化有关。 对于均匀导电媒质,介电常数 和电导率 都
5
如果体积的厚度可以忽略, 可以认为电荷在面上运动,形成面电流。 密度为 的面电荷 以速度 v 运动, 形成面电流密度 K , 定义 K v 。 如图所示, db0 是垂直于 v 方向的线段元。
6
dl db0 dl dS dq dI K v dt dtdb0 dtdb0 dtdb0 db0
4
7
7
7
3
7
10 5
1.03× 10
7
10 15
16
3.2 恒定电场的基本方程
1.局外场
要维持导电媒质中的恒定电流,就必须有恒定 的电场强度。 (作用:克服运动中的阻力) 在电场的作用下,正自由电荷沿电场强度方向 运动, 负自由电荷沿相反方向运动。 对于金属导体, 主要是自由电子沿电场相反方向运动。
工程电磁场-恒定磁场

例2 分析铁磁媒质与空气分界面情况。
μ0 α2
α1
μfe
铁磁媒质与空 气分界面
解:
tan 2
2 1
tan 1
0 fe
tan 1
0
2 0
表明 只要 1 90 ,空气侧的B
与分界面近似垂直,铁磁媒质表面
近似为等磁面。
2023/10/27
34/119
例 3 在两种媒质分界面两侧,
1 50,2 30
即 H2 H2yey H2xex 10ex 4ey A/m
B2 2H2 0(30ex 12ey ) T
M1 ∆l2
磁化电流是一种等效电流,是大量分子电流磁效应的表示。 有磁介质存在时,场中的 B 是传导电流和磁化电流共同 作用在真空中产生的磁场。
2023/10/27
20/119
4) 磁偶极子与电偶极子对比
模型
电量
电
偶
极
子
p qd
ρp - P p P en
电场与磁场
磁 偶
Jm M
极 子
Bx
0Ky 2
dx (x2 y2)
B
0K
2
ex
0K
2
e
x
y0 y0
2023/10/27
7/119
3.2 安培环路定律 Ampere’s Circuital Law 1. 真空中的安培环路定律
B dl l
l
0 I 2
e
dl
0I d l 2
0I
2
2
0 d 0 I
α
I dΦ
Bdl
解: 平行平面磁场,且轴对称,故
图3.2.19 磁场分布
工程电磁场第三章解读

3.1 Electric Flux Density
9. Example 3.1: find D in the region about a uniform line charge of 8nC/m lying along the z axis in free space. 10. Exercise: D3.1, D3.2
3. Electric Flux Density D (coulombs/square meter):direction (the
direction of the flux lines at that point) and magnitude (the number of flux lines crossing a surface normal to the lines divided by the S. area).
Ds S
The total flux passing through the closed surface is d closed Ds dS
surface
3.2 Gauss’s Law 4.To a gaussian surface, the mathematical formulation of Gauss’s law DS dS charge closed Q( Qn L dL S dS d )
4. Shown in the right figure
Q D r a a (inner ) 2 r 4a Q D r b a (outer ) 2 r 4b Q D a ( a r b) 2 r 4r
3.1 Electric Flux Density
工程电磁场PPT课件

eρ
a b
a
Jc
E
U 0 ln b
eρ
a b
a
R 1 1 1 ln b G Cll 2l a
Cl
U0
2
ln b
a
第19页/共91页
2.接地电阻 接地技术是保障人身和设备的一项电气安全措施,为电 力系统正常工作提供了零电位基准参考点。计算接地体 的接地电阻是恒定电场计算的一项重要工作。
第11页/共91页
例3-2:设一平板电容器由两层非理想介质串联构成,
如图所示。其介电常数和电导率分别为1,1和2,2, 厚度分别为d1和d2,外施恒定电压U0,忽略边缘效应。
试求:(1)两层非理想介质中的电场强度;(2)单位体积 中的电场能量密度及功率损耗密度;(3)两层介质分界 面上的自由电荷面密度。
b a
Jc
td
tU0
ln
b a
厚度为t的导电片两端面的电阻为:
R
U0 I
S
U0 Jc • dS
b a
U 0
U0
e td
e
tln b
a
第4页/共91页
2.电功率
在恒定电流场中,沿电流方向截取一段元电流管,如图所示。该元电流管中的电 流密度J可认为是均匀的(E,F不变),其两端面分别为两个等位面。在电场力作 用下,dt时间内有dq电荷自元电流管的左端面移至右端面,则电场力作功为:
第20页/共91页
下面计算图示埋于大地的半球形接地体的接地电阻。由镜象法得:
当r≥a时
4r 2Jc
2i, Jc
i
2r 2
,E
i
2r 2
,
E • dr
r
3工程电磁场 课后答案(王泽忠 全玉生 卢斌先 著) 清华大学出版社

工程电磁场答案第1章梯度:x y z u u u gradu e e e u x y z∂∂∂=++=∇∂∂∂; 散度:y x z A A A divA A x y z∂∂∂=++=∇⋅∂∂∂ ; 旋度:xy zxy ze e e rotA A x y z A A A ∂∂∂==∂∂∂ ∇⨯ 1-1(1)解:,T xy = ∴等温线方程为T x ,y c ==解得cy x=为双曲线族 (2)解:21T 2x y=+ , ∴等温线方程为221T c x y ==+,解得221x y c +=为半径的圆族 1-2(1)解:1u ax by cz=++ ,∴等值面方程为1u c ax by cz==++,解得, 110ax by cz c ++-=所以它为平行平面族(2)解:u z =-,∴等值面方程为u z c ==,解得()222x y z c +=-,顶点在(的圆锥面族)0,0,c (3)解: ()222ln u x y z=++,∴等值面方程为,()222ln u x y z =++c =解得222cx y z e ++=, 所以它为球心在原点的球面族1-3解:由题意可得,,x y z 2A x A y A z ===,又x y zdx dy dz A A A ==,即2dx dy dzx y z ==, ,2dx dy dx dzx y x z∴==, 212,y c x z c x ==, 过()1.0,2.0,3.0M 122,3c c ∴==,即22,3y x z x ==(联立)1-4解:由题意可知22,,x y z 2A y x A x y A y z ===,,x y zdx dy dz A A A ==即222dx dy dz y x x y y z ==,,dx dy dx dzy x x z∴==, 可得2212,x y c z c -==x (联立) 1-5 解:|621M ux z x ∂=+=∂2, 0|2M uz y ∂=-=-∂6,|222M uz y x z ∂=-+=∂4,余弦cos αβγ===,所以方向导数为0|1264M u l ∂=-=∂ 1-6 解:000|5,|4,|M M M u u uy z x z x y x y z∂∂∂=+==+==+=∂∂∂3, 过点(), 1.0,2.0,3.0余弦cos α==,cos β==cos γ==543+=1-7 解:0|22,24,2M u u u y x z x y z∂∂∂==-===-=-∂∂∂2), 设点到点的方向余弦为()2.0, 1.0.1.0-(3.0,1.0. 1.0-1cos 3α==,22cos ,cos 33βγ==-, 所以方向导数为()12222333⎛⎫⨯-++-⨯-= ⎪⎝⎭103, 由题意可知。
工程磁场学第三章(2)
21
21
与 I 1 成正比。
M
I 21 1
M
21
21
I1
式中,M21 为互感,单位:H(亨利)
同理,回路2对回路1的互感可表示为
M
12
12
I2
可以证明
M
12
M
图3.7.5 电流I1 产生与回路2交链的磁链
21
互感是研究一个回路电流在另一个回路所产生的磁效应,它不仅与两个回路的
由 由
H 1t H
2t
,
得 得
1
I 2 r
I 2 r
sin
I 2 r
I
sin
I 2 r
sin
I cos
21 I
I I I
B1n B 2 n
cos 1
2 1 2 1
I
2 r
cos 2
dρ
外磁链
o
d
o
d
o
a
0I
2
ld ρ
0 Il
2
ln
b a
缆芯中的内磁链 i :
在距轴线为 的场点上的磁场强度为
H
i
1
2
2 a
2
I 2a
2
2
通过长度为1,宽为d’ 的面积元dS’ 与部分电流 链的元磁通
d
i
I
a
2
I
交
a
2
2
d
i
a
3
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简单证明: 对J E 两边取面积分
左边 J dS I S
右边 E dS U dS S U GU
S
Sl
l
所以 U RI
7
3. 2恒定电场的基本方程 1. 局外场
要维持导电媒质中的恒定电流。就必须有恒定的电场强度。 在一个闭合回路中库仑电场的电场强度E闭合线积分为零。要维持恒定电流,电荷 在沿闭合回路运动时,还必须受到局外力的作用。
在电源中,除局外电场外,也存在库仑电场,故总的电场强度为 在电源以外的其他区域,只存在库仑电场,故总的电场强度
如果积分路径经过电源,则电场强度的闭合线积分等于电源的电动势
9
考虑电源以外的空间 电源以外的恒定电场是无旋场
10
3.电流连续性 根据电荷守恒原理,自然界中电荷量是守恒的。给定任意闭合面,设闭合面内的
密度为ρ的体电荷以速度v运动形成体电流密度J
穿过面积S的电流就是电流密度J在该面积上的通量
4
如果体积的厚度可以忽略,则可以认为电荷在面上运动,形成面电流,有面电流密度 如果面的宽度可以忽略,则可以认为电流在线上运动,形成线电流。
5
2.电流密度与电场强度的关系 要维持恒定电流,导电媒质中必须有电场强度。 电场强度也是恒定电场的基本场矢量。
积累自由电荷的体密度与 的空间变化有关。
14
• D • E • E • E • E • E
•
E
2
•
E
•
J
积累自由电荷的体密度与 的空间变化有关。
例 在均匀恒定电流场中,电流密度为1,沿 x 方向。 在 x 从 0 到 1 的区域,媒质电导率从1均匀增加到 2 , 介电常数保持 0 不变,试求自由电荷体密度。 解 据电流连续性,整个区域电流密度不随 x 变化,
12
4.恒定电场的基本方程及辅助方程 在电源以外的导电媒质中,恒定电场的基本方程微分形式为
微分形式
积分形式为
辅助方程 辅助方程在电源内部成立
电源以外空间恒定电场的电 位满足拉普拉斯方程
电源以外空间(包括导电媒质)的 恒定电场是由电荷产生的库仑场, 空间电场也应满足高斯通量定理
13
5.不均匀导电媒质内部积累电荷 在恒定电场建立过程中,当导电媒质不均匀时,其内部积累自由电荷。
电荷量为q,空间的电流密度为J,则
这是电流连续性方程的积分形式。等式左边是单位时间从闭合面流出的电荷量,等 式右侧为单位时间闭合面内减少的电荷量。
应用散度定理
考虑电荷体密度为ρ,有
11
对于恒定电场,电荷的分布不随时间变化
上式适合于电源和电源以外恒定电场的任何区域。电流连续即电流密度的散度为零, 说明恒定电流场是无散场,场内任一点不产生电流密度线,也不终止电流密度线, 即电流密度线处处连续。
2
恒定电场知识结构
基本物理量 J、 E
欧姆定律
J 的散度
基本方程
E 的旋度
边界条件
边值问题
电位
一般解法
电导与接地电阻
特殊解(静电比拟)
3
3 .1电流与电流密度 1.电流与电流密度 电荷有规则的运动形成电流; 导电媒质中的电流称为传导电流; 不导电空间电荷运动形成的电流称为运流电流; 不随时间变化的电流是恒定电流,维持恒定电流的电场称为恒定电场。
第三章 恒定电场的基本原理 定义电流和电流密度 电源的电动势和局外电场强度 恒定电场的电流连续性 恒定电场的基本方程 恒定电场的导电媒质分界面条件 讨论边值问题
重点掌握电流密度的定义和恒定电场的基本性质,学会将 恒定电流场表述为边值问题。
1
3 恒定电场的基本原理
本章提示:
电荷有规则运动形成电流,定义电流和电流密度。 维持恒定电流的条件,引出电动势和局外电场强度; 由电荷守恒原理导出恒定电场的电流连续性; 从而得到恒定电场的基本方程。 导出恒定电场的导电媒质分界面条件。 最后边值问题。
15
由
E
1
J
,
1
x
,得
E
Байду номын сангаас
1 1
x
e
x
,
D
0 1
x
ex
。计算自由电荷体密度
D
x
( 0 ) 1 x
(1
0 x)2
图中画出了电位移矢量分布 情况,
随着 x 的增大,
电位移矢量数值变小, 说明有?值的自由体电荷。
16
3. 3导电媒质分界面条件 1.分界面条件
在不同导电媒质的分界面上,存在自由面电荷,也可能存在束缚面电荷。这造成 分界面两侧场矢量不连续。这种场矢量的不连续性虽然不会影响积分形式基本方程 的应用,却使微分形式的基本方程在不同电介质分界面处遇到困难。 第一,讨论电场强度E应满足的分界面条件。
提供局外力的装置就是电源。在电源中,其他形式的能量(如化学能、机械能和光 能等)转换为电能。在整个闭合回路中,电能又转换为别的形式的能量。
8
2.电动势 图3-2-1所示为一个典型的导电回路。
为了衡量电源将其他能量转换为电能的能力, 我们把单位正电荷从电源负极运动到 正极,局外力所做的功定义为电源的电动势, 用e表示,且
媒质分界面上才没有自由面电荷 一般情况下这一关系不满足,媒质分界面上存在自由面电荷。
20
3.媒质分界面的两种特殊情况 首先,讨论良导体和不良导体分界面的情况。 根据分界面条件,得
在分界面处,当电流从良导体γ1进入不良导体γ2时,电流密度的法向分量不变,而 切向分量改变为原来的γ2/ γ1倍。对于良导体与不良导体分界面,因γ1远大于γ2, γ2/ γ1很小,所以一般情况下J2t可以忽略。因此可得如下结论:
(1)从不良导体一侧看,进入的电流线近似与分界面垂直。 (2)在不良导体中放入良导体电极,从不良导体一侧看,可以认为电流 线垂直进入或流出电极表面,电极表面可作为等位面处理。
γ称为导电媒质的电导率,单位是西/米,S/m
式中ρR称为导电媒质的电阻率,单位是欧·米,Ω˙m 电导率和电阻率互为倒数。上式称为欧姆定律的微分形式,是导电媒质中恒
定电场的辅助方程。
6
在线性媒质中
J E 欧姆定律 微分形式。
U RI 欧姆定律 积分形式。
J 与 E 共存,且方向一致。
J 与 E 之关系
17
第二,讨论电流密度J应满足的分界面条件。 第三,讨论电位Ф应满足的分界面条件。
18
由 l E dl 0 SJ dS 0
E1t E 2t
得
J1n J 2n
说明 分界面上 E 切向分量 连续,J 的法向分量连续。
折射定律
tan1 1 tan2 2
电流线的折射
19
2.导电媒质分界面积累自由面电荷 在恒定电场建立过程中,导电媒质分界面上积累自由面电荷,当达到平衡状态时,根据
