理论力学竞赛辅导5综合应用-资料.ppt
合集下载
工程力学竞赛辅导-材料力学拓展与提高PPT课件

d
32ml
3G (d2
d1 )
1 ( d13
1
d
3 2
)
思考:两端直径分别为d1、d2的圆锥形杆,受分布力 偶m的作用,如何求杆的总扭转角。
d T (x) dx
GI p ( x)
㈡超静定问题的变形协调条件
如图所示,一实心圆杆1在其外表面紧套空心圆管2。设杆的 拉压刚度分别为E1A1和E2A2 。此组合杆承受轴向拉力F,试求 其长度的改变量。(假设圆杆和圆管之间不发生相对滑动)
解: (1) 对节点C进行受力分析
2
3
列平衡方程 (2) 根据胡克定律,列出各杆的绝对变形
,
1
300
C 1000
F
FN2
FN3
FN1
C
F C
(3) 变形协调条件 l3 l2 sin 300 (l2 cos 300 l1)ctg300
简化后得:
△l3
△l1 C1
300
△l2
C2
1杆实际受压,2杆和3杆受拉。
解: 由平衡条件
F
2 1
F
l
变形协调条件
最后得到 l FN1l
Fl
E1 A1 E1 A1 E2 A2
㈡超静定问题的变形协调条件
设有一实心钢管,在其外表面紧套一铜管。材料的弹性模量和
线膨胀系数分别为E1,E2和αl1 ,αl2.且αl2 > αl1 。两管的横截
面面积均为A。如果两者紧套的程度不会发生相互滑动,试证
桩的总的缩短量∆l,以P、l、E、A表示。
P
y
f ky2
l
f
dy dy
y (a)
y f
0 (b)
理论力学竞赛指导-PPT课件

2 k 2 0 x ( )x m
当 2
2k m
牵连惯性力大于弹簧的弹性恢复力,
物块不能在x´=0处附近作自由振动,物块在x´=0处 的平衡是不稳定的。 当
2
2k m
牵连惯性力等于弹簧的弹性恢复力
物块在x´=0处为随遇的平衡位置。
4、水流以体积流量qV通过内径为d1管
z
ω
北
解:3. 分析加速度
绝对加速度aa -所要求的 未知量;
z´ ae ar
vr
相对加速度ar - ar=vr2/R 方向指向地心;
牵连加速度ae - ae=Rcos2ae 矢量垂直于 Oz´轴,方向指向Oz´; 科氏加速度aC - aC=2vrsin方向沿过P点纬 线的切向,指向西。
aC
k
P O
k
y´
k x´
解: 1. 非惯性参考系-O x´ y´ 动点-物块P 2. 分析相对速度和各种加速 度: 相对速度vr -沿着x´正向
OP kk
P x´
aIC
牵连加速度aen-由大盘 转动引起
vr
aen
科氏加速度aIC -2m vr
y´ k x´ 解: 3. 分析质点(物块)受力: F -弹簧力F=2k x´ FIC aIC vr aen F FN -槽对物块的约束力 FIC -科氏力 FIen -法向牵连惯性力 FIen=m 2 x´
1
qv
1
2
2
解:分析以喷嘴的左右截面(1-1 和2-2)为边界所包含的质量流根据 体积流量与速度和管道横截面积的 关系,有
2 2 π d π d q v A v A v 1 v 2 V 1 1 2 2 1 2 4 4
当 2
2k m
牵连惯性力大于弹簧的弹性恢复力,
物块不能在x´=0处附近作自由振动,物块在x´=0处 的平衡是不稳定的。 当
2
2k m
牵连惯性力等于弹簧的弹性恢复力
物块在x´=0处为随遇的平衡位置。
4、水流以体积流量qV通过内径为d1管
z
ω
北
解:3. 分析加速度
绝对加速度aa -所要求的 未知量;
z´ ae ar
vr
相对加速度ar - ar=vr2/R 方向指向地心;
牵连加速度ae - ae=Rcos2ae 矢量垂直于 Oz´轴,方向指向Oz´; 科氏加速度aC - aC=2vrsin方向沿过P点纬 线的切向,指向西。
aC
k
P O
k
y´
k x´
解: 1. 非惯性参考系-O x´ y´ 动点-物块P 2. 分析相对速度和各种加速 度: 相对速度vr -沿着x´正向
OP kk
P x´
aIC
牵连加速度aen-由大盘 转动引起
vr
aen
科氏加速度aIC -2m vr
y´ k x´ 解: 3. 分析质点(物块)受力: F -弹簧力F=2k x´ FIC aIC vr aen F FN -槽对物块的约束力 FIC -科氏力 FIen -法向牵连惯性力 FIen=m 2 x´
1
qv
1
2
2
解:分析以喷嘴的左右截面(1-1 和2-2)为边界所包含的质量流根据 体积流量与速度和管道横截面积的 关系,有
2 2 π d π d q v A v A v 1 v 2 V 1 1 2 2 1 2 4 4
理论力学竞赛辅导全

II
B
A I
选择题28: 长方体I面上的A点作用 一该平面内的汇交力系,II面上的B 点也作用有一该面内的汇交力系,则 该力系最多有几个独立的平衡方程? A:2个 B:3个 C:4个 D:5个
B A
地面光滑
18
BUAA
虚位移原理
虚位移原理:具有双面、完整、 定常、理想约束的静止的 质点系, 在给定位置保持平衡的充要条件是:该质点系所 有主动力在系统的任何虚位移上所作的虚功之和等于零。
思考题13:判断在图示位置系统是否 有可能平衡.(F,M 均不为零)
C
CF
AM
B
A F
2020/10/18
0
MOx(F ) 0
MOy(F ) 0
M x(F) 0 M y (F ) 0,
Fz 0
MOz(F ) 0
M z(F) 0
注:正交条件是充分的,不是必要的。
2020/10/18
9
BUAA
空间汇交力系的平衡条件
空间汇交力系平衡条件的讨论
FR FRxi FRy j FRzk 0
A
O RC
mg
1. 不倒翁的质量m 2. 半圆球的半径R 3. 重力加速度g 4. 重心的位置h
2020/10/18
21
BUAA
静力学的思考题与例题
题15:在下列图示结构中,构件AC上作用有一已知力偶(构 件自重不计),试确定铰链A处约束力的方向。
AB AC, AC AB
思考题16:上述结构中,哪个结构中A点的约束力最大?
FR FR2x FR2y FR2z 0
FRx Fx FRy Fy FRz Fz
空 FRx Fx 0
间
力
全国周培源大学生力学竞赛辅导力学竞赛-静力学专题PPT共150页

竞赛-静力学专题
36、“不可能”这个字(法语是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
39、没有不老的誓言,没有不变的承 诺,踏 上旅途 ,义无 反顾。 40、对时间的价值没有没有深切认识 的人, 决不会 坚韧勤 勉。
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
36、“不可能”这个字(法语是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
39、没有不老的誓言,没有不变的承 诺,踏 上旅途 ,义无 反顾。 40、对时间的价值没有没有深切认识 的人, 决不会 坚韧勤 勉。
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
理论力ppt课件

力矩对时间的累积等于物体角 动量的变化率。
角动量守恒的条件
系统不受外力矩或所受外力矩 的矢量和为零。
角动量守恒定律
不受外力矩作用的系统,其总 角动量保持不变。
应用领域
广泛应用于航天、航空、航海 等领域,用于分析系统的旋转
运动规律和设计。
CHAPTER 04
质点和刚体的动力学应用
质点和刚体的直线运动
理论力学的历史与发展
理论力学的起源可以追溯到古代,如阿基米德等人的贡献。 然而,真正意义上的理论力学是在牛顿发表《自然哲学的数 学原理》之后发展起来的。
随着数学和物理学的不断发展,理论力学也不断完善和深化 ,形成了多个分支。近年来,随着计算机科学的进步,理论 力学与数值计算方法的结合为解决复杂问题提供了更有效的 手段。
弹性力学的基本方程
01
02
03
平衡方程
根据牛顿第二定律,描述 了物体在力的作用下保持 平衡的状态。
几何方程
描述了物体在外力作用下 产生的变形。
物理方程
描述了物体的应力与应变 之间的关系。
弹性力学的应用实例
桥梁和建筑物的设计
材料科学的研究
通过弹性力学,可以分析桥梁和建筑 物的受力情况,从而设计出更加安全 和经济的结构。
连续性假设
物质没有空隙地连续充满所占据的空 间,或者说物质所占据空间的场内, 物质分布函数的值是连续的。
完全弹性假设
当外力撤去后,所有的变形全部恢复 ,并且不出现残余的应变。
各向同性假设
弹性性质与方向无关,也就是说,在 各个方向上,弹性模量是常数。
小变形假设
物体在外力作用下产生的变形量远远 小于物体原来的尺寸,即可以忽略不 计。
基础运动形式
角动量守恒的条件
系统不受外力矩或所受外力矩 的矢量和为零。
角动量守恒定律
不受外力矩作用的系统,其总 角动量保持不变。
应用领域
广泛应用于航天、航空、航海 等领域,用于分析系统的旋转
运动规律和设计。
CHAPTER 04
质点和刚体的动力学应用
质点和刚体的直线运动
理论力学的历史与发展
理论力学的起源可以追溯到古代,如阿基米德等人的贡献。 然而,真正意义上的理论力学是在牛顿发表《自然哲学的数 学原理》之后发展起来的。
随着数学和物理学的不断发展,理论力学也不断完善和深化 ,形成了多个分支。近年来,随着计算机科学的进步,理论 力学与数值计算方法的结合为解决复杂问题提供了更有效的 手段。
弹性力学的基本方程
01
02
03
平衡方程
根据牛顿第二定律,描述 了物体在力的作用下保持 平衡的状态。
几何方程
描述了物体在外力作用下 产生的变形。
物理方程
描述了物体的应力与应变 之间的关系。
弹性力学的应用实例
桥梁和建筑物的设计
材料科学的研究
通过弹性力学,可以分析桥梁和建筑 物的受力情况,从而设计出更加安全 和经济的结构。
连续性假设
物质没有空隙地连续充满所占据的空 间,或者说物质所占据空间的场内, 物质分布函数的值是连续的。
完全弹性假设
当外力撤去后,所有的变形全部恢复 ,并且不出现残余的应变。
各向同性假设
弹性性质与方向无关,也就是说,在 各个方向上,弹性模量是常数。
小变形假设
物体在外力作用下产生的变形量远远 小于物体原来的尺寸,即可以忽略不 计。
基础运动形式
高中物理竞赛辅导力学解题步骤 课件 新人教版全套PPT

A
A
手控制kx到2 脱mg离m时13:a
m(1 a g)
x2
3 k
B
x1
x2
1(1a)t2 23
t2 m k
• 起始时整体:
kx1(M m )gF 1(M m )1 3a F1M(g13a)23ma
刚脱离时隔离BM:g
F2
M
1a 3
F2
M(g
1a) 3
若要两力方向相反:F 2 0
F1 0
1.研究对象的选取: 隔离法与整体法
• 当多个物体的加速度不相同时用隔离法! • 当涉及两个物体之间作用力时用隔离法! • 不涉及物体之间作用力和加速度相同时也能
用隔离法! • 若能用整体法解决问题的,隔离法也能解
决.只是步骤多了一些而已!
• 【例1】如图,在光滑水平面上,有质量为M,长 度为L的木板.在木板上有一个质量为m的物体,
是恒力.求作用力F的最大值和最小值.
刚F 开始时F最小F:(Mm)a弹簧原先:kx1(Mm)g
脱离时隔离AFmgma脱离时:kx2MgMa
A B
x1
x2
1 2
at 2
F m in (M m )a 0 .5 7 5 N
mg a
1 kt2 M 2
0.25m/s2 F m axm (ga )3 .0 7 5N
a 3g
2ma M(1ag)
3
3
m a 3g M2
• 【训练6】一个竖立的弹簧上端有一质量为M=2kg 的木板,木板上放一个质量为m=0.3kg的砝码,原来 静止.今用一个竖直向上的力F拉砝码.使砝码以加
速度 做匀a 加速运动,已知轻弹簧的劲度系数
为 k500N/m,F在最初的 0 . 2 s 内是变力,以后都
《理论力学全面实用》课件

3
第三章:弹性力学
弹性力学的基本概念和定律,材料的弹性特性及变形和应力分析。
实例演示
结构设计实例
通过实际工程示例,展示如何应 用理论力学知识进行结构设计和 分析。
流体力学案例
通过流体力学案例,讲解流体流 动的力学原理和计算方法。
应力分析示例
应力分析实例,帮助学员了解如 何通过力学理论分析材料的应力 状态。
总结与展望
在本课程中,我们通过详细的理论讲解、实际案例和实例演示,全面介绍了理论力学的基本概念、原理和应用。 接下来,您可以进一步拓展自己的学术和实践能力,并将所学知识应用到实际工作中。
《理论力学全面实用》 PPT课件
欢迎来到《理论力学全面实用》PPT课件,本课程将帮助您深入了解理论力学, 掌握实用技巧,并提供丰富的案例演示和实例讲解,让您成为该领域的专家。
课程介绍
这一部分将介绍本课程的背景、目的以及适合的受众群体。了解课程的整体框架和目标,能够帮助您更好地理 解和应用相关内容。
课程大纲
基础理论
力学基本概念和定律,运动学 和动力学,力的作用和计算方 法。
力学分支
刚体力学,弹性力学,流体力 学和热力学等力学的不同分支 领域。
实际应用
力学在实际工程和科学研究中 的应用,如结构设计、材料力 学、流体流动等。
教学方法
1 理论讲解
通过课堂讲解,详细介绍力学的基本概念和定律,并深入解读其背后的原理和应用。
2 案例分析
通过实例演示和案例分析,帮助学员将理论知识应用到实际问题的分析和解决中。
3 小组讨论
引导学员进行小组讨论,促进彼此间的交流和学习,培养团队合作及解决问题的能力。
课件内容
1
第一章:力学基础
周培源力学竞赛辅导龙江省.ppt
A xdA 0
A z xdA 0
M z A y xdA 0
x
y
(4)
x E x
EE21
x x
A1 A2
(5)
(1) (2) (3)
(4) 代入(5) 代入(3) 1 M z E1I z1 E2I z2
x1
M z E1 E1I z1 E2I z2
y
, x2
M z E2 E1I z1 E2I z2
tan
式式((98))
MzIy M yIz
M y I yz M z I yz
讨论:
x
(M zIy
M
y I yz ) y (M y I z
IyIz
I
2 yz
M z I yz )z
3) 截面无对称轴 但弯矩在形心主惯性平面内
y、z为形心主轴
M y 0 , M z M , I yz 0
tan
辅导课
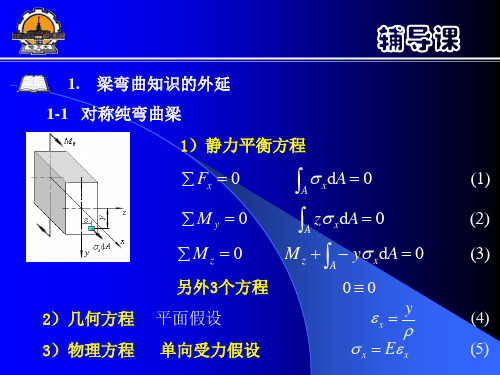
1. 梁弯曲知识的外延 1-1 对称纯弯曲梁
1)静力平衡方程
Fx 0
A xdA 0
(1)
My 0
A z xdA 0
(2)
Mz 0
M z A y xdA 0
(3)
另外3个方程
00
2)几何方程 平面假设 3)物理方程 单向受力假设
x
y
(4)
x E x
(5)
辅导课
1. 梁弯曲知识的外延
IyIz
I
2 yz
(9)
(8)、(9)代入(5)
x
(M zIy
M
y I yz ) y (M
I
yIz
I
2 yz
yIz
M z I yz )z
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8
BUAA
运动学的应用
问题7:设计相关的参数,使得当摇杆BD铅垂时,滑枕向右移动 的速度是向左移动速度的2倍,并求此时滑枕的加速度和摇杆的 角加速度。已知曲柄OA的角速度为常量ω(逆时针转动)
D
设 O : R A , O L B
H
A O
B 2021/1/2
v左
R H
LR
v右
R H
LR
L3R a滑枕0
b a s i n b c os
(usin )tb
f'() a co b s si 0 n
uasinVbbcos
tan a
b
u Vb a2 b2
2021/1/2
7
BUAA
运动学的应用
问题6:设计一个机构,使得将转动转换成往复移动或摇动。
2021/1/2
摇杆0
9
BUAA
动力学的应用
问题8 :两轮电动车中的力学问题 设:电机转子与车轮固连,其定子 与车身固连。
2021/1/2
10
BUAA
动力学的应用
问题8—1 :无人使用时,车体能在铅垂位置平衡的力学原理 是什么?
2021/1/2
问题8—2 :人站在车上时,车体在 铅垂位置平衡是否是稳定的?
11
BUAA
2021/1/2 问题3:该磅秤在设计上存在还哪些不足,如何改进3。
BUAA
静力学的应用
问题3:该磅秤在设计上存在还哪些不足,如何改进。
2021/1/2
4
BUAA
静力学的应用
2021/1/2
5
BUAA
静力学的应用
问题4:轧钢机械中的力学问题
θ
bθ
a
d
tan d2(dab)2
dab
2021/1/2
BUAA
第五讲 应用篇
• 静力学的应用 • 运动学的应用 • 动力学的应用
2021/1/2
1
BUAA
静力学的应用
问题1:设计一个机构或结构,实现施加一个很小的力, 产生一个很大的作用力?
β
β
2021/1/2
2
BUAA
静力学的应用
例题2:试设计一台秤,使称重结果与大象站立位置无关。 1、台秤应用的是什么原理? 2、若使称重结果与大象站的位置无关,应用什么样的机构? 3、应用什么原理最容易确定大象重量与秤砣重量间的关系? 4、给出台秤必要的几何参数。 5、给出测试数据与大象重量的关系。
习的过程中实践,在实践的基础上创新。
2021/1/2
17
BUAA
祝大家取得好成绩
谢谢
2021/1/2
18
相对质心C动量矩守恒:
取圆盘为动系,甲虫A为动点
r C A m A v a r C O m O v O J O ω ( 5 )
由5式并利用2式和3式,化简可得:3R u0(6 )
2021/1/2
由5、6和1式,可得:
3uR,vOva
u 3
15
BUAA
运动学中思考题40:
设计一个平面运动机构,该机构由若干个刚体构成,使得仅在图
17. 3 18. 圆周, u/3 19. 圆周,u/3 20. 平面,u/3R
21. 2mu2/9R 22. 2pi/3 23. u 24. 6u/L 25. gf/3 26. -8gf/3L
2021/1/2
14
BUAA
四、综合分析题(A)
由于合外力为零,因此系统的动量守恒,对质心的动量矩也守恒
示瞬时,下列情况同时成立:
• 刚体1的角速度不为零,但角加速度为零: 1 0 ,
• 刚体2的角速度为零,但角加速度不为零: 2 0 ,
• 刚体3的角速度和角加速度均为零:
3 0,
A
cos(t)
C
1 0 2 0 3 0
D
E
O
B
2021/1/2
16
BUAA
结束语
• 在学习中挖掘知识的内涵
动力学的应用
问题8—3:若车轮在地面上纯滚动,已知:车轮轮心的加速度为
a,人体和车体(不含电机和车轮)的总质量为mC,电机和车轮
的质量为mA,对转轴的转动惯量为J,车轮半径为R,AC=L
C θ
mCg
A
若车身视为平移。求: 1、电机的驱动力矩M 2、人体与车体总重心C 前倾的角度θ。 3、地面作用在车轮上 的摩擦力。
1、 若钢板能进入碾轧机,利 用的是什么力学概念? 2、轧轮和钢板间的摩擦系数 为f,确定a,b,d ,f间的关系。
ftam na x tan
6
BUAA
运动学的应用
问题5:已知车队以速度V 匀速行驶,车宽为b,车距为a, 若人要
匀速沿直线行走穿过马路,求人过马路的最小速度u,并确定过
马路的方向。
au
– 掌握基本理论与方法的适用条件(基本假设在理论推 导中的作用)
– 建立各知识点间的内在联系,形成知识结构体系
• 在实践中提高分析问题和解决问题的能力
– 分析因果关系,建立力学模型,选择解决问题的方法 – 勤思考,多总结,掌握解决某类问题的普遍方法 – 在探索的过程中学习(不要认可知识与方法),在学
2021/1/2
12
BUAA
动力学的应用
1、电机的驱动力矩M 应用动能定理微分形式:
T1 2m Cv21 2m Av21 2JAR v2 dWM d
T m Cv am Av aJAR v2aW MMRv
M(mCRmARR J)a
C θ
mCg
a A
F
2、求倾角θ 应用动静法:研究车身
M A0, FICmCa
FIC
C
θ
3、求摩擦力 mCg
F Ay
研究整体,应
m CgsLinFIC Lco sM0 M
A
用动量定理 F Ax
2021/1/2
13
BUAA
竞赛试题答案
1. 非 2. 非 3. 非 4. 是 5. 是 6. D 7. C 8. C 9. C 10. A
11.(tanθ)/2 12.2a/b 13.δrA 14. R 15. mRω2/2pi 16. gsin450
C为系统的质心
动量守恒: m A vam O vO0
vr u
vO
Avr va
vavO0(1 )
ve
速度合成定理: vavevr (2)
C O
v e v O r O A (3 )
x 将2式和3式代入1式: r O A v r 2 v O 0
该式在x轴投影: R u 2 v O 0(4 )
