第六章 系统的状态变量分析 (1)
第6章状态变量分析法

间变化而描述的路径,称为状态轨迹。
6
通信与信息基础教学部
状态与状态空间(3) 状态变量分析法的一般步骤
用状态变量来描述和分析系统的方法称为状态变量分 析法。当已知系统的模型及激励,用状态变量分析法时, 一般分两步进行:
一是选定状态变量,并列写出用状态变量描述系统特 性的方程,一般是一阶微分(或差分)方程组,它建立了 状态变量与激励之间的关系;同时,还要建立有关响应与 激励、状态变量关系的输出方程,一般是一组代数方程;
M
M
M
M
M
yr (t) cr1x1 (t) cr2 x2 (t) L crn xn (t) dr1 f1 (t) dr2 f2 (t) L drm fm (t)
11
Байду номын сангаас
通信与信息基础教学部
连续系统状态方程的一般形式(4)
状态方程、输出方程(P323)
x1
x
Mxx2n
a11
16
通信与信息基础教学部
由电路图建立状态方程(1) 由电路直接建立状态方程的步骤
(1) 选择独立的电容电压和电感电流作为状态变量;
(2)
对于电容C应用KCL写出该电容的电流
iC
C
dvC dt
与其它状态
变量和输入变量的关系式;
(3)
对于电感L应用KVL写出该电感的电压
vL
L
diL dt
与其它状态
变量和输入变量的关系式;
(4) 消除非状态变量(称为中间变量); (5) 整理成状态方程和输出方程的标准形式。
17
通信与信息基础教学部
由电路图建立状态方程(2)
M
M
M
M
系统的状态变量分析法
出
状
方
态
程
方
程
9-1 连续系统状态空间方程建立
一、引例 t<0,K在2;t=0,K从2打到1。求t>0时,电压uR和uL。
(
状
态
方
程
)
( 输 出
uR t Ri(t)
方 程
uL t Ri(t) uc (t) us (t)
)
状态方程和输出方程通称为
状态空间方程
uc(t)和i(t)称为状态变量
说明:同一系统函数或微分方程,可以有不同的模拟图或信号流图,所以 可以得到不同的状态方程和输出方程,但特征根相同,同一系统,它的系 统矩阵A相似。
练习1:列写状态方程和输出方程,已知系统函数为
状态变量:选积分器输出。
练习2:已知系统函数,用级联型信号流图列写状态方程和 输出方程
状态变量:选积分器输出。来自3、系统函数矩阵与单位冲激响应矩阵 1)系统函数矩阵
2)单位冲激响应矩阵: 3)系统自然频率:
意义:第j个激励单独作用时 与所产生的第i个响应之间的 关系。
3、状态方程:描述系统状态变量和激励与状态变量一阶导数关系 的微分方程组。
4、输出方程:描述系统状态变量和激励与输出响应关系的代数方程组。 5、状态向量:由状态变量做分量所构成的向量。(n维) 6、状态空间:状态变量所有取值的集合。即状态向量所在的空间。 7、状态轨迹:在状态空间中状态向量端点随时间变化所形成的轨迹。
(2)便捷的运用到多输入多输出系统; (3)可以分析系统的“可观测性”和“可控制性”; (4)可以描述非线性系统和时变系统; (5)便于计算机求解(一阶微分方程、差分方程)。
4、分析方法:状态变量法
以系统内部的状
第6章系统的状态变量分析法

写成标准形式
d λ1 (t ) R R 1 = − 1 λ1 (t ) − λ 2 ( t ) + 1 x1 ( t ) dt L L L d λ 2 (t ) 1 1 1 = λ1 ( t ) − λ 2 (t ) + x 2 (t ) dt C R2C R2C
例如:电路如图中所示,以两电阻上的电压为输出,试列出电路的
iL L x1
R1 R2
C
y1
vc
y2
状态方程与输出方程。
x2
解:⑴ 选择状态变量。选择电感电 流与电容电压为状态变量
λ1 (t ) = iL (t )
λ 2 (t ) = v c (t )
⑵ 列状态方程。列包含电感支路的回路电压方程,
L di L ( t ) = [ x 1 ( t ) − i L ( t )] R 1 − v c ( t ) dt
二、 状态方程
系统的状态方程,是一组一阶微分方程组。以状态变量与激励 的线性组合,表示一个状态变量的导数。 例如:串联的RLC回路,可以由以下的状态方程描述。
⎛ c11 c12 ⎜ c22 ⎜c C = ⎜ 21 M M ⎜ ⎜c ⎝ L1 cL 2
R
L
iL (t )
C
L
diL (t ) = − RiL (t ) − uC (t ) + x(t ) dt duC (t ) = iL (t ) dt
X (s)
bM
s −1 λ N
a N −1
aN −2
bM −1
s −1 λ N −1 λ2 s −1 λ1 b0
武大信号系统(郑君里)考与不考的章节

武大信号与系统考点分布
读下面三段三遍以上,不想学习的时候再读读:
一、根据往年考题的情况,以下几章是不考的:《信号与系统》郑君里第二版,上册的第六章“信号的矢量空间分析”;下册的第九章“离散傅里叶变换以及其离散正交变换”;第十章“模拟与数字滤波器”;第十一章“反馈系统”(但是这一章里的画信号流图和劳斯表每年基本必考);第十二章“系统的状态变量分析”(这一章只要求你会列状态方程,不要求你去解状态方程)
二、根据往年考题的情况,大题一般的分布情况:第三章与第五章傅里叶变换及应用每年绝对的大题,甚至不止一道;第二章与第四章可能是一道大题可以用时域解也可以用S域解,看你的选择方法,往往就是给你电路图每年必考一道或两道大题;第七章,主要是考列解差分方程,每年一道大题,有时考文字叙述的应用题;第八章,每年基本两道大题,很重要;第十一章,十二章,每年一道信号流图加劳斯表,列状态方程的大题;第一章的关于线性,连续,时不变,稳定等系统的判断也常考。
三、课后习题,考过的真题要熟练。
1、做题养成好习惯,步骤过程清晰,计算要仔细
2、重复一下第1条,因为真的很重要,步骤过程认真仔细,开始想不犯错很难,要尽量少犯错
3、容易出错的题型多动笔做做,这几年题型都很基础,熟练就能得高分。
系统的信号流图

例3
H (z)
z2 z3+3z2
2z
,画出直接形式、
串联形式和并联形式信号流图。
解:(1)
H (z)
z3 z3+3z2
= z2 3z3 2z 1 3z1 2z2
(2)
H (z)
z3 z3+3z2
2z
z(z
z3 2)(z
1)
1 z
z z
3 2
1 z 1
z 1
1 1
3z 1 2 z 1
1
z
1 s1
1 s1
根据梅森公式分别画出 2
1 3s1
2 1 s1
的流图,并联起来
1 F(s)
1
s-1
1/2 -3
Y(s)
s-1
1/2
-1
系统的状态变量分析
例2
H
(s)
s(s
2s 3 3)(s
2)
,画出直接形式、串联
形式和并联形式信号流图。
解:(1)
H (s)
s(s
2s 3 3)(s
2)
s3
1
1
z-1
z-1
z-1
F(z)
Y(s)
-3
4
2
H(z)
z2 2
Y(z)
z3 2z2 3z 4
-3
1 s-1 s-1 1
F(s)
-2
s-1 1 Y(s)
-1
H
(s)
1
s 1
s 3 5s 2
2 s 3
系统的状态变量分析
三、系统函数计算
1.列节点方程(由加法器输出端)
2.梅森公式
H 1
k
数字逻辑 第六章习题答案
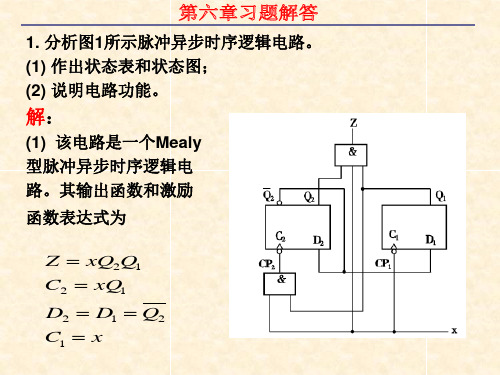
根据真值表画出激励函数和输出函数卡诺图(略),化简后可 得:
(5) 画出逻辑电路图 根据激励函数和输出函数表达式,可画出实现给定功能的逻 辑电路如图11所示。该电路存在无效状态10,但不会产生挂 起现象,即具有自启动功能。
7 试用与非门构成的基本R-S触发器设计一个 脉冲异步模4加1计数器。 解(1) 设电路输入脉冲为x,状态变量为 y1y0,其状态表如表9所示。
(2)该电路的状态图、状态表
(3)该电路是一个“x1—x2—x3”序列检测器。
4 分析图7所示脉冲异步时序电路,作出时间 图并说明该电路逻辑功能。
解:(1) 该电路是一个 Moore型脉冲异步时序逻辑 电路,其输出即电路状态。激 励函数表达式为
(2)电路次态真值表
(3)时间图
(4)该电路是一个模4计数器。
(4) 确定激励函数和输出函数 确定激励函数和输出函数时注意: ● 对于多余状态y2y1=10和不允许输入x2x1=11,可作为无关条 件处理; ● 当输入x2x1=00时,电路状态保持不变; ● 由于触发器时钟信号作为激励函数处理,所以,可假定次态 与现态相同时,触发器时钟信号为0,T端为d。 据此,可列出激励函数和输出函数真值表如表8所示。
(2) 根据状态表和RS触发器的功能表,可列出激 励函数真值表如表10所示。
Байду номын сангаас
(3)化简后,可得激 励函数最简表达式为:
(4)根据激励函数表达式,可画出逻辑电路 图如图12所示。
5 用D触发器作为存储元件,设计一个脉冲异 步时序电路。该电路在输入端x的脉冲作用 下,实现3位二进制减1计数的功能,当电 路状态为“000”时,在输入脉冲作用下输 出端Z产生一个借位脉冲,平时Z输出0。
1第一节动态系统的状态变量和状态变量模型概论

条件:ⅰ、在任意时刻 t0 ,这组变量的值完全确定系统在该时刻 的状态;ⅱ、当 t t0 的输入u(t)和初始状态 x1(t0 ), x2 (t0 ),..., xn (t0 )
给定时,系统未来时刻的状态可完全唯一的被确定下来。
Sunday, November 08, 2020
13
[线性系统动态方程的方块图]: 1、MIMO系统:
D
U
B
•
X X
A
2、SISO系统:
d
u
B
•
X X
A
C Y
X•
AX
BU
Y CX DU
y
C
X•
AX
Bu
y CX du
Sunday, November 08, 2020
14
小结
动态系统 状态、状态变量(向量)、状态方程和输出方程 状态变量的性质
最小变量组; 个数唯一,选择不唯一; 个数与系统独立储能元件个数同。
动态方程(状态空间表达式)的一般形式和方块 图表示
Sunday, November 08, 2020
15
Sunday, November 08, 2020
11
[动态方程的一般形式]:
X•
AX
BU
Y CX DU
式中:X [x1, x2 ,..., xn ]T
Y [ y1, y2 ,..., ym ]T U [u1, u2 ,..., ur ]T
分别表示n维、m维和r 维状态、输出和输入 列向量。
Sunday, November 08, 2020
7
连续系统的状态变量方程求解

连续系统的状态变量方程求解连续系统的状态变量方程求解通常采用数值方法,例如龙格-库塔法(Runge-Kutta)等。
在这个过程中,需要将连续系统的状态方程离散化,即将连续时间步长的微分方程转化为离散时间步长的离散方程。
求解离散方程可采用递推的方式,根据系统的初始条件和上一时刻的状态变量值,计算出当前时刻的状态变量值。
以下是一个求解连续系统状态变量方程的步骤:1. 确定连续系统的状态变量方程。
例如,给定线性定常系统dx/dt = Ax + Bu,其中x为状态变量,A和B为系统矩阵。
2. 离散化。
将状态变量方程转化为离散方程。
常见的离散化方法有前项差分变换、后项差分变换和Tustin变换。
具体变换方法取决于系统的特性以及所需的数值稳定性和精度。
例如,使用Tustin变换将连续系统离散化,得到离散状态方程x[k+1] = A*x[k] + B*u[k]。
3. 初始化。
给定初始条件,如x[0] 和u[0],初始化状态变量值。
4. 数值求解。
使用数值方法(如龙格-库塔法)递推计算离散方程,得到一系列状态变量值x[1], x[2], ...,以及对应的输出值y[1], y[2], ...。
5. 分析结果。
根据求解得到的状态变量值和输出值,分析系统的性能,如稳定性、收敛速度等。
在MATLAB中,可以使用ode45等函数求解连续系统的状态变量方程。
以下是一个简单的示例:```MATLAB定义系统矩阵A、B和输入信号uA = [1 0; -1 1];B = [0 1];u = [1; 0.5];定义初始条件x0 = [1; 2];设置求解参数tspan = [0, 10];options = odeset('RelTol', 1e-6, 'AbsTol', 1e-6);求解状态变量方程[x, u] = ode45(@(t, x) A*x + B*u, tspan, x0, options);绘制状态变量曲线figure;plot(t, x(:, 1), 'b', 'LineWidth', 2);hold on;plot(t, x(:, 2), 'r', 'LineWidth', 2);xlabel('Time');ylabel('State Variables');legend('x1', 'x2');```这个示例中,我们使用ode45函数求解了一个线性定常系统在给定输入信号下的状态变量演化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§ 6-2 连续时间系统状态方程的建立
3.由信号流图建立状态方程 n n -1 b s + b s + + bn-1 s + bn 1 3.1直接型结构 H s 0
s n + a1 s n-1 + + an-1 s + an
b0 b1 1 b2 bk-2 bk-1
e(t)
s-1
-a1 xk
§ 6-1 引 言
e(t)
R +
L
iL(t) + C
uc(t)
-
3.基本概念
-
串联谐振电路: 了解系统内部储能元件动态特性,可列出方程: ' iC t CuC t
RiL t + LiL ' t + uC t e t
R 1 1 ' iL t - iL t - uC t + e t L L L u ' t 1 i t C C C
§ 6-1 引 言
3.基本概念
X ' t AX t + Be t
通常把系统状态方程以下述矩阵-矢量形式书写
R 1 1 ' i t i t u t + e t L C L L L L u ' t 1 i t C C C
2 x1 t + x1' t + x3 t e1 t 1 ' x2 t + x2 t + e2 t x3 t 3 1 ' x3 t + x2 t x1 t 2 r t x2 t + e2 t
1
-a2
r t b0 xn t + bi xn +1-i t b0 e t + bi - b0 ai xn +1-i t
i 1
n
§ 6-2 连续时间系统状态方程的建立
3.由信号流图建立状态方程 x t x t 3.1直接型结构 x t x t
C 0 1 , D 0
§ 6-1 引 言
4.状态变量分析方法的优点
便于研究系统内部物理量的动态变化特性。 与系统复杂程度无关,差别仅在于系统激励矢量和
状态矢量的维数不同,无论是SISO、SIMO、MISO或 MIMO都可用同一形式的状态方程描述。 适用于时变系统或非线性系统,此时状态方程及/ 或输出方程是时变的或非线性的。 状态方程的特性参数鲜明地表征了系统关键性能, 尤其是系统稳定性、系统可控性和系统可观测性。 为系统的CAA或CAD提供了有效途径。
§ 6-1 引 言
e(t)
R +
L
iL(t) + C
uc(t)
-
-
3.基本概念
串联谐振电路,若只关心于系统激励 et 和响应 u t 之间的关系,则有系统微分方程描述
C
R ' 1 1 uC t + uC t + uC t e t L LC LC
"
是一种输入-输出描述法,它只能得到系统输出如何 随系统输入变化,无法了解系统内部发生的变化及 由此引起的输出变化,更无法得知如何控制系统内 部变化来达到所需的系统输出。
s-1
xk-1 -a2 -ak-2 -ak-1 x3
s-1
x2
s-1
x1 bk
r(t)
-ak
§ 6-2 连续时间系统状态方程的建立
3.由信号流图建立状态方程 3.1直接型结构 选取图中每个积分器 1 s e(t) x -a 的输出为状态变量
-1
b0 b1 b2 bk-2 bk-1
s-1
k
s-1
xk-1 x3 -ak-2 -ak-1 -ak x2
§ 6-1 引 言
1.经典系统分析方法的缺陷 经典系统分析方法包括时域法和变域法,它研 究LTI系统的冲激响应、阶跃响应、零输入响应 和零状态响应等时域特性及系统传递函数、幅 频特性、相频特性等频域特性(尤其是频率响 应特性)的概念。 经典的线性系统理论不能揭示系统内部特性, 不能有效地处理多输入-多输出系统,也不易推 广应用于分析时变系统或非线性系统。它仅适 合于分析单输入-单输出的线性时不变系统的外 部特性,具有相当大的局限性。
' 1 2 ' 2 3
' xn -1 t xn t n ' xn t e t - ai xn +1-i t i 1
n n ' i 1 i 1
r t b0 xn t + bi xn +1-i t b0 e t + bi - b0 ai xn +1-i t
§ 6-2 连续时间系统状态方程的建立
3.由信号流图建立状态方程 由系统微分方程或系统函数可得其直接型、 串联型、并联型或并串型实现的信号流图。 3.1直接型结构
b0 s n + b1 s n-1 + + bn-1 s + bn H s n s + a1 s n-1 + + an-1 s + an
c11 c12 c c22 21 C cn1 cn 2
c1k d11 d c2 k , D 21 cnk d n1
d12 d1m d 22 d 2 m d n 2 d nm
X ' t AX t + Be t r t CX t + De t
a1k b11 b12 b b a2 k , B 21 22 akk bk 1 bk 2
b1m b2 m bkm
2.由电路图直接建立状态方程 对含有RLC的电路,选取电容电压和电感电 流为状态变量; 对于仅含LC的电路,选取电容电荷和电感磁 链为状态变量。注意,为确保矩阵 A 可逆, 每个状态变量必须是独立变量。
§ 6-2 连续时间系统状态方程的建立
2.由电路图直接建立状态方程 通常,首先选取所有电容电压和电感电流为 自变量; 然后根据KCL和KVL列写电路方程; 最后,判断矩阵 A 是否非奇异,若非奇异, 则所选变量就是状态变量;否则消去多余自 变量,只留下状态变量和输入变量,经整理 后就得到所需的系统状态方程。
§ 6-2 连续时间系统状态方程的建立
1.状态方程的一般形式 n 维输出的动态系统可一般地表示 一个有 m维输入、 为矢性一阶非线性时变微分方程: ' X 状态方程: t f X t , e t , t 输出方程: r t h X t , e t , t k 维状态矢量:X t x t x t x t
§ 6-1 引 言
2.状态变量分析理论的重要意义 卡尔曼(Kalman)提出的以状态变量分析为核心 的现代系统理论用描述系统内部特性的状态变量 取代了描述系统外部特性的系统函数 这种描述可方便地运用于分析多输入-多输出系统 进一步提出的可控性和可观测性概念完整地揭示 了系统内部特性 状态空间法也能成功地应用于分析时变系统或非 线性系统 能方便地使用计算机求解系统
§ 6-2 连续时间系统状态方程的建立
2.由电路图直接建立状态方程 例6-1:给定电路图,列写状态方程和以 r t 为输出的输出方程。 1H — 1H 3 选择状态变量:
i1 t X t i2 t vC t
2Ω x1(t) 1F — 2 i1(t) ic + x3(t) i2(t) x2(t) 1Ω + e2(t) r(t) +
第六章 系统的状态变 量分析 复习
学习要点:
1. 2. 3. 4. 5. 6.
依据电路的独立储能器件选择状态变量,并列写相应的连续系统状 态方程; 依据系统最简的传递函数、信号流图、或实现框图,列写相应的连 续系统或离散系统的状态方程; 使用变域技术或凯莱-哈密顿定理,计算系统状态转移矩阵; 使用时域法或变域法,求解系统状态方程; 线性变换对状态方程的影响; 状态方程描述的系统稳定性判断方法。
§ 6-2 连续时间系统状态方程的建立
1.状态方程的一般形式
X ' t AX t + Be t r t CX t + De t
D(t) X´ (t) X(t) r(t)
e(t)
B(t)
积分
A(t)
C(t)
§ 6-ห้องสมุดไป่ตู้ 连续时间系统状态方程的建立
T 1 2 k
m 维输入矢量: e t e t
1
e2 t em t
T
n 维输出矢量: r t r t
1
r2 t rn t
T
§ 6-2 连续时间系统状态方程的建立
1.状态方程的一般形式 k 维非线性时变函数矢量 f X t , e t , t f X t , e t , t f X t , e t , t
s-1
x1 bk
r(t)
x1 t x2 t ' x2 t x3 t ' xn -1 t xn t n ' xn t e t - ai xn +1-i t i 1
