由一道课本习题引发的思考
由一道课本习题引发的探究

学 习活动 中 , 常常 N _ Y Y 各种 困惑与 不解 , 这 正是我 们提 高认 识 的切 入点 作 为学 生 , 一 定要 有探 究意 识
与探 究精 神 , 抓 住 适合 探究 的节 点开展 探 究活 动才能 真正 培养 我们 的探 究意 识
问题 提 出
图1
解 法1 ( 向量法 ) : 设痢 : A 魂 : A ( ) , 则劢 = + : ( 1 一 A ) .
有A 1 l , A 2 -  ̄ - , / . e 2 .事 实 上 ( A 1 1 ) P l = ( A 2 - p a ) e : , 而e l , e 2 不共 线 , 所 有 必 有
用 向量 的 方 法 证 明 : M是 B D的一 个
三 等 分 点.
C
④ 问题探究
平面 向量基本定理的前提条件
是 两个 平 面 向量e , e 2 不共 线 , 结论 有
赢, / / 葫, 所以有 = - F d , 从而
AE- - CF .
例2 ( 2 0 0 4 年全 国数学联 赛 ) 设 点。 在A A B C 的内部 , 且有 + 2 十 3 = 0 , 则 AA B C 的面积 与△A O C 的
于 , 求证 : E
地 选择 解题 方法.如 果 不这 样做 , 我
们 对 向 量 的 探 索欲 望 就 会 大 打 折
C
而显得麻烦 ,体现不出向量 的优势. 比如 苏 教 版 必 修 4 第6 7 页习题2 . 2 第 l l 题 .它的求解 就让我们 十分 困惑 向量法是否真的简单.
一
个很好的方法 。 下 面提供3 个例题
由一道教材例题引起的思考

由一道教材例题引起的思考新课程改革已经在我省全面展开,笔者认为新课程目标下,最基本的还是应该重视对教材资源的充分挖掘和利用。
这也是实现注意从学生已有的经验出发,让他们在熟悉的情景中感受物理思想的重要性,了解物理与日常生活的密切关系,逐步学会分析和解决与物理有关的一些简单的实际问题。
”的教学理念和实现高中新课程教育目标的基础与关键。
我以高中新课标教材《物理选修-3-4》为例,分别对新教材例题的研究;新教材概念的深入挖掘;新教材插图的充分利用,谈谈我的看法和做法。
一、重视教材例题习题我们虽然总是在提素质教育,可真正教学时,很容易让学生陷入题海当中。
如果我们能充分挖掘教材潜力,以课本为纲,让学生知道什么是最重要的。
实现让学生可以从教材走出去,也可以从容走回来。
教材例题是编委从大量习题中精选出来的,有很强的代表性。
我们应该从例题出发,触类旁通,举一反三。
我想这也是给学生减负的好方法。
笔者最近和学生曾经讨论一道习题,感受颇丰。
原题是这样的。
“井底之蛙”这个成语常被用来讽刺没有见识的人,现有井口大小和深度相同的两口井,一口是枯井,一口是水井(水面在井口之下),两井底都各有一只青蛙,则( )a.枯井中青蛙觉得井口大些b.水井中青蛙觉得井口大些c.晴天的夜晚,枯井中青蛙能看到更多的星星d.晴天的夜晚,水井中青蛙能看到更多的星星学生们开始普遍感到无从下手。
而我在备课时想尽量降低学生理解的难度,从学生熟悉的知识入手。
后来我发现如果从教材一道例题出发就能很好的解决问题。
教材原题是一个储油桶的底面直径与高均为d.当桶内没有油时,从某点a恰能看到桶底边缘的某点b. 如图(a)所示,当桶内油的深度等于桶高的一半时,仍沿ab方向看去,恰好看到桶底上的点c, 如图(b)所示,c、b两点相距d/4.求油的折射率和光在油中传播的速度。
这是一道很常规的习题,学生很容易入手,当时讲的时候学生也普遍接受。
现在我换一个角思维问题。
第一步按着题中所说开始c点看不到a,a也看不到c。
由一道课本试题引发的思考

由一道课本试题引发的思考七年级学生经常会在练习题中遇到这样的一道几何习题(例1),此题是全等三角形的经典习题,从它上面,我们可以发掘更多、更深的知识。
笔者在实际教学中对此题的讲解,深得学生的赞赏,现将此题拿出来,跟广大师生读者分享,希望大家能获得更多的解题心得。
图1例1如图1,在△ABC中,已知AB=AC,BE=CD。
求证:AD=AE。
??分析:此题的常规思路是通过说明△ABD≌△ACE来证明AD=AE。
显然求证条件是足够的,在△ABC中,AB=AC已经隐含了∠B=∠C,加之BE=CD,即BD+DE=DE+EC,实际上就是BD=CE,故△ABD≌△ACE(SAS)。
当然如果考虑到AD,AE是△ADE的两边时,那么说明△ADE是等腰三角形也不失为一种方法,但要说明△ADE是等腰三角形时,就要证明∠ADE=∠AED,而要证明∠ADE=∠AED,就得证明∠ADB=∠AEC,其实就是说明△ABD≌△ACE,可见我们回到了第一种方法上,当我们把题目多角度思考时,总会收获许多知识。
另外,从等腰三角形的性质入手,也可以找到解题途径;通过作底边上的高,可以得到多个直角三角形,再结合其他条件(BE=CD)就可以解讲问题。
??证明:由AB=AC?荨?B=∠C。
??BE=DC(BD+DE=DE+CE)??BD=CE。
??在△ABD和△ACE中,AB=AC,??∠B=∠C,??BD=CE?荨?ABD≌△ACE(SAS)。
??图2另证:如图2,取BC的中点F,连结AF,则BF=CF,AF ⊥BC。
(△ABC是等腰三角形)??∵BE=BF+EF,CD=CF+DF,CD=BE,??∴DF=EF,∴在??Rt??△AEF和??Rt??△ADF中,??AF=AF,?ぁ?AFD=∠AFE,??FO=FE,∴??Rt??△AEF≌??Rt??△ADF。
??∴AD=AE。
??笔者在第一题的基础上,稍作改变,得到了以下两道新题,这两个题目的解题思路可以极大地丰富我们对全等三角形及相关知识点的认识。
一道课本例题教学所引发的思考

一道课本例题教学所引发的思考——为学生打开自主学习的空间浙江省天台中学王修凯摘要:新课程改革遵循“以学生发展为本”的理念,大力倡导建立自主、合作、探究的学习方式,改变原有的单一、被动的学习方式,促进学生主动地、富有个性的学习。
自主学习以学生自己的认知与经验来建构活动过程的,通过亲身体验、讨论、反思实现由感性认识发展到理性认识。
自主学习能激活、诱导学生的学习积极性,促进学生思维能力的发展,提高学生探究的意识。
关键词:自主学习优化反思转变观念现在,整个教育界都在提倡创新教育,自主探究式学习,我也曾经尝试着在课堂上渗透让学生自主学习的思想,我也曾努力创设情景给学生们多一些创新的机会,允许并鼓励他们在课堂上提出自己的看法,但课堂教学,特别是目前仍受考试压力影响的高中课堂中,教师和学生依然面临着升学压力。
无奈的现实让我很难在课堂上落实这些“理念”:毕竟学生这么多、课时这么少、教学任务又如此之重,作出一个教学决定又要考虑方方面面的因素,权衡各种关系。
可一次偶然的机会,让我彻底改变了原先的观念,原来,教育的机会就在平时普通的课堂中。
一、例题教学的再现例题高中新课本《数学》第二册(上)第106页例3一炮弹在某处爆炸,在A处听到爆炸声的时间比在B处晚2s。
(1)爆炸点应在什么样的曲线上?(2)已知A、B两地相距800m,并且此时声速为340m/s,求曲线的方程。
如何通过这道例题的讲解,为学生打开自主学习的空间呢?首先设爆炸点为P,那么在A处听到爆炸声比在B处晚2s,说明什么问题?学生思考后很快说出点P在距A处较远、距B处较近的位置上,且点P到A处的距离与它到B处的距离的差是一个常数3402⨯m。
我进一步问道,那么点P在怎样的曲线上?学生回答,点P在以A、B为焦点的双曲线上,且在离B处较近的一支上。
显然,这种解答不够全面,接下去是老师讲出正确答案,还是让学生讨论探讨出其他的可能性呢?我用鼓励的目光望着大家,问:大家还有其他想法吗?过了一会,有同学提出了不同意见:点P不一定在双曲线上,因为由题意只能知道点P 到A处的距离与它到B处的距离的差是一个常数3402⨯m,但并未说明这个常数小于A、B 两处的距离。
一道课本例习题教学引发的思考

一道课本例习题教学引发的思考摘要:课本中例习题是从数不清的数学题中海选出来,就赋予所选出来的都是典型性和启示性,因此在“活”用课本例习题应当注意特别是变式教学时要注重如何更好的形变,如何更好的在“度”、“宽”上的掌控,让学生从不同角度、不同层面去看问题,从学会更好地解决问题。
关键词:数学;课本例习题;反思课本中例习题是从数不清的数学题中海选出来,就赋予所选出来的都是典型性和启示性,因此在教学过程中对教材中的例题,习题可以从多个角度来挖掘其深层次的数学本质,并结合利用变式教学通过改变数学表征问题,来达到更好地揭示数学本征问题的目的。
下面以八年级上册第十三章轴对称13.3.2等边三角形习题13.3综合运用(P83)12题为例谈谈针对一道课本例习题教学引发的一些思考:一、注重引导,寻思关键在课本例习题教学中,教师要先指引学生从题设出发,通过观察图形,自主学习与探讨交流,然后写出证明过程。
本题对于学生来说,没有障碍,由已知条件等边三角形自然联想到其性质:三条边相等,三个角相等,学生由图形自主探究构建全等三角,再进行合作交流,找出间边与角之间对应关系,且角的相等是证明全等的关键。
课本这道例习题的教学价值在于学生通过学习后能够完成文字语言与符号语言之间的转换,检验学生对基本概念知识、方法的掌握情况,目的在于让学生学会观察、分析、概括、归纳,提升语言表达能力。
二、深入挖掘,一题多解数学教学中,为了激发学生的思维和建构知识间的链接,往往是在解决问题时从多角度促使知识间的联系。
因此十分有必要对课本中例习题进一步进行挖掘,比如八年级上册第十三章轴对称13.3.2等边三角形习题13.3综合运用(P83)12题,这是一道基础题,如若在教学过程中教师讲过就将之抛在一旁,那乃是捡了芝麻丢了西瓜之举。
在数学课堂中,时常用来拓展学生数学思维形成的教学策略之一是一题多解,这种教学策略能很好地引导学生从不同角度看待问题、解决问题。
一道教材练习题的再思考

一道教材练习题的再思考杨伟达(花都区第二中学 广东广州市 510820)内容摘要: 三角形是中小学教材中最常见、最简单的图形。
就是这样一个图形,它却成了不少高考命题者的第一视觉,成了学生每年高考的必考题。
在翻阅高中数学教材时笔者找到了一道不起眼的练习题,引起笔者的注意,激发笔者的深思,品味着三角形带来的乐趣。
关键词: 教材 习题 思考俗话说:高考试题源于教材,又高于教材。
纵观近几年高考数学题,许多高考试题在教材中都有呈现,进而找到了试题的“活化石”。
因此,回归教材就是在高考题中找到教材中的“活化石”,感悟着“活化石”带来的数学味道。
一、题目再现题目 (高中人教版必修5 P18练习第2题) 一块四边形土地的形状如图所示,它的三条边的长度分别是50m ,60m ,70m ,两个内角是127°和132°,求四边形的面积(精确到0.01)。
分析 这是一道生活中的数学题。
笔者在翻阅教材时引起了笔者的注意,于是捡回了此题,查阅教师教学用书,可在教参里只提供了答案,没有详细的解答过程,或许该题运算繁杂、方法复杂,或许是练习题的缘故,没有引起师生重视。
对此笔者感到在生活中数学无处不在,加上解决此题的思想、方法来自生活实践,笔者觉得很值得探讨。
二、解法探究思路一 (分割+正、余弦定理)分析 对于这样的不规则的四边形,没有直接计算面积方法,采用分割法把四边形分成两个三角形,分别求出两个三角形的面积,以和的形式求得四边形的面积。
解法1 如图1,连结AC在△ADC 中 根据余弦定理得: ADC DC AC DC AD AC ∠⋅⋅-+=cos 2222127c o s 60502605022⨯⨯⨯-+= 89.9710=所以54.98=AC m再根据正弦定理得: D AC ACD AD ∠=∠sin sin 即:︒=∠127sin 54.98sin 50ACD 求得:4052.0sin =∠ACD所以 ︒=∠9.23ACD (锐角) A BC图1 D因为︒⋅=︒⋅-︒=∠-=∠1108923132132DCA ACB所以ACB ACD A S S ∆∆+=S BCD 四边形 ACB CD AC ADC CD AD ∠⨯⨯⨯+∠⨯⨯⨯=sin 21sin 21 ︒⋅⨯⨯⋅⨯+︒⨯⨯⨯=1108sin 70549821127sin 605021 =4476.19 m 2思路二 (补形+正弦定理)分析 对于这样的不规则的四边形,没有直接计算面积方法,采用补形法把四边形补角还原成一个大三角形,分别求出两个三角形的面积,以差的形式求得四边形的面积。
一道课本立体几何题引发的思考讲解
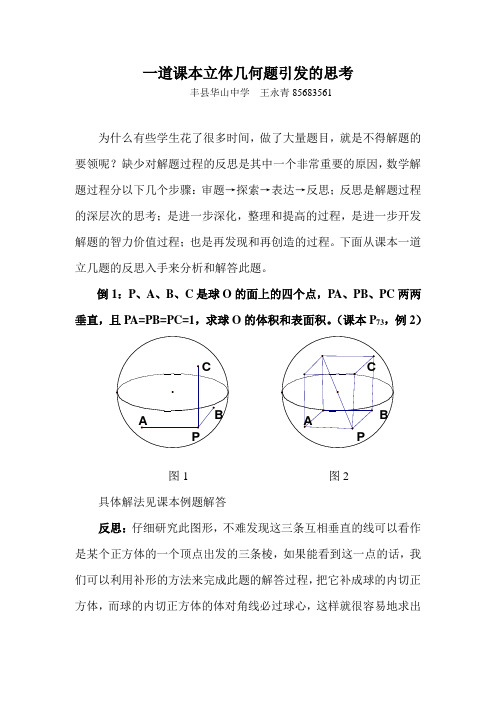
一道课本立体几何题引发的思考丰县华山中学王永青85683561为什么有些学生花了很多时间,做了大量题目,就是不得解题的要领呢?缺少对解题过程的反思是其中一个非常重要的原因,数学解题过程分以下几个步骤:审题→探索→表达→反思;反思是解题过程的深层次的思考;是进一步深化,整理和提高的过程,是进一步开发解题的智力价值过程;也是再发现和再创造的过程。
下面从课本一道立几题的反思入手来分析和解答此题。
倒1:P、A、B、C是球O的面上的四个点,PA、PB、PC两两垂直,且PA=PB=PC=1,求球O的体积和表面积。
(课本P73,例2)图1 图2具体解法见课本例题解答反思:仔细研究此图形,不难发现这三条互相垂直的线可以看作是某个正方体的一个顶点出发的三条棱,如果能看到这一点的话,我们可以利用补形的方法来完成此题的解答过程,把它补成球的内切正方体,而球的内切正方体的体对角线必过球心,这样就很容易地求出D球的直经,从而求出球的体积S=3 。
由此可见在立几中,正、长方体是立几中的重要模型,教学积累使我们感到有不少 的数学问题通过构建正、长方体,可使复杂的问题简单化,抽象问题直观化,实施问题的有效转换,使问题的解决变的简捷易行。
此为课本立几中的一例题,在此题中我们感受到立几中的基本图形的重要性,同时要对基本图形有一个比较深刻的了解,能感受到它的内部结构,这样就可用补形的方法来完成解题的过程。
变式1:P 、A 、B 、C 是球O 的面上的四个点,PA 、PB 、PC 两两垂直,且PA=1,PB=2,PC=3,求球O 的体积和表面积。
(构建球内接长方体可解)变式2:已知球面上的四点O 、A 、B 、C 满足OA 、OB 、OC 两两垂直,且球面上一点P ,到OA 、OB 、OC 的距离分别为3、4、5,求球的直径。
例2:一个正方体如图那样截去四个三棱锥,得到一个正三棱锥A-BCD ,则截得到的正三棱锥的体积是正方体体积的几分之几。
一道课本问题的解决引发的思考

一道课本问题的解决引发的思考摘要:数学课程改革应倡导教学探究,让学生在探究过程中理解数学的本质。
笔者认为这里的探究的含义是多方面的,对我们一线教师而言对课本上的知识生成、例习题解法以及涉及的思想方法的探究意义尤为重要。
关键词:探究;课本问题;多种方法;数学思想中图分类号:g427 文献标识码:a 文章编号:1992-7711(2012)23-068-1选自苏教《选修1-1》p90 练习8:已知海岛a与海岸公路bc的距离为ab为50km b,c间的距离为100km.从a 到c,先乘船,船速为25km/h50km/h分析:易知点p一定在b,c之间,可设bp=x,则水路ap=2500+x 2公里,陆路pc=(100-x)公里,将这里的总时间y表示成关于x的函数,得y=2500+x225+100-x50,这里由题意可知x∈(0,100),下面就是如何解函数的最小值问题了。
方案1 由于我们刚刚学习过导数,我们可以对函数进行求导y′=12(2500+x2)′252500+x2-150=x252500+x2-150,令y′=0则x2500+x2=12,x=5033(负值舍去)当x∈(0,5033)时,y′0。
所以当x=5033时,函数有最小值。
所以当登陆点距离b点x=5033km这种处理问题的方式是用导数来研究函数的最值,学生容易想到这种处理方案。
“这个世界本不缺少美,只是缺少发现的眼睛”,同样,我们是不是少了探索的眼睛呢?是不是我们对问题的解决就仅限如此呢?方案2 u=22500+x2-x,为了求解u的最小值,除了平方,我们还可以考虑把根式里面的式子配成完全平方式,联想到1+tan 2θ=sec2θ,我们可以将函数关系变形为u=22500+x 2-x=1001+(x50)2-x,令x50=tanθ,θ∈(0,arctan 2),则u=1001+tan2θ-50tanθ=100secθ-50sinθ=100cosθ-50sinθcosθ=50·2-sinθcosθ上面两种方案中我们都是选择的长度为变量,实际上我们在处理这种图形类应用题时经常选择一个活动的角为变量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由一道课本习题引发的思考
九年义务教育八年级数学上配套练习册 P 65第11题:
已知:如图1,点C 为线段AB 上一点,△ACM, △CBN 都是等边三角形,
思考 由命题的条件,根据平行线判定定理易知: AM/CN MC/ NB,由此得命题1: 命题1已知:如图1,点C 为线段AB 上一点,△ACM, △:BN 都是等边三角形, 求证:AM CN ,MC /NB
思考二
由命题的条件结合三角形全等的判定定理可知,有三对全等三角形,故得命题: 命题2已知:如图2,点C 为线段AB 上一点,△ACM, △:BN 都是等边三角形,AN 、 CM 交于点E,CN 、BM 交于点F.
求证:△ACN 也血CB, △AEC 也 JMFC, △ECN 也△CB
思考三
由命题2的结论,根据全等三角形的性质,可得到一些相等的线段和相等的角, 从而得到
命题:
命题3已知:如图2,点C 为线段AB 上一点,△ACM, △:BN 都是等边三角形,AN 、 CM 交于点E,CN 、BM 交于点F.
求证:⑴ AN=BM,CE=CF,AE=MF,NE=FB, (2)/NAC= /BMC; ZANC= JMBC; ZAEC= / MFC; 山东省五莲县洪凝初中 王爱仁
求证:
图1
JCEN= /CFB
思考四
因为/ ACM # NCB=60 ,所以/ MCN=6D ,再由命题3的结论可知CE=CF 则△ ECF 为等边三 角形,得命题:
命题4已知:如图3,点C 为线段AB 上一点,△ACM, △CBN 都是等边三角形,AN 交
思考五 _
由命题4的结论知,/ EFC=60°,故/ EFC=/FCB ,所以EF I AB ,得命题:
命题5已知;如图3,点C 为线段AB 上一点,^ACM, ACBN 是等边三角形,AN 交MC 于点 BM 交CN 于点F.
求证:AN=BM
MrzT
-[y
、. 思考八 由^ ACN^A MCB 可知,/ CAN=/ CMB 所以/ A0B2 MAO £
AMO ^ MAO £ AMC :+ CMB ^ MAO 乂 CAN # AMChMAC+^AMC=60 +60° =120° ,可得命题:
命题6已知;如图4,点C 为线段AB 上一点,AACM, ACBN 是等边三角形,AN,BM 相交于 点O.
MC 于点 E ,BM 交CN 于点F.
⑴求证: AN=BM;
(2)求证: △CEF 为等边三角形
若AN 、MC 交于点E,BM 、 NC 交于点F ,求证:EF IAB
图4
求/AOB 的度数
思考七
由(1)证得 △ AC 华△ MCB 可得 AN=BM , S ^ ACN=A MCB 如果由点C 分别向AN BM 作垂线,垂足分别为 H 、G 即? AN • CH=?BM ・CG /• CF=CG •••点C 在/ AOB 的平分线上,可得命题:
命题7已知,如图5,点C 为线段AB 上一点,△ACM > △CBN 为等边三角形,连结BM 交AN 于P 点,连结CP.
V/ ACM=6° =/ BCN,/./ ACM :+ MCNM BCN# MCN 即 / ACN / BCM V AC=MC,CN=C/,ACN/ BCM
/. △ ACN^A MCB/. / 1=/ 2
V/ 仁/ 2,BE=NP,BC=NC ;. A BCE^A NCP
••• CP=CE/ ECB/ PCN
V/ ECB/ NCE=60 , // PCN/ NCE= 60 ,即 / PCE=60 , •••△
PCE 是等边三角形,二PC=PE
••• BP=BE+PE=PN+PC
从而可得命题: 命题八 已知;如,7,点C 为线段AB 上一点,△XCM, △CBN
点。
求证:BP=CP+NP 思考九
是等边三角形,AN,BM 相交于P
求证:PC 平分/APB
图6
在原命题中,分别取 AN 、BM 的中点P 、Q ,连接P 、C 、Q 、易证△CPN ◎△ CQB ,可 得 CP=CQ ,思考十 在原命题中,如果让让△ CBN 绕点C 旋转成图10的情形,结果又如何?通过探究可得命
题: 命题10⑴已知:如图9,点C 为线段AB 上一点,△ACM, △CBN 都是等边三角形,
求证:AN=BM
(2)如果去掉“点C 为线段AB 上一点”的条件,而是让△CBN 绕点C 旋转成图8的情形,还 有AN=BM ”的结论吗?如果有,请给予证明.
图10
思考十
命题11如图a ,^ABC 和MEF 是两个大小不等的等边三角形,且有一个公共顶点
C , 连接AF 和BE.
⑴线段AF 和BE 有怎样的大小关系?请证明你的结论; / PCN=/BCQ ,可得/ PCQ=/ NCB=60。
,二△ PCQ 是等边三角形,可得命题:
命题九 已知:如图 8,点C 为线段AB 上一点,AACM, △CBN 都是等边三角形,P 、Q 分别是AN 、 MB 的中点, 求证:△PCQ 是等边三角形
如果△KBC 和 △CEF 在BC 的两旁, 结果又如何呢?通过探究可得命题:
图8
图9
⑵ 将图a中的△CEF绕点C旋转一定角度,得到图b,⑴中的结论是否成立?作出判断
并说明理由;
⑶ 若将图a中的AABC绕点C旋转一定的角度,请你画出一个旋转后不同于图b的图形
C(草图即可),⑴中的结论是否还成立?作出判断并说明理由
F
思考十二
在原命题中,去掉等边三角形的条件,改为AB=AC AD=AE/ BAC/ DAE可得命题:
命题12 已知,如图11 所示,在 A ABC 和 A ADE 中,AB=AC , AD=AE,/BAC= /DAE , 且点B、A、D在一条直线上,连接BE、CD,M、N分别为BE、CD的中点。
求证:①BE=CD ②AM=AN
在图11的基础上,其他条件不变,将 A ADE绕点A按顺时针方向旋转180。
,得到图12 所示的图形,请直接写出⑴中的两个结论是否成立?
2
?
图11
图12。
